Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the development of a gold-standard potential energy surface for the OH− + CH3I reaction†
Domonkos A.
Tasi
 ,
Tibor
Győri
,
Tibor
Győri
 and
Gábor
Czakó
and
Gábor
Czakó
 *
*
MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: gczako@chem.u-szeged.hu
First published on 27th January 2020
Abstract
We report a story where CCSD(T) breaks down at certain geometries of the potential energy surface (PES) of the OH− + CH3I reaction. To solve this problem, we combine CCSD-F12b and Brueckner-type BCCD(T) methods to develop a full-dimensional analytical PES providing method- and basis-converged statistically-accurate SN2 and proton-transfer cross sections.
The knowledge of the potential energy surface (PES) is essential to compute the dynamics and mechanisms of chemical reactions. For bimolecular nucleophilic substitution (SN2) reactions, the use of the direct dynamics approach became popular due to its black-box nature and widespread applicability.1–6 Direct dynamics simulations determine the potential gradients on-the-fly along the trajectories using an electronic structure program package, which is very time consuming, and thus only a low level of theory can be afforded. Therefore, in 2013, we started to develop analytical PESs for SN2 reactions by fitting high-level ab initio energy points,7 thereby allowing efficient classical and/or quantum dynamics simulations.7–13 We have already reported full-dimensional global PESs for the F− + CH3Y [Y = F, Cl, Br, I] reactions, which accurately describe both the SN2 and proton-transfer channels.8,14–16 The millions of trajectories computed on these PESs revealed a new retention mechanism for SN2 reactions, called double inversion,8 front-side complex formation,12 an unexpected leaving group effect,9 and unprecedented agreement with crossed-beam experiments.9,17
Moving beyond the six-atomic systems, in the present study, we aim to develop a full-dimensional analytical ab initio PES for the OH− + CH3I reaction. Following the pioneering direct dynamics studies3,5,18,19 as well as crossed-beam3,5,20 and selected ion flow tube18 experiments, the present PES will be the first analytical surface for the title reaction, and moreover the first PES for a 7-atomic SN2 reaction. The efficient PES development is made possible by utilizing Robosurfer,15 our very recently developed program package enabling automatic construction of analytical PESs for reactive systems. Our plan is to build a PES at the MP2/aug-cc-pVDZ level of theory21,22 and then to re-compute the energy points using the more accurate and more time-consuming CCSD(T)-F12b/aug-cc-pVTZ level of theory.23 Using this strategy, we develop a good MP2/aug-cc-pVDZ surface, which performs very well in quasiclassical trajectory (QCT) simulations. However, unexpectedly, the CCSD(T)-F12b PES gives many unphysical trajectories, for example, at zero impact parameter (b = 0) about 10% of the trajectories break up to many energetically forbidden fragments. Does the CCSD(T) method,24 often called the gold-standard of quantum chemistry, fail to provide an accurate PES for the OH− + CH3I reaction? Is there a solution to this problem? Can we develop an accurate analytical PES for this system? The answer for the third question is a yes. If one is interested in knowing how, we describe the details below along with the answers to the other two questions.
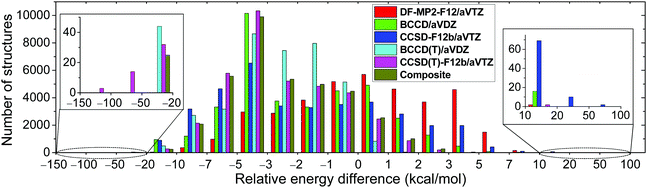
We develop a full-dimensional ab initio PES for the title reaction by fitting roughly 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MP2/aug-cc-pVDZ energy points using the permutationally invariant polynomial approach,25,26 while the fitting set is generated via the Robosurfer program system.15 The computational details of the automated PES development are given in the ESI.† The PES points are recomputed using the explicitly-correlated CCSD(T)-F12b/aug-cc-pVTZ level of theory and the distributions of the differences between the CCSD(T)-F12b and MP2 relative energies are shown in Fig. 1. The root-mean-square (RMS) energy difference is 4.5 kcal mol−1, which is typical when one compares MP2 and CCSD(T) relative energies. However, we find 17 CCSD(T)-F12b points with potential energies below the corresponding MP2 data by more than 50 kcal mol−1. Such energy points may cause deep holes on the CCSD(T)-F12b PES, which may be responsible for the large fraction of unphysical trajectories. Indeed, upon the removal of the aforementioned 17 configurations from the dataset, the probability of the unphysical b = 0 trajectories drops from 6–13% to 2–3%. To get a deeper insight into the origin of this issue, we recompute the energy points using the DF-MP2-F12/aug-cc-pVTZ,27 BCCD/aug-cc-pVDZ,28 CCSD-F12b/aug-cc-pVTZ,23 and BCCD(T)/aug-cc-pVDZ28 levels of theory. Using the CCSD-F12b method, the 17 low-energy points disappear, and we do not find any configuration whose relative energy is at least 20 kcal mol−1 below the MP2 results (Fig. 1). Thus, we find that the perturbative (T) correction is too negative in some cases, and this is the reason why the CCSD(T)-F12b PES breaks down in certain regions. This finding is not unprecedented as similar wrong (T) behavior was reported for potential energy curves of BH, HF, OH−, F2, C2, and BN.29–31 To solve this problem, we investigate the performance of the Brueckner coupled cluster doubles (BCCD) and BCCD with perturbative triples (BCCD(T)) methods.28
000 MP2/aug-cc-pVDZ energy points using the permutationally invariant polynomial approach,25,26 while the fitting set is generated via the Robosurfer program system.15 The computational details of the automated PES development are given in the ESI.† The PES points are recomputed using the explicitly-correlated CCSD(T)-F12b/aug-cc-pVTZ level of theory and the distributions of the differences between the CCSD(T)-F12b and MP2 relative energies are shown in Fig. 1. The root-mean-square (RMS) energy difference is 4.5 kcal mol−1, which is typical when one compares MP2 and CCSD(T) relative energies. However, we find 17 CCSD(T)-F12b points with potential energies below the corresponding MP2 data by more than 50 kcal mol−1. Such energy points may cause deep holes on the CCSD(T)-F12b PES, which may be responsible for the large fraction of unphysical trajectories. Indeed, upon the removal of the aforementioned 17 configurations from the dataset, the probability of the unphysical b = 0 trajectories drops from 6–13% to 2–3%. To get a deeper insight into the origin of this issue, we recompute the energy points using the DF-MP2-F12/aug-cc-pVTZ,27 BCCD/aug-cc-pVDZ,28 CCSD-F12b/aug-cc-pVTZ,23 and BCCD(T)/aug-cc-pVDZ28 levels of theory. Using the CCSD-F12b method, the 17 low-energy points disappear, and we do not find any configuration whose relative energy is at least 20 kcal mol−1 below the MP2 results (Fig. 1). Thus, we find that the perturbative (T) correction is too negative in some cases, and this is the reason why the CCSD(T)-F12b PES breaks down in certain regions. This finding is not unprecedented as similar wrong (T) behavior was reported for potential energy curves of BH, HF, OH−, F2, C2, and BN.29–31 To solve this problem, we investigate the performance of the Brueckner coupled cluster doubles (BCCD) and BCCD with perturbative triples (BCCD(T)) methods.28
As shown in Fig. 1, unlike CCSD(T)-F12b, the BCCD(T) method does not give relative energies below the MP2 data by more than 50 kcal mol−1. Thus, BCCD(T) seems to be a promising method to incorporate the (T) correction without making “holes” on the PES. Since an explicitly-correlated version of the BCCD(T) method is not widely available in quantum chemistry software and the 2.9 kcal mol−1 RMS difference between DF-MP2-F12/aug-cc-pVTZ and MP2/aug-cc-pVDZ relative energies indicates significant basis set effects, we propose a composite ab initio method defined as
| CCSD-F12b/aug-cc-pVTZ + BCCD(T)/aug-cc-pVDZ − BCCD/aug-cc-pVDZ, | (1) |
To further investigate the accuracy of the different levels of electronic structure theory, we select several representative geometries and compute their relative energies using various ab initio methods and basis sets. Two representative examples are shown in Fig. 2 and additional results are presented in the ESI.† On the one hand, the left panel of Fig. 2 shows a typical case where all the ab initio levels provide relative energies within a 4 kcal mol−1 window, BCCD(T) agrees with CCSD(T) within 0.1 kcal mol−1, and CCSD(T) differs from CCSDT by only 0.01 kcal mol−1 showing the excellent performance of the perturbative (T) approximation. On the other hand, the right panel of Fig. 2 shows an extreme configuration with strong correlation effects. Using the aug-cc-pVDZ basis set, the HF method32 provides an energy of 94.2 kcal mol−1 relative to the reactants, the corresponding MP2 result is only 61.8 kcal mol−1, which is relatively close to the {CCSD, BCCD, OQVCCD} values of {56.5, 51.2, 51.0} kcal mol−1, where OQVCCD denotes optimized-orbital quasi-variational coupled cluster doubles.33 However, considering the (T) corrections, striking differences are found. The {CCSD(T), BCCD(T), OQVCCD(T)} methods give relative energies of {−61.0, 19.2, 14.7} kcal mol−1, showing the breakdown of the CCSD(T) method. If we do not use the pertubative (T) approximation and perform the full CCSDT computations with single, double, and triple excitations,34 the above relative energy becomes 29.7 kcal mol−1, which clearly shows the issue with the CCSD(T) method. The best agreement between CCSDT and the (T) methods is found for BCCD(T) as seen from the above data and also supported by several additional test computations reported in the ESI† (Fig. S1). This motivated us to define the composite energy as given in eqn (1), which provides a relative energy of 31.1 kcal mol−1 in good agreement with the CCSDT value (29.7 kcal mol−1) even in this problematic case.
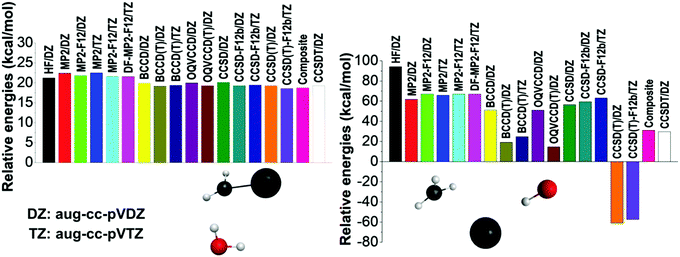 | ||
| Fig. 2 Energies of two representative structures relative to the reactants obtained by different ab initio levels of theory. | ||
To get into the physical insight, we can conclude that the failure of the traditional perturbative (T) approximation occurs at homolytic bond (e.g., C–I) dissociation, where HF orbital quasi-degeneracy and/or wrong t-amplitudes cause the breakdown of the perturbation theory.29 This problematic behavior is also related to significant multi-reference character predicted by large T1-diagnostic35 values (>0.03) as shown in Table S2 (ESI†). In these strongly correlated cases, the use of the non-HF Brueckner reference, which provides the best overlap with the exact wave function, may be more robust than the traditional HF-based approaches.
After the above-described ab initio investigations, we develop eight different analytical PESs by fitting MP2/aug-cc-pVDZ, DF-MP2-F12/aug-cc-pVTZ, BCCD/aug-cc-pVDZ, CCSD-F12b/aug-cc-pVTZ, BCCD(T)/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVTZ, CCSD(T)-F12b/aug-cc-pVTZ′, and composite [eqn (1)] ab initio data, where ′ denotes the removal of the 17 outlier configurations. The classical relative energies of the stationary points corresponding to the SN2 pathways of the OH− + CH3I reaction obtained on the different PESs are shown in Fig. 3. Our all-electron CCSDT(Q)/complete-basis-set-quality benchmark data are also available for comparison.36 Electron correlation effects are significant for the product region, and both MP2 and CCSD methods differ from the benchmark data by 2–3 kcal mol−1 in the case of the CH3OH⋯I− minimum and the CH3OH + I− products. (T) correction is needed to achieve accuracy within 0.7 kcal mol−1. Basis set effects are important for the front-side (FS) attack and double-inversion (DI) TSs as, without explicit correlation, the DZ results differ from the TZ ones by about 1.5 (FSTS) and 2.5 (DITS) kcal mol−1, respectively. Thus, as seen, the (T) method with a TZ-quality basis and/or explicit correlation is needed to obtain a chemically accurate PES. Indeed, the CCSD(T)-F12b/aug-cc-pVTZ′ PES provides stationary-point relative energies with only 0.43 kcal mol−1 RMS and 0.66 kcal mol−1 maximum deviations from the benchmark data. However, as we discussed above, CCSD(T)-F12b fails at certain non-stationary regions of the PES, where only the composite method defined in eqn (1) performs satisfactorily. Therefore, it is comforting to find that the composite PES also provides excellent stationary-point energies, in agreement with the benchmark data with only 0.47 kcal mol−1 RMS and 0.62 kcal mol−1 maximum deviations. We can conclude that when CCSD(T)-F12b performs well, the present composite method provides the same energies as CCSD(T)-F12b/aug-cc-pVTZ within 0.1 or 0.2 kcal mol−1 (Fig. 3), whereas in certain regions where CCSD(T)-F12b suffers from serious breakdown, the glory of the composite method is obvious (Fig. 2, right panel).
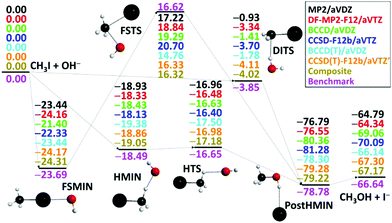 | ||
| Fig. 3 Classical relative energies (kcal mol−1) of the stationary points characterizing the OH− + CH3I SN2 reaction obtained on the different analytical PESs. The composite PES energies are defined in eqn (1) and the benchmark data are taken from ref. 36. | ||
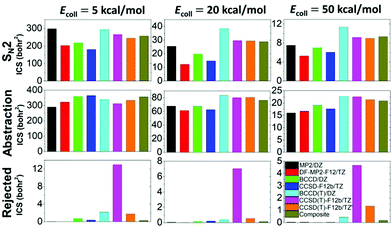
In total, more than 1 million trajectories are computed for the OH− + CH3I reaction on the eight different PESs at collision energies (Ecoll) of 5, 20, and 50 kcal mol−1. Computational details and opacity functions (Fig. S2, ESI†) are given in the ESI,† and cross sections for the SN2 and proton-abstraction channels are shown in Fig. 4. Furthermore, Fig. 4 also shows the cross sections of the rejected unphysical trajectories (resulting in energetically non-available products), which allows the assessment of the quality of the PESs. The original CCSD(T)-F12b PES gives large cross sections of 13.0, 7.0, and 4.7 bohr2 for these unphysical products at collision energies of 5, 20, and 50 kcal mol−1, respectively. At the highest Ecoll, the cross-section of the unphysical trajectories is comparable to those of the SN2 (9.2 bohr2) and abstraction products (22.5 bohr2). Removing 17 low-energy outliers from the CCSD(T)-F12 dataset reduces the unphysical cross sections to 1.8, 0.5, and 1.3 bohr2, in the above order. Fortunately, using the composite PES, these troublesome values become negligible such as 0.3, 0.1, and 0.2 bohr2, respectively. Despite the different unphysical cross sections, it is important and comforting to find that the reactive SN2 and proton-abstraction cross sections are almost the same on the CCSD(T)-F12b, CCSD(T)-F12b′, and composite PESs as seen in Fig. 4. Considering the lower-level PESs, which can be important to assess the accuracy of direct dynamics studies, significant basis-set effects are found for the SN2 channel, because the DZ basis overestimates the TZ cross sections by 10–100%, depending on the ab initio method and Ecoll. Electron correlation effects are found to be more pronounced at higher collision energies, and the (T) correction increases the SN2 cross sections by 50–100%. Due to the opposite effects of the basis and correlation, the error cancelation improves the accuracy of the MP2/aug-cc-pVDZ cross-section predictions. For the proton-abstraction channel, the reactivity shows less significant method- and basis-set dependence (Fig. 4). Both the SN2 and proton-abstraction cross sections decrease with increasing Ecoll, as expected in the case of exothermic, barrier-less reactions. Note that unlike in the case of the X− + CH3Y reactions,37 where X and Y are halogens, for OH− + CH3I, the proton-abstraction channel is slightly exothermic.3,18 At Ecoll = 5 kcal mol−1 the SN2 and abstraction reactivity is similar, whereas at higher collision energies, the energetically less favored proton-abstraction channel clearly dominates over the SN2 reaction, as the CH2I−/I− product cross section ratios, on the most accurate composite PES, are 1.4, 2.7, and 2.2 at Ecoll of 5, 20, and 50 kcal mol−1, respectively. This finding is in qualitative agreement with the B97-1/ECP/d direct dynamics results of the Hase group, as they reported CH2I−/I− ratios of 0.6, 2.3, 1.7, and 2.0, at Ecoll of 1, 12, 23, and 46 kcal mol−1, respectively.3 Considering the absolute cross sections, direct dynamics found SN2 cross sections of 38.9 ± 11.1 and 15.4 ± 3.6 bohr2 at Ecoll = 23 and 46 kcal mol−1, respectively, which may be compared to our composite results of 28.7 and 9.3 bohr2 corresponding to Ecoll = 20 and 50 kcal mol−1, respectively. This comparison indicates that B97-1 overestimates the SN2 reactivity. For the proton-abstraction channel the trend is less obvious, because direct dynamics gives 64.6 ± 11.4 and 31.4 ± 5.7 bohr2,3 whereas the composite PES provides 76.2 and 20.9 bohr2, in order at the above Ecoll values. One may notice the large error bars of the direct dynamics cross sections resulting from the relatively low total number of trajectories (3736),3 whereas the present analytical PESs make the computation of more than a million trajectories possible, thereby providing results without any significant statistical uncertainty.
The present methodology tests may provide guidance for future PES developments for similar challenging systems and the new high-level ab initio PES opens the door for detailed classical and/or quantum dynamics investigations allowing critical comparisons with experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the NKFIH, K-125317, the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT, the Momentum (Lendület) Program of the Hungarian Academy of Sciences, and the National Young Talent Scholarship (NTP-NFTÖ-18-B-0399 for D. A. T.) for financial support.References
- J. Xie and W. L. Hase, Science, 2016, 352, 32 CrossRef CAS
.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960 CrossRef CAS
.
- J. Xie, R. Sun, M. R. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162 CrossRef CAS
.
- Y.-T. Ma, X. Ma, A. Li, H. Guo, L. Yang, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2017, 19, 20127 RSC
.
- J. Xie, J. Zhang, R. Sun, R. Wester and W. L. Hase, Int. J. Mass Spectrom., 2019, 438, 115 CrossRef CAS
.
- H. Tachikawa and M. Igarashi, Chem. Phys., 2006, 324, 639 CrossRef CAS
.
- I. Szabó, A. G. Császár and G. Czakó, Chem. Sci., 2013, 4, 4362 RSC
.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef
.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151 CrossRef CAS
.
- Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322 CrossRef CAS
.
- Y. Li, Y. Wang and D. Y. Wang, J. Phys. Chem. A, 2017, 121, 2773 CrossRef CAS
.
- I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917 CrossRef PubMed
.
- B. Olasz and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 1578 RSC
.
- I. Szabó, H. Telekes and G. Czakó, J. Chem. Phys., 2015, 142, 244301 CrossRef PubMed
.
- T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51 CrossRef PubMed
.
- B. Olasz, I. Szabó and G. Czakó, Chem. Sci., 2017, 8, 3164 RSC
.
- M. Stei, E. Carrascosa, A. Dörfler, J. Meyer, B. Olasz, G. Czakó, A. Li, H. Guo and R. Wester, Sci. Adv., 2018, 4, eaas9544 CrossRef PubMed
.
- J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019 CrossRef CAS PubMed
.
- J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 378, 14 CrossRef CAS
.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534 CrossRef CAS PubMed
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef
.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef
.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS
.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577 Search PubMed
.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094 RSC
.
- H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102 CrossRef
.
- K. A. Brueckner, Phys. Rev., 1954, 96, 508 CrossRef CAS
.
- J. B. Robinson and P. J. Knowles, J. Chem. Phys., 2013, 138, 074104 CrossRef
.
- D. A. Mazziotti, Phys. Rev. Lett., 2008, 101, 253002 CrossRef PubMed
.
- D. Kats, D. Kreplin, H.-J. Werner and F. R. Manby, J. Chem. Phys., 2015, 142, 064111 CrossRef PubMed
.
-
W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed
.
- J. B. Robinson and P. J. Knowles, Phys. Chem. Chem. Phys., 2012, 14, 6729 RSC
.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041 CrossRef CAS
.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, S23, 199 Search PubMed
.
- D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773 CrossRef CAS
.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details, discussion, and ab initio test results as well as opacity functions. See DOI: 10.1039/c9cp07007a |
| This journal is © the Owner Societies 2020 |