Ab initio modelling of local interfaces in doped organic semiconductors

Abstract

Doping in organic semiconductors remains a debated issue from both an experimental and ab initio perspective. Due to the complexity of these systems, which exhibit a low degree of crystallinity and high level of disorder, modelling doped organic semiconductors from first-principles calculations is not a trivial task, as their electronic and optical properties are sensitive to the choice of initial geometries. A crucial aspect to take into account, in view of rationalizing the electronic structure of these materials through ab initio calculations, is the role of local donor/acceptor interfaces. We address this problem in the framework of state-of-the-art density-functional theory and many-body perturbation theory, investigating the structural, electronic, and optical properties of quaterthiophene and sexithiophene oligomers doped by 2,3,5,6-tetrafluoro-7,7,8,8-tetracyano-quinodimethane (F4TCNQ). We consider different model structures ranging from isolated dimers and trimers, to periodic stacks. Our results demonstrate that the choice of the initial geometry critically impacts the resulting electronic structure and the degree of charge transfer in the materials, depending on the amount and on the nature of the local interfaces between donor and acceptor species. The optical spectra appear less sensitive to these parameters at least from a first glance, although a quantitative analysis of the excitations reveals that their Frenkel or charge-transfer character is affected by the characteristics of the donor/acceptor interfaces as well as by the donor length. Our findings represent an important step forward towards an insightful first-principles description of the microscopic properties of doped organic semiconductors complementary to experiments.

---

1 Introduction

Understanding the microscopic properties of doped organic semiconductors (OSCs) is the key to disclosing and ultimately controlling the fundamental doping mechanisms in these materials.^1–3 Relentless efforts in the last decade have brought noticeable advances in this field, unraveling correlations between the chemical nature and concentration of the dopant species and the observed ion-pair formation or creation of charge-transfer complexes.^2,4–13 This intensive research has made it apparent that such complexity demands reliable theoretical models that are able to address it in a predictable and insightful way. Ab initio quantum mechanical methods, such as density-functional theory (DFT) and many-body perturbation theory (MBPT), offer the unique advantage of an accurate and parameter-free description of the electronic-structure of materials given only their chemical composition and structural arrangement. In this sense, results obtained with first-principles approaches are regarded as complementary to experimental findings. However, besides theoretical and numerical approximations, the match between first-principles and experimental results is determined by the geometries chosen to model the systems under study. While this problem is negligible when dealing with ordered crystalline structures, in the case of doped organic semiconductors, which typically exhibit a low degree of crystallinity and a high level of disorder,^14–18 the initial geometry adopted in the calculations may influence the outcome and hence bias the interpretation of the investigated physical effect. A common choice in modelling doped OSCs is to consider an isolated dimer formed by a donor and an acceptor molecule interacting with each other.^12,19–21 Representing OSC with an isolated dimer implicitly assumes that the system can be reproduced by a single molecular interface. This model turned out to be successful in describing the level alignment of the donor/acceptor interfaces,¹⁹ the spatial distribution of the resulting frontier states,¹² and also in rationalizing the role of the donor conjugation length.²⁰ However, in this way, it is not possible to capture in full the behavior of extended donor/acceptor stacks, nor to reproduce the chemical environment of a molecule surrounded by more than one dopant.²² This is a non-negligible issue, considering that local interactions at donor/acceptor interfaces are known to critically impact the doping mechanism in organic semiconductors.^7,11,14,15

We investigate the effects of local interactions between donor and acceptor species on the electronic and optical properties of doped OSCs using ab initio many-body theory, focusing on prototypical charge-transfer complexes (CTCs) formed by oligothiophene molecules doped by the electron acceptor 2,3,5,6-tetrafluoro-7,7,8,8-tetracyano-quinodimethane (F4TCNQ). We consider trimer structures with different alternations of donors and acceptors, which are meant to model different types of interfaces. For comparison, we contrast these structures with isolated dimers and idealized periodic stacks formed by alternating donor and acceptor moieties. In the framework of hybrid DFT, we determine the nature and the spatial distribution of the frontier states and we quantitatively predict the degree of charge transfer in these systems. With the aid of MBPT applied on top of DFT, we provide an accurate description of the single-particle energy levels and of the optical excitations, including absorption spectra and character of the (bound) electron–hole pairs.

2 Systems

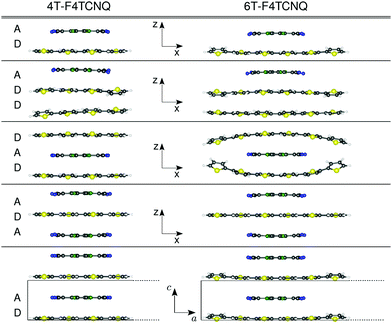
We study isolated dimers, trimers, and periodic stacks of CTCs formed by quaterthiophene (4T) and sexithiophene (6T) molecules doped by F4TCNQ. The choice of considering these two donor species is stimulated by the results of ref. 20, which show the sensitivity of the ground- and excited-state properties of these complexes to the donor length. We assume that initial geometries where the donor and acceptor species face each other are held together by π–π interactions, and have the respective centers of mass aligned on top of each other in the center of the CTC. The systems considered in this work are depicted in Fig. 1: a reference D–A dimer, analogous to the one adopted in ref. 20; three trimer configurations formed by (i) an acceptor molecule adsorbed on two stacked donors (D–D–A), (ii) an acceptor sandwiched between two donors (D–A–D), and (iii) a donor sandwiched between two acceptors (A–D–A); a periodic stack aligned in the normal direction with respect to the molecular planes, represented by the unit cell with lattice parameters a = 35 Å in 4T-F4TCNQ and a = 45 Å in 6T-F4TCNQ, and b = 25 Å in the two non-periodic directions, including about 20 Å of vacuum to avoid spurious interactions between the replicas. The lattice constant along the stacking direction, c = 6.66 Å, accounts for twice the π–π distance between the donor and acceptor molecules.

Fig. 1 Ball-and-stick representation of the optimized geometries of the considered CTCs with 4T (left panel) and 6T (right panel) as donors. Sulfur, carbon, nitrogen, fluorine, and hydrogen atoms are depicted in yellow, dark gray, blue, green, and white, respectively. In the bottom panel, the unit cell of one-dimensional periodic structures is outlined.

3 Theoretical background and computational details

3.1 Theoretical background

The results presented in this work are calculated using DFT²³ and MBPT.²⁴ In the framework of DFT, we optimize the structures and compute the electron density, which is the main ingredient to determine the character and the spatial distribution of the single-particle wave-functions and also to quantify the degree of charge transfer (CT) in the ground state using the Bader charge analysis.^25–28 The variation of the Bader charges within the acceptor/donor unit(s) in the CTCs with respect to the isolated cases is defined as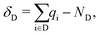andrespectively. In eqn (1) and (2), is the Bader charge calculated by integrating the charge density within the Bader volume V_i associated to the ith atom in the acceptor (donor), and N_A (N_D) is the total number of valence electrons in the acceptor (donor) moiety. As the total number of electrons must be conserved, eqn (1) and (2) obey the condition δ_A + δ_D = 0.

The solutions of the Kohn–Sham equations²⁹ of DFT represent the starting point for the MBPT calculations. The quasi-particle (QP) electronic structure of the CTCs is obtained by computing the self-energy from the single-shot G₀W₀ approximation.³⁰ This is the baseline for the construction and the solution of the Bethe–Salpeter equation (BSE), which gives access to the exitonic wave-functions and energies, and hence to the optical absorption spectra. This method, initially conceived for crystalline solids,^24,31–33 has successfully been applied to isolated molecules and organic materials in the last two decades.^20,34–56 Formally, the BSE is the equation of motion for the two-particle Green's function, L = L₀ + L₀KL, where K is the BSE interaction kernel composed by the repulsive exchange term, given by the bare Coulomb potential v, and by the direct screened Coulomb potential W, which accounts for the electron–hole attraction, and L₀ is the non interacting two-particle Green's function.^31,57 In practice, this problem is mapped into an effective two-particle Hamiltonian whose eigenvalues and eigenvectors describe the excitation energy and the character of the electron–hole pairs, respectively.³³ With this information, one can calculate the hole and electron densities^20,58,59 as

andrespectively. A^λ_αβ are the BSE coefficients associated to the λth excited state and the index α (β) runs over all occupied (empty) states ϕ_α (ϕ_β) included in the transition space. To ensure charge conservation, the hole and the electron densities integrate always to unity. In order to quantify the degree of localization of the hole (electron) on the donor (acceptor) in the λth excited state, we introduce the hole and electron localization index (LI) obtained by summing up the Bader partial charges associated to the hole and the electron, respectively, asand

In eqn (5) (eqn (6)), is the charge associated to the hole (electron) density integrated within the Bader volume V_i of the ith atom in the donor (acceptor) unit(s) of the CTC. As the hole and electron densities must integrate to unity, the hole and electron LIs are constrained to be always less than or equal to 1. The optical excitations computed from the BSE can be further analyzed through the transition density^60,61

This quantity is helpful to retrive information about the spatial and symmetry character of the considered excited state.

3.2 Computational details

The results reported in this work are obtained following a three-step computational approach. The first step consists in a ground-state calculation with structural optimization. All systems are optimized with the all-electron code FHI-aims⁶² by minimizing the interatomic forces until they are smaller than 10⁻³ eV Å⁻¹. In these calculations, we employ the TIER2 basis sets⁶³ with a tight integration mesh, the Perdew–Burke–Ernzerhof⁶⁴ (PBE) generalized gradient approximation for the exchange–correlation (xc) functional, and the Tkatchenko–Scheffler scheme⁶⁵ to account for the van der Waals interactions. For the periodic systems, the Brillouin zone (BZ) is sampled by a 1 × 1 × 6 k-grid.

The second step consists in computing the QP electronic structure from MBPT. In the isolated systems, these calculations are performed with the code MOLGW.⁶⁶ We use augmented double-ζ polarized Gaussian basis set aug-cc-pVDZ,⁶⁷ with frozen-core and resolution-of-identity⁶⁸ approximations. QP energies are calculated adding the perturbative QP correction obtained from G₀W₀ to the underlying DFT calculation with the range separated hybrid xc functional CAM-B3LYP.⁶⁹ In the periodic stacks the ground-state electronic structure is computed using the plane-wave pseudopotential code Quantum Espresso,^70,71 using a cutoff for the wave-functions (electron density) of 40 Ry (160 Ry), norm conserving pseudopotentials,⁷² and a 1 × 1 × 12 k-grid. This is the starting point for the GW calculations performed with the code Yambo,^73,74 where the truncated Coulomb potential method^73,75 is adopted, defining a box-like region with a vertical dimension of 24 Å and a lateral size of 35 Å and 44 Å for 4T-F4TCNQ and 6T-F4TCNQ, respectively. The QP correction in the periodic stacks is calculated through the partially self-consistent G_nW₀ approximation, where only the single particle Green's function G is updated at each iteration using the QP energies from the previous iteration with a convergence threshold of 10 meV. To improve the convergence of the self-energy with respect to the number of bands, the Bruneval–Gonze terminator technique⁷³ is adopted with 400 bands in total. The Godby–Needs plasmon-pole approximation⁷⁶ is employed to approximate the frequency-dependence of the dielectric function, that is used to describe the screening function W₀. A cutoff of 40 Ry (5 Ry) for the exchange (correlation) part of the self-energy is chosen.

In the third and final step, the optical properties of the considered materials are calculated from the solution of the BSE on top of the QP electronic structure. For this purpose, the MOLGW⁶⁶ and the Yambo^73,74 codes are used for the isolated and periodic stacks, respectively. In solving the BSE, the Tamm–Dancoff approximation (TDA) is adopted, such that the coupling between resonant and anti-resonant transitions is neglected. In organic materials, the TDA is known to cause a (rigid) blue-shift of a few hundred meV in the excitation energies and a slight redistribution of the oscillator strength. However, it has typically no impact on the nature of the excitations.^{20,40,77–79} In building the BSE Hamiltonian for the periodic stacks with Yambo, we consider an electron–hole transition space composed of 20 occupied and 40 unoccupied states. In this case, to alleviate the poor starting-point dependence of the underlying PBE calculation, the QP correction is adjusted by the application of a scissors operator of 1.86 (1.51) eV and dimensionless stretching factors S_v = 1.31 (1.60) and S_c = 1.29 (1.26) for doped 4T (6T) stacks. The values of the scissors operators are evaluated as Δ = Δ_GW + Δ_PBE0–PBE, where Δ_GW is the QP correction to the gap on top of PBE, whereas Δ_PBE0–PBE is the difference between PBE0⁸⁰ and PBE band gaps. The PBE0 band gap for the periodic stacks is computed with FHI-aims.⁶² The optical absorption spectra with Yambo are obtained assuming an incident electric field polarized along the a and c directions (see the coordinate system at the bottom of Fig. 1), and calculated by the inversion of the BSE Hamiltonian using the Haydock-Lanczos iterative algorithm.⁸¹

4 Results

4.1 Structural properties

We start our analysis by investigating the structural properties of the optimized CTCs shown in Fig. 1. In the CTCs formed by 4T, which has a size comparable to F4TCNQ, the donor remains essentially planar regardless of the stacking sequence and the interface with the acceptor (see the left side of Fig. 1). On the contrary, doped 6T exhibits more pronounced deviations from planarity, with the exception of the F4TCNQ-6T-F4TCNQ trimer, in which the donor remains flat. In the 6T-F4TCNQ dimer and in the 6T-6T-F4TCNQ trimer, the edges of the donor interacting with F4TCNQ are twisted by 14° and 18°, respectively. However, the most prominent effect is seen in the 6T-F4TCNQ-6T sequence, where the edges of the 6T oligomers are significantly distorted in the out-of-plane direction, as visible on the right side of Fig. 1. We explain this behavior in terms of van der Waals attraction between the edge rings of the donor, which exceeds the length of the acceptor molecule, approaching a mutual distance of 3.81 Å. The periodic stacks behave similarly as their isolated dimer counterparts, although the periodic boundary conditions effectively reduce the distortions. In all the considered CTCs, the smallest intermolecular distance between C atoms at the center of each donor and acceptor molecule ranges from 3.33 Å to 3.39 Å. The shortest donor–acceptor distance is obtained in the D–A dimer and D–D–A trimer, which exhibit analogous interface structures. The distance between the two donor moieties in the D–D–A trimer amounts to 3.6 Å. In the D–A–D sequence, the distances between the donors and the acceptors range between 3.35 Å and 3.39 Å, and increase with the donor length.

4.2 Electronic properties

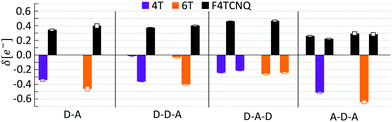
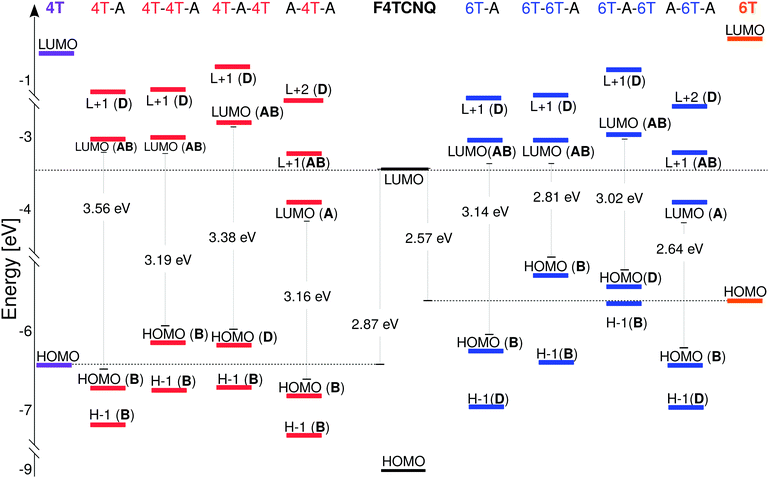
In the next step of our analysis we focus on the electronic properties of the CTCs and start with the estimation of the degree of charge transfer in the ground state. This quantity has a particular relevance in the field of doped OSCs, as it represents the main parameter to assess the nature and the effectiveness of the doping mechanism. For this purpose we use here the Bader charge analysis (see Section 3). For each complex, we define the Bader charge variation δ as the amount of charge transferred from the donor(s) to the acceptor(s) in the ground state. The results reported in Fig. 2 (further details in the ESI†) are grouped according to the stacking type. In this way it is possible to capture at a glance how the CT is related to the stacking sequence. While all complexes exhibit partial charge transfer, as expected from the nature of the involved species,¹³ the actual amount of charge transfer is rather sensitive to the type and number of donor/acceptor interfaces. In the D–A dimers, the charge is equally distributed between the two constituents and the CT slightly increases with the donor length. The trimers exhibit a more diverse behavior. In the D–D–A configuration, the charge transfer takes place almost exclusively between the donor and the acceptor directly facing each other. The second donor, which is farther away and less strongly interacting with F4TCNQ, loses less than 0.05e. On the other hand, in the D–A–D (A–D–A) configuration, the acceptor (donor) receives (donates) charge from both neighboring donor (acceptor) molecules. The results in Fig. 2 indicate an uneven distribution of the transferred charge from the donor to the acceptors, with differences of the order of 0.05e. However, as this value is of the same order as the numerical error on the Bader charges, this finding should not be over-interpreted. The results described above represent a clear indication that the effectiveness of the charge transfer is determined by the amount of donor–acceptor interfaces and by the nature of the species involved, rather than by the number of stacked molecules. The increase of the donor length impacts very slightly the amount of transferred charge. This effect can be understood considering the stronger interaction between the acceptor and the donor when the latter has a more extended backbone and hence a larger charge density, which in turn gives rise to an enhanced charge redistribution in the whole complex.

Fig. 2 Charge transfer in the ground state quantified through the Bader analysis of the partial charges on the donor(s) to the acceptor(s) in the CTCs analyzed in this work. The empty portions of the bar indicate the error in the numerical integration of the total charge density, performed on a finite spatial mesh.

We continue our analysis with the electronic properties of the considered CTCs, starting from the level alignment of the non-periodic systems computed from G₀W₀ on top of hybrid DFT (see Fig. 3). We show the energies of the frontier states of the CTCs with those of their building blocks [4T (left), 6T (right), and F4TCNQ (center)] computed at the same level of theory. In this way, the type-II alignment between the donor and acceptor species is clearly evident. In the dimers, both the HOMO and the LUMO are hybridized with bonding and anti-bonding character, respectively,^{13,19,20,82–84} (see Fig. 4) and they are energetically comprised between the frontier orbitals of the constituents. The situation is again more faceted in the trimers, where the number and the characteristics of the donor/acceptor interfaces influence the level alignment and also the nature and the spatial distribution of the frontier orbitals. In both D–D–A and D–A–D sequences, the HOMO of the CTC lies above the HOMO of the donor, while the LUMO is between the lowest-unoccupied levels of the building blocks. The scenario is reversed in the A–D–A trimer, where the LUMO of the complex is energetically lower than that of the acceptor, while the HOMO lies in between the HOMO energy levels of the donor and the acceptor (see Fig. 3). As a result, we obtain a larger band gap for the dimers compared to all the trimers. Among the latter, the A–D–A configuration exhibits a smaller gap, mainly due to the sizable downshift of the LUMO with respect to the individual components.

Fig. 3 Energy level alignment computed from G₀W₀ on top of DFT (CAM-B3LYP functional) for all the considered CTCs. The labels associated to the electronic states indicate the character of the orbitals, which can be bonding (B) or anti-bonding (AB), as well as localized on the acceptor (A) or donor (D) molecules.

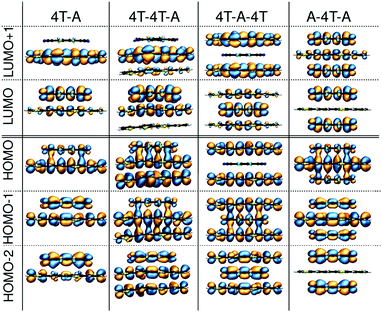Fig. 4 Molecular orbitals of dimers and trimers composed of quarterthiophene (4T) doped by the acceptor F4TCNQ.

These findings suggest that the relative concentration of the donor and acceptor molecules in the complex impacts the level alignment and the overall energy levels of the CTCs with respect to their constituents. Interestingly, the character of the orbitals in the trimers also depends on the stacking sequence. At the frontier, only the D–D–A trimer behaves as the dimer, with the HOMO and LUMO bearing bonding and anti-bonding character, respectively. In the D–A–D (A–D–A) stack the LUMO (HOMO) has anti-bonding (bonding) nature, while the HOMO (LUMO) is localized solely on the donor (acceptor) molecule: The bonding (anti-bonding) state is now the HOMO−1 (LUMO+1) – see Fig. 4. The trends discussed above appear in both classes of CTCs formed by doped 4T and 6T. The main effect of the donor length on the electronic properties of the complexes is to systematically reduce the size of the band gaps²⁰ (see Fig. 3, right panel).

We now turn to the periodic arrangements, where the electronic properties are analyzed in terms of the band structure shown in Fig. 5 for the case of the 4T-F4TCNQ stack. The corresponding plot for 6T-F4TCNQ can be found in the ESI.† We focus once again on the band gap, on the character of the frontier states, and also on the band dispersion which originates both from the π–π interactions between the molecules along the periodic stacking direction, and also from the non-negligible spatial overlap at the interface between the molecular orbitals of the species involved. In accordance with the results obtained with the same approach on other CTCs,⁸⁴ the fundamental gap, which amounts to about 2 eV in 4T-F4TCNQ, appears at Z, namely at the edge of the BZ, rather than at Γ, where the energy separation between the highest-occupied and the lowest-unoccupied bands increases up to approximately 3 eV. The nature and distribution of the Kohn–Sham wave-functions at Γ, shown in Fig. 5, resemble that of the isolated dimer in terms of bonding and anti-bonding character of the frontier states (see Fig. 4). On the contrary, the valence band maximum (VBM) and conduction band minimum (CBM) at Z are significantly more localized on the donor and acceptor molecules, respectively, compared to their counterparts at Γ. This character approaches the behavior of the HOMO and LUMO of the D–A–D and A–D–A trimer, respectively.

Fig. 5 Quasi-particle band structure of the periodic 4T-F4TCNQ stack. The square modulus of the highest-occupied and lowest-unoccupied Kohn–Sham states at Γ (left) and at Z (right) is shown.

4.3 Optical properties

The analysis of the electronic structure presented before provides us with all the ingredients to understand the optical properties of the isolated and periodic CTCs considered in this work. In Fig. 6 we report the absorption spectra of the isolated dimers and trimers. Remarkably, all spectra look rather similar to each other around the absorption onset, where two weak peaks appear regardless of the number of stacked molecules, their interfaces, and the donor length. An intense peak characterizes all spectra between 3.0 eV and 3.5 eV on both the left and right panels of Fig. 6. Its large oscillator strength is due to the enhanced wave-function overlap between the orbitals involved in the optical transitions and due to the polarization of the excitations along the longitudinal axis of the CTC. A detailed analysis of these peaks is reported in the ESI.† Here, we focus on the lowest-energy region of the spectra, where the optical transitions between the bonding and anti-bonding orbitals at the frontier are found. In all spectra, the lowest-energy excitation, labelled P₁ in Fig. 6, is optically active and exhibits similar energy and oscillator strength. Its frequency decreases by a few hundred meV going from the dimer to the trimers, while its intensity concomitantly increases by a slight amount. Notably, the gaps do not follow the red-shift of the energy of P₁ (see Fig. 6), implying different binding energies of this excitation in different arrangements. The largest binding energy of P₁ is obtained in the dimers, as expected, considering the enhanced confinement and the reduced screening produced by two molecules instead of three. Among the trimers, P₁ is most strongly bound in the A–D–A configuration, where, especially in the case of 6T, the binding energy is almost as large as in the dimer. On the other hand, the reduced exciton binding energy of P₁ in the D–D–A trimer results from the screening due to the second donor molecule. The second peak, P₂, is characterized in all spectra by an oscillator strength similar to P₁. However, its energy difference with respect to both P₁ and the gap (E_gap) varies from system to system.

Fig. 6 Optical absorption spectra of isolated dimer and trimer structures with 4T (left) and 6T (right) as donor species. In each spectrum, the energy of the QP gap (E_gap) is marked by a vertical dashed line. A broadening of 0.1 eV is applied to all spectra to mimic the excitation lifetime.

To better understand the nature of these excitations, we summarize in Table 1 their energy, oscillator strength, and composition in terms of single-particle transitions. In all CTCs, P₁ corresponds to the HOMO–LUMO transition. However, as discussed in Section 4.2, the character and spatial distribution of the frontier orbitals in the complexes is particularly sensitive to the stacking sequence and to the number of D–A interfaces. Hence, the nature of P₁ varies accordingly: In the D–A dimer and in the D–D–A trimer, where the frontier orbitals have bonding and anti-bonding character, this excitation has Frenkel-like character.²⁰ On the other hand, in the D–A–D trimers, where the HOMO is localized on the donor molecules and the LUMO is an anti-bonding state delocalized on the CTC, P₁ has charge-transfer character, with the hole fully localized on the donors and the electron mostly localized on the acceptor. The A–D–A trimer exhibits a behavior opposite to the D–A–D one, as far as P₁ is concerned: the HOMO has bonding character and the LUMO is fully localized on the acceptors. All this information is summarized in Fig. 7 where the electron and hole densities, calculated according to eqn (5) and (6), respectively, are displayed.

Table 1 Excitation energy, oscillator strength (OS), and composition in terms of single-particle transitions of the P₁ and P₂ excitations marked in Fig. 6

	Excitation	Energy [eV]	OS	Composition
4T-A	P1	1.23	0.19	H → L
	P2	2.02	0.19	H−1 → L
4T-4T-A	P1	1.19	0.23	H → L
	P2	1.94	0.18	H−2 → L
4T-A-4T	P1	1.11	0.28	H → L
	P2	2.14	0.17	H−2 → L
A-4T-A	P1	0.94	0.25	H → L
	P2	2.01	0.10	H−1 → L+1
6T-A	P1	1.12	0.18	H → L
	P2	1.57	0.37	H−1 → L
6T-6T-A	P1	1.07	0.22	H → L
	P2	1.49	0.30	H−2 → L
6T-A-6T	P1	0.93	0.19	H → L
	P2	1.67	0.28	H−2 → L
A-6T-A	P1	0.76	0.23	H → L
	P2	1.47	0.29	H−1 → L+1

---

Fig. 7 Hole, electron, and transition densities of the excitations associated to the first (P₁) and second (P₂) peaks in the optical spectra of the CTCs shown in Fig. 6.

In the case of P₂ the situation is more elaborate. As shown in Table 1, this excitation has a different composition depending on the stacking type. In the dimers, P₂ is formed by the transition between the HOMO−1 and the LUMO. As the character of the former changes with the length of the donor (see Fig. 3), in 4T-F4TCNQ, the HOMO−1 is delocalized over the whole CTC, while in 6T-F4TCNQ, it becomes more localized on the 6T. As a result, in 4T-F4TCNQ, P₂ is an exciton with more Frenkel-like charcater, while in 6T-F4TCNQ, P₂ has mainly CT nature. In the trimers, on the other hand, P₂ has a different composition depending on the type and sequence of molecular interfaces. It stems from HOMO−1 → LUMO+1 in F4TCNQ-4T-F4TCNQ, while it stems from HOMO−2 → LUMO in the 4T-4T-F4TCNQ and 4T-F4TCNQ-4T complexes. In all trimers formed by 4T, the occupied states involved in P₂ are delocalized on the whole complex while the unoccupied ones have anti-bonding nature (see Fig. 4). Hence, P₂ always has a Frenkel-like character, as seen from the hole and electron densities depicted in Fig. 7. In the CTCs formed by doped 6T, the situation is slightly different: While in all configurations, the composition of P₂ is the same as in the 4T counterparts, the spatial distribution of the occupied orbitals involved in the corresponding optical transition changes (see Table 1). Due to the increasing donor length, the HOMO−1 in the dimer and in the A–D–A trimer, and the HOMO−2 in the D–D–A and D–A–D trimers become more localized on the donor(s) species (see the ESI†). As a result, P₂ has a Frenkel-like character in all CTCs formed by doped 4T, whereas in those including 6T, the spatial separation between the hole and the electron increases and hence the CT character is more pronounced.

In the spectra of the D–D–A trimers, an additional weak peak, labeled P₁*, is visible between P₁ and P₂. It stems from the transition between the HOMO−1 and the LUMO. In the D–D–A trimers, the HOMO−1 has a bonding character similar to the HOMO (see Fig. 4), although it is slightly more localized on the donor molecules than on the acceptor. As a result, the reduced spatial overlap between HOMO−1 and LUMO explains the lower oscillator strength of P₁*, compared to P₁. More details are provided in the ESI.†

To support these observations, we quantify the localization of the hole on the donor(s) and of the electron on the acceptor(s) with the LIs defined in eqn (5) and (6). The results for P₁ and P₂ are reported in Table 2. In the dimers, the values of LIs for both the hole and electron densities associated to P₁ are close to 1.0, which suggests the CT character of this excitation. On the other hand, the frontier orbitals contributing to this transition have bonding and anti-bonding nature due to the large degree of hybridization (see Fig. 4). From the combined analysis of the electron and hole densities shown in Fig. 7 and of the LIs in Table 2, it is evident that P₁ bears a very peculiar nature, which can hardly be labeled as purely Frenkel- or charge-transfer-like. The D–D–A trimers exhibit a similar behavior to the dimers. However, in this case, the presence of two donor molecules stacked on top of each other enhances the localization of the hole on their side, such that the corresponding LI is even closer to 1.0 (see Table 2). On the other hand, the electron is as localized on the acceptor as in the dimer, as reflected by the values of the associated LI. In the D–A–D (A–D–A) trimers, the CT nature of P₁ is confirmed by the LI being equal to 1.0 for the hole (electron), while the electron (hole) exhibits about 0.8 localization on the acceptor (donor). Turning now to P₂, its Frenkel (CT) nature in 4T-F4TCNQ (6T-F4TCNQ) is confirmed by the LI equal to 0.6 (0.95) of the hole on the donor, with the electron being also largely localized on the acceptor. In the trimers formed by doped 4T, the values of LI for P₂ as shown in Table 2 point to a balanced distribution of the hole and of the electron on both donor and acceptor species, resulting in an overall delocalization of this excitation on the whole complex. On the other hand, in the trimers formed by doped 6T the results of Table 2 for P₂ quantify the enhanced segregation of the hole and electron on the donor and acceptor molecules, respectively. The LI associated to the hole, in particular, is very close to 1.0 in all these trimers, thus confirming the CT-like character of P₂. This analysis of the LIs suggests that a simple visual inspection of the hole and the electron densities, or even only of the orbitals contributing to the optical transitions, is insufficient to determine the character of the excitations. The calculation of the LIs represents a much more robust and reliable approach to analyze the excitations.

Table 2 Localization index associated to the hole (L_h) and electron density (L_e) on the donor and acceptor species, respectively, for P₁ and P₂ marked in 6

4T-A	0.86	0.84	0.62	0.78
6T-A	0.85	0.82	0.95	0.82
4T-4T-A	0.92	0.83	0.79	0.80
6T-6T-A	0.90	0.80	0.97	0.80
4T-A-4T	1.00	0.81	0.60	0.75
6T-A-6T	1.00	0.80	0.93	0.80
A-4T-A	0.83	1.00	0.68	0.74
A-6T-A	0.78	1.00	0.95	0.74

---

We finally analyze the optical properties of the CTCs modeled by periodic arrangements (see the bottom of Fig. 1). The absorption spectra shown in Fig. 8 (left panel) are computed considering different polarizations of the incident electric field, namely along the stacking direction (c axis in Fig. 1, solid lines in Fig. 8), and along the long molecular axis (a axis in Fig. 1, dashed lines in Fig. 8). The average spectrum obtained from these two is also displayed for comparison. The first excitation, labeled E₁, is bright and very intense. It is polarized along the stacking direction, as shown by the corresponding transition density in Fig. 8. Energetically, it is red-shifted with respect to P₁ in the spectra of the corresponding dimers, which can be regarded as a manifestation of J-aggregate behavior.^56,85,86 As summarized in Table 3, E₁ is mainly the result of transitions from the highest-occupied band to the lowest-unoccupied band around the high-symmetry point Z in the BZ, where the band gap appears (see Fig. 5). The binding energy of E₁, evaluated as the energy difference with respect to the QP gap, is of the order of 1 eV, i.e., significantly reduced compared to P₁ in the isolated CTCs (see Fig. 6). This is a reasonable behavior, considering the larger screening exerted by the periodic alternation of donor and acceptor molecules in comparison with isolated dimers or trimers. The second and third bright excitations in the spectra of the periodic stacks, labeled E₂ and E₃, respectively, are much weaker than E₁ and, as such, hardly visible in Fig. 8. Similar to E₁, E₂ is also polarized along the stacking direction, and stems from the transitions between the highest-occupied band and the lowest-unoccupied band in the vicinity of Γ (see Table 3). E₁ and E₂ can be associated to the splitting of P₁ in the isolated dimers due to intermolecular coupling in the periodic stacks.^87–89 Analogously, the third excitation E₃ results from the splitting of P₂ in the dimer: as shown in Table 3, it stems from multiple transitions between the second highest-occupied band and the lowest-unoccupied one over the entire BZ.

Fig. 8 (left) Optical absorption spectra of periodic 4T- and 6T-F4TCNQ stacks. Black solid (dashed) lines indicate the absorption with polarization along the c (a) axis in the unit cell (see the reference system at the bottom of Fig. 1), while in color, we depict the average between the two. Dashed bars mark the energy of the QP gaps. (right) Transition densities of the excited states highlighted in the spectra.

Table 3 Excitation energy, oscillator strength (OS) and composition in terms of single-particle transitions (band and k-point) of the first three excitations E₁, E₂ and E₃ highlighted in Fig. 8. The labels VB and CB stand for the highest valence band and the lowest conduction band, respectively. The coordinates of the k-points are expressed in reciprocal lattice units, where Γ = (0,0,0) and Z = (0,0,0.5). Only the transitions with weight larger than 10% are reported

	Excitation	Energy [eV]	OS	Composition	Weight	k-Point
4T-A	E1	0.81	1.57	VB → CB	46%	Z
				VB → CB	21%	(0, 0, ±0.42)
	E2	2.14	0.07	VB → CB	20%	Γ
				VB → CB	17%	(0, 0, ±0.08)
	E3	2.27	0.06	VB-1 → CB	15%	(0, 0, ±0.25)
				VB-2 → CB	14%	(0, 0, ±0.50)
				VB-1 → CB	11%	(0, 0, ±0.33)
6T-A	E1	0.64	2.25	VB → CB	69%	Z
				VB → CB	13%	(0, 0, ±0.42)
	E2	1.67	0.15	VB → CB	50%	Γ
				VB → CB	23%	(0, 0, ±0.08)
	E3	1.90	0.11	VB-1 → CB	20%	Γ
				VB-1 → CB	15%	(0, 0, ±0.08)

---

To deepen the analysis on the excitations in the periodic stacks in comparison with those in the isolated dimers and trimers, we consider the transition densities depicted on the right panel of Fig. 8 and contrast them with those reported in Fig. 7. From the transition-density plots, the polarization of E₁ and E₂ along the stacking direction is evident and so is the larger oscillator strength of the first excitation compared to the second one. Reflecting the character of the electronic states involved in the corresponding optical transitions, the transition density of E₁ is significantly more extended along the stacking direction than the one of E₂ due to the more pronounced wave-function overlap. The transition densities of both excitations exhibit similarities with the one of P₁ in the isolated dimers and trimers, even in the D–A–D and A–D–A arrangements where the lowest-energy excitation has a CT character (see Fig. 7). On the other hand, E₃ is evidently polarized along the long molecular axis (see Fig. 8, right panel), analogously to P₂ in the non-periodic structures (see Fig. 7).

5 Discussion and conclusions

The results presented in this work demonstrate the sensitivity of the electronic and optical properties of doped OSCs on the number and nature of the local donor–acceptor interfaces in the structures adopted in the first-principles calculations. The electronic structure of dimers, trimers, and periodic stacks varies accordingly. Bonding and anti-bonding frontier orbitals are formed only by donor and acceptor molecules interacting with each other through one single interface. This is obviously the case in the dimers^13,19,20 and also in the trimers formed by one acceptor molecule adsorbed on top of two donors. On the other hand, when one donor (acceptor) is sandwiched between two acceptor (donor) molecules, the LUMO (HOMO) of the complex is localized solely on the latter species, that are present in larger amount, with the LUMO+1 (HOMO−1) exhibiting anti-bonding (bonding) character. The orbital energies are correspondingly affected by these characteristics, which are also reflected in the relative level alignment of the CTCs with respect to their constituents, and also in the resulting band gaps. The optical spectra are, at a first glance, hardly influenced by the type and amounts of donor–acceptor interfaces in the model structure. For a given donor molecule, the absorption onset is within a window of less than 500 meV regardless of the number of stacked molecules and their arrangement, and the corresponding peak has comparable oscillator strength in all systems. However, in spite of these common characteristics, a quantitative inspection reveals a different nature of the first excitation, corresponding to the transition between the HOMO and the LUMO, depending on the aforementioned character of the frontier orbitals. As a result, excitons with more pronounced Frenkel or charge-transfer character are obtained depending on the number of local interfaces: One donor–acceptor interface promotes bonding and anti-bonding states at the frontier and hence Frenkel excitons localized in the CTC. Conversely, the double interface of a donor (acceptor) molecule with two acceptor (donor) species enhances the spatial segregation of the LUMO (HOMO) on the acceptors (donors), thus enhancing the CT nature of the excitons.

Charge-transfer complexes modelled by idealized periodic structures exhibit additional features in the electronic structure, such as dispersive bands and the systematic reduction of the QP-gap energy. The fundamental gap appears at the zone edge along the reciprocal axis of the periodic direction rather than at the zone center Γ, similar to the other D–A complexes investigated in previous work.⁸⁴ The character of the wave-functions at the frontier varies across the Brillouin zone, being more remarkably bonding and anti-bonding at Γ than at the zone edge Z, where the highest-occupied and lowest-unoccupied bands become more segregated on the donors and on the acceptors, respectively. The optical spectra of the periodic stacks exhibit a pronounced maximum at the onset, corresponding to a bright excitation polarized along the stacking direction. The relative intensity of the first peak is enhanced compared to the non-periodic CTCs, due to the increase of wave-function overlap and delocalization along the periodic direction.

In conclusion, our study highlights the remarkable complexity of modelling organic donor/acceptor complexes using first principles. Our main finding is that the electronic and optical properties of doped OSCs depend critically on the local interface structure. Hence, the models adopted in the ab initio calculations should be chosen critically depending on the characteristics of the system under study (e.g., the dopant concentration) and/or the effect to be investigated (e.g., local or global properties of the materials). The implications of our work in the context of ab initio studies of the doped OSCs are therefore evident. Our findings are also relevant from an experimental perspective, as they demonstrate that a detailed description of the local structures is crucial for addressing and unraveling the microscopic physical processes in doped OSCs. If existing experimental evidence is able to clarify the specific local interface structure, it should be used to guide the ab initio modelling. On the other hand, if no experimental reference is available, our results provide a useful rationale to anticipate the role played by the model structures and thus to support the physical intuition in designing them.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge fruitful discussions with Andreas Opitz, Norber Koch, Dieter Neher, Ahmed Mansour, and Malavika Arvind. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 182087777 – SFB 951 and 286798544 – HE 5866/2-1. Computational resources were provided by the North-German Supercomputing Alliance (HLRN), through the projects bep00060 and bep00076.

Notes and references

1. B. Lüssem, M. Riede and K. Leo, Phys. Status Solidi A, 2013, 210, 9–43.
2. I. E. Jacobs and A. J. Moulé, Adv. Mater., 2017, 29, 1703063.
3. I. Salzmann and G. Heimel, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 208–222.
4. E. Aziz, A. Vollmer, S. Eisebitt, W. Eberhardt, P. Pingel, D. Neher and N. Koch, Adv. Mater., 2007, 19, 3257–3260.
5. K.-H. Yim, G. L. Whiting, C. E. Murphy, J. J. M. Halls, J. H. Burroughes, R. H. Friend and J.-S. Kim, Adv. Mater., 2008, 20, 3319–3324.
6. P. Pingel, L. Zhu, K. S. Park, J.-O. Vogel, S. Janietz, E.-G. Kim, J. P. Rabe, J.-L. Brédas and N. Koch, J. Phys. Chem. Lett., 2010, 1, 2037–2041.
7. J. Gao, J. D. Roehling, Y. Li, H. Guo, A. J. Moulé and J. K. Grey, J. Mater. Chem. C, 2013, 1, 5638–5646.
8. P. Pingel and D. Neher, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115209.
9. D. T. Duong, C. Wang, E. Antono, M. F. Toney and A. Salleo, Org. Electron., 2013, 14, 1330–1336.
10. I. Salzmann, G. Heimel, S. Duhm, M. Oehzelt, P. Pingel, B. M. George, A. Schnegg, K. Lips, R.-P. Blum, A. Vollmer and N. Koch, Phys. Rev. Lett., 2012, 108, 035502.
11. I. Salzmann, G. Heimel, M. Oehzelt, S. Winkler and N. Koch, Acc. Chem. Res., 2016, 49, 370–378.
12. H. Méndez, G. Heimel, A. Opitz, K. Sauer, P. Barkowski, M. Oehzelt, J. Soeda, T. Okamoto, J. Takeya, J.-B. Arlin, J.-Y. Balandier, Y. Geerts, N. Koch and I. Salzmann, Angew. Chem., Int. Ed., 2013, 52, 7751–7755.
13. H. Méndez, G. Heimel, S. Winkler, J. Frisch, A. Opitz, K. Sauer, B. Wegner, M. Oehzelt, C. Röthel, S. Duhm, D. Többens, N. Koch and I. Salzmann, Nat. Commun., 2015, 6, 8560.
14. I. E. Jacobs, C. Cendra, T. F. Harrelson, Z. I. Bedolla Valdez, R. Faller, A. Salleo and A. J. Moulé, Mater. Horiz., 2018, 5, 655–660.
15. B. Neelamraju, K. E. Watts, J. E. Pemberton and E. L. Ratcliff, J. Phys. Chem. Lett., 2018, 9, 6871–6877.
16. D. P. McMahon and A. Troisi, ChemPhysChem, 2010, 11, 2067–2074.
17. A. Fediai, F. Symalla, P. Friederich and W. Wenzel, Nat. Commun., 2019, 10, 4547.
18. S. Hood, N. Zarrabi, P. Meredith, I. Kassal and A. Armin, J. Phys. Chem. Lett., 2019, 10, 3863–3870.
19. L. Zhu, E.-G. Kim, Y. Yi and J.-L. Brédas, Chem. Mater., 2011, 23, 5149–5159.
20. A. M. Valencia and C. Cocchi, J. Phys. Chem. C, 2019, 123, 9617–9623.
21. C. Dong and S. Schumacher, J. Phys. Chem. C, 2019, 123, 30863–30870.
22. M.-S. Niu, K.-W. Wang, X.-Y. Yang, P.-Q. Bi, K.-N. Zhang, X.-J. Feng, F. Chen, W. Qin, J.-L. Xia and X.-T. Hao, J. Phys. Chem. Lett., 2019, 10, 7100–7106.
23. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
24. G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659.
25. R. F. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press, 1990.
26. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
27. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
28. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
29. W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, A1133–A1138.
30. L. Hedin, Phys. Rev., 1965, 139, A796–A823.
31. W. Hanke and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4656–4673.
32. M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315.
33. M. Rohlfing and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944.
34. J. C. Grossman, M. Rohlfing, L. Mitas, S. G. Louie and M. L. Cohen, Phys. Rev. Lett., 2001, 86, 472.
35. P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. Lett., 2002, 89, 056405.
36. K. Hummer, C. Ambrosch-Draxl, G. Bussi, A. Ruini, M. J. Caldas, E. Molinari, R. Laskowski and N. Christensen, Phys. Status Solidi B, 2005, 242, 1754–1758.
37. M. L. Tiago and J. R. Chelikowsky, Solid State Commun., 2005, 136, 333–337.
38. K. Hummer and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 081202.
39. C. Ambrosch-Draxl, D. Nabok, P. Puschnig and C. Meisenbichler, New J. Phys., 2009, 11, 125010.
40. M. Palummo, C. Hogan, F. Sottile, P. Bagalà and A. Rubio, J. Chem. Phys., 2009, 131, 084102.
41. X. Blase and C. Attaccalite, Appl. Phys. Lett., 2011, 99, 171909.
42. I. Duchemin, T. Deutsch and X. Blase, Phys. Rev. Lett., 2012, 109, 167801.
43. I. Duchemin and X. Blase, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245412.
44. C. Faber, P. Boulanger, I. Duchemin, C. Attaccalite and X. Blase, J. Chem. Phys., 2013, 139, 194308.
45. F. Bruneval, S. M. Hamed and J. B. Neaton, J. Chem. Phys., 2015, 142, 244101.
46. D. Hirose, Y. Noguchi and O. Sugino, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205111.
47. L. Pithan, C. Cocchi, H. Zschiesche, C. Weber, A. Zykov, S. Bommel, S. J. Leake, P. Schäfer, C. Draxl and S. Kowarik, Cryst. Growth Des., 2015, 15, 1319–1324.
48. C. Cocchi and C. Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205126.
49. L. Hung, H. Felipe, J. Souto-Casares, J. R. Chelikowsky, S. G. Louie and S. Öğüt, Phys. Rev. B, 2016, 94, 085125.
50. C. Cocchi, T. Moldt, C. Gahl, M. Weinelt and C. Draxl, J. Chem. Phys., 2016, 145, 234701.
51. V. Ziaei and T. Bredow, J. Chem. Phys., 2016, 145, 174305.
52. T. Rangel, K. Berland, S. Sharifzadeh, F. Brown-Altvater, K. Lee, P. Hyldgaard, L. Kronik and J. B. Neaton, Phys. Rev. B, 2016, 93, 115206.
53. C. Cocchi and C. Draxl, J. Phys.: Condens. Matter, 2017, 29, 394005.
54. C. Cocchi, T. Breuer, G. Witte and C. Draxl, Phys. Chem. Chem. Phys., 2018, 20, 29724–29736.
55. S. Sharifzadeh, J. Phys.: Condens. Matter, 2018, 30, 153002.
56. M. Guerrini, C. Cocchi, A. Calzolari, D. Varsano and S. Corni, J. Phys. Chem. C, 2019, 123, 6831–6838.
57. G. Strinati, La Rivista del Nuovo Cimento (1978–1999), 1988, 11, 1–86.
58. C. Cocchi, D. Prezzi, A. Ruini, M. J. Caldas and E. Molinari, J. Phys. Chem. Lett., 2011, 2, 1315–1319.
59. M. De Corato, C. Cocchi, D. Prezzi, M. J. Caldas, E. Molinari and A. Ruini, J. Phys. Chem. C, 2014, 118, 23219–23225.
60. I. Fischer-Hjalmars, J. Mol. Spectrosc., 1971, 39, 321–331.
61. A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037.
62. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
63. V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379.
64. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
65. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
66. F. Bruneval, T. Rangel, S. M. Hamed, M. Shao, C. Yang and J. B. Neaton, Comput. Phys. Commun., 2016, 208, 149–161.
67. F. Bruneval, J. Chem. Phys., 2012, 136, 194107.
68. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183.
69. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
70. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
71. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
72. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
73. D. Sangalli, A. Ferretti, H. Miranda, C. Attaccalite, I. Marri, E. Cannuccia, P. Melo, M. Marsili, F. Paleari, A. Marrazzo, G. Prandini, P. Bonfà, M. O. Atambo, F. Affinito, M. Palummo, A. Molina-Sánchez, C. Hogan, M. Grüning, D. Varsano and A. Marini, J. Phys.: Condens. Matter, 2019, 31, 325902.
74. A. Marini, C. Hogan, M. Grüning and D. Varsano, Comput. Phys. Commun., 2009, 180, 1392–1403.
75. C. A. Rozzi, D. Varsano, A. Marini, E. K. U. Gross and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205119.
76. R. W. Godby and R. J. Needs, Phys. Rev. Lett., 1989, 62, 1169–1172.
77. B. Baumeier, D. Andrienko, Y. Ma and M. Rohlfing, J. Chem. Theory Comput., 2012, 8, 997–1002.
78. T. Rangel, S. M. Hamed, F. Bruneval and J. B. Neaton, J. Chem. Phys., 2017, 146, 194108.
79. T. Lettmann and M. Rohlfing, J. Chem. Theory Comput., 2019, 15, 4547–4554.
80. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
81. C. Lanczos, J. Res. Natl. Bur. Stand., Sect. B, 1950, 45, 255–282.
82. S. Shibahara, H. Kitagawa, T. Kubo and K. Nakasuji, Inorg. Chem. Commun., 2007, 10, 860–862.
83. C. S. Jacobsen, H. J. Pedersen, K. Mortensen and K. Bechgaard, J. Phys. C, 1980, 13, 3411–3425.
84. P. Beyer, D. Pham, C. Peter, N. Koch, E. Meister, W. Brutting, L. Grübert, S. Hecht, D. Nabok, C. Cocchi, C. Draxl and A. Opitz, Chem. Mater., 2019, 31, 1237–1249.
85. F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376–3410.
86. E. E. Jelley, Nature, 1936, 138, 1009–1010.
87. M. Kasha, Radiat. Res., 1963, 20, 55–70.
88. A. S. Davydov, Soviet Physics – Uspekhi, 1964, 7, 145–178.
89. M. Guerrini, A. Calzolari, D. Varsano and S. Corni, J. Chem. Theory Comput., 2019, 15, 3197–3203.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary figures and tables with additional analysis of the electronic structure and optical excitations of the investigated materials. See DOI: 10.1039/c9cp06655a

---