Open Access Article
Open Access ArticleA microfluidic study of synergic liquid–liquid extraction of rare earth elements†
Asmae
El Maangar
 ab,
Johannes
Theisen
ab,
Johannes
Theisen
 ab,
Christophe
Penisson
ab,
Thomas
Zemb
ab,
Christophe
Penisson
ab,
Thomas
Zemb
 b and
Jean-Christophe P.
Gabriel
b and
Jean-Christophe P.
Gabriel
 *acd
*acd
aUniv. Grenoble Alpes, IRIG-MEM, F-38054 Grenoble, France
bICSM, CEA, Univ Montpellier, CNRS, ENSCM, Marcoule, France
cUniversité Paris-Saclay, CEA, CNRS, NIMBE, 91191, Gif-sur-Yvette, France. E-mail: jean-christophe.gabriel@cea.fr
dNanyang Technological University, ERI@N, Singapore
First published on 5th February 2020
Abstract
A microfluidic technique is coupled with X-ray fluorescence in order to investigate the origin of the so-called synergy effect observed in liquid–liquid extraction of rare earth elements (REEs) when special combinations of two extractants – one solvating and one ionic – are used. The setup enables kinetic studies by varying the two phases’ contact time. The results obtained are compared with those obtained using a standard batch extraction method at identical contact time. We then determine variations of free energies of transfer for five rare earth elements present in a solution together with a non-target ion (Fe3+) at different pH. Analysis of the effect of temperature and of surface charge density of the coexisting cations allows separating electrostatic effects from complexation effects. We finally show that all non-linear (synergic) effects are quadratic in mole fraction. This demonstrates that in-plane mixing entropy of the bent extractant film, in the first nanometer around rare earth ions, is the determining term in the synergy effect. Surprisingly, even when the third phase is present, free energies of transfer could still be measured in the dilute phase, which is reported for the first time, to our knowledge. We hence show that the extractive power of the dense third phase is stronger than that of conventional reverse aggregates in equilibrium with excess water.
Introduction
With increased scarcity and/or strategic importance of many chemical elements of the periodic table,1–4 there is a large thrust in research efforts for new economically viable processes for the recycling of such elements from the “Urban Mine”, i.e. our wastes.5–7 A critical example can be found in the case of rare earth elements (REEs) that are key elements in so many applications surrounding us, especially in the electronic and energy sector.3,8,9 Many of such processes are based on liquid–liquid extraction,10–14 hence making use of very complex formulations, often referred to as complex fluids.13,15 Ion transfer between two phases and its driving force have been the subject of many kinetic, thermodynamic, theoretical, and modeling studies which require years of research with yet many remaining unknowns.11,16–22 In addition to this complexity, even when promising hydrometallurgy processes are described, their use by the recycling industry is hindered by the cost associated with the use of very low pH and the variability in the elemental composition from one waste lot to the other. The industry is therefore not only in need of more efficient approaches that can work at higher pH and show higher performances but also of methods enabling a faster speed of process development or adjustment. In order to reduce time and volume, relying on microfluidic devices represents a very promising route.15,22–31 Indeed, since the pioneering work of Ismagilov and co-workers,22 microfluidics has been developed as a popular method to save quantities of test materials needed to complete experimental plans in formulating efficient processes. The main difficulties in using microfluidics instead of the old “batch” method are related to the adsorption of electrolytes on all interfaces present and to the sensitivity required in elemental analysis. These effects contribute to uncertainty in the final results.32 The precise control of kinetic effects limited by diffusion in thin channels depends on the design strategy chosen (membrane, membrane-less, bubble, and droplet). In a preliminary paper, we have shown that the presence of a membrane may not limit the transfer observed and can be considered as an alternative to the most popular strategy based on droplets.33In this paper we report on the interest of chemical analysis of all four microfluidic channels (aqueous/oil, in & out), which enables accurate measurements of the concentration ratio [Ion]out/[Ion]in (both in water and oil). We show that such a microfluidic study, here applied to a very promising synergic system formed by two different extracting molecules,34 allows for: (i) classical yield measurements, but also, for the first time to the best of our knowledge; (ii) the measurement of Gibbs free energies of transfer reactions and thus not only for Winsor II but also Winsor III data points.14,35,36
Experimental
Chemicals
The solvating extractant N,N′-dimethyl-N,N′-dioctylhexyl-ethoxymalonamide (DMDOHEMA) was purchased from Panchim SARL (Lisses, France) with a purity higher than 99%, determined by gas chromatography coupled to mass spectrometry (GC-MS). The cation exchanger bis(2-ethylhexyl)phosphoric acid (HDEHP) was purchased from Sigma Aldrich with a purity higher than 97%. Isane® IP175 was purchased from Total Special fluids. Water was deionized using a Millipore Milli-Q purification system (Merck Millipore, Billerica, MA). All other chemicals were purchased from commercial sources: 70% nitric acid HNO3 (Sigma Aldrich), lanthanum(III) nitrate hexahydrate La(NO3)3·6H2O (Sigma Aldrich; purity, >99.99%), neodymium(III) nitrate hexahydrate Nd(NO3)3·6H2O (Sigma Aldrich; purity, >99.9%), europium(III) nitrate hexahydrate Eu(NO3)3·6H2O (Sigma Aldrich; purity, >99.9%), dysprosium(III) nitrate hexahydrate Dy(NO3)3·6H2O (Sigma Aldrich; purity, >99,9%), ytterbium(III) nitrate hexahydrate Yb(NO3)3·6H2O (Sigma Aldrich; purity, >99.9%) and iron(III) nitrate nonahydrate Fe(NO3)3·9H2O (Sigma Aldrich; purity, >99.999%). All chemical products were used without further purification.Solution preparation
For all samples, organic phases containing both extracting molecules DMDOHEMA and HDEHP were prepared with a well-defined quantity of the two extractants at different molar fractions of DMDOHEMA varying from 0 to 1 in steps of 0.25 (as reported in Table S1 of the ESI†) diluted in Isane® IP175. Solutions of both extractants were prepared so that their total concentration in extractant molecules, (Ctot = CDMDOHEMA + CHDEHP) was fixed to 0.9 mol L−1. This latter concentration is chosen to be above critical aggregation concentrations (CACs) for both extractants.34,37In order to measure all selectivities in a simulated although realistic case, we chose a reference aqueous solution composition that contained five lanthanides and a typical non-target ion, Fe3+. Ln(III) and iron(III) aqueous solutions were obtained by dissolving La(NO3)3·6H2O, Nd(NO3)3·6H2O, Eu(NO3)3·6H2O, Dy(NO3)3·6H2O, Yb(NO3)3·6H2O and Fe(NO3)3·9H2O in an aqueous solution of nitric acid at different concentrations ([HNO3] = 0.03, 0.3 and 3 M), so that each of their respective concentrations in the aqueous phase was 10 mmol L−1. The initial concentration of the different salts in the aqueous phase was verified by both X-ray Fluorescence (XRF) and Inductively Coupled Plasma Atomic Emission Spectrophotometry (ICP-OES) analyses.
Microfluidic system
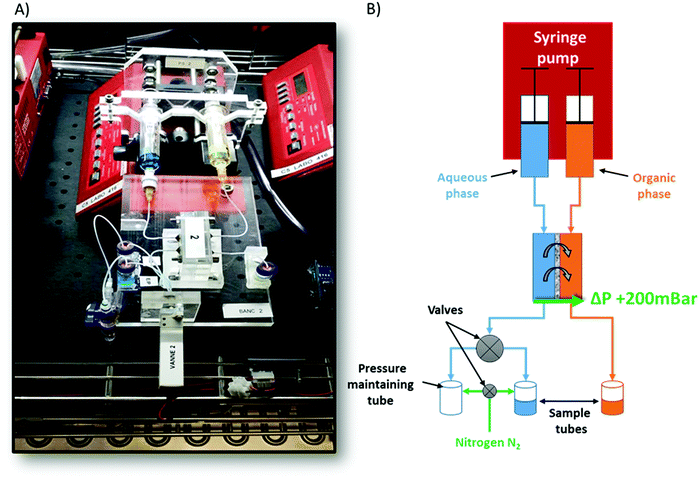
We used a set-up as illustrated in Fig. 1 and previously described in detail, as well as validated, elsewhere.32,33 Typically, the oil and aqueous channels are micromachined in poly(methyl methacrylate) (PMMA) blocks, which are chemically compatible with nitric acid and Isane® IP175. The two channels are separated by a hydrophobic and porous PTFE membrane with a thickness of 30 μm, a pore size of 20 nm and a porosity of 55% (Commercially available from Cobetter filtration, China). It acts as capillary separation between the microfluidic channels. The thickness of this membrane was previously optimised to 30 μm so as to: (i) be easy to handle and (ii) not become the limiting factor in the mass transfer kinetics.33 Connectors between the microfluidic ship and PTFE tubing were made of a stainless-steel tubing sealed with epoxy resin (Fig. 2).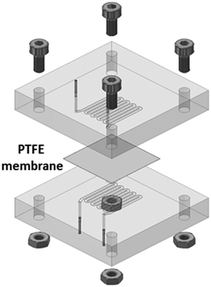 | ||
| Fig. 2 3D sketch of a microfluidic extraction circuit card with: PTFE membranes; four tightening bolts for mechanical stability; PMMA blocks milled with microfluidic serpentine channels; input/output stainless steel tubes. The volume of each channel within the phase contact area is 35.7 μL. Reprinted from ref. 34, Copyright 2019, with permission from Elsevier. | ||
Our validated microfluidic liquid–liquid extraction procedure can be summarized as follows:32,33 the first step of any of our microfluidic extractions consisted in loading the aqueous and oil phases – classically an extractant at predetermined composition and a “diluent” – into gas-tight 5 mL glass syringes equipped with a PTFE plunger (Hamilton Bonaduz, syringe 1005TLL). Then, both syringes were placed on a syringe pump (NE1000, New Era Pump Systems, modified to enable simultaneous use of two syringes) to deliver desired flow rates and injection volumes. Both syringes were connected to the microfluidic device with a PTFE tubing of internal diameter 0.65 mm and known overall length. The aqueous sample was introduced first, manually, into the aqueous channel in order to avoid the organic phase passing through the membrane. Indeed, the latter may occur whenever the oil phase is introduced first while the aqueous channel is either left empty or if it is under pressurized. Hence, a slight back-pressure of 200 mbar must be applied to the aqueous channel, thus maintaining the oil–water interface within the membrane. This back-pressure was applied by connecting the output sample septum vial to a pressure regulated nitrogen (N2) reservoir (Fig. 1). Then the organic phase was injected into the organic channel. When both microfluidic channels were filled, both syringes were perfused simultaneously and at equal flow rates by computer-controlled automation. For each data point, the microfluidic device was (i) fully flushed with twice its internal volume, in order to assure reaching a steady state; (ii) further flushed until 600 μL of each phase was retrieved in collecting output vials, for off-line XRF or ICP-OES analysis (see the ESI† for more details about the XRF analysis).32,38,39 The necessary overall time required to obtain each sample varies according to the flow rate used (always equal, by construction, for both phases (Fig. 1)) which in our case varies from 34 μL min−1 to 0.57 μL min−1 (see Table S2 of the ESI†). For all experimental studies, both aqueous and organic samples were sampled out for five different contact times between the two phases, i.e. after 1, 3, 10, 30, and 60 minutes, respectively. When all flow rates for a given composition have been sampled, the device shown in Fig. 2 was disassembled, cleaned and its membrane replaced to proceed to another composition within the phase diagram. All microfluidic extractions were performed within a large (1 m3) thermostated chamber (Memmert, IPP 750 Plus), regulated at the set experimental temperature ± 0.1 °C.
It should be noted that the collection of 600 μL from the microfluidic platform was the main data point acquisition time's limiting factor. Such a large volume was indeed required to perform off-line characterization. In future implementations, this data point experimental time should be reduced to whichever is the limiting factor: (i) the time required to acquire an on-line XRF spectrum, once XRF is integrated to the platform; or (ii) the time to reach a steady state when using very slow flow rates. This will be the case in the next generation of our platform. Other groups have already integrated an online ICP-MS, but with the issue that it only measures the aqueous channel which further often requires a dilution before performing the measurement.40
It should be noted that a blank experiment, in which only pure oil was used – i.e. without extracting molecules – was performed and showed that no metals were extracted from the aqueous phase. Such a loss of metals can sometimes be observed due to their adsorption onto channels’ surfaces. This is usually avoided as long as the thicknesses of the microfluidic channels are more than 0.05 mm. Here, we used channels with a rectangular cross-section of 0.4 mm in width and 0.2 mm in depth and with a contact section 171 mm long. Hence we did not need to correct data for absorbed cations in the porous membrane or elsewhere.
It should be noted that in some cases, organic phase samples obtained at the organic channel output were decanted in both extractant-poor and extractant-rich phases. The latter viscous phase is often referred to as a Winsor III instability phase, which is at the origin of the so-called “Third phase” occurring in hydrometallurgy processes involving a dense and viscous phase, expelling a lighter and fluid organic phase. This phase separation was not observed by the naked eye within the organic channel of the device during the extraction process. Due to its increased density, it also leads to a reduced volume of the collected organic sample, i.e. less than 600 μL. After settling, the two organic phases were separated and recovered by decantation to measure their respective ion concentrations by XRF.
Batch extractions
Batch extractions were performed in parallel to microfluidic extractions to use them for additional comparison and further validation. These batch samples were prepared using identical compositions to the initial solutions (fifteen aqueous batch samples to be brought into contact with fifteen organic batch samples) as previously described in detail:34 typically, we used a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio between the aqueous and the organic phases – the volume of each phase being 2.5 mL. The contact time of the two phases within a test tube was set to 1 h, using permanent mechanical shaking, to maintain a good emulsification, at room temperature. In the case of low acidity, extraction kinetics is slower. In order to achieve equilibrium, additional batch extractions were performed for contact times of 120, 180 and 480 min.
1 volume ratio between the aqueous and the organic phases – the volume of each phase being 2.5 mL. The contact time of the two phases within a test tube was set to 1 h, using permanent mechanical shaking, to maintain a good emulsification, at room temperature. In the case of low acidity, extraction kinetics is slower. In order to achieve equilibrium, additional batch extractions were performed for contact times of 120, 180 and 480 min.
Then, in all cases, the two phases were separated by centrifugation (8000 rpm for 30 minutes) and recovered separately by decantation. The results were compared to those of microfluidic extraction having a one hour contact time. All experiments were carried out at room temperature (25 ± 1 °C) or, when other temperatures were studied, in a temperature controlled closed chamber (Memmert, IPP 750 Plus).
XRF
The commercial XRF spectrometer used to analyse both aqueous and organic phases after extraction is a SPECTRO XEPOS (AMETEK) model. It is commercially equipped with an energy dispersive X-ray analyser (ED-XRF) that used the energy loss of the X photon in a silicon material to determine the spectrum by a suitable signal processing. Secondary targets reduce background noise compared to the output signal from the tube and improve fluorescence detection. Liquid samples were placed in 6 mm diameter cups, the bases of which consisted of a 4 μm thick prolene film. The XRF spectrometer was used to analyse a series of eleven cups in sequence, using a rotating carousel that positions the sample to be measured above the inverted optical part. A volume of 100 μL of each of the samples was placed in the micro-cups for analysis for a duration of 40 minutes. The X-ray tube generator was set at 40 kV and an intensity of 0.160 mA. The Zirconium secondary target was monitored between 15 and 17 keV to visualize the fluorescence of all lanthanides and iron: between 4 keV and 10 keV.ICP-OES
Rare earth extraction was also analysed by ICP-OES: aqueous solution ion concentrations were measured before and after extraction. The commercial tool used for this study is a SPECTRO ARCOS ICP-OES, which is equipped with a circular detector consisting of 32 linearly aligned CCDs, each having a resolution of 3648 pixels covering wavelengths ranging from 130 to 770 nm. The resolution of the detector is 8.5 pm from 130–340 nm and 15 pm from 340–770 nm with an intensity dynamic range of eight orders of magnitude. CCDs were read out simultaneously and a complete spectrum was generated in under two seconds. The circular polychromator (Paschen-Runge design, optical components: MgF2, Zerodur structure) has a focal distance of 750 mm. The radio frequency generator works at a frequency of 27.12 MHz and has a power output of 0.7 to 1.7 kW with an efficiency of 70% and a stability of 0.1%.A typical sample analysis was carried out as follows: the sample was diluted to an appropriate concentration ranging between 5 and 15 mg L−1 using 2% HNO3 in water. Before each run a calibration was performed with metal standards made from a calibrated solution (1000 mg L−1) which was diluted to obtain standards at 0, 1, 5 and 15 mg L−1. Each sample was measured three times for statistical reasons and after each measurement, the system was purged with 2% HNO3.
Results and discussion
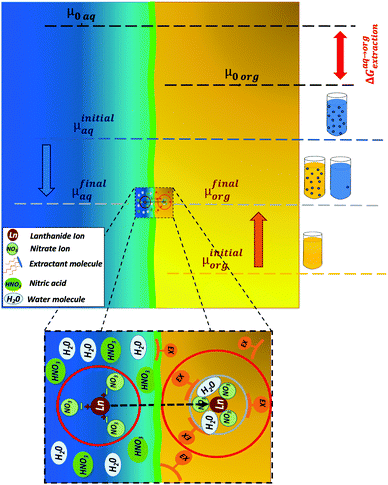
Currently, there are seventeen categories identified strategically for formulating efficient complex fluids for liquid–liquid extraction.15,35,41 The vast majority of these efficient formulations combine a solvating extractant and an ionic exchanger extractant that can modify the overall reaction mechanism and lead to either a synergic or an antagonist effect.35,42–45 Synergy – for which no predictive theory exists yet – is strongly affected by various parameters such as aqueous phase acidity and amounts of extractants as well as temperature.43 Most of these effective processes rely on combining two extractants and an optimized “diluent” with the so-called modifiers.10,11,46–49 To optimize a process, both “yield”, expressed in mass extracted by unit of time, and “selectivity” in differentiating “target” from “non-target” elements are considered.50 In the absence of general predictive theory for the selectivity of multi-component complex fluids,34,43,51 optimization requires very lengthy experimental plans.Anyhow, selectivity can be understood by comparing the “double differences” of free energies of transfer between the water and the oil phases (ΔΔG0R) for the two elements considered.16 The methodology is illustrated in Fig. 3, it gives an overview of how an extraction process can be coupled with thermodynamic driving forces. On the left side, the Gibbs free energy of transfer between the water and oil phase is calculated using the ienaics approach: from the difference between the reference chemical potentials of each phase (eqn (2))-since the reference chemical potential reflects the intrinsic affinity of the solute towards the aqueous or oil phase-. In Fig. 3, the reference chemical potential of a solute in the initial aqueous phase μinitialAq (blue bar) is higher than the reference chemical potential of a solute in the final organic phase after contact μfinalOrg (grey bar). Thus, it is transferred into the organic phase, as it is thermodynamically favourable (see ref. 16 for further details on the ienaics approach). At the input of the microfluidic device, ions have an initial state which is represented by an initial chemical potential in each phase, i.e. μinitialAq and μinitialOrg, during the transfer, the ion will reach thermodynamic equilibrium and will have the same chemical potential in both phases at the output of the liquid–liquid extraction microfluidic zone (eqn (1)).
The chemical potential can then be split into the reference chemical potential in the designated phase and a second term related to the activity. Such a rearrangement of eqn (1) leads to an expression of the free energy of transfer, ΔG0R (eqn (2)), in which, assuming ideal behaviour (i.e. no interactions of the solute molecules between each other), the activity can be reduced to the solute's concentration. Thus, the free energy of transfer can be expressed using only the ratio of the considered ion's concentration in each individual phase (eqn (3)–(5)).
| μfinalAq = μfinalOrg | (1) |
This explains the final aim of this microfluidic investigation: to explore the phase diagram of a synergic extraction system with regard to its ion free energies of transfer from the water to the oil phase, and thus as fast as the kinetics of the extraction allows (typically from a few minutes to a few hours in worse cases).
Also, since our microfluidic chip allows precise control of solution contact times, it therefore also enables studying transient states and establishing extraction time dependence.
Studying such transient behaviours, at constant total molarity of the extractant, allows identifying asymptotic values, thereby characterizing the thermodynamic equilibrium and thus for various acid concentrations, temperatures and molar fractions. It therefore allows determining the Gibbs free energy of transfer.
| ΔG0R (J mole−1) = μ0,Aq − μ0,Org | (2) |
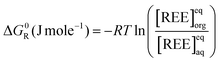 | (3) |
For the sake of clarity, it should be noted that the reaction Gibbs energy of the transfer ΔG0R standard state is defined for a solvent containing all the species but the rare earth nitrate salt. It is therefore the free energy per mole of the transferred species and not the raw difference of a given sample versus a reference state, as classically noted μ0 or ΔG0 in thermochemistry. There is no assumption considering a dominant supramolecular extraction equilibrium that would take into account all other species present in the solution. The ratio of extracted to remaining species defines the reference free energy linked to the advancement of the reaction. Here, all other species than the one considered are considered part of the solvent and participate in defining the reference state, as explained previously.
One particular interest of this work is that we performed chemical analysis of both fluids coming out of the liquid–liquid extraction device, in order to improve the measurement of the free energy of transfer (see ESI,† 1.4). Indeed, when [REE]org is well below the standard error of the measurement of [REE]aq, measuring only [REE]aq can lead to significant measurement errors of [REE]org, and hence of both the [REE]org/[REE]aq ratio and Gibbs free energies of transfer (see ESI,† 1.4). Ion concentrations are measured by X-ray fluorescence.
The latter approach differs from most reports available in the literature that focus on mass balances for which some lack of precision in the measurement of the aqueous residual concentrations of ions left after extraction is acceptable (since efficiency >90%). In such case, the “remaining” species in the aqueous phase are highly diluted and hence difficult to accurately measure to enable a precise calculation of the ion concentration in the organic phase. To precisely quantify the ion concentration of the organic phase, another chemical preparation, such as back extraction, is usually performed prior to capillary chromatography in an aqueous medium and quantification via inductively coupled plasma (ICP).
To avoid this and enable accurate measurement of the ratio between extracted and non-extracted ions, an absolute method working for both phases is then needed, such as X-ray fluorescence (XRF).52 See ESI,† 1.4 for more details on how the calculation of the free energies of transfer from the concentrations of the two phases allows reducing the errors of measurements by comparing the method used in this study to the classical one, i.e. measuring aqueous concentrations only.
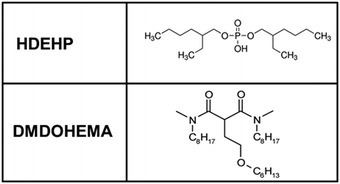
In this study, the synergic extraction system investigated is composed of the solvating extractant DMDOHEMA and the cation exchanger HDEHP (Fig. 4). We selected these as they form a well-studied synergic system based on DMDOHEMA, the latter being known to be efficient to extract lanthanides with high actinide/lanthanide selectivity. More generally DMDOHEMA is a good example of diamine extractants which are known to show high actinide/lanthanide selectivity. This is a crucial property required when long-lived and short-lived radioactive species coexist in large quantities, such as in closed nuclear cycle that is associated with any fourth generation nuclear plant. Furthermore the viscosity of solutions containing typically 30% of DMDOHEMA in a solvent is acceptable for process design.53,54 Moreover, modern predictive approaches exist: (i) to calculate the viscosities observed when solutions are loaded with uranium;55,56 (ii) to derive the critical micellar concentration (cmc) of extractants in different solvents, not only alkanes and solvo-surfactants, but also ionic liquids (such as COSMO-RS).57
Overall, our study allows determining the influence of (i) the molar fraction, XDMDOHEMA, of the solvating extractant (eqn (4)); (ii) the acidity and; (iii) the temperature, on the kinetics, efficiencies and selectivities of the extraction.
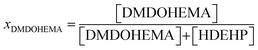 | (4) |
In this article, the efficiency is defined as a distribution ratio expressed in standard free energy difference:58
ΔG0R (J mole−1) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KD) ln(KD) | (5) |
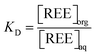 | (6) |
Note that iron is ten times more concentrated than the rare earths, in order to be representative of typical conditions for recycling of wind-mill magnets.59 It is an active field of research due to the very large amount of expensive rare earths (neodymium and dysprosium, for example) that can be recycled from them.60,61 However, due to (i) overlap of X-ray fluorescence peaks and; (ii) the very low, or very slow, extraction of iron, extracted iron concentrations were too small to be measured either by ICP or XRF. Therefore, one cannot calculate the selectivity of the five lanthanides versus iron.
Comparison of microfluidic versus macroscopic liquid–liquid extraction approaches
Various microfluidic approaches to carry out liquid–liquid extraction have already been proposed, each with advantages and disadvantages, which have already been critically reviewed.25,26 To summarize, the main advantages of microfluidic over the batch approach are that most microfluidic platforms enable: (i) a good control and possible variation of the contact time between the two phases (by control of the flow); (ii) a known effective surface of contact. Hence, it enables the quantification of extraction kinetics and interfacial mass transfer rate constants, otherwise fairly difficult to quantify. More specifically, advantages of the microfluidic platform used in this article are: (i) a large range of contact time can be investigated (which is not the case when the two phases are directly brought into contact in a co-flow microchannel);27,31,62,63 (ii) the assembly of the cell and technology required are simple and do not need complex handling/building procedures or expansive process controls such as what is required when using alternating phase droplets.22 Hence, it should be noted that our simple design and assembly method, using only four screws to hold in place and squeeze the membrane, proved to be very efficient and therefore economical as it enabled us to perform all seventy-five microfluidic extraction experiments, including fifteen membrane exchanges, without any disabling leaking issue. This saves a considerable amount of time and effort when compared to the non-reversible method of assembly such as gluing or thermal bonding. Importantly, we recently reported that the use of a thin membrane to separate the two phases, such as the one used here, is not a limiting factor, hence it does not modify extraction kinetics.33To compare our microfluidic extraction results with those of standard approaches, we measured extraction efficiencies for various molar fractions of microfluidic extraction experiments and systematically reproduced these using the macroscopic standard so-called “batch method” in flasks.
From ICP-OES or XRF ion concentration measurements of samples obtained from both organic and aqueous phases using our microfluidic procedure, one can calculate an extraction percentage for each measured data point. The extraction percentage, %E (eqn (7)), also called the recovery factor, is defined, for any given ion, as the ratio of its concentrations, at equilibrium, in the organic phase [REE]Outorg to its concentration in the input aqueous solution [REE]Inaq:
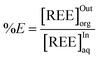 | (7) |
Examples of extraction percentages for all studied ions, obtained for various contact times and at 0.03 M in nitric acid, are calculated, plotted and presented in Fig. 5. Additional results for other acidities (0.3 and 3 M in HNO3) can be found in the ESI,† 1.3. At such acidic concentrations, pH values are well below 3 where lanthanides and iron ions are trivalent.
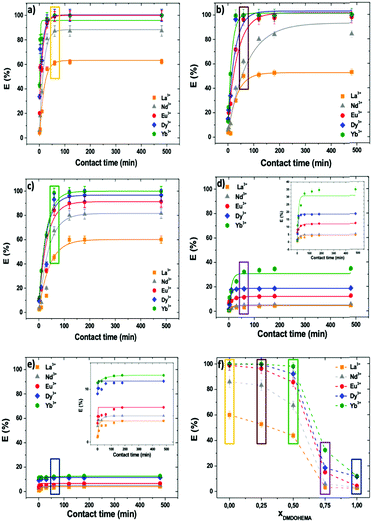 | ||
| Fig. 5 Extraction percentage versus time obtained in microfluidics, with [HNO3] = 0.03 M, T = 25 °C, for different lanthanides (La3+, Nd3+, Eu3+, Dy3+, and Yb3+) and molar fractions, xDMDOHEMA = 0 (a), 0.25 (b), 0.5 (c), 0.75 (d), and 1 (e). (f) Extraction percentages obtained using the batch method (1 h). Comparing the contents of same colour rectangles in graphs (a–e) with the ones in (f) allows visual assessment of reproducibility of microfluidic extraction versus batch extraction measurements (for quantitative data comparisons, see Table 1). | ||
Comparison of the results of microfluidic and batch methods was made for a contact time of 1 h. Microfluidic extraction percentages at extraction time identical to standard batch extractions (1 h) are highlighted in coloured boxes in Fig. 5(a)–(e). They can be compared to values obtained using the standard batch method and are given in Fig. 5(f). Quantitatively, the data set acquired using both our microfluidic device and in batch samples for all cations present in the solution coincide within experimental uncertainty of the analysis and the difference between the two methods is never more than 8% (see Table 1). For example, for Ytterbium, this represents at most 0.5 kT (= 1.2 kJ mole−1) in free energy of transfer.22
| x DMDOHEMA | La | Nd | Eu | Dy | Yb |
|---|---|---|---|---|---|
| 0.00 | 0.0109 | 0.0116 | 0.0008 | 0.0000 | 0.0000 |
| 0.25 | 0.0270 | 0.0131 | 0.0002 | 0.0003 | 0.0001 |
| 0.50 | 0.0153 | 0.0016 | 0.0151 | 0.0091 | 0.0036 |
| 0.75 | 0.0002 | 0.0094 | 0.0369 | 0.0025 | 0.0028 |
| 1.00 | 0.0063 | 0.0162 | 0.0111 | 0.0057 | 0.0024 |
| Ion | La3+ | Nd3+ | Eu3+ | Dy3+ | Yb3+ |
|---|---|---|---|---|---|
| Entropy coefficient (A) | 7.1 | 6.2 | 6.3 | 5.5 | 1.5 |
Study of the parameters influencing the extraction properties
Such an influence of the pH on extraction kinetics has previously been explained as being linked to the ion exchange mechanism: at low pH, the concentration of H+ in extractant aggregates's polar cores is high which facilitates cation exchange.20 Although observed curves can show some irregularities, which are likely to be attributed to measurment artefacts, it should be noted that the difference in kinetics for the considered ions could be exploited to enhance selectivity by using a contact time that maximises it (instead of working at thermodynamic equilibrium): for example in the absence of DMDOHEMA, fast extraction allows targetting of heavy rare earths. Such an observation cannot be obtained using the standard batch approach in the case of fast kinetics. From these, new process protocols of separation and purification could be derived that would work away for the thermodynamic equilibrium.
Furthermore, in order to go beyond a qualitative analysis and enable a more quantitative analysis of the influence of the nitric acid concentration on lanthanide extraction with the HDEHP and DMDOHEMA mixed system, free energies of transfer of lanthanides are measured at various nitric acid concentrations from 0.03 M to 3 M in the Isane diluent. Extractions were carried out using the same model aqueous phase and with 0.9 M of the total extractant concentration. The results will be discussed and linked to the behaviour of the extractant molecules and the electrolyte composition.
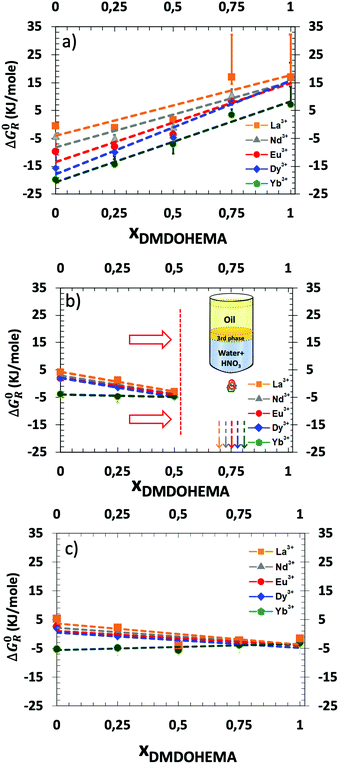
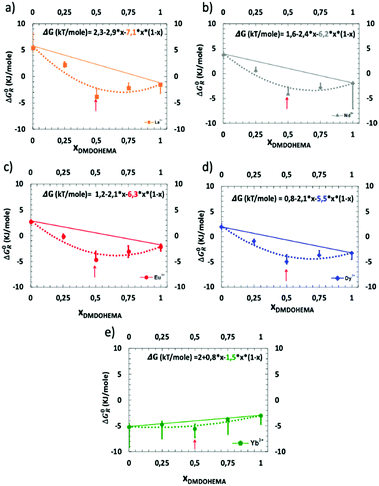
Hence, Fig. 6 represents the standard-state Gibbs free energy of transfer ΔG0R (eqn (5)) as a function of the molar fraction of DMDOHEMA and for three different nitric acid concentrations. For each lanthanide and in the absence of the solvating extractant DMDOHEMA (xDMDOHEMA = 0), one can observe that 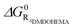 value increase significantly when changing [HNO3] from 0.03 (Fig. S3 in the ESI† and Fig. 6(a)) to 0.3 M (Fig. 6(b)). Less variations are observed when increasing [HNO3] further (Fig. 6(c)). According to eqn (3), this therefore indicates that [REE]org/[REE]aq decreases when acidity increases, and thus that the extraction efficiency of lanthanides decreases with the increased acidity and becomes maximum at [HNO3] = 0.03 M.
value increase significantly when changing [HNO3] from 0.03 (Fig. S3 in the ESI† and Fig. 6(a)) to 0.3 M (Fig. 6(b)). Less variations are observed when increasing [HNO3] further (Fig. 6(c)). According to eqn (3), this therefore indicates that [REE]org/[REE]aq decreases when acidity increases, and thus that the extraction efficiency of lanthanides decreases with the increased acidity and becomes maximum at [HNO3] = 0.03 M.
This has previously been explained as coming from the competition between the transfer of H+ from the solvent to aqueous phase and the extraction of lanthanides.64 More generally, it is often observed when using a cationic exchanger system.65–67
The general evolution of the Gibbs free energy ΔG0R as a function of the molar fractions however differs for each of the three acid concentrations studied. We discuss this behaviour in more detail hereafter.
The two to three-phases transition can be understood as a Winsor II to Winsor III equilibrium. Winsor II is the coexistence of two fluid phases: a water-poor microemulsion in an oil-continuous medium coexisting with an aqueous phase in excess.72 Winsor III is a three-phases equilibrium. The Winsor-II equilibrium enables standard liquid–liquid extraction processes while entering the Winsor-III domain is the root cause of the so called “third-phase” accident, stopping plants for very long times since all reservoirs must be cleaned. Transition from Winsor II to Winsor III in a liquid–liquid extraction process is due to attraction and coalescence between molecular aggregates producing the splitting of the organic phase into two phases, an extractant-rich and an extractant-poor one, respectively. The latter dilute organic phase has its extractant concentration below the cmc, so all aggregates decompose into monomers.73 Most Winsor III studied in the literature have been obtained using equal volumes of water and solvent, but they also coexist at low water proportion, even for water volume fractions of less than 10%.74,75 Comparing Fig. 7(a)–(c), it was found that a Winsor III regime is only observed at intermediate pH, namely [HNO3] = 0.3 M. Erlinger et al.71 have already studied similar systems and explained that at low acidity there is not enough extracted species to induce such a phase transition by van der Waals forces whereas at high acidity, the coalescence due to interfacial film bending is not strong enough. In classical microemulsions, these are called liquid–liquid phase separation and emulsification failure, respectively.76,77
As recently detailed by Spadina et al., the free energy of transfer can be expressed as the sum of different terms: (i) complexation term; (ii) bulk term which represents the reduction of the accessible volume solute confinement in cores of aggregates; and (iii) other electrostatic terms.79 This is also valid in the case of mixed micelles with two extracting molecules.79 In this latter case, according to Spadina et al., the sum of the entropic part of these three terms seems to be dominant which enhanced synergy extraction due to the increase of configurational entropy for extracted ions.
The configurational mixing entropy inside the aggregate formed by the extractant in the first and second coordination spheres80 can be expressed as follows:78,81–83
| ΔS = A·k·T·x(1 − x) | (8) |
Such excess in configuration entropy can be associated with the many possible arrangements of the ion in the polar core of the aggregate, which is intrinsically included in molecular dynamics, but neglected in quantum chemistry (second coordination sphere).79 Hence, since in that case (i) synergy is reported to be mostly due to configurational entropy and not to a specific unique stoichiometry of defined complexes as used in the parametric model;30 and (ii) we assume that the main contribution to entropy is from the extractant present in the aggregate and not from co-extracted nitric acid or water, then we can evaluate the configuration excess mixing entropy according to:34,78
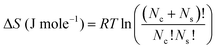 | (9) |
Considering (i) the expression of the extractant entropy given in eqn (9) and (ii) the hypothesis that aggregates are made of about ten interacting molecules of both solvating extractants (Ns) and charged surfactants (Nc): Ns + Nc = 10, one can tabulate the entropy as a function of the number of charged surfactants per aggregate (Table 3). N.B. we assumed that number since, according to ref. 84, most efficient extraction systems have local water in the oil cylindrical microstructure, with both the typical cylinder diameter and length per extracted ion in the order of one nanometre. From this, the number of complexing molecules in the first and second coordination positions can easily be calculated to be between eight and ten. From Table 3, expected values for the entropy should be between 2 and 5 and furthermore, one can also observe that it is maximum for Nc = 5, similar to the experimentally determined synergy which is also maximum for a molar ratio of 0.5.
| N c | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| ΔScalc | 2.3 | 3.8 | 4.78 | 5.34 | 5.6 | 5.3 | 4.78 |
Since entropy experimental values, listed in Table 2 (ranging between 1.5 and 7 for Ytterbium and Lanthanum, respectively), and the calculated ones are of a similar order of magnitude, this is coherent with the fact that surface excess mixing entropy is the dominant term responsible for the synergy effect.79 Further mechanism studies of surface mixing entropy are however yet required to explain the variability of synergy versus ionic radius of the lanthanides.
The results presented and fitted in Fig. 7 and discussed above demonstrate also the interest of precise measurement of ΔG0R as a function of the molar fraction. Indeed, we just showed that it enables the estimation of the extracting aggregates’ composition for which a drastic enhancement of separation efficiency is observed. Indeed, in the case of Dysprosium (Fig. 7(d)), at a molar fraction of 0.5, one can measure a Synergic Gibbs free energy variation, written ΔΔG0R, which is the difference between the experimental Gibbs free energy measured with the one calculated from linear interpolation at x = 0.5, see Fig. 7. In the latter case, ΔΔG0R is equal to 4. This means that the extraction efficiency is improved by almost two orders of magnitude (×50).
Effect of temperature
The Gibbs free energies of transfer for the five lanthanides were determined for three different temperatures ranging from 15 °C to 35 °C, with [HNO3] = 3 mol L−1, a DMDOHEMA's molar fraction of 0.5 and a total amount of extractants of 0.9 M. The plotted results are presented in Fig. 8 and precise values for each data point are given in the ESI.† The increasing of the free energy of transfer with the temperature indicates an exothermic nature of the extraction process (Fig. 8).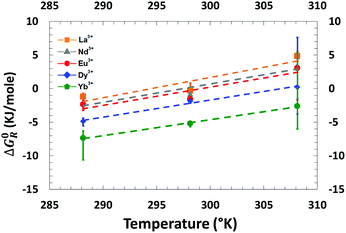 | ||
| Fig. 8 Evolution of the free energy of transfer as a function of the temperature for the five lanthanides and for a total extractant concentration of 0.9 M (50% DMDOHEMA) in Isane. | ||
According to the literature, all lanthanide extractions by amides or mixed extractants are enthalpy driven,51,85,86 with yet unpredictable effects of solvent branching or monomer isomerisation.87 In classical thermodynamics and when considering the extraction process as a whole, the standard van’t Hoff derivation used for simple fluids can be used only when (i) all aggregation effects are negligible and (ii) enthalpy itself has no temperature dependence. With these two restrictions, all entropy variations can be calculated from the derivatives of the free energy with respect to the temperature. It should be noted that this van’t Hoff approach is only valid for ideal fluids, it is not numerically correct and no more valid when aggregation or electrostatic effects are more than 2–5 kJ mole−1. If we suppose that configurational mixing entropy of the extraction is much larger than other contributions such as complexation entropy, then we can be discussed in a classical thermodynamics framework. Considering the linear dependence of the Gibbs free energies of transfer of lanthanides versus temperature (eqn (10)), the plot of ΔG0R as a function of temperature leads to a straight line from which: (i) the entropy of complexation (ΔS0) can be measured directly as its slope and; (ii) the enthalpy of complexation (ΔH0) is equal to the intercept values.
| ΔG0 = ΔH0 − TΔS0 | (10) |
Negative values measured for ΔH indicate the exothermic nature of the extraction process. Furthermore, one can observe that all slopes are positive (measured ΔS0 are given in Table 4). Since strong slopes are indicative of strong entropic contributions to the extraction process (Fig. 8 and Table 4), this is coherent with extraction efficiency maximum at the lowest temperature values accessible experimentally.
| Ion | La3+ | Nd3+ | Eu3+ | Dy3+ | Yb3+ |
|---|---|---|---|---|---|
| ΔS0measured (J mol−1) | −302 | −274 | −271 | −254 | −237 |
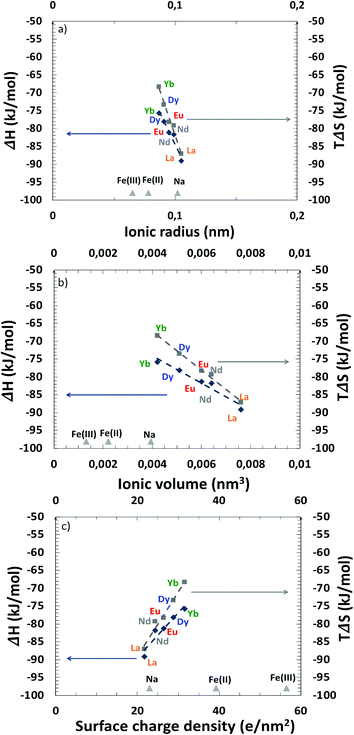
As said before, one must however be careful when using this approach88 as it only applies when the solvent's structuration is independent of the temperature. Nevertheless, it allowed us to determine quantitatively the averaged thermodynamic parameters. All measured averaged thermodynamic parameters ΔS0 and ΔH0 for extraction are given in the ESI† and are plotted in Fig. 9versus various characteristics of the considered REEs.
From these measured values and for all lanthanides tested here, it has been found that REE extractions are mainly driven by strong enthalpies of complexation, although they are also associated with negative entropy terms, which favours the initial state in water. A higher exothermic enthalpy value (−ΔH0) for lanthanum suggests its stronger binding with the mixed system compared to dysprosium for example. The negative entropy change (ΔS0) may be associated with a loss of translation and rotation entropy of the mixed extractant system during complexation in the volume of the extracted species.
The Yb(III) – DMDOHEMA/HDEHP complex seems to be more favourable than the La(III) – DMDOHEMA/HDEHP one, since −ΔG0 for ytterbium is larger than that for lanthanum.
If we compare behaviours within the lanthanide family, three quantities are typically discussed regarding the origin of selectivity:89 ionic radius (Fig. 9(a)), ionic volume (Fig. 9(b)) and surface charge density (Fig. 9(c)). All plots are linear for enthalpy and entropy so the dominant mechanism cannot be directly determined from these plots. The effect of surface charge density shown in Fig. 9(c) leads to larger extraction of lanthanides versus iron. Since the charge effect seems to be little, this indicates that non-electrostatic complexation is dominant but it is not the only important effect, since complexation also follows Pearson's HSAB principle.90–93
In any case, one of the core properties of the ieanics approach is that the speciation of the different complexes in the water phase is not needed in order to interpret the free energy of transfer of the solute. Moreover, the ieanics approach does not suppose any “dominant” reaction: it considers the energy of transfer in the presence of a large number of coexisting polydisperse W/O aggregates. There are therefore hundreds of competing equilibria between weak aggregates and there is no reason to presuppose the existence of a single stoichiometric “reaction mechanism” similar to monodisperse “complexes” that sometimes co-crystallize with water and salts.33,64,71
Additional findings
A microfluidic set-up was designed for the study of phase diagrams in the Winsor II regime allowing efficient extraction and stripping. Surprisingly, our results indicate that the Winsor III16,71,94,95 regime could also be obtained, although in the collecting tube of the solvent phase. This liquid–liquid instability of the solvent phase occurs therefore spontaneously and without the need of mixing and emulsification. The top phase is nearly pure solvent and contains only extractant monomers. The latter coexists with the third phase. Even without gentle centrifugation, it was possible to take a sample for analysis with a syringe. Due to the unique dynamic range of XRF, and the absence of need for further preparation, the concentration of both the diluted phase and the concentrated optically birefringent mesophase could be obtained. It should be noted that the phase separation was not visible by the naked eye in the channels of the microfluidic device. Its occurrence was also cross-checked with the batch method where, after extraction, the extractant-rich and extractant-poor phases could be collected separately and our XRF analysis protocol used. Hence, in this regime, the free energy of transfer could even be obtained in the dilute phase, for the first time to the best of our knowledge.Fig. 6(b) illustrates the case where the acid concentration is equal to 0.3 M but for molar fractions of DMDOHEMA strictly greater than 0.5 and where a concentrated “third phase” is formed which coexists with a diluted organic solution as a Winsor III equilibrium.14,71,96Fig. 10 shows the observed free energies of transfer in the dilute phase (light yellow), which range between ∼−0.5 and −1.5 kJ mole−1. Regarding the third phase (orange), made of interconnected polar cylinders,84 Gibbs free energy is too strong to be measured with ion concentrations in the organic phase that are too low to be measured (hence free energies of transfer values diverge, which we represented with arrows pointing down going all the way).
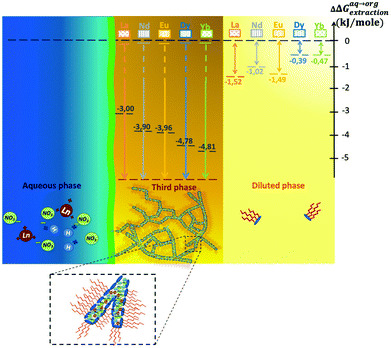 | ||
| Fig. 10 Relation between the driving force for extraction observed in three different cases: bold black dashed levels represent the best measured extraction efficiencies (see eqn (5)) in the Winsor II equilibria situated at the limit of the phase ([HNO3] = 0.3 M, xDMDOHEMA = 0.25); for the third condensed phase made from interconnected polar cylinders, the chemical potential step is too large to be measured (hence the infinite arrows); in the dilute phase, free energy steps are small but measurable (coloured dotted lines). | ||
We assembled graphically the main findings of this work in a schematic form in Fig. 10, including free energies of transfer of the Winsor III dilute phase. Ion exchanges occur between aqueous (in blue) and solvent-rich phases (orange and light yellow). Kinetic barrier and asymmetry in the transfer rate are due to the thin interfacial domain, also called the interphase,23 which is schematized as a green line.97,98 Again, in the dilute phase, complexation versus entropy balance results in low but measurable energy of transfer.81,82 Moreover, as previously reported,35 the domain where extraction is most efficient and optimum for liquid–liquid formulation in industrial plant feed is close to the third phase appearance point.
Conclusions
In this report, after presenting a simple although versatile microfluidic assembly enabling the study of liquid–liquid extraction, we then report its use for the study of a synergetic extracting system hereby enabling:(i) The acquisition of kinetics data, otherwise difficult to obtain using the standard batch method or other more complex microfluidic systems.
(ii) To study the influence of acid concentrations, molar fractions and temperature, thus giving access to pieces of information on the stoichiometry of the aggregates forming in organic solvents.
(iii) To prove the interest of measuring the concentrations in both aqueous and organic phases by a constrained fit which increases result's precision down to 2 kJ mole−1 (1 kT molecule−1) (see the ESI† 1.4).
(iv) A simultaneous study of multiple chemical element solution and therefore of realistic models or real lixiviates. Do note that measured ion specifics' kinetics can enable new separation processes that cannot otherwise be performed at equilibrium.
(v) To greatly reduce the amount of chemicals used for such a study (only 10.86 g of DMDOHEMA, 7.25 g of HDEHP and 73 mL of Isane/water were used in total here. This could further be reduced by about one order of magnitude with on-line XRF).
Finally, it appears that this device is also adapted in the case when the solvent channels are the locus of a phase separation. Thus this device could also be used for the collection and study of the Winsor III equilibria. Although, if in the classical extraction regime (Winsor II), we have shown in a previous paper that the chosen membrane is not a limiting factor,33 it has recently been evidenced that liquid–liquid and liquid–solid interfaces increase the domain of stability of the liquid crystals that constitute the “third phase”.23 Therefore, the results concerning experiments where a third phase may be present in the pores of the membrane will have to be considered with care and with some uncertainty regarding the exact composition of the final equilibrium state.
Once fully integrated with computer controlled mixing capability and online characterization methods such as hollow waveguide FTIR,24,99 XRF,32 and ultimately small angle X-ray scattering, we anticipate that phase diagram exploration can be fully automatized, with very little down time. It would furthermore also give access to kinetics information and interfacial mass transfer rate constants, otherwise difficult to obtain. Ultimately, a two stage system would allow studying simultaneously both extraction and back-extraction, as well as the recycling of the organic extractant. Hence such tools should accelerate the study of liquid–liquid extraction processes, a key factor to enable the recycling of highly variable waste stream lixiviates.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
All the authors would like firstly to pay their gratitude to Helmuth Möhwald, who passed away in March 2018, for helpful scientific discussions and counselling, and secondly to thank Sandrine Dourdain, Béatrice Baus-Lagarde, Jean-François Dufrêche and Stéphane Pellet-Rostaing (CEA/DRF/ICSM) for help in AEM and CP's initial training in batch extraction, XRF, ICP-OES and consortium meeting discussions. AEM, JT, CP and JCG would like to thank Frédéric Né, Nicolas Verplanck, François Boizot and Manuel Alessio at CEA/DRT/LETI for help with microfluidics manufacturing, as well as final year intern Gabriel Bernard for incremental improvement of the microfluidic platform (design & implementation of the counter pressure control, and syringe pump modification) and preliminary extraction testing. CP thanks D. Kirsanov for helpful exchange on XRF data treatment. All experimental research leading to these results was performed at CEA and received funding from the European Research Council under the European Union's 7th Framework Program (FP/2007–2013)/ERC Grant Agreement No. [320915] “REE-CYCLE”: Rare Earth Element reCYCling with Low harmful Emissions. JCG acknowledge financial support, while at NTU where this article's writing effort took place, from SCARCE, which is supported by the National Research Foundation, Prime Minister's Office, Singapore, the Ministry of National Development, Singapore, and National Environment Agency, Ministry of the Environment and Water Resource, Singapore under the Closing the Waste Loop R&D Initiative as part of the Urban Solutions & Sustainability – Integration Fund (Award No. USS-IF-2018-4).Notes and references
- Z. Sun, H. Cao, Y. Xiao, J. Sietsma, W. Jin, H. Agterhuis and Y. Yang, ACS Sustainable Chem. Eng., 2017, 5, 21–40 CrossRef CAS.
- S. Gloser, L. T. Espinoza, C. Gandenberger and M. Faulstich, Resour. Policy, 2015, 44, 35–46 CrossRef.
- T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493 CrossRef CAS PubMed.
- J. Lucas, P. Lucas, T. Le Mercier, A. Rollat, W. Davenport, J. Lucas, P. Lucas, T. LeMercier, A. Rollat and W. Davenport, Rare Earth Production, Use and Price, 2015 Search PubMed.
- C. Tunsu, M. Petranikova, M. Gergoric, C. Ekberg and T. Retegan, Hydrometallurgy, 2015, 156, 239–258 CrossRef CAS.
- W. J. Albery and R. A. Choudhery, J. Phys. Chem., 1988, 92, 1142–1151 CrossRef CAS.
- N. Urasaki and C. P. Wong, Separation of low molecular siloxanes for electronic application by liquid–liquid extraction, IEEE, 1999 Search PubMed.
- K. Binnemans, P. T. Jones, B. Blanpain, T. Van Gerven, Y. Yang, A. Walton and M. Buchert, J. Cleaner Prod., 2013, 51, 1–22 CrossRef CAS.
- J. Lucas, P. Lucas, T. L. Mercier, A. Rollat and W. G. Davenport, Rare Earths, 1st edn, Elsevier, 2014 Search PubMed.
- H. S. Yoon, C. J. Kim, K. W. Chung, S. D. Kim, J. Y. Lee and J. R. Kumar, Hydrometallurgy, 2016, 165, 27–43 CrossRef CAS.
- A. M. Wilson, P. J. Bailey, P. A. Tasker, J. R. Turkington, R. A. Grant and J. B. Love, Chem. Soc. Rev., 2014, 43, 123–134 RSC.
- J. Veliscek-Carolan, J. Hazard. Mater., 2016, 318, 266–281 CrossRef CAS PubMed.
- H. F. Eicke and H. Christen, Helv. Chim. Acta, 1978, 61, 2258–2263 CrossRef CAS.
- C. Bauer, P. Bauduin, J. F. Dufreche, T. Zemb and O. Diat, Eur. Phys. J.: Spec. Top., 2012, 213, 225–241 CAS.
- G. Gompper and M. Schick, Phase transitions and critical phenomena, Self-assembling amphiphilic systems, Academic Press, London, 1994, vol. 16, pp. 1–181 Search PubMed.
- T. Zemb, C. Bauer, P. Bauduin, L. Belloni, C. Dejugnat, O. Diat, V. Dubois, J. F. Dufreche, S. Dourdain, M. Duvail, C. Larpent, F. Testard and S. Pellet-Rostaing, Colloid Polym. Sci., 2015, 293, 1–22 CrossRef CAS.
- R. J. Ellis, Y. Meridiano, J. Muller, L. Berthon, P. Guilbaud, N. Zorz, M. R. Antonio, T. Demars and T. Zemb, Chem. – Eur. J., 2014, 20, 12796–12807 CrossRef CAS PubMed.
- R. J. Ellis, Y. Meridiano, R. Chiarizia, L. Berthon, J. Muller, L. Couston and M. R. Antonio, Chem. – Eur. J., 2013, 19, 2663–2675 CrossRef CAS PubMed.
- B. F. Qiao, J. V. Muntean, M. O. de la Cruz and R. J. Ellis, Langmuir, 2017, 33, 6135–6142 CrossRef CAS PubMed.
- M. Špadina, K. Bohinc, T. Zemb and J.-F. Dufrêche, Langmuir, 2018, 34, 10434–10447 CrossRef PubMed.
- R. Motokawa, T. Kobayashi, H. Endo, J. J. Mu, C. D. Williams, A. J. Masters, M. R. Antonio, W. T. Heller and M. Nagao, ACS Cent. Sci., 2019, 5, 85–96 CrossRef CAS PubMed.
- K. P. Nichols, R. R. Pompano, L. Li, A. V. Gelis and R. F. Ismagilov, J. Am. Chem. Soc., 2011, 133, 15721–15729 CrossRef CAS PubMed.
- M. Corti, A. Raudino, L. Cantu’, J. Theisen, M. Pleines and T. Zemb, Langmuir, 2018, 34, 8154–8162 CrossRef CAS PubMed.
- V. Kokoric, J. Theisen, A. Wilk, C. Penisson, G. Bernard, B. Mizaikoff and J. C. P. Gabriel, Anal. Chem., 2018, 90, 4445–4451 CrossRef CAS PubMed.
- D. Ciceri, J. M. Perera and G. W. Stevens, J. Chem. Technol. Biotechnol., 2014, 89, 771–786 CrossRef CAS.
- C. Xu and T. L. Xie, Ind. Eng. Chem. Res., 2017, 56, 7593–7622 CrossRef CAS.
- G. Hellé, C. Mariet and G. Cote, Procedia Chem., 2012, 7, 679–684 CrossRef.
- D. Mark, S. Haeberle, G. Roth, F. von Stetten and R. Zengerle, Chem. Soc. Rev., 2010, 39, 1153–1182 RSC.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- M. Tokeshi and T. Kitamori, in Handbook of capillary and microchip electrophoresis and associated microtechniques, ed. J. P. Landers, Taylor & Francis, Boca Raton, 3rd edn, 2007, ch. 35, pp. 1021–1036, DOI:10.1201/9781420004953.
- F. Corne, A. Lelias, A. Magnaldo, C. Sorel, N. D. Raimondi and L. Prat, Chem. Eng. Technol., 2019, 42(10), 2223–2230 CrossRef CAS.
- C. Penisson, PhD thesis, Université de Grenoble Alpes, 2018.
- J. Theisen, C. Penisson, J. Rey, T. Zemb, J. Duhamet and J. C. P. Gabriel, J. Membr. Sci., 2019, 586, 318–325 CrossRef CAS.
- J. Rey, S. Dourdain, J.-F. Dufrêche, L. Berthon, J. M. Muller, S. Pellet-Rostaing and T. Zemb, Langmuir, 2016, 32, 13095–13105 CrossRef CAS PubMed.
- Solvent Extraction Principles and Practice, Revised and Expanded, ed. J. Rydberg, M. Cox, C. Musikas and G. R. Choppin, Marcel Dekker Inc., New York, 2004 Search PubMed.
- B. Abecassis, F. Testard, T. Zemb, L. Berthon and C. Madic, Langmuir, 2003, 19, 6638–6644 CrossRef CAS.
- L. Berthon, L. Martinet, F. Testard, C. Madic and T. Zemb, Solvent Extr. Ion Exch., 2007, 25, 545–576 CrossRef CAS.
- D. Kirsanov, V. Panchuk, M. Agafonova-Moroz, M. Khaydukova, A. Lumpov, V. Semenov and A. Legin, Analyst, 2014, 139, 4303–4309 RSC.
- D. Kirsanov, V. Panchuk, A. Goydenko, M. Khaydukova, V. Semenov and A. Legin, Spectrochim. Acta, Part B, 2015, 113, 126–131 CrossRef CAS.
- G. Helle, C. Mariet and G. Cote, Talanta, 2015, 139, 123–131 CrossRef CAS PubMed.
- H. F. Eicke, Topics in current chemistry, 1980, vol. 87, pp. 85–145 Search PubMed.
- J. M. Muller, C. Berthon, L. Couston, D. Guillaumont, R. J. Ellis, N. Zorz, J. P. Simonin and L. Berthon, Hydrometallurgy, 2017, 169, 542–551 CrossRef CAS.
- J. Rey, S. Atak, S. Dourdain, G. Arrachart, L. Berthon and S. Pellet-Rostaing, Solvent Extr. Ion Exch., 2017, 35, 321–331 CrossRef CAS.
- S. Dourdain, I. Hofmeister, O. Pecheur, J. F. Dufreche, R. Turgis, A. Leydier, J. Jestin, F. Testard, S. Pellet-Rostaing and T. Zemb, Langmuir, 2012, 28, 11319–11328 CrossRef CAS PubMed.
- J. Muller, PhD thesis, Université Pierre et Marie Curie, Paris VI, 2012.
- G. J. Lumetta, A. V. Gelis and G. F. Vandegrift, Solvent Extr. Ion Exch., 2010, 28, 287–312 CrossRef CAS.
- P. Bauduin, F. Testard and T. Zemb, J. Phys. Chem. B, 2008, 112, 12354–12360 CrossRef CAS PubMed.
- A. V. Gelis and G. J. Lumetta, Ind. Eng. Chem. Res., 2014, 53, 1624–1631 CrossRef CAS.
- M. K. Jha, A. Kumari, R. Panda, J. R. Kumar, K. Yoo and J. Y. Lee, Hydrometallurgy, 2016, 165, 2–26 CrossRef CAS.
- T. Zemb, M. Duvail and J. F. Dufreche, Isr. J. Chem., 2013, 53, 108–112 CrossRef CAS.
- J. Rey, M. Bley, J.-F. Dufrêche, S. Gourdin, S. Pellet-Rostaing, T. Zemb and S. Dourdain, Langmuir, 2017, 33, 13168–13179 CrossRef CAS PubMed.
- S. E. Mann, M. C. Ringo, G. Shea-McCarthy, J. Penner-Hahn and C. E. Evans, Anal. Chem., 2000, 72, 1754–1758 CrossRef CAS PubMed.
- M. Duvail, T. Dumas, A. Paquet, A. Coste, L. Berthon and P. Guilbaud, Phys. Chem. Chem. Phys., 2019, 21, 7894–7906 RSC.
- R. Malmbeck, D. Magnusson, S. Bourg, M. Carrott, A. Geist, X. Heres, M. Miguirditchian, G. Modolo, U. Mullich, C. Sorel, R. Taylor and A. Wilden, Radiochim. Acta, 2019, 107, 917–929 CAS.
- M. Pleines, W. Kunz, T. Zemb, D. Benczedi and W. Fieber, J. Colloid Interface Sci., 2019, 537, 682–693 CrossRef CAS PubMed.
- M. Pleines, W. Kunz and T. Zemb, J. Surfactants Deterg., 2019, 22, 1011–1021 CAS.
- M. Grabda, M. Panigrahi, S. Oleszek, D. Kozak, F. Eckert, E. Shibata and T. Nakamura, Fluid Phase Equilib., 2014, 383, 134–143 CrossRef CAS.
- B. Moeser and D. Horinek, Biophys. Chem., 2015, 196, 68–76 CrossRef CAS PubMed.
- T. Zemb and J.-C. P. Gabriel, Final Report Summary ERC 320915: REE-CYCLE, Rare Earth Element reCYCLing with Low harmful Emissions European Union, 2019.
- Y. X. Yang, A. Walton, R. Sheridan, K. Guth, R. Gauss, O. Gutfleisch, M. Buchert, B. M. Steenari, T. Van Gerven, P. T. Jones and K. Binnemans, J. Sustain. Metall., 2017, 3, 122–149 CrossRef.
- M. Panigrahi, M. Grabda, D. Kozak, A. Dorai, E. Shibata, J. Kawamura and T. Nakamura, Sep. Purif. Technol., 2016, 171, 263–269 CrossRef CAS.
- Y. Kikutani, K. Mawatari, A. Hibara and T. Kitamori, Microchim. Acta, 2008, 164, 241–247 CrossRef.
- X. Wang, C. Saridara and S. Mitra, Anal. Chim. Acta, 2005, 543, 92–98 CrossRef CAS.
- C. Dejugnat, S. Dourdain, V. Dubois, L. Berthon, S. Pellet-Rostaing, J. F. Dufreche and T. Zemb, Phys. Chem. Chem. Phys., 2014, 16, 7339–7349 RSC.
- A. E. Visser, R. P. Swatloski, S. T. Griffin, D. H. Hartman and R. D. Rogers, Sep. Sci. Technol., 2001, 36, 785–804 CrossRef CAS.
- A. Rout, J. Kotlarska, W. Dehaen and K. Binnemans, Phys. Chem. Chem. Phys., 2013, 15, 16533–16541 RSC.
- D. F. Peppard, G. W. Mason, J. L. Maier and W. J. Driscoll, J. Inorg. Nucl. Chem., 1957, 4, 334–343 CrossRef CAS.
- R. J. Ellis, T. Demars, G. Liu, J. Niklas, O. G. Poluektoy and I. A. Shkrob, J. Phys. Chem. B, 2015, 119, 11910–11927 CrossRef CAS.
- D. C. Steytler, D. L. Sargeant, G. E. Welsh, B. H. Robinson and R. K. Heenan, Langmuir, 1996, 12, 5312–5318 CrossRef CAS.
- D. C. Steytler, T. R. Jenta, B. H. Robinson, J. Eastoe and R. K. Heenan, Langmuir, 1996, 12, 1483–1489 CrossRef CAS.
- C. Erlinger, L. Belloni, T. Zemb and C. Madic, Langmuir, 1999, 15, 2290–2300 CrossRef CAS.
- S. A. Safran and L. A. Turkevich, Phys. Rev. Lett., 1983, 50, 1930–1933 CrossRef CAS.
- S. Prevost, M. Gradzielski and T. Zemb, Adv. Colloid Interface Sci., 2017, 247, 374–396 CrossRef CAS PubMed.
- K. Osseo-Asare, Adv. Colloid Interface Sci., 1991, 37, 123–173 CrossRef CAS.
- M. Duvail, L. Arleth, T. Zemb and J. F. Dufreche, J. Chem. Phys., 2014, 140, 164711 CrossRef.
- A. Jada, J. Lang, S.-J. Candau and R. Zana, Colloids Surf., 1989, 38, 251–261 CrossRef CAS.
- A. Jada, J. Lang and R. Zana, J. Phys. Chem., 1990, 94, 381–387 CrossRef CAS.
- K. A. Dill and S. Bromberg, Molecular driving forces, Garland Science, Taylor & Francis [distributor], New York, London, 2010 Search PubMed.
- M. Špadina, K. Bohinc, T. Zemb and J.-F. Dufrêche, ACS Nano, 2019, 13, 13745–13758 CrossRef.
- J. Rey, S. Dourdain, L. Berthon, J. Jestin, S. Pellet-Rostaing and T. Zemb, Langmuir, 2015, 31, 7006–7015 CrossRef CAS.
- L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2015, 20, 3–10 CrossRef CAS.
- L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2016, 22, 80–87 CrossRef CAS.
- S. Sukenik, L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2013, 18, 495–501 CrossRef CAS.
- P. Guilbaud, L. Berthon, W. Louisfrema, O. Diat and N. Zorz, Chem. – Eur. J., 2017, 23, 16660–16670 CrossRef CAS PubMed.
- S. Vafaei, B. Tomberli and C. G. Gray, J. Chem. Phys., 2014, 141, 154501 CrossRef.
- H. Singh, S. L. Mishra and R. Vijayalakshmi, Hydrometallurgy, 2004, 73, 63–70 CrossRef CAS.
- M. S. Tyumentsev, M. R. S. J. Foreman, B.-M. Steenari and C. Ekberg, J. Chem. Thermodyn., 2019, 131, 133–148 CrossRef CAS.
- M. S. Tyumentsev, M. R. S. Foreman, B. M. Steenari and C. Ekberg, J. Chem. Thermodyn., 2019, 131, 133–148 CrossRef CAS.
- Y. Marcus, Ions in Solution and their Solvation, John Wiley & Sons Inc., Hoboken, Nex Jersey, 2015 Search PubMed.
- R. D. Hancock and A. E. Martell, Chem. Rev., 1989, 89, 1875–1914 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 581 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 643 CrossRef CAS.
- C. Erlinger, D. Gazeau, T. Zemb, C. Madic, L. Lefrancois, M. Hebrant and C. Tondre, Solvent Extr. Ion Exch., 1998, 16, 707–738 CrossRef CAS.
- M. R. Antonio, R. Chiarizia and F. Jaffrennou, Sep. Sci. Technol., 2010, 45, 1689–1698 CrossRef CAS.
- Y. Chevalier and T. Zemb, Rep. Prog. Phys., 1990, 53, 279–371 CrossRef CAS.
- P.-M. Gassin, R. Champory, G. Martin-Gassin, J.-F. Dufrêche and O. Diat, Colloids Surf., A, 2013, 436, 1103–1110 CrossRef CAS.
- A. Paquet, O. Diat, L. Berthon and P. Guilbaud, J. Mol. Liq., 2019, 277, 22–35 CrossRef CAS.
- A. W. C. Penisson, J. Theisen, V. Kokoric, B. Mizaikoff and J. C. P. Gabriel, Water activity measurement of NaCl/H2O mixtures via substrate-integrated hollow waveguide infrared spectroscopy with integrated microfluidics, Anaheim, CA, USA, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06569e |
| This journal is © the Owner Societies 2020 |