Do defects in PAHs promote catalytic activity in space? Stone–Wales pyrene as a test case

Abstract

Using density functional theory (DFT), we studied the formation of Stone–Wales defects in pyrene, as a prototype PAH molecule. In addition, we studied the reactivity of the defective and pristine pyrenes toward hydrogenation, a process that can occur in some regions of the interstellar medium. We found that the formation of the defect requires overcoming energies of the order of 8.4 eV, but the defective structure is stable due to the high reverse reaction barrier (approx. 6 eV). We also found that the presence of the defect decreases the sticking barrier for the first hydrogenation and promotes more stable singly and doubly hydrogenated intermediates with respect to that of the pristine pyrene. Finally, our results show that both Stone–Wales pyrene and pristine pyrenes can lead to the formation of H₂ through an extraction mechanism involving H atoms attached on distal carbon atoms with energy barriers below 2 eV.

---

1 Introduction

Among the different types of sp² carbon nanomaterials, polycyclic aromatic hydrocarbon (PAH) molecules are of particular interest in astrophysics since they are responsible for a family of infrared emission bands in the 3–20 μm range, the so-called aromatic infrared bands, which are observed everywhere in our galaxy and beyond.^1–3 PAHs are ubiquitous in space and, thus, they should participate in the chemistry of the interstellar medium (ISM). Indeed, they have been proposed as sources of small carbon chains⁴ and even fullerenes.⁵ PAHs act as catalytic surfaces where H₂, the most abundant interstellar molecule, can be formed.⁶ It has been proposed that both neutral and cationic PAH molecules can first react with atomic hydrogen with little (few meV) to no barrier becoming superhydrogenated and, then, promote barrierless H₂ abstraction through the Eley–Rideal mechanism.^7,8 Since detailed photochemical evolution models of PAHs in the ISM have questioned the efficiency of the Eley–Rideal H₂ abstraction,⁹ more recently other mechanisms have been invoked, such as photodissociation of H₂ from normally hydrogenated PAHs.¹⁰

Stone–Wales (SW) defects are topological changes in the structure ubiquitous in sp² carbon materials such as fullerene, graphene, nanoribbons, and carbon nanotubes.^11–13 They are also studied in materials that have graphene-like structures but different compositions, e.g. boron nitrides.¹⁴ The defect is produced upon a 90° rotation of a C–C bond located in a hexagonal carbon ring, creating two seven-membered and two five-membered rings. The generation of SW defects can cause a curvature of the material that hosts it, but in the case of graphene or other planar hexagonal materials this defect results in a planar structure. Ma et al.¹⁵ proved that, in 2D materials, the formation of SW defects is inducted in non-equilibrium conditions by irradiation or the effect of mechanical strain. Experimental and theoretical studies conducted on fullerene and PAHs have shown that an extra hydrogen or carbon atom, chemisorbed on the molecule, induces a structure promoting the formation of the SW defect with a lower energy barrier than the formation of the defect in the pristine material.^16,17 Defects are known to change the physical and chemical properties; for example, they can open band gaps and exhibit increased reactivity toward oxygen and hydrogen atoms.^18–20 Theoretical studies have shown that PAH containing 5,7-membered rings are stable enough to survive interstellar conditions and they might be responsible for two of the AIBs, at 6.9 and 16.4 μm.^21,22

In this study, we used density functional theory (DFT) to determine the mechanism leading to the formation of Stone–Wales defects in a prototypical PAH molecule, pyrene. We investigated the effect of the SW defect on the reactivity of pyrene toward hydrogenation (single and double) and its ability to catalyse the formation of molecular hydrogen in an interstellar environment.

2 Theoretical methods

We employed density functional theory (DFT) implemented in the Gaussian 16,²³ to estimate barrier, binding and reaction energies. We used the hybrid meta exchange–correlation functional M06-2X developed by Truhlar and coworkers,²⁴ with the segmented polarization-consistent double zeta basis set pcseg-1 optimized for DFT and developed by Jensen.²⁵ M06-2X proved to be accurate when compared with CCSD(T) calculations for the investigation of hydrogen chemisorption on graphene-like structures such as PAHs.²⁶ We corrected all calculated energies for zero point vibrational energy and for basis-set superposition error, using the counterpoise method.^27,28

The geometry optimization of minima and transition states (TSs) in the potential energy surface (PES) were calculated using the Berny algorithm²⁹ and their nature in the PES were characterized by analyzing the normal modes (i.e. one imaginary frequency for the TS and no imaginary frequencies for the minima). All calculations were carried out using the unrestricted approach (UHF) and in order to produce a correct UHF wavefunction for blue singlet open-shell biradical systems in the case of TSs, we mixed the HOMO and LUMO destroying α–β orbitals and spatial symmetries (see the ESI†).³⁰

The vibrational frequencies, molecular structures, and intra- and intermolecular distances were analyzed with Molden.^31,32 Binding energy, energy barrier and reaction energy were calculated according to the following equations:

ΔE_bind = [(E_H + E_reagent) − E_{nH– pyrene}]

ΔE_bar = [E_TS − (E_H + E_reagent)]

ΔE_r = [E_product − (E_H + E_reagent)]

where ΔE_bind is the binding energy, ΔE_bar is the energy barrier and ΔE_r is the reaction energy. E_H is the energy of the isolated hydrogen, E_reagent is the energy of the isolated pyrene, E_nH–pyrene is the energy of pyrene with one or two atomic hydrogens chemisorbed, E_TS is the energy of the transition state structure and E_product is the energy of pyrene with two atomic hydrogen atoms chemisorbed. The binding energies are considered exoergic when they are positive as opposed to the reaction energies that are negative for exoergic processes. Barrier energies are always positive for the definition of transition state.

3 Results

3.1 Formation of PAHs with Stone–Wales defects

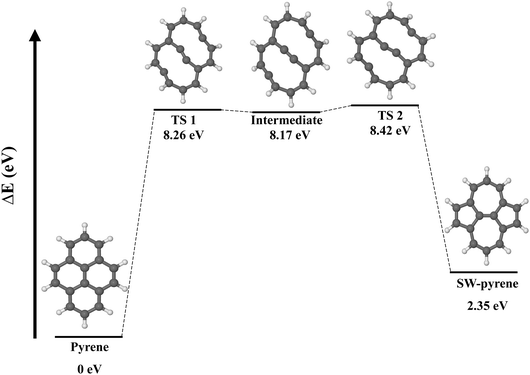
Pyrene (C₁₆H₁₀) is an organic molecule belonging to the D_2h point group (Fig. 1). The system can undergo a Stone–Wales transformation,³³ through the in-plane 90° rotation of the bond formed by C(2) and C(4) to a Stone–Wales defect in the structure, characterized by the presence of two seven-membered rings and two five-membered rings.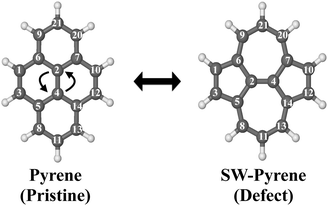

Fig. 1 Labeled optimized structures of pyrene and SW–pyrene. The arrows show the Stone–Wales formation.

The formation of a SW defect in the neutral pyrene molecule features two concerted transition states (Fig. 2) of the first order, connected by a shallow minimum. A similar mechanism was proposed in a previous study using a modified G4(MP2) method,²² but in that case only transition states of the second order were obtained. The first transition state (TS 1) is a non-planar structure characterized by the partial breaking of two carbon–carbon bonds C(2)–C(7) and C(5)–C(4) (now 2.42 Å apart) and an energy barrier of 8.26 eV, slightly higher than that calculated before.²² The mechanism, then, proceeds with the formation of a high-energetic intermediate (8.17 eV) with a bicyclic structure of two ten-membered rings. Once this intermediate is formed, 0.25 eV is required to overcome a second barrier associated with a second non-planar transition state (TS 2) featuring the partial formation of bonds C(2)–C(5) and C(4)–C(7) with elongation of 2.32 Å. Overcoming the second energy barrier leads to the production of SW–pyrene, which lies 2.35 eV above the pristine structure. Thus the formation of pyrene is an endoergic process, requiring 8.42 eV. Nevertheless, once the defective structure is created, 6.07 eV is needed to revert to the pristine structure. During the formation of the defect, all equivalent carbon–carbon distances are contracted down to 1.38 Å with respect to pristine pyrene where these carbon–carbon distances are 1.43 Å, similar to what is observed in graphene.³⁴

Fig. 2 Potential energy surface for the formation of a Stone–Wales defect starting from pristine pyrene, illustrated with optimised molecular structures. Energies are calculated with respect to pristine pyrene.

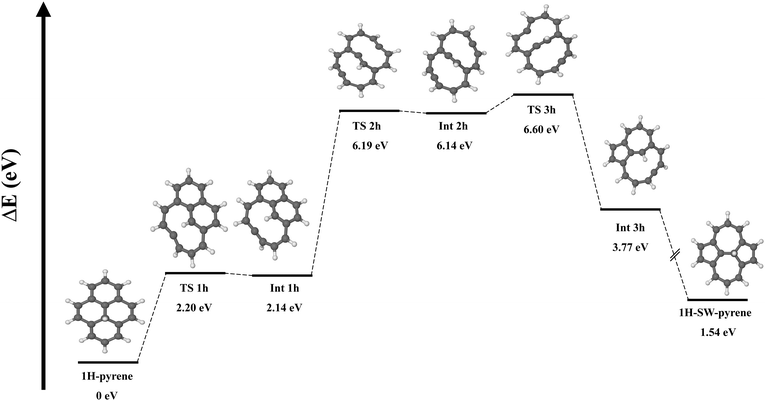
It has been proposed that the presence of additional H chemisorbed on carbonaceous material can catalyze the formation of a SW defect.¹⁶ As we are interested here in defective PAHs and their reactivity, we investigated this mechanism for pyrene. We started with a molecular structure where a hydrogen atom is chemisorbed on one of the inner carbon atoms (C(2) or C(4)) involved in the SW transformation (Fig. 3). Starting from this structure, the reaction goes through a transition state (TS 1 h) lying 2.20 eV above the reactant. For comparison, an energy barrier of 6.8 eV was found to break a central carbon–carbon bond in a graphene nanoflake with a chemisorbed H atom.²⁰ In our system the TS is characterised by the partial breaking of a carbon–carbon bond, where the carbons are 2.33 Å apart. After TS 1 h, intermediate INT 1 h is formed at 2.14 eV, featuring a ten-membered ring structure. From there, an additional 4.05 eV is needed to break a second carbon–carbon bond and form intermediate INT 2h, a shallow minimum with a bicyclic structure. After overcoming 0.46 eV (TS 3 h) a new carbon–carbon bond is created, leading to the formation of a pentagonal ring. In the end, we have the formation of a more stable intermediate (Int 3h) geometrically structured by a five membered-ring, a seven membered-ring and a ten membered-ring. The process ends with the barrierless formation of the SW–pyrene with a hydrogen chemisorbed on the inner carbon (1H–SW–pyrene).

Fig. 3 Potential energy surface for the formation of a Stone–Wales defect starting from hydrogenated pyrene illustrated with optimised molecular structures. The symbol (//) indicates the absence of energy barriers.

To summarize, the creation of a Stone–Wales defect in neutral pyrene requires an energy of 8.42 eV and the overcoming of two transition states. Once the shallow intermediate structure is formed, due to the small difference in barriers, the rate of the forward (creation of SW–pyrene) and backward reaction (creation of pyrene) should be comparable. The addition of a chemisorbed H atom catalyzes the process, which requires a total energy of 6.60 eV. However due to symmetry breaking, the process requires several additional steps. In particular, after the formation of INT 1H, the energy difference between TS 1h (0.06 eV) and TS 2h (4.05 eV) indicates that the former is more likely to happen, thus making the formation of 1H–SW–pyrene unlikely.

3.2 Hydrogenation process

First hydrogen attachment. Due to the symmetry of the SW–pyrene, there are five non-equivalent carbon sites, C(2), C(5), C(8), C(11) and C(12) available for interaction with a radical hydrogen atom; we calculated the binding and barrier energies for H chemisorbed on these sites. The most reactive carbon sites are the one possessing the highest binding energies and the lowest energy barriers. Table 1 reports the values for the different sites for SW–pyrene and pristine pyrene for comparison. In both structures, edge carbons C(12) and C(8) are the most reactive sites with binding energies of 1.55 and 1.45 eV and energy barriers of 0.18 and 0.19 eV, respectively. To follow, C(5), C(11) and C(2) have lower binding energies and slightly higher energy barriers, up to 0.27 eV in the case of C(5). Thus, the addition of the H atom to edge carbons C(8) and C(12) produces the most stable isomers, in line with previous studies.^7,35–37 In any case, all the energies calculated are exoergic and favorable.

Table 1 Binding energies (ΔE_bind) and energy barriers (ΔE_bar) for the hydrogenation of different carbon sites of Stone–Wales and pristine pyrene

C site	SW pyrene		Pristine pyrene
	ΔEbind (eV)	ΔEbar (eV)	ΔEbind (eV)	ΔEbar (eV)
C(12)	1.55	0.18	1.23	0.23
C(8)	1.45	0.19	1.24	0.22
C(5)	1.14	0.27	—	—
C(11)	1.10	0.25	—	—
C(2)	1.04	0.21	0.26	0.43

---

The energetics for H adsorption on three different sites (2 edge and 1 graphene-like carbon) of pristine pyrene were also calculated, to evaluate the effect of the SW defect on reactivity. The values reported for the binding energies (Table 1) are consistently lower by 0.25 eV with respect to previous calculations,³⁸ while the barrier energies are consistently higher by 0.16 eV. This is expected since the previous work used a different functional (PBE) and in our work a correction for zero-point vibrational energy is also included. Binding energies for singly hydrogenated SW–pyrene are always larger than those in the pristine molecules and energy barriers are smaller in accordance with the general Brønsted–Evans–Polayni rule^39,40 that in a reaction lower energy barriers are connected to larger exoergicity. In particular, when C(2) is hydrogenated in the SW–pyrene the binding energy is 1.04 eV compared to only 0.26 eV in the pristine molecule, and the energy barrier is halved, 0.21 versus 0.43 eV.

To understand the origin of this difference we looked at the structural differences in the two molecules. Indeed, in a PAH molecule the addition of a H atom changes the hybridization of the C atom where it is bonded from sp² to sp³, leading to a tetrahedral puckering of the carbon skeleton. This structure relaxation is fundamental as it creates the correct condition for the binding to happen. Both the defect and pristine pyrene are planar and hydrogenation triggers the creation of a much rippled structure for SW–pyrene. The hydrogenation of C(2) generates a puckering of 0.40 Å in the SW structure versus 0.46 Å in the pristine pyrene. In addition, in the SW-structure, edge carbon atoms forming the pentagons, C(1), C(3), C(10) and C(12), experience a downward motion of 0.29 Å, while for the pristine pyrene C(21) and C(11) move downward by 0.21 Å, and C(9) and C(20) by 0.10 Å. The larger puckering of C(2) in the pristine pyrene is likely responsible for the higher energy barrier.³⁸ As for the larger binding energy, we hypothesize that the flexibility of SW–pyrene permits the downward motion of the five-membered rings, thus, releasing part of the strain caused by the H-addition in the molecule. Thus this results in more stable hydrogenated intermediates, with the extreme case of C(2), in the SW molecule. Our calculations confirm that introducing a Stone–Wales defect increases consistently the reactivity of a PAH as it happens for graphene.⁴¹

Second hydrogen attachment. The attachment of a H atom to SW–pyrene generates an open-shell doublet structure with an unpaired electron that is susceptible to the attack of another H atom. As we are interested in the ability of SW–PAHs to catalyse H₂, we considered both adjacent and non-adjacent carbon sites, which are illustrated in Fig. 4.

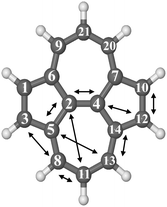Fig. 4 Optimized molecular structure of SW–pyrene with arrows indicating the different carbon pairs considered in this study.

A spin population analysis (values are reported in the ESI†) based on the Mulliken partitioning scheme for the single hydrogenated species of SW–pyrene and pristine pyrene (Fig. 7 and 8) shows a population of spin-up and spin-down electrons on the carbon framework. Specifically, for 1H–C2–SW–pyrene and 1H–C5–SW–pyrene a larger population of spin-up is localized in the carbons adjacent to the hydrogenated site (Fig. 7a and b, respectively); this is also true for 1H–C12–pyrene (Fig. 8b). These are the sites where we expect that the second hydrogen will most likely chemisorb as seen for coronene and pentacene molecules.^26,42 The other isomers analysed have the population of spin-up electrons distributed more uniformly over the entire carbon framework.

We first attempted to calculate the energy barrier for the attachment of the second H atom to a different site. Due to the computational issues of dealing with bi-radical systems in a singlet spin state, not all the calculations reached convergence (see ESI†). In isomer 1H–C12–SW (Fig. 5) the attachment of a second H atom on C(14) has an energy barrier of 0.033 eV, while there is no barrier when, on 1H–C2–SW, the second H atom attaches on C(4). If the second H is attached to an edge C atom that was hydrogenated previously, the reaction is found to be barrier-less. In pristine pyrene it is found that in 1H–C(2)–pristine, the energy barrier to attach the second H to C(4) is calculated to be 0.19 eV, whereas we do not find transition state structures for the edge carbons of the pristine pyrene due to convergence issues. A previous study³⁸ found that all the second H-addition reactions to singly-hydrogenated pyrene are barrier-less, while for our study this is true only when the reaction involves edge carbons. The difference is likely due to the different methods used and the lack of zero-point correction in the previous study. Incidentally, we note that the observed small barriers of 5 and 33 meV (Table 2) are below the barrier height error of M06-2X (0.06 eV) estimated by Mardirossian et al.⁴³ with the hydrogen transfer barrier heights database (HTBH38) and, therefore, these small energy barrier values obtained here can be approximated to 0 eV.

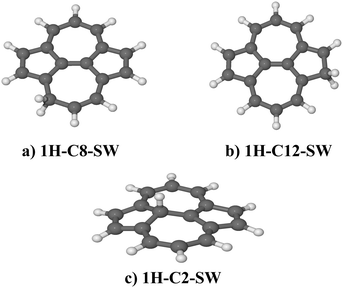Fig. 5 Optimized molecular model of different isomers of hydrogenated SW–pyrene with an atomic hydrogen bonded on C(8) (a), C(12) (b) and C(2) (c). All belong to the C_s point group.

Table 2 Energy barrier (ΔE_bar), binding energy (ΔE_bind) and carbon–carbon distance (d) values for distal (|) and adjacent (–) carbon pairs of SW–pyrene hydrogenated with two extra hydrogen atoms

C pairs	ΔEbar (eV)	ΔEbind (eV)	d (Å)
a Denotes calculations that did not converge. b Values to be considered 0 eV (see main article text).
C(12)|C(4)	0.033^b	2.00	2.49
C(5)–C(2)		2.21	1.56
C(8)|C(3)		2.41	2.66
C(11)|C(2)		2.49	3.27
C(2)–C(4)	0.005^b	2.59	1.55
C(8)–C(11)	0.005^b	3.00	1.53
C(5)|C(13)	0.005^b	3.02	2.91
C(12)–C(10)	0.005^b	3.18	1.52

---

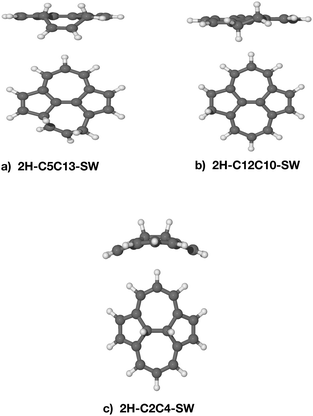
The stability of the doubly-hydrogenated defective species in terms of binding energy is summarised in Table 2 together with the carbon–carbon distance. There is no correlation between the stability of the intermediates and the carbon–carbon distances. All the double hydrogenated isomers have non-planar structures (see Fig. 6 for some examples). As to be expected,^7,38 the most stable species are 2H–C12C10–SW and 2H–C8C11–SW, where the dihydrogenation occurs at the edge.⁴⁴ The isomer 2H–C5C13–SW has a similar binding energy even if the 2 H atoms are attached to distal carbons. The dihydrogenation of the C(2)–C(4) junction follows at 2.59 eV. The presence of the SW defect significantly decreases the energy barrier in the C(2)–C(4), thus, increases the reactivity of the molecule. Calculations on equivalent carbon sites in pristine pyrene reveals that the dihydrogenation on C(5)|C(13) has a binding energy of 2.21 eV, C(8)–C(11) of 2.70 eV and C(2)–C(4) of 1.72 eV, hence, showing less stability than the same positions calculated on SW–pyrene. Surprisingly, the binding energy for the 2H–C12C10 isomer is 3.59 eV, 0.41 eV more stable than the equivalent isomer of SW–pyrene. In this last case, the inversion of reactivity might be attributed to the added strain on the already perturbed pentagonal ring in the SW–pyrene. The high binding energy of 2H–C5C13–SW (Fig. 6) suggests that the heptagonal ring can provide additional flexibility and, hence, a larger stability for the isomer. Indeed in this isomer the part of the hydrogenated heptagon that deviates significantly from planar has bond angles C(5)–C(8)–C(11) = 121.19° and C(13)–C(11)–C(8) = 121.77°, closer to the internal angles of a hexagon (120°) than those of a heptagon. We thus confirm that the most stable species are formed due to the largest electronic affinity of the atomic hydrogen for the carbons located on the edges.³⁷ Furthermore, in the case of the second hydrogenation, introducing a Stone–Wales defect appears to increase the reactivity and in most cases the stability of the dihydrogenated species.

Fig. 6 (a) Side and top views of optimized molecular structures for different isomers of hydrogenated SW–pyrene with two extra atomic hydrogens bonded on C(5) and C(13) (a), C(12) and C(10) (b) and C(2) and C(4) (c).

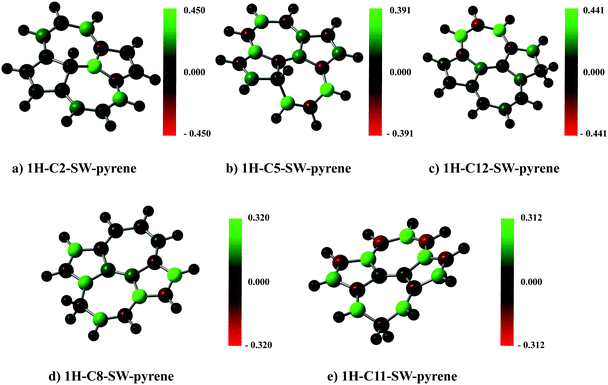Fig. 7 Spin population analysis for each optimized geometry of single hydrogenated species of SW–pyrene. The colour scale shows the distribution of spin-up (green) and spin-down (red) for each atom.

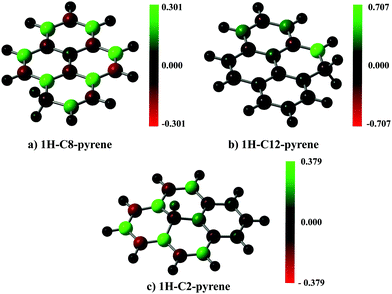Fig. 8 As in Fig. 7, but for each optimized geometry of single hydrogenated species of pristine pyrene.

3.3 Molecular hydrogen formation

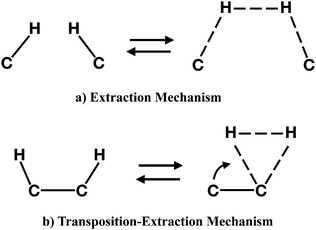
To follow, we investigated the formation of molecular hydrogen from the dihydrogenated intermediates discussed in the previous section. The formation of H₂ in these molecules can occur through two different mechanisms. The first type of mechanism is the extraction process that can involve H atoms attached either to neighbouring or distal carbons. This mechanism is characterized by a concerted transition state formed by the partial formation of a H–H bond and the partial break of C–H bonds (Fig. 9, top panel). The second type of mechanism occurs only for adjacent carbon pairs, in particular on C(2)–C(4), C(5)–C(8) and C(8)–C(11), and can be defined as a transposition-extraction (Fig. 9, bottom panel). In the transition state of this mechanism one H atom is transposed to the adjacent carbon where there is the partial formation of a H–H bond and the partial rupture of a C–H bond. This eventually leads to the extraction of H₂.

Fig. 9 Schematic representation of the process that leads to the formation of transition state for the molecular hydrogen formation: the extraction (a) and the transposition-extraction (b) mechanisms.

Table 3 shows the values for energy barriers and reaction energies (i.e. the difference in energy between the products and the reagents) together with the carbon–carbon distances in the transition state and the type of reaction. The extraction of H₂ from adjacent carbons in the edge – as in the case for C(12)–C(10) and C(8)–C(11) – is the most energetically expensive, with energy barriers of almost 5 eV and slightly endoergic products. On adjacent, internal carbon atoms, the extraction of H₂ requires almost 3 eV and the reaction is quite exoergic, with the products being almost 1 eV more stable than the reactants. This is to be expected, since the release of H₂ would remove the strain in the molecules caused by the sp³ hybridisation at the single hydrogenation site. Interestingly, we found that distal carbon atoms promote the formation of H₂, with a barrier lower than 2 eV and exoergic reactions.

Table 3 Values of energy barrier (ΔE_bar), and reaction energy (ΔE_r) for the extraction of H₂ in different isomers of doubly hydrogenated SW–pyrene. Also reported are distances between the two carbon atoms where the extra hydrogen atoms are attached (d) in the transition state and the type of mechanism involved in the formation (see Fig. 9). The symbols – and | identify adjacent and distal carbons, respectively

Stone–Wales
C pairs	ΔEbar (eV)	ΔEr (eV)	d (Å)	Type
C(12)–C(10)	4.87	0.28	1.44	(a)
C(8)–C(11)	4.60	0.10	1.48	(a)
C(5)–C(8)	3.46	0.03	1.51	(b)
C(2)–C(4)	2.94	−0.72	1.51	(b)
C(5)–C(2)	2.42	−1.00	1.55	(a)
C(8)|C(3)	2.58	−0.49	2.42	(a)
C(12)|C(4)	2.07	−0.80	2.28	(a)
C(5)|C(13)	1.84	−0.21	2.83	(a)
C(11)|C(2)	1.96	−0.77	2.85	(a)

---

We evaluated energy barriers and reaction energies for selected dihydrogenated isomers in the pristine pyrene for comparison (Table 4). Energy barriers for H₂ extraction are slightly lower than the values found for the same process in defective pyrene, with a maximum difference of 0.39 eV when considering the C pair C(8)–C(11). The reaction is also more exoergic; in particular for the same reaction type (a) and bond length, the extraction of H₂ from the C-pair C(2)–C(4) has a reaction energy of −0.72 eV in the defective pyrene and of −2.33 eV in the pristine molecule. This is the result of the high stability of the pristine pyrene with respect to its hydrogenated counterparts. The energy barriers for the H₂ formation found on pristine pyrene are slightly higher than what was found previously on graphene;^45,46 this confirms that small graphene-nanoflakes like pyrene behave like graphene when H₂ formation is considered.

Table 4 Values of energy barrier (ΔE_bar), reaction energy (ΔE_r) and carbon–carbon distance (d) in the transition state for the extraction of molecular hydrogen in pristine pyrene

Pristine
C pairs	ΔEbar (eV)	ΔEr (eV)	d (Å)	Type
C(12)′–C(10)′	4.89	0.48	1.45	(a)
C(8)′–C(11)′	4.21	−0.28	1.50	(b)
C(2)′–C(4)′	2.71	−2.33	1.57	(b)
C(5)′|C(13)′	1.67	−0.77	2.61	(a)

---

Fig. 10 shows the potential energy surface for the formation of H₂ on defective and pristine pyrene, considering hydrogenation on the same ring (left) and on the SW junction C(2)–C(4). In the case of SW–pyrene, the energy barrier for the first hydrogenation, namely 0.2 eV, is the limiting barrier for the formation of H₂ independently, if we consider carbons belonging to the same ring or the SW junction. For pristine pyrene, on the other side, the limiting barrier is 0.7 eV, represented by the transition state for the formation of H₂ on the hydrogenated intermediates. If distal carbon atoms are considered, H₂ formation has a submerged barrier, with a value comparable to what is seen in SW–pyrene. As seen in Section 3.2, the addition of H atoms on the reactive SW–pyrene results in stable isomers and the subsequent formation of H₂ has a submerged barrier.

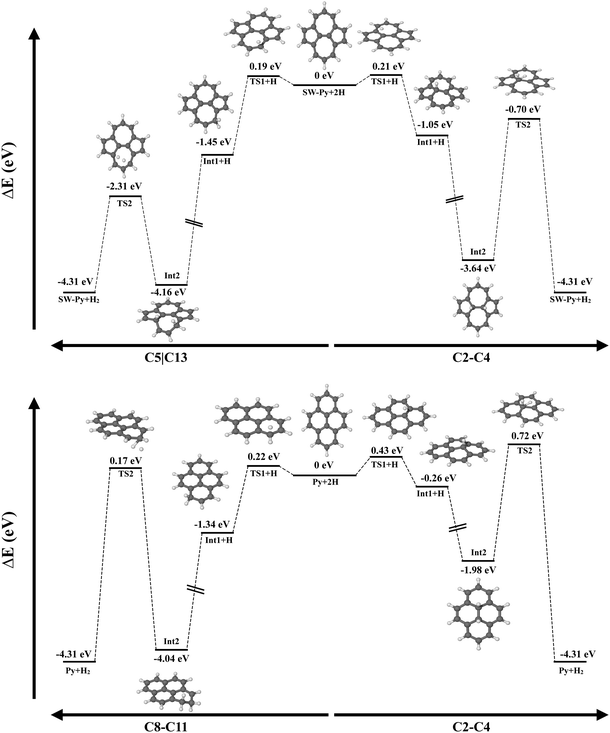Fig. 10 Comparison between the potential energy surfaces for the formation of molecular hydrogen from SW (top) and pristine pyrene (bottom).

3.4 Astrophysical implications

Observed infrared spectra of astronomical objects have been interpreted as revealing the presence of SW–PAHs.^47,48 We calculated the infrared spectra of pristine and Stone–Wales pyrene (see ESI†) and their spectra can be identified apart, thanks to the presence of a strong mode around 1375 cm⁻¹ in pristine pyrene (see also ref. 22). The same is true for 1H–C2–SW pyrene that shows strong activity in the 1300–1600 cm⁻¹ region, while 1H–C2 pristine pyrene as little to no activity there. Hopefully the James Webb Space Telescope that will observe the AIB spectrum in the full 3–20 μm region at high spectral resolution (R > 1550) will allow astronomers to confirm the presence of SW–PAHs. Defective PAHs as pristine PAH molecules should take part in the chemistry happening in space. Astrochemical models based on combustion chemistry⁴⁹ suggest that PAHs and carbon soot should be efficiently formed in the inner regions of carbon-rich giant stars.⁵⁰ Defective PAHs can be created starting from 6-membered ring species through a process requiring energies of the order of ≈8 eV (Fig. 2). To evaluate the stability of the mechanism, we calculated the Rice–Ramsperger–Kassel–Marcus (RRKM) rates⁵¹ as functions of internal energy for the backward and forward reactions when the system is in the intermediate state (Fig. 2). Once the intermediate is formed and possess enough internal energy, roughly a third of the time the mechanism will go forward and a defective structure will be created. The timescale needed for the intermediate to revert back to pristine pyrene is comparable with the timescales to share the excess energy among the other modes of the molecule, few tens of picoseconds.⁵² At internal energies above 30 eV the process is even more frequent. On graphene the energy needed to perform a Stone–Wales transformation is calculated to be 5 eV¹⁵ and this might hint at the size dependence of the energy involved in the SW rearrangement. Nevertheless, the high barrier derived here makes it unlikely that SW–PAHs are formed in the interstellar medium itself. An alternative route could be the formation through energetic processing of 6-membered ring species. Indeed, molecular dynamics simulations show that interaction of PAHs with a sub-keV ion can break C–C bonds without perturbing the rest of the structure⁵³ and can promote the formation of the 5 and 7 member rings.⁵⁴ Clearly more studies are needed to identify a precise pathway for the formation of SW–PAHs through energetic processes. Once SW–PAHs are formed, they can survive for a long time due to the higher barrier required for the conversion to the unaltered 6-membered PAHs and, thus, take part in the AstroPAH populations (Fig. 11).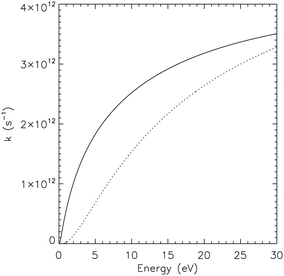

Fig. 11 Comparison between reaction rates for the forward reaction toward SW–pyrene (solid line) and for the reverse reaction toward pristine pyrene (dashed line) as a function of internal energies. Rates were calculated using the RRKM formalism^51,55 starting from the energies and vibrational analysis performed in this paper at the M06-2X/pcseg-1 level.

Both neutral and cationic PAHs have been put forward as catalytic surfaces where H₂ can be efficiently formed via an Eley–Rideal mechanism after initial hydrogenation (see the recent review by Wakelam et al, ref. 6). The key resides in the very low sticking barrier when the H is on the edge, calculated to be a few tens of meV, and the barrierless abstraction of H₂, as seen from both experiments and theory. Photochemical evolution models of PAHs in photodissociation regions show that the Eley–Rideal mechanism is effective only when the gas temperature is enough to overcome addition and extraction barriers.⁹ Accurate DFT calculations including zero point vibrational energy correction, like the one presented here and also elsewhere²⁶ give sticking barriers one order of magnitude higher (few hundreds of meV) than what were used in photochemical models in the past.^9,56,57 This means that even higher gas temperatures are needed for the process to happen. Also, the efficiency of the Eley–Rideal mechanism depends on the incident direction of the H that impinges on the superhydrogenated PAH molecule. If the molecule is heavily superhydrogenated, this is not much of an issue. However, astronomical observations of PAHs and the aforementioned photochemical models show that PAHs are scarcely superhydrogenated, with up to 4 additional hydrogen atoms in the shielded region (A_v > 4). Thus, while the energetics of the Eley–Rideal H₂ formation are very favourable, its efficiency is below 1%.⁹

Other mechanisms, such as H₂-loss from photodissociation of normally hydrogenated PAHs¹⁰ and protonated PAHs^58,59 have been invoked to explain the enhanced H₂ formation rates in some photodissociation regions.⁶⁰ In addition, PAH molecules can exist in the form of aggregates or clusters in the denser part of the photodissociation regions^61,62 and they might catalyse the formation of H₂. The study of the specific reactions involved and the interplay with competing channels is interesting and could have important implications for H₂ formation; however it is beyond the scope of the present work and should be addressed in a separate publication.

Here we have shown that Stone–Wales defects in PAHs can facilitate the catalytic formation of H₂. First, the presence of the defect lowers the difference in the H addition barrier between internal and edge carbons, which is 0.05 eV compared to pristine pyrene where the difference is 0.2 eV. Second, singly and doubly hydrogenated intermediates in SW–pyrene are located in a deeper well of the PES than in the case of pristine pyrene. The largest differences are seen for the 1H–C2–SW and 2H–C2C4–SW, where the H atoms are attached on the Stone–Wales rotated C2–C4 bond (Fig. 10, upper right). Moreover, the 2H–C2C4–SW intermediate needs slightly higher energy, in the order of 0.2 eV, to either lose a H atom or form H₂ than in the same isomer for the pristine case. This may imply that superhydrogenated Stone–Wales PAH species may have a longer lifetime against dehydrogenation than superhydrogenated pristine PAH in the interstellar medium and that they can be a sink for additional hydrogen atoms also in the case of diffusion.⁴⁴ Finally, in SW–pyrene the catalytic formation of H₂ is limited only by the barrier for first hydrogen attachment, which is of the order of 0.2 eV. H₂ formation from 2H–C2C4–SW pyrene requires 2.9 eV, comparable to the energy needed to photodissociate H₂ from a PAH cation.⁵⁵ An additional favourable channel for catalytic H₂ formation was found in both SW and pristine pyrenes, in the case where hydrogenation occurs on distal carbon atoms (2H–SW–C5C13 and 2H–SW–C11C2, see Tables 3 and 4). The energy barrier for this reaction, that proceeds through an extraction mechanism, is typically below 2 eV with the lowest for pristine pyrene at 1.67 eV. This type of reaction might help to increase the amount of H₂ formed in the interstellar region where superhydrogenated PAHs are present.

There are other processes that can compete with the formation of H₂ on hydrogenated SW–PAHs. Specifically, H-loss and H-roaming might be important reactions to be considered.^55,63,64 For SW–pyrene, H-loss can be a competitive channel when H₂ is formed on the C2–C4 junction, as the difference between the two reactions is 0.35 eV, which favours the H-loss. This is not the case for the formation of H₂ on distal carbons, where the energy difference is 0.88 eV, favouring the H₂ formation (Fig. 10). Calculations of energy barriers and reaction energies for H-roaming from C4 to C7 on 2H–SW–C2C4 are 0.92 and 0.40 eV, while for the reverse reaction they are 0.52 and −0.40 eV, respectively. This means that H will move rapidly to the nearby tertiary carbon position but likely go back to position C4. This will slow down the formation of molecular hydrogen. Calculations for H roaming along the edge in 2H–SW–C5C13 gives higher values, 1.65 eV for the energy barrier and 1.00 eV for the reaction energy. The reverse reaction has a barrier of 0.65 eV and a reaction energy of −1.00 eV. The difference in energy barrier between H-roaming and H₂ formation is only 0.2 eV and thus competition might be less important. We defer a detailed modelling of the kinetics of the processes involved to a future study.

Finally, we want to note that in this study we provided binding and barrier energies for H₂ extraction that can be useful for astrochemical modelling. We note that cross-over quantum mechanical temperature ranges between 397 and 534 K for SW–pyrene and between 400 and 571 K for pristine pyrene (see ESI†). For lower temperatures a proper evaluation of the reaction rate coefficient has to take tunneling effects into account.

4 Conclusions

We studied, using computational chemistry, the formation mechanism and catalytic properties of a prototype PAH with a Stone–Wales defect, pyrene. We calculated binding energies and barrier energies indispensable for subsequent astronomical modelling studies. We found:

• The creation of a SW defect requires 8.42 eV. Moreover, the addition of one atomic hydrogen on the inner carbon of pristine pyrene reduces the energy barrier for the creation of the SW defect by 1.82 eV.

• The C–C bond involved in the creation of the SW defect has enhanced reactivity, which translates to a lower H addition barrier for the first hydrogenation (the second is barrierless) and more stable singly hydrogenated SW–pyrene with respect to the pristine molecule. Thus, the SW defect “normalises” the differences in sticking barriers and stability seen between edge and central carbon atoms in pristine PAHs.

• Catalytic formation of H₂ in SW–pyrene is limited only by the barrier of the first hydrogen addition, in the order of 0.2 eV.

• An additional mechanism for H₂ formation involves hydrogenation of distal carbon atoms and has an energy below 2 eV, both in pristine and SW–pyrenes.

In the interstellar medium, due to their enhanced reactivity towards hydrogenation and stability, SW-containing PAHs can act as H sinks in regions of moderate irradiation. In this region, together with pristine PAHs, they can promote the catalytic formation of H₂ in addition to the Eley–Rideal mechanism.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank X. Tielens, T. Lamberts, I. L. ten Kate and the two referees for the useful comments and suggestions that improved the quality of the paper and D. Duca for reading an earlier version of the manuscript. D.C. acknowledges financial support from the EU under the Horizon 2020 Marie Skłodowska-Curie ITN EUROPAH (grant number 722346). A. C. acknowledges the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) for a VENI grant (639.041.543). This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative (project 16260) and the CINECA award IPCM2, under the ISCRA initiative, for the availability of high performance computing resources and support.

References

1. B. van Diedenhoven, E. Peeters, C. Van Kerckhoven, S. Hony, D. M. Hudgins, L. J. Allamandola and A. G. G. M. Tielens, Astrophys. J., 2004, 611, 928–939.
2. A. Candian, J. Zhen and A. G. G. M. Tielens, Phys. Today, 2018, 71, 38–43.
3. C. Boersma, J. Bregman and L. J. Allamandola, Astrophys. J., 2018, 858, 67.
4. J. Pety, D. Teyssier, D. Fossé, M. Gerin, E. Roueff, A. Abergel, E. Habart and J. Cernicharo, Astron. Astrophys., 2005, 435, 885–899.
5. O. Berné and A. G. G. M. Tielens, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 401–406.
6. V. Wakelam, E. Bron, S. Cazaux, F. Dulieu, C. Gry, P. Guillard, E. Habart, L. Hornekær, S. Morisset, G. Nyman, V. Pirronello, S. D. Price, V. Valdivia, G. Vidali and N. Watanabe, Mol. Astrophys., 2017, 9, 1–36.
7. E. Rauls and L. Hornekær, Astrophys. J., 2008, 679, 531–536.
8. N. Foley, S. Cazaux, D. Egorov, L. M. P. V. Boschman, R. Hoekstra and T. Schlathölter, Mon. Notices Royal Astron. Soc, 2018, 479, 649–656.
9. H. Andrews, A. Candian and A. G. G. M. Tielens, Astron. Astrophys., 2016, 595, A23.
10. P. Castellanos, A. Candian, H. Andrews and A. G. G. M. Tielens, Astron. Astrophys., 2018, 616, A167.
11. H. F. Bettinger, J. Phys. Chem. B, 2005, 109, 6922–6924.
12. V. V. Pokropivny and A. L. Ivanovskii, Russ. Chem. Rev., 2008, 77, 837–873.
13. J. N. B. Rodrigues, P. Goncalves, N. F. G. Rodrigues, R. M. Ribeiro, J. M. B. Lopes dos Santos and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155435.
14. R. Cortese, D. Campisi and D. Duca, ACS Omega, 2019, 4, 14849–14859.
15. J. Ma, D. Alfé, A. Michaelides and E. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 033407.
16. B. R. Eggen, M. I. Heggie, G. Jungnickel, C. D. Latham, R. Jones and P. R. Briddon, Sci., 1996, 272, 87–90.
17. S. Stanković, S. Marković, I. Gutman and S. Sretenović, J. Mol. Model., 2010, 16, 1519–1527.
18. X. Qi, X. Guo and C. Zheng, App. Surf. Sci., 2012, 259, 195–200.
19. E. J. Duplock, M. Scheffler and P. J. D. Lindan, Phys. Rev. Lett., 2004, 92, 225502.
20. A. J. M. Nascimento and R. W. Nunes, Nanotechnology, 2013, 24, 435707.
21. H. Yu and G. Nyman, Astrophys. J., 2012, 751, 1–7.
22. S. Oettl, S. E. Huber, S. Kimeswenger and M. Probst, Astron. Astrophys., 2014, 568, 1–8.
23. M. J. Frisch, G. W. Trucks, H. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. J. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Account, 2008, 120, 215–241.
25. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085.
26. P. A. Jensen, M. Leccese, F. D. S. Simonsen, A. W. Skov, M. Bonfanti, J. D. Thrower, R. Martinazzo and L. Hornekær, Mon. Notices Royal Astron. Soc., 2019, 486, 5492–5498.
27. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
28. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
29. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
30. S. Yamanaka, T. Kawakami, H. Nagao and K. Yamaguchi, Chem. Phys. Lett., 1994, 231, 25–33.
31. G. Schaftenaar, E. Vlieg and G. Vriend, J. Comput.-Aided Mol. Des., 2017, 31, 789–800.
32. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
33. A. J. Stone and D. J. Wales, Chem. Phys. Lett., 1986, 128, 501–503.
34. S. Letardi, M. Celino, F. Cleri and V. Rosato, Surf. Sci., 2002, 496, 33–38.
35. C. W. Bauschlicher, Jr., Astrophys. J., 1998, 509, L125–L127.
36. J. A. Sebree, V. V. Kislov, A. M. Mebel and T. S. Zwier, J. Phys. Chem. A, 2010, 114, 6255–6262.
37. M. Bonfanti, S. Casolo, G. F. Tantardini, A. Ponti and R. Martinazzo, J. Chem. Phys., 2011, 135, 164701.
38. J. A. Rasmussen, G. Henkelman and B. Hammer, J. Chem. Phys., 2011, 134, 164703.
39. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24.
40. R. P. Bell, Proc. R. Soc. Lond. A., 1936, 154, 414–429.
41. P. A. Denis and F. Iribarne, THEOCHEM, 2009, 907, 93–103.
42. D. Campisi, F. D. S. Simonsen, J. D. Thrower, R. Jaganathan, L. Hornekær, R. Martinazzo and A. G. G. M. Tielens, Phys. Chem. Chem. Phys., 2020, 22, 1557–1565.
43. N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303–4325.
44. M. Bonfanti, R. Martinazzo, G. F. Tantardini and A. Ponti, J. Phys. Chem. C, 2007, 111, 5825–5829.
45. L. Hornekær, Z. Šljivančanin, W. Xu, R. Otero, E. Rauls, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 96, 156104.
46. J. Petucci, S. Semone, C. LeBlond, M. Karimi and G. Vidali, J. Chem. Phys., 2018, 149, 014702.
47. A. Ricca, C. W. Bauschlicher, Jr and L. J. Allamandola, Astrophys. J., 2011, 729, 94.
48. H.-G. Yu and G. Nyman, Astrophys. J., 2012, 751, 3.
49. M. Frenklach, Phys. Chem. Chem. Phys., 2002, 4, 2028–2037.
50. I. Cherchneff, EAS Publications Series, 2011, 177–189.
51. T. Baer and P. M. Mayer, J. Am. Soc. Mass Spectrom, 1997, 8, 103–115.
52. A. H. Zewail, Femtochemistry, 1994, 3–22.
53. J. Postma, PhD thesis, Rijksuniversiteit Groningen, 2011.
54. S. E. Huber, A. Mauracher and M. Probst, AIP Adv., 2013, 3, 122104.
55. P. Castellanos, A. Candian, J. Zhen, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys, 2018, 616, A166.
56. L. Boschman, S. Cazaux, M. Spaans, R. Hoekstra and T. Schlathölter, Astron. Astrophys., 2015, 579, A72.
57. J. Montillaud, C. Joblin and D. Toublanc, Astron. Astrophys., 2013, 552, A15.
58. M. Vala, J. Szczepanski, J. Oomens and J. D. Steill, J. Am. Chem. Soc., 2009, 131, 5784–5791.
59. J. Szczepanski, J. Oomens, J. D. Steill and M. T. Vala, Astrophys. J., 2011, 727, 12.
60. E. Habart, F. Boulanger, L. Verstraete, C. M. Walmsley and G. Pineaudes Forêts, Astron. Astrophys., 2004, 414, 531–544.
61. M. Rapacioli, F. Calvo, F. Spiegelman, C. Joblin and D. J. Wales, J. Phys. Chem. A, 2005, 109, 2487–2497.
62. P. Pilleri, C. Joblin, F. Boulanger and T. Onaka, Astron. Astrophys., 2015, 577, A16.
63. G. Trinquier, A. Simon, M. Rapacioli and F. X. Gadéa, Molecular Astrophysics, 2017, 7, 27–36.
64. S. D. Wiersma, A. Candian, J. M. Bakker, G. Berden, J. Oomens, W.-J. Buma and A. Petrignani, Astron. Astrophys., 2020 DOI:10.1051/0004-6361/201936982.

---

Footnote

† Electronic supplementary information (ESI) available: Technical suggestions for the convergence blue of open-shell biradical systems and Cartesian coordinates of the most relevant intermediates and transition states. See DOI: 10.1039/c9cp06523g

---