 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature effects on the ionic conductivity in concentrated alkaline electrolyte solutions†
Yunqi
Shao
 a,
Matti
Hellström
a,
Matti
Hellström
 bc,
Are
Yllö
a,
Jonas
Mindemark
bc,
Are
Yllö
a,
Jonas
Mindemark
 a,
Kersti
Hermansson
a,
Kersti
Hermansson
 a,
Jörg
Behler
a,
Jörg
Behler
 b and
Chao
Zhang
b and
Chao
Zhang
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Uppsala University, Box 538, 751 21 Uppsala, Sweden. E-mail: chao.zhang@kemi.uu.se
bUniversität Göttingen, Institut für Physikalische Chemie, Theoretische Chemie, Tammannstr. 6, 37077 Göttingen, Germany
cSoftware for Chemistry and Materials B. V., De Boelelaan 1083, 1081HV Amsterdam, The Netherlands
First published on 19th December 2019
Abstract
Alkaline electrolyte solutions are important components in rechargeable batteries and alkaline fuel cells. As the ionic conductivity is thought to be a limiting factor in the performance of these devices, which are often operated at elevated temperatures, its temperature dependence is of significant interest. Here we use NaOH as a prototypical example of alkaline electrolytes, and for this system we have carried out reactive molecular dynamics simulations with an experimentally verified high-dimensional neural network potential derived from density-functional theory calculations. It is found that in concentrated NaOH solutions elevated temperatures enhance both the contributions of proton transfer to the ionic conductivity and deviations from the Nernst–Einstein relation. These findings are expected to be of practical relevance for electrochemical devices based on alkaline electrolyte solutions.
Because of their excellent ionic conductivity and high room-temperature solubility, alkaline electrolyte solutions are widely used in electrochemical devices such as rechargeable batteries and alkaline fuel cells.1,2 The electrochemically active ion in alkaline electrolytes is the hydroxide ion.3 OH− has an anomalously high mobility in aqueous solution, as it can diffuse via Grotthuss mechanism which is composed of a series of proton transfer events.4 Major progress in the understanding of OH− solvation and mobility at low concentration was made by molecular dynamics (MD) simulations based on density functional theory5–9 and reactive force fields,10,11 which highlighted the importance of “presolvation”, i.e., a thermally induced hydrogen-bond fluctuation, in the diffusion of hydroxide ions.7,10–12
Although ionic conductivity at low concentrations is well-described by the Nernst–Einstein equation, which links the conductivity σ to the self-diffusion coefficients D+ and D− of cations and anions, respectively, this simple picture is no longer valid at concentrations typically used in electrochemical devices. At higher concentrations, several types of non-ideal phenomena like ion-pairing,13 in which cations and anions associate and form metastable neutral pairs, and, more generally, cross-correlations of the movements of different ions (of equal or opposite charge) can notably alter the ionic conductivity. Moreover, the working temperature of alkaline batteries and fuel cells can be much higher than room-temperature (293 K).14 Therefore, it is desirable to understand the temperature effects on proton transfer and ion-pairing in alkaline electrolyte solutions and their implications concerning the ionic conductivity at high concentrations and elevated temperatures.
Simulations of electric properties, such as ionic conductivity, necessitate long time-scales and, except for cases at extreme conditions,15 are normally beyond reach of the standard density-functional theory (DFT)-based MD. One way to tackle this time-scale challenge is to explore finite-field DFTMD simulations to speed up the convergence of the polarization P, which has been successfully applied to compute the dielectric constant of polar liquids and the capacitance of electrified solid–electrolyte interfaces.16 The other approach to solve this problem is to make use of reactive force fields to access longer time-scales.10,11,17 One promising approach in this direction is to devise high-dimensional neural network potentials (NNPs) with DFT quality as proposed by Behler and Parrinello.18 Here, we use this approach, and by means of MD simulations using a NNP for the prototypical case of aqueous NaOH solutions19 and show how different factors together lead to the surprising behavior of the ionic conductivity in concentrated NaOH aqueous solutions at elevated temperatures.
The details of the construction and validation of the NNP for NaOH solutions using DFT calculations at the dispersion-corrected GGA level have previously been discussed in detail19–21 (see also a brief summary in ESI†). The present MD simulations were performed using LAMMPS22 together with an extension for high-dimensional NNPs.23 The cubic simulation box contained between 272 and 496 water molecules, and between 8 and 120 NaOH formula units, depending on concentration (see Table S1 in the ESI†). The length of cubic simulation box has been fixed using the experimental densities of NaOH solutions at the given composition and temperature24 (see Table S1 in the ESI†). Production runs with a timestep of 0.5 fs in the NVT ensemble lasted for 15 ns at each combination of composition and temperature after the equilibration. The Bussi–Donadio–Parrinello thermostat25 which has shown an excellent control of kinetic energy and little effect on the dynamical properties was employed. The trajectory frames were saved every 0.01 ps for later analysis. Each trajectory was split into 5 uncorrelated segments with length of 3 ns each. The standard deviations of observables from the different segments were used as an error estimate. Note that nuclear quantum effects were not included in the MD simulations.
To accompany the simulations, we have also performed conductivity measurements of NaOH solutions of concentrations up to 25 molality (m). The conductivity meter probe used is a 4 pole InLab 738-ISM by (Mettler Toledo) which has a sensitivity range from 0.01–1000 mS cm−1 and gives accurate measurements up to 373 K. The mean and the standard deviation of five independent measurements after calibration were reported for each given NaOH solution at both 293 K and 323 K.
When comparing simulation and experimental results, it is important to realize that the ionic conductivity can be computed using different formulas which have different applicabilities. As mentioned at the beginning, the Nernst–Einstein equation for the ionic conductivity of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 symmetric electrolyte is valid only at low concentration and can be written as
1 symmetric electrolyte is valid only at low concentration and can be written as
| σN−E = q2ρβ(D+ + D−), | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte.
1 electrolyte.
D + can be obtained by integrating the velocity auto-correlation function as
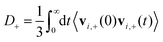 | (2) |
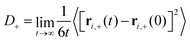 | (3) |
D − can be computed analogously according to eqn (2) and (3). We defined the positions of OH− ions by the position of O atoms bonded only to a single H atom. All bonds in the system were defined by assigning each hydrogen atom to its nearest oxygen atom, which gave either water molecules or hydroxide ions. Upon proton transfer reactions, the trajectories of OH− were traced in a fashion similar to how was done in ref. 21, i.e. based on “the Hungarian algorithm” as introduced by König in 1916 and Egerváry in 1931 and elaborated by Kuhn in 1955.26
The Nernst–Einstein equation becomes approximate at high concentrations, for which ion-pairing and cross-correlated ion motions play an important role.27–29 A more general equation for the conductivity, which is valid at both low and high concentrations, is the Green–Kubo formula
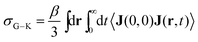 | (4) |
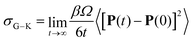 | (5) |
Unlike σN–E, σG–K includes ion-pairing and cross-correlated ion motions from the so-called distinct diffusion coefficients of cations Dd+, anions Dd− and cation–anion pairs Dd±, which can be computed from MD simulations.28,32 The name “distinct” means it is cross-correlation between two different ions, even within the same species.
This leads to a decomposition of the Green–Kubo conductivity as
| σG–K = q2ρβ(D+ + D− + Dd+/2 +Dd−/2 − Dd±) | (6) |
| = σN–E + σd+ + σd− + σd± | (7) |
After elaborating on the difference between the Nernst–Einstein conductivity and the Green–Kubo conductivity, we are now ready to compare the ionic conductivity calculated from MD simulations to those measured in experiments. The results are shown in Fig. 1. In Fig. 1a, the calculated ionic conductivities from MD simulations agree well with conductivity measurements, especially at 293 K. Considering that the NNP19 was generated using only DFT calculations at the dispersion-corrected GGA level as the reference, this agreement is quite encouraging. Further improvement might be achieved with higher-level functionals.33 Note that we have neglected the finite-size correction34 to the Nernst–Einstein conductivity showed in Fig. 1a, because of the relatively large simulation box that we used and the high viscosity of concentrated NaOH solutions (see Fig. S1 in the ESI†).
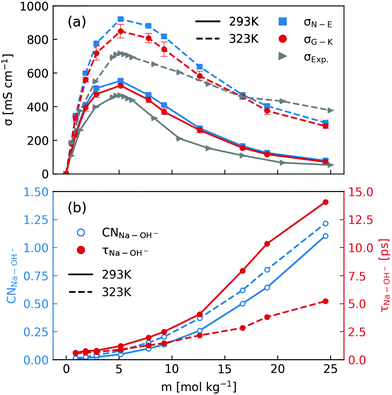 | ||
| Fig. 1 (a) Comparison of concentration-dependent ionic conductivities calculated using the Nernst–Einstein formula (eqn (1) and (3)) and the Green–Kubo formula (eqn (5)) from MD simulations and those measured in experiments at 293 K and 323 K; (b) calculated Na+–OH− coordination numbers and residence time. | ||
When inspecting the simulation results at both 293 K and 323 K (Fig. 1), one can see that the Nernst–Einstein conductivity is always larger than the Green–Kubo conductivity, as expected. However, there are several interesting observations specific to NaOH solutions. First, the absolute difference between the Nernst–Einstein conductivity and the Green–Kubo conductivity becomes smaller at higher concentrations which is counter-intuitive. Second, the difference is in general larger at higher temperature (323 K) than at lower temperature (293 K). Third, near the solubility limit (25 m) at room-temperature, the ionic conductivity at 323 K is still substantial while at 293 K it becomes quite small.
One way to rationalize these observations is to consider ion-pairing. For this reason, we calculated the coordination number of OH− around Na+ ions as well the residence time of Na+–OH− pairs. The coordination number (CN) was calculated by integrating the radial distribution function to its first minimum and the residence time τ was calculated by following the stable states picture formalism.35 As is described in ref. 20, a time correlation function C(t) was calculated to give the probability that a “stable” hydroxide ion at time t does not escape the first coordination shell of Na+ through either ligand exchange or proton transfer within the interval t0 and t0 + t. C(t) was then fitted to a biexponentially decaying function to extract the residence time. As shown in Fig. 1b, the number of OH− coordinating Na+ at both 293 K and 323 K can exceed one near the room-temperature solubility limit. However, the residence time at 293 K increases much more rapidly with the concentration than that at 323 K. Based on these observations, one may speculate that the effect of ion-pairing on the ionic conductivity would be stronger at 293 K.
In order to dissect the contributions of proton transfer reactions and cross-correlated ion motions, we exploited the fact that proton transfer contributes to the mean squared displacement (MSD, eqn (3)) but not to the corresponding velocity correlation function (VCF, eqn (2)). As shown in Fig. 2a and b, the scaled self-diffusion coefficients of Na+ are the same regardless whether they are computed from MSD or from VCF. In contrast, the scaled self-diffusion coefficients of OH− computed from MSD and VCF are different and their difference quantifies the contribution from proton transfer reactions. Comparing to the case at 323 K, one can clearly see that the proton transfer contribution to the self-diffusion coefficient of OH− becomes negligible at 293 K in concentrated NaOH solutions. This is the main reason why the ionic conductivity near the room-temperature solubility limit at 323 K is still significant while at 293 K it becomes severely diminished.
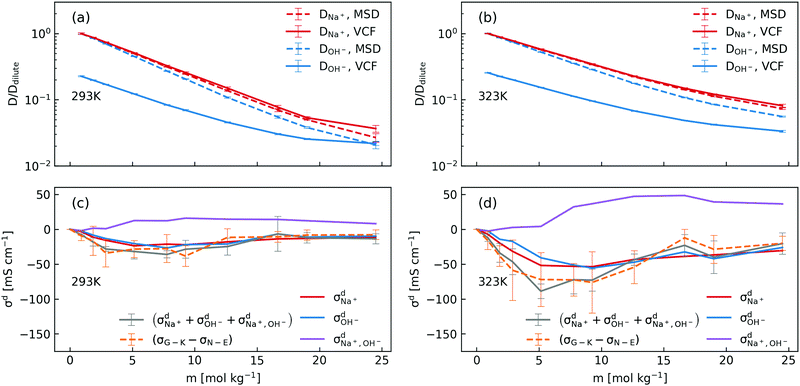 | ||
| Fig. 2 (a) and (b) Scaled concentration-dependent self-diffusion coefficients of Na+ and OH− at 293 K and 323 K obtained from VCF (eqn (2)) and from MSD (eqn (3)), where the self-diffusion coefficients were scaled by the corresponding value in the dilute solution; (c) and (d) contributions of distinct diffusion coefficients to the ionic conductivity at 293 K and 323 K as shown in eqn (7) and calculated from VCFs. Detailed definition of distinct diffusion coefficients can be found in ref. 28 and 32. Note that (σG–K − σN–E) were obtained from Fig. 1a for the purpose of comparison. | ||
We then used the same technique to evaluate the contributions of the distinct diffusion coefficients to the ionic conductivity from VCFs, as shown in Fig. 2c and d. It is found that 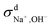 at both 293 K and 323 K are positive instead of negative as a simple picture of ion-pairing would suggest, similar to what was seen in ionic liquids.32 Further,
at both 293 K and 323 K are positive instead of negative as a simple picture of ion-pairing would suggest, similar to what was seen in ionic liquids.32 Further, 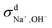 is much more positive at 323 K than that at 293 K. These suggest that in spite of the existence of ion-pairs in concentrated NaOH solutions, the effect of ion-pairing on the ionic conductivity should not be taken for granted.
is much more positive at 323 K than that at 293 K. These suggest that in spite of the existence of ion-pairs in concentrated NaOH solutions, the effect of ion-pairing on the ionic conductivity should not be taken for granted.
When comparing the sum of 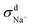 ,
, 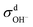 and
and 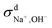 calculated from VCFs to the absolute difference between σG–K and σN–E calculated from the MSD, one can see a good agreement within the statistical error. Note that (σG–K − σN–E) has a larger error bar than its counterpart
calculated from VCFs to the absolute difference between σG–K and σN–E calculated from the MSD, one can see a good agreement within the statistical error. Note that (σG–K − σN–E) has a larger error bar than its counterpart 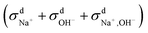 , because the former is the difference of two large numbers (Fig. 1a). The agreement between these two quantities means that the cross-correlated ion motions are hydrodynamic in nature and not determined by proton transfer reactions in NaOH solutions. We suspect that the counter-intuitive observation that (σG–K − σN–E) becomes smaller at high concentration is related to the rapid increment of the viscosity in NaOH solutions (see Fig. S2 in the ESI†). Since the viscosity decreases at elevated temperatures, this may also explain a larger difference between the Nernst–Einstein conductivity and the Green–Kubo conductivity at 323 K as seen in Fig. 1a. Nevertheless, future investigations are needed to identify the factors affecting the cross-correlated ion motions and subsequent deviations from the Nernst–Einstein relation.36
, because the former is the difference of two large numbers (Fig. 1a). The agreement between these two quantities means that the cross-correlated ion motions are hydrodynamic in nature and not determined by proton transfer reactions in NaOH solutions. We suspect that the counter-intuitive observation that (σG–K − σN–E) becomes smaller at high concentration is related to the rapid increment of the viscosity in NaOH solutions (see Fig. S2 in the ESI†). Since the viscosity decreases at elevated temperatures, this may also explain a larger difference between the Nernst–Einstein conductivity and the Green–Kubo conductivity at 323 K as seen in Fig. 1a. Nevertheless, future investigations are needed to identify the factors affecting the cross-correlated ion motions and subsequent deviations from the Nernst–Einstein relation.36
Conflicts of interest
There are no conflicts to declare.Acknowledgements
CZ thanks Uppsala University (UU) for a start-up grant and funding from the Swedish National Strategic e-Science programme eSSENCE. MH acknowledges funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 798129. KH acknowledges funding from the Swedish Research Council (VR). JB acknowledges the DFG for a DFG Heisenberg professorship (Be3264/11-2, project 329898176). The simulations were performed on the resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC.Notes and references
- G. Merle, M. Wessling and K. Nijmeijer, J. Membr. Sci., 2011, 377, 1–35 CrossRef CAS.
- A. R. Mainar, O. Leonet, M. Bengoechea, I. Boyano, I. de Meatza, A. Kvasha, A. Guerfi and J. A. Blázquez, Int. J. Energy Res., 2016, 40, 1032–1049 CrossRef CAS.
- E. Hückel, Z. Elektrochem. Angew. Phys. Chem., 1928, 34, 546–562 Search PubMed.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- M. E. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Phys.: Condens. Matter, 1994, 6, A93–A100 CrossRef CAS.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- D. Marx, A. Chandra and M. E. Tuckerman, Chem. Rev., 2010, 110, 2174–2216 CrossRef CAS PubMed.
- A. Hassanali, M. K. Prakash, H. Eshet and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20410–20415 CrossRef CAS PubMed.
- M. Chen, L. Zheng, B. Santra, H.-Y. Ko, R. A. D. Jr, M. L. Klein, R. Car and X. Wu, Nat. Chem., 2018, 10, 413–419 CrossRef CAS PubMed.
- T. J. F. Day, U. W. Schmitt and G. A. Voth, J. Am. Chem. Soc., 2000, 122, 12027–12028 CrossRef CAS.
- S. T. Roberts, P. B. Petersen, K. Ramasesha, A. Tokmakoff, I. S. Ufimtsev and T. J. Martinez, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15154–15159 CrossRef CAS PubMed.
- R. Biswas, Y.-L. S. Tse, A. Tokmakoff and G. A. Voth, J. Phys. Chem. B, 2016, 120, 1793–1804 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS.
- S. V. Guaitolini and J. F. Fardin, in Advances in Renewable Energies and Power Technologies, ed. I. Yahyaoui, Elsevier, 2018, pp. 123–150 Search PubMed.
- V. Rozsa, D. Pan, F. Giberti and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6952–6957 CrossRef.
- C. Zhang, J. Hutter and M. Sprik, J. Phys. Chem. Lett., 2019, 10, 3871–3876 CrossRef CAS PubMed.
- W. Zhang and A. C. T. van Duin, J. Phys. Chem. C, 2015, 119, 27727–27736 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- M. Hellström and J. Behler, J. Phys. Chem. Lett., 2016, 7, 3302–3306 CrossRef PubMed.
- M. Hellström and J. Behler, J. Phys. Chem. B, 2017, 121, 4184–4190 CrossRef PubMed.
- M. Hellström, M. Ceriotti and J. Behler, J. Phys. Chem. B, 2018, 122, 10158–10171 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Singraber, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 1827–1840 CrossRef CAS.
- R. H. Perry, D. W. Green and J. O. Maloney, Perry's Chemical engineers' handbook, McGraw-Hill, New York, 6th edn, 1984 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. W. Kuhn, Nav. Res. Logist. Q., 1955, 2, 83–97 CrossRef.
- J. P. Hansen and I. R. McDonald, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 2111–2123 CrossRef.
- E. C. Zhong and H. L. Friedman, J. Phys. Chem., 1988, 92, 1685–1692 CrossRef CAS.
- S. Chowdhuri and A. Chandra, J. Chem. Phys., 2001, 115, 3732–3741 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 2017 Search PubMed.
- J.-M. Caillol, J. Chem. Phys., 1994, 101, 6080–6090 CrossRef CAS.
- H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS PubMed.
- T. Duignan, G. K. Schenter, J. Fulton, T. Huthwelker, M. Balasubramanian, M. Galib, M. D. Baer, J. Wilhelm, J. Hutter, M. D. Ben, X. S. Zhao and C. J. Mundy, ChemRxiv, 2019 DOI:10.26434/chemrxiv.7466426.v2.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 7697–7701 CrossRef CAS PubMed.
- Y. Shao, K. Shigenobu, M. Watanabe and C. Zhang, ChemRxiv, 2019 DOI:10.26434/chemrxiv.8217152.v2.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06479f |
| This journal is © the Owner Societies 2020 |
