DFT modelling of explicit solid–solid interfaces in batteries: methods and challenges
Abstract
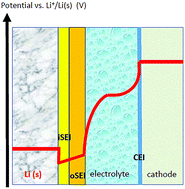
Density Functional Theory (DFT) calculations of electrode material properties in high energy density storage devices like lithium batteries have been standard practice for decades. In contrast, DFT modelling of explicit interfaces in batteries arguably lacks universally adopted methodology and needs further conceptual development. In this paper, we focus on solid–solid interfaces, which are ubiquitous not just in all-solid state batteries; liquid-electrolyte-based batteries often rely on thin, solid passivating films on electrode surfaces to function. We use metal anode calculations to illustrate that explicit interface models are critical for elucidating contact potentials, electric fields at interfaces, and kinetic stability with respect to parasitic reactions. The examples emphasize three key challenges: (1) the “dirty” nature of most battery electrode surfaces; (2) voltage calibration and control; and (3) the fact that interfacial structures are governed by kinetics, not thermodynamics. To meet these challenges, developing new computational techniques and importing insights from other electrochemical disciplines will be beneficial.
- This article is part of the themed collections: PCCP Perspectives, 2020 PCCP HOT Articles and Frontiers in Molecular Simulation of Solvated Ions, Molecules and Interfaces


 Please wait while we load your content...
Please wait while we load your content...