Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rapid and accurate molecular deprotonation energies from quantum alchemy†
Guido Falk
von Rudorff
 and
O. Anatole
von Lilienfeld
*
and
O. Anatole
von Lilienfeld
*
Institute of Physical Chemistry and National Center for Computational Design and Discovery of Novel Materials (MARVEL), Department of Chemistry, University of Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: anatole.vonlilienfeld@unibas.ch
First published on 19th December 2019
Abstract
We assess the applicability of alchemical perturbation density functional theory (APDFT) for quickly and accurately estimating deprotonation energies. We have considered all possible single and double deprotonations in one hundred small organic molecules drawn at random from QM9 [Ramakrishnan et al., JCTC, 2015]. Numerical evidence is presented for 5160 deprotonated species at both HF/def2-TZVP and CCSD/6-31G* levels of theory. We show that the perturbation expansion formalism of APDFT quickly converges to reliable results: using CCSD electron densities and derivatives, regular Hartree–Fock calculations are outperformed at the second or third order for ranking all possible doubly or singly deprotonated molecules, respectively. CCSD single deprotonation energies are reproduced within 1.4 kcal mol−1 on average within third order APDFT. We introduce a hybrid approach where the computational cost of APDFT is reduced even further by mixing first order terms at a higher level of theory (CCSD) with higher order terms at a lower level of theory only (HF). We find that this approach reaches 2 kcal mol−1 accuracy in absolute deprotonation energies compared to CCSD at 2% of the computational cost of third order APDFT.
1 Introduction
Proton affinity as an inherent property of a molecule determines its protonation state, enthalpic contribution to pKa,1,2 and reaction dynamics,3 and impacts proton transport.3,4 Evaluating which sites have the lowest energetic barrier for deprotonation is one part of predicting the overall protonation state of a molecule. The proton affinity Epa is given as| Epa≡ −ΔH = ΔE + ΔEZPVE + H(H+) | (1) |
| ΔH = H(AH) − H(A−) − H(H+) | (2) |
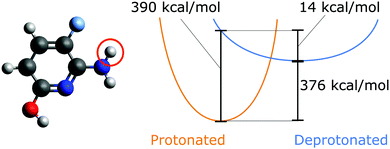
Previous work has shown that only high levels of theory afford deprotonation energies which are accurate enough to allow comparison to experiments with chemical accuracy.8 These calculations, however, are expensive, since almost all practically relevant molecules can be deprotonated at multiple sites, which drastically increases the computational cost. For example, in the case of the QM9 database9,10 which contains organic molecules with up to nine heavy atoms (not counting hydrogens), on average nine protons are available per molecule. If up to two sites are allowed to be deprotonated, this yields 9 + 9 × 8/2 = 45 possible protonation states. For larger molecules where the protonation state is relevant, e.g. for molecular packing11,12 or conformational structure of proteins,13 this number quickly becomes so large that the systematic enumeration of all protonation states is rendered computationally prohibitive.
Recently, alchemical perturbation density functional theory (APDFT)14 has been developed which offers a way to drastically reduce the computational cost of such screening efforts. The core idea is to treat a change in nuclear charges as a perturbation to a molecular Hamiltonian where all other degrees of freedom such as geometry and number of electrons are fixed. This is achieved by defining a new mixed electronic Hamiltonian Ĥ:
| Ĥ ≡ λĤt + (1 − λ)Ĥr, | (3) |
Contrary to the typical computational quantum alchemy application which modifies nuclear charges or pseudo-potentials of heavy elements, we here focus on the annihilation of protons only. More specifically, the overall difference between the energy Et of a target molecule, i.e. any of the many possible deprotonated anions, and the energy Er of the neutral reference molecule can be written according to ref. 14 as
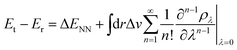 | (4) |
So far, the density derivatives ∂λρ implicitly depend on the target compound, since they denote the density derivatives in the direction of the target molecule. However, by virtue of the chain rule, we can express the first two orders as
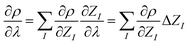 | (5) |
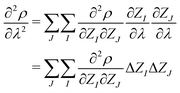 | (6) |
In the context of APDFT, deprotonation is equivalent to changing the nuclear charge of the hydrogen site to zero while keeping the total number of electrons fixed. This means that either ΔZI = 0 (for heavy atoms or protons that stay in place for a given target) or ΔZI = −1 (for sites which are deprotonated).
2 Methods
To numerically assess this approach, we chose 100 random molecules (full list in the ESI,† five examples in Fig. 3) from the QM9 database9 in the B3LYP local minimum geometries given in that database. All of these molecules have been evaluated on two levels of theory: HF/def2-TZVP45 and CCSD/6-31G*,46–48 as provided by the Basis Set Exchange.49–51 For CCSD, we chose a smaller basis set to reduce the overall computational cost of the self-consistent results to which we compare our APDFT results. The def2-TZVP basis set is parametrically optimized at the HF level, i.e. partial derivatives of the energy with respect to the basis set parameters are designed to be zero at the HF level. This makes the def2 family particularly accurate for APDFT at the HF level, which is why it has been chosen in this work.We used the APDFT code52 and PySCF53 to calculate the electron density and its first two derivatives for both levels of theory (details in the ESI†). For a subset thereof, the electron densities and their derivatives have been validated with both MRCC54 and Gaussian55 and the same corresponding levels of theory.
For each molecule, all unique singly and doubly deprotonated configurations have been evaluated explicitly (i.e. self-consistently) by iterating over all sites, in total 5'160 for each level of theory. All these evaluations have been done vertically, i.e. in the geometry of the fully protonated molecule as found in the QM9 database. Upon deprotonation, the basis functions of the hydrogen atoms in question have been removed together with the nucleus. The density derivatives are obtained from central finite differences where the nuclear charges are perturbed by 0.05e, which requires 1'816 calculations for all molecules for the first order and 8'304 calculations for the second order contributions. Note that none of these molecules feature intramolecular hydrogen bonds (IMHB) in the geometries we investigated. With the energy contribution of IMHB being significant for relative ranking of conformers but much smaller in magnitude than the overall deprotonation energy, we expect some but no large differences between the alchemical derivatives for removing a proton that is and one that is not part of an IMHB.
All integrals have been evaluated analytically by calculating the electrostatic potential at the nuclei for all obtained electron densities.
3 Results and discussion
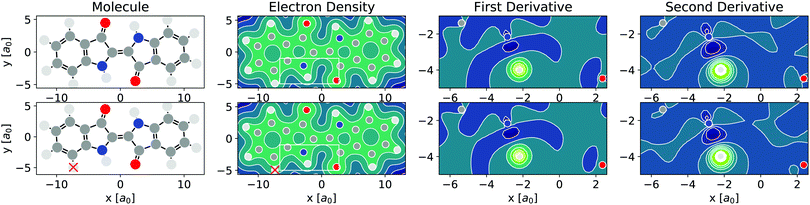
As per eqn (4), APDFT requires the electron density derivatives with respect to the nuclear charges. Fig. 2 shows how these derivatives look like for hydrogen sites. One can think of these derivatives being the electron density response upon adding a proton at that location. In the first derivative, electron density gets concentrated around the proton, which satisfies Kato's cusp theorem56 that any nuclear charge needs to create a singularity in the electron density. The electron density that is built up around the hydrogen atom mostly comes from the atom it is bonded to and (to a lesser extent) from the bond axis. The second derivative (which has a smaller absolute magnitude than the first derivative) then polarises the electron density around the hydrogen atom more strongly by depleting the electron density at the side facing the bonded atom and accumulating density at the opposite side. This means that the vast majority of the density rearrangement upon protonation is happening along the bond axis of that hydrogen and, as such, is highly local. Interestingly, this applies to both first and second order density derivatives in a part of the molecule that is in close vicinity to regions of high electron density like the oxygen atom. Since the change in energy obtained via APDFT depends on these density derivatives only, the observation of highly localised electron density derivatives is an indication of deprotonation energies being additive. As shown in Fig. 2, the density derivatives due to a deprotonation are largely unaffected by already deprotonated sites nearby. This means that the electron density derivatives constituting the second step in formation of a doubly deprotonated molecule are still highly localised and similar to a single deprotonation event. This points towards a high transferability of the density derivatives across molecular environments.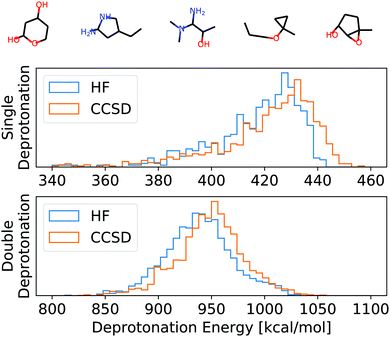 | ||
| Fig. 3 Top: Example molecules used for the evaluation of HF, CCSD, and APDFT (full list in the ESI†). Bottom: Histogram of the deprotonation energies for single and double deprotonation in the data set considered. Data shown for HF/def2-TZVP and CCSD/6-31G*. | ||
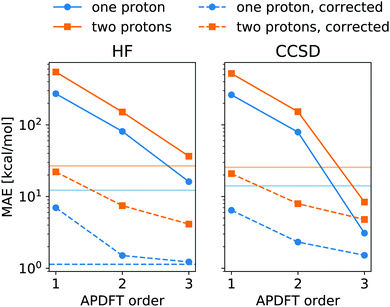
The energy expression of APDFT, eqn (4), is a sum of infinitely many terms. With more and more higher order terms, the expression becomes more accurate, but also more expensive to evaluate. To be practically relevant, this sum needs to be quickly converging. Fig. 4 shows the mean absolute error (MAE) for APDFT systematically decreasing with the order n in eqn (4), since more and more of the electron density response is taken into account. This is the case for both singly and doubly deprotonated molecules which are separated in the figure. Consistently, i.e. regardless of method and APDFT order, stripping two protons from the molecule carries a significantly larger error. This is because if two sites are alchemically changed at the same time, these changes interact. In APDFT, the first two orders only contain per-site terms, while the third order is the first to contain pairwise terms.
The residual error of APDFT, however, is systematic in nature. This allows for a simple correction where each value is shifted by the median error of comparable results, which captures the average contributions from higher orders in the APDFT expression. This correction brings down the MAE by one order of magnitude. With 1.4 kcal mol−1 accuracy, APDFT is quantitative for the deprotonation energy of one site comparable to HF which reaches a residual error of 1.3 kcal mol−1. In practice, when searching for site-specific deprotonation energies, this only requires a few calibrating calculations to find the median error for a given APDFT order which can then be applied to the remaining data set. Since the median is a robust metric, i.e. only marginally affected by outliers, very few such calibration calculations will stabilise the value for this correction.
To set this accuracy into perspective, Fig. 3 shows the histogram of deprotonation energies for the molecules in our data set. They span 120 kcal mol−1 for single deprotonation and 200 kcal mol−1 for double deprotonation. By comparison, the APDFT accuracy of 1.4 kcal mol−1 is nearly two orders of magnitude smaller than the value range.
In the context of APDFT, the success of this simple correction can be understood physically. Let us consider the case where the first two orders are included explicitly for single deprotonation. Then the energy expression is
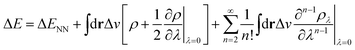 | (7) |
To set the MAE into perspective, Fig. 4 also shows the standard deviation of the deprotonation energies in our dataset. If one were to estimate deprotonation energies by their average, an error of that magnitude would be expected. Interestingly, the absolute values without the correction only come close to (HF) or improve upon (CCSD) this level of accuracy at third order APDFT. After the correction, however, even first order APDFT is better than this estimate even though first order APDFT carries nearly no computational cost and only uses the electron density of the reference molecule. While the first order term is not sufficient to obtain practically useful deprotonation energies, this illustrates how quickly relevant physics is captured in the sum of the APDFT energy expression.
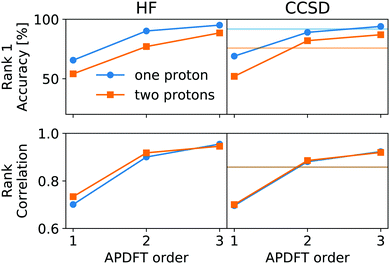
This correction, however, is only required if absolute deprotonation energies are required. The typical use case is to identify the one proton of a molecule that can be stripped away most easily. This requires ranking the deprotonation energies of all sites in a given molecule. Fig. 5 shows the performance of APDFT in this regard. Interestingly, the rank 1 accuracy exceeds 50% even at the first order, i.e. without the inclusion of any density derivative at all. For both levels of theory investigated in this work, the accuracy reaches 94% after inclusion of the median-corrected third order of APDFT for single deprotonation. This is remarkable, since HF itself is correct in 85% of the cases when CCSD ranking is the reference. This way, using APDFT on CCSD data is more accurate than doing all calculations self-consistently with Hartree–Fock calculations. Therefore, it can be more efficient to invest in few higher-quality calculations and then use APDFT for the derivatives for all individual targets than to brute-force the enumeration over all possible targets at some intermediate level of theory.
For two protons being removed at the same time, the APDFT predictions systematically improve with order as well. Note that the ranking improvement by including the third order terms is not as large as the improvement seen in Fig. 4 for absolute energies. This points towards the first two orders recovering the overall ranking and the third order mostly shifting deprotonation energies to be more accurate.
Fig. 5 also shows Kendall's τ as the metric of the overall accuracy of the ranking, not only of one particular rank. Kendall's τ57 has been chosen since it is more resilient against effects of the small number of ranks to consider than, e.g., the Spearman rank. The picture for the overall ranking is very consistent with the rank 1 accuracy: starting from the second order terms, APDFT on CCSD data is more accurate than self-consistent Hartree–Fock calculations when compared to the CCSD reference results. Again, the ranking improvement of the third order terms is noticeable, but a sufficient ranking accuracy is already established at the second order.
Generally, the spatial electron densities are quite similar across methods, while the total energies associated with these densities vary widely. If the electron densities are similar between methods, then their derivatives must be similar as well in order to keep that similarity across chemical space. In the APDFT energy expression, the first order term establishes the total energy baseline for any target molecule, while the higher order terms give density-based corrections to that first estimate. Note that no total energy of any level of theory enters the expression for the higher order terms. Now if densities and their derivatives are more similar between methods than the total energies are, then it is a promising route to obtain the first order term from high quality calculations (e.g. CCSD) and the higher orders being approximated by the density derivatives obtained at a lower and cheaper level of theory (e.g. HF).
To this end, we shall give any density or density derivative with the level of theory at which it has been obtained as superscript. Then the first three orders for the deprotonation energy ΔE as obtained from central finite difference derivatives with a finite difference stencil of Δλ are given by
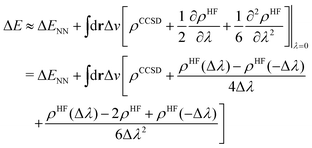 | (8) |
Fig. 6 shows the resulting accuracy for deprotonation energies following this approach. In direct comparison to CCSD density derivatives, this mixed approach is of comparable quantitative accuracy. Moreover, the median correction outlined above is still applicable for the results of mixed levels of theory. Since the difference between CCSD and HF is the inclusion of correlation energy in the former, this means that the correlation energy needs to be highly similar between different deprotonated targets, even though it can vary arbitrarily between neutral molecules. Despite the purely Coulombic expression in eqn (4), APDFT recovers all energy contributions covered by the level of theory at which the density derivatives have been evaluated. Consequently, the electron density derivatives only include physical effects that are part of the level of theory at which they have been evaluated. Therefore, this mixed approach is only likely to work for those cases where the correlation energy is substantial enough to require the inclusion of it in the first order but also locally constant in chemical space, i.e. of comparable value for nearby target molecules.
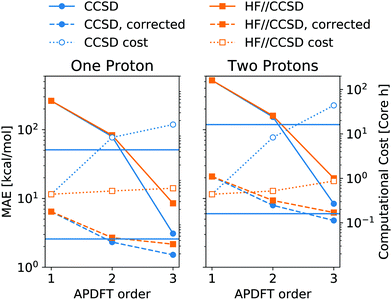 | ||
| Fig. 6 Mean absolute error (MAE) of deprotonation energies obtained from APDFT with CCSD/6-31G* data for the first order and HF/def2-TZVP data for higher orders, denoted HF//CCSD. Exact expression given in eqn (8). Median-corrected (see text) data shown as dashed lines. Computational cost of APDFT shown with dotted lines. Upper/lower horizontal line refers to brute-force full SCF with CCSD/6-31G* and HF/6-31G*, respectively. Reference data are CCSD/6-31G* deprotonation energies for both panels. | ||
As shown in Fig. 6, this mixed approach requires 2% of the computational cost of third order APDFT for the 6-31G* basis set used. Note that this speedup becomes more and more pronounced with larger basis sets and larger molecules, since the inherent scaling of CCSD is worse than the scaling of HF with respect to the number of basis functions. While for very small molecules, a brute-force calculation of all possible single deprotonations can be cheaper than APDFT, since the number of derivatives APDFT requires is comparably high in small molecules, the hybrid approach HF//CCSD is always significantly cheaper. Most importantly, due to the chain rule trick, APDFT scales with the combinatorial increase of possible deprotonations for multiple protons being removed: Fig. 6 shows second order non-APDFT to be more expensive than brute-force CCSD for single deprotonations, but already for double protonations, APDFT is cheaper. The hybrid approach, however, is computationally more efficient in all cases.
4 Conclusion
In the context of deprotonation of small organic molecules, this work suggests the use of the quantum alchemy method APDFT to quantify deprotonation energies ΔE and rank the individual sites by using high-quality reference calculations and the density derivatives only instead of calculating deprotonated species explicitly with a medium level method. If required, the computational cost can be reduced further by evaluating higher order derivatives at a lower level of theory. The systematic contribution of higher order terms in APDFT that are not evaluated at all can be treated by shifting results by their molecule-independent median deviation from reference results. In the case of CCSD and HF, this procedure yields more reliable results at a substantially lower computational cost.The accuracy for absolute deprotonation energies of 1.4 kcal mol−1 is on a par with quantum chemical calculations with large basis sets when compared to experiments1 and substantially outperforms semiempirical methods.6 In terms of ranking, the quantum alchemy predictions from APDFT based on CCSD derivatives are found to be more accurate than explicit HF calculations. This means that APDFT gives energies close to the explicitly calculated reference values which in turn are closer to experiment values if the level of theory is able to capture more relevant physical effects. This could be particularly helpful for cases like metal centers where only high-level reference methods are able to describe the electronic structure sufficiently accurately.
As an outlook, our findings are also promising for enabling ensemble calculations of free energies throughout chemical compound space, generating extensive lists of pKa estimates58 for entire molecular libraries. Future work will deal with more systematic assessments of the hybrid approach for larger sets of molecules.
We acknowledge support from the Swiss National Science foundation (No. PP00P2_138932, 407540_167186 NFP 75 Big Data, 200021_175747 and NCCR MARVEL). Some calculations were performed at sciCORE (http://scicore.unibas.ch/) scientific computing core facility at the University of Basel.
Conflicts of interest
There are no conflicts to declare.References
- A. Moser, K. Range and D. M. York, J. Phys. Chem. B, 2010, 114, 13911 CrossRef CAS PubMed.
- M. Sulpizi and M. Sprik, J. Phys.: Condens. Matter, 2010, 22, 284116 CrossRef PubMed.
- C. M. Carlin and M. S. Gordon, J. Phys. Chem. A, 2016, 120, 6059 CrossRef CAS PubMed.
- G. F. von Rudorff, R. Jakobsen, K. M. Rosso and J. Blumberger, J. Phys. Chem. Lett., 2016, 7, 1155 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, M. Diedenhofen and M. E. Beck, J. Phys. Chem. A, 2003, 107, 9380 CrossRef CAS PubMed.
- K. Range, D. Riccardi, Q. Cui, M. Elstner and D. M. York, Phys. Chem. Chem. Phys., 2005, 7, 3070 RSC.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef PubMed.
- K. Range, C. S. López, A. Moser and D. M. York, J. Phys. Chem. A, 2006, 110, 791 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864 CrossRef CAS PubMed.
- J. Zhang, Q. Zhang, T. T. Vo, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2015, 137, 1697 CrossRef CAS PubMed.
- D. Sadhukhan, M. Maiti, G. Pilet, A. Bauzá, A. Frontera and S. Mitra, Eur. J. Inorg. Chem., 2015, 1958 CrossRef CAS.
- N. V. D. Russo, D. A. Estrin, M. A. Martí and A. E. Roitberg, PLoS Comput. Biol., 2012, 8, e1002761 CrossRef PubMed.
- G. F. von Rudorff and O. A. von Lilienfeld, 2018, arXiv:1809.01647v4.
- L. L. Foldy, Phys. Rev., 1951, 83, 397 CrossRef CAS.
- E. B. Wilson, J. Chem. Phys., 1962, 36, 2232 CrossRef CAS.
- S. T. Epstein, A. C. Hurley, R. E. Wyatt and R. G. Parr, J. Chem. Phys., 1967, 47, 1275 CrossRef CAS.
- P. Politzer and R. G. Parr, J. Chem. Phys., 1974, 61, 4258 CrossRef CAS.
- P. Politzer and M. Levy, J. Chem. Phys., 1987, 87, 5044 CrossRef CAS.
- P. Politzer, P. Lane and M. C. Concha, Int. J. Quantum Chem., 2002, 90, 459 CrossRef.
- O. A. von Lilienfeld, R. Lins and U. Rothlisberger, Phys. Rev. Lett., 2005, 95, 153002 CrossRef PubMed.
- A. Beste, R. J. Harrison and T. Yanai, J. Phys. Chem., 2006, 125, 074101 CrossRef CAS PubMed.
- O. A. von Lilienfeld and M. E. Tuckerman, J. Chem. Phys., 2006, 125, 154104 CrossRef PubMed.
- O. A. von Lilienfeld, J. Chem. Phys., 2009, 131, 164102 CrossRef PubMed.
- M. Lesiuk, R. Balawender and J. Zachara, J. Comp. Physiol., 2012, 136, 034104 CrossRef PubMed.
- O. A. von Lilienfeld, Int. J. Quantum Chem., 2013, 113, 1676 CrossRef CAS.
- K. Chang and O. A. von Lilienfeld, Chimia, 2014, 68, 602 CrossRef CAS PubMed.
- M. Munoz and C. Cardenas, Phys. Chem. Chem. Phys., 2017, 19, 16003 RSC.
- S. Fias, S. Chang and O. A. von Lilienfeld, J. Phys. Chem. Lett., 2019, 10(1), 30–39 CrossRef CAS PubMed.
- V. Marcon, O. A. von Lilienfeld and D. Andrienko, J. Comp. Physiol., 2007, 127, 064305 Search PubMed.
- K. Leung, S. B. Rempe and O. A. von Lilienfeld, J. Comp. Physiol., 2009, 130, 204507 Search PubMed.
- D. Sheppard, G. Henkelman and O. A. von Lilienfeld, J. Comp. Physiol., 2010, 133, 084104 Search PubMed.
- F. Weigend, C. Schrodt and R. Ahlrichs, J. Chem. Phys., 2004, 121, 10380 CrossRef CAS PubMed.
- F. Weigend, J. Chem. Phys., 2014, 141, 134103 CrossRef PubMed.
- A. Solovyeva and O. A. von Lilienfeld, Phys. Chem. Chem. Phys., 2016, 18, 31078 RSC.
- M. Baben, J. O. Achenbach and O. A. von Lilienfeld, J. Comp. Physiol., 2016, 144, 104103 Search PubMed.
- K. Y. S. Chang, S. Fias, R. Ramakrishnan and O. A. von Lilienfeld, J. Chem. Phys., 2016, 144, 174110, DOI:10.1063/1.4947217.
- K. Saravanan, J. R. Kitchin, O. A. von Lilienfeld and J. A. Keith, J. Phys. Chem. Lett., 2017, 8, 5002 CrossRef CAS PubMed.
- C. D. Griego, K. Saravanan and J. A. Keith, Adv. Theory Simul., 2018, 1800142 Search PubMed.
- Y. S. Al-Hamdani, A. Michaelides and O. A. von Lilienfeld, J. Chem. Phys., 2017, 147, 164113 CrossRef PubMed.
- S. Fias, F. Heidar-Zadeh, P. Geerlings and P. W. Ayers, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11633 CrossRef CAS PubMed.
- R. Balawender, M. Lesiuk, F. D. Proft and P. Geerlings, J. Chem. Theory Comput., 2018, 14, 1154 CrossRef CAS PubMed.
- K. S. Chang and O. A. von Lilienfeld, Phys. Rev. Mater., 2018, 2, 073802 CrossRef.
- G. F. von Rudorff and O. A. von Lilienfeld, J. Phys. Chem. B, 2019, 123(47), 10073–10082 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59(11), 4814–4820 CrossRef CAS PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045 CrossRef CAS PubMed.
- https://github.com/ferchault/APDFT .
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K. Chan, Pyscf: the python-based simulations of chemistry framework, 2017, DOI:10.1002/wcms.1340.
- M. Kállay, P. R. Nagy, Z. Rolik, D. Mester, G. Samu, J. Csontos, J. Csóka, B. P. Szabó, L. Gyevi-Nagy, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and B. Hégely, Mrcc, a quantum chemical program suite, 2019, http://www.mrcc.hu Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. Kato, Commun. Pure Appl. Math., 1957, 10, 151 CrossRef.
- M. G. Kendall, Biometrika, 1938, 30, 81 CrossRef.
- M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06471k |
| This journal is © the Owner Societies 2020 |