Open Access Article
Open Access ArticleBenchmark and performance of long-range corrected time-dependent density functional tight binding (LC-TD-DFTB) on rhodopsins and light-harvesting complexes†
Beatrix M.
Bold
 a,
Monja
Sokolov
a,
Sayan
Maity
a,
Monja
Sokolov
a,
Sayan
Maity
 b,
Marius
Wanko
c,
Philipp M.
Dohmen
a,
Julian J.
Kranz
ad,
Ulrich
Kleinekathöfer
b,
Marius
Wanko
c,
Philipp M.
Dohmen
a,
Julian J.
Kranz
ad,
Ulrich
Kleinekathöfer
 b,
Sebastian
Höfener
b,
Sebastian
Höfener
 a and
Marcus
Elstner
a and
Marcus
Elstner
 *ad
*ad
aInstitute of Physical Chemistry, Karlsruhe Institute of Technology (KIT), Kaiserstrasse 12, 76131 Karlsruhe, Germany. E-mail: marcus.elstner@kit.edu
bDepartment of Physics and Earth Science, Jacobs University Bremen, 28759 Bremen, Germany
cNano-Bio Spectroscopy Group and ETSF, Dpto. Material Physics, Universidad del País Vasco, 20018 San Sebastiàn, Spain
dInstitute of Biological Interfaces (IBG2), Karlsruhe Institute of Technology (KIT), Kaiserstrasse 12, 76131 Karlsruhe, Germany
First published on 13th January 2020
Abstract
The chromophores of rhodopsins (Rh) and light-harvesting (LH) complexes still represent a major challenge for a quantum chemical description due to their size and complex electronic structure. Since gradient corrected and hybrid density functional approaches have been shown to fail for these systems, only range-separated functionals seem to be a promising alternative to the more time consuming post-Hartree–Fock approaches. For extended sampling of optical properties, however, even more approximate approaches are required. Recently, a long-range corrected (LC) functional has been implemented into the efficient density functional tight binding (DFTB) method, allowing to sample the excited states properties of chromophores embedded into proteins using quantum mechanical/molecular mechanical (QM/MM) with the time-dependent (TD) DFTB approach. In the present study, we assess the accuracy of LC-TD-DFT and LC-TD-DFTB for rhodopsins (bacteriorhodopsin (bR) and pharaonis phoborhodopsin (ppR)) and LH complexes (light-harvesting complex II (LH2) and Fenna–Matthews–Olson (FMO) complex). This benchmark study shows the improved description of the color tuning parameters compared to standard DFT functionals. In general, LC-TD-DFTB can exhibit a similar performance as the corresponding LC functionals, allowing a reliable description of excited states properties at significantly reduced cost. The two chromophores investigated here pose complementary challenges: while huge sensitivity to external field perturbation (color tuning) and charge transfer excitations are characteristic for the retinal chromophore, the multi-chromophoric character of the LH complexes emphasizes a correct description of inter-chromophore couplings, giving less importance to color tuning. None of the investigated functionals masters both systems simultaneously with satisfactory accuracy. LC-TD-DFTB, at the current stage, although showing a systematic improvement compared to TD-DFTB cannot be recommended for studying color tuning in retinal proteins, similar to some of the LC-DFT functionals, because the response to external fields is still too weak. For sampling of LH-spectra, however, LC-TD-DFTB is a viable tool, allowing to efficiently sample absorption energies, as shown for three different LH complexes. As the calculations indicate, geometry optimization may overestimate the importance of local minima, which may be averaged over when using trajectories. Fast quantum chemical approaches therefore may allow for a direct sampling of spectra in the near future.
1 Introduction
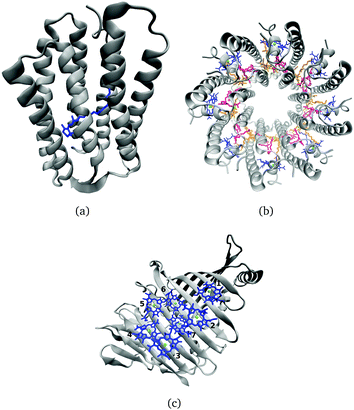
Many biological processes are triggered by the absorption of photons. Two prominent and well studied protein classes involving these processes are rhodopsins and light-harvesting (LH) complexes. Microbial rhodopsins consist of seven transmembrane helices (Fig. 2) embedded in a membrane, forming an internal binding pocket, where the chromophore all-trans retinal (Fig. 1) is bonded via a Schiff base (SB) to an ε-amino group of a lysine side chain. They are mainly classified through their retinal conformation and binding pocket. In organic solvents the absorption maximum of the chromophore retinal is about 450 nm,1 while in proteins it varies from 360 to 635 nm.2 As rhodopsin models in this work, bacteriorhodopsin (bR) and pharaonis phoborhodopsin (ppR), are chosen. The binding pockets of bR and ppR differ in only 10 amino acids within 5 Å of the retinal and features the same arrangement of counter ions. Despite the similarity, the absorption maximum of ppR (497 nm)3 is blue shifted by about 70 nm relative to bR (568 nm),4 which has been attributed to a number of small contributions that all add up in a constructive manner. The overall shift between these two proteins hence poses a critical test as the experimental value is less likely achieved due to error cancellation as, e.g., the shift from vacuum to the protein (opsin shift).5,6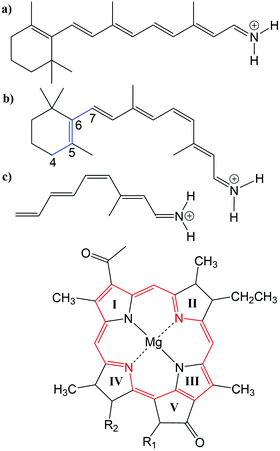 | ||
Fig. 1 Top: (a) all-trans retinal, (b) 6-s-cis-11-cis retinal, in blue: twisted dihedral angle (C4–C5–C6–C7), (c) PSB5 model; bottom: BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a; in red diaza18-annulene substructure visible; full model: R1 = COOMe, R2 = phytyl-tail; model with truncated phytyl-tail: R1 = COOMe, R2 = COOMe; truncated model: R1 = H, R2 = CH3. a; in red diaza18-annulene substructure visible; full model: R1 = COOMe, R2 = phytyl-tail; model with truncated phytyl-tail: R1 = COOMe, R2 = COOMe; truncated model: R1 = H, R2 = CH3. | ||
LH complexes are aggregates of proteins and chromophores, i.e., often bacteriochlorophyll (BChl) or chlorophyll (Chl) chromophores, which are mainly responsible for photosynthesis in bacteria and plants. They absorb light and collect the energy to transfer it to the photosynthetic reaction center (RC) using an excitation energy transfer (EET) mechanism.7 The absorption spectra of (bacterio)chlorophylls exhibit two key features, which are the Soret-band in the near UV region and the Q-bands in the visible region. The labeling of the absorption peaks is based on the four-orbital model for porphyrin derivatives proposed by Gouterman et al.8,9 While in free-base porphyrins the two highest occupied molecular orbitals (HOMOs) and lowest unoccupied molecular orbitals (LUMOs) are energetically degenerated, in (bacterio)chlorophylls this degeneracy is lifted due to the reduced symmetry leading to a splitting of the Q-bands into the so-called Qx and Qy bands. In this work, only the Qy state, i.e., the lowest excited state, is considered. In organic solvents the absorption maximum of BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (Fig. 1) is at around 770 nm.10
a (Fig. 1) is at around 770 nm.10
In the present work, two LH2 complexes of Rs. molischianum and Rps. acidophila and the FMO complex of C. tepidum are chosen (Fig. 2). The LH2 complex of Rs. molischianum (in brackets are given the values for Rps. acidophila) contains 24 (27) BChls, arranged in two rings, called B800 (1.55 eV) and B850 (1.46 eV) corresponding to their respective absorption maxima. The B800 ring consists of eight (nine) BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores with an inter-chromophore distance of about 20 Å, while the B850 ring consists of 16 (18) BChl
a chromophores with an inter-chromophore distance of about 20 Å, while the B850 ring consists of 16 (18) BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores with a distance of about 9 Å. The FMO complex used here consists of a monomer including seven BChls, which are separated by about 10–20 Å and arranged asymmetrically in contrast to the LH2 complex. The absorption maxima of the FMO complex are found experimentally in a range of 790 nm to 825 nm (1.50–1.57 eV).11 The reason for the red-shift compared to the one in organic solvents (770 nm (1.61 eV)10) is found to be originating from the protein environment and the excitonic inter-chromophore coupling. In the case of LH2, the absorption shift of the B850 ring mainly originates from the exciton couplings, while the absorption shift of the B800 ring and the ones occurring in the FMO complex are to a large extent caused by the protein environment.12–14
a chromophores with a distance of about 9 Å. The FMO complex used here consists of a monomer including seven BChls, which are separated by about 10–20 Å and arranged asymmetrically in contrast to the LH2 complex. The absorption maxima of the FMO complex are found experimentally in a range of 790 nm to 825 nm (1.50–1.57 eV).11 The reason for the red-shift compared to the one in organic solvents (770 nm (1.61 eV)10) is found to be originating from the protein environment and the excitonic inter-chromophore coupling. In the case of LH2, the absorption shift of the B850 ring mainly originates from the exciton couplings, while the absorption shift of the B800 ring and the ones occurring in the FMO complex are to a large extent caused by the protein environment.12–14
The individual chromophores in these biological systems exhibit very specific absorption spectra. In principle, there are several factors determining the absorption maximum, which are (i) the chromophore structure, influenced by the protein environment, (ii) the interaction with the electrostatic environment due to ionic, polar or polarizable groups of amino acids, and (iii) direct hydrogen-bonding or van der Waals (vdW) interactions and (iv) exciton couplings. All these factors are responsible for “color-tuning” of the respective chromophores within their protein environment. The detailed mechanism of “color-tuning” is experimentally not fully available and computational studies are thus of interest for a deeper understanding. Computational methods can disentangle those factors, however the choice of the method is important in order to confirm that the form of the spectrum results from correct physical description and not due to error cancellation. The computational methods should therefore be sufficiently efficient to allow for sampling of the conformational space. Single structures, e.g., computed by QM/MM geometry optimization may not be representative for ensemble averages, and information about the peak widths can only be gained from standard deviations.
Both chromophores, retinal and BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a have been shown to be particularly cumbersome for an accurate quantum chemical description. Often even obtaining ground state geometries is a non-trivial task as various methods yield very different values for the bond-length alternation (BLA), which is defined as the difference between the average single- and double bond lengths along a conjugation chain or ring, and has a sizable impact on excitation energies. Excited states can exhibit multi-reference character, while charge transfer is important, in particular for retinal. In principle, this would require multi-reference configuration interaction methods (MRCI). Complete-active space self-consistent field (CASSCF) together with second-order perturbation theory (CASPT2) yields excited state properties in agreement with experimental results for retinal, however, at high computational costs.15–17 An alternative method to study retinal is the ab initio spectroscopy oriented configuration interaction (SORCI) method, which yields the same accuracy as CASPT2 but at reduced computational effort.18 In contrast to retinal, BChl has a large active space, which makes it difficult for MRCI methods to investigate its properties in the excited state. MRCI methods used in previous studies are e.g., RASSCF/RASPT2,19,20 or DFT/MRCI.21 Similarly, optimized geometries have to be computed at a computationally less expensive level of theory.
a have been shown to be particularly cumbersome for an accurate quantum chemical description. Often even obtaining ground state geometries is a non-trivial task as various methods yield very different values for the bond-length alternation (BLA), which is defined as the difference between the average single- and double bond lengths along a conjugation chain or ring, and has a sizable impact on excitation energies. Excited states can exhibit multi-reference character, while charge transfer is important, in particular for retinal. In principle, this would require multi-reference configuration interaction methods (MRCI). Complete-active space self-consistent field (CASSCF) together with second-order perturbation theory (CASPT2) yields excited state properties in agreement with experimental results for retinal, however, at high computational costs.15–17 An alternative method to study retinal is the ab initio spectroscopy oriented configuration interaction (SORCI) method, which yields the same accuracy as CASPT2 but at reduced computational effort.18 In contrast to retinal, BChl has a large active space, which makes it difficult for MRCI methods to investigate its properties in the excited state. MRCI methods used in previous studies are e.g., RASSCF/RASPT2,19,20 or DFT/MRCI.21 Similarly, optimized geometries have to be computed at a computationally less expensive level of theory.
Single-reference methods with in many cases sufficient accuracy such as the second-order approximate coupled cluster singles and doubles (CC2) can describe retinal excited states for a mostly planar retinal configuration or without the inclusion of the β-ionone ring.22–24 The optimization of the retinal geometry in the ground and excited state is only accurate if far away from the conical intersection region.23,25 Hence, the popular CC2 method is not applicable to all intermediate steps required when studying, e.g., the isomerization of retinal. In the case of BChl, CC2 can successfully describe the excitation energies of truncated BChl structures,26 while it shows weaknesses in the application to the complete BChl structure, as it occurs in proteins due to the sensitivity on the multi-configurational character of BChl.21
Density functional theory (DFT) methods, although computationally efficient, can only be applied with care: DFT in the generalized gradient approximation (GGA) significantly underestimates the BLA, while hybrid functionals result in improved predictions of the BLA when an increasing amount of exact exchange is included.6,27 Excitation energies obtained with the response formalism (TD-DFT) are only reasonable for mostly planar retinal structures.24 The response of the excitation energies on the electrostatic interaction, is grossly underestimated with standard TD-DFT functionals,18 making these methods effectively useless for color tuning studies. For BChl, however, hybrid functionals seem to perform reasonably well, when taking DFT/MRCI as reference.21 Problems with hybrid functionals occur especially when investigating the carotenoids, which are also present in LH complexes.12
The failure of TD-DFT methods, when using standard GGA or hybrid functionals, is rooted with their inability to capture charge transfer excitations which play a role in rhodopsins and to some extend also in LH complexes.14,18 For charge transfer excitations in organic molecules, an improvement is provided by long-range corrected (LC) functionals,28,29 and even for the isomerization of retinal.30 A study investigating the excited state relaxation of retinal shows that LC-BLYP31 provides results in accordance with CASPT2.32 In a benchmark study on BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a in FMO, CAM-B3LYP33 was reported to yield results in accordance with DFT/MRCI.21 Furthermore, CAM-B3LYP can reproduce experimental results for excitation energies of BChl
a in FMO, CAM-B3LYP33 was reported to yield results in accordance with DFT/MRCI.21 Furthermore, CAM-B3LYP can reproduce experimental results for excitation energies of BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a in different solvents.34
a in different solvents.34
Using ab initio and TD-DFT approaches, excitation energies are often computed for single structures, e.g., for QM/MM optimized geometries of chromophore and protein environment. The computation of excitation energies of sampled structures obtained by molecular dynamics (MD) simulations is required not only to determine correct averages and widths of the absorption spectra, but also to investigate, e.g., temperature effects as reported in previous studies.35,36 Therefore, methods with low computing costs based on semi-empirical Hamiltonians are frequently applied. In LH complexes, ZINDO/S-CIS37,38 is often used to sample excitation energies.27,39–41 In previous studies on retinal proteins, some of us have used OM2/MRCI for sampling of excitation energies, since its performance for relative excitation energies is comparable to SORCI,18,42 while absolute excitation energies are blue shifted. The semi-empirical TD-DFTB method faces the same problems as TD-DFT methods using GGA functionals, since TD-DFTB is based on the PBE exchange–correlation expression.43
Recently, a LC functional has been implemented into the density functional tight binding (LC-DFTB) method and has been extended to the time-dependent scheme (LC-TD-DFTB), which is about three orders of magnitude faster than the LC-TD-DFT method.44,45 The newly implemented LC-TD-DFTB allows for extensive sampling of absorption spectra and also for direct propagation of excitons, as recently shown for an anthracene crystal.46 It is therefore a promising method to study rhodopsins and LH complexes. LC-TD-DFTB has already been successfully benchmarked for a test set of small organic molecules involving charge-transfer excitations45 and found its application in the computation of gas-phase relaxation dynamics of cycloparaphenylen molecules.47 Since TD-DFTB is based on GGA and does not work for retinal proteins, ZINDO/S-CIS likely overestimates electrostatic effects on BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) absorption spectra,21 a thorough test of LC-TD-DFTB seems desirable. Even though previous studies on both retinal and BChl proteins showed that LC functionals lead to an improved description over standard functionals,21,30,32,36,48,49 there is still no systematic benchmark regarding the factors of color tuning.
absorption spectra,21 a thorough test of LC-TD-DFTB seems desirable. Even though previous studies on both retinal and BChl proteins showed that LC functionals lead to an improved description over standard functionals,21,30,32,36,48,49 there is still no systematic benchmark regarding the factors of color tuning.
In the present work, we perform a benchmark study on both the isolated chromophores retinal and BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a as well as on the biological systems, to determine the accuracy of LC-TD-DFT and LC-TD-DFTB for describing color-tuning effects. The article is structured as follows: First, the benchmark study of LC-TD-DFT and LC-TD-DFTB on retinal and BChl
a as well as on the biological systems, to determine the accuracy of LC-TD-DFT and LC-TD-DFTB for describing color-tuning effects. The article is structured as follows: First, the benchmark study of LC-TD-DFT and LC-TD-DFTB on retinal and BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a is presented on computing excitation energies with respect to geometry effects and electrostatic effects. Second, a benchmark of LC-TD-DFTB for the computation of excitonic couplings is performed. Finally, the performance of LC-TD-DFT and LC-TD-DFTB is demonstrated on two rhodopsins, bR and ppR, and two LH complexes, the LH2 and FMO complex.
a is presented on computing excitation energies with respect to geometry effects and electrostatic effects. Second, a benchmark of LC-TD-DFTB for the computation of excitonic couplings is performed. Finally, the performance of LC-TD-DFT and LC-TD-DFTB is demonstrated on two rhodopsins, bR and ppR, and two LH complexes, the LH2 and FMO complex.
2 Computational details
2.1 Models and geometry optimization
The three retinal model systems used in Section 3, displayed in Fig. 1, were taken from ref. 18. The rhodopsin model systems used in Section 4, bR (PDB code 1C3W) and ppR (PDB code 1H68), were taken from ref. 5. Concerning the chromophore BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, geometry optimizations were carried out using the Turbomole program package50 using HF and DFT, employing the functionals BH-LYP, B3LYP and BLYP together with the Karlsruhe basis sets def2-SV(P), def2-SVP, and def2-TZVP.51,52 Additionally, geometry optimizations were carried out at the SCC-DFTB level of theory,53 denoted DFTB in the following, and at the DFT level of theory using the range-separated CAM-B3LYP functional together with the def2-SVP and def2-TZVP basis sets, as implemented in the ORCA program package.54 For these different geometries, the diaza[18]-annulene substructure of BChl
a, geometry optimizations were carried out using the Turbomole program package50 using HF and DFT, employing the functionals BH-LYP, B3LYP and BLYP together with the Karlsruhe basis sets def2-SV(P), def2-SVP, and def2-TZVP.51,52 Additionally, geometry optimizations were carried out at the SCC-DFTB level of theory,53 denoted DFTB in the following, and at the DFT level of theory using the range-separated CAM-B3LYP functional together with the def2-SVP and def2-TZVP basis sets, as implemented in the ORCA program package.54 For these different geometries, the diaza[18]-annulene substructure of BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,55 see Fig. 1 in red, was used to calculate the BLA. To account for protein environment effects on the excitation energies of BChl
a,55 see Fig. 1 in red, was used to calculate the BLA. To account for protein environment effects on the excitation energies of BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, the QM/MM optimized structures of the FMO complex (PDB code 3EOJ) of P. aesturii were taken from ref. 21.
a, the QM/MM optimized structures of the FMO complex (PDB code 3EOJ) of P. aesturii were taken from ref. 21.
For the benchmark study (Section 3.2.3) of the exciton couplings of the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores, a model system was constructed. The model system contains a BChl
a chromophores, a model system was constructed. The model system contains a BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a structure (see Fig. 1), where all substituents are replaced by hydrogen atoms except of the carbonyl group of ring V. This structure was firstly optimized using SCC-DFTB. Subsequently, dimers were build differing in the inter-dimer distance.
a structure (see Fig. 1), where all substituents are replaced by hydrogen atoms except of the carbonyl group of ring V. This structure was firstly optimized using SCC-DFTB. Subsequently, dimers were build differing in the inter-dimer distance.
The LH complexes used in Section 4 were QM/MM optimized, which are the FMO complex from C. tepidum (PDB code 3ENI) and the LH2 complexes from Rs. molischianum (PDB code 1LGH) and Rps. acidophila (PDB code 1NKZ). All QM/MM optimizations were performed using the DFTB3/3OB method for the QM region as implemented in the GROMACS package (version 2017.1).56,57 The QM regions of the FMO complex and the LH2 complex contain a single BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophore, while the respective phythyl tail is not part of the QM region. Neglecting the phythyl tail in the QM region saves computational cost and does not significantly effect the excitation energies, cf.ref. 27 and 39. Both systems have been QM/MM minimized using the steepest descent (SD) algorithm (100
a chromophore, while the respective phythyl tail is not part of the QM region. Neglecting the phythyl tail in the QM region saves computational cost and does not significantly effect the excitation energies, cf.ref. 27 and 39. Both systems have been QM/MM minimized using the steepest descent (SD) algorithm (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with a tolerance of 1000 kJ mol−1 nm−1).
000 steps with a tolerance of 1000 kJ mol−1 nm−1).
2.2 Classical and QM/MM MD simulations
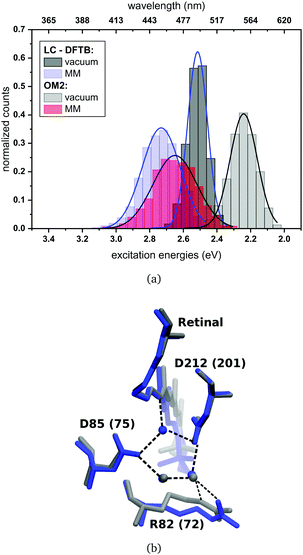
For rhodopsins, QM/MM MD simulations of both models were performed, since failures of force-field-only descriptions of the active site of retinal proteins were previously reported.35,58,59 Moreover, a well-chosen QM region is important for retinal proteins to be able to investigate effects like charge transfer, protein polarization and dispersion interaction.6 In the present study, the QM region includes retinal, the counter ions near the retinal Schiff base (RSBH+) (D85 and D212 for bR, D75 and D201 for ppR), the three water molecules near the RSBH+ and a third amino acid close to the active site (R82 for bR and R72 for ppR), see Fig. 8(b). The remaining parts of the system were treated with MM using the CHARMM36 force field.60 The QM/MM MD simulations were carried out with the DFTB3/3OB method (extended self-consistent-charge Density-Functional Tight-Binding)61–63 for the QM region, implemented in the GROMACS package.57 DFTB3/3OB is known to produce a reliable model of hydrogen bonded structures, which are present in rhodopsins, since it is able to describe hydrogen-bonded networks with similar accuracy as full DFT calculations performed with medium sized basis sets.61 The QM/MM MD trajectories had a time length of 1 ns. A QM/MM sampling of the LH complexes would require a multichromophoric QM region, which is not easily possible within the current approach. Therefore, classical MD simulations were performed with a time length of 1 ns. Computational details concerning the equilibration of the systems can be found in the ESI,† see Section S1.1. The classical MD simulations were carried out using the GROMACS package (version 2016.3)64 and the CHARMM27 force-field.652.3 Excitation energies
Vertical excitation energies were performed at the HF/CIS, ZINDO/S-CIS,37,38 TD-DFT (BP86, B3LYP) and LC-TD-DFT (CAM-B3LYP, ωB97X, LC-BLYP) level of theory as implemented in the ORCA program package.54 ZINDO/S is a short hand notation for ZINDO/S-CIS and LC-TD-DFT is abbreviated as LC-DFT in the following. For the HF/CIS computations, the def2-SVP basis set51 was chosen. For the ZINDO/S calculations an active space of (10,10), i.e., including the 10 highest occupied and the 10 lowest unoccupied states, was employed, which yields a sufficient agreement with experimental results for both BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a and retinal.41,66
a and retinal.41,66
The Tamm–Dancoff approximation (TDA)67 has been invoked for all TD-DFT calculations together with the resolution of identity (RI)68 to speed up the computations. We used the def2-TZVP basis set52 and have considered RIJCOSX69 for the Coulomb integral and HF exchange terms as well as def2/J as an auxiliary basis set70 in the RI approximation. In order to avoid large errors due to possible charge-transfer contributions in vertical excitations, long-range corrected functionals such as CAM-B3LYP, ωB97X and LC-BLYP were employed. These functionals are compared in the present work as they differ in the amount of exact exchange. For example, LC-BLYP contains 0% exact exchange at short range and 100% at long-range,31 ωB97X contains 16% exact exchange at short range and 100% at long-range71 and CAM-B3LYP consists of 19% exact exchange at short range and 65% at long-range.33 Vertical excitation energies were furthermore performed using the time-dependent generalization of DFTB (TD-DFTB)72 without and with long-range corrected functionals (LC-TD-DFTB).44,45,73 LC-TD-DFTB is abbreviated as LC-DFTB in the following. In LC-DFTB, the local BNL functional74,75 for the short-range part and a conventional non-local Hartree–Fock exchange for ω → ∞ for the long-range part was implemented.46 The range-separation parameter ω is set to ω = 0.3/a0 for the computation of the electronic parameters, which was already used in previous work.46 DFTB uses a minimal atomic orbital basis set, which is computed from atomic Kohn–Sham equations, and an additional harmonic potential is introduced to confine the basis function.
The DFT/MRCI calculations were performed with a parallel version of the DFT/MRCI code using an interface to the ORCA program package.76 For the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores we use a protocol similar to that recently reported for a Chl a chromophore.77 The first SCF step for vacuum and in the QM/MM framework were performed in ORCA 4.0 using the BH-LYP functional together with a def2-SV(P) split valence basis set.51 The latest Hamiltonian (R2018) and the “short” parameter sets were employed with a 0.8 Eh threshold for the initial and production DFT/MRCI run with 12 roots required for all structures in the present study. The reference space has been considered as eight HOMOs and six LUMOs including single and double excitations.
a chromophores we use a protocol similar to that recently reported for a Chl a chromophore.77 The first SCF step for vacuum and in the QM/MM framework were performed in ORCA 4.0 using the BH-LYP functional together with a def2-SV(P) split valence basis set.51 The latest Hamiltonian (R2018) and the “short” parameter sets were employed with a 0.8 Eh threshold for the initial and production DFT/MRCI run with 12 roots required for all structures in the present study. The reference space has been considered as eight HOMOs and six LUMOs including single and double excitations.
In order to provide reference values for vertical excitation energies, wavefunction methods are often applied. Since in the present study large systems are investigated, only low-scaling wavefunction methods could be applied to guarantee applicability for the entire set of models used. Therefore, the reference method for small molecules is a second-order approximate coupled-cluster singles and doubles (CC2) method and the algebraic diagrammatic construction scheme of second order, denoted ADC(2).78,79 Both methods employ RI. Since with increasing system size even these efficient excited-state methods can become unfeasible, these schemes are employed in the scaled-opposite-spin approximation in combination with the Laplace transformation (LT) to reduce the computational scaling, i.e., LT-SOS-RICC2 and LT-SOS-RIADC(2).80,81 In the following, these methods are denoted SOS-CC2 and SOS-ADC(2) since the RI and LT introduce only deviations significantly below the method error. All these wavefunction based methods are performed using the Turbomole program package.50 The vertical excitation energies are based on geometries obtained with the def2-SVP basis set. No significant difference were found when performing, as an exemplary comparison, the same calculations using the def2-TZVP basis set.
For the computation of the vertical excitation energies on the chromophores within their protein environment, the QM region were chosen as described above. The electrostatic environment was considered as the reminder of the protein included as fixed MM point charges for rhodopsins and the FMO complex. In the case of the LH2 complex a charge sphere around the Mg atom with a size of 20 Å was chosen as MM environment. In order to obtain proper thermal averages, structures were extracted from classical (LH complexes) as well as the QM/MM MD trajectories (rhodopsins). Along these 1 ns-long trajectories, 1000 snapshots were used for the computation of the vertical excitation energies.
In the case of rhodopsins, LC-DFTB and OM2/MRCI calculations were employed for the computation of the vertical excitation energies. The OM2/MRCI calculations were carried out using the MNDO2005 program package82,83 with an active space of (20,20).84 Due to missing Mg parameters, the OM2/MRCI approach can presently not be used for the computation of the vertical excitation energies of LH complexes. In this case, the computation were performed using LC-DFTB and ZINDO/S as detailed above.
2.4 Exciton couplings
In a next step we focus on the determination of excitonic couplings. Supermolecular calculations were performed on the model system, Section 3.2.3, using DFT/MRCI with the same setup as described above, HF/CIS with the basis set def2-SVP, TD-DFT (B3LYP) and LC-DFT (ωB97X, CAM-B3LYP) with the basis set def2-TZVP employing the TDA as implemented in the ORCA program package.54 Furthermore, the RI has been taken into account to speed up the TD-DFT calculations. As in the case of individual chromophores, we used the RIJCOSX for the Coulomb integral and HF exchange and def2/J as an auxiliary basis set in the RI approximation. Additionally, supermolecular calculations were performed using TD-DFTB and LC-DFTB.For LC-DFTB, two different parameter sets have been employed for the computation of Coulomb couplings and supermolecular calculations. The original LC-DFTB parameters reported in ref. 46, yield very good vertical excitation energies and also quite accurate Coulomb couplings, but achieve this by using quite compact atomic orbital basis sets. They were generated by a homogeneous scaling of the original GGA parameter set mio-0-1 of all radii.46 It has been shown, however, that using such a confined basis set leads to an underestimation of electron-transfer couplings.85 For this type of property, more diffuse basis functions are required since it depends on the overlap of molecular fragments in vdW distance. Therefore, a parameter set was generated using fully uncompressed radii. This parameter set was used for the supermolecular calculations.
For larger inter-chromophore distances, the excitonic couplings can be approximated by the respective Coulomb coupling only. For the model systems, Section 3.2.3, these Coulomb couplings were computed using LC-DFTB based on Mulliken transition charges and an approximation to second order Coulomb interaction described by a γ-function.45,46 We further tested the TrESP approaches (transition charges from electrostatic potentials)41,86 as well as a very similar approach based on Mulliken rather than electrostatic charges (Tr-Mulliken). To be able to perform a systematic benchmark, we refrained from rescaling the TrESP or Mulliken charges to match the experimental values of the dipole moment as done in the original TrESP scheme. For a discussion of these rescaling and screening factors, see, e.g., ref. 87. The computations of TrESP and Tr-Mulliken charges on the transition densities between ground and first excited state are performed using B3LYP and CAM-B3LYP functionals as implemented in the ORCA program package. Subsequently, the atomic transition charges were obtained using a fitting procedure implemented in the Multiwfn program package.88 Additionally, both the TrESP and the Tr-Mulliken charges have been fitted for the actual conformation of one of the two identical monomers. For the TrESP approach this procedure is slightly unusual since the charges are normally fitted for the equilibrium geometry which would potentially lead to some (model) differences between the TrESP and the supermolecular results. Details concerning the computation of the respective Coulomb couplings can be found in the ESI,† see Section S1.2.
In addition, supermolecular calculations were performed directly on a biological system, Section 3.2.4, i.e., on the B850 ring system belonging to the LH2 complex, where we considered only pairs of neighboring chromophores. The B850 ring consists of so-called α and β chromophores which have slightly varying properties due to differences in their environments. Thus the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a dimer exciton couplings V are subdivided into two groups denoted as, cf.ref. 36: inter-dimer couplings V1, where BChl
a dimer exciton couplings V are subdivided into two groups denoted as, cf.ref. 36: inter-dimer couplings V1, where BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a α and β are arranged together with one BChl
a α and β are arranged together with one BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a of the B800 ring, and intra-dimer couplings V2, with only one α- and β BChl
a of the B800 ring, and intra-dimer couplings V2, with only one α- and β BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophore. For the biological system supermolecular computations are performed with LC-DFT and LC-DFTB with the computational setups as described for the model system. For TrESP, however, the charges have been calculated only for the equilibrium conformations and then mapped onto all other conformations. This procedure is sometimes termed “frozen” TrESP approach.89 This scheme was chosen here since it is usually employed when computing Coulomb couplings along trajectories, as described above.
a chromophore. For the biological system supermolecular computations are performed with LC-DFT and LC-DFTB with the computational setups as described for the model system. For TrESP, however, the charges have been calculated only for the equilibrium conformations and then mapped onto all other conformations. This procedure is sometimes termed “frozen” TrESP approach.89 This scheme was chosen here since it is usually employed when computing Coulomb couplings along trajectories, as described above.
3 Benchmark
The aim of this section is to investigate the accuracy of LC-DFTB for different model systems. In particular, it is studied whether LC-DFTB can yield qualitatively correct excitation energies for different geometries and point charges used to model a protein environment. In Section 3.1 these influences are investigated for a retinal model, followed by an analysis using BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a in Section 3.2 for which also excitonic couplings are compared.
a in Section 3.2 for which also excitonic couplings are compared.
3.1 Retinal
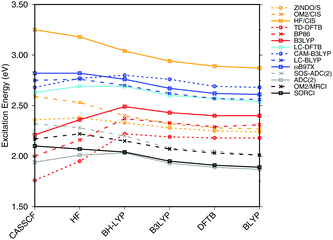 | ||
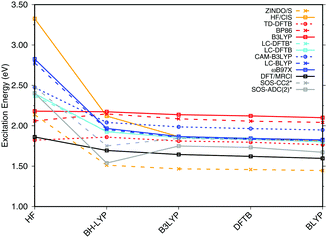
| Fig. 3 Influence of the optimization method on the excitation energies: the results for the BP86, DFTB, B3LYP, OM2/CIS, HF/CIS, OM2/MRCI, and SORCI calculations have been taken from ref. 18. | ||
SORCI as the reference method displays an expected blue shift that increases with the BLA.18 HF-based single-reference methods show the same trend. While CIS overestimates the excitation energies by a factor of about 1.5, SOS-ADC(2) agrees more quantitatively with SORCI, which also applies to OM2/MRCI. Without spin-component scaling ADC(2) agrees very well with SORCI for small BLA, however, yields a red shift for CASSCF and HF optimized structures (−0.16 eV). GGA, hybrid DFT functionals and TD-DFTB excitation energies are red-shifted by up to 0.4 eV with CASSCF geometries.
The ab initio LC functionals, LC-BLYP and ωB97X, which use 100% HF exchange in the long-range limit, obtain the same trend as SORCI, while CAM-B3LYP with only about 60% HF exchange still has a qualitative problem. The same trend as described by CAM-B3LYP is obtained by LC-DFTB, however, showing a significant improvement for the HF and CASSCF optimized retinal structures compared to the DFT-GGA and TD-DFTB based on GGA functional. As expected, absolute excitation energies are overestimated by LC functionals.
An important property is the change in excitation energy due to variation in BLA, which shows up, e.g., in the width of the absorption band due to fluctuations. SORCI has a range of Δ = 0.21 eV. SOS-ADC(2) overestimates this range, while ZINDO/S as well as CAM-B3LYP and LC-DFTB underestimate it. A similar range compared to SORCI is obtained by LC-BLYP as well as ωB97X.
To investigate the effect of delocalization on the excitation energies, a 6-s-cis-11-cis PSB model with different dihedral twist angles has been taken from ref. 18. The results of the methods tested are shown in Fig. 4. The corresponding numerical values can be found in the ESI† (Table S2). ADC(2) shows a very good agreement with SORCI, as well as SOS-ADC(2), which is only slightly blue-shifted. Moreover, CIS-based methods follow also the same trend as SORCI with higher absolute excitation energies as obtained in the case of the optimized all-trans retinal structures in Fig. 3. The failure of standard DFT functionals is visible in a red shift of the excitation energies by the retinal twist. As for the BLA, LC-DFT functionals as well as LC-DFTB show an improvement obtaining a blue shift for the twisted retinal configuration.
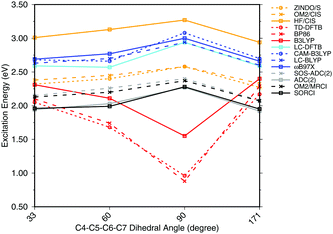 | ||
| Fig. 4 Excitation energies of a 6-s-cis-11-cis PSB in vacuum for different twist angles. The results for the BP86, DFTB, B3LYP, OM2/CIS, HF/CIS, OM2/MRCI, and SORCI calculations have been taken from ref. 18. | ||
This failure of hybrid and GGA TD-DFT approaches is even more dramatic as in the case of BLA. In many retinal proteins, i.e., in bovine rhodopsins a blue shift of absorption energy is found due to a twist in the retinal conformation around the C6–C7 single bond.90 The latter is induced by steric interaction of the environment with the retinal chromophore and represents one effective way of color tuning. It is therefore encouraging to see that the LC-DFT methods and LC-DFTB are able to reproduce this feature.
For meaningful benchmarks, a simple counterion model has been proposed, which consists of a PSB5 analog and a single point charge, see Fig. 1 interacting with a point charge in its immediate environment. The PSB5 geometry was reoptimized with DFTB using a charge of −1.1 a.u. at a distance of 2.22 Å to the SB proton,18 which results in a shift when computing the excitation energy of the reoptimized model compared to the model in vacuum. When adiabatically calculating the shift in excitation energy caused by an external field, two effects contribute, (i) the change in geometry and (ii) the interaction of the excitation-induced charge transfer with the external field. When using HF-based methods, these two contributions add up constructively whereas with GGA functionals they can partially cancel out. To show this, we first only include the point charge in the ground-state geometry optimization (column with shift “0.0” in Table 1), then also in the excited-state calculation (columns with shifts “−0.5” and “−1.1”).
| Chargeb | VEE | Shifts | ||
|---|---|---|---|---|
| 0.0c | −0.5c | −1.1 | ||
| a Taken from ref. 18. b Charges in atomic units. c Vertical excitation energy with downscaled charge but geometry optimized in presence of the full charge of −1.1 e. | ||||
| ZINDO/S | 2.78 | +0.02 | +0.13 | +0.31 |
| TD-DFTBa | 2.77 | −0.09 | +0.00 | +0.11 |
| LC-DFTB | 3.24 | +0.03 | +0.15 | +0.28 |
| CAM-B3LYP | 3.34 | −0.01 | +0.10 | +0.27 |
| LC-BLYP | 3.30 | +0.03 | +0.18 | +0.37 |
| ωB97X | 3.36 | +0.04 | +0.18 | +0.37 |
| SOS-ADC(2) | 2.74 | +0.09 | +0.35 | +0.71 |
| ADC(2) | 2.61 | +0.04 | +0.28 | +0.60 |
| OM2/MRCIa | 2.61 | +0.07 | +0.39 | +0.73 |
| SORCIa | 2.67 | +0.03 | +0.28 | +0.58 |
SORCI, considered to be the reference method, shows a blue shift of +0.58 eV with a charge of −1.1 a.u. ADC(2) and SOS-ADC(2) nicely reproduce this shift, whereas TD-DFT using GGA and hybrid functionals grossly underestimate the shift with values of less than 0.2 eV, see ref. 18. TD-DFTB reproduces this failure, and ZINDO/S shifts which are only half of the ones of the SORCI approach. An improvement is observed with LC-DFT functionals as well as LC-DFTB. LC-BLYP and ωB97X with +0.4 eV show a larger shift than CAM-B3LYP and LC-DFTB (+0.3 eV). However, the shifts are still substantially smaller, which implies a weakness of the LC functionals. In short, this finding can be termed “color-weakness”. In conclusion, TD-DFT with GGA and hybrid functionals are not able to predict color-tuning effects. Furthermore, LC-DFT cannot be considered a quantitative method in this respect neither.
3.2 Bacteriochlorophyll a (BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) a)
a)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, the use of a multi-reference method like SORCI is impossible due to the large active space required for this chromophore. Thus, we consider DFT/MRCI as a reference, as previously suggested in a benchmark study on BChl
a, the use of a multi-reference method like SORCI is impossible due to the large active space required for this chromophore. Thus, we consider DFT/MRCI as a reference, as previously suggested in a benchmark study on BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, cf.ref. 21. The performance of DFT/MRCI, however, is dependent on the particular Hamiltonian used and the choice of method specific parameters. To consolidate the reference calculations, we therefore also consider the wavefunction-based methods SOS-CC2 and SOS-ADC(2). These are single-reference methods and their reliability is therefore sensitive to the multi-reference character of the ground-state wavefunction, indicated by the D1 diagnostic.92 However, this D1 value is not a strict measure. To avoid distorted structures which lead to a multi-reference ground state, we have, following ref. 26, truncated some substituents, see Fig. 1, which break the symmetry of the BChl
a, cf.ref. 21. The performance of DFT/MRCI, however, is dependent on the particular Hamiltonian used and the choice of method specific parameters. To consolidate the reference calculations, we therefore also consider the wavefunction-based methods SOS-CC2 and SOS-ADC(2). These are single-reference methods and their reliability is therefore sensitive to the multi-reference character of the ground-state wavefunction, indicated by the D1 diagnostic.92 However, this D1 value is not a strict measure. To avoid distorted structures which lead to a multi-reference ground state, we have, following ref. 26, truncated some substituents, see Fig. 1, which break the symmetry of the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophore. When comparing the excitation energies of the truncated and the full geometries using LC-DFTB, we find that the truncation does not lead to significant changes, see ESI† (Table S3).
a chromophore. When comparing the excitation energies of the truncated and the full geometries using LC-DFTB, we find that the truncation does not lead to significant changes, see ESI† (Table S3).
Most methods show a continuous blue shift of excitation energies with increasing BLA, with the exception of the GGA and hybrid DFT methods and the ADC and CC variants. For small to intermediate BLA values, all methods perform similarly. This behavior may be relevant when sampling excitation energies along MD simulations, since the BLA changes along the C–C stretch modes, which is one of the relevant modes in the molecular dynamics. The blue shift is largest for CIS and ZINDO/S, and seems to depend on the HF-amount in the LC functionals, which becomes apparent when comparing e.g., ωB97X and CAM-B3LYP. LC-DFTB shows a behavior quite close to that of CAM-B3LYP, which resembles the change of excitation energy with BLA closely to DFT-MRCI. DFT in general has be considered to been robust with respect to the multi-configurational character, in particular for BChl chromophores,21,27,93 it can be concluded that LC-DFT and LC-DFTB are sufficiently accurate for these systems.
Fig. 6(a) shows the excitation energies of the isolated BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores (solid lines) in comparison with the excitation energies calculated including the protein electrostatic field represented by point charges (dashed lines). The corresponding numerical values can be found in the ESI† (Table S4). The axial ligand or the amino acids hydrogen bonded to the BChl
a chromophores (solid lines) in comparison with the excitation energies calculated including the protein electrostatic field represented by point charges (dashed lines). The corresponding numerical values can be found in the ESI† (Table S4). The axial ligand or the amino acids hydrogen bonded to the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophore seem to have a small impact on the excitation energy, as reported before.20,21,93 This behavior can partially be explained by the transition dipole moment of 6 D of BChl
a chromophore seem to have a small impact on the excitation energy, as reported before.20,21,93 This behavior can partially be explained by the transition dipole moment of 6 D of BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,94,95 which is only about 50% of the transition dipole moment of retinal (12 D).96 B3LYP, CAM-B3LYP as well as LC-DFTB and TD-DFTB lead to accurate vacuum excitation energies, being in agreement with the DFT/MRCI method, which predicts only a small variation in the excitation energies of less than 0.1 eV. Slightly larger variations are obtained for LC-DFT methods with larger fractions of HF exchange, e.g., in the case of ωB97X for the BChl
a,94,95 which is only about 50% of the transition dipole moment of retinal (12 D).96 B3LYP, CAM-B3LYP as well as LC-DFTB and TD-DFTB lead to accurate vacuum excitation energies, being in agreement with the DFT/MRCI method, which predicts only a small variation in the excitation energies of less than 0.1 eV. Slightly larger variations are obtained for LC-DFT methods with larger fractions of HF exchange, e.g., in the case of ωB97X for the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores 5 and 6. A significantly different behavior is obtained using SOS-ADC(2), being similar to CC2, cf.ref. 21.
a chromophores 5 and 6. A significantly different behavior is obtained using SOS-ADC(2), being similar to CC2, cf.ref. 21.
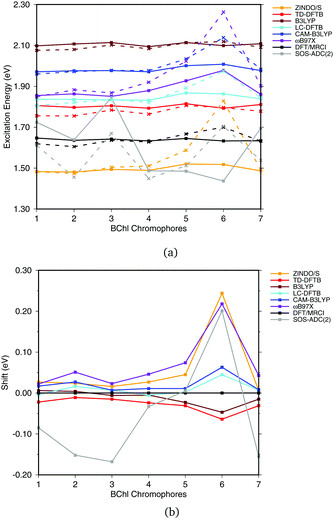 | ||
| Fig. 6 (a) Excitation energies of the chromophores from the FMO complex including (solid lines) and not including (vacuum, dashed lines) the surrounding point charges. (b) Shifts of excitation energies due to the protein electrostatic field, displayed with respect to the respective DFT/MRCI values. Structures taken from ref. 21. | ||
To better visualize the behavior, we show the shifts in excitation energies due to the protein environment w.r.t. the DFT/MRCI reference method in Fig. 6(b), values see ESI,† Table S5. Due to the interaction with the environment, chromophore 6 is the most blue shifted one, and this shift is clearly dependent on the method used. ZINDO/S shows the strongest response to the electrostatic field, as previously reported, cf.ref. 21. B3LYP slightly underestimates the shift with respect to DFT/MRCI. For the LC functionals, the amount of exact exchange plays a significant role. For example, ωB97X leads to a larger shift than CAM-B3LYP, and LC-DFTB reproduces the CAM-B3LYP behavior quite well, deviating only up to 0.05 eV from DFT/MRCI.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores, also denoted as excitonic coupling. Due to the large separation of the BChl
a chromophores, also denoted as excitonic coupling. Due to the large separation of the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a monomers, both, supermolecular or Coulomb couplings can be used to compute the exciton splittings. In the supermolecular approach, the exchange contribution to the coupling is formally included but in practice is negligible for the systems studied here.97
a monomers, both, supermolecular or Coulomb couplings can be used to compute the exciton splittings. In the supermolecular approach, the exchange contribution to the coupling is formally included but in practice is negligible for the systems studied here.97
To benchmark LC-DFT as well as LC-DFTB, we first consider a model system consisting of parallel displaced dimers of truncated BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores, as described in Section 2.1, to avoid any intra-molecular influences on the exciton coupling. The ADC(2) method is excluded from the assessment of the excitonic couplings due to the large deviations of excitation energies in the protein electrostatic environment compared to all other methods, see Section 3.2.2.
a chromophores, as described in Section 2.1, to avoid any intra-molecular influences on the exciton coupling. The ADC(2) method is excluded from the assessment of the excitonic couplings due to the large deviations of excitation energies in the protein electrostatic environment compared to all other methods, see Section 3.2.2.
In Table 2 results are collected, which have been obtained from supermolecular calculations for which excitonic coupling are determined as half of the energy splitting of the lowest two states, at least for a homogeneous dimer. The exciton couplings become smaller with increasing distance between the dimers. Compared to DFT/MRCI, CIS slightly overestimates the couplings, while all other DFT methods (hybrid and LC functionals) reproduce the reference quite well. TD-DFTB significantly underestimates the coupling, most likely due to the GGA functional applied, since the absence of exact exchange leads to an underestimation of the energy splittings, a further problem is the state mixing.98 LC-DFTB is in good agreement with CAM-B3LYP and improves significantly over TD-DFTB.
| Distance (Å) | 7 | 8 | 9 | 10 |
|---|---|---|---|---|
| CIS | 0.069 | 0.051 | 0.040 | 0.031 |
| DFT/MRCI | 0.046 | 0.035 | 0.028 | 0.022 |
| ωB97X | 0.059 | 0.044 | 0.034 | 0.027 |
| CAM-B3LYP | 0.058 | 0.044 | 0.034 | 0.026 |
| B3LYP | 0.051 | 0.039 | 0.030 | 0.023 |
| LC-DFTB | 0.063 | 0.048 | 0.037 | 0.030 |
| TD-DFTB | 0.031 | 0.024 | 0.019 | 0.015 |
Having assessed the accuracy of the supermolecular energy splittings, the same model system is used to investigate the accuracy of LC-DFTB, TrESP and Tr-Mulliken for Coulomb couplings describing the energy splittings. The Coulomb couplings are collected in Table 3. The TrESP method without any scaling factor can reproduce the corresponding supermolecular results since for the large inter-chromophore distances the exchange contributions can be neglected. This was already reported in a previous study employing the B3LYP functional.87 For CAM-B3LYP and B3LYP using TrESP, the Coulomb couplings are, as expected, slightly smaller than those computed with the supermolecular approach. The difference is not big, indicating that the point charge representation of transition densities is a good approximation for these distances. Further, there is no significant difference between ESP and Mulliken charges, indicating that the transition dipole is a quite robust quantity. However, in the case of LC-DFTB it is vice versa. LC-DFTB also uses transition charges computed from a Mulliken charge analysis. In TrESP, these charges are fitted to transition densities using larger basis sets, which seems to be a good approximation. The LC-DFTB Coulomb couplings, however, differ from the Tr-Mulliken calculations in two aspects: first, a minimal basis set is used to compute the Mulliken charges and second, the TD-DFT amplitudes enter the calculation of the Coulomb couplings46 as well. LC-DFTB Coulomb couplings possibly can be improved by investigating the applied charge model in more detail.
| Distance (Å) | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|
| TrESP | B3LYP | 0.050 | 0.038 | 0.029 | 0.023 |
| CAM-B3LYP | 0.056 | 0.043 | 0.033 | 0.026 | |
| Tr-Mulliken | B3LYP | 0.047 | 0.036 | 0.028 | 0.022 |
| CAM-B3LYP | 0.054 | 0.041 | 0.032 | 0.025 | |
| — | LC-DFTB | 0.082 | 0.063 | 0.049 | 0.039 |
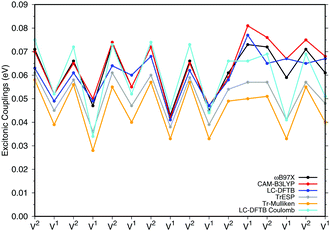
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a dimers (B850 ring), for which results are shown in Fig. 7, the values are collected in the ESI† (Table S6). The results for the biological system show significant differences compared to the model system in Section 3.2.3. Depending on the relative orientation of the BChl
a dimers (B850 ring), for which results are shown in Fig. 7, the values are collected in the ESI† (Table S6). The results for the biological system show significant differences compared to the model system in Section 3.2.3. Depending on the relative orientation of the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a monomers, the values of the couplings range from about 0.04 eV to about 0.08 eV. These values are mostly larger than those in the model system. LC-DFTB values compare quite well with ωB97X and CAM-B3LYP results. LC-DFTB slightly overestimates the couplings in the model system, which is not the case for the dimers in the B850 ring, and LC-DFTB also reproduces the correct trend of the couplings in the ring system.
a monomers, the values of the couplings range from about 0.04 eV to about 0.08 eV. These values are mostly larger than those in the model system. LC-DFTB values compare quite well with ωB97X and CAM-B3LYP results. LC-DFTB slightly overestimates the couplings in the model system, which is not the case for the dimers in the B850 ring, and LC-DFTB also reproduces the correct trend of the couplings in the ring system.
Fig. 7 also includes Coulomb couplings. TrESP and Tr-Mulliken methods reproduce the coupling fluctuations along the ring quite well, however, now systematically underestimating the coupling strengths. This may be related to the ‘frozen’ TrESP approach, where transition charges are only computed for the equilibrium geometry and then mapped to the actual conformer. There is, however, a second factor which may be responsible for the deviation: since exchange effects depend on the mutual overlap of electron densities, which may be dominated by the densities of the highest occupied orbitals, we expect a sensitive geometry dependence of this property. This is less pronounced for the Coulomb couplings, because those are only dependent on the relative orientations of the transition dipole moments. A more detailed study on dimers of organic molecules100 seem to support this argument.
Both approaches, TrESP and LC-DFTB, have certain shortcomings, namely the use of transition charges determined for an equilibrium conformation (‘frozen’ TrESP approach) and the application of a minimal basis set as discussed in Section 3.2.3. However, the mean absolute error (MAE) (see ESI,† Table S6) computed for all methods with respect to the supermolecular ωB97X and CAM-B3LYP calculations are small, while LC-DFTB supermolecular as well as LC-DFTB Coulomb couplings show only half of the MAE value compared to TrESP and Tr-Mulliken.
The LC-DFTB Coulomb couplings are in agreement with those obtained from a transition density cube (TDC) approach without an additional scaling factor in ref. 49. A detailed comparison with couplings computed in previous studies, as summarized in Tables S7 and S8 in the ESI,† is difficult due to the frequent use of screening factors.
4 Performance of LC-DFTB in biological model systems
In this section, the performance of LC-DFTB on biological model systems, i.e., on rhodopsins and LH complexes is discussed. Due to the efficiency of the LC-DFTB method, not only single-point excitation energies can be computed for minimized geometries but also a statistical average of several thousands structures as obtained by classical or QM/MM MD simulations.4.1 Rhodopsin models
| Exp. | Wavefunction | DFT | DFTB | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SORCI | OM2/MRCI | CC2 | SOS-CC2 | ADC(2) | SOS-ADC(2) | ωB97X | CAM-B3LYP | LC-DFTB | TD-DFTB | ||
| a Ref. 104. b Ref. 4. c Ref. 3. d Ref. 5. | |||||||||||
| bR | |||||||||||
| Vacuum | 2.00a | 1.86d | 2.22d | 2.08 | 2.25 | 1.89 | 2.13 | 2.65 | 2.64 | 2.58 | 2.04 |
| Protein | 2.18b | 2.34d | 2.66d | 2.48 | 2.76 | 2.35 | 2.64 | 2.94 | 2.85 | 2.77 | 2.22 |
| Shift | +0.18 | +0.48 | +0.44 | +0.40 | +0.51 | +0.46 | +0.51 | +0.29 | +0.21 | +0.19 | +0.18 |
| ppR | |||||||||||
| Vacuum | 2.00a | 1.91d | 2.24d | 2.08 | 2.30 | 1.92 | 2.20 | 2.67 | 2.65 | 2.60 | 2.00 |
| Protein | 2.50c | 2.63d | 2.96d | 2.80 | 3.11 | 2.70 | 3.01 | 3.18 | 3.06 | 2.95 | 2.37 |
| Shift | +0.50 | +0.72 | +0.72 | +0.72 | +0.81 | +0.78 | +0.81 | +0.51 | +0.39 | +0.35 | +0.37 |
| Δ(ppR − bR) | +0.32 | +0.29 | +0.30 | +0.32 | +0.35 | +0.35 | +0.37 | +0.24 | +0.21 | +0.18 | +0.16 |
The latter observation is consistent with the underestimated response of the model chromophore to external charges, as described in Section 3.1.3, whereas the first one requires a different explanation. Based on our earlier results, the opsin shift should be underestimated by DFT methods rather than overestimated by all other methods. Here, we refer to previous works, which have shown that point charges obtained by electronic embedding over-polarize the chromophore region. This can be improved by a polarizable embedding. When replacing the point charges in the binding pocket by the electron density of a separate QM region,102 or by a polarizable force field,103 significantly lower excitation energies are obtained. When the chromophore is described with SORCI and the rest of the protein with the polarization model, excitation energies of 2.16 and 2.42 eV have been reported for bR and ppR, respectively.102,103 Compared to vacuum (2.00 eV),104 this corresponds to shifts of 0.16 and 0.42 eV, which are in good agreement with the experiment.
The comparison of calculated and measured properties for the purpose of validating theoretical methods is often hampered by experimental measurements in solution. In the present case, the MM modeling of the protein environment introduces errors that can be of the same order of magnitude as those associated with the applied QM methods. Rather than validating, the following discussion therefore attempts to rationalize the results of the different methods and we will employ SORCI shifts as a reference point.
The shifts obtained with OM2/MRCI, CC2, and ADC(2) are in the range of the SORCI ones, with an average deviation of 0.02–0.04 eV. The SOS variants of CC2 and ADC(2) yield shifts larger by 0.06 eV on average. Moreover, the LC functionals ωB97X and CAM-B3LYP underestimate the shifts by 0.20 and 0.30 eV on average, respectively. TD-DFTB underestimates the shift by even up to 0.35 eV with respect to SORCI. Surprisingly, LC-DFTB does not improve the shifts.
Otherwise, these trends are similar to the ones shown in the previous section for the model chromophore in presence of a single point charge and consistent with previous works (see ref. 18 and references therein), which show that also CIS (based on HF or an OM2 Hamiltonian) underestimates the shift in bR. Therefore, it is not surprising that the shift obtained with LC functionals is larger than that of pure or fixed-hybrid DFT functionals but still significantly lower than that of higher-level methods, like SORCI or CASPT2. Regarding the shifts, the ωB97X functional performs better than CAM-B3LYP due to its larger amount of HF-X in the long-range limit, but this improvement is paid with a larger error in absolute excitation energies.
The absorption maxima of the retinal chromophore in bR and ppR in vacuum differ by about ±0.02 eV for each method. This result is expected, since the retinal conformations are similar in bR and ppR. In comparison with the QM/MM optimized models, OM2/MRCI displays a slight blue shift of +0.02 eV and LC-DFTB a red shift of about −0.06 eV for the vacuum excitation energies. The same behavior is obtained for the absorption maxima including the protein environment.
In bR and ppR the inclusion of the protein environment results in a blue shift for both methods. In the case of bR, OM2/MRCI leads to a slightly smaller blue shift (0.41 eV) compared to the QM/MM optimized models (0.44 eV). Whereas in the case of ppR, LC-DFTB computes a slightly higher blue shift (0.40 eV) compared to the QM/MM optimized models (0.35 eV). The slight deviations compared to the QM/MM optimized models of both rhodopsins bR and ppR is mainly reflected by the strong hydrogen bond network (see Fig. 8(b)) in the active site confining the chromophore retinal in its structural fluctuation. In this case the QM/MM MD simulations describe only an oscillation of the chromophore retinal around the energy minimum.5 However, it has to be mentioned that rhodopsins exist, e.g., channelrhodopsin-2 wild-type (ChR2-WT), exhibiting a very flexible structure and therefore needs sampling by QM/MM MD simulations.84 The difference of the absorption maxima between both rhodopsins (ppR-bR) obtained by OM2/MRCI (+0.33 eV) is as expected in agreement to the experimental shift (+0.32 eV). LC-DFTB shows with +0.20 eV a smaller shift of the absorption maxima between bR and ppR. Here, the color-weakness of LC-DFTB is again visible.
The computed excitation energies of the sampled structures are plotted as histograms in Fig. 8(a) for bR. The histogram for ppR is shown in the ESI† (Fig. S3). In the case of OM2/MRCI, a broad simulated absorption spectrum is obtained, while LC-DFTB tends to yield less broad absorption spectra, especially when considering only the retinal chromophore without the protein environment. The width of the absorption spectra reflects in the case of vacuum, the different obtained retinal conformations differing in their BLA. The inclusion of the protein environment includes then also the fluctuation of the protein itself. Hence, weaknesses of LC-DFTB become visible also in this property since it cannot reproduce the same width as OM2/MRCI.
4.2 Light-harvesting complexes
To asses the performance of LC-DFTB, we focus on the energy ranges of three LH complexes, LH2 complex of Rs. molischianum and Rps. acidophila and the FMO complex of C. tepidum. To this end, we analyze the energy range spanned by all individual uncoupled BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores with and without the protein environment as well as the energy range of the excitons.
a chromophores with and without the protein environment as well as the energy range of the excitons.
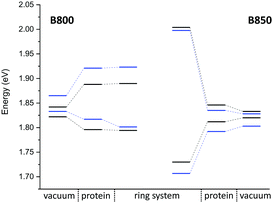
QM/MM optimized model. In a first step, we considered a DFTB-QM/MM optimized structure for the complex and computed excitation energies for the B800 and B850 ring systems using LC-DFTB as summarized in Table 6. More detailed information can be found in the ESI† (Tables S9 and S10). The BChl
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a structures are not significantly influenced by the protein environment and thus the excitation energies show only a minute standard deviation of 0.01 eV due to structural effects. The electrostatic interaction based on the QM/MM point charge model leads to a larger variation of the excitation energies, which is also illustrated in Fig. 9. It leads to a larger range for the B800 ring (0.092 eV) than for the B850 ring (0.034 eV). This finding can be explained by a more pronounced influence of the protein environment in B800, since the chromophores are less densely packed than in B850 and thereby exposed to a more polar protein environment.105,106 As expected from the benchmark results (Section 3), ZINDO/S overestimates the effect of the electrostatic tuning and results in a larger variation as shown in Table S11, ESI.†
a structures are not significantly influenced by the protein environment and thus the excitation energies show only a minute standard deviation of 0.01 eV due to structural effects. The electrostatic interaction based on the QM/MM point charge model leads to a larger variation of the excitation energies, which is also illustrated in Fig. 9. It leads to a larger range for the B800 ring (0.092 eV) than for the B850 ring (0.034 eV). This finding can be explained by a more pronounced influence of the protein environment in B800, since the chromophores are less densely packed than in B850 and thereby exposed to a more polar protein environment.105,106 As expected from the benchmark results (Section 3), ZINDO/S overestimates the effect of the electrostatic tuning and results in a larger variation as shown in Table S11, ESI.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a structures of the B800 and B850 ring systems. Shown are the excitation energies for the individual BChl
a structures of the B800 and B850 ring systems. Shown are the excitation energies for the individual BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores with and without the influence of the protein environment. In addition, excitonic energies (in eV), i.e., the lowest eigenvalues are shown for the ring system. The excitation energies have been computed using LC-DFTB, Coulomb couplings with LC-DFTB and TrESP
a chromophores with and without the influence of the protein environment. In addition, excitonic energies (in eV), i.e., the lowest eigenvalues are shown for the ring system. The excitation energies have been computed using LC-DFTB, Coulomb couplings with LC-DFTB and TrESP
LC-DFTB Coulomb couplings are about 0.006 eV for neighboring BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a in a B800 ring, while we find a range of 0.033–0.075 eV for the B850 ring. TrESP gives smaller Coulomb couplings, as expected from the benchmark study (Section 3), which are around 0.004 eV for the B800 ring and 0.038–0.061 eV for the B850 ring. The excitonic energies resulting from the diagonalization of the Hamiltonian for the two individual ring systems show a range of excitonic energies of 0.096 eV for B800, and 0.274 eV for B850. A similar energy range of 0.317 eV for the B850 ring was already reported previously.107 Although for LH2 of Rs. molischianum no experimental data is known regarding the excitonic energy range, experimental data for the bacterium Rps. acidophila suggests an energy range of about 0.179 eV for the B850 ring at low temperatures.108 Therefore, LC-DFTB overestimates this range of energies, and the reason for this overestimation is two-fold: first, the spread of the excitation energies of the individual chromophores may be slightly overestimated due to the QM/MM point charge electrostatics, i.e., inclusion of polarizable embedding may damp this spread slightly.36,102,103 Second, LC-DFTB overestimates the values of the Coulomb couplings, as seen in Section 3. The Coulomb couplings are larger than the LC-DFTB supermolecular couplings, which in turn are in very good agreement with full LC-DFT couplings. Moreover, effects of polarization on the couplings are neglected. But all these effects are small (0.01–0.02 eV), but they accumulate when determining the eigenvalues of the Hamiltonian of the ring system. Therefore, we expect that our approach overestimates the spread of eigenvalues by about 0.1 eV.
a in a B800 ring, while we find a range of 0.033–0.075 eV for the B850 ring. TrESP gives smaller Coulomb couplings, as expected from the benchmark study (Section 3), which are around 0.004 eV for the B800 ring and 0.038–0.061 eV for the B850 ring. The excitonic energies resulting from the diagonalization of the Hamiltonian for the two individual ring systems show a range of excitonic energies of 0.096 eV for B800, and 0.274 eV for B850. A similar energy range of 0.317 eV for the B850 ring was already reported previously.107 Although for LH2 of Rs. molischianum no experimental data is known regarding the excitonic energy range, experimental data for the bacterium Rps. acidophila suggests an energy range of about 0.179 eV for the B850 ring at low temperatures.108 Therefore, LC-DFTB overestimates this range of energies, and the reason for this overestimation is two-fold: first, the spread of the excitation energies of the individual chromophores may be slightly overestimated due to the QM/MM point charge electrostatics, i.e., inclusion of polarizable embedding may damp this spread slightly.36,102,103 Second, LC-DFTB overestimates the values of the Coulomb couplings, as seen in Section 3. The Coulomb couplings are larger than the LC-DFTB supermolecular couplings, which in turn are in very good agreement with full LC-DFT couplings. Moreover, effects of polarization on the couplings are neglected. But all these effects are small (0.01–0.02 eV), but they accumulate when determining the eigenvalues of the Hamiltonian of the ring system. Therefore, we expect that our approach overestimates the spread of eigenvalues by about 0.1 eV.
In order to estimate the B800–B850 energy splitting, we use the lowest eigenvalues of the two ring Hamiltonians. As shown in Table 6, this range is close to the experimental value, i.e., the errors cancel out to some extent. The reason can be understood by inspecting Fig. 9. On the one hand, the Coulomb couplings are overestimated, partially due to neglect of polarization. This significantly affects the B850 excitonic energies, i.e., additionally lowering the lowest energy states. Since the couplings between the B800 chromophores are much smaller, this spectrum is not much affected. The neglect of polarization, on the other hand, also lowers the energies of the individual chromophores, i.e., the site energies of the excitonic Hamiltonian: this, as discussed above, affects mostly B800 energies. Therefore, the energies of both ring systems are artificially lowered due to computational errors, i.e., for the B800 the site energies are mostly affected, for B850 the couplings. Since in both cases, the excitonic energies are lowered, we find a cancellation of errors.
The computation of such small energy differences, i.e., below 0.1 eV, is very challenging for these large systems, where approximations are inevitable. A recent study36 on the LH2 complex of Rps. acidophila reported an overestimation of the experimental gap, while the computed excitonic couplings are smaller than ours (around 0.05 eV) due to the consideration of polarization effects. Since it is interesting to see how different approaches perform for the same system, we also studied the LH2 complex of Rps. acidophila. A detailed discussion and comparison of methods can be found in the ESI.† The monomer excitation and excitonic energies of this complex are shown in Fig. 9. Although the two LH2 complexes studied here differ in conformation and number of chromophores, the spectra are quite similar.
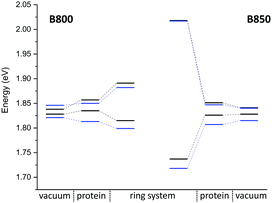
Classical MD simulation. QM/MM MD simulations for multi-chromophoric complexes are not straightforward, since a QM approach with multiple QM regions would be required which is not implemented in the present DFTB scheme. Therefore, we use classical MD trajectories to sample the excitation energies. The corresponding average excitation energies and standard deviations are shown in Table 7. Moreover, in Fig. 10 histograms based on snapshots of the BChl
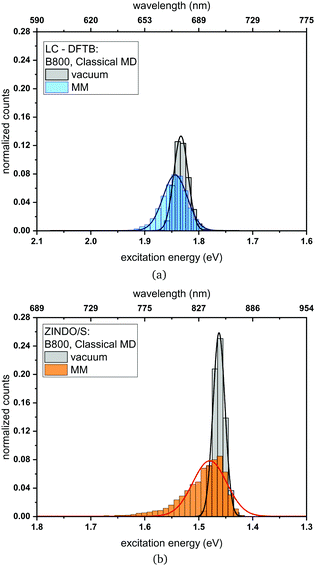
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores belonging to the B800 ring using a 1 ns-long MD trajectory are displayed. The results for the B850 ring are given in the ESI† (Fig. S4). While the vacuum excitation energy distribution is similar for LC-DFTB and ZINDO/S, the different response of both methods to the electrostatic field of the protein, as discussed in Section 3, is clearly visible. Both methods show a broadening while ZINDO/S shows a strongly asymmetric distribution with a long tail towards higher energies as reported earlier.41,110
a chromophores belonging to the B800 ring using a 1 ns-long MD trajectory are displayed. The results for the B850 ring are given in the ESI† (Fig. S4). While the vacuum excitation energy distribution is similar for LC-DFTB and ZINDO/S, the different response of both methods to the electrostatic field of the protein, as discussed in Section 3, is clearly visible. Both methods show a broadening while ZINDO/S shows a strongly asymmetric distribution with a long tail towards higher energies as reported earlier.41,110
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores with and without the influence of the protein environment. The average excitation energies are obtained by averaging the maxima of Gaussian fits of the distributions of the respective chromophore. In addition, the excitonic energies (in eV), i.e., the lowest eigenvalues are shown for the Hamiltonians considering Coulomb couplings between the BChl
a chromophores with and without the influence of the protein environment. The average excitation energies are obtained by averaging the maxima of Gaussian fits of the distributions of the respective chromophore. In addition, the excitonic energies (in eV), i.e., the lowest eigenvalues are shown for the Hamiltonians considering Coulomb couplings between the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores within one ring system. The excitonic energies are extracted as the maxima of the Gaussian fits to the exciton energy distributions. The excitation energies have been computed using LC-DFTB, Coulomb couplings with LC-DFTB and TrESP
a chromophores within one ring system. The excitonic energies are extracted as the maxima of the Gaussian fits to the exciton energy distributions. The excitation energies have been computed using LC-DFTB, Coulomb couplings with LC-DFTB and TrESP
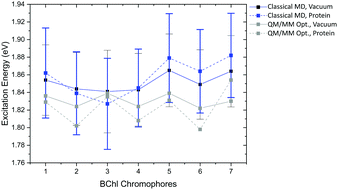
Compared to the QM/MM optimized structures, the standard deviations (Table 7) are reduced for the average excitation energies with and without the protein environment. For LC-DFTB, the diagonal disorder, i.e., the range of excitation energies, is smaller compared to that of the QM/MM optimized structures, as can be seen from Fig. 11. It seems, that optimization leads to local minima, where excitation energy differences between the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores are more pronounced. Hence, the differences between both LH2 complexes are reduced, comparing Fig. 11 and 9 (more details, see Table S15, ESI†).
a chromophores are more pronounced. Hence, the differences between both LH2 complexes are reduced, comparing Fig. 11 and 9 (more details, see Table S15, ESI†).
The sampled Coulomb couplings over the classical MD trajectory clearly show differences when comparing LC-DFTB and TrESP. An example plot is given in the ESI† (Fig. S5). The LC-DFTB couplings fluctuate in a range of 0.004–0.008 eV for B800 and 0.060–0.080 eV for B850, while the TrESP couplings show lower fluctuations of 0.0018–0.0025 eV for B800 and 0.035–0.045 eV for B850. The variation arises only from geometric changes, since the LC-DFTB computed couplings undergo changes due to changes in the transition charges, while in the case of TrESP the transition charges are constant. Please note, that we found the TrESP approach to lead to smaller couplings already for the model systems presented above. The B800–B850 energy splitting estimated from the sampled structures is higher in the case of LC-DFTB compared to the QM/MM optimized model and closer to the experimental value. As discussed above, error cancellation might also be responsible for the better agreement with the experimental energy range.
The resulting excitonic energy range computed using LC-DFTB decreases after sampling compared to the QM/MM optimized model in the case of B800, while it slightly increase in the case of B850 (see ESI,† Table S14). As discussed for the QM/MM optimized model, the diagonal disorder is dominant in the B800 ring, since the couplings do not contribute much. Since the excitation energy splitting of the protein environment decreased after sampling, the excitonic splitting decreased as well. In the case of B850, smaller differences are observed compared to the QM/MM optimized model. For B850, the off-diagonal disorder is smaller through the more tight packing105,106 (see also discussion above), the chromophores are less exposed to the fluctuations of the protein electrostatic field. Thus, at the LC-DFTB level, there is no significant change in the exciton splitting when compared to the QM/MM optimized case, which can be seen by comparing Fig. 11 and 9. For the TrESP couplings, however, a sizable decrease is found upon sampling, where the exciton splitting of 0.163 eV is closer to the experimental value at room temperature of about 0.158 eV.108 This however, may be an accidential agreement, since the TrESP couplings are much smaller than those from supermolecular calculations.
One has to note, however, that the averaging process for the excitonic energies is ambiguous in itself: one can average the Hamiltonian and then compute its eigenvalues or one can average the excitonic energies computed for every snapshot. The latter one is used in the present work. Since the diagonalization is a non-linear operation, the two approaches lead to different results (Table S14, ESI†). Thus, these two averaging procedures do not commute. In the first case, the deviations from the average value will not receive an appropriate weight in the exciton formation, while in the second case an instantaneous response of the electronic structure to the nuclear motion is assumed. This is a time-scale problem occurring typically, when a transport process is coupled to nuclear motions: how to treat fluctuations, e.g., in the context of Marcus theory111 or Landauer tunneling.112 When the time scales of the fluctuations in the electronic structure, resulting for the nuclear motion, and transport of the charge or energy are on the same time scale, non-adiabatic methods seem to be more appropriate.
QM/MM optimized model. Next we analyze the excitation energies of the individual BChl
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores from the FMO of C. tepidum. In Fig. 12, the results for the DFTB QM/MM optimized FMO complex are depicted, computed in vacuum and within the protein environment using LC-DFTB. As observed for the LH2 complex, the BChl
a chromophores from the FMO of C. tepidum. In Fig. 12, the results for the DFTB QM/MM optimized FMO complex are depicted, computed in vacuum and within the protein environment using LC-DFTB. As observed for the LH2 complex, the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a geometries are not significantly influenced by the protein environment, since the BLA values are in the same range. Furthermore, the ZINDO/S results show a stronger response to the electrostatics (see ESI,† Table S18).
a geometries are not significantly influenced by the protein environment, since the BLA values are in the same range. Furthermore, the ZINDO/S results show a stronger response to the electrostatics (see ESI,† Table S18).
The respective minimum and maximum of the energy range obtained in vacuum and with the protein environment are presented in Table 8. As expected, the resulting energy range in vacuum of 0.017 eV is smaller than the experimental range of 0.060 eV.113 The consideration of the electrostatic environment increases this value to 0.056 eV. A previous study using QM/MM optimized structures of the FMO complex of P. aesturii reporting an energy range of about 0.025 eV using CAM-B3LYP and including polarization contribution.48 Therefore, using point charges only, the protein electrostatic effect may be overestimated, since polarization is neglected here.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores of the FMO complex. LC-DFTB is used for the computation of excitation energies without (vacuum) and with the protein environment as fixed MM point charges. Coulomb couplings are computed using LC-DFTB and TrESP
a chromophores of the FMO complex. LC-DFTB is used for the computation of excitation energies without (vacuum) and with the protein environment as fixed MM point charges. Coulomb couplings are computed using LC-DFTB and TrESP
For LC-DFTB Coulomb couplings, a range of values between 0.019 eV and 0.044 eV is obtained for the strongest couplings, i.e., for the neighboring BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores. In the case of TrESP a range of 0.012–0.029 eV is found showing lower values than LC-DFTB as expected from the benchmark study, see Section 3. The Hamiltonian and the excitonic energies of the QM/MM optimized model computed with LC-DFTB are given in the ESI† (Tables S17 and S21, ESI†). The resulting energy range between the maximum and the minimum of the excitonic energies overestimates the experimental energy range, see Table 8, as expected, due to the overestimation of the Coulomb couplings and the neglect of polarization effects, similar to the LH2 case discussed above.
a chromophores. In the case of TrESP a range of 0.012–0.029 eV is found showing lower values than LC-DFTB as expected from the benchmark study, see Section 3. The Hamiltonian and the excitonic energies of the QM/MM optimized model computed with LC-DFTB are given in the ESI† (Tables S17 and S21, ESI†). The resulting energy range between the maximum and the minimum of the excitonic energies overestimates the experimental energy range, see Table 8, as expected, due to the overestimation of the Coulomb couplings and the neglect of polarization effects, similar to the LH2 case discussed above.
Classical MD simulation. In a next step, we analyze the excitation energies for the single BChl
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores sampled along a classical MD trajectory. The maxima of Gaussian fits to the distributions with the respective standard deviations are plotted in Fig. 12. LC-DFTB was used for the computation of the excitation energies of the sampled structures with and without protein environment. Again, ZINDO/S shows a stronger response to the electrostatic environment as shown by the broader excitation energy distributions depicted in the ESI† (Fig. S9–S11). However, the standard deviations of both LC-DFTB and ZINDO/S are similar, showing values of about 0.048 eV. The vacuum excitation energy range of the BChl
a chromophores sampled along a classical MD trajectory. The maxima of Gaussian fits to the distributions with the respective standard deviations are plotted in Fig. 12. LC-DFTB was used for the computation of the excitation energies of the sampled structures with and without protein environment. Again, ZINDO/S shows a stronger response to the electrostatic environment as shown by the broader excitation energy distributions depicted in the ESI† (Fig. S9–S11). However, the standard deviations of both LC-DFTB and ZINDO/S are similar, showing values of about 0.048 eV. The vacuum excitation energy range of the BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a chromophores is in the case of LC-DFTB slightly larger (0.024 eV) than for the QM/MM optimized model (0.017 eV), see Table 9 due to the fluctuations.
a chromophores is in the case of LC-DFTB slightly larger (0.024 eV) than for the QM/MM optimized model (0.017 eV), see Table 9 due to the fluctuations.
The energy range computed for the protein environment is similar to that obtained by the QM/MM optimized model (see Tables 8 and 9). The results are consistent with those from a previous study cf.ref. 114, which also did not include polarization effects. As already mentioned polarization effects reduce this range to 0.025 eV.115
The average Coulomb couplings sampled along the trajectories are slightly smaller than for the QM/MM optimized model, see ESI† (Table S19). These are plotted together with Coulomb couplings obtained by previous studies using TD-DFT/MMPol115 and PDA,116 see ESI† (Fig. S8). LC-DFTB obtains qualitatively the same trend, however overestimates the Coulomb couplings by about a factor of 2. In the case of FMO, the Coulomb couplings seems to be slightly more overestimated than for the LH2 complex, when comparing to previous studies.36,49 Protein polarization leads to a screening of electrostatic interactions, which can be represented by a screening factor specific for the chromophores in different protein environments. Jurinovich et al.,115 reported a screening factor of about 1.7 for the FMO complex, which is larger than the screening factor obtained for the LH2 complex of 1.47.36 This indicates a higher influence of polarization, which explains the different deviations of our results.
The energy range resulting from the average excitonic energies (see ESI,† Table S21), i.e., the exciton energy range from the coupled FMO chromophores shown in Table 9, is larger than the experimental energy range. It is even larger compared to the energy range obtained by the QM/MM optimized model. In the case of FMO, the off-diagonal disorder is dominant, leading to an increase of the exciton energy range compared to the QM/MM optimized model. Furthermore, the Coulomb couplings might have been overestimated more severely in the FMO complex compared to the LH2 aggregate due to the above discussed polarization influence.
5 Summary
In this study, we have investigated the performance of LC-DFT and LC-DFTB for two major light-activated protein classes, rhodopsins and light-harvesting complexes. Both present significant challenges for a theoretical description: rhodopsins show a large variance in absorption energies, i.e., have a sophisticated mechanism of color tuning depending on chromophore geometry and interaction with the environment, while light-harvesting complexes are less responsive to the interaction with the environment, but are large in size and to a large extent change color by inter-chromophore coupling. For both systems, standard DFT functionals give non-satisfactory results while range-separated functionals seem to be a promising alternative.For retinal, GGA and hybrid DFT functionals both fail to describe color tuning w.r.t. changes in geometry and protein electrostatic interactions, while LC-DFT and LC-DFTB, in contrast, give a quite good account for geometrical changes. However, the correct response to the protein electrostatic field is sensitively dependent on the amount of exact exchange. Therefore, the ωB97X and LC-BLYP functionals come close to the reference methods and might be useful in applications, while for CAM-B3LYP and LC-DFTB the response to the protein electrostatic field is too weak, therefore, these methods are not suitable for studies of retinal protein color tuning.
For BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, the changes of absorption energies w.r.t. geometries are well reproduced by LC-DFT and LC-DFTB. Electrostatic effects are much smaller than in retinal proteins but still relevant, since small energy differences lead to sizable effects in the red part of the spectrum. Taking DFT/MRCI as reference, it seems that less exact exchange in the LC-DFT functionals leads to a better agreement, so that CAM-B3LYP and LC-DFTB yield comparably the best results. Therefore, CAM-B3LYP might be the LC reference method of choice. For the calculation of excitonic couplings in BChl
a, the changes of absorption energies w.r.t. geometries are well reproduced by LC-DFT and LC-DFTB. Electrostatic effects are much smaller than in retinal proteins but still relevant, since small energy differences lead to sizable effects in the red part of the spectrum. Taking DFT/MRCI as reference, it seems that less exact exchange in the LC-DFT functionals leads to a better agreement, so that CAM-B3LYP and LC-DFTB yield comparably the best results. Therefore, CAM-B3LYP might be the LC reference method of choice. For the calculation of excitonic couplings in BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, the choice of the LC-DFT functional is not critical, and they are also quite well described by LC-DFTB. Coulomb couplings computed from LC-DFTB, however, are slightly overestimated.
a, the choice of the LC-DFT functional is not critical, and they are also quite well described by LC-DFTB. Coulomb couplings computed from LC-DFTB, however, are slightly overestimated.
Therefore, the LC functionals have to be chosen carefully according to the target systems, since the correct description of absorption energies of retinal and BChl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a depends on the amount of exact exchange. This is in inherited by LC-DFTB due to the particular choice of the LC functional.
a depends on the amount of exact exchange. This is in inherited by LC-DFTB due to the particular choice of the LC functional.
The low computational cost of semi-empirical methods allows for extensive sampling of absorption spectra along MD trajectories, but also for a direct propagation of the exciton wavefunction on relevant time-scales.46 We have performed QM/MM MD simulations to sample rhodopsin absorption energies using LC-DFTB and OM2/MRCI as fast quantum methods. While OM2/MRCI performs quite well, LC-DFTB computed spectra have to be considered carefully, due to the too small response to the protein electrostatic fields.
Considering the LH complexes, in a first step we have QM/MM optimized their structures iteratively, by successively selecting one chromophore in the QM region. The calculated excitation energies for these QM/MM optimized structures indicate, that the diagonal disorder in the excitonic Hamiltonian is overestimated. This leads to an overestimation of the width of the computed spectrum. It seems, that geometry optimization drives the geometries into local minima, which show a large variation of excitation energies among the chromophores. These may be shallow minima, which seem to contribute less when averaging over trajectories at 300 K. A problem, which can be solved by either imposing symmetry36 or by averaging. We tested this for both LH complexes studied here, showing a clear reduction of energy range differences after sampling. We sampled the excitation spectra using trajectories from classical MD, since QM/MM MD simulations for the entire LH complexes are not possible at the moment. A multi-chromophore QM region would be required, work is in progress to make this property available in DFTB.
The comparison of exciton splittings for both LH2 and FMO computed with LC-DFTB and ZINDO/S show clear differences: since ZINDO/S shows a stronger response to the electrostatic environment, the width of the exciton spectrum is overestimated. LC-DFTB seems to be a good alternative method to ZINDO/S representing the electrostatic interaction in a more balanced way. Up to now, effects of protein polarization, which we included in our previous studies on retinal proteins101–103 have not been taken into account. However, chromophore excitation energies and exciton couplings are affected by polarization. Both, diagonal disorder and the coupling strength are slightly reduced when considering protein polarization effects, therefore, not taking polarization into account leads to an overestimation of the exciton bandwidth.
Interestingly, the experimental B800–B850 energy splitting is reproduced quite well, since polarization effects tend to cancel. This is not the case for the FMO complex, where the width of the exciton band is overestimated. Therefore, LC-DFTB will most likely give quite accurate results for LH complexes excited states properties, if polarization is included in future work.
In summary, LC-DFTB is an accurate and efficient method for studying exciton spectra and dynamics in LH complexes, since it is about three orders of magnitude faster than the full TD-DFT scheme with a minimum loss in accuracy.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge support by the DFG through the joint grant EL 206/18-1 and KL-1299/18-1, the DFG-Research Training groups 2247 “Quantum Mechanical Materials Modelling”, 2039 “Molecular architecture for fluorescent cell imaging”, 2450 “Tailored Scale-Bridging Approaches to Computational Nanoscience” and the DFG-SFB 1249 “N-Heteropolyzyklen als Funktionsmaterialien” (Projects B02 and B07). Moreover, support by the state of Baden-Württenberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/467-1 FUGG (JUSTUS cluster) is gratefully appreciated. The project has been supported in part by the bwHPC initiative and the bwHPC-C5 project. We thank N. H. List for providing us with the structures and benchmark data of the FMO complex from ref. 21.Notes and references
- S. L. Logunov, L. Song and M. A. El-Sayed, J. Phys. Chem., 1996, 100, 18586–18591 CrossRef CAS.
- G. G. Kochendoerfer, S. W. Lin, T. P. Sakmar and R. A. Mathies, Trends Biochem. Sci., 1999, 24, 300–305 CrossRef CAS PubMed.
- I. Chizhov, G. Schmies, R. Seidel, J. R. Sydor, B. Lüttenberg and M. Engelhard, Biophys. J., 1998, 75, 999–1009 CrossRef CAS PubMed.
- R. R. Birge and C. F. Zhang, J. Chem. Phys., 1990, 92, 7178–7195 CrossRef CAS.
- M. Hoffmann, M. Wanko, P. Strodel, P. H. Konig, T. Frauenheim, K. Schulten, W. Thiel, E. Tajkhorshid and M. Elstner, J. Am. Chem. Soc., 2006, 128, 10808–10818 CrossRef CAS PubMed.
- M. Wanko, M. Hoffmann, T. Frauenheim and M. Elstner, J. Comput. Aided Mol. Des., 2006, 20, 511–518 CrossRef CAS PubMed.
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, John Wiley & Sons, 2014 Search PubMed.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- M. Gouterman and G. H. Wagnière, J. Mol. Spectrosc., 1963, 127, 108–127 CrossRef.
- M. Umetsu, Z. Wang, K. Yoza, M. Kobayashi and T. Nozawa, Biochim. Biophys. Acta, 2000, 1457, 106–117 CrossRef CAS.
- E. Thyrhaug, K. Žídek, J. Dostál, D. Bína and D. Zigmantas, J. Phys. Chem. Lett., 2016, 7, 1653–1660 CrossRef CAS PubMed.
- J. Neugebauer, ChemPhysChem, 2009, 10, 3148–3173 CrossRef CAS PubMed.
- M. T. Milder, B. Brüggemann, R. van Grondelle and J. L. Herek, Photosynth. Res., 2010, 104, 257–274 CrossRef CAS.
- C. Curutchet and B. Mennucci, Chem. Rev., 2017, 117, 294–343 CrossRef CAS PubMed.
- M. Schreiber and V. Buss, Int. J. Quantum Chem., 2003, 95, 882–889 CrossRef CAS.
- N. Ferré and M. Olivucci, J. Am. Chem. Soc., 2003, 125, 6868–6869 CrossRef PubMed.
- A. J. A. Aquino, M. Barbatti and H. Lischka, ChemPhysChem, 2006, 7, 2089–2096 CrossRef CAS PubMed.
- M. Wanko, M. Hoffmann, P. Strodel, A. Koslowski, W. Thiel, F. Neese, T. Frauenheim and M. Elstner, J. Phys. Chem. B, 2005, 109, 3606–3615 CrossRef CAS PubMed.
- A. Anda, T. Hansen and L. De Vico, J. Chem. Theory Comput., 2016, 12, 1305–1313 CrossRef CAS PubMed.
- A. Anda, L. De Vico and T. Hansen, J. Phys. Chem. B, 2017, 121, 5499–5508 CrossRef CAS PubMed.
- N. H. List, C. Curutchet, S. Knecht, B. Mennucci and J. Kongsted, J. Chem. Theory Comput., 2013, 9, 4928–4938 CrossRef CAS.
- R. Send and D. Sundholm, Phys. Chem. Chem. Phys., 2007, 9, 2862–2867 RSC.
- R. Send and D. Sundholm, J. Phys. Chem. A, 2007, 111, 27–33 CrossRef CAS.
- R. Send, D. Sundholm, M. P. Johansson and F. Pawlowski, J. Chem. Theory Comput., 2009, 5, 2401–2414 CrossRef CAS PubMed.
- O. Valsson and C. Filippi, J. Chem. Theory Comput., 2010, 6, 1275–1292 CrossRef CAS.
- C. M. Suomivuori, N. O. Winter, C. Hättig, D. Sundholm and V. R. Kaila, J. Chem. Theory Comput., 2016, 12, 2644–2651 CrossRef CAS.
- J. Linnanto and J. Korppi-Tommola, Phys. Chem. Chem. Phys., 2006, 8, 663–687 RSC.
- D. Jacquemin, E. A. Perpète, G. Scalmani, M. J. Frisch, R. Kobayashi and C. Adamo, J. Chem. Phys., 2007, 126, 0–12 Search PubMed.
- D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed.
- I. V. Rostov, R. D. Amos, R. Kobayashi, G. Scalmani and M. J. Frisch, J. Phys. Chem. B, 2010, 114, 5547–5555 CrossRef CAS PubMed.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- O. Valsson, C. Filippi and M. E. Casida, J. Chem. Phys., 2015, 142, 144104 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. Higashi, T. Kosugi, S. Hayashi and S. Saito, J. Phys. Chem. B, 2014, 118, 10906–10918 CrossRef CAS.
- T. Wolter, M. Elstner, S. Fischer, J. C. Smith and A.-N. Bondar, J. Phys. Chem. B, 2015, 119, 2229–2240 CrossRef CAS.
- L. Cupellini, S. Jurinovich, M. Campetella, S. Caprasecca, C. A. Guido, S. M. Kelly, A. T. Gardiner, R. Cogdell and B. Mennucci, J. Phys. Chem. B, 2016, 120, 11348–11359 CrossRef CAS PubMed.
- A. D. Bacon and M. C. Zerner, Theor. Chim. Acta, 1979, 53, 21–54 CrossRef CAS.
- M. C. Zerner, G. H. Loew, R. F. Kirchner and U. T. Mueller-Westerhofflc, J. Am. Chem. Soc., 1980, 102, 589–599 CrossRef CAS.
- M. G. Cory, M. C. Zerner, X. Hu and K. Schulten, J. Phys. Chem. B, 1998, 102, 7640–7650 CrossRef CAS.
- C. Olbrich, T. L. C. Jansen, J. Liebers, M. Aghtar, J. Strümpfer, K. Schulten, J. Knoester and U. Kleinekathöfer, J. Phys. Chem. B, 2011, 115, 8609–8621 CrossRef CAS PubMed.
- C. Olbrich and U. Kleinekathöfer, J. Phys. Chem. B, 2010, 114, 12427–12437 CrossRef CAS PubMed.
- K. Welke, J. S. Frähmcke, H. C. Watanabe, P. Hegemann and M. Elstner, J. Phys. Chem. B, 2011, 115, 15119–15128 CrossRef CAS PubMed.
- T. Niehaus, THEOCHEM, 2009, 914, 38–49 CrossRef CAS.
- T. A. Niehaus and F. Della Sala, Phys. Status Solidi B, 2012, 249, 237–244 CrossRef CAS.
- J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, J. Chem. Theory Comput., 2017, 13, 1737–1747 CrossRef CAS PubMed.
- J. J. Kranz and M. Elstner, J. Chem. Theory Comput., 2016, 12, 4209–4221 CrossRef CAS PubMed.
- L. Stojanović, S. G. Aziz, R. H. Hilal, F. Plasser, T. A. Niehaus and M. Barbatti, J. Chem. Theory Comput., 2017, 13, 5846–5860 CrossRef PubMed.
- C. Steinmann and J. Kongsted, J. Chem. Theory Comput., 2015, 11, 4283–4293 CrossRef CAS.
- F. Segatta, L. Cupellini, S. Jurinovich, S. Mukamel, M. Dapor, S. Taioli, M. Garavelli and B. Mennucci, J. Am. Chem. Soc., 2017, 139, 7558–7567 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- J. Almlöf, T. H. Fischer, P. G. Gassman, A. Ghosh and M. Häser, J. Phys. Chem., 1993, 97, 10964–10970 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- T. Kubař, K. Welke and G. Groenhof, J. Comput. Chem., 2015, 36, 1978–1989 CrossRef PubMed.
- M. Eichinger, P. Tavan, J. Hutter and M. Parrinello, J. Chem. Phys., 1999, 110, 10452–10467 CrossRef CAS.
- H. C. Watanabe, K. Welke, D. J. Sindhikara, P. Hegemann and M. Elstner, J. Mol. Biol., 2013, 425, 1795–1814 CrossRef CAS PubMed.
- J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS.
- M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS PubMed.
- M. Gaus, X. Lu, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2014, 10, 1518–1537 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- C. S. López, O. N. Faza, S. L. Estévez and A. R. De Lera, J. Comput. Chem., 2006, 27, 116–123 CrossRef.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- T. A. Niehaus, S. Suhai, F. Della Sala, M. Elstner, G. Seifert and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–9 CrossRef.
- V. Lutsker, B. Aradi and T. A. Niehaus, J. Chem. Phys., 2015, 143, 184107 CrossRef CAS.
- R. Baer and D. Neuhauser, Phys. Rev. Lett., 2005, 94, 2–5 CrossRef.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1394 Search PubMed.
- S. Maity, A. Gelessus, V. Daskalakis and U. Kleinekathöfer, Chem. Phys., 2019, 526, 110439 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- N. O. C. Winter and C. Hättig, J. Chem. Phys., 2011, 134, 184101 CrossRef PubMed.
- N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630 RSC.
- A. Koslowski, M. E. Beck and W. Thiel, J. Comput. Chem., 2003, 6, 714–726 CrossRef PubMed.
- W. Weber and W. Thiel, Theor. Chem. Acc., 2000, 103, 495–506 Search PubMed.
- Y. Guo, F. E. Beyle, B. M. Bold, H. C. Watanabe, A. Koslowski, W. Thiel, P. Hegemann, M. Marazzi and M. Elstner, Chem. Sci., 2016, 7, 3879–3891 RSC.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105 CrossRef PubMed.
- M. E. Madjet, A. Abdurahman and T. Renger, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS PubMed.
- E. P. Kenny and I. Kassal, J. Phys. Chem. B, 2016, 120, 25–32 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- H. Kitoh-Nishioka, D. Yokogawa and S. Irle, J. Phys. Chem. C, 2017, 121, 4220–4238 CrossRef CAS.
- S. Ahuja, M. Eilers, A. Hirshfeld, E. C. Y. Yan, M. Ziliox, T. P. Sakmar, M. Sheves and S. O. Smith, J. Am. Chem. Soc., 2009, 131, 15160–15169 CrossRef CAS PubMed.
- L. H. Andersen, I. B. Nielsen, M. B. Kristensen, M. O. El Ghazaly, S. Haacke, M. B. Nielsen and M. Å. Petersen, J. Am. Chem. Soc., 2005, 127, 12347–12350 CrossRef CAS.
- C. L. Janssen and I. M. Nielsen, Chem. Phys. Lett., 1998, 290, 423–430 CrossRef CAS.
- J. Neugebauer, J. Phys. Chem. B, 2008, 112, 2207–2217 CrossRef CAS PubMed.
- R. S. Knox and B. Q. Spring, Photochem. Photobiol., 2003, 77, 497–501 CrossRef CAS PubMed.
- R. G. Alden, E. Johnson, V. Nagarajan and W. W. Parson, J. Phys. Chem. B, 1997, 101, 4667–4680 CrossRef CAS.
- R. Mathies and L. Stryer, Proc. Natl. Acad. Sci. U. S. A., 1976, 73, 2169–2173 CrossRef CAS PubMed.
- P. A. Plötz, T. Niehaus and O. Kühn, J. Chem. Phys., 2014, 140, 174101 CrossRef PubMed.
- T. Kubař, P. B. Woiczikowski, G. Cuniberti and M. Elstner, J. Phys. Chem. B, 2008, 112, 7937–7947 CrossRef PubMed.
- B. Moore and J. Autschbach, ChemistryOpen, 2012, 1, 184–194 CrossRef CAS.
- N. Schieschke, B. M. Bold, D. Holub, M. Hoffman, A. Dreuw, M. Elstner and S. Höfener, to be published.
- J. S. Frähmcke, M. Wanko, P. Phatak, M. A. Mroginski and M. Elstner, J. Phys. Chem. B, 2010, 114, 11338–11352 CrossRef PubMed.
- M. Wanko, M. Hoffmann, T. Frauenheim and M. Elstner, J. Phys. Chem. B, 2008, 112, 11462–11467 CrossRef CAS.
- M. Wanko, M. Hoffmann, J. Frähmcke, T. Frauenheim and M. Elstner, J. Phys. Chem. B, 2008, 112, 11468–11478 CrossRef CAS PubMed.
- I. B. Nielsen, L. Lammich and L. H. Andersen, Phys. Rev. Lett., 2006, 96, 13–16 CrossRef PubMed.
- A. Damjanović, I. Kosztin, U. Kleinekathöfer and K. Schulten, Phys. Rev. E, 2002, 65, 1–24 CrossRef PubMed.
- L. Janosi, I. Kosztin and A. Damjanović, J. Chem. Phys., 2006, 125, 14903 CrossRef PubMed.
- A. Damjanović, T. Ritz and K. Schulten, Phys. Rev. E, 1999, 59, 3293–3311 CrossRef.
- M. Pajusalu, M. Rätsep, G. Trinkunas and A. Freiberg, ChemPhysChem, 2011, 12, 634–644 CrossRef CAS PubMed.
- J.-p. Zhang, R. Fujii, P. Qian, T. Inaba, T. Mizoguchi, Y. Koyama, K. Onaka, Y. Watanabe and H. Nagae, J. Phys. Chem. B, 2000, 104, 3683–3691 CrossRef CAS.
- S. Chandrasekaran, M. Aghtar, S. Valleau, A. Aspuru-Guzik and U. Kleinekathöfer, J. Phys. Chem. B, 2015, 119, 9995–10004 CrossRef CAS PubMed.
- S. S. Skourtis, D. H. Waldeck and D. N. Beratan, Annu. Rev. Phys. Chem., 2010, 61, 461–485 CrossRef CAS PubMed.
- P. B. Woiczikowski, T. Kubař, R. Gutiérrez, R. A. Caetano, G. Cuniberti and M. Elstner, J. Chem. Phys., 2009, 130, 215104 CrossRef PubMed.
- D. Hayes and G. S. Engel, Biophys. J., 2011, 100, 2043–2052 CrossRef CAS PubMed.
- C. W. Kim, B. Choi and Y. M. Rhee, Phys. Chem. Chem. Phys., 2017, 20, 3310–3319 RSC.
- S. Jurinovich, C. Curutchet and B. Mennucci, ChemPhysChem, 2014, 15, 3194–3204 CrossRef CAS.
- X. Jia, Y. Mei, J. Z. H. Zhang and Y. Mo, Sci. Rep., 2015, 5, 1–10 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05753f |
| This journal is © the Owner Societies 2020 |