Effect of crystallization on the electronic and optical properties of archetypical porphyrins

Abstract

Thin porphyrin films as employed in modern optical devices or photovoltaic applications show deviating electronic and optical properties from the gasphase species. Any understanding of the physical origin may pave way to a specific engineering of these properties via ligand or substituent control. Here we investigate the impact of crystallization of prototypical porphyrins on the electronic levels and optical properties in the framework of density functional theory and many-body perturbation theory. Crystallization substantially shrinks the HOMO–LUMO gap based on polarization effects. We find a shift of the HOMO to higher energy is consistent with recent experiment of MgTPP multilayer film on Ag (100) [A. Classen et al., Phys. Rev. B, 2017, 95, 115414]. Calculated excitation spectra demonstrate a significant redshift of excitation bands except for the Q bands. These lowest excitation bands, in stark contrast to the strong HOMO–LUMO gap renormalization, remain essentially the same as in the gas phase. Our work underlines the possibility of band-gap engineering via ligand-controlled modification of the polarizability.

---

1 Introduction

Free-base and metallated porphyrins are versatile molecules that have been successfully used in 0D applications^1–3 such as emitters in organic light-emitting diodes (OLEDs),^4,5 label-free fluorescence probe for DNA analytics,⁶ sensitizers in dye-sensitized solar cells⁷ and electron transfer centers in catalytic transformations.^8,9 Functional layers and nanostructures on surfaces using 2D molecular engineering lead to sensors, and nanoscale optical and magnetic materials.¹⁰ 3D structures made from porphyrins are used in controlling and manipulating light at subwavelength dimensions.^11–13 Porphyrin assemblies can be manufactured to act both as a passive and active waveguide simultaneously.¹⁴ In general, layered van der Waals (vdW) bound 3D materials promise, among other applications, highly efficient yet thin solar energy harvesters.¹⁵ Ground and excited state energy levels play a key role in such applications as they directly influence optical properties and charge-transfer dynamics of the material. For the porphyrin molecules, these are captured by a robust symmetry cascade model called the Gouterman four-orbital model.¹⁶ However, the influence of the supramolecular packing on the energy levels even in the fundamental crystal form¹⁷ has not been thoroughly explored.

Archetypal free-base tetraphenylporphyrin (H2TPP) and Magnesium meso-tetraphenylporphyrin (MgTPP) represent naturally occurring porphyrins frequently encountered in biology. A recent experiment reveals that when H2TPP and MgTPP form thick films on Ag(100) substrate, the quasiparticle band gap shrinks compared to gas phase.^18,19 These experiments identify a ∼0.5 eV upshift of the HOMO in the multilayer films with respect to the molecules in the gas phase independent of the film thickness.

In fact, level shifts and a corresponding band-gap renormalization were observed for a wide range molecular crystals in photo emission experiments²⁰ and was attributed to the polarization energy due to the ionization of molecules in the crystal. Recent state of the art calculations using high-level methods such as many body perturbation theory or DFT with optimal tuning of range separated hybrid functionals were able to access these effects,^21,22 whereas using semi-local and hybrid exchange–correlation energy functionals failed to capture level-shifts and band gap renormalization. How these effects manifest themselves in the electronic and optical properties of the porphyrin crystals is, however, unclear.

In this article we address the impact of the supramolecular packing on the electronic and optical spectra of archetypical porphyrins H2TPP and MgTPP. We focus on the experimentally reported molecular crystal¹⁷ and various other packings of the molecules in the crystalline phase. Besides the fundamental interest in the properties of the porphyrin crystal, the results are also applicable to the modeling of a thick film on a substrate. Indeed, substrate–film interaction effects couple weakly to the bulk part of the film owing to the VdW bonding between the molecules. We demonstrate that the deviation between the gas phase data and the multilayer films in experiment is due to intermolecular interactions. The quasiparticle DOS features for the experimental crystalline packing align well with the photoemission spectra on thick films,^19,23 in particular regarding the HOMO position. In the experimental crystalline packing, the vertical transitions of the visible part of the spectrum remains unchanged, whereas in the UV region redshifts by more than 1 eV do occur.

2 Theoretical methods

The structural properties of the porphyrins packing are investigated at the DFT-level with empirical dispersion corrections using VASP.²⁴ We have applied different flavors of dispersion correction schemes, and the best consistency was obtained using DFT-D3²⁵ and the many-body dispersion energy method (MBD@rSC)²⁶ as described in the ESI.† The cell shape, volume and ionic positions of the crystal structure are optimized starting from the experimental crystal structure.¹⁷

The electronic properties of the isolated molecules and crystals are obtained within the sc-GW₀²⁷ level of theory using LDA orbitals as a starting point (cf. ESI,† Section S2, for details). This level of theory reproduces NIST calibration data²⁸ for the molecules in the gas phase. In the crystal, the band structure is obtained by interpolating the quasiparticle levels along the k-path trajectory using the maximally localized Wannier functions (MLWFs) method of Marzari and Vanderbilt.²⁹ The details of the parameters and procedures can be found in the ESI,† Section S3.

The optical properties in the visible and UV regions are calculated by solving the Bethe–Salpether equation³⁰ (BSE). Due to the complex nature of the excited state potential energy surface of porphyrins, we restrict the investigation to vertical transitions.

3 Results and discussion

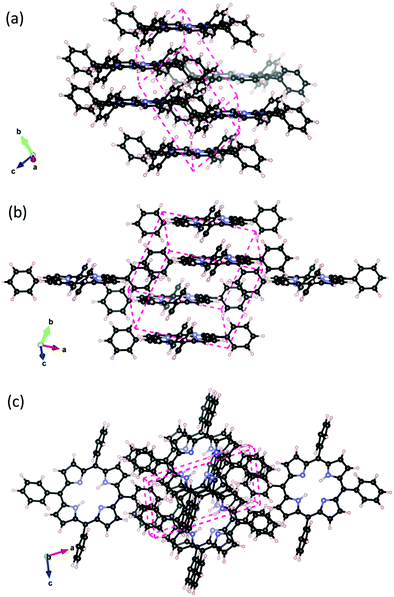
Porphyrins aggregate as a result of the strong attractive π–π van der Waals interaction further enhanced by the unique properties of the porphine skeleton. The H2TPP crystal is reported¹⁷ to have a P1̄ triclinic unit cell. From the experiments, the packing scheme shown in Fig. 1 was deduced, in which the interacting H2TPP assume an offset cofacial configuration. Experimental crystallographic data was not available for MgTPP. Inspired by the observation for similar behaving metal centers,³¹ we obtained its crystal lattice by metalating and re-optimizing the H2TPP crystal.

Fig. 1 H2TPP crystal with P1̄ triclinic crystal structure. Interacting porphyrins arrange cofacially in the crystal. (a) and (b) different views parallel to the macrocycle plane, and (c) view onto the macrocycle plane. The orientation of the lattice vectors a⃑, b⃑, and c⃑ as well as the shape of the unit cell (dashed line) are indicated.

In addition to the P1̄ triclinic crystal structure, we investigate three additional possible scenarios for thick MgTPP films following the strong and weak interaction idea from Perepogu and Bangal:³² (1) The simple stack where porphyrin molecules are directly on top of each other. (2) Rotated stack, where porphyrin layers are rotated by 90° with respect to each other (3) Herringbone where each porphyrin is coordinated with the phenyl rings of another porphyrin perpendicular to it. The binding energies of the models are reported in the ESI,† Table S5. The experimentally reported crystal packing, which can be considered as an offset form of the simple stack, is the most favorable energetically.

In the following we focus on the experimentally observed P1̄ triclinic crystal structure. The experimental and calculated unit cell parameters are reported in the ESI,† Table S1. The porphine skeleton of H2TPP is significantly distorted in the crystal compared to the isolated molecule and assumes a saddle shape. The point group becomes C_i whereas the gas phase H2TPP has the point group D_2h and the porphine macrocycle has D_4h. Our calculations identify the strong VdW interaction both between macrocycles and between phenyl ring substituents as the major driving force behind this distortion. In the ESI,† Fig. S1 and Table S2, we report key interatomic distances within the phenyl, and pyrrole sections of the molecule as well as the orientation of the phenyl rings with respect to the macrocycle plane, and the overall macrocycle size. The distorted molecule in the crystal (cf. Table S3, ESI†) shows a significant change in the orientation of the phenyl rings of 10° with respect the isolated molecule and only small changes in bond distances.

In comparison with the experimental structural parameters, the calculated values for the volume and inter molecular distances using the D3 or MDB@rSC dispersion correction variants are slightly smaller: the crystal volume is by 6% lower and the distance between adjacent macro cycles is by 4–5% shorter. On the other hand, the calculated intramolecular bond distance result slightly larger than the corresponding experimental values (cf. ESI† Tables S2). For the latter, the different VdW schemes have little effect and the results follow the common tendency of the PBE exchange–correlation functional. The other structural parameters hinge on the flavor of the VdW scheme (cf. ESI† Tables S1 and S2). Note, however, that the structure optimisation does not account for zero point vibrations, effects of anharmonic vibrations or other thermal effects that are contained in the experimental data.

An interesting aspect is the energy cost for cleaving the layered material (cleavage energy) which we determine based on DFT-VdW calculations. The calculated cleavage energy of the H2TPP and the MgTPP crystal is 0.198 J m⁻² and 0.207 J m⁻² respectively (cf.Fig. 2). Using the same level of approximation yields a cleavage energy of 0.324 J m⁻² for graphite (0.36 J m⁻² experimentally). Although the calculated values are smaller than the value for graphite, they are still within the range of other commercially interesting layered materials.

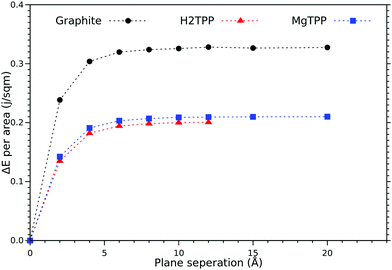Fig. 2 Calculated cleavage energy of the H2TPP and MgTPP crystals, and graphite as a function of the layer separation (symbols as obtained with DFT-D3, lines guide the eye only).

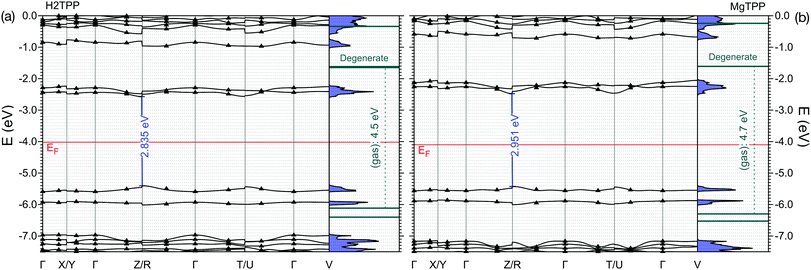
Now, we turn our attention to the electronic properties of the P1̄ triclinic crystal. The comparison of the gas phase quasiparticle levels with the DOS in crystalline phase (along with relevant experimental values) is presented in Fig. 3. The band structure of the crystal is presented in Fig. 4. All levels are aligned with respect to the vacuum level as a common reference potential. Note that our approach replicates the available NIST data²⁸ for all similar porphyrins in the gas phase as indicated in Fig. 3. The crystalline porphyrin H2TPP is an indirect band-gap semiconductor with a band gap of 2.84 eV, which is more than 1.6 eV smaller compared to the gas phase. The band gap of the crystal at the Γ-point is slightly larger than the indirect gap (+0.3 eV). At the PBE-VdW level we obtain an indirect band gap of the H2TPP crystal (cf. Table S6, ESI†) that is only 0.3 eV smaller than that of the gas phase molecule. This difference is comparable to the dispersion of the highest occupied and lowest unoccupied bands obtained at this level of theory (cf. Table S6, ESI†). The failure to reproduce the band-gap renormalization or level shifts at this DFT-level of theory is not unexpected and is in par with earlier findings.^21,33

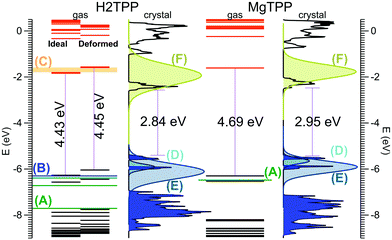Fig. 3 Calculated molecular levels and crystal DOS (sc-GW₀) aligned to the vacuum level. For the H2TPP molecule, levels are reported both in the gas phase geometry, and the distorted geometry found in the crystal. Gas phase experiments: (A) ref. 36 (B) ref. 37 (C) ref. 38. Multi-layer film on Ag(100) from ref. 18 (D) HOMO, (E) HOMO−1, and (F) LUMO; the reported peak positions are broadened using Gaussians according to the corresponding peak width given in ref. 18. Peak height is adjusted for clarity.

Fig. 4 Band structure of the (a) H2TPP and (b) MgTPP crystals. Bands obtained via Wannierization of sc-GW₀ calculation are aligned to the vacuum level. The exact sc-GW₀ values on the k-path are indicated by triangles. For comparision the levels of the isolated molecules are shown.

The HOMO level of the gas phase H2TPP is shifted upwards by ∼0.9 eV and the LUMO level is shifted downwards by ∼0.7 eV in the crystal. Similary the HOMO level of gas phase MgTPP upshifts by ∼0.9 eV and the LUMO level downshifts by ∼0.9 eV. The bands in the crystal are slightly dispersive (for details cf. ESI† Section S2, Table S6 and Fig. S2). This manifests itself as an uneven broadening in the DOS. There are a number of level crossings between LUMO and LUMO+1 bands which are degenerate orbitals in the gas phase. The band structure of the MgTPP crystal is quite similar to that of the H2TPP crystal, with a band gap of 2.95 eV.

Note that a very similar band-gap renormalization is observed in the simple stacking scheme of MgTPP, where the HOMO–LUMO gap reduces to 3.0 eV. The packing density seems to be more relevant to the band-gap renormalization than the exact molecular packing. This suggests that ligand controlled modification of the packing density is a viable strategy for band-gap engineering.

In order to understand the large band-gap renormalization of 36%, we considered the influence of the significant distortion of the molecule in the crystal and intermolecular interaction. A comparison of the energy levels of the isolated H2TPP molecule in its fully relaxed configuration and the distorted geometry in the crystal showed that the distortion into a saddle shape and the rotation of the phenyl rings have negligble effect (cf.Fig. 3). Our finding of a weak dispersion at the GW- and DFT-levels of theory furthermore show that weak interaction between the molecules that causes this band dispersion does not explain the band-gap renormalization or the distinct shifts of the HOMO and LUMO bands. This is in par with similar calculations for other molecular crystals and is explained there by electronic polarization effects.^34,35

The calculated HOMO band energy position of both H2TPP and MgTPP crystal fit with photoemission experiments on thick films on Ag(100)¹⁸ (cf.Fig. 3). In these experiments the LUMO states were investigated using two-photon photoemission spectroscopy (2PPE).¹⁸ As shown in Fig. 3 the broad LUMO peaks are centered at somewhat higher energies than the calculated values, however, the discrepancy is less than the peak width. The LUMO peaks are broadened most likely due to unresolved vibrational modes given their Gaussian shape.¹⁸ Besides the high level of vibrational excitation in the LUMO peak, the unknown film structure may also contribute to the deviation. Nevertheless, a reduction of the HOMO–LUMO gap of 1.0 eV and 0.5 eV is also reported¹⁸ for the thick MgTPP and H2TPP films, respectively, which although being smaller, confirms the trend found in our calculations for the pure crystalline structures.

Now we focus on the optical properties. The porphyrins share similar features in their optical spectra, namely two peaks in the visible region (Q bands), a very intense peak (B or Soret band), a shoulder on the B band (N band), and two other small peaks, the L and M bands. Q bands are often considered of critical importance for energy harvesting and lighting applications. The origin of these typical features are well captured by the Gouterman model¹⁶ which involves the two uppermost occupied orbitals and the two lowest unoccupied orbitals of the porphine skeleton. The effect of the substituents on these features are limited and often indirect.

We calculate the vertical optical transitions using BSE presented in Fig. 5. We observe that, the important Q band vertical transitions are not effected by the formation of the crystal, apart from an additional small feature at 2.5 eV. On the contrary, the effect of crystallization is clearly observed in the Soret band. It redshifts from UV by 0.5 eV and moves into the visible range. Furthermore the reduced symmetry and anisotropic screening in the layered crystal lead, in the case of MgTPP, to an anisotropic splitting of the Soret band. It is interesting to note that the shift in the Soret band aligns with the purple appearance of crystalline H2TPP.

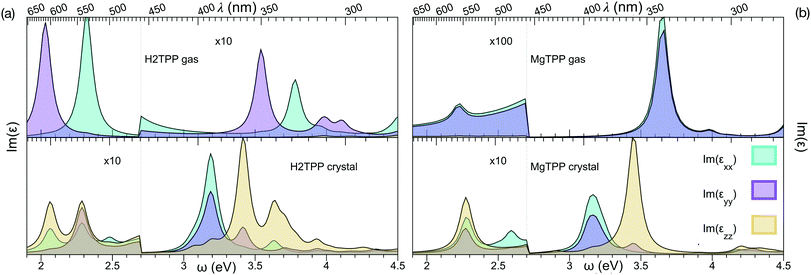Fig. 5 Imaginary part of the dielectric response, obtained from Bethe–Salpether equation: (a) H2TPP gas phase and crystal and (b) MgTPP gas phase and crystal.

In recent experiments the optical properties of H2TPP and MgTPP films were investigated.^39,40 Note that a direct comparison of the optical spectra presented in this and the experimental works requires incorporation of the vibronic effects, since vibronic enhancement of orders of magnitude in Q bands is well known in porphyrins. Furthermore, the excited states are dynamic Jahn–Teller active.⁴¹ Given the flexibility of the macrocycle and the low impact of the distortion on the quasiparticle levels, we expect nevertheless that the trends we describe are robust. Indeed, also in these experiments^39,40 only a very small shift in the Q bands (H2TPP films:³⁹ <70 meV) and a much larger shift in the Soret band (MgTPP films:⁴⁰ ∼200 meV) were observed in the mostly amorphous films. Although the effect in the Soret band of the amorphous MgTPP film is by a factor of two smaller than predicted for the crystal, most likely due to the more isotropic screening in the amorphous film, the experiments match our findings.

4 Conclusions

In summary, we investigated the effect of H2TPP and MgTPP crystallization on the electronic and optical properties using density functional theory with semi-empirical dispersion corrections and many body perturbation theory at the sc-GW₀ and BSE levels. We find a band-gap renormalization due to polarization effect of more than 1.6 eV upon crystallization in the P1̄ triclinic lattice. The crystals are indirect band gap semiconductors with dispersive conduction and valence bands. Our qualitative analysis shows that the band edges are Gouterman-like, with a dispersive component mostly due to phenyl–phenyl and phenyl–pyrrole interactions. Calculated sc-GW₀ energy bands explain the shift in HOMO and HOMO−1 in the photoemission experiment¹⁸ on multi-layer films on Ag(100) compared to the gas phase values. Experiments also indicate a band-gap renormalization.

The impact of crystallization on electronic levels and optical transitions are qualitatively different. Despite of the large band-gap renormalization, optical Q band vertical transitions remain at the same energy with an additional low intensity transition. The Soret band, however, redshifts towards blue in the crystal, which makes the purple/blue spectral region accessible in solar applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge valuable discussions with Th. Fauster. This project is part of DFG Research unit FOR 1878, and has been funded by Deutsche Forschungs Gemeinschaft (grant: BO 1851/4-1) and Austrian FWF (grant: I3385). Computer time was provided on the HPC cluster at the RRZE of Friedrich-Alexander University Erlangen-Nürnberg and on the Doppler-Cluster of the Paris-Lodron University Salzburg.

Notes and references

1. K. M. Kadish, K. M. Smith and R. Guilard, Handbook of Porphyrin Science, World Scientific, 2010.
2. J. M. Gottfried, Surf. Sci. Rep., 2015, 70, 259–379.
3. W. Auwarter, D. Ecija, F. Klappenberger and J. V. Barth, Nat. Chem., 2015, 7, 105–120.
4. Porphyrin materials for organic light emitting diodes: a route to phosphorescent emission, ed. B. Tuffy, LAMBERT Academic Publishing, Saabrucken, 2011.
5. A. G. Coutsolelos, A. Charisiadis, A. Bagaki, E. Fresta, K. T. Weber, G. Charalambidis, C. Stangel, A. G. Hatzidimitriou, P. A. Angaridis and R. D. Costa, ChemPlusChem, 2018, 83, 254–265.
6. Y. Guo, L. Deng, J. Li, S. Guo, E. Wang and S. Dong, ACS Nano, 2011, 5, 1282–1290.
7. M. Urbani, M. Gratzel, M. K. Nazeeruddin and T. Torres, Chem. Rev., 2014, 114, 12330–12396.
8. D. A. Duncan, P. S. Deimel, A. Wiengarten, R. Han, R. G. Acres, W. Auwarter, P. Feulner, A. C. Papageorgiou, F. Allegretti and J. V. Barth, Chem. Commun., 2015, 51, 9483–9486.
9. B. E. Murphy, S. A. Krasnikov, N. N. Sergeeva, A. A. Cafolla, A. B. Preobrajenski, A. N. Chaika, O. Lubben and I. V. Shvets, ACS Nano, 2014, 8, 5190–5198.
10. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671–679.
11. F. S. Kim, G. Ren and S. A. Jenekhe, Chem. Mater., 2011, 23, 682–732.
12. G. C. La Rocca, Nat. Photonics, 2010, 4, 343–345.
13. D. M. Coles, N. Somaschi, P. Michetti, C. Clark, P. G. Lagoudakis, P. G. Savvidis and D. G. Lidzey, Nat. Mater., 2014, 13, 712–719.
14. N. Chandrasekhar, S. Basak, M. A. Mohiddon and R. Chandrasekar, ACS Appl. Mater. Interfaces, 2014, 6, 1488–1494.
15. B. E. Hardin, H. J. Snaith and M. D. McGehee, Nat. Photonics, 2012, 6, 162–169.
16. P. G. Seybold and M. Gouterman, J. Mol. Spectrosc., 1969, 31, 1–13.
17. K. Kano, K. Fukuda, H. Wakami, R. Nishiyabu and R. F. Pasternack, J. Am. Chem. Soc., 2000, 122, 7494–7502.
18. A. Classen, R. Poschel, G. Di Filippo, T. Fauster, O. B. Malcioglu and M. Bockstedte, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 115414.
19. G. Di Filippo, A. Classen, R. Poschel and T. Fauster, J. Chem. Phys., 2017, 146, 064702.
20. N. Sato, K. Seki and H. Inokuchii, J. Chem. Soc., Faraday Trans., 1981, 77, 1621–1633.
21. L. Kronik and J. B. Neaton, Annu. Rev. Phys. Chem., 2016, 67, 587–616.
22. X. Blase, C. Attaccalite and V. Olevano, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115103.
23. M. Nardi, R. Verucchi, C. Corradi, M. Pola, M. Casarin, A. Vittadini and S. Iannotta, Phys. Chem. Chem. Phys., 2010, 12, 871–880.
24. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
25. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
26. A. Ambrosetti, A. M. Reilly, R. A. DiStasio, Jr. and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508.
27. M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235102.
28. W. E. Acree and J. S. Chickos, Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, GaithersburgMD, 20899, retrieved March 6, 2019.
29. N. Marzari and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 12847–12865.
30. T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209.
31. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
32. A. K. Perepogu and P. R. Bangal, J. Chem. Sci., 2008, 120, 485–491.
33. J. B. Neaton, M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216405.
34. S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081204(R).
35. S. Bhandari, M. S. Cheung, E. Geva, L. Kronik and B. D. Dunietz, J. Chem. Theory Comput., 2018, 14, 6287.
36. S. C. Khandelwal and J. L. Roebber, Chem. Phys. Lett., 1975, 34, 355–359.
37. Y. Nakato, K. Abe and H. Tsubomura, Chem. Phys. Lett., 1976, 39, 358–360.
38. H. L. Chen, Y. H. Pan, S. Groh, T. E. Hagan and D. P. Ridge, J. Am. Chem. Soc., 1991, 113, 2766–2767.
39. K. Tanimura, T. Kawai and T. Sakata, J. Phys. Chem., 1980, 84, 751–756.
40. K. Stallberg, G. Lilienkamp and W. Daum, J. Phys. Chem. C, 2015, 119, 21626–21632.
41. P. Rosenow, P. Jakob and R. Tonner, J. Phys. Chem. Lett., 2016, 7, 1422–1427.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06040e

‡ Present address: METU Orta Dogu Teknik Universitesi, Fizik Bolumu, Ankara, Turkey.

§ Present address: Institute for Theoretical Physics, Johannes Keppler University, Linz, Austria.

---