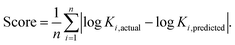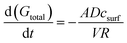Applying support-vector machine learning algorithms toward predicting host–guest interactions with cucurbit[7]uril

Abstract

Machine learning is a valuable tool in the development of chemical technologies but its applications into supramolecular chemistry have been limited. Here, the utility of kernel-based support vector machine learning using density functional theory calculations as training data is evaluated when used to predict equilibrium binding coefficients of small molecules with cucurbit[7]uril (CB[7]). We find that utilising SVMs may confer some predictive ability. This algorithm was then used to predict the binding of drugs TAK-580 and selumetinib. The algorithm did predict strong binding for TAK-580 and poor binding for selumetinib, and these results were experimentally validated. It was discovered that the larger homologue cucurbit[8]uril (CB[8]) is partial to selumetinib, suggesting an opportunity for tunable release by introducing different concentrations of CB[7] or CB[8] into a hydrogel depot. We qualitatively demonstrated that these drugs may have utility in combination against gliomas. Finally, mass transfer simulations show CB[7] can independently tune the release of TAK-580 without affecting selumetinib. This work gives specific evidence that a machine learning approach to recognition of small molecules by macrocycles has merit and reinforces the view that machine learning may prove valuable in the development of drug delivery systems and supramolecular chemistry more broadly.

---

Introduction

The applications of machine learning in biology and chemistry have rapidly expanded in recent years due to the potential of data science to improve small molecule drug discovery, identify more efficient synthetic pathways, create proteins with greater binding affinity to specific substrates, and other applications.^1–5 One application that has not yet been explored is predicting the molecular recognition of small molecules with macrocyclic hosts.

Cucurbiturils are a class of symmetric macrocycles that have applications within drug delivery, biosensing, catalysis, and energy.^6,7 These macrocycles have many advantages over their non-symmetric counterparts such as cyclodextrins, including temperature stability and robustness at acidic and basic pH values,⁶ such as those that occur naturally in physiology. The use of cucurbiturils to change the release kinetics or pharmacokinetics of drugs has been previously reported for chemotherapies such as temozolomide.^8,9 Cucurbituril acts as a competitive substrate and binds to the active ingredient. This binding can reduce the effective concentration and increase the half life of biologic and hydrophobic small molecule drugs.¹⁰ Predicting whether a molecule will bind to any cucurbituril, in particular cucurbit[7]uril (CB[7]), a priori could be a valuable tool in developing new chemical or material systems.¹¹

In this work, we show that support vector machines (SVMs) can be used to provide utility towards predicting 1 : 1 complexation of small organic molecules with CB[7]. Finding no comprehensive, compiled body of data that could be used for regression, we first created one using much of the published literature on small molecules that bind to CB[7].⁶ We also report the utility of this regression in predicting the binding of two new small molecule drugs that have received promising results in the clinic and verify these predictions with experimental data. Finally, we provide a qualitative example of the potential use of these predictions in developing cocktail drug therapies against a pediatric low grade glioma cell model.

Methods and model

A principal challenge for any machine learning application is in building a sufficiently large training data set that approximates the entire problem domain with as little bias as possible.¹² To start such an effort, we performed density functional theory (DFT) calculations on 146 molecules (Fig. S1–S10, ESI,† corresponding to nomenclature in ref. 6). These molecules had 194 total equilibrium binding coefficients to CB[7]; some molecules had multiple values because they were tested at multiple different experimental conditions (Table S1, ESI†).^6,13,14 Seeing a lack of negative controls in the literature,⁶ we also synthesised and/or tested three molecules that could not bind to CB[7] and set these undetectable binding events to output values of 0 to not skew the algorithm with extreme values (Fig. S11, ESI†). Critical to the binding affinity of molecules with CB[7] are the size, aromaticity, and charge of the guest. Other, non-intrinsic parameters such as solution temperature, pH, salt and/or buffer concentration may also effect the equilibrium binding constant.^6,15 We sought to capture both intrinsic and environmental properties of the binding event as potential predictive features (Fig. S12, ESI†). Many reports in the literature fail to disclose critical environmental details such as temperature or pH, which limited our ability to make a cohesive body of data covering the environmental properties. The simulated body of data were unified as we homogenously ran DFT calculations and extracted identical parameters from the optimised results (Table S1, ESI†).

With 194 molecular samples consisting of 17 experimental and structural features, the constructed data set is small sample-wise with a relatively high-dimensional feature space. Without heavily sub-setting the feature space and losing potentially integral feature-interaction information, training a model to find a subspace parameterising the underlying binding dynamics is difficult without strong inductive biases provided a priori. We instead looked to kernel methods to provide a more sample-efficient learning paradigm that can still capture the dynamics of the feature space through the lens of properly-defined sample similarity. A mathematical background for kernel methods is provided (ESI†).

Kernel featurisation provides a non-linear representation of the samples within some inner-product space. Support Vector Machines (SVMs) are a family of models that can capitalize on this expressive kernel structure by representing examples as points in this space and determining an optimal but well-behaved mapping that best describes the differences between individual points. Although originally designed for classification tasks, SVMs have a natural extension to regression. Given the mathematical framework developed (ESI†), we explored the capacity of SVMs to predict the equilibrium binding constants of published molecules.⁶ We performed a search over features to determine the best-performing subset of the feature space in coordination with grid search over hyperparameters within the model pipeline, namely γ, ε, C, |θ|, σ, and all permutations of addition or multiplication of each kernelised feature. The optimal hyperparameters (ESI†) were chosen based on 5-fold cross-validation with respect to mean absolute error.

The environmental data were largely incomplete due to the fact that many experiments in the literature do not report at least one and often several of the environmental parameters such as temperature or pH. For samples missing this information, we assumed temperatures of 298.15 K, and pH values of 7. We also set other values, such as salt concentration, to zero. These assumptions resulted in an environmental feature set that was sparse and largely uniform (Fig. 3, Supplementary data set, ESI†). Viewing environmental factors as a single feature vector, we also explored how the addition of environmental information affected prediction performance.

Results and discussion

A leave-one-out analysis was performed to subset the model features and choose the optimal model. Each model was trained on the entire training set less one sample, for all possible held out samples. The log of the equilibrium constant, log K, was then predicted by the model for each held-out sample. The mean absolute error of all held-out runs was calculated across every combination of the features listed in Table S1 (ESI†), and the subset with the lowest error score was chosen to go forward (Fig. S18 and S19, ESI†). While this combination, (1), (3), (4), and (6) (see Table S1, ESI†), contains some redundant information, it performed slightly better than the next best of (3), (4), and (6), and we chose to highlight its results here (see data processing for more information). Plots for the combinations of these parameters are shown in Fig. S13–S16, ESI.† For a predicted set of n members, the score was defined as the mean absolute deviation:
We chose mean absolute error as the scoring function due to both its intuitive simplicity and, because it equally scales the residuals, its consistent comparison across any magnitude split of left out data. We found other error measures behave similarly to this score.

Because the available environmental data lack diversity and are unnaturally uniform across samples, their usage as an additional feature often masked the underlying predictive capacity of the structural features. This process of feature reduction resulted in an optimal model consisting of 4 features derived from DFT calculations (1), (3), (4), and (6) only (Fig. S18, ESI†). These results are intuitive: both the size and electron distribution of small molecule organics are key in determining binding to cucurbit[7]uril.⁶ Environmental parameters including salt concentration are known to affect the binding of some molecules.⁶ However, the extent of changes is less than the error of our model, so environmental parameters were not considered going forward.

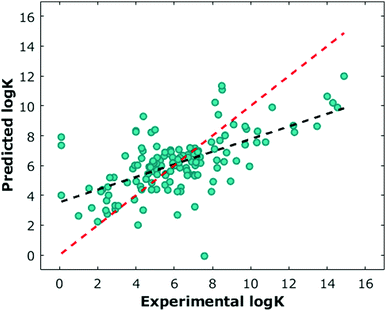
Optimised orientation was a large driver of model accuracy in predicting log K (ESI†). In pursuit of better intuition regarding model performance, the equivalent SVM classifier was trained using the same process as above. The confusion matrix in Fig. S19 (ESI†) is largely diagonal, with a bias towards over-predicting samples with a low value for log K. Also of interest was the extent to which the preprocessing methods provided separation between samples. Fig. S17 (ESI†) shows non-linear 2D projections of the combined kernels as well as the pre-kernelised and post-kernelised features for the optimised DFT orientation.¹⁶ It is evident from these plots that the featurisation process creates useful separation between high and low values of log K.

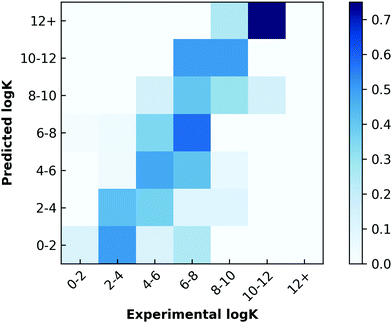
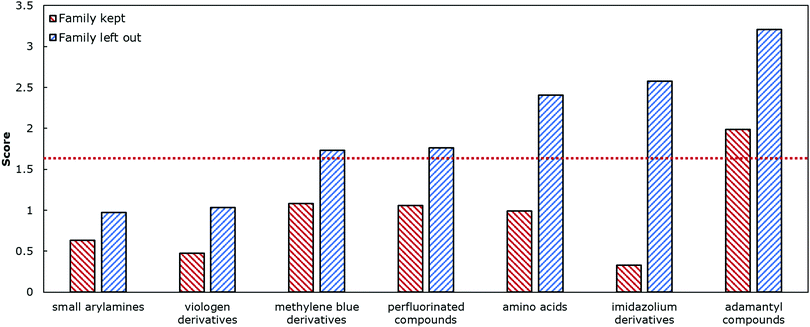
We next sought to challenge the model and identify its limits. We first removed any duplicate molecules at different conditions and set the true log K as the average of all the reported values. For example, methyl viologen was reported 14 times at different parameters such as temperature or salt concentration, and so instead of having methyl viologen appear 14 times, it appeared once (ESI†). Interestingly, and perhaps expectedly, the optimal model in this duplicate-free data set remained the same. The duplicate-free data set was chosen for subsequent analysis and the performance, confusion matrix, and corresponding receiver operating characteristic/area under the curve (ROC-AUC) plot are reported (Fig. 1, 2 and Fig. S17, ESI†). These classification results demonstrate the nature of the model's performance. Error accumulates primarily at either extemum of the log K distribution, but large errors are uncommon and performance in the denser parts of the training distribution is higher. Next, we removed classes of families and tested the model's ability to predict any one member of that family (Table 1, Fig. 4 and Table S2, ESI†). Given the limited size of the data set, we expect this algorithm to be useful in identifying the binding of molecules which a supramolecular chemist might expect to bind to cucurbiturils a priori. For example, molecules with extended aromaticity are generally hypothesised to have some interactions with cucurbiturils.¹⁵ This analysis shows that in order to capture binding of molecules such as imidazolium derivatives and adamantyl compounds, a data set containing these molecules is required. Imidazolium derivatives performed the best out of all the groups considered when their family was included in the training, and their error increases more than 5 times when left out, suggesting the algorithm is particularly sensitive to training on these types of molecules. Small arylamines and viologen derivatives performed better than the average data set regardless if the family was kept in or out, suggesting analysis of these kinds of molecules is robust and the physics of their binding is well-captured with the remaining data relative to the other families.

Fig. 1 Prediction performance for optimal leave-one-out experiments. The line of best fit based on predicted points is shown in black, and the line representing perfect prediction is shown in red (score = 1.6266, R² = 0.3820).

Fig. 2 Normalised confusion matrix for the optimal SVM model trained as a classifier.

Fig. 3 Prediction performance for leave-one-out experiments for environmental parameters only. The line of best fit based on predicted points is shown in black, and the line representing perfect prediction is shown in red (score = 2.1938, R² = −0.0665).

Table 1 Summary of different subclasses of molecules identified in the data set that were used to challenge the model

Family of molecules	Unique entries
Small arylamines	4
Viologen derivatives	6
Methylene blue derivatives	9
Perfluorinated compounds	13
Amino acids	10
Imidazolium derivatives	8
Adamantyl compounds	12

---

Fig. 4 The score describes the mean difference between predicted log K and actual log K when each class of families is kept or left out. Dashed red line is the average score of the model utilising all the data.

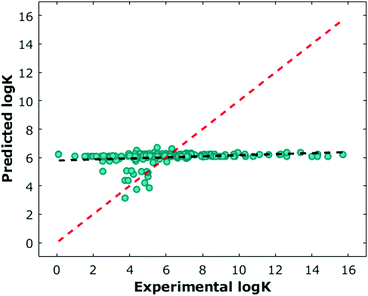
We next performed classical machine learning controls.¹⁷ We first tested the performance of environmental parameters alone, which contain no chemical information about the guest. We found they had poor predictive capabilities (Fig. 3). We also tested whether we could predict the log K by counting the number of carbons in each molecule (Fig. S21, ESI†). Similarly, we found poor predictive capabilities with this approach. Both models performed worse than models which considered 3D structural data. One potential bias in the data that could be leading to the difference in the controls' performance is the slight negative relationship of molecular weights of guests (Fig. S22, ESI†) to log K. Finally, we generated a random data set of identical dimension with the same log K outputs and found this had poor predictive capabilities (Fig. S23, ESI†). We also randomly reassigned log K values to different input data and found this reshuffling had, as expected, poor predictive capabilities (Fig. S24, ESI†).

We then compared whether there were similarities among the top 10 performing models based on score (of the 127 models considered when no environmental parameters are included). All the 10 best models utilised the electric field gradient and a geometry, while seven also used electrons condensed to atoms. No other parameters were used in 50% or more of the top 10 models. While we chose to highlight the results from the top performing model, the differences between the top 10 are small. This shows that the identity of the top performing model is less important than identifying which features consistently improve performance. We conclude from these results that these spatial and electronic data about each molecule improve the predictive capabilities of the algorithm. Five of these top 10 also had among the highest 10 R² values, including the top model based on score. All of the top 10 models had among the top 25 R² values.

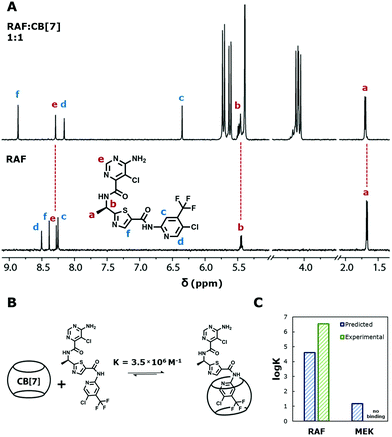
Within the domain of utility, our results suggest these models may has some predictive ability towards binding constants of molecules we might suspect a priori have binding to cucurbiturils. We next used the top model to predict whether binding can occur between CB[7] and two small molecule organics recently identified as potentially promising drugs against pediatric low-grade gliomas: a type II RAF inhibitor TAK-580 (formerly MLN2480; referred to here as RAF), and a MEK inhibitor selumetinib (also called AZD6244; referred to here as MEK).^18,19 Sun and colleagues recently reported RAF as a more promising therapy than type I RAF inhibitors due to its ability to bind to both fused and truncated v600.¹⁸ Banerjee and colleagues also recently reported a promising phase I clinical trial of MEK in children with low-grade gliomas.¹⁹ We performed DFT geometry optimisations on these two molecules and applied the SVM model. It was predicted that RAF would be a good guest to CB[7] with a log K of 4.61, while MEK would have very poor binding with a log K of 1.18 (Fig. 5C). Similar values were obtained if duplicate inputs were considered (Fig. S20, ESI†). Synergistic drug cocktails have more potent responses than the sum of their individual components.²⁰ A key challenge in developing drug cocktails is in their delivery because drugs have different therapeutic windows requiring different release kinetics.^21,22 The ability to independently modulate release kinetics is an invaluable tool in the development of combination drugs. Different binding constants with macrocycles such as CB[7] is one promising approach to independently modulate these kinetics. This prediction that two promising drugs (Fig. S25, ESI†) against pediatric low grade gliomas is a potentially promising ‘hit’ in combination drug delivery.

Fig. 5 (A) ¹H NMR spectra of RAF alone (bottom) in D₂O with 2% DMSO-d₆, and with CB[7] in a 1 : 1 molar ratio (top) in the same solution. Red text and dashed lines indicate peaks that did not shift. Blue text corresponds to peaks that did shift. (B) Illustration showing geometrically accurate binding of RAF with CB[7]. (C) Predicted and experimental log K of RAF and MEK.

We experimentally validated whether these predictions on the strong and poor CB[7] binding of RAF and MEK were accurate. Upon addition of CB[7] to an aqueous solution of RAF (1 : 1 molar ratio), the drug's aromatic ¹H NMR peaks remained sharp and well resolved. The proton signals of CB[7] split into two sets of equivalent peaks (Fig. 5A). These two observations strongly suggest that RAF and CB[7] bind favorably and statically.¹⁵ Isothermal titration calorimetry (ITC) revealed that K_CB[7] = 3.5 × 10⁶ M⁻¹ (Fig. S29, ESI†). We also sought to identify precisely where RAF was binding with CB[7]. No information on ¹H or ¹³C NMR peak assignments could be found on RAF from the manufacturer or in the literature, and so further characterisations were carried out utilising 1D and 2D NMR techniques (ESI,† Section S3: Binding analyses via NMR). Our results show that CB[7] binds statically at the trifluoromethyl-substituted ring in a 1 : 1 fashion (Fig. S29, ESI†). Surprised by this result, we sought to understand why CB[7] preferentially bound to the bulkier trifluoromethyl-substituted ring if there was an alternative pyrimidine with a positively charged amine.⁶ Deuterated hydrochloric acid solution (0.1 M) was titrated into a solution of RAF alone (Fig. S30, ESI†). The aromatic peak meta to the primary amine shifted after a reduction to pH ≤ 2. This suggests that the primary amine is, in fact, uncharged, which may be a reason why CB[7] does not bind at the pyrimidine ring. We then investigated whether RAF could bind to CB[8] (Fig. S31, ESI†). The aromatic peaks of the drug do not remain well resolved as in the case with CB[7], but rather they broaden and disappear. This suggests that RAF does interact with CB[8] with low affinity and in a highly dynamic manner. Thus, CB[8] is not a good carrier for RAF, while CB[7] is an excellent one.

We then validated whether the SVM prediction for MEK was correct. MEK was added to an aqueous solution of excess CB[7] to determine whether any interactions were occurring (Fig. S32, ESI†). In depth analysis is described in the ESI.† These data demonstrated that the drug does not bind to CB[7], confirming that the SVM predicted poor binding of MEK with CB[7]. We then screened its binding to CB[8] (Fig. S33, ESI†). The shift and retention of sharp peaks in the ¹H NMR spectra suggested that the MEK inhibitor binds more strongly and statically to CB[8] than RAF. The downfield shifts of protons c, g, and h suggested that the extended imidazole ring is located near but outside the CB[8] cavity. The upfield shift of protons a and b suggested that the ethylene glycol unit is inside the CB[8] cavity. The minimal changes in protons d, e, and f were consistent with the hypothesis that the bromo-substituted ring was not inside or near the CB[8] cavity. It is well known that CB[8] can thread poly(ethylene glycol) chains.⁶ The thermodynamically favorable interactions between ethylene glycol repeat units and CB[8] may explain why CB[8] preferentially binds to the ethylene glycol unit of MEK. After addition of CB[8] in ratios greater than 1 : 1, little change occurs in the spectra, which suggested MEK and CB[8] bind in a 1 : 1 fashion. These data show that two different drugs with different therapeutic windows bind to different CB macrocycles. MEK shows no binding with CB[7], yet RAF and CB[7] bind strongly in a 1 : 1 fashion. Conversely, MEK binds to CB[8] more statically than RAF. Combining these two drugs into one therapy could give rise to a paradigm that provides a unique opportunity to selectively tune the release or residence time of one drug independently of the other by simply tuning the concentrations of CB[7] and CB[8] in the system.

We next sought to provide a qualitative example of the potency of these drugs, and why modulating drugs to have different release kinetics is an important capability in the development of combination therapies. RAF/MEK combination therapies have been found to be efficacious against other malignancies.^23,24 In this work we explore whether such a combination is potent in a pediatric glioma model. We screened for combinations of RAF and MEK against a v600e mutant and identified a synergistic effect at 10² nM concentration of both RAF and MEK together (Fig. S34, ESI†). This result suggests that by co-delivering RAF and MEK, the total drug concentration required can be reduced. Further optimisations may yield further reductions in required concentrations.

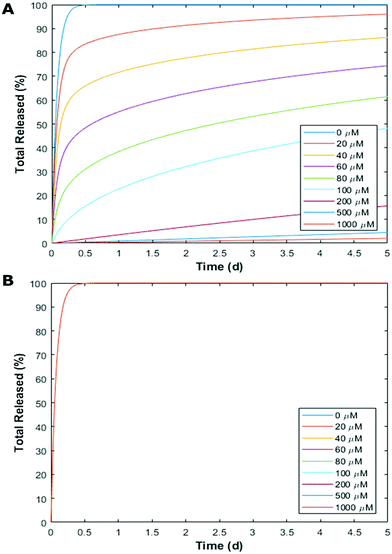
Finally, we utilised a simple mass transport model to showcase how with these binding affinities, CB[7] can be used to independently tune the release kinetics of one drug without changing the kinetics of the other (Fig. 6). We modeled a spherical, non-degradable hydrogel depot 0.375 mL in volume²⁵ with CB[7] bound within the matrix and 100 μM loaded drug concentrations (G_total). Our lab has recently shown that divalent crosslinkers can form hydrogels loaded with CBs,^26–28 however the gel modeled here differs from these previous reports as the CB does not participate in the non-covalent network (ESI†). This model leads to an initial value problem, which is dictated by the differential equation (full derivation in ESI†):

c_surf = f(K,G_total,CB[7]_total)

where hydrogel radius (R) and volume (V), surface area (A), and species diffusivity (D) are constants. Experimentally derived association equilibrium constants (K) were used in the model for RAF (binding) and MEK (no binding). c_surf is the drug concentration at the hydrogel boundary. The concentration of loaded CB[7] was varied. Across different concentrations of CB[7], the release kinetics of RAF changed several orders of magnitude in timescale (Fig. 6A and Fig. S35, ESI†). By contrast, changing the concentration of CB[7] did not change the release kinetics of MEK (Fig. 6B). One limitation of this approach is that the fast equilibrium assumption fails in the limit of no CB[7] or no binding to CB[7]. Given that the parameter of interest is total drug released (Fig. 6) and not the spatial distribution of drug within the hydrogel depot, and given a lack of kinetic information, this assumption was tolerated in this limit. Determining the changes in release profile observed when the fast equilibrium assumption is relaxed is the basis for future work. Nonetheless, this numerical result shows that preferential binding is a valuable tool that can be exploited to tune kinetics of drugs independently of one another over time scales of interest for local drug delivery.²¹

Fig. 6 (A and B) Simulated time-resolved release kinetics of RAF and MEK with different concentrations of CB[7]. The RAF or MEK were free guests in the hydrogel depot, whereas the CB[7] was tethered to the network and did not diffuse out with the guest. Pseudo-steady state and fast equilibrium assumptions reduced the differential equation into a non-linear initial value problem which was solved numerically. Figure shows five day result of (A) RAF and (B) MEK. MEK shows no change in concentrations as it does not bind to CB[7] (note: all plots are overlapping in panel B).

Conclusion

In this work, DFT calculations were used as training data to predict equilibrium binding constants of small molecule organics to CB[7] with machine learning. A library was developed and used in an engineering-approach to identify parameters which may provide predictive capability. We find that publicly available data creates a set likely too small for robust, accurate prediction of binding, though utilising SVMs may confer some predictive ability. The top algorithm was highlighted and used to predict the binding of two promising small molecule drugs in the clinic against pediatric low grade glioma. The algorithm predicted strong binding for the type II RAF inhibitor, and poor binding for the MEK inhibitor, which was experimentally validated. It was also discovered that CB[7] is partial to binding the RAF inhibitor, and CB[8] is partial to binding the MEK inhibitor, suggesting an opportunity for tunable release kinetics by introducing different concentrations of CB[7] or CB[8] into the system, perhaps in a hydrogel depot. Finally, we qualitatively demonstrated that these two drugs have different therapeutic windows and may have utility in concert against low grade gliomas. Machine learning may prove valuable in the development of drug delivery materials for combination therapies in the future, as well as non-biomedical applications that require predicting the binding of small molecules to macrocycles. As data sets continue to be generated and refined, the opportunities of data science in supramolecular chemistry will continue to grow.

Author contributions

A. T., T. G., M. P. S., H. B., P. A., D. H. R., and O. A. S. conceived and planned the studies, wrote, or edited the manuscript. A. T., C. R., G. W., and V. K. R. created the chemical library. C. R. performed the DFT calculations and pre-processed the data. M. P. S., C. R., V. K. R., A. T. and T. G. analysed the processed DFT data. T. G. and C. B. designed and implemented the machine learning framework and analysed the results. A. T. and G. W. performed the experimental chemical characterisations and analysis. A. T. and H. B. performed the biological assays, with the support of C. H. who plated the cells, supported the creation of cell culture media, and is acknowledged. A. T. performed the mass transfer release analysis.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

A. T. and M. P. S. thank The Winston Churchill Foundation of the United States. A. T. thanks the National Science Foundation graduate research fellowship, the MIT Chemical Engineering first year fellowship, and the Churchill College post-graduate grant program. G. W. thanks the Leverhulme Trust (project: ‘Natural material innovation for sustainable living’). V. K. R. thanks the Swiss National Science Foundation (P2EZP2_168784). O. A. S. acknowledges EPSRC Programme grant Nano-Optics to controlled Nano-Chemistry (NOtCH, EP/L027151/1) for funding. The authors thank Prof. Lucy Colwell (Cambridge) for fruitful discussions on machine learning controls, Prof. Charles Stiles (Harvard) for providing API stocks, Prof. Jeremy Baumberg (Cambridge) for support with DFT calculations, Prof. Dane Wittrup and Aditya M. Limaye (MIT) for support with kinetic modeling, and Clement Hallou (Cambridge) for support with cell experiments. The authors also thank Prof. Connor Coley (MIT), Dr Magdalena Olesińska (Cambridge), and Dr Stefan Mommer (Cambridge) for engaging and useful discussions.

Notes and references

1. C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443.
2. A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau and S. Thrun, Nature, 2017, 542, 115.
3. C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 5.
4. A. Y. Hannun, P. Rajpurkar, M. Haghpanahi, G. H. Tison, C. Bourn, M. P. Turakhia and A. Y. Ng, Nat. Med., 2019, 25, 65–69.
5. C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. J. Hart, T. F. Jamison and K. F. Jensen, Science, 2019, 365, eaax1566.
6. S. J. Barrow, S. Kasera, M. J. Rowland, J. del Barrio and O. A. Scherman, Chem. Rev., 2015, 115, 12320–12406.
7. A. Palma, M. Artelsmair, G. Wu, X. Lu, S. J. Barrow, N. Uddin, E. Rosta, E. Masson and O. A. Scherman, Angew. Chem., Int. Ed., 2017, 56, 15688–15692.
8. E. A. Appel, M. J. Rowland, X. J. Loh, R. M. Heywood, C. Watts and O. A. Scherman, Chem. Commun., 2012, 48, 9843–9845.
9. K. I. Kuok, S. Li, I. W. Wyman and R. Wang, Ann. N. Y. Acad. Sci., 2017, 1398, 108–119.
10. M. Werle and A. Bernkop-Schnürch, Amino Acids, 2006, 30, 351–367.
11. H. S. Muddana, A. T. Fenley, D. L. Mobley and M. K. Gilson, J. Comput. – Aided Mol. Des., 2014, 28(4), 305–317.
12. A. Ng, deeplearning.ai, 2018, vol. 1, pp. 1–61.
13. M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., Gaussian 09, Gaussian Inc., Wallingford CT, 2009.
14. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
15. G. Wu, M. Olesińska, Y. Wu, D. Matak-Vinkovic and O. A. Scherman, J. Am. Chem. Soc., 2017, 139, 3202–3208.
16. L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605.
17. K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603.
18. Y. Sun, J. A. Alberta, C. Pilarz, D. Calligaris, E. J. Chadwick, S. H. Ramkissoon, L. A. Ramkissoon, V. M. Garcia, E. Mazzola, L. Goumnerova, M. Kane, Z. Yao, M. W. Kieran, K. L. Ligon, W. C. Hahn, L. A. Garraway, N. Rosen, N. S. Gray, N. Y. Agar, S. J. Buhrlage, R. A. Segal and C. D. Stiles, Neuro-Oncology, 2017, 19, 774–785.
19. A. Banerjee, R. I. Jakacki, A. Onar-Thomas, S. Wu, T. Nicolaides, T. Young Poussaint, J. Fangusaro, J. Phillips, A. Perry, D. Turner, M. Prados, R. J. Packer, I. Qaddoumi, S. Gururangan, I. F. Pollack, S. Goldman, L. A. Doyle, C. F. Stewart, J. M. Boyett, L. E. Kun and M. Fouladi, Neuro-Oncology, 2017, 19, 1135–1144.
20. K. N. Sugahara, T. Teesalu, P. P. Karmali, V. R. Kotamraju, L. Agemy, D. R. Greenwald and E. Ruoslahti, Science, 2010, 328, 1031–1035.
21. A. Tabet, M. P. Jensen, C. C. Parkins, P. G. Patil, C. Watts and O. A. Scherman, Adv. Healthcare Mater., 2019, 8, 1801391.
22. A. Tabet and C. Wang, Adv. Healthcare Mater., 2019, 8, 1800908.
23. G. Gibney, J. Messina, I. Fedorenko, V. Sondak and K. Smalley, Nat. Rev. Clin. Oncol., 2013, 10, 390–399.
24. A. Ribas, D. Lawrence, V. Atkinson, S. Agarwal, W. H. Miller, M. S. Carlino, R. Fisher, G. V. Long, F. S. Hodi, J. Tsoi, C. S. Grasso, B. Mookerjee, Q. Zhao, R. Ghori, B. H. Moreno, N. Ibrahim and O. Hamid, Nat. Med., 2019, 25, 936–940.
25. For leuprolide acetate formulation specifications, see: https://www.rxlist.com/eligard-drug.htm#indications. Accessed: 2018-11-26.
26. J. Liu, C. Soo Yun Tan, Z. Yu, Y. Lan, C. Abell and O. A. Scherman, Adv. Mater., 2017, 29, 1604951.
27. J. Liu, C. Soo Yun Tan, Z. Yu, N. Li, C. Abell and O. A. Scherman, Adv. Mater., 2017, 29, 1605325.
28. A. Tabet, S. Mommer, J. A. Vigil, C. Hallou, H. Bulstrode and O. A. Scherman, Adv. Healthcare Mater., 2019, 8, 1900068.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05800a

‡ These authors contributed equally to this work.

---