Open Access Article
Open Access ArticleEnergetics of paramagnetic oxide clusters: the Fe(III) oxyhydroxy Keggin ion†
C. André
Ohlin

Umeå University, Umeå, Sweden. E-mail: andre.ohlin@umu.se
First published on 20th January 2020
Abstract
The energetics of the different spin states of the five Baker–Figgis isomers of the iron(III) Keggin ion, [Fe(O4)(Fe(OH)2(OH2))12]7+, have been investigated using density functional theory in order to demonstrate how the energy landscape of medium-to-large discrete paramagnetic transition metal oxide clusters with large numbers of antiferromagnetically coupled centres can be resolved. Antiferromagnetic coupling causes the energies to span a surprisingly large range of 30 kcal mol−1, as determined by calculating the energies of all 664 unique spin configurations based on determination of the antiferromagnetic coupling constants by density functional theory. A program which simplifies the resolution of the energetics of this type of system is also provided.
Introduction
Paramagnetic systems are challenging to model computationally. Although multiconfigurational wave function methods can give good results in the computations of relative spin state energies, they are computationally expensive and density functional theory is often the only realistic method for investigating the properties of medium and large transition metal clusters.1 In addition to method-specific issues the potentially large number of coupled spins in transition metal compounds further complicates the investigation of the energetics of clusters containing paramagnetic centres.In this study a methodical approach to resolving the energy landscape of systems composed of multiple antiferromagnetically coupled centres is described and investigated. This is particularly pertinent to the investigation of transition metal oxide clusters with antiferromagnetically coupled centres, which include catalysts and molecular magnets incorporating first-row metals such as manganese, iron and cobalt, which are at the centre of applied inorganic research today. As an example of such a discrete transition metal cluster target system containing multiple antiferromagnetically coupled centres the hypothetical iron(III) oxyhydroxy Keggin ion has been chosen, for the reasons outlined below.
Ferrihydrite is a metastable ferric mineral which serves as a precursor to the rock and soil minerals haematite and goethite.2 While the details of the poorly crystalline structure are still under debate, it forms through the condensation of mono- and oligomeric ferric (hydr)oxo species. How this occurs is not clear, and because the Keggin motif appears to be present, albeit not as a discrete unit, in ferrihydrite, the discrete oxyhydroxy iron(III) Keggin ion has been suggested to form in solution and act as a building block.
This iron(III) Keggin ion, [Fe(O4)(Fe(OH)2(OH2))12]7+ (Fe13) (Fig. 1), has in fact long been predicted as the Keggin ions are important species in the aqueous chemistry of Al(III).3 However, while the δ motif is incorporated as part of larger structures in the models of the important but metastable iron mineral ferrihydrite,4,5 until recently no discrete iron(III) Keggin ion had been isolated.
However, in 2015 Sadeghi et al. isolated the first example of an iron(III)-oxo Keggin ion, α-[Bi6FeO4(FeO(OH)(Cl3CCOO))12]+, from a solution at pH ca. 1.4, and recrystallised it from tetryhydrofuran.6 This was quickly followed by the isolation of two more iron(III) Keggin ions, α-[Bi6FeO4(FeO(OH)(CF3COO))12]+ and the closely related α-[Bi6FeO4(FeO(OH)(CF3COO))10(FeO(OH)(H2O))2]3+, which were found to be stable at pH 1–3.7 The authors attributed the isolation of these clusters in large parts to the protective effect of the Bi3+ ion, which prevents the clusters from aggregating. In the absence of bismuth it was suggested, based on SAXS data, that dimerisation, and isomerisation to the δ isomer, of the clusters occurred through a lacunary intermediate.6
Bandeira et al.8 determined the electronic spin coupling constants for the two fully carboxylated cluster species using the approach by Ruiz et al.,9,10 and compared the results to experimentally and computationally determined coupling constants for the related α-[FeO4(FeF2(OCH)3)12]5− ion.11,12 Three antiferromagnetic coupling interactions were considered based on a view of the α Keggin ion as four triads, each consisting of three Fe(III) octahedrals, organised around a central tetrahedral Fe(III) centre: intratriad, intertriad and tetrahedral-to-octahedral coupling. They found in all cases that intertriad coupling is relatively weak (ca. −10 to −6 cm−1), whereas intertriad coupling ranged from −90 cm−1 for the CF3COO-species to −20 cm−1 for the CH3O-capped species. Tetrahedral-to-octahedral coupling was fairly constant at around −40 to −30 cm−1. Experimental determination of coupling constants for the methanoate complex using a model only incorporating intratriad and tetrahedral-to-octahedral coupling yielded values of −30 and −43 cm−1, respectively.12
The three cases of iron(III) bismuth halocarboxylate clusters that have been isolated all exist as the Keggin α isomer,6,7 but there are five potential Baker–Figgis Keggin isomers,13,14 – α, β, γ, δ and ε –, which are related by the π/3 rotation of a triad of metal sites as one progresses from the α isomer, in which no edge-sharing sites exist, to the ε isomer in which no corner-sharing sites exist (see Fig. 1 and Fig. S1, ESI†).
Whereas Al(III) is generally found as the ε isomer in solution, isomers with fewer edge sharing centres, such as the α-isomer, are generally favoured owing to decreased Coloumbic repulsion between the metal centres relative to the edge-sharing isomers, such as ε, which is particularly important for species with high charges and large radii.15 For example, the heteropolyacid Keggin ions, PM12OO403−, of Mo(VI) and W(VI) are found as the α isomer, in agreement with computational prediction for the phosphotungstate ion.16 On the other hand, edge-sharing is favoured for small species such as Al(III). Given the larger Shannon radius of high-spin Fe(III) (78.5 pm) vs. Al(III) (67.5 pm),17 isomers with fewer edge-sharing sites, such as α or β, should be favoured for iron(III).
The goal of the present study is to be able to generate the complete space of energies due to spin configuration and geometrical isomerism. It would be a monumental task to calculate this directly – by estimate there are 85, 119, 177, 209 and 74 unique spin configurations for the Keggin α, β, γ, δ and ε isomers, respectively – so instead the coupling constants for each type of antiferromagnetic coupling in each isomer are first determined, and then used to predict the energies for all unique spin configurations.
In this study the energies of a large number of spin configurations for all five Baker–Figgis isomers of the Fe13 Keggin isomers have been calculated using the broken symmetry method by Noodleman et al.18 as developed by Ruiz et al.9 with the goal to determine what isomer and spin configuration are the lowest energy ones and, by extension, which is the most likely hypothetical species in solution. This is also important from a theoretical perspective, as this is required information when computationally investigating the energetics of the condensation of monomeric and oligomeric iron clusters (see e.g. Das et al.19).
Methods
Computations were carried out using unrestricted density functional theory (DFT) with combinations of the exchange correlation (XC) functionals PBE0,20 B3LYP,21 M06,22 PBE,23,24 or BP86,25,26 with the basis sets def2-svp and def2-tzvp,27 together with implicit solvation through the SMD model by Marenich et al.,28 for M06, or the polarizable continuum model (PCM) by Tomasi et al.29 for all other XC functionals as implemented in G16 rev. B.01 with molecular symmetry turned off, but otherwise with the default settings.30 Initial guesses were generated by dividing each molecule into 14 fragments, 13 of which correspond to an iron centre, with defined spins. The iron centres were organised so that {1,2,3}, {4,5,6}, {7,8,9} and {10,11,12} form triads and iron centre 13 is the tetrahedral iron unit at at the centre of the Keggin ion. All structures were optimised at the same level of theory as energies are reported for. The basis set combination def2-tzvp + svp uses def2-tzvp for the iron centres and def2-svp for all other atoms.The method by Ruiz et al. for the evaluation of coupling constants in polynuclear clusters,9,10 which is based on the Noodleman et al.18 concept of broken symmetry analysis, was used. The concept of broken symmetry refers to the breaking of symmetry by introducing anti-parallel spins, rather than all spins being parallel, which would be the highest symmetry state.
In brief, the difference in energy, ΔE, between the highest spin multiplicity configuration of the cluster, where all spins are parallel (ESmax), and the energy of an arbitrary broken symmetry spin configuration i, EBSi, in which some spins are anti-parallel, is given by eqn (1), which is reproduced here as formulated by Bencini.31 Here Si and Sj are the spins (±5/2 for high-spin iron(III)) of atomic centres i and j, which couple by constant Jij. Jij is zero if there is no antiferromagnetic coupling between the centres. λij is also zero if the spins are parallel, but is exactly one if they are not. Thus, only interacting spins which are antiferromagnetically coupled contribute to the energy difference between the Smax state and the broken symmetry state.
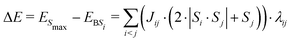 | (1) |
Eqn (1) thus expresses the energy change as a function of a linear equation of the form. which is dependent on the antiferromagnetic coupling constants and corresponding prefactors. By looking at a range of broken symmetry states, a set of linear equations is obtained which can be solved by fitting to yield the corresponding antiferromagnetic coupling constants. In the present case sets of linear equations were generated for each isomer using the Python software J_generator.py, which is supplied as a code in the ESI,† and fitting was carried out using gnuplot 5.0 (pathlevel 5).32 Usage of the J_generator.py software is briefly described in the ESI,† together with a description of how it can be modified for other systems.
The coupling constants can in turn be used to predict the energies of all possible spin configurations, and the lowest predicted spin configurations can be identified, and then computationally optimised to confirm the predictions. The general workflow is as follows:
(1) Define the coupling matrix and generate all possible expressions for ΔE as a function of the coupling constant.
(2) Select computational targets based on the maximum variation in dependence on different coupling constants, and optimise geometries using DFT.
(3) Fit coupling constants based on computed DFT energies.
(4) For all possible spin configurations, calculate ΔE.
(5) Computationally optimise the targets which are predicted to have the lowest energies to confirm predictions.
In this study four types of antiferromagnetic coupling paths between iron(III) centres and corresponding coupling constants J are considered: intratriad coupling (J1a), intertriad coupling between corner-sharing triads (J1b), intertriad coupling between edge-sharing triads (J1d), and coupling between the central tetrahedral iron centre and all other iron centres (J2). Schematic views of coupling in the different isomers and the corresponding coupling matrices are given in the ESI.†
Examples of the antiferromagnetic coupling paths for the different Keggin isomers are given in Fig. 2.
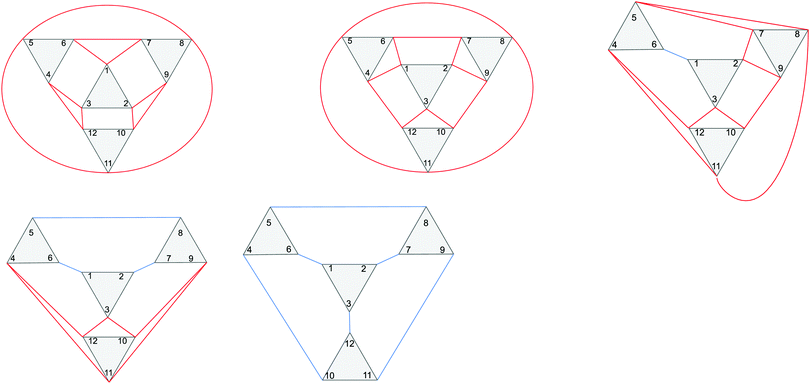 | ||
| Fig. 2 Schematic view of the coupling paths in the α (top left), β (top middle), γ (top right), δ (bottom left) and ε (bottom right) isomers. Intratriad J1a couplings are shown as black lines, intertriad J1b couplings for corner-sharing triads are shown as red lines, and intertriad J1d couplings for edge-sharing triads are shown as blue lines. Fe(III) centres 1–12 all couple to centre 13 via J2, which is not shown. The figure is reproduced in a larger format in the ESI.† | ||
Results and discussion
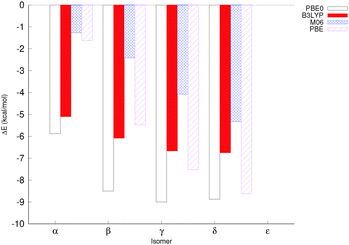
The relative energies of the different isomers in the highest spin state (Smax) – where the spins of all iron centres are parallel to one another – were computed with different exchange correlation (XC) functionals using the def2-tzvp basis set for Fe, and the def2-svp basis set for all other atoms. Two XC functionals, PBE0 and B3LYP, were chosen as well-established hybrid functionals, PBE was chosen as an example of a pure DFT functional, and M06 was chosen as an example of a popular parametrised functional. All four XC functionals gave very similar qualitative trends, although in particular the magnitude by which the ε isomer was disfavoured varied (Fig. 3 and Table S1, ESI†). For B3LYP, M06 and PBE, the lowest energy isomer was δ, whereas PBE0 favours the γ isomer by 0.2 kcal mol−1 over the δ isomer. The closeness in energies of the different isomers and the large number of potential sources of error, such as explicit solvent interactions and the effect of counterions, mean that there is little real difference in energy between several of the isomers.Ten broken symmetry spin configurations were generated for the α isomer, the prefactors were determined according to eqn (1) and the structures were optimised at a few different levels of theory. Trends were consistent across levels of theory, although energies for def2-tzvp+svp were generally somewhat smaller in magnitude than energies computed at either def2-svp or def2-tzvp (see Fig. S9 and Tables S8 and S9, ESI†). Using these data, antiferromagnetic coupling constants were determined (Fig. 4 and Table S11, ESI†).
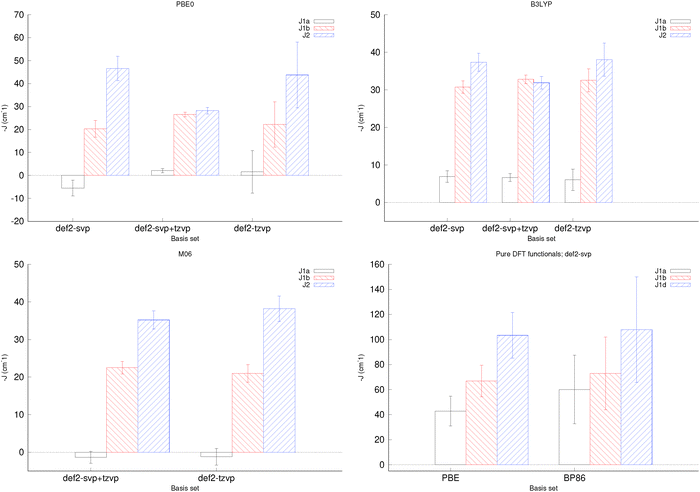
For PBE0 and B3LYP, in particular, the uncertainties in the fitted coupling constants were noticeably smaller if def2-tzvp+svp was used, than either def2-svp or def2-tzvp. While this does not provide any information about which method provides more accurate results, the goal of this work is the prediction of energies. Low uncertainty is thus a goal in itself. It should also be noted that while the fitted coupling constants for B3LYP remain consistent between different basis set combinations, for PBE0 the results obtained at either def2-svp or def2-tzvp were noticeably different from those obtained at def2-tzvp+svp. Use of M06 with def2-svp was associated with considerable SCF convergence issues, and was not further investigated, but the results were otherwise not found to be basis-set dependent. Fitting using M06-computed data – in contrast with B3LYP and PBE0, with one exception – yielded positive J1a coupling constants, which disagrees with the findings of van Slageren et al.,12 although their coupling model was different from the one used here. Finally, PBE and BP86 yielded coupling constants much larger in magnitude than those obtained using hybrid XCs.
With this in mind, B3LYP/def2-tzvp+svp was chosen for the rest of the study as a method with potentially good predictive properties in terms of spin state energies, and has the added benefit of being very similar to the one used by Banderia et al.,8 making it easier to compare the results obtained in this study with theirs. This does not, however, presume that the B3LYP/def2-tzvp+svp results are closer than those at the other levels of theory to in vitro coupling constants, which are generally not known with great confidence or precision.
Using the J_generator program, which is given in the ESI,† sets of linear equations for the calculations of ΔE were generated for each isomer for all possible different spin configurations for the chosen coupling model. A selection of these spin configurations were chosen for each isomer to get a good range of dependencies of ΔE on different combinations of J1a, J1b, J1d and J2, and optimised computationally. The energies obtained were then used to fit J1a, J1b, J1d and J2 for each isomer (see Table 1). All the energies, coupling matrices and pre-factors for the linear equations are reported in the ESI.†
| Isomer | J 1a ± σ | J 1b ± σ | J 1d ± σ | J 2 ± σ |
|---|---|---|---|---|
| a def2-tzvp was used for all Fe atoms; def2-svp was used for all other atoms. 1 cm−1 corresponds to ca. 2.86 × 10−3 kcal mol−1. | ||||
| α | −6.64316 ± 1.154 | −33.8603 ± 1.186 | — | −30.6934 ± 1.083 |
| β | −8.99948 ± 3.445 | −25.7675 ± 4.675 | — | −30.0717 ± 3.295 |
| γ | −6.27393 ± 1.026 | −29.4497 ± 0.9103 | −23.3231 ± 4.839 | −31.6417 ± 0.4647 |
| δ | −4.92424 ± 0.7783 | −29.7590 ± 0.9269 | −18.8791 ± 1.995 | −29.5641 ± 0.5541 |
| ε | −3.14517 ± 0.5585 | — | −19.3922 ± 1.115 | −27.5094 ± 0.4107 |
| All isomers | −6.62805 ± 1.006 | −31.3688 ± 1.175 | −12.3721 ± 2.97 | −29.3623 ± 0.7858 |
In the original draft of this manuscript only entries denoted as ‘BS’ in the ESI† were used in the fitting of coupling constants. Following comments by a referee, additional computations were carried out, only ca. half of which were used for fitting (indicated by a * in the relevant table in the ESI†), and the rest of which were used to check the predictive capability of the method. All data are provided in the ESI.† Half of the additional spin configurations were selected using a random number generator, and the other half were selected manually to provide a good range of permutations. For the fitting sets, the data were sorted in terms of energies, and every second computation was selected, in order to get a wide range of data.
The tetrahedral-to-octahedral coupling constant J2 and the inter-triad coupling constant J1b vary relatively little between the isomers, spanning ranges of ca. −32 to −28 cm−1 and −34 to −27 cm−1, respectively. The inter-triad coupling constant J1d, which is not present for the α and β isomers, varies from ca. −23 cm−1 for the γ isomer to −19 cm−1 for the δ and ε isomers. Likewise, the intra-triad coupling constant J1a varies from ca. −9 cm−1 in the β-isomer to −3 cm−1 in the ε isomer. When using the data for all isomers, J1a, J1b, and J2 are consistent with the fitted values obtained for each isomer. However, the fitted value for J1d does not resemble those obtained for the γ, δ or ε isomers.
In general, the coupling constants are expected to vary between the isomers since the inter-atomic distances also vary, but there is no clear correlation between the variation in J1a and J1d and trends in Fe–Fe distances for different coupling types (Fig. S7, ESI†), nor is there any correlation between the spread in distances for a particular coupling type and the uncertainty in the fit of the corresponding coupling constant. The variability may also be due to the inaccuracy of the model used to resolve the antiferromagnetic coupling constants, which assumes that the energies computed correspond to those free of spin contamination and that only iron centres possess a net spin. This is not the case since the framework oxygen atoms also become spin polarised. Allowing for more types of coupling to account for this may improve the fitting process, but will also require a larger set of computations to avoid the improved fit simply being due to overdetermination, in particular if the magnitudes of the oxygen-centered coupling constants are small.
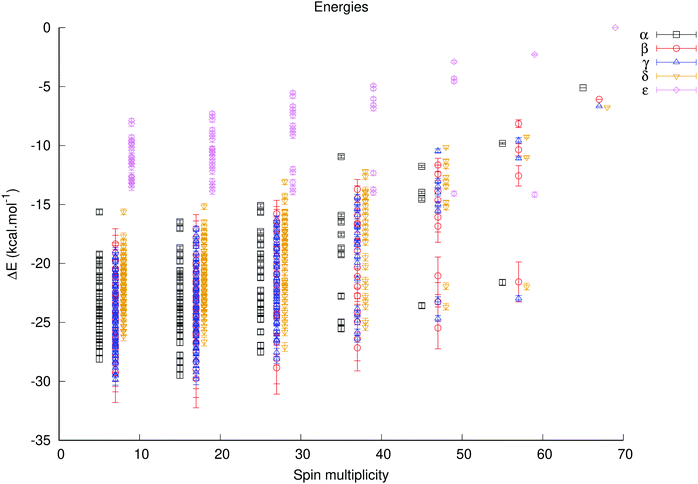
Using the fitted antiferromagnetic coupling constants the complete range of energies for all unique spin configurations could be generated with the J_generator software, either relative to the Smax state for each isomer (Fig. S11 and 12, ESI†) – in order to gauge how much the energy of each isomer varies – or relative to the Smax state of the α isomer in order to determine the lowest energy isomer and spin configurations (Fig. 5).
The predicted energies of each isomer relative to the Smax state of each isomer varies by ca. 25–27 kcal mole−1 for the α, β and γ isomers, 20 kcal mole−1 for the δ isomer and by less than 16 kcal mole−1 for the ε isomer. These ranges are simply a consequence of a larger magnitude of the J1b constant relative to the J1d constant; the former corresponds to a type of coupling which is more important for isomers with more corner-sharing triads (found in α–δ isomers), and the latter is present for edge-sharing triads (found in γ–ε isomers).
The predicted lowest energy spin configurations relative to the energy of the Smax state of the ε isomer – the highest energy species – are given in Table 2. The α, β and γ isomers are the predicted lowest energy ones, and the difference between the computed lowest state configurations for the α, β and γ isomers is less than 0.8 kcal mol−1, which is likely beyond the precision of this method. The predicted energies are very close to the observed ones, but as the actual energies of these spin configurations were used in the fitting of the coupling constants, this serves primarily to indicate that the chosen model is reasonable.
| Isomer | Inverted spin centresb | Multiplicity | ΔEa (kcal mol−1) | |||
|---|---|---|---|---|---|---|
| Predictedc | PBE0 | B3LYP | M06 | |||
| a Relative to the energy of the Smax state of the ε-isomer. b The iron centres in the Keggin ions are organised into the following triads: {1,2,3}, {4,5,6}, {7,8,9} and {10,11,12}. Centre 13 is a tetrahedral iron centre in the centre of the ion. PCM was used for PBE0 and B3LYP; SMD was used for M06. c Predicted energies based on fitted coupling constants at B3LYP/def2-tzvp+svp, relative to the ε isomer in the Smax spin configuration. | ||||||
| α | 1, 4, 9, 11, 13 | 17 | −29.5 ± 0.3 | −26.30 | −29.22 | −20.59 |
| β | 2, 4, 6, 11, 13 | 16 | −29.8 ± 2 | −27.57 | −28.73 | −19.76 |
| γ | 3, 4, 7, 8, 9, 13 | 7 | −29.9 ± 0.45 | −28.42 | −29.52 | −21.41 |
| δ | 3, 4, 9, 13 | 27 | −27.0 ± 0.4 | −26.00 | −26.90 | −24.31 |
| ε | 13 | 57 | −14.0 ± 0.2 | −12.20 | −14.07 | −14.95 |
Furthermore, the predicted energies are based only on the fitted coupling constants – if these are under- or overestimated the predicted trends will change. As shown (see Fig. 4 and Table S11, ESI†), the magnitude of the coupling constants varies with the chosen method. It would thus be imprudent to state with certainty which isomer and spin state are the most stable ones. What the current study shows is that there are a fairly limited range of candidates for the lowest energy configuration, and that some isomers and spin configurations are disfavoured. This latter point will be discussed later.
The results presented thus far have centred on computations at the B3LYP/def2-tzvp+svp level of theory. However, as shown in Fig. 3, while the levels of theory investigated in this study yield similar qualitative trends for the relative stability of the different Keggin isomers in their highest spin states, there are quantitative differences. These also extend to the determination of the spin coupling constants. The lowest energy spin configuration for each isomer, as predicted by B3LYP/def2-tzvp+svp, was thus optimised at M06, PBE0 and B3LYP with the def2-tzvp+svp basis set combination to provide a clearer picture of the difference between the methods.
The configuration and energies of the lowest spin configurations for each isomer are given in Table 2 and in Fig. S13 and S14 (ESI†). The energies of the lowest spin configurations deviate from the Smax energy trends largely by PBE0 and B3LYP disfavouring the δ isomer, and by B3LYP favouring the α isomer compared to the case with the Smax spin configuration.
Looking at the spin configurations corresponding to the lowest energies in Table 2 and comparing them with the coupling constants in Table 1, the reasons behind why the different spin configurations are the lowest ones become clear. For the ε isomer the configuration where only the central tetrahedral iron centre is antiferromagnetically coupled is the lowest one in energy because of the magnitude of the J2 coupling constant relative to the intratriad J1d and intertriad J1a coupling. For all the other isomers the lowest energy configuration is a compromise between maximising either intertriad J1b or tetrahedral-to-octahedral J2 coupling. For the α isomer all triads couple through J1b, and so the configuration of each triad is identical. The β isomer has a somewhat different configuration, where one triad with all positive spins couples with three triads with mixed spins, and a central antiferromagnetic tetrahedral iron centre.
For the γ isomer three of the negative spins belong to the same triad ({7,8,9}), which antiferromagnetically couples to centres 2, 5, 10 and 11. Centres 3 and 4 belong to different triads ({1,2,3} and {4,5,6}, respectively) and couple antiferromagnetically to centres in the same triad (11 and 12, and 10 and 12, respectively). Spins 1 and 6 would couple through J1d only, which is weaker than J1b, in particular if the values obtained through fitting data for the δ and ε isomers are considered.
In the case of the δ isomer only the following centres couple through J1b: centre 4 with centres 10 and 12, centre 3 with centres 11 and 12, and centre 9 with centres 10 and 11 (Fig. S5, ESI†). This is reflected by the negative spins for centres 3, 4 and 9 for the δ isomer in Table 2.
The large J2 causes centre 13 to have a negative spin in all cases.
Conclusions
This study demonstrates how coupling constants, whether comparable in magnitude to experimental ones or not, can be used to generate a potential energy map of all spin configurations for a system with a limited number of computations, and that this can be used to inform the computation of the energetics of a system with good apparent predictive capacity. Considering all potential coupling configurations for systems with multiple antiferromagnetic coupling paths can thus be done with reduced computational cost, and improves the energetic description of the system.For the iron(III) Keggin cluster which may play a role in the formation of ferrihydrite, antiferromagnetic coupling breaks symmetry and stabilises each isomer up to ca. 25 kcal mol−1. While the ε isomer does not appear to be a thermodynamically favoured isomer, all other isomers achieve spin configurations of very similar energies, suggesting that a hypothetical solution of Fe13 may contain all of them in comparable concentrations if isomerisation barriers are low, or the formation from smaller building blocks is perfectly reversible. If, on the other hand, isomerisation barriers are high or if the formation of the Fe13 Keggin ion is irreversible, then a specific isomer and spin configuration may well dominate. Resolving the Fe13 Keggin system experimentally may prove to be very challenging indeed, assuming that the ion exists in nature.
In the present case a likely, but not confirmed, species has been investigated owing to the potential importance of this species in the solution chemistry of iron(III) as well as in the formation of proto-mineral nucleation species, but the approach is equally applicable to the solution chemistry of other paramagnetically coupled systems, such as those involving manganese, where the formation of extended phases from discrete starting materials is key to the formation of an active water oxidation catalyst.33 Using an approach as demonstrated here investigating such systems is, if not trivial from a theoretical point of view, feasible and quite affordable in terms of computational cost.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks the Kempe foundation for generous support via grant JCK-1719 and the referees for perceptive comments. This work was made possible by resource allocation grants SNIC 2019/3-344 and SNIC 2019/3-264 by the National Supercomputer Centre at Linköping university and the High Performance Computing Centre North at Umeå University, respectively.References
- M. Swart and M. Gruden, Acc. Chem. Res., 2016, 49, 2690–2697 CrossRef CAS PubMed.
- J. L. Jambor and J. E. Dutrizac, Chem. Rev., 1998, 98, 2549–2586 CrossRef CAS PubMed.
- W. H. Casey, Chem. Rev., 2006, 106, 1–16 CrossRef CAS PubMed.
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, Science, 2007, 316, 1726–1729 CrossRef CAS PubMed.
- J. S. Weatherill, K. Morris, P. Bots, T. M. Stawski, A. Janssen, L. Abrahamsen, R. Blackham and S. Shaw, Environ. Sci. Technol., 2016, 50, 9333–9342 CrossRef CAS PubMed.
- O. Sadeghi, L. N. Zakharov and M. Nyman, Science, 2015, 347, 1359–1362 CrossRef CAS PubMed.
- O. Sadeghi, C. Falaise, P. I. Molina, R. Hufschmid, C. F. Campana, B. C. Noll, N. D. Browning and M. Nyman, Inorg. Chem., 2016, 55, 11078–11088 CrossRef CAS PubMed.
- N. A. G. Bandeira, O. Sadeghi, T. J. Woods, Y.-Z. Zhang, J. Schnack, K. Dunbar, M. Nyman and C. Bo, J. Phys. Chem. A, 2017, 121, 1310–1318 CrossRef CAS PubMed.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed.
- A. Bino, M. Ardon, D. Lee, B. Spingler and S. J. Lippard, J. Am. Chem. Soc., 2002, 4578–4579 CrossRef CAS PubMed.
- Y. V. Rakitin and J. van Slageren, Russ. J. Coord. Chem., 2004, 810–812 CrossRef CAS.
- J. F. Keggin, Nature, 1933, 131, 908–909 CrossRef CAS.
- L. C. W. Baker and J. S. Figgis, J. Am. Chem. Soc., 1970, 92, 3794–3797 CrossRef CAS.
- D. L. Kepert, Inorg. Chem., 1969, 8, 1556–1558 CrossRef CAS.
- X. Lopez and J. M. Poblet, Inorg. Chem., 2004, 43, 6863–6865 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- L. Noodleman, D. A. Case and A. Aizman, J. Am. Chem. Soc., 1988, 110, 1001–1005 CrossRef CAS.
- B. Das, J. Phys. Chem. A, 2018, 122, 652–661 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6159 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- A. Bencini and F. Totti, J. Chem. Theory Comput., 2009, 5, 144–154 CrossRef CAS PubMed.
- T. Williams and C. Kelley, http://sourceforge.net/projects/gnuplot/, 2014.
- R. K. Hocking, R. Brimblecombe, L.-Y. Chang, A. Sing, M. H. Cheah, M. H. Chech, C. Glover and L. Spiccia, Nat. Chem., 2011, 3, 461–466 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05795a |
| This journal is © the Owner Societies 2020 |