Effect of sodium thiocyanate and sodium perchlorate on poly(N-isopropylacrylamide) collapse

Abstract

The T(collapse) of poly(N-isopropylacrylamide), PNIPAM, shows a nonlinear dependence on the concentration of NaSCN or NaClO₄; in the case of NaClO₄, for example, at very low concentrations of the salt, T(collapse) increases with the concentration, while it has an opposite trend at higher NaClO₄ concentrations [J. Am. Chem. Soc., 2005, 127, 14505]. These puzzling experimental data can be rationalized by considering that low charge density and poorly hydrated ions, such as thiocyanate and perchlorate, interact preferentially with the surface of the polymer, and cause an increase of the magnitude of the energetic term that stabilizes swollen conformations at low salt concentrations. However, as both swollen and collapsed PNIPAM conformations are accessible to such ions in view of their large conformational freedom, the difference in the number of ions bound to PNIPAM surface upon collapse changes little on increasing the salt concentration. Thus, the energetic term that favors swollen conformations increases with salt concentration to a lesser extent than the solvent-excluded volume term (linked to the density increase caused by salt addition to water), that favors collapsed conformations, leading to a nonlinear trend of T(collapse).

---

Introduction

It is firmly established that poly(N-isopropylacrylamide), PNIPAM, chains dissolved in water undergo a coil-to-globule collapse transition on increasing the temperature,^1,2 with T(collapse) = 31 °C. Soon after collapse, PNIPAM globules aggregate, giving rise to a lower critical solution temperature, LCST, behavior; it has been shown that these two temperatures prove to be closely similar.³ Experimental DSC measurements⁴ indicate that the process can be considered as a first-order phase transition in view of its cooperativity^4,5 (i.e., two-state behavior), and is characterized by a positive latent heat (i.e., it is endothermic), and a positive entropy change. In other words, PNIPAM collapse is a paradigmatic example of entropy-driven phase transition.^5,6 The chains in the globule state ensemble, G-state, should possess less conformational entropy than those in the coil state ensemble, C-state, and so the entropy increase has to be attributed to water molecules. Interestingly, neutron scattering data indicate that the water molecules constituting the hydration shell of nonpolar moieties are not characterized by a structural order (i.e., orientational and/or rotational) greater than that of water molecules in the bulk phase (and this should be true also for the isopropyl groups in PNIPAM side chains).^7–9 On light of this piece of data, the reason behind the entropy increase has to be found in a different mechanism.

In previous papers, we have already proposed that the increase in entropy is related to an increase in translational entropy of water molecules caused by the decrease in solvent-excluded volume associated with PNIPAM collapse (i.e., an expansion of the available configurational space).^6,10 The solvent-excluded volume can reliably be measured by the solvent-accessible surface area of the molecule,^11,12 that in the case of water is named WASA. Computer simulations on all-atom models have shown that the average WASA of the conformations populating the C-state is significantly larger than the average WASA of the conformations populating the G-state.^13,14 This means that water molecules gain translational entropy on pushing PNIPAM chains to collapse. This entropic driving force has a geometric ground and can be captured by means of a theoretical approach that uses simple geometric models,^6,10 and analytic relationships from classic scaled particle theory,^15–17 SPT. Indeed, the solvent-excluded volume effect can be measured by calculating the reversible work associated with cavity creation in a liquid¹⁸ (including water and aqueous solutions), ΔG_c. A fundamental point is that, on keeping fixed the van der Waals volume, V_vdW, of the cavity and changing its shape, the ΔG_c magnitude is markedly affected.¹¹ Specifically, on increasing the cavity WASA (i.e., passing from a spherical cavity to prolate spherocylindrical cavities of increasing length), the ΔG_c magnitude increases in an almost linear manner.¹¹ Therefore, the solvent-excluded volume effect is not measured by the cavity V_vdW, but by the cavity WASA. In addition: (a) the ΔG_c magnitude is larger in water than in other liquids as a consequence of its larger number density, originating in the small size of water molecules and the strength of H-bonds;^18–21 (b) the ΔG_c magnitude in water increases with temperature because the density decreases to a very small extent over the 0–100 °C temperature range, due to the strength of H-bonds in comparison to the random thermal energy.^18–21 According to this theoretical approach, the density of water and aqueous solutions and its temperature dependence play a fundamental role for the energetics of PNIPAM collapse. Its application has provided a coherent rationalization of several features of such transition: (a) the effect of several sodium salts on T(collapse);¹⁰ (b) the effect of urea, tetramethylurea and TMAO on T(collapse);^6,22,23 (c) the co-non-solvency phenomenon in water–methanol solutions around room temperature.^24,25

However, other experimental results have not been yet addressed in their entire complexity. Interesting results by Cremer and co-workers^26,27 showed that: (a) NaSCN causes a small increase in T(collapse) at low concentration and, on further increasing the NaSCN concentration, the T(collapse) value remains practically constant; in other words, NaSCN addition causes a small stabilization of the C-state at low salt concentration, but it has no effect at 1 M concentration; (b) NaClO₄ causes a small increase in T(collapse) at very low concentration and, on further increasing the NaClO₄ concentration, the T(collapse) value decreases significantly; in other words, NaClO₄ stabilizes the C-state at very low concentration, but stabilizes the G-state at high concentration. This means that, for both salts, the dependence of T(collapse) on salt concentration is non-linear, in contrast with the linear decrease caused by the addition of salts like NaCl, consisting of well hydrated ions (see Fig. 1). It is important to underscore that: (a) the NaSCN effect on PNIPAM T(collapse) was first detected by Schild and Tirrell;³ (b) Cremer and co-workers obtained qualitatively similar results also for elastin-like polypeptides,²⁸ regardless of the chemical heterogeneity of the latter in comparison to PNIPAM chemical homogeneity.

Fig. 1 Trend of PNIPAM T(collapse) as a function of salt concentration for NaCl, NaSCN and NaClO₄, for polymer samples with a weight-average molecular weight of 170 kDa; data are from ref. 27.

These findings are very interesting because: (a) both NaSCN and NaClO₄ are denaturing agents of globular proteins^29–31 (i.e., thiocyanate and perchlorate are at the far-right end of the Hofmeister anion series²⁶); (b) PNIPAM is considered to be a simplified model of globular proteins;^4,5 (c) the two salts, at high concentration, do not stabilize the C-state of PNIPAM, that should resemble the denatured state of globular proteins. In the present study, we analyze the effect of NaSCN and NaClO₄ on PNIPAM collapse over a large salt concentration range by means of our theoretical approach, providing an interesting and reliable explanation.

Theory section

The developed theoretical approach^6,10 leads to the following formula for the Gibbs energy change associated with collapse transition, ΔG_tr (the formula is written considering that the G-state is stable when ΔG_tr is positive; for a complete derivation see ref. 23):

ΔG_tr = [ΔG_c(C) − ΔG_c(G)] − T·ΔS_conf + [E_a(C) − E_a(G) + ΔE(intra)] = ΔΔG_c − T·ΔS_conf + ΔE_a (1)

where ΔG_c(C) and ΔG_c(G) represent the reversible work to create in water or aqueous solutions a cavity suitable to host the C-state and the G-state, respectively; these two quantities have a different magnitude because the conformations belonging to the two states have different shape and so cause a different solvent-excluded volume effect^10,11 (for more, see below); ΔS_conf represents the conformational entropy gain of PNIPAM chains upon swelling; E_a(C) and E_a(G) represent the energetic interactions (i.e., both van der Waals attractions and H-bonds) among the C-state or the G-state of PNIPAM and surrounding water and co-solute molecules; ΔE(intra) is the difference in intra-chain energetic interactions between the C-state and the G-state. The reorganization of water–water H-bonds is characterized by an almost complete enthalpy–entropy compensation,^32,33 and so it does not affect ΔG_tr. At T(collapse) a perfect balance between the three contributions in eqn (1) has to hold, so that ΔG_tr = 0. It is worth noting that it is no possible to arrive at an explicit expression of T(collapse) starting from the above relationship; this may appear as a drawback of the approach, that, nevertheless, contains all the physics needed for a general description.

It is necessary to devise a reliable procedure to calculate the three terms in eqn (1). The ΔΔG_c = ΔG_c(C) − ΔG_c(G) contribution is calculated by means of a simple geometric model:^6,10 the G-state is a sphere, and the C-state is a prolate spherocylinder, having the same V_vdW of the sphere representing the G-state, but a significantly larger WASA. As in previous applications, a PNIPAM chain of 40 monomers in the G-state is modelled as a sphere of radius a = 10 Å, V_vdW = 4189 ų and WASA = 1633 Ų, whereas the C-state is modelled as a prolate spherocylinder of radius a = 5 Å, cylindrical length l = 46.7 Å, V_vdW = 4189 ų and WASA = 2393 Ų (experimental measurements³⁴ show that the volume change associated with PNIPAM collapse in water is negligibly small). The geometric models for the G-state and the C-state (rough and rigid representations of the average geometric properties possessed by chains populating the two ensembles) are assumed to be not affected by salt addition to water (this assumption should work because, in water, the interior volume of G-state contains a lot of water molecules, which will gradually be replaced by anions on adding salt). Note that the ΔΔG_c contribution: (a) is always positive because ΔG_c increases with cavity WASA, even though the cavity V_vdW is kept fixed;¹¹ (b) is calculated by means of the classic SPT formulae for spherical and spherocylindrical cavities in a hard sphere fluid mixture^16,17 (the pressure–volume term is neglected for its smallness at P = 1 atm). A fundamental variable is the volume packing density of the hard sphere fluid mixture (i.e., aqueous solutions) ξ₃ = (π/6)·∑ρ_j·σ_j³, where ρ_j is the number density, in molecules per ų, of the species j and σ_j is the corresponding hard sphere diameter; ξ₃ represents the fraction of the total liquid volume actually occupied by ions and molecules. The physical reliability of classic SPT formulae is grounded in its geometric basis.^11,35

Experimental values of the density of water,³⁶ and the considered aqueous salt solutions,³⁷ have been used to perform calculations over the 5–40 °C temperature range. The use of experimental density is important because it allows one to take into account, even though in an indirect way, the actual interactions existing among molecules and ions that determine the liquid density.^10,20–24 The following effective hard sphere diameters have been used and considered to be temperature-independent: (a) σ(H₂O) = 2.80 Å,³⁸ corresponding to the position of the first maximum in the oxygen–oxygen radial distribution function of water,³⁹ at room temperature and 1 atm; (b) σ(Na⁺⁾ = 2.02 Å, which is two times the ionic radius first proposed by Wasastjerna;⁴⁰ (c) σ(SCN⁻) = 3.94 Å, corresponding to the effective hard sphere diameter of carbon dioxide;⁴¹ (d) σ(ClO₄⁻) = 4.80 Å, which is the Pauling-type diameter reported by Marcus.⁴²

The T·ΔS_conf term is calculated by considering that each monomer gains a temperature-independent conformational entropy upon swelling (i.e., the coupling between the conformational degrees of freedom of the backbone and those of the side chains is neglected):

T·ΔS_conf = T·N_res·ΔS_conf(res) (2)

where N_res = 40 and ΔS_conf(res) = 4 J K⁻¹ molres⁻¹, the same value used in all our previous applications of this approach.^6,10,22–24 It is assumed that this term is not affected by the addition of cosolutes or salts to water (i.e., the conformational entropy is an intrinsic property of the PNIPAM chain). It is worth noting that, according to large-scale computer simulations,⁴³ an average value for ΔS_conf(res) in the case of globular proteins would be around 19 J K⁻¹ molres⁻¹. Of course, the large difference between the two numbers is due to the large conformational entropy characterizing the G-state of PNIPAM in comparison to the unique 3D structure of the native state of globular proteins.

In our previous studies,^6,10,22–24 the ΔE_a quantity was fixed to −166.5 kJ mol⁻¹ in pure water, and was considered to be temperature-independent in view of the limited temperature range important for PNIPAM collapse. The ΔE_a quantity was considered to be not affected by the addition to water of high charge density anions,¹⁰ because the latter have strong and preferential electrostatic attractions with water molecules. In contrast, the ΔE_a quantity is expected to be larger in magnitude in aqueous solutions containing NaSCN or NaClO₄, because the low charge density and poorly hydrated^44,45 thiocyanate and perchlorate anions should have preferential attractions with PNIPAM isopropyl groups, as already pointed out by means of both experimental and computational studies.⁴⁶ However, no theoretical relationship is used to arrive at the ΔE_a values in NaSCN or NaClO₄ aqueous solutions; the adopted procedure will become clear in the following.

Results and discussion

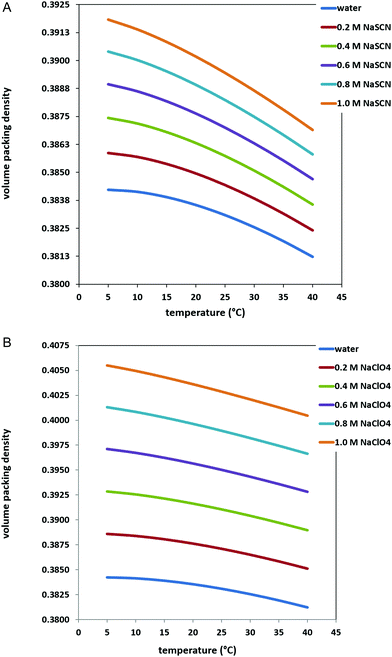
Experimental measurements indicate that the addition of NaSCN or NaClO₄ to water causes a density increase,³⁷ which translates in an increase of the volume packing density ξ₃ of the solutions. This is shown in Fig. 2 and 3 for the two sodium salts over the 0–1 M concentration range, in the 5–40 °C temperature range. The corresponding ΔΔG_c values are shown in Fig. 4, panel A for NaSCN aqueous solutions, and panel B for NaClO₄ aqueous solutions (see also Tables 1 and 2). In both cases, ΔΔG_c increases together with salt concentration, and this occurs to a larger extent in the case of NaClO₄, because the volume packing density of perchlorate solutions is larger than that of thiocyanate solutions³⁵ (compare the two panels of Fig. 3). Therefore, the ΔΔG_c contribution tends to stabilize the G-state upon the concentration increase of the two sodium salts. This stabilizing effect is the same used for rationalizing the behavior of well hydrated, high charge density anions, such as Cl⁻, SO₄²⁻ and CO₃²⁻, as discussed in our previous study.¹⁰ On the other hand, the stabilizing effect of ΔΔG_c is counterbalanced by the destabilizing effect of ΔE_a, produced by the energetic attractions of SCN⁻ and ClO₄⁻ ions to PNIPAM surface. These low charge density and highly polarizable anions have weak electrostatic attractions with water molecules,^44,45 but good dispersion attractions with nonpolar moieties,^46–50 such as PNIPAM isopropyl groups (as well as nonpolar side chains in proteins). Interestingly, these direct energetic attractions are considered to be the molecular origin of the thiocyanate and perchlorate denaturing action towards the native state of globular proteins.¹⁷ Unfortunately, reliable calculations of ΔE_a contribution are very difficult to obtain using theoretical relationships because, for instance, a large set of PNIPAM conformations belonging to both the G-state and the C-state would be needed, together with a qualitatively good estimation of the fraction of PNIPAM surface interacting with water molecules rather than with SCN⁻ or ClO₄⁻ ions. Also large scale computer simulation approaches have limitations due to force field inaccuracies,⁵¹ and the slow dynamics of PNIPAM chains.⁵²

Fig. 2 Experimental density of water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaSCN solutions over the 5–40 °C temperature range and 1 atm (panel A); experimental density of water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaClO₄ solutions over the 5–40 °C temperature range and 1 atm (panel B); data are from ref. 36 and 37.

Fig. 3 Values of the volume packing density, ξ₃, for water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaSCN solutions over the 5–40 °C temperature range and 1 atm (panel A); values of the volume packing density, ξ₃, for water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaClO₄ solutions over the 5–40 °C temperature range and 1 atm (panel B).

Fig. 4 Temperature dependence of the ΔΔG_c functions for PNIPAM in water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaSCN solutions, over the 5–40 °C temperature range and 1 atm (panel A); temperature dependence of the ΔΔG_c functions for PNIPAM in water and aqueous 0.2, 0.4, 0.6, 0.8 and 1 M NaClO₄ solutions, over the 5–40 °C temperature range and 1 atm (panel B).

Table 1 Experimental density of aqueous NaSCN solutions at 20 °C and 1 atm, from ref. 37; experimental values of T(collapse) at different NaSCN concentrations, for PNIPAM samples with a weight-average molecular weight of 170 kDa, from Fig. 1c of ref. 27; classic SPT-ΔΔG_c values and T·ΔS_conf values at T(collapse), estimates of the ΔE_a term obtained by means of eqn (1) and (2). See text for further details

[NaSCN]/M	d(20 °C)/g ml^−1	T(collapse)/°C	ΔΔGc/kJ mol^−1	T·ΔSconf/kJ mol^−1	ΔEa/kJ mol^−1
0	0.9982	31.0	215.2	48.7	−166.5
0.1	1.0025	31.7	215.7	48.8	−166.9
0.2	1.0067	31.9	216.2	48.8	−167.4
0.4	1.0150	32.0	217.0	48.8	−168.2
0.6	1.0233	31.8	217.4	48.8	−168.6
0.8	1.0315	31.5	218.1	48.7	−169.4
1.0	1.0395	31.0	218.9	48.7	−170.2

---

Table 2 Experimental density of aqueous NaClO₄ solutions at 20 °C and 1 atm, from ref. 37; experimental values of T(collapse) at different NaClO₄ concentrations, for PNIPAM samples with a weight-average molecular weight of 170 kDa, from Fig. 1c of ref. 27; classic SPT-ΔΔG_c values and T·ΔS_conf values at T(collapse), estimates of the ΔE_a term obtained by means of eqn (1) and (2). See text for further details

[NaClO4]/M	d(20 °C)/g ml^−1	T(collapse)/°C	ΔΔGc/kJ mol^−1	T·ΔSconf/kJ mol^−1	ΔEa/kJ mol^−1
0	0.9982	31.0	215.2	48.7	−166.5
0.1	1.0060	31.0	216.1	48.7	−167.4
0.2	1.0138	30.5	217.2	48.6	−168.6
0.4	1.0293	29.0	219.1	48.3	−170.8
0.6	1.0447	27.0	220.6	48.0	−172.6
0.8	1.0601	24.5	222.0	47.6	−174.4
1.0	1.0754	22.0	223.4	47.2	−176.2

---

DSC measurements have shown that the enthalpy change associated with PNIPAM collapse transition, ΔH_tr, decreases slightly on increasing the NaSCN concentration, and the process becomes less cooperative, as indicated by DSC peak broadening.^53,54 It is worth noting that the macroscopic ΔH_tr quantity cannot be considered an exact measure of the ΔE_a quantity with a changed sign because the former accounts also for the energy change due to the water–water and water–ion structural reorganization associated with PNIPAM collapse.

Taking into account both the experimental T(collapse) values in the presence of the two salts and the grounds of the theoretical approach [i.e., the T·ΔS_conf contribution is not affected by salt addition to water, and ΔG_tr = 0 at T(collapse) because PNIPAM collapse is a first-order phase transition], it is possible to arrive at the ΔE_a estimates that are listed in the last column of Tables 1 and 2, in the assumption that the classic SPT-ΔΔG_c values are correct. Even though the ΔE_a values are just estimates, not to be used for quantitative analysis, they can help to provide a qualitative but reliable picture. Looking at the numbers and keeping in mind that the positive ΔΔG_c quantity rises significantly with temperature (see Fig. 4), one can state that: (a) on increasing the NaSCN concentration, the increase in the ΔE_a magnitude is almost entirely counterbalanced by the ΔΔG_c increase (note that the ΔH_tr decrease measured via DSC^53,54 does not contrast with the increase in the ΔE_a magnitude); (b) on increasing the NaClO₄ concentration, the increase in the ΔE_a magnitude is overwhelmed by the ΔΔG_c increase. The difference between SCN⁻ and ClO₄⁻ ions mainly comes from the larger size of the latter and its better attractions with water molecules (i.e., the NaClO₄ solubility in water is larger than that of NaSCN); these two factors lead to larger ξ₃ values (see Fig. 3), and so to larger ΔΔG_c values (see Fig. 4) that stabilize the G-state. In general, it should be recognized that such differences are not large because the PNIPAM conformational stability is ruled by a delicate balance of contrasting quantities [see eqn (1)].

At first sight, the emerged scenario does appear strange because PNIPAM is considered to be a simplified model of globular proteins, and NaSCN and NaClO₄ are denaturing agents of the native state of globular proteins^29–31 (i.e., in the latter case the destabilizing ΔE_a quantity overwhelms the stabilizing ΔΔG_c one on increasing the salt concentration). The point to recognize and underscore is that the G-state of PNIPAM does not resemble the native state of globular proteins. Quasi-elastic neutron scattering measurements,⁵⁵ and MD simulations^56,57 have shown that PNIPAM G-state is characterized by an ensemble of different globular conformations, containing in their interior volume a lot of water and cosolute molecules or ions. In other words, PNIPAM G-state does not resemble a “crystal molecule”⁵⁸ in view of its large conformational freedom. This means that: (a) low charge density and highly polarizable ions, not having strong electrostatic attractions with water molecules, such as SCN⁻ and ClO₄⁻, are present inside globular conformations, where they have attractive interactions with PNIPAM moieties; (b) in the case of PNIPAM, the ΔE_a magnitude is not large and does not increase significantly on increasing the salt concentration because the difference in accessibility of the two PNIPAM states to SCN⁻ or ClO₄⁻ anions is smaller than expected; (c) this interpretation is supported by the experimental finding that T(collapse) nonlinearity versus NaSCN and NaClO₄ concentration depends on PNIPAM molecular weight (see Fig. 7e and f in ref. 59); the structural organization of PNIPAM chains in the G-state should depend on their length and the accessibility to SCN⁻ or ClO₄⁻ anions is expected to increase on increasing the molecular weight, in line with the measured, stronger decrease of T(collapse);⁵⁹ (d) in the case of globular proteins, the ΔE_a magnitude is large because there is a marked difference in accessibility between the native state and the denatured one to SCN⁻ or ClO₄⁻ anions (i.e., the interior volume of native state proves to be inaccessible to water and cosolute molecules or ions since it is very well packed⁶⁰). In other words, the important structural differences existing between the G-state of PNIPAM and the native state of globular proteins do not manifest themselves in the collapse thermodynamics in water, but in the response of T(collapse) to the addition of cosolutes or salts to water. In fact, the addition of urea, a well-known denaturing agent of globular proteins, stabilizes the G-state of PNIPAM,²² such as the addition of a significant NaClO₄ quantity. The reliability of this analysis is also supported by the experimental finding that NaClO₄ addition to water causes the stabilization of the molten globule state of cytochrome c,⁶¹ and staphylococcal nuclease,⁶² by recognizing that the molten globule state of globular proteins should somewhat resemble the G-state of PNIPAM.

The effect of NaSCN and NaClO₄ addition on the collapse transition of PNIPAM has already been analyzed by two groups. On one side, Cremer and co-workers^26–28,59 fitted their own T(collapse) experimental data by means of a heuristic relationship consisting of a constant, a linear, and a nonlinear term. The linear term should describe the G-state stabilization due to depletion effects of the added ions, whereas the nonlinear term has the shape of a Langmuir binding isotherm to describe the binding of low charge density ions to PNIPAM surface. The linear term was considered to account for effects related to the increase in surface tension caused by salt addition to water,⁶³ and to the negative hydration entropy of the anions.⁶⁴ Even though there is no clear theoretical ground behind their heuristic T(collapse) expression, Cremer and co-workers²⁶ found that SCN⁻ or ClO₄⁻ anions possess the largest values of binding constant to PNIPAM surface, in line with the present analysis. On the other side, Heyda and Dzubiella¹³ devised an approximate expression for T(collapse), resembling the one used by Cremer and co-workers, starting from a second order Taylor expansion of ΔG_tr, considered to be a function of temperature and salt concentration, and used it to fit experimental data. The approximate T(collapse) expression of Heyda and Dzubiella is indeed very interesting (something similar has recently been used in a different context⁶⁵), but unfortunately it cannot provide a molecular rationalization of the phenomenon because it is not grounded in statistical mechanics. For instance: (a) it makes direct use of the experimental value of the entropy change associated with PNIPAM collapse transition,¹³ that is a macroscopic quantity coming from diverse molecular contributions; (b) its linear term in salt concentration, the m-value, is positive for both NaSCN and NaClO₄, the derivative (∂m/∂C_salt) proves to be negative for both salts, but markedly larger in magnitude for NaClO₄, without any explanation proposed (look at Table 3 in ref. 13). This fitting exercise cannot be considered satisfactory to arrive at a complete understanding.

In conclusion, coherent application of our theoretical approach leads to the following rationalization. For very low concentrations of NaSCN or NaClO₄, T(collapse) increases because the ΔE_a magnitude increases to a greater extent than the ΔΔG_c one. However, poorly hydrated ions, such as SCN⁻ or ClO₄⁻, interact so well with PNIPAM surface that they are bound in a significant manner to both the C-state and the G-state, and the difference in the number of ions bound to PNIPAM surface changes little on increasing the salt concentration. This implies that the ΔE_a magnitude increases with salt concentration to a lesser extent than the ΔΔG_c quantity, leading to a nonlinear trend of T(collapse). In other words, beyond a given salt concentration, ΔΔG_c becomes dominant in the Gibbs energy balance. At this particular concentration point, the salt changes its qualitative action: it does not stabilize the C-state, but starts to stabilize the G-state, as in the case of sodium perchlorate.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The work is supported by the research funds of the Università del Sannio, FRA 2018. The article is dedicated to the memory of Professor Attilio Immirzi, born October 28, 1938 and died March 1, 2019, who played a key role in the academic career of Giuseppe Graziano.

References

1. S. Fujishige, K. Kubota and I. Ando, J. Phys. Chem., 1989, 93, 3311–3313.
2. M. Meewes, J. Ricka, M. de Silva, R. Nyffenegger and T. Binkert, Macromolecules, 1991, 24, 5811–5816.
3. H. G. Schild and D. A. Tirrell, J. Phys. Chem., 1990, 94, 4352–4356.
4. E. I. Tiktopulo, V. N. Uversky, V. B. Lushchik, S. I. Klenin, V. E. Bychkova and O. B. Ptitsyn, Macromolecules, 1995, 28, 7519–7524.
5. G. Graziano, Int. J. Biol. Macromol., 2000, 27, 89–97.
6. A. Pica and G. Graziano, Polymer, 2017, 124, 101–106.
7. A. K. Soper and J. L. Finney, Phys. Rev. Lett., 1993, 71, 4346–4349.
8. J. L. Finney, A. K. Soper and J. Z. Turner, Pure Appl. Chem., 1993, 65, 2521–2526.
9. P. Buchanan, A. Aldiwan, A. K. Soper, J. L. Creek and C. A. Koh, Chem. Phys. Lett., 2005, 415, 89–93.
10. A. Pica and G. Graziano, Phys. Chem. Chem. Phys., 2015, 17, 27750–27757.
11. G. Graziano, J. Mol. Liq., 2015, 211, 1047–1051.
12. B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379–400.
13. J. Heyda and J. Dzubiella, J. Phys. Chem. B, 2014, 118, 10979–10988.
14. C. Dalgicdir, F. Rodriguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2017, 121, 7741–7748.
15. H. Reiss, Adv. Chem. Phys., 1965, 9, 1–84.
16. J. L. Lebowitz, E. Helfand and E. Praestgaard, J. Chem. Phys., 1965, 43, 774–779.
17. G. Graziano, Phys. Chem. Chem. Phys., 2011, 13, 12008–12014.
18. B. Lee, J. Chem. Phys., 1985, 83, 2421–2425.
19. B. Lee, Biopolymers, 1985, 25, 813–823.
20. G. Graziano, Phys. Chem. Chem. Phys., 2014, 16, 21755–21767.
21. G. Graziano, Pure Appl. Chem., 2016, 88, 177–188.
22. A. Pica and G. Graziano, Phys. Chem. Chem. Phys., 2016, 18, 14426–14433.
23. A. Pica and G. Graziano, J. Mol. Liq., 2019, 285, 204–212.
24. A. Pica and G. Graziano, Phys. Chem. Chem. Phys., 2016, 18, 25601–25608.
25. A. Pica and G. Graziano, Soft Matter, 2017, 13, 7698–7700.
26. Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, J. Am. Chem. Soc., 2005, 127, 14505–14510.
27. Y. Zhang and P. S. Cremer, Annu. Rev. Phys. Chem., 2010, 61, 63–83.
28. Y. Cho, Y. Zhang, T. Christensen, L. B. Sagle, A. Chilkoti and P. S. Cremer, J. Phys. Chem. B, 2008, 112, 13765–13771.
29. P. H. von Hippel and K. Y. Wong, J. Biol. Chem., 1965, 240, 3909–3923.
30. M. Senske, D. Constantinescu-Aruxandei, M. Havenith, C. Herrmann, H. Weingartner and S. Ebbinghaus, Phys. Chem. Chem. Phys., 2016, 18, 29698–29708.
31. S. Cozzolino, R. Oliva, G. Graziano and P. D. Vecchio, Phys. Chem. Chem. Phys., 2018, 20, 29389–29398.
32. A. Ben-Naim, Biopolymers, 1975, 14, 1337–1355.
33. B. Lee, Biophys. Chem., 1994, 51, 271–278.
34. P. Kujawa and F. M. Winnik, Macromolecules, 2001, 34, 4130–4135.
35. G. Graziano, J. Chem. Phys., 2008, 109, 084506.
36. G. S. Kell, J. Chem. Eng. Data, 1975, 20, 97–105.
37. P. Novotny and O. Sohnel, J. Chem. Eng. Data, 1988, 33, 49–55.
38. G. Graziano, Chem. Phys. Lett., 2004, 396, 226–231.
39. J. M. Sorenson, G. Hura, R. M. Glaeser and T. Head-Gordon, J. Chem. Phys., 2000, 113, 9149–9161.
40. J. A. Wasastjerna, Commentat. Phys.-Math., 1923, 38, 1–25.
41. E. Wilhelm and R. Battino, J. Chem. Phys., 1971, 55, 4012–4017.
42. Y. Marcus, Chem. Rev., 1988, 88, 1475–1498.
43. M. C. Baxa, E. J. Haddadian, J. M. Jumper, K. F. Freed and T. R. Sosnick, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15396–15401.
44. A. Botti, S. E. Pagnotta, F. Bruni and M. A. Ricci, J. Phys. Chem. B, 2009, 113, 10014–10021.
45. J. T. Kelly, M. Mayer, A. C. Kennedy, C. Schemel and K. R. Asmis, J. Chem. Phys., 2018, 148, 222840.
46. H. I. Okur, J. Hladilkova, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014.
47. K. D. Collins, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 5553–5557.
48. S. Woelki and H. H. Kohler, Chem. Phys., 2004, 306, 209–217.
49. R. Zangi, M. Hagen and B. J. Berne, J. Am. Chem. Soc., 2007, 129, 4678–4686.
50. G. Graziano, Chem. Phys. Lett., 2010, 491, 54–58.
51. C. Dalgicdir and N. F. A. van der Vegt, J. Phys. Chem. B, 2019, 123, 3875–3883.
52. Y. Kang, H. Joo and J. S. Kim, J. Phys. Chem. B, 2016, 120, 13184–13192.
53. I. Shechter, O. Ramon, I. Portnaya, Y. Paz and Y. D. Livney, Macromolecules, 2010, 43, 480–487.
54. S. Z. Moghaddam and E. Thormann, Langmuir, 2017, 33, 4806–4815.
55. K. Kyriakos, M. Philipp, L. Silvi, W. Lohstroh, W. Petry, P. Müller-Buschbaum and C. M. Papadakis, J. Phys. Chem. B, 2016, 120, 4679–4688.
56. F. Rodriguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2014, 118, 7327–7334.
57. S. Micciulla, J. Michalowsky, M. A. Schroer, C. Holm, R. von Klitzing and J. Smiatek, Phys. Chem. Chem. Phys., 2016, 18, 5324–5335.
58. A. M. Liquori, Q. Rev. Biophys., 1969, 2, 65–92.
59. Y. Zhang, S. Furyk, L. B. Sagle, Y. Cho, D. E. Bergbreiter and P. S. Cremer, J. Phys. Chem. C, 2007, 111, 8916–8924.
60. F. M. Richards and W. A. Lim, Q. Rev. Biophys., 1994, 26, 423–498.
61. D. Hamada, S. Kidokoro, H. Fukada, K. Takahashi and Y. Goto, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 10325–10329.
62. H. Maity and M. R. Eftink, Arch. Biochem. Biophys., 2004, 431, 119–123.
63. R. L. Baldwin, Biophys. J., 1996, 71, 2056–2063.
64. Y. Marcus and A. Loewenschuss, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 1984, 81, 81–135.
65. E. A. Oprzeska-Zingrebe, S. Meyer, A. Roloff, H. J. Kunte and J. Smiatek, Phys. Chem. Chem. Phys., 2018, 20, 25861–25874.

---