Superhydrogenation of pentacene: the reactivity of zigzag-edges

Abstract

Investigating the hydrogenation of carbonaceous materials is of interest in a wide range of research areas including electronic device development, hydrogen storage, and, in particular, astrocatalytic formation of molecular hydrogen in the universe. Polycyclic Aromatic Hydrocarbons (PAHs) are ubiquitous in space, locking up close to 15% of the elementary carbon. We have used thermal desorption measurements to study the hydrogenation sequence of pentacene from adding one additional H to the fully hydrogenated pentacene species. The experiments reveal that hydrogenated species with an even number of excess H atoms are highly preferred over hydrogenated species with an odd number of H atoms. In addition, the experiments show that specific hydrogenation states of pentacene with 2, 4, 6, 10, 16 and 22 extra H atoms are preferred over other even numbers. We have investigated the structural stability and activation energy barriers for the superhydrogenation of pentacene using Density Functional Theory. The results reveal a preferential hydrogenation pattern set by the activation energy barriers of the hydrogenation steps. Based on these studies, we formulate simple concepts governing the hydrogenation that apply equally well for different PAHs.

---

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) are an important class of carbon bearing molecules which are ubiquitous in the universe and lock up close to 15% of the cosmic carbon.¹ PAHs also play an important role in the chemistry of space.² The role of PAHs in the formation of H₂, the most abundant molecule in the universe, in the interstellar medium (ISM) has been studied extensively.^3–8 PAHs are of general interest to the scientific community due to their pollutant and carcinogenic properties in terrestrial environments.⁹ In this context, the reduction (hydrogenation) sequence that leads to the formation of aliphatic compounds¹⁰ and the reduction of PAHs by metal free catalysts¹¹ have been studied, showing that the hydrogenation of these compounds leads to a less toxic mixture of saturated and unsaturated species. Owing to their photo-physical and structural properties, PAHs are also of interest for applications in hydrogen storage¹² and in optoelectronic devices.^13–16

In this work, we focus, specifically, on one specific kind of linear catacondensed PAH, pentacene (C₂₂H₁₄), representative of a class called acenes. These compounds, consisting of a linear row of condensed six membered rings,¹⁷ are characterized by zigzag edges and they are representative of the smallest graphene nanoribbon. Zigzag edges are a structural repetition of carbon atoms already bound to a single hydrogen atom, well known in the literature as “solo sites”,¹⁸ and bridge carbon atoms that are not bound to any hydrogen atoms. The zigzag edges are important in astrophysics since they have strong infrared signatures that have been clearly detected in astronomical spectra.¹⁹ Specifically, the strong C–H out-of-plane bending mode at 11.2 μm is characteristic of C–H groups that belong to zigzag edges^20–22 and this band dominates the observed IR spectra of HII regions, YSOs and reflection nebulae (RNe) as well as the diffuse ISM.¹⁸ The presence of zigzag edges is also of interest to the chemistry community since they allow charge localization at the edges of the PAHs, and that increases their reactivity.

In contrast to catacondensed PAHs such as the acenes, some pericondensed PAHs (e.g. coronene) have no zigzag edges and their structure is characterized by duo carbons (two adjacent hydrogenated carbon sites) with strong CH modes in the 12–13 μm range.^20,21 Both catacondensed and pericondensed PAHs are susceptible to hydrogenation by hydrogen atoms under interstellar conditions, but the hydrogenation sequence differs due to their different structures.^23,24 For instance, a recent study demonstrated that the hydrogenation sequence of coronene, a pericondensed PAH, starts from the duo carbons²⁴ with delayed hydrogenation of the other carbon sites. For catacondensed species, the hydrogenation sequence begins from the central aromatic ring, saturating both inner and edge carbons.^23,25

Superhydrogenated PAHs are important since they might be responsible for the formation of molecular hydrogen in Photodissociation Regions (PDRs).²⁶ PDRs are regions where the ultraviolet radiation from nearby bright stars influences the chemical and physical properties of the present molecular structures.²⁷ It is well appreciated that, because of the high UV flux, molecular hydrogen has to be rapidly reformed and that the normal routes considered for H₂ formation in the ISM do not suffice to account for its observed abundance.^28,29 As astronomical observations have revealed a spatial correlation between the H₂ formation rate and interstellar PAHs emission in these regions, PAHs have been suggested as possible catalysts for H₂ formation.^29,30 Different mechanisms have been studied in order to understand the formation of molecular hydrogen on PAHs, including reactions between two chemisorbed atomic hydrogen atoms through Langmuir–Hinshelwood (LH) and Eley–Rideal (ER) mechanisms. These mechanisms have been studied for pyrene³¹ and for coronene,^3,5 demonstrating that Eley–Rideal abstraction is a viable pathway for PAH catalyzed molecular hydrogen formation. Moreover, Rasmussen²⁵ studied the correlation of the increase in hydrogen binding energy with increasing zigzag edge length, using several acenes with different length as models. Therefore, it is crucial to study the aromatic–aliphatic character of PAHs when they are in a hydrogen rich environment in order to shed light on the sequence that leads to the so called “Magic Numbers” in the hydrogenation sequence of these species.³²

This study aims to determine and understand the hydrogenation sequence of pentacene that leads to complete superhydrogenation of the molecule, using a combination of experimental and theoretical techniques. Specifically, temperature programmed desorption (TPD) is employed to directly determine the sequence of products of hydrogen addition to pentacene while density functional theory (DFT) calculations are used to investigate the hydrogenation sequence. This also serves as a test of simple concepts that may be applicable to other aromatic species featuring a bipartite lattice (e.g. carbon sp² structured as a graphene lattice).

2 Experimental and theoretical methods

2.1 Thermal desorption measurements

Experimental investigations of superhydrogenation of pentacene were conducted using temperature programmed desorption (TPD) measurements under ultra high vacuum (UHV) conditions; p < 10⁻⁹ mbar. A few multilayers of commercially available pentacene (C₂₂H₁₄; Sigma-Aldrich; triple-sublimed grade, ≥99.995%) were deposited onto highly oriented pyrolytic graphite (HOPG), held at 290 K, using a home-built Knudsen-type effusion cell. The HOPG substrate was cleaved in air prior to mounting and then annealed in UHV to 1100 K before each measurement. Typically 2–3 pentacene multilayers were obtained after 2 minutes deposition with the molecular doser at 135 °C (408 K). A monolayer could then be consistently produced by annealing the sample to 330 K for 5 minutes, removing the multilayers.

The monolayer of pentacene on HOPG was then exposed to a beam of atomic hydrogen (H) using a hydrogen atom beam source (HABS).³³ The HABS was operated at ≈2200 K, producing a hot atomic H beam which was subsequently cooled collisionally, through a quartz nozzle, to an estimated temperature of ≈1400 K.

TPD measurements were performed with a linear ramp of β = 1 K s⁻¹ until reaching 1100 K. To mass-selectively detect the species that leave the surface a quadrupole mass spectrometer (QMS) (Extrel CMS LLC) was used, scanning the range 258–340 atomic mass units (amu) per charge. The TPD spectra within the given mass range are integrated and averaged over the relevant desorption temperature range to give the presented mass spectra.

2.2 Density functional theory calculations

Theoretical investigations were conducted using density functional theory (DFT) as implemented in the Gaussian 16 software suite.³⁴ In order for our calculations to have sufficiently high accuracy, we used the exchange correlation functional M06-2X.³⁵ This functional has been proven to provide an accurate description of PAH hydrogenation since it has been found to be in close agreement with coupled-cluster calculations.²⁴ All calculations were carried out using the unrestricted (UHF) formalism. We employed the new pcseg-1³⁶ basis set, a segmented polarization consistent double zeta basis set optimized for DFT. All geometries were optimized using the Berny algorithm³⁷ and, in order to characterize the minima and saddle points, normal modes were analyzed within the harmonic approximation. All energies were corrected in order to reduce the basis set superposition error (BSSE) using the counterpoise scheme^38,39 implemented in Gaussian 16. We employed the molden^40,41 software package to visualize molecular structures and normal modes.

The theoretical part of this work is divided into two sections: the first describes the sequence of H addition that leads to fully hydrogenated pentacene while the second describes the hydrogenation sequence of superhydrogenated species based on a binding energy and energy barrier analysis.

The binding energies are defined as:

E_bind = [(E_H + E_reagent) − E_nH-pentacene]

E_bind is the binding energy, E_H is the energy of atomic hydrogen in gas phase, E_reagent is the energy of the reactant that is interacting with the atomic hydrogen. Positive values of binding energies indicate exoergic processes, while negative values indicate endoergic ones.

The energy barriers are defined as:

E_barr = [E_TS − (E_H + E_reagent)]

E_barr is the energy barrier, E_TS is the energy of the transition state structure calculated as a first order saddle point, while E_H and E_reagent are the energy of the minima for the hydrogen atom and reactant, respectively. For the definition of transition state, the energy barrier is always positive.

Finally, the formation energy is defined as:

E_f = [E_product − (E_H + E_reagent)]

E_f is the formation energy, E_product is the energy of the product, while E_H and E_reagent are the energies of the hydrogen atom and reactant, respectively. In the case of the formation energy, negative values indicate exoergic processes, whereas positive values indicate endoergic ones. For simplicity, we label the hydrogenated species of pentacene as nH-pentacene where n is a whole number (e.g. 3H-pentacene, is pentacene with 3 extra hydrogen atoms attached, namely C₂₂H₁₇). We use the term syn (cis position) when the extra hydrogen are chemisorbed on the same side of the molecule, while, we use the term anti for the hydrogens chemisorbed on opposite sides (trans position).

In order to gain broader insights into the hydrogenation process, the sequence of hydrogenation was rationalized with simple concepts derived from a tight-binding model where the most reactive site is related to the smallest π-coordination number (number of carbon atoms connected to a carbon center) and the highest hypercoordination number (number of second carbon atom neighbours that have the same coordination number) for closed-shell systems.⁴² Attaching a hydrogen on a closed-shell system (i.e. all odd extra hydrogens chemisorbed) generates an unpaired electron (mid-gap state) that localizes preferentially in the ortho- or para-positions respect to the already extra hydrogen attached. Therefore, the odd hydrogenations were predicted using the coordination and hyper-coordination rule, whereas the even hydrogenations were predicted using the ortho–para localization. Finally, these simple rules were confirmed through the binding energy and energy barrier analysis. The latter are correlated by the Bell–Evans–Polanyi principle according to which larger energy barriers are associated with lower binding energies.^43,44

3 Experimental results

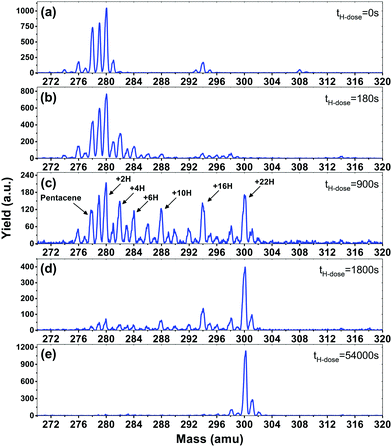
In Fig. 1, mass spectra for pentacene monolayers exposed to increasing H atom fluences are displayed. The initial mass spectrum before hydrogenation can be seen in Fig. 1(a). In the mass spectrum prominent peaks are seen at masses: 278 amu (the pentacene molecule, C₂₂H₁₄), 280 amu (6,13-dihydropentacene (DHP), C₂₂H₁₆), 294 amu (6-hydroxypentacene C₂₂H₁₄O), and 308 amu (pentacenequinone (PQ), C₂₂H₁₂O₂). Mass 279 contains contributions from both the fragmentation of DHP during the ionization step in the QMS and from pentacene with the naturally occurring isotope ¹³C (¹³C is also seen in DHP as mass 281 in Fig. 1(a)). All masses detected below 278 amu, e.g. 276 amu, are ascribed to fragmentation in the QMS. The commercially available pentacene batches are known to have the oxidized species PQ as a main contaminant,⁴⁵ and more oxidised and/or superhydrogenated species are known to form when pentacene is exposed to air and light.⁴⁶ DHP is also present in commercially available pentacene and is known to be a byproduct of sublimation.⁴⁷

Fig. 1 Mass spectra showing the mass distribution of a pentacene monolayer after different H-atom exposure times presented in the figure. (a) Mass distribution of a monolayer of pentacene (mass 278) with the prominent contaminants dihydropentacene (mass 280) and 6-hydroxypentacene (mass 294). (b–e) Mass distributions shifting towards higher masses with increasing H atom fluences, eventually reaching mass 300 corresponding to fully superhydrogenated pentacene.

Fig. 1(b–e) show the mass distribution of superhydrogenated pentacene after hydrogenation times of (b) 180 s, (c) 900 s, (d) 1800 s and (e) 54 000 s (17 hours). Fig. 1(b) shows a small degree of hydrogenation for both the pentacene and the oxidized species. The species with even masses such as 280, 282 and 284 are seen to be more prominent than the odd. This is consistent with the fact that superhydrogenated pentacene molecules with an odd mass will be open-shell, and hence exhibit a radical behaviour and therefore be more reactive towards the addition of a subsequent H atom. By contrast, the even mass species are less prone to further hydrogenation. The odd–even oscillation is clearly visible in Fig. 1(c) where the mass distribution covers the entire range from pristine pentacene, mass 278, to fully superhydrogenated pentacene, C₂₂H₃₆, with mass 300. While the odd–even oscillation is clearly visible, it is also evident that some specific species (with specific superhydrogenation degrees) appear more prominently than others. The most prominent species are: 280 (+2H), 282 (+4H), 284 (+6H), 288 (+10H), 294 (+16H) and 300 (+22H), also indicated in Fig. 1(c).

After extended H atom exposure, see Fig. 1(d–e), the mass distribution is pushed towards mass 300, corresponding to fully superhydrogenated pentacene C₂₂H₃₆. In Fig. 1(e) the peak at mass 300 completely dominates the spectrum. The smaller peaks seen at masses 301–302 and 298–299 are ascribed to the ¹³C isotope and fragmentation in the QMS, respectively. Hence, the fact that it is possible to drive the entire mass distribution to fully superhydrogenated pentacene for long H deposition times (see Fig. 1(e)) reveals that H atom addition reactions dominate over H atom abstraction for superhydrogenated pentacene.

4 Theoretical results

4.1 Hydrogenation sequence

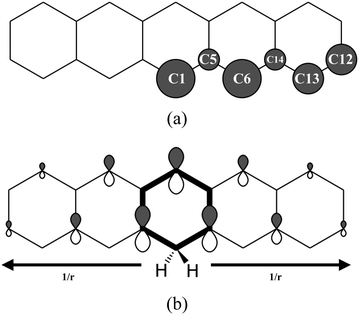
The hydrogenation sequence found for pentacene is schematically shown in Fig. 2. At the first hydrogenation, the carbon sites more inclined to be hydrogenated are C1 and C6 (Fig. 3(a)) with the highest hyper-coordination. The least inclined carbon atoms to be hydrogenated are the inner carbons C5 and C14 (Fig. 3(a)) since they have the highest coordination numbers. The carbon atoms C13 and C12, have intermediate propensity to be hydrogenated (a detailed description of the sequence is reported in the ESI†). The first hydrogenation and all odd hydrogenation steps are the single addition of a hydrogen atom to a closed-shell species and are, therefore, associated with the formation of a mid-gap state (singly occupied molecular orbital) which is represented schematically in Fig. 3(b). The mid-gap state generated is in a radical open-shell system and will react readily with a radical species such as a further hydrogen atom. The mid-gap state formation increases the electron affinity of the carbon sites where an unpaired electron is localized, but this affinity decreases as the distance from the hydrogenated carbon sites increases.⁴² For instance, the highest probability that an atomic hydrogen will be chemisorbed are those carbon sites nearby the already extra hydrogen chemisorbed. This tendency is illustrated in Fig. 3(b). Hence, for even hydrogenation reactions, the sequence is led by ortho–para localization of the unpaired electron by the mesomeric effect with respect to the already chemisorbed extra hydrogen. Therefore, the mid-gap state drives the reactivity to specific carbon sites in the molecule. The second atomic hydrogen might chemisorb in ortho or in para with respect to the already chemisorbed extra hydrogen (Fig. 3(b)).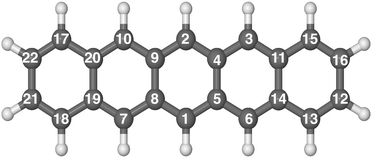

Fig. 2 Optimized molecular structure of pentacene in balls and sticks. The numerical labels reported indicate the full hydrogenation sequence of pentacene.

Fig. 3 (a) Schematical representation of the affinity of the carbon atoms to be chemisorbed by the first hydrogen atom. Larger balls indicates higher hydrogenation affinity. (b) Graphical representation of localized mid-gap states for the second hydrogenation. The arrows show decreasing effect of mid-gap state with increasing distance from the first hydrogenated carbon site.

The hydrogenation sequence follows a simple rule: first hydrogenation of the carbon in the solo position (CH bonded H where adjacent C atoms do not have a H), followed by hydrogenation of the neighboring inner carbons (bridge carbons). The latter step reflects that an inner carbon is under-coordinated upon hydrogenation of a neighbour carbon site. This is in line with the study carried out by Klærke et al.⁴⁸ and Bonfanti et al.⁴² confirming that it is easier to hydrogenate edge carbons than bridge ones.

The highest binding energy found is associated with the chemisorption of the extra hydrogen in position 2 (Fig. 2), which is para with respect to carbon 1. Once carbons 1 and 2 are hydrogenated, two topologically disconnected systems are generated. The molecule now consists of two naphthalene units, bound to the hydrogenated non-aromatic ring, outlined in bold in Fig. 4(a). These two naphthalene units are equivalent and therefore, we considered the chemisorption of the third hydrogen atom on C3 (Fig. 4(a)) which has the highest hyper-coordination. Fig. 4(a) also reports graphically the propensity of the carbon atoms to be hydrogenated (details reported in the ESI†) where it is clearly shown that C3 and C15 have higher affinity (high hyper-coordination) compared to the inner carbon site C11 as the latter has the highest coordination number, while, C16 and C4 have lower propensity to be hydrogenated since these carbon sites have lower hyper-coordination. The fourth hydrogen atom, then, chemisorbs on the least coordinated carbon site (labeled C4 in Fig. 4(a)) that is a bridge carbon. The sequence, schematically shown in Fig. 2, continues with the system tending to preserve the aromaticity of individual rings as long as possible. Moreover, during the hydrogenation, disconnected systems are created, as naphthalene and benzene rings (shown in bold in Fig. 4(b)), and the hydrogenation sequence might change accordingly. A complete overview of the sequence is reported in the ESI.†

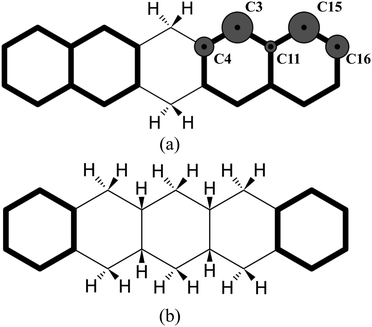Fig. 4 (a) Graphical representation of disconnected naphthalene units and their propensity to be hydrogenated. (b) Graphical representation of disconnected benzene units.

4.2 syn and anti conformation

In our experiments, a pentacene molecule is exposed to a flux of hydrogen atoms on only one side as the monolayer is deposited on a graphite surface. Therefore, one could argue, from a geometric perspective, that superhydrogenation only occurs on one side. Initially, we studied the reaction sequence by chemisorbing hydrogen atoms on a single side of the molecule (syn path). The complete hydrogenation of pentacene leads to the formation of a bent structure as reported in Fig. 5.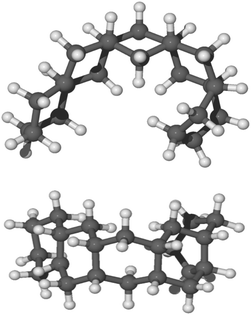

Fig. 5 Side view and top view of the optimized molecular structure of syn-22H-pentacene in balls and sticks.

As it may be relevant for the hydrogenation of gaseous pentacene, we also considered binding the hydrogen atoms to the bridging carbon atoms of the molecule on alternating sides of the molecular plane (trans-hydrogenation), referred to here as “anti position”, and shown in Fig. 6. The anti conformation in the case of pentacene is relevant only in carbon sites where no hydrogen atoms are already bound. In fact, in the case of edge carbons where two hydrogen atoms are attached, the hydrogen atoms are topologically equivalent.

The hydrogenation sequence for the anti path begins with the 4th hydrogenation since the hydrogen atoms already chemisorbed are topologically equivalent. Specifically, the hydrogen atom may chemisorb on carbon 4 (Fig. 2) from the bottom side with respect to the plane of the molecule. The addition of the next hydrogen atom to carbon 5, proceeds from the top of the molecule with respect to the molecular plane. Hence, if the hydrogen atom chemisorbs on the bottom side of the molecule, specifically on carbon atoms 4, 8, 11 and 20, we can observe a more linear structure with all rings in arm-chair conformation. A complete description of why those hydrogenated species are formed, based on the analysis of binding energies and energy barriers, is reported in the next section and a more complete description of the sequence is reported in the ESI.†

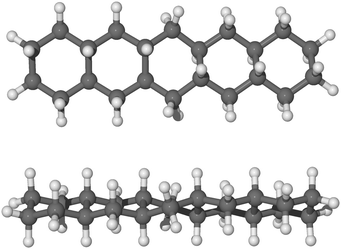Fig. 6 Side view and top view of optimized molecular structure of anti-22H-pentacene in balls and sticks.

4.3 Quasi-nanotubular formation

Furthermore, the formation of these topologically disconnected systems may cause an intramolecular homo-coupling (i.e. formation of C–C bond inside the same molecule). Specifically, we found that for radical species, syn-9H-pentacene, syn-11H-pentacene, syn-13H-pentacene and syn-15H-pentacene (see ESI†), further hydrogenation takes place in the ring disconnected from the already present unpaired electron and an intramolecular radical–radical reaction will occur leading to the formation of a nanotubular structure during the chemisorption of the 12th hydrogen radical (e.g. that shown in Fig. 7). The disconnected systems do not allow the localization of the unpaired electron within the molecule and thus results in the formation of such a nanotubular structure. As discussed in the ESI,† several nanotubular structures could be formed during the hydrogenation process.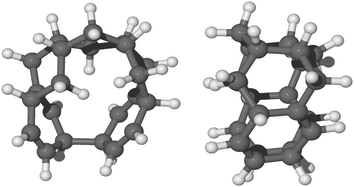

Fig. 7 Front view and side view, respectively, of the optimized molecular structure in balls and sticks of quasi-nanotube formed by the chemisorption of 12th hydrogen on a less reactive carbon site of syn-11H-pentacene (see section 12th hydrogenation in the ESI†).

Table 1 provides the exoergic formation energies, indicating that the formation of quasi-nanotubular structures is thermodynamically favourable, especially during the addition of the 16th hydrogen atom in a less reactive carbon site (more details are reported in ESI†). Moreover, the formation of these nanotubular structures occurs only in the gas-phase and involves an intramolecular homo-coupling (formation of a carbon bond within a molecule). In a similar study, the formation of intermolecular homo-coupling (formation of a carbon bond between two molecules) between two pentacene molecules on Au(111), resulting from superhydrogenation, has been investigated.⁴⁹ In this case, intermolecular homo-coupling dominates on a surface. This process is not important in the gas phase as collisions are rare. Instead, in the gas phase, intramolecular nanotubular formation dominates.

Table 1 Formation energy (ΔE_f) of quasi-nanotubes from pentacene with n numbers of extra H atoms chemisorbed on the same side

Hn	ΔEf (eV)
10	−2.39
12	−1.20
14	−2.50
16	−2.70

---

4.4 Analysis of superhydrogenated species

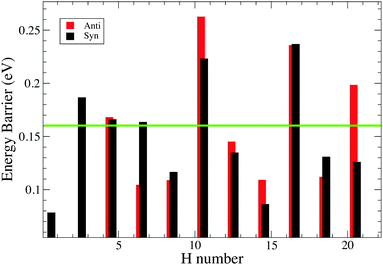
Fig. 8 shows the trend of energy barrier for the syn and anti path. We do not expect energy barriers of activation for odd to even hydrogenation since 1H-pentacene is an open-shell radical ready to react through a barrier-less reaction with another radical (atomic hydrogen), which is in line with the studies conducted on coronene and pyrene.^3,24,31 From chemical principles, we expect that this is a general rule and we have focused our calculations on determining energy barriers involved in the formation of odd hydrogenated species.

Fig. 8 Calculated energy barriers in the hydrogenation from an even to an odd number of H's on pentacene. H number indicates the number of extra hydrogens chemisorbed on pentacene. The green line represents energy barrier relevant under our experimental conditions. Note that there is no energy barrier for the hydrogenation from an odd to an even number of H atoms.

syn path. Pentacene is particularly reactive for the first two hydrogenation reactions, as indicated by the presence of 6,13-dihydropentacene (syn-2H-pentacene) as a contaminant in the experiments. Once syn-2H-pentacene is formed, hydrogenation proceeds until larger energy barriers are difficult to overcome under the experimental conditions. Specifically, energy barriers higher than 0.16 eV (green line in Fig. 8) are less accessible in our experiment with a 1400 K atomic hydrogen beam. In fact, the peaks related to +2H, +4H, +6H, +10H, +16H are observed in the mass spectra reflect the difficulty to overcome barrier heights for further hydrogenation processes.

syn-21H-pentacene can react through a barrierless reaction with another radical to produce the fully hydrogenated pentacene with a mass of 300 amu. The peak corresponding to mass 300 amu becomes prominent as exposure times to atomic hydrogen increases. The presence of magic numbers in the hydrogenation of pentacene reflects that the energy barriers are particularly high whenever a new aromatic ring has to be attacked.

The values of binding energies reported in Fig. 9 suggest that all even hydrogenated species are more favourable than the odd hydrogenated species and have binding energies between 3 and 4.5 eV. The species with an odd number of extra hydrogen atoms attached display smaller binding energies between 2.5 eV and 1 eV. This trend was studied and confirmed on several neutral PAHs,^3,25,31 while for the cation the opposite is found as expected for an open shell species.^32,50 Within the odd and even sequences there are small variations in binding energy which are due to high affinity of these carbon sites toward the hydrogenation. However, these differences are small and, at the temperature of the experiment, are unlikely to be relevant for the discussion of the magic numbers.

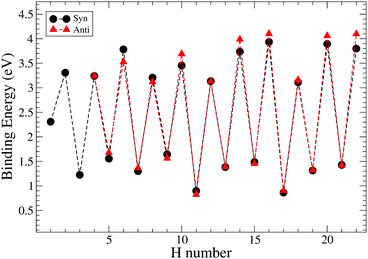Fig. 9 Trend of binding energies for the hydrogenation of pentacene for two different paths: syn and anti. H number indicates the number of extra hydrogens chemisorbed on pentacene.

Our study of the binding energies reveals that superhydrogenation is energetically favorable for all species. The odd–even pattern and the presence of magic numbers in the even sequence reflects the pattern of energy barriers in the production of odd species from even ones. The lowest energy barriers found in this work are related to the chemisorption of the hydrogen on aliphatic carbon and, in particular, for the case of the formation of syn-9H, syn-13H, syn-15H and syn-19H-pentacene.

anti path. The hydrogenation sequence in gas phase space environments may reflect the fact that both sides of the pentacene molecule can be attacked by radical hydrogen atoms. Therefore, we investigated an alternative path where the hydrogen atoms chemisorbed on the bridge carbons are in anti conformation respect to the plane of the molecule, as shown in Fig. 6. The energy barriers for the addition of hydrogen atoms to the anti hydrogenated pentacene follow the same trend as that of the syn path with some significant exceptions.

Table 2 reports the difference in energy barrier between anti and syn. The trend revels significant differences between syn and anti that cannot explain the magic numbers found in our experiment. Specifically, based on this trend we should not expect the presence of anti-6H-pentacene due to the lower barrier with respect to the syn counterpart, whereas we might expect the anti-20H-pentacene due to the difficulties associated with further hydrogenation. For a complete overview, see Fig. 8.

Table 2 Difference of energy barriers between the anti and syn hydrogenation (ΔE^anti_bar − ΔE^syn_bar). Hn indicates the number of extra hydrogens chemisorbed on pentacene

Hn	ΔE^antibar − ΔE^synbar (eV)
7	−0.070
11	0.039
13	0.010
15	0.019
21	−0.072

---

The anti path has the same trend in binding energies as the syn path. We show that anti-6H, anti-10H, anti-12H, anti-14H, anti-16H and anti-20H-pentacene have large binding energies (larger than 3.4 eV), while anti-11H and anti-17H have lower binding energies by 1 eV. Table 3 shows the difference of binding energies between syn and anti hydrogenation, indicating that the anti chemisorption of hydrogen atoms might be more favourable for some hydrogenations.

Table 3 Difference of binding energies between the syn and anti hydrogenation of pentacene (ΔE^anti_bind − ΔE^syn_bind). Hn indicates the number of extra hydrogens chemisorbed on pentacene

Hn	ΔE^antibind − ΔE^synbind (eV)
5	0.12
10	0.24
14	0.25
16	0.17
20	0.16
22	0.30

---

Some hydrogenation steps are not included in Table 3 as the energy differences are small (∼0.007–0.09 eV). The observed pattern of magic numbers in the hydrogenation of pentacene adsorbed on graphite is fully consistent with our expectation that, because of steric reasons, hydrogenation will occur following the syn sequence. Specifically, we observed a dominant peak at the mass of 6H-pentacene and only a minor peak corresponding to 20H-pentacene in accordance with the syn-sequence, but not the anti-sequence.

5 Astrophysical implications

Massive stars have a profound influence on their nascent clouds. Specifically, far-ultraviolet photons with energies in the range 6 to 13.6 eV do not have enough energy to ionize atomic hydrogen but can photo-dissociate molecules and heat the gas in the surrounding molecular cloud.⁵¹ Hydrogen is atomic in the surface layers of these so-called photodissociation regions (PDRs) while carbon is singly ionized (C⁺). Going into the PDR, the dissociating and ionizing far-UV photons are attenuated by small dust grains and atomic hydrogen is converted into H₂ and, eventually, C⁺ into CO. Gas temperatures in the atomic H and molecular H₂ zones of PDRs range from 200–500 K depending on the star involved, while the dust is 30–75 K. Deeper in, where CO has formed, the gas cools down to 40 K. Observationally, PDRs shine brightly in the vibrational transitions of UV-pumped PAH molecules, the far-infrared fine-structure transitions of abundant atoms (C⁺, O), the ro-vibrational transitions of H₂, and molecular rotational lines of e.g., CO.⁵¹

Analysis of this data has revealed that H₂ must be very efficiently made in these surface layers.²⁹ This is not understood as the dust in PDRs is too warm to allow efficient H₂ formation.²⁸ This observed efficient H₂ formation in PDR surfaces has been ascribed to the catalytic activity of PAHs and detailed studies have appeared in the astronomical literature.^8,52–54 The present study is geared towards elucidating the interaction of atomic H with PAHs and quantitative measuring of the molecular parameters involved that are needed for these astronomical models. Our results show that addition of the first two hydrogens will be very efficient as the energy barriers involved are small and the kinetic temperature of the gas is quite high. However, adding the third hydrogen has a prohibitive energy barrier (Fig. 8) even at gas temperatures relevant for PDRs (200–500 K). To estimate the importance of quantum mechanical tunneling, we have evaluated the cross-over temperatures for the reactions involved and these are reported in ESI.† Typically these vary from 136 to 213 K and hence, quantum mechanical tunneling is not expected to play a role in the warm gas of PDRs but it may play more of a role in cold molecular clouds. We note also that the binding energies of these extra H's are relatively low and these are readily lost in strong radiation field of a PDR.^8,53 Detailed astronomical modeling will be required to assess the balance of reactions of atomic H with PAHs and the UV photolysis in a PDR environment as well as the importance of hydrogenation of PAHs in PDRs for the formation of H₂. The experimental and theoretical results reported here will form the basis for such a modeling effort. We defer this to a follow up study that will be reported in an appropriate journal.

6 Discussion and conclusion

The experimental and theoretical study conducted here has elucidated the steps that will be relevant for the hydrogenation of pentacene. We do stress that the goal of this study is to provide fundamental parameters, as energy barriers and binding energies, useful for astronomical modeling such as Andrews et al. addressed for coronene's family.⁸ In fact, in space, superhydrogenation of PAHs is a balance between H addition and UV photolysis, energy barriers and binding energies will each play their role in setting the hydrogenation pattern of PAHs in space.

Specifically, we found that even hydrogenated species of pentacene are more preferred than the odd hydrogenated species since chemisorbing odd hydrogens on pentacene leads to the formation of reactive open-shell radicals. These extremely reactive species interact with further hydrogen atoms forming preferred species (species with magic numbers seen to dominate the mass spectra). The analysis of binding energies and energy barriers carried out in this study have confirmed the validity of the hypercoordination and coordination rule (discussed in detail in the ESI†), demonstrating that these simple concepts are applicable to small condensed and linear systems. These concepts are validated for systems formed by hexagonal aromatic rings and are applicable during the hydrogenation sequence for all benzene-like structures that still present bipartite lattices. However, we emphasize that these simple concepts are useful tools and can guide the choice of hydrogenation sites, but they cannot replace a deeper analysis of binding energies and energy barriers. Specifically, energy barriers calculation provide insights into the hydrogenation sequence, showing which species are more likely to form. We found that the energy barrier required for hydrogenating an aliphatic carbon is lower (<0.13 eV) than the energy required for hydrogenating aromatic carbons (up to 0.15 eV). Hence, the presence of magic numbers in the mass spectra are explained by the energy barriers rather than the binding energies. In fact, the absence in the mass spectra of the peaks corresponding to the masses of 12H, 14H, 18H and 20H-pentacene was confirmed by our theoretical calculations since a further hydrogenation (11H, 13H, 17H and 19H-pentacene) requires the highest energy barrier, up to 0.16 eV. Our theoretical results also suggest that both anti and syn confirmations are possible in the gas phase. The sequence found for the syn-path in our calculation matches the magic numbers found in the mass spectra for the hydrogenation of pentacene, whereas the anti-path might be more relevant for the hydrogenation sequence that will occur in the gas phase.

Furthermore, we noticed differences in the hydrogenation sequence that occurs in pentacene with respect to pericondensed PAHs such as coronene.²⁴ The hydrogenation scheme tends at first, in these aromatic molecules, to break the aromaticity of the central aromatic ring of pentacene through addition to solo sites. In contrast in coronene, where such sites are not present, this occurs for the aromatic rings located at the edges. Moreover, pentacene is more reactive at the first hydrogenation with a barrier of only 109 meV with respect to coronene.²⁴ As a last difference, coronene has a barrierless reaction for the addition of the last odd hydrogen. Therefore, zigzag edges are significantly more reactive for the first hydrogen addition reaction with respect to pericondensed PAHs.

We also discovered a pathway that leads to the formation of quasi-nanotubular structures during the hydrogenation of pentacene in the gas phase. This is due to the formation of two topologically separated structures in the molecule. The two unpaired electrons located in two different systems cannot be shared any longer. Therefore, a spontaneous curling up of the structure occurs with the formation of a quasi-nanotube.

We discovered that the flexibility of the molecule provides extra structural stability with respect to more rigid molecules as coronene or graphene. Zigzag edges present on linear and flexible molecules may provide extra reactivity that may correlate the presence of H₂ with the formation of superhydrogenated species.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Dr Alessandra Candian, Dr Inge Loes ten Kate, Mirko Leccese and Dr Thanja Lamberts for useful discussions. The CINECA award IPCM under the ISCRA initiative, for the availability of high performance computing resources and support, the financial support from The Danish Council for Independent Research (grant no. 5137-00049B), the European Research Council (CoG GRANN, grant no. 648551), and the E.U. under the Horizon2020 Marie Skłodowska-Curie ITN EUROPAH (grant number 722346).

References

1. A. Candian, J. Zhen and A. G. G. M. Tielens, Phys. Today, 2018, 71, 38–43.
2. A. G. G. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081.
3. E. Rauls and L. Hornekær, Astrophys. J., 2008, 679, 531–536.
4. C. W. Bauschlicher, Jr., Astrophys. J., 1998, 509, L125–L127.
5. J. D. Thrower, B. Jørgensen, E. E. Friis, S. Baouche, V. Menella, A. C. Luntz, M. Andersen, B. Hammer and L. Hornekær, Astrophys. J., 2012, 752, 1–6.
6. V. Menella, L. Hornekær, J. Thrower and M. Accolla, Astrophys. J., Lett., 2012, 745, 1–5.
7. L. Boschman, S. Cazaux, M. Spaans, R. Hoekstra and T. Schlathölter, Astron. Astrophys., 2015, 579, A72.
8. H. Andrews, A. Candian and A. G. G. M. Tielens, Astron. Astrophys., 2016, 595, A23.
9. S. K. Samanta, O. V. Singh and R. K. Jain, Trends Biotechnol., 2002, 20, 243–248.
10. M. J. Jacinto, O. H. C. F. Santos, R. Landers, P. K. Kiyohara and L. M. Rossi, Appl. Catal., B, 2009, 90, 688–692.
11. Y. Segawa and D. W. Stephan, Chem. Commun., 2012, 48, 11963–11965.
12. L. G. Scanlon, P. B. Balbuena, Y. Zhang, G. Sandi, C. K. Back, W. A. Feld, J. Mack, M. A. Rottmayer and J. L. Riepenhoff, J. Phys. Chem. B, 2006, 110, 7688–7694.
13. D. Knipp, R. A. Street, A. Völkel and J. Ho, J. Appl. Phys., 2003, 93, 347–355.
14. J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048.
15. P. Samorí, N. Severin, C. D. Simpson, K. Müllen and J. P. Rabe, J. Am. Chem. Soc., 2002, 124, 9454–9457.
16. W. Pisula, X. Feng and K. Müllen, Chem. Mater., 2011, 23, 554–567.
17. H. F. Bettinger and C. Tönshoff, Chem. Rec., 2015, 15, 364–369.
18. A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
19. F. Salama, E. L. O. Bakes, L. J. Allamandola and A. G. G. M. Tielens, Astrophys. J., 1996, 458, 621–636.
20. S. Hony, C. Van Kerckhoven, E. Peeters, A. G. G. M. Tielens, D. M. Hudgins and L. J. Allamandola, Astron. Astrophys., 2001, 370, 1030–1043.
21. A. Candian and P. J. Sarre, Mon. Not. R. Astron. Soc., 2015, 448, 2960–2970.
22. M. J. Shannon, D. J. Stock and E. Peeters, Astrophys. J., 2016, 824, 111.
23. R. M. Ferullo, C. E. Zubieta and P. G. Belelli, Phys. Chem. Chem. Phys., 2019, 21, 12012–12020.
24. P. A. Jensen, M. Leccese, F. D. S. Simonsen, A. W. Skov, M. Bonfanti, J. D. Thrower, R. Martinazzo and L. Hornekær, Mon. Not. R. Astron. Soc., 2019, 486, 5492–5498.
25. J. A. Rasmussen, J. Phys. Chem. A, 2013, 117, 4279–4285.
26. C. Joblin, A. G. G. M. Tielens, J. D. Thrower, L. Nilsson, B. Jørgensen, S. Baouche, R. Balog, A. C. Luntz, I. Stensgaard, E. Rauls and L. Hornekær, EAS Publ. Ser., 2011, 46, 453–460.
27. D. J. Hollenbach and A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 1997, 35, 179–215.
28. V. Wakelam, E. Bron, S. Cazaux, F. Dulieu, C. Gry, P. Guillard, E. Habart, L. Hornekær, S. Morisset, G. Nyman, V. Pirronello, S. D. Price, V. Valdivia, G. Vidali and N. Watanabe, Mol. Astrophys., 2017, 9, 1–36.
29. E. Habart, F. Boulanger, L. Verstraete, C. M. Walmsley and G. Pineau des Forêts, Astron. Astrophys., 2004, 414, 531–544.
30. A. L. Skov, J. D. Thrower and L. Hornekær, Faraday Discuss., 2014, 168, 223–234.
31. J. A. Rasmussen, G. Henkelman and B. Hammer, J. Chem. Phys., 2011, 134, 164703.
32. S. Cazaux, L. Boschman, N. Rougeau, G. Reitsma, R. Hoekstra, D. Teillet-Billy, S. Morisset, M. Spaans and T. Schlathölter, Sci. Rep., 2016, 6, 1–7.
33. K. Tschersich, J. Appl. Phys., 2000, 87, 2565–2573.
34. M. J. Frisch, G. W. Trucks, H. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. J. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
35. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
36. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085.
37. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
38. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
39. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
40. G. Schaftenaar, E. Vlieg and G. Vriend, J. Comput.-Aided Mol. Des., 2017, 31, 789–800.
41. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
42. M. Bonfanti, S. Casolo, G. F. Tantardini, A. Ponti and R. Martinazzo, J. Chem. Phys., 2011, 135, 164701.
43. R. P. Bell, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429.
44. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24.
45. O. D. Jurchescu, J. Baas and T. T. M. Palstra, Appl. Phys. Lett., 2004, 84, 3061–3063.
46. F. De Angelis, M. Gaspari, A. Procopio, G. Cuda and E. Di Fabrizio, Chem. Phys. Lett., 2009, 468, 193–196.
47. L. B. Roberson, J. Kowalik, L. M. Tolbert, C. Kloc, R. Zeis, X. Chi, R. Fleming and C. Wilkins, J. Am. Chem. Soc., 2005, 127, 3069–3075.
48. B. Klærke, Y. Toker, D. B. Rahbek, L. Hornekær and L. H. Andersen, Astron. Astrophys., 2013, 549, A84.
49. C. Sánchez-Sánchez, J. I. Ignacio Martínez, N. R. del Arbol, P. Ruffieux, R. Roman Fasel, M. F. López, P. L. de Andres and J. A. Martín-Gago, J. Am. Chem. Soc., 2019, 141, 3550–3557.
50. A. Ricca, E. L. O. Bakes and C. W. Bauschlicher, Jr., Astrophys. J., 2007, 659, 858–861.
51. D. J. Hollenbach and A. G. G. M. Tielens, Rev. Mod. Phys., 1999, 71, 173–230.
52. P. Castellanos, A. Candian, J. Zhen, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys., 2018, 616, A166.
53. J. Montillaud, C. Joblin and D. Toublanc, Astron. Astrophys., 2013, 552, A15.
54. V. L. Page, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2009, 704, 274–280.

---

Footnote

† Electronic supplementary information (ESI) available: Sequence analysis of the hydrogenation of pentacene. Crossover temperatures and Cartesian coordinates of the optimized geometries of minima and transition states of the hydrogenation of syn and anti-nH-pentacene. See DOI: 10.1039/c9cp05440e

---