p-Type conductivity mechanism and defect structure of nitrogen-doped LiNbO3 from first-principles calculations†
Weiwei
Wang
a,
Yang
Zhong
a,
Dahuai
Zheng
 b,
Hongde
Liu
b,
Hongde
Liu
 *a,
Yongfa
Kong
*ab,
Lixin
Zhang
a,
Rupp
Romano
cd and
Jingjun
Xu
*ab
*a,
Yongfa
Kong
*ab,
Lixin
Zhang
a,
Rupp
Romano
cd and
Jingjun
Xu
*ab
aMOE Key Laboratory of Weak-Light Nonlinear Photonics and School of Physics, Nankai University, Tianjin 300071, China. E-mail: liuhd97@nankai.edu.cn; kongyf@nankai.edu.cn; jjxu@nankai.edu.cn
bTEDA Institute of Applied Physics, Nankai University, Tianjin 300457, China
cFaculty of Physics, Vienna University, Wien, A-1090, Austria
dDepartment of Complex Matter, Jozef Stefan Institute, Ljubljana, Slovenia
First published on 25th October 2019
Abstract
Most metal-doped lithium niobates (LiNbO3, LN) exhibit n-type conductivity. The absence of p-type conductive LiNbO3 limits its application. Based on the finding that p-type conductive LiNbO3 can be realized by doping with a non-metallic element N, we investigate the most stable defect configurations and formation energies of LiNbO3 doped with non-metal nitrogen (LN:N) by first-principles calculations. Nitrogen substitution, interstitial and quasi-substitution point defects in different sites and their effects were explored. The results show that N prefers to occupy the oxygen site with only little lattice distortion. Ab initio molecular dynamics (AIMD) simulations confirm the structural stability of an N ion occupying the O site. The charge-state transition level ε(0/−1) slightly above the valence band maximum (VBM) indicates that N point defects would contribute to p-type conductivity of LiNbO3. The analysis of the band structure reveals that the partially filled impurity levels can accommodate electrons that jump from valence bands and result in holes to become the main charge carriers. The calculation not only explains the occurrence of p-type conductivity in LN:N but also provides a simple and efficient way to discover p-type conductive candidates in numerous doped LiNbO3 crystals.
Introduction
Lithium niobate (LiNbO3, LN) is considered as one of the promising platforms for integrated photonics.1,2 Many photonic devices, such as waveguides, couplers, wavelength converters, and electro-optical modulators, have been fabricated with LN in the past few decades.3–10 However, the aforementioned devices are passive components and the absence of p-type conductive LN limits its application in active components. Various methods, such as irradiation by ultraviolet light and strong doping with various optical damage resistant ions have been tried, but the photoinduced hole carrier concentration is too low to be detected by the Hall effect. Thermoelectric oxidation to achieve p-type LN is also hard to realize due to heavy out-diffusion of lithium.11–15 Anyhow, it remains a great challenge to fabricate stable p-type LN of high quality. Recently, Li et al. have successfully fabricated a p-type LN film on a Si substrate by doping with nitrogen atoms,16 thus introducing non-metallic doping in LN, and promoting the fabrication of integrated devices based on LN thin films. However, the origin of p-type conductivity and the defect structures in LiNbO3 doped with non-metal nitrogen (LN:N) are not clear yet.As we know, many efforts have been devoted to the theoretical calculation of LN to explain some experimental phenomena and to provide a predictive guidance for the experiments in the past few years.17–20 Most of these computational studies concentrated on the replacement of Li or Nb cations in doped LN. Xu et al. reported the structures, energies and site preferences of Er defects in LiNbO3.19 And according to the report of Li et al., non-photorefractive ions generally prefer the Li site.18 Despite the cationic dopants being different from each other, all of them resulted in n-type conductivity.18–20 Little attention was paid to the relationship between the conductivity type and dopants. For non-metallic dopants, there is no relevant report to show their site occupation in LN, and the exploration of its impact on the properties of the non-metallic doped LN.
Non-metallic dopants have also played an important role in improving the properties of compounds. For example, graphene doped with nitrogen can open the band gap from zero, change the electronic structure of graphene and improve the free carrier density of graphene.21,22 The N element also plays a role in improving the band structure of titanium dioxide metal compounds.23,24 Due to the distinctive p-type conductivity performance of LN:N it is of importance to explore its p-type conductivity mechanism and its defect structure.
In this paper, employing first-principles calculations, we investigate the formation energies of nitrogen point defects: substitution of anions, N as interstitials and quasi-substitutions. The local atomic relaxations and their effects on the electronic structure of each defect are explored. The charge states of N dopants corresponding to the analysis of the band structure are also examined. The interaction between the dopants and the inherent atoms has also been studied. Finally, we discuss the p-type conductivity mechanism of LN:N through an analysis of the electronic properties.
Method
The Vienna ab initio Simulation Package (VASP) is employed to perform the density functional theory (DFT) calculation.25,26 The results are obtained from the projector-augmented-wave (PAW) formalism.27–29 Based on the standard PAW method, the Li 2s1, Nb 4p64d45s1, O 2s22p4, and N 2s22p3 states are treated as valence electrons. The wave functions are expanded in a plane wave basis set with a cutoff energy of 400 eV. The force convergence criterion to optimize the structure is set as 0.01 eV Å−1. The hexagonal supercells containing 120 atoms with a 4 × 4 × 4 k-points mesh are employed in the calculations of the charge state energies of the N substitution and interstitial point defects within the density functional theory-generalized gradient approximation (DFT-GGA). The Perdew–Burke–Ernzerhof (PBE) functional is used to model the electron exchange–correlation energy within the GGA.29 The atomic concentration of nitrogen is 0.83% to simulate the experimental results where the concentration is 0.87% as obtained from X-ray Photoelectron Spectroscopy (XPS).16 A larger supercell containing 240 atoms is used to simulate substitution, interstitial and quasi-substitution of N point defects and defect complexes with intrinsic defects. The hexagonal supercell employed here is a = b = 10.308 Å, c = 27.754 Å, in which the length of the c-axis is more than twice the length of the a and b axis; thereby, a 2 × 2 × 1 k-point mesh over the Brillouin zone with half the number of k points in the z direction (c axis) as in x and y directions generated by the Monkhorst–Pack scheme is employed.30 The usually used local functional underestimates the band gap of the semiconductors. Thus the Heyd–Scuseria–Ernzerhof (HSE06) screened hybrid functional was implemented in the electronic structure calculations.31,32 Although the band gaps calculated with DFT-PBE and HSE06 are 3.28 eV and 4.74 eV, respectively, the positions of the defect levels related to the VBM are nearly the same. Therefore, the partial density of states of N substituting O atoms with intrinsic defect clusters are calculated using DFT-PBE to reflect the main characters of the electronic structures. The test on the pseudopotential selection for the atom Nb and the dispersion effect can be found in the ESI.†Defect formation energy (DFE) is related to the difficulty of forming defect clusters, and a lower formation energy corresponds to a more stable defect complex.33 The DFEs of different point defects and defect complexes are calculated to explore the most stable defect complex formed in LN:N. The DFE of defect complex X with charge q is calculated using34,35
 | (1) |
 | (2) |
 | (3) |
 | (4) |
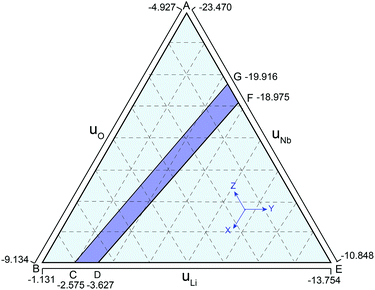
Bringing all the stability criteria together, we plotted the thermodynamically stable region of the LN in Fig. 1 according to the method in ref. 36 and 37. As shown in Fig. 1, the purple region CDFG is an area that meets the limitation of the equilibrium equation of lithium oxide, niobium oxide, and LN, and the line DF shows the Nb-rich condition while the line CG represents the Li-rich condition. Since the as-grown crystals and films are Li-deficient compositions, the chemical potentials of Nb and Li are chosen according to the line DF.36,37 The chemical potential of N atoms is assumed to be half of that of N2 (gas). The chemical potentials of Nb, Li, O and N elements are listed in Table 1. Similar results have been reported by other researchers.33,37
| Condition | Atom species | Chemical potential (eV) |
|---|---|---|
| Li-Deficient | Li | −3.63 |
| Nb | −18.96 | |
| O | −5.59 | |
| N | −8.33 |
Due to the total internal energies obtained from DFT calculations corresponding to the Helmholtz free energy at zero temperature, there is a difference between the VASP work environment and real conditions. Therefore, the free energy (F = E − TS) should be taken into account. Strain effects can be considered ignorable in the large supercell, and electronic entropy is negligible due to the large band gap of LiNbO3, too. The free energy is mainly related to the entropy which is related to the configuration contributions of point defects and defect clusters. Boltzmann's entropy can be calculated using17,37,38
S = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W W | (5) |
The ab initio molecular dynamic (AIMD) simulation with a canonical ensemble is performed by using the Nóse algorithm. The temperature of the system is maintained at 300 K.39 The 240-atom supercell with the Γ point is implemented here in the whole AIMD calculation. The time step is 1.0 fs and the total simulation time is 10.0 ps.
Results and discussion
Point defects of LN:N
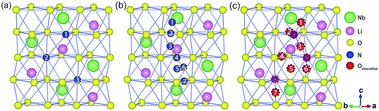
As N is adjacent to O in the periodic table, they have many similarities in physical and chemical properties, such as the size of atoms, the electronic affinity, and the chemical valence state. This suggests that N may substitute O sites and plays a similar role to O by forming N substitutional or the quasi-substitutional point defects. On the other hand, the atomic radius of N is much smaller than those of Li and Nb, and thus N may exist as interstitial atoms. In LN crystals, the O atoms form three different kinds of octahedron structures: a Li-centered octahedron, an Nb-centered octahedron, and a hollow octahedron. In Fig. 2, three isolated sites of point defects around these three oxygen octahedra are shown: the substitutional N (Fig. 2(a)), the interstitial N (Fig. 2(b)), and the quasi-substitutional N (Fig. 2(c)).40,41As shown in Fig. 2(a), numbers 1–3 present three different O sites that can be substituted by N (marked as NO) corresponding to the three different oxygen octahedron. The DFEs of the three NO point defect models are 5.64, 5.64 and 5.63 eV, respectively, showing a weak difference. This indicates that there is no obvious difference in the position of NO point defects, and the structure of NO point defects is fairly stable. The models for N as an interstitial (named as Ni) are shown in Fig. 2(b). Due to the limitation of the N atomic size, the possible interstitial sites distribute between two different O atoms in the same layer (labeled as 2, 4, 7 in Fig. 2(b)) or different O layers (labeled as 1, 3, 6 in Fig. 2(b)), and N interstitials can also exist at the center of oxygen octahedron, for example, number 5 in Fig. 2(b). The formation energies change significantly: the lowest formation energy is 4.68 eV. The most stable structure corresponds to the model where Ni lies between O atoms and it is close to the O hollow octahedron. The results show that there may be a positional priority for Ni point defects. With N as quasi-substitutions (Nq), N occupies the normal site of the O, while the original O atom becomes an interstitial at the same time. In Fig. 2(c), the different combinations of the N substitution and O interstitial are displayed. The distribution of O interstitials is the same as that of N interstitials. For comparison, the example where an O interstitial is far away from the N substitution is given in Table 2. Fig. 2(c) and Table 2 show that the formation energies of Nq point defects change significantly. The case of N as quasi-substitution usually comes along with strong lattice distortions that will seriously destroy the lattice structure of LiNbO3. Therefore, it is difficult to form N quasi-substitutions in the crystals. As seen from the formation energies, N lying in the specific location as an interstitial point defect has the lowest formation energy, while the distribution of NO is the most stable.
| Model | Substitutional | Interstitial | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ① | ② | ③ | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | |
| Formation energy (eV) | 5.75 | 5.75 | 5.74 | 5.16 | 5.81 | 7.26 | 5.71 | 7.53 | 4.79 | 10.82 |
| Quasi-substitutional | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | A + ① | A + ② | A + ③ | B + ③ | B + ④ | B + ⑥ | C + ⑤ | C + ⑦ | C + far away |
| Formation energy (eV) | 5.16 | 7.52 | 5.20 | 5.16 | 7.68 | 5.21 | 5.24 | 5.20 | 9.71 |
Besides knowing their formation energies, it is also important to know how N point defects influence the crystal lattice. The knowledge of the lattice distortion around point defects greatly contributes to the understanding of their interaction with inherent atoms. The local structures of point defect NO before and after structure relaxation are shown in Fig. 3(a) and (b), respectively. As shown in Fig. 3(b), NO defects cause only a quite slight local distortion of the LN lattice. In detail, the distances from the upper O layer decrease while the distances from the lower O layer increase. The largest distortion is only 1.15% compared to that in the pristine crystals. In addition to the change in the distances of O atoms between different layers, the distances between the same layers of O atoms are increased, which indicates an increase of the O octahedral volume. As a whole, NO point defects are fairly stable. This fact can be ascribed to the similarity between N and O atoms.
Fig. 3(c) and (d), clearly show the lattice relaxation of Ni point defects. In Fig. 3(d), the Ni point defect moves against the z-direction due to the ferroelectric distortion and the distance between Ni and the nearest-neighboring O atoms along the z-direction increases. Due to the Coulomb repulsion of the electrons around N and O atoms, the O plane undergoes serious changes, in which some O atoms get out of the original O plane. Compared with lattice distortions of NO, Ni point defects have a stronger influence. This effect on the lattice structure is mainly reflected in the influence of O atoms, which means the influence on crystal electronic properties. We ignore the situation of Nq because of its strong distortion of the lattice structure.
Based on the above analysis, NO defects are superior to interstitial and quasi-substitution point defects because of their lower and more stable formation energies, and substitutions have the least influence on LN crystals compared with the other two forms of point defects. The charge states of the NO and Ni point defects are studied further to investigate their changes.
AIMD simulations were done to investigate the stability of the NO defect structure. On the basis of first-principles calculations and AIMD simulation, Fig. 4 shows the stability of the NO defect structure at a temperature of 300 K. The oscillation of energy (red line) tends to be stable, and the similarity of the two structures before and after 10 ps AIMD simulation indicates that it is fairly suitable for N ions to substitute O atoms.
 | ||
| Fig. 4 Total energy fluctuation during AIMD simulations of LN:N at a temperature of 300 K. The structural snapshots of the LN:N crystal at times of 0 and 10 ps during AIMD simulation. | ||
Charge states of N point defects
Differently from metal dopants replacing Nb or Li ions with a positive charge state, N prefers to occupy O atoms or to be an isolated interstitial. The charge states of the further two possible point defects NO and Ni were explored, too. Fig. 5 shows the formation energies of NO and Ni point defects in all charge states at the most stable charge states. We can find that the charge states of the point defects vary with the increase of the Fermi energy from the VBM towards the CBM, a range that corresponds to the band gap of LN with an experimental value of 3.8 eV.42,43 This value is somewhat larger than the calculated result of 3.28 eV, but the difference is in allowable error scope.44,45 The multiple charge states of the point defects NO and Ni indicate that they can form acceptors in LN crystals.In general, the formation energy of the point defect NO is lower than that of point defect Ni throughout the whole Fermi energy range. Therefore, the existence of NO is more plausible. Due to the limitation of the doping concentration, the concentration of the Ni point defect can be considered negligible. The transition levels ε(q1/q2) are defined as the points q1 and q2 where the formation energy and Fermi energy become equal.
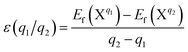 | (6) |
Defect clusters
In the growth process of LN, the preparation conditions result in a large number of intrinsic point defects and defect complexes. Under Nb2O5 rich conditions, intrinsic defect niobium antisite (NbLi4+) is supposed to be considered, and it is usually compensated by four lithium vacancies (VLi−) to maintain a neutral environment in LN crystals.47,48 In LN:N, NbLi4+ can also be complemented by point defects NO−. Table 3 lists the different clustering patterns, in which NbLi4+ co-exists with VLi− and NO−. Similar to point defects, the defect formation energy is the main criterion considered here to indicate structural stability.| Clusters | The formation energy (eV per defect) |
|---|---|
| NbLi4+ + 4VLi− | 2.60 |
| NbLi4+ + 3VLi− + 1NO− | 2.95 |
| NbLi4+ + 2VLi− + 2NO− | 3.46 |
| NbLi4+ + VLi− + 3NO− | 3.94 |
| NbLi4+ + 4NO− | 4.35 |
The formation energy of the intrinsic defect cluster NbLi4+ + VLi− is 2.60 eV, remaining to be the most stable defect cluster compared with the defect clusters including the N point defects. With the increase of NO− and the decrease of VLi−, the formation energy becomes higher and higher, indicating a more unstable structure. The results show that it is difficult for N dopants to form a defect cluster with intrinsic defects, and N dopants cannot improve the situation of lithium deficiency.
Corresponding to the defect clusters above, the partial density of states (PDOSs) of the main single atomic states including O 2p, Nb 4d, and N 2p that can reflect the contributions of different atoms in electron density are shown in Fig. 6. Based on the PDOS, we can discriminate whether LN contains only intrinsic defects or also N point defects. The magnified area shows that the introduction of N atoms not only leads to the formation of the new energy level in the band gap, but also causes a strong interaction between N 2p and O 2p electrons. Most N 2p electrons and some O 2p electrons contribute to the defect energy level. With the increase in the number of N point defects, some 4d electrons of Nb ions take part in the formation of defect levels that get closer and closer to the bottom of the conduction band. Although the area of defect levels expands, there is not much overlap between these defect levels as O atoms. This may indicate a preference for isolated N point defects.
Based on the defect formation energies and PDOS analysis, we found that N point defects do not form so easily defect clusters with intrinsic defects or other N point defects. As we know, the formation of defect clusters has a close relationship with the concentration of N atoms, and the results provide an answer to the question why it is difficult to introduce N atoms into LN and why N dopants were experimentally observed to maintain at a relatively low concentration.
Mechanism of p-type conductivity in LN:N
N ions have significantly improved the properties of LN, and its most distinctive property is p-type conductivity, which will now be explored. In the part above analyzing the charge state of N point defects, the charge state transition of the N point defect from 0 to −1 already indicates that the conductive type of LN:N is p-type. In order to find out the mechanism of p-type conductivity, we study the band structure and the PDOS of LN:N in Fig. 7(a) and (b). In the band structure of LN:N, the bandgap is about 4.74 eV. The new energy level in the band gap is 3.75 eV away from the bottom of the conduction band.The new energy level displays an important role in improving the proprieties of LN. Seen from the PDOS, we can find that the contribution of N 2p electrons and O 2p electrons to the defect level of LN:N is almost the same. The interaction between N 2p and O 2p electrons is obvious. N ions influence the electronic distribution of the valence band, especially the electrons near the VBM, and the electrons of N enhance the activity of valence electrons. The existence of new energy levels is associated with the electronic transition in LN:N. The defect levels are approximately 0.39 eV above the VBM, which provides an opportunity for the O 2p electrons to transfer from the valence band with little energy which can easily be obtained from thermal activation. The result of the valence band electron transition leaves a large number of holes as the main carriers for LN:N. In addition, the occupation of defect energy levels has been explored. The occupation states of the valence band and the conduction band are 2 and 0, thus representing the full occupation state and the empty occupation state, respectively. In the band structure, we can clearly see that there are two energy lines. The occupation of the upper one changes from 0.27 to 1.95, and the other does not also have a fully occupied energy level either. Obviously, the holes in the energy level have a good chance to be thermally activated from the valence band.
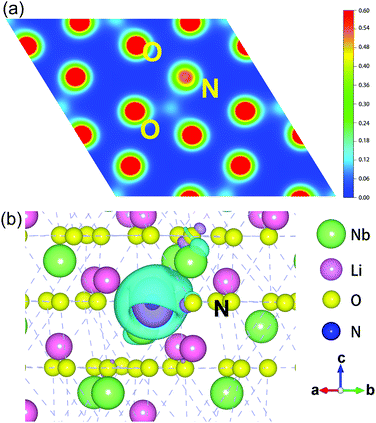
Based on the analysis above, we infer that N dopants have a strong influence on the distribution of electrons in LN:N. Therefore, the electronic transformation of NO point defects has been studied. The charge density distributions of an O plane that include N atoms and the electronic charge difference49 between the LN:N and pristine system are given in Fig. 8.
For the NO point defect, N takes the responsibility of the O atom as an electron-withdrawing center. In a sense, NO guarantees the basic charge-transfer in crystals. Fig. 8(a) shows that there is an electron cloud gathering around NO, but it is smaller than the charge density of O atoms. Hence, compared with normal O sites, there is a clear depletion in the O site occupied by N. This is consistent with the conclusion we obtained above that the N point defect shows a −1 charge state. As shown in Fig. 8(b), the yellow ellipsoid around N ions presents the electron depletion compared to the original O site. While the yellow area is surrounded by a blue ellipsoid, it indicates aggregation of electrons between N and O atoms, which enables easy formation of covalent bonds.
In general, the charge density and the electronic charge difference prove the electronic interaction between N and O atoms and confirm that N plays a similar role to O with a negative charge state. Therefore, some of the O 2p electrons have the chance to transit from the valence band to the defect levels, leaving holes in the valence band as the main carriers.
Conclusions
In summary, we have performed the detailed first-principles calculations exploring the possible site preferences of isolated defects and their corresponding charge state in LN:N. We discussed the mechanism leading to p-type conductivity in LN:N based on the analysis of its band structure and of the density of states. The formation energy calculation indicates that the most plausible structure to be formed is N occupying the site of O with only a tiny lattice distortion. In addition, N as the isolated point defect is more reasonable in LN:N for lower formation energies. We found that the transition level ε(0/−1) is near the VBM, which proves that LN:N is a candidate p-type material, and the analysis of the band structure confirms that the defect energy level is close to the VBM. This leads to p-type conductivity in LN:N. Owing to the electron overlap of N and O atoms, the defect level includes a contribution of O. Therefore not all occupation states can be thermally activated from the valence band electrons, leaving a large number of positive holes in the valence band. These are then the dominant charge carriers. N doping opens a reliable pathway for producing LN crystals with p-type conductivity, which may find important applications in integrated optics. Our study on N-doped LN presents a powerful example on how to discover good candidates for p-type conductivity in LN among yet unknown dopants.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge financial support from the National Natural Science Foundation of China with grant number [11674179] and [61705116], and the Program for Changjiang Scholars and the Innovative Research Team in University with grant number [IRT_13R29], and the Slovenian research agency (ARRS, grant P1-0192).References
- M. Zhang, C. Wang, R. Cheng, A. Shams-Ansari and M. Lončar, Optica, 2017, 4, 1536 CrossRef CAS.
- A. Guarino, G. Poberaj, D. Rezzonico, R. Degl'Innocenti and P. Guenter, Nat. Photonics, 2007, 1, 407 CrossRef CAS.
- Y. Park, B. Min, K. J. Vahala and H. A. Atwater, Adv. Mater., 2006, 18, 1533 CrossRef CAS.
- M. F. Volk, S. Suntsov, C. E. Rüter and D. Kip, Opt. Express, 2016, 24, 1386 CrossRef CAS.
- R. Wu, J. Zhang, N. Yao, W. Fang, L. Qiao, Z. Chai, J. Lin and Y. Cheng, Opt. Lett., 2018, 43, 4116 CrossRef CAS.
- Z. Chen, Y. Wang, Y. Jiang, R. Kong and H. Hu, Opt. Mater., 2017, 72, 136 CrossRef CAS.
- C. Wang, M. Zhang, X. Chen, M. Bertrand, A. Shams-Ansari, S. Chandrasekhar, P. Winzer and M. Lončar, Nature, 2018, 562, 101 CrossRef CAS.
- R. Wolf, Y. Jia, S. Bonaus, C. S. Werner, S. J. Herr, I. Breunig, K. Buse and H. Zappe, Optica, 2018, 5, 872 CrossRef.
- A. Ashkin, G. D. Boyd, J. M. Dziedzic, R. G. Smith, A. A. Ballman, J. J. Levinstein and K. Nassau, Appl. Phys. Lett., 1966, 9, 72 CrossRef CAS.
- C. Wang, M. Zhang, B. Stern, M. Lipson and M. Lončar, Opt. Express, 2018, 26, 1547 CrossRef CAS.
- D. L. Staebler and J. J. Amodei, J. Appl. Phys., 1972, 43, 1042 CrossRef CAS.
- Y. Kong, S. Wu, S. Liu, S. Chen and J. Xu, Appl. Phys. Lett., 2008, 92, 251107 CrossRef.
- F. Liu, Y. Kong, W. Li, H. Liu, S. Liu, S. Chen, X. Zhang, R. Rupp and J. Xu, Opt. Lett., 2010, 35, 10 CrossRef CAS.
- J. Deng, J. Wen, Z. Wu and H. Wang, Appl. Phys. Lett., 1994, 64, 2622 CrossRef CAS.
- Z. Pei, Q. Hu, Y. Kong, S. Liu, S. Chen and J. Xu, AIP Adv., 2011, 1, 032171 CrossRef.
- W. Li, J. Cui, W. Wang, D. Zheng, L. Jia, S. Saeed, H. Liu, R. Rupp, Y. Kong and J. Xu, Materials, 2019, 12, 819 CrossRef.
- A. F. Kohan, G. Ceder, D. Morgan and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 15019 CrossRef CAS.
- L. Li, Y. Li and X. Zhao, Phys. Chem. Chem. Phys., 2018, 20, 17477 RSC.
- H. Xu, D. Lee, S. B. Sinnott, V. Gopalan, V. Dierolf and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 144104 CrossRef.
- F. Bridges, C. Mackeen and L. Kovács, Phys. Rev. B, 2016, 94, 014101 CrossRef.
- D. Wei, Y. Liu, Y. Wang, H. Zhang, L. Huang and G. Yu, Nano Lett., 2016, 9, 1752 CrossRef.
- C. Zhou, J. Kong, E. Yenilmez and H. Dai, Science, 2000, 290, 1552 CrossRef CAS.
- R. Asahi, T. Mikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269 CrossRef CAS.
- M. Batzill, E. H. Morales and U. Diebold, Phys. Rev. Lett., 2006, 96, 026103 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393 CrossRef CAS.
- Q. Li, B. Wang, C. H. Woo, H. Wang and R. Wang, J. Phys. Chem. Solids, 2007, 68, 1336 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- H. Xu, A. Chernatynskiy, D. Lee, S. B. Sinnott, V. Gopalan, V. Dierolf and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 184109 CrossRef.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- H. Xu, D. Lee, J. He, S. B. Sinnott, V. Gopalan, V. Dierolf and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174103 CrossRef.
- Y. Li, W. G. Schmidt and S. Sanna, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094111 CrossRef.
- J. He, R. K. Behera, M. W. Finnis, X. Li, E. C. Dickey, S. R. Phillpot and S. B. Sinnott, Acta Mater., 2007, 55, 4325 CrossRef CAS.
- D. Bucher, L. C. T. Pierce, J. A. McCammon and P. R. L. Markwick, J. Chem. Theory Comput., 2011, 7, 890 CrossRef CAS.
- Y. Bar-Yam and J. D. Joannopoulos, Phys. Rev. Lett., 1984, 52, 1129 CrossRef CAS.
- R. Car, P. Kelly and A. Oshiyama, Phys. Rev. Lett., 1984, 52, 1814 CrossRef CAS.
- D. Redfield and W. J. Burke, J. Appl. Phys., 1974, 45, 4566 CrossRef CAS.
- A. Dhar and A. Mansingh, J. Appl. Phys., 1990, 68, 5804 CrossRef CAS.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 1985, 55, 1418 CrossRef CAS.
- R. W. Godby, M. Schlüter and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10159 CrossRef.
- P. Rinke, A. Janotti, M. Scheffler and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 026402 CrossRef.
- D. M. Smyth, Prog. Solid State Chem., 1984, 15, 145 CrossRef CAS.
- H. Donnerberg, S. M. Tomlinson, C. R. A. Catlow and O. F. Schirmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 11909 CrossRef CAS.
- X. Li and S. Li, J. Mater. Chem. C, 2019, 7, 1630 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05019a |
| This journal is © the Owner Societies 2020 |