Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
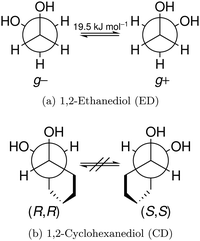
The reduced cohesion of homoconfigurational 1,2-diols†
Beppo
Hartwig
 a,
Manuel
Lange
a,
Anja
Poblotzki
a,
Robert
Medel
a,
Manuel
Lange
a,
Anja
Poblotzki
a,
Robert
Medel
 a,
Anne
Zehnacker
a,
Anne
Zehnacker
 b and
Martin A.
Suhm
b and
Martin A.
Suhm
 *a
*a
aInstitut für Physikalische Chemie, Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: msuhm@gwdg.de
bInstitut des Sciences Moléculaires d'Orsay, CNRS, Université Paris-Sud, Université Paris-Saclay, Orsay, France
First published on 12th December 2019
Abstract
By a combination of linear FTIR and Raman jet spectroscopy, racemic trans-1,2-cyclohexanediol is shown to form an energetically unrivalled S4-symmetric heterochiral dimer in close analogy to 1,2-ethanediol. Analogous experiments with enantiopure trans-1,2-cyclohexanediol reveal the spectral signature of at least three unsymmetric homochiral dimers. A comparison to signal-enhanced spectra of 1,2-ethanediol and to calculations uncovers at least three transiently homochiral dimer contributions as well. In few of these dimer structures, the intramolecular OH⋯O contact present in monomeric 1,2-diols survives, despite the kinetic control in supersonic jet expansions. This provides further insights into the dimerisation mechanism of conformationally semi-flexible molecules in supersonic jets. Racemisation upon dimerisation is shown to be largely quenched under jet cooling conditions, whereas it should be strongly energy-driven at higher temperatures. The pronounced energetic preference for heterochiral aggregation of vicinal diols is also discussed in the context of chirality-induced spin selectivity.
1 Introduction
Most complex molecules are chiral and when they dimerise via non-covalent interactions, the relative chirality of the two monomers matters.1 For small, weakly interacting molecules, this phenomenon of chirality recognition2 is usually quite subtle, typically amounting to less than 10% of the total binding energy. It has recently been argued that there is a fundamental energetical contribution with preference for homochiral pairings in the contact area between the molecules due to chirality-induced spin selectivity (CISS),3 although the size of this effect remains quite uncertain4 and it has not been detected unambiguously in the gas phase, so far.5 It is therefore questionable whether this systematic effect will distort the otherwise expected more or less random preference for homo- or heterochiral aggregation due to the individual interplay of electrostatic, induction, dispersion and Pauli forces for different molecules. We note that empirical evidence at the level of macroscopic crystals actually points to an opposite preference for heterochiral assemblies,6 although perhaps not as pronounced as previously thought.7 On the theoretical side, it is not clear which level of quantum chemistry is needed to capture the CISS effect accurately, whereas it is believed that the interaction will not be contained in typical mechanical force fields.4 In this context, and more generally towards a better understanding of chirality recognition phenomena, the aggregation of axially chiral 1,2-diols via conventional hydrogen bonds is of particular interest, because they offer a multitude of directional intermolecular hydrogen bond patterns. This can have interesting consequences in the solid. E.g., the simplest 1,2-diol, HO–CH2–CH2–OH, crystallises in separate left-handed and right-handed, extended hydrogen-bonded networks,8 although its chirality is only transient in the liquid.In a molecular dimer of 1,2-diols, the limited hydrogen bond pattern is complemented by secondary, less directional London dispersion interactions,9,10 which can be modulated by alkyl substitution next to the C–C bond which connects the two OH groups. In this way, flexible hydrogen bond patterns can be favoured relative to rigid hydrogen bond networks because only the former allow for the co-optimisation of distant secondary interactions. This may lead to subtle intermolecular energy balances11 between different hydrogen bond patterns connecting the two 1,2-diols. Furthermore, alkyl substitution can modulate the barriers between different conformations and thus switch between transient and permanent chirality on different time and temperature scales by an interplay of dispersive and repulsive interactions.9
It has recently been shown computationally12 that there is a strong energetic preference for heterochiral pairing in the simplest representative 1,2-ethanediol (ED), on the order of 20% of the total interaction energy. The cyclic hydrogen bond motif responsible for this stability differs from structural motifs observed in crystalline diols.13 Experimentally, the heterochiral dimer shows a high spectral visibility, when probed by linear infrared and Raman spectroscopy in supersonic jets.12 The homochiral dimer could not be assigned in the spectra at the time and it was speculated that it largely converts into the more stable heterochiral dimer by some bimolecular or perhaps even termolecular relaxation mechanism. This may not be considered surprising for transiently chiral vicinal diols at room temperature, where racemisation barriers can be overcome more easily than in the less fluxional binaphthyl compounds.14 However, in contrast to environmental equilibrium conditions, supersonic jet expansion efficiently suppresses such relaxation processes on its characteristic microsecond timescale,15 once the interconversion barrier exceeds 5–10 kJ mol−1. This is the case in ED and the only way to rationalise the spectral elusiveness of homochiral dimers besides band overlap and low spectral visibility were promotion of torsional relaxation by the dimerisation energy or monomer exchange via transient trimers.12 We note that for the related aminoethanol system with a stronger intramolecular hydrogen bond, a (non-exhaustive) search has identified a homochiral dimer with only two intermolecular hydrogen bonds as the most stable structure, whose IR spectrum is consistent with experiment.16 This contrasts the heterochiral preference in ED dimers.
In this work, we investigate the phenomenon systematically by studying cyclohexane analogues of ED, where the axial chirality of the ED unit can be controlled and homochiral dimers can be enforced. Specifically, trans-1,2-cyclohexanediol (hereafter abbreviated CD) is studied as a racemate and in thermally stable enantiopure form, the latter only enabling homochiral dimers. Fig. 1 illustrates the similarities between ED and CD by showing the Newman projection of the enantiomer pairs. The infrared and Raman results for CD shed new light onto the previous ED case, for which improved spectra are also presented.
CD has been of considerable interest by itself and has been studied previously by X-ray diffraction,17 matrix isolation spectroscopy18 and in more or less inert solvents.18–23 As our work confirms as a side effect (see ESI†), there are substantial spectral shifts induced by such environments.24 Furthermore, the energy sequence between cyclic and open intermolecular hydrogen bond patterns is likely to change by adding a solvent or matrix enclosure which can act as a hydrogen bond acceptor. While matrix isolation can be powerful for the study of intramolecular diastereoisomerism,25 the present work addresses more subtle intermolecular diastereoisomerism. Therefore it is essential to study these diols in the low temperature gas phase for the best match between theory and experiment. This is ambitious, because CD has no easily accessible UV chromophore for double resonance studies26,27 and its preferred dimer has a negligible dipole moment, thus counteracting microwave studies.28,29 Its solid state properties have been nicely summarised before.17 There is evidence for a higher stability and thus lower volatility of the racemic crystal, but also of polymorphism, which has to be kept in mind when comparing jet expansions from heated samples.
Technical improvements of linear vibrational spectroscopy techniques are important because the rarefied gas flows in a supersonic expansion require a high detection sensitivity, which is difficult to achieve for FTIR spectroscopy with incoherent light sources or for spontaneous Raman scattering. Furthermore, large molecules have limited volatility, which must be overcome by heating the gas flow and expansion nozzle. There are several successful realisations of heatable slit nozzles30 in infrared absorption spectroscopy, initially in combination with narrow-band laser sources.31,32 More recently, jet FTIR spectroscopy has also been combined with nozzle heating.33–36 Our own heatable jet-FTIR setup12,37,38 was previously restricted to short double-slit nozzles with a limited column density of molecular clusters. This limitation is overcome in the present study.
2 Experimental techniques
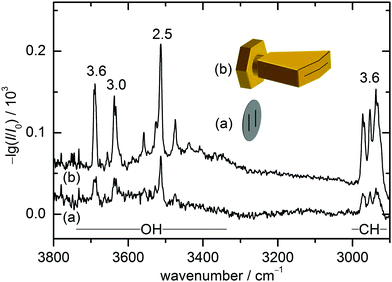
The present combination of FTIR and Raman slit jet spectroscopy is similar to those used for the identification of alcohol clusters39 or amide trimers,40 the latter making use of a heated Raman setup. The lower volatility of ED and in particular of CD species requires a heated sample chamber and nozzle for the FTIR spectroscopy as well. This was previously realised by a short double-slit nozzle probed perpendicular to the central jet flow plane.12,37 Two new concepts to increase the optical pathlength for heated nozzles in FTIR spectroscopy are explored in this work. Both involve the use of a wedged pre-expansion chamber which matches the focused IR beam profile. In one case, the established concept of flowing a pre-heated gas pulse through a poppet-enclosed stationary sample reservoir (popcorn-jet37) is kept. However, the flow is now redirected through a fan-like pre-expansion channel. In the other case, applicable only to liquid samples like ED, a small amount of the liquid sample is injected through a high pressure valve into the heated pre-expansion chamber where it is picked up by a pulse of turbulent carrier gas flow.As this is the first detailed report on the two new FTIR nozzle variants, some technical aspects are discussed (see also Table S2.1 in the ESI† for detailed differences in the experiments). In the first variant, the previously used double-slit nozzle plate is replaced by an individually heatable nozzle attachment. Thereby, an additional temperature control stage is introduced to the setup design, which provides a further variable to tune the cluster formation in the supersonic expansion. The nozzle geometry is changed from a double 0.5 mm × 10 mm slit (with slits 10 mm apart)12 to a single 0.2 mm × 60 mm slit with an angle of 162° to fit the approximate shape of the FTIR beam (V-nozzle). The gas pulse is synchronised such that the opening time (316 ms) coincides with one scan of a Bruker IFS 66 v/S spectrometer (double-sided-fast-return mode). For the V-nozzle the opening time has been shortened (200 ms) such that the valves are open only during the interferogram recording time for a more efficient substance use. Additionally, the opening pressure of the downstream poppet valve has been reduced from 10 psi to 5 psi. The signal enhancement by these changes can be seen in Fig. 2 for ED expansions in helium together with cartoons of the slit geometries. Although the spectrum recorded with the old design (a) contains a higher compound concentration due to a higher sample chamber temperature, the path length enhancement of the new design (b) still leads to a more than threefold higher total column density, recognisable for the aggregation-insensitive CH stretching bands. This is reproduced for the OH stretching bands of the monomer, which dominates both expansions. For the more IR-visible dimer, the column density enhancement from (a) to (b) is somewhat less due to the higher dilution in (b). That is actually welcome because it provides a better suppression of the unwanted larger cluster background. Therefore, the spectrum from the V-nozzle design variant of the popcorn-jet (b) is much improved and supports the present detection of homochiral dimers considerably.
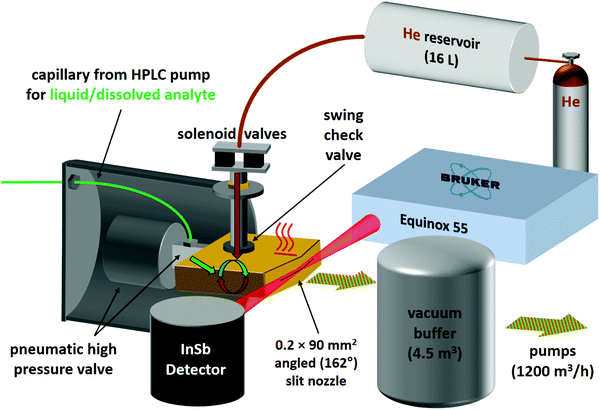
For the second variant, nicknamed risotto-jet (rapid injection of solutions into a turbulent flow oven), a scheme is shown in Fig. 3. The liquid sample is pressurised with an HPLC pump to 90 bar and a small amount (estimated to be in the single-digit microlitre range) is rapidly injected through a capillary with 0.18 mm internal diameter and a pneumatic high pressure valve (60 ms opening time) into a heated (200 °C) evacuated flow oven, where it is vaporised. At the end of the injection the vapour is picked up by a pulse of the carrier gas, coming from a 16 L reservoir at 800 mbar through twin solenoid valves and a swing check valve, the latter preventing the vapour from entering non-heated parts of the setup. The mixture is expanded through a symmetrically wedged 0.2 mm × 90 mm slit nozzle into vacuum. The supersonic jet is probed by a 62 ms scan of a Bruker Equinox 55 spectrometer (single-sided-fast-return mode) and the wedged nozzle allows for a close approach to the focused beam profile. By tuning the double synchronisation between droplet injection, carrier gas pulse and interferometer scan, different concentrations in the expansion can be probed for the same temperature settings. The spectral resolution is currently limited to 3.5 cm−1 to reduce the effect of mechanical vibrations.
As illustrated in Fig. S4.1 in the ESI,† for ED, the risotto-jet setup is already capable of providing spectra of comparable quality as the previous popcorn jet design with a short double slit nozzle, despite a smaller stagnation pressure and a higher nozzle temperature. Significant potential for improvement remains due to the longer slit length, but this potential is currently restricted due to limitations of the employed spectrometer with less IR throughput than the popcorn-jet spectrometer, the mechanical vibrations associated with the liquid injection and turbulent gas mixture, and the size of the temporal window which offers the best mixing ratio. Once these limitations are overcome, the risotto-jet offers the possibility to study binary liquid solutions with different volatility of the components because full evaporation allows for complete control of the gas phase composition. This is currently not the case for the popcorn-jet, where the gas phase mixing ratio is proportional to the partial vapour pressure of the components, because the solid or liquid components are enclosed in a common heated reservoir. Therefore, the risotto-jet setup has the potential to directly reveal solution effects by comparing the FTIR spectra in solution to those of jet-cooled molecules and aggregates of the constituents generated from the same solution (see ESI† Table S2.8 for the size of such effects). Another potential advantage of the risotto-jet is the restriction of compound heating to fractions of a second, rather than hours. This might in some cases allow extending the range of substances to be studied by FTIR jet spectroscopy to less thermostable compounds, in particular with improved μL injection methods.
To prepare the gas mixtures for the Raman jet spectroscopy,40 a heatable saturator had to be thermostatted at 40 °C for ED and 80 °C for CD. The tubing (length 265 cm) connecting the saturator to the slit-nozzle including the nozzle body itself was kept 10 °C (ED) and 20 °C (CD) higher than the saturator to avoid condensation and to control aggregation. Stagnation pressures of 1.0 bar (ED) and 1.4 bar (CD) were needed to optimise the formation of cold dimers. Unlike the IR experiments, the expansion for Raman spectroscopy is continuous to ensure a stable cluster composition during the long exposures needed for the low spontaneous Raman scattering photon flux. A Spectra Physics Millenia 25 eV 532 nm laser was used, operating at 25 W (continuous wave) to maximise the photon flux. The distance between the slit nozzle and the parallel laser beam was set to 2.0 mm (ED) and 1.25 mm (CD). The scattered light was collected perpendicular to the laser and the nozzle flow via a camera lens and focused onto a 1 m monochromator (McPherson) which disperses the photons for a LN2-cooled CCD-camera (Princeton, PyLoN 400). The camera was operated in vertical binning mode. The combination of laser and monochromator results in a resolution of about 1 cm−1. Exposure times of 10 min (ED) and 4 min (CD) were used and co-added over 10 (ED and enantiopure CD) and 7 (CD racemate) exposures. To calibrate the raw spectra in the frequency domain neon lines were measured and compared to the known vacuum transitions of the NIST database.41 Spikes due to cosmic rays were eliminated by comparing multiple exposures for the same pixel column.
3 Computational techniques
Structure optimisations based on manually chosen starting geometries and harmonic frequency calculations were carried out with the ORCA (version 4.0.1.2) program package.42,43 The B3LYP functional44,45 was used which has proven to yield reliable energies and frequencies in the past.12,40 To account for London dispersion, Grimme's D3 correction including three-body terms in conjunction with Becke–Johnson damping was used (B3LYP-D3).46,47 Comprehensive theoretical benchmarks by Burns et al. and Mardirossian et al. further show the suitability of this combination for capturing non-covalent interactions.48,49 The def2-TZVP and def2-QZVP basis sets were employed, also to assess residual (small) BSSE and other basis set incompleteness effects on structures, energies and wavenumbers.50 To speed-up the calculations, density fitting (RIJCOSX)51 was used with the corresponding auxiliary basis set.52 Due to the way ORCA computes Raman activities, numerical frequency calculations had to be carried out. Furthermore the double harmonic approximation implying linear dipole functions was used. Pre-optimisations for a fast screening of many possible conformations were obtained by the recently proposed B97-3c functional.53 Example inputs for the ORCA calculations can be found in the ESI† (see Table S2.2).The computed Raman activities are subsequently converted to differential (per unit angle) cross sections (σ′ in m2 sr−1). Hereby we account for the perpendicular laser polarisation relative to the scattering plane, the method of detection (i.e. photon counting), an estimated vibrational temperature (100 K) and the polarisation and frequency dependence of the grating.54 The grating is less efficient for parallel polarised light, which is corrected for by dividing the parallel component of the Raman activity by a recently reevaluated empirically determined polynomial function.55 Hence in the case of strongly polarised totally symmetric vibrations (depolarisation ratio of 0) no grating correction would be required.
To validate that no relevant structures had been overlooked by the manual structure search, molecular dynamics simulations were carried out with the GFN2-xTB (Geometries Frequencies Non-covalent Interactions version 2 – extended Tight Binding)56,57 semi-empirical method coupled with the CREST (Conformer-Rotamer Ensemble Sampling Tool) program.58 The standard iMTD-GC (iterative Meta-Dynamic – Genetic Crossing) workflow was used. Cluster structures found in this manner were pre-optimised as before and followed up by a B3LYP optimisation.
To obtain transition states the reaction path was calculated using Woelfling in the TURBOMOLE (version 7.2) program package.59 The transition states obtained in this manner were then optimised using ORCA. Reported energy barriers include harmonic ZPE correction for all positive curvatures at the B3LYP-D3/def2-QZVP level of computation. No correction for the (small) basis set superposition error (BSSE) was made.
Furthermore, symmetry adapted perturbation theory (SAPT) was applied to the B3LYP geometries to compare the influence of London forces between the different conformers of ED and CD. In particular we used SAPT2+/aug-cc-pVDZ as implemented in the psi4 (version 1.3.2) program package.60 This variant was chosen as a compromise between accuracy and computational cost based on the benchmark of Parker et al.,61 who tested many different levels of SAPT as well as basis sets. Density fitting and the frozen core approximation were used for a speedup of the calculations.
4 Results and discussion
4.1 Predicted conformational and configurational preferences
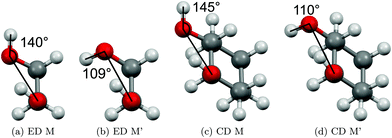
The two most stable monomer conformations of ED and CD are structurally closely related, both featuring a weak intramolecular hydrogen bond or at least bridge from the donor OH to the acceptor OH. The associated ∠OHO angle is (109 ± 2)° for the four structures, and thus very similar. This weak and strained contact slightly prefers a roughly collinear orientation (M, ∠OOH ≈ 140°) over a more perpendicular orientation (M′, ∠OOH ≈ 110°) of the interacting OH groups, which is illustrated in Fig. 4. We draw the border between these two OH/OH orientations, which will also play a role in the dimers, at an OOH angle of 120°.Compared to ED, the flexibility of CD is reduced and coupled to the ring conformation. To realise an intramolecular hydrogen bridge, the OH groups in CD have to assume a doubly equatorial chair conformation. The diaxial conformations come with an energy penalty of more than 12 kJ mol−1 due to the missing hydrogen bridge and unfavourable diaxial interactions. They will therefore be neglected in this work. M and M′ differ in energy by about 1 kJ mol−1 for ED and CD19,62 with significant zero point vibrational energy (ZPVE) contributions, as elaborated in Tables S2.3 and S2.4 in the ESI.† The interconversion barrier between M and M′ is around 4 kJ mol−1 such that equilibration in the jet will be feasible to some extent, further assisted by the short interconversion path and small associated mass and largely equivalent for ED and CD. The observed relative abundance of M′ and M is expected to fall somewhere in between the thermal equilibrium at the nozzle temperature and exclusive population of the global minimum conformer M (including ZPVE). Indeed, using computed energy differences and spectroscopic cross sections,11,15 effective conformational temperatures around 100–150 K are obtained (Table S2.3 in the ESI†).
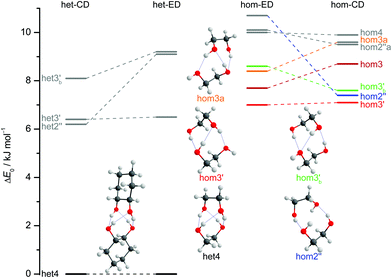
The dimers of ED and CD require several conformational specifications for a unique identification, but for simplicity we focus on relative chirality (hom or het) of the two OCCO torsion angles and hydrogen bond pattern (2 isolated, 3 openly, or 4 cyclically arranged intermolecular hydrogen bonds), adding a subscript b (for bifurcated) if a dangling OH is doubly coordinated by two OH groups of the other molecule, thus breaking the cooperativity chain, which is realised when no b is added. A prime (′) is added for each dangling (or just intramolecularly connected) terminal OH if the intermolecular OOH arrangement resembles the intramolecular one for M′ by having an OOH angle smaller than 120°. If a label reoccurs for a higher energy conformation (using CD at B3LYP-D3/def2-QZVP level as a naming reference), an ‘a’ is added to the name of this conformation. Thus, hom3′ involves two monomers of the same OCCO helicity forming a sequence of OH⋯OH⋯OH⋯OH hydrogen bonds, where the terminal OOH angle is less than 120°. A homochiral structure with two intermolecular hydrogen bonds and two dangling arrangements (non-intermolecular hydrogen bonds) with OOH angles less than 120° is denoted hom2′′ and the most stable heterochiral bonding pattern is named het4. The label hom3 stands for a torsional isomer related to hom3′ with the terminal OH oriented more in line with the coordinating OH and hom3a is a higher energy variant of it. The key difference between hom3 and its hom3a variant is that the CC backbones of the monomers are oriented rather parallel in the case of hom3a whereas they have an orthogonal arrangement for hom3 (see ESI† Fig. S1.1).
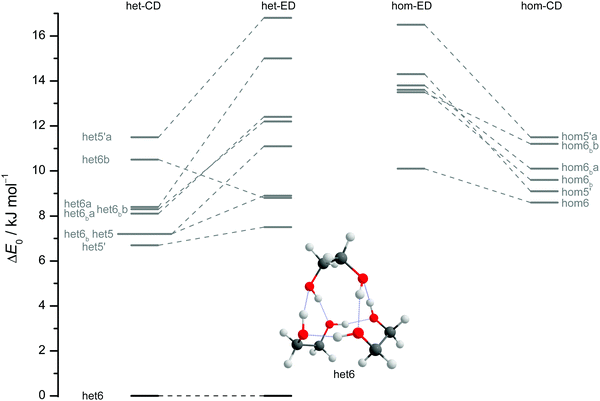
The results of extensive searches for energetically low-lying dimers of ED and CD yield a qualitatively similar energy pattern, which is compared in Fig. 5. The dashed lines in Fig. 5 illustrate the effect of moving from ED to CD. Interactive as well as static representations of the dimer structures are provided in the ESI† (interactive: Fig. S1.1 and S1.2; static: Fig. S1.1a and S1.2a). By far the most stable dimer is het4 in both cases, featuring an S4-symmetric cyclic hydrogen bond pattern with significant strain.12 Beyond a gap of >6 kJ mol−1, a larger number of het and hom dimers with 2 or 3 intermolecular hydrogen bonds follows. All electronic and ZPE corrected energy values can be found in the ESI† (see Table S2.5). A major difference between CD and ED is the stabilisation of flexible 2-fold hydrogen-bonded structures, likely caused by interactions due to the cyclohexyl rings. They thus compete with the most stable 3-fold hydrogen-bonded structures for CD, which is not the case for ED.12
 | ||
| Fig. 5 ZPV-corrected relative energies of the lowest 11 dimer structures for ED (inner) and CD (outer columns) at B3LYP-D3/def2-QZVP level, distinguishing between heterochiral (left) and homochiral (right) pairings. For ease of identification the colour coding corresponds to that from Fig. 7. Energy levels in grey indicate that those structures are not relevant for the experimental spectra. Since hom3 may spectrally overlap with hom3′ it is shown in dark red and not visualised. Dashed lines connect corresponding ED and CD structures and thus visualise the effect of the cyclohexyl substitution. | ||
Of particular interest is the 2 kJ mol−1 window above the lowest het and hom structure, respectively. In the het case, there is no competitor to het4, even in a threefold larger window. In the hom case, there are four competing structures with quite some variation from ED to CD (see Fig. S1.1 in the ESI†). For both compounds, the global hom minimum is hom3′ with its characteristic zig-zag hydrogen bond pattern. In ED, it is closely followed by a slightly twisted terminal OH arrangement (hom3), which is shifted to rank 4 in CD, presumably due to interactions with the cyclic residue. A backbone puckering variant of hom3, hom3a, is placed third in ED, but shifted out of the window in CD. Instead, a somewhat unfavourable floppy ED dimer with only two intermolecular hydrogen bonds (hom2′′) is predicted to be the second-most stable hom structure in CD. Finally, a bifurcated hydrogen bond pattern where the dangling OH group is intermolecularly coordinated at both lone electron pairs gains slightly from ED to CD, but this hom3b′ structure is always in the 2 kJ mol−1 window.
The aforementioned stabilisation of hom2′′ in the CD case, as well as its heterochiral analogue, is likely caused by an interplay of the deformation energy (EDef with ED as reference) relative to the two monomer subunits realised in het4 and long range dispersion interactions between the cyclohexyl residues. The deformation energy is the amount of energy that is needed to transform two of the most stable monomers (M) to the conformation that is found in each dimer.63–65 As M and M′ for ED and CD are almost isoenergetic, we define the deformation energy relative to M. For the computation of the deformation energies single point calculations were performed on the monomers. As CD is more rigid than ED the deformation energy for the highly strained het4 dimer increases (see ESI† Fig. S3.1). This results in a relative stabilisation of all other important CD dimers with respect to het4 in comparison to ED, which is indicated by the negative sign of EDef in Fig. 6. The intermolecular dispersion energies (EDisp) are taken from SAPT2+/aug-cc-pVDZ calculations. In both, the ED and the CD case, het4 profits most from dispersion interactions (see ESI† Fig. S3.2) due to its compactness. In ED and CD, all dimers with three hydrogen bonds exhibit similar but lower EDisp, because they are less compact. This is also the case for dimers with two hydrogen bonds. In CD, however, hom2′′, het2′′ and hom3b′ gain significantly in comparison to het4 of ED, resulting in negative values for EDisp in Fig. 6 for these conformers. Although hom3b′ benefits significantly from dispersion the deformation energy contribution is much smaller than for hom2′′ and het2′′. Overall het2′′ and hom2′′ are expected to be lower in energy by at least a factor of two in comparison to most other conformers, in this double difference. Therefore an interplay of dispersion and deformation energies yields a plausible qualitative explanation for their stabilisation. An identical analysis as in Fig. 6 can be found in the ESI,† with results from sSAPT0/jun-cc-pVDZ calculations (see Fig. S3.3, ESI†) as well as EDisp estimated by the D3(BJ,abc) terms (see Fig. S3.4, ESI†), which qualitatively yield the same results. Furthermore the ESI† (see Fig. S3.5) includes correlation plots for optimised geometries (including ZPE) without dispersion correction, which also indicate the stabilising effect of London forces on het4.
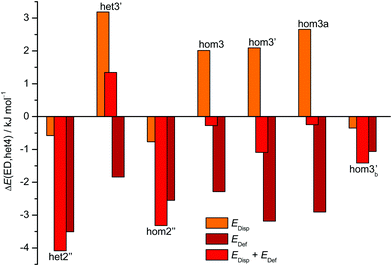 | ||
| Fig. 6 Overview of the CD dispersion contributions (orange), deformation energies (dark red) and the resulting sum (red). All values are given relative to the corresponding ED value and relative to the effect for het4. The absolute components for this double difference are provided in the ESI† (Fig. S3.1 and S3.2). Negative values indicate a stabilisation by deformation (dark red) or London dispersion (orange) or both (red) relative to het4 and relative to the ED case. het2′′ and hom2′′ profit most from the net effect of deformation and dispersion. | ||
The robustness of the harmonic B3LYP-D3/def2-QZVP prediction is discussed in the ESI,† by comparing it to a def2-TZVP (see ESI† Fig. S3.6) and to the former Pople (see ESI† Fig. S3.7) basis set results for ED.12 It is found that the hom/het gap increases with smaller basis set, indicative of more pronounced BSSE and other basis set incompleteness effects for the compact structure. In the hom-quartet, there is some rearrangement, but the lowest hom3′/hom3 pair persists for ED.
The interconversion barrier from the hom3 to the hom3′ structure is on the order of 1 kJ mol−1, indicative of efficient relaxation under jet-cooling conditions. However, the two structures are also predicted within 1 kJ mol−1 of each other and therefore most likely remain populated in the jet, similar to the M/M′ monomer pair. For the higher energy hom dimer conformers, observation in the jet will depend on both, their relative energy and their barrier for structural relaxation.11,15
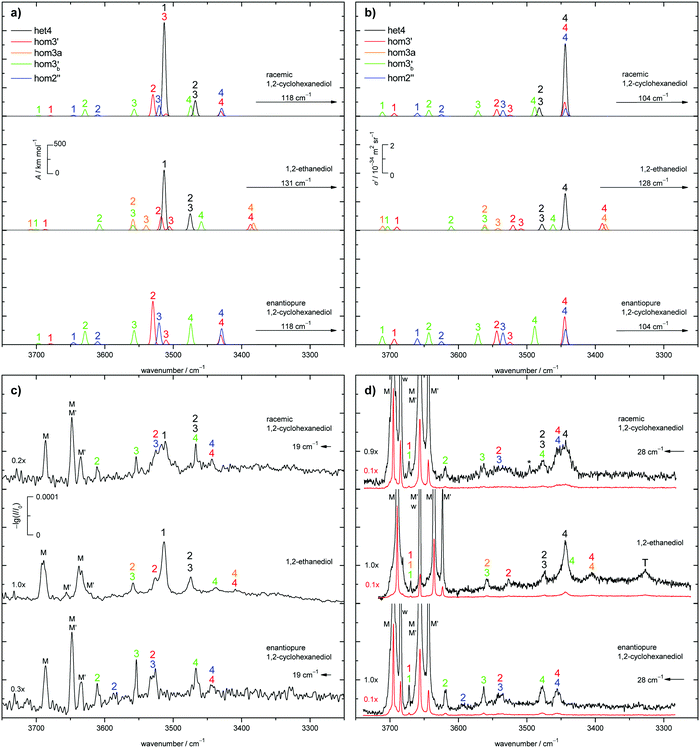
The judgement about which secondary hom-dimers survive the jet expansion will therefore depend on a comparison of the theoretical harmonic spectra with the experimental ones. Fig. 7 provides such theoretical IR spectra in a three panel comparison. The centre panel shows calculated double harmonic OH-stretching IR band-strengths for het4 (black) and three of the four structures which are most stable for hom ED dimers (hom3′, hom3a, hom3b′). hom3 is not simulated explicitly because of its likely relaxation to hom3′ and their spectral similarity. For comparison, the upper panel shows the corresponding CD dimer spectra for het4, hom3′, hom2′′, hom3b′, again leaving out the unstable hom3 contribution. Bear in mind that hom3a is now replaced by hom2′′ as a consequence of the cyclohexyl substitution. The lower panel corresponds to the upper one, with the heterochiral contribution of het4 removed and the hom-contributions thus doubled in intensity. Note that all harmonic spectra are shifted on the wavenumber axis such that the main het4 signal always agrees with the experimentally observed ED peak. This downshift (131 cm−1 for ED and 118 cm−1 for CD) accounts for anharmonicity and electronic structure error and in the CD case also for the substitution effect.
The het4-matched spectra demonstrate several aspects which are favourable for a CD-inspired ED hom-dimer reanalysis. The predicted OH stretching IR pattern is qualitatively similar among ED and CD dimers and sufficiently spread out to identify different conformations. The cumulated OH intensity for each conformation with more than two intermolecular hydrogen bonds is relatively similar (within ±30%, see ESI† Table S2.5) such that all potentially observable conformations have a similar IR and Raman visibility. The most stable hom3 dimers may be partially hidden underneath the dominant het4 band and enantiopure CD investigation is necessary to uncover this overlap.
Before moving to the comparison with experiment, we briefly discuss a previous computational investigation. Jesus and Redinha report one cyclic CD homo dimer with 2 intermolecular hydrogen bonds (not hom2′′ presented here) and one open dimer with a single intermolecular hydrogen bond at the B3LYP/6-311G** level of computation.19 This is very different from the present findings. Likely reasons are the omission of dispersion correction in the primary B3LYP search and the use of M06-2X only for reoptimisations. In addition, it appears probable that their conformational search building on crystallographic data66,67 as well as the CFF91 force field68,69 was incomplete, because their reported dimer structures show large amounts of surviving intramolecular hydrogen bonds which our study does not support for the lowest energy structures. Given that CFF91 focuses mainly on proteins it might also be inherently inadequate for dimers/trimers of diols. Further sampling issues may apply. The fact that they still find good agreement between theory and solution phase spectroscopy underscores the limited conclusiveness and discrimination power of the latter. This is largely due to the thermally induced broadening of spectra caused by the sensitivity of hydrogen bond shifts to excitation, but also due to solvent-induced shifts, which are not so easy to model (see ESI† Table S2.8). It clearly calls for a supersonic jet study as presented in this work, although even this suffers from conformational overlap and therefore only allows for cautious interpretations.
4.2 Experimental dimer conformational and configurational preferences
With the robust theoretical IR and Raman predictions in Fig. 7 (see ESI† Fig. S4.2 for an analogous plot at B3LYP-D3/def2-TZVP level, where BSSE and other basis set incompleteness effects may be somewhat more pronounced), we can turn to the experimental spectra. The previous assignments of the monomer bands of ED remain the same.12 Compared to room temperature gas phase fundamental spectra,70 the jet cooling helps in resolving the two conformers M and M′, as does overtone spectroscopy.71 In case of CD only three monomer bands can be observed in contrast to the four of ED, as seen in Fig. 7. For a better visibility of the monomer signals in the experimental Raman spectra, scaled spectra are shown in red. The frequency calculations for CD predict an overlap of the bound OH-stretching vibration of M with the free OH vibration of M′. A relaxation study revealed that this is indeed the case (see ESI† Fig. S4.3). The fourth band (w) is due to water impurities.72 The predicted shifts as well as the energetic order are in good agreement with the experiment (see ESI† Table S2.3 and Fig. S4.5, S4.6).The introduction of the cyclohexyl backbone leads to permanent chirality, which allows us to enforce the formation of homochiral dimers by using enantiopure CD. In case of the racemate homo- and heterochiral dimers are expected to form largely statistically with a ratio close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It follows that the intensity of the homochiral dimer bands should roughly double for enantiopure CD in comparison to the racemate if the volatility is similar. The energy gap of more than 6 kJ mol−1 above het4 may prevent formation, stabilisation or detection of the less stable hetero dimers. The shallow 2.0 kJ mol−1 barrier for het3 certainly prevents stabilisation in the expansion. Depending on the level of theory het3 exists as a shallow minimum slightly lower in energy than het3′ along its (het3′) relaxation pathway to het4. Due to this fact het3 is not shown in Fig. 5. For the homo-dimers hom3′, hom2′′ and hom3b′ are energetically feasible, only 0.5 kJ mol−1 apart from each other. hom3 is 1.6 kJ mol−1 higher, but poorly separated from hom3′ by a 0.3 kJ mol−1 barrier. Due to the close energetic proximity of the three remaining dimers, their populations are estimated to be roughly equal, even if relaxation within the hom family modifies statistical formation. This leads to simplified statistical weights for het4
1. It follows that the intensity of the homochiral dimer bands should roughly double for enantiopure CD in comparison to the racemate if the volatility is similar. The energy gap of more than 6 kJ mol−1 above het4 may prevent formation, stabilisation or detection of the less stable hetero dimers. The shallow 2.0 kJ mol−1 barrier for het3 certainly prevents stabilisation in the expansion. Depending on the level of theory het3 exists as a shallow minimum slightly lower in energy than het3′ along its (het3′) relaxation pathway to het4. Due to this fact het3 is not shown in Fig. 5. For the homo-dimers hom3′, hom2′′ and hom3b′ are energetically feasible, only 0.5 kJ mol−1 apart from each other. hom3 is 1.6 kJ mol−1 higher, but poorly separated from hom3′ by a 0.3 kJ mol−1 barrier. Due to the close energetic proximity of the three remaining dimers, their populations are estimated to be roughly equal, even if relaxation within the hom family modifies statistical formation. This leads to simplified statistical weights for het4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom3′
hom3′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom3b′
hom3b′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom2′′ of 3
hom2′′ of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which are chosen in Fig. 7a and b (top panel). It should be noted that the overall IR and Raman visibility of the hom2′′ dimer is comparatively weak with respect to the other dimers (see ESI† Table S2.5).
1, which are chosen in Fig. 7a and b (top panel). It should be noted that the overall IR and Raman visibility of the hom2′′ dimer is comparatively weak with respect to the other dimers (see ESI† Table S2.5).
The strong het4 bands 1 and 4 are the most prominent in the simulated and experimental IR and Raman spectra, respectively. Band 4 (A species) is not visible in the IR, due to the S4-symmetry of het4. Although not ruled out by symmetry, band 1 (B species) is hardly Raman active. The doubly degenerate band 2/3 (E species) is visible in both cases. Interestingly, all het4 bands overlap to some degree with homo-dimers. By comparing the experimental racemate and enantiopure spectra this becomes evident. The overlap is especially prominent for band 1 in the IR and band 4 in the Raman spectra with hom2′′ and hom3′ in either case. The broad structure in the centre of the experimental Raman spectrum of the racemate can be explained by an overlap of band 2 and 3 of hom3′ and hom2′′, respectively. Bands 4 of the two dimers also overlap. In the IR some intensity increase is visible when switching to the enantiopure CD. This slight increase might be due to some overlap with the most stable hetero-trimer which is not present in the enantiopure case, therefore increasing to a lesser degree. Since band 1 and 2 of hom2′′ exhibit fairly low intensities they cannot be observed in the racemate. Band 1 also likely overlaps with monomer bands and hence cannot be seen. Because of the intensity increase for the enantiopure CD expansion, band 2 becomes visible. hom3b′ exhibits fairly similar calculated intensities, except for 1 which is missing in the IR. This is in good agreement with the experiment as well as the predicted shifts (see ESI† Fig. S4.6). An overlap of band 1 by hom3′ and hom3b′ is also possible and might explain the fairly high experimental Raman intensity in comparison to the simulation. The proposed intensity increase by a factor of 2 in the enantiopure spectra cannot be observed, although a rise is clearly present (e.g. band 1 increases roughly by a factor of 1.5 in the Raman spectrum). Overlap with het-bands is a possible reason. Furthermore the effective vapour pressure of the enantiopure CD is most likely lower, as indicated by lower monomer signals (i.e. racemate scaled by 0.7 (IR) and 0.9 (Raman)). At first glance, this is nicely parallel to ED, which is a conglomerate former when crystallised.8 However, in the case of CD there is evidence in the literature that the racemic form is more stable and thus less volatile.17 Therefore, the concentration probed in the jet is more likely a consequence of different effective contact areas in the sample pickup. Also, the expansion conditions might have slightly varied between the two experiments. All this can explain the quantitative deviations from the statistically expected factor of 2.
As previously mentioned het4 remains the most stable dimer when switching from CD to ED. het3′ can easily relax to het4 under jet conditions (barrier 1.5 kJ mol−1). Therefore het4 should be the dominant hetero-dimer present in the expansion. As in CD, four homo-dimers are energetically feasible, namely hom3′, hom3, hom3a and hom3b′. hom3 is neglected for simplicity due to its shallow (0.9 kJ mol−1) barrier to hom3′. Since the three hom dimers are energetically separated by only 1.6 kJ mol−1, equal population is approximated. This leads to coarse statistical weights for het4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom3′
hom3′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom3a
hom3a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hom3b′ of 3
hom3b′ of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 which are shown in Fig. 7 (middle panel). Thus the only major change from CD to ED is that hom2′′ is substituted by hom3a.
1 which are shown in Fig. 7 (middle panel). Thus the only major change from CD to ED is that hom2′′ is substituted by hom3a.
het4 can again be easily spotted in the experimental IR and Raman spectra of ED (see Fig. 7c and d). The predicted shifts with regard to M (see ESI† Fig. S4.5) as well as the intensities are in good agreement with the experiment. The intensity pattern of het4 is similar to CD although the (absolute) predicted intensities are smaller than for CD in both the IR and Raman spectra. Between the monomer signals in the Raman spectrum a band is present which could consist of an overlap of the dangling hydroxyl groups from all three homo-dimers. The fairly high experimental intensity in contrast to the simulated spectra indicates that this is indeed the case. The free OH-stretching vibration cannot be observed in the predicted and experimental IR-spectra. Furthermore band 2 of hom3′ again overlaps with band 1 of het4 in the IR visible as a shoulder. It is also present in the Raman spectrum. An overlap with band 4 of het4 in the Raman spectra does not take place since band 4 is shifted towards lower wavenumbers in comparison to CD. Band 4 of hom3b′ is likely present as a small shoulder of band 4 of het4 since it is visible in the IR as a small band. However band 2 of hom3b′ is not visible due to its low intensity. Band 4 of hom3′ and hom3a, which overlap, can be observed as a distinct signal in the Raman spectrum, whereas in the IR they are hardly visible. Their presence in the IR can only be inferred from the position of the Raman signal. Given the comparatively low intensities of band 3 of hom3′ and hom3a it is unlikely to be observed in the experimental spectra. The most prominent remaining band is possibly caused by an overlap of band 2 of hom3a and band 3 of hom3b′. This overlap could partially explain the comparatively high experimental intensity in comparison to the simulations but the assignment remains tentative. The signal marked with T is due to a trimer or larger cluster which can be shown by more dilute spectra (see ESI† Fig. S4.4). An overview of all assigned bands can be found in the ESI† (see Table S2.6). Confirmation for the correct assignments comes from the systematic correlation of the harmonic predictions for downshifts relative to the free monomer OH signal with the experimental anharmonic downshifts (Fig. S4.5 and S4.6 in the ESI†). It reflects the characteristic slight overestimation of B3LYP for such hydrogen bonding effects39 and should not be blamed only on the harmonic approximation but rather on an intrinsic deficiency of such density functionals, which is only partly relieved by the hybrid Hartree–Fock character of B3LYP.
In summary, the close analogy between the CD and ED spectra despite a blocked OCCO interconversion for CD suggests that formation of ED dimers is also largely statistical in terms of the OCCO angle. No interconversion between the helical enantiomers has to be invoked to explain the spectra. This interpretation is qualitatively supported by the close similarity of the spectra obtained by the three different jet-FTIR techniques explored in this work, as demonstrated in Fig. S4.1 in the ESI,† for the transiently chiral ED. If interconversion between transient hom and het dimers were feasible under jet expansion conditions, one would expect significant differences between hot low pressure expansions (risotto-jet) and colder expansions at higher pressure (popcorn-jet variants) (Table S2.1 in the ESI†).
The spectral analogies between ED and CD help to identify previously unassigned bands as hom dimers. The previous elusiveness of these hom pairs can now be explained by the fact that the spectral intensity is distributed over three to four conformations with partial het overlap, whereas most of the het dimer population appears to collapse into a single dominant het4 structure with symmetry- and cooperativity-enhanced prominent bands.
4.3 Implications for chirality-induced spin selectivity
Regular electrostatic, induction, London dispersion and exchange repulsion mechanisms should more or less randomly favour homochiral and heterochiral dimers in terms of global minimum structure, when averaged over all conceivable transiently or permanently chiral molecular systems. However, there is an empirical preference for racemic crystals6 which might indicate systematically better packing for heterochiral pairings. On the other hand, it was proposed that CISS could add an extra term which always favours homochiral pairings,4 because favourable concerted electron fluctuations giving rise to dispersion interactions generate preferentially spin-paired contact surfaces between homochiral entities and thus reduce Pauli repulsion relative to heterochiral contacts. The class of 1,2-diol dimers could represent a suitable testing system for this issue, because they exhibit up to 4 hydrogen bonds which provide a rigid and intense contact between the chiral units, at which CISS effects could develop. There are two major challenges to turn this situation into a CISS testing ground. The energy gap between the homo and hetero structures has to be closed and the interconversion barrier between them12 has to be lowered. Both goals might be achieved if chemical substitution reduces the preferred OCCO torsional angle further. Once a suitable system has been identified and studied, one could compare different computational models with the experimentally observed preference.Alternatively, one could use spectral fingerprints to detect such CISS effects, because spectral trends may be more sensitive to deficiencies in theory than some energetical trends.5 For the clusters of CD and ED, we have not observed any systematic chirality-sensitive deviations of B3LYP-D3 spectral predictions from experiment, although the dispersion at least at long range is treated in a force-field and thus spin-insensitive manner.
4.4 Tentative trimer evidence
Energetic chirality recognition cannot only be observed for the CD dimers but for CD trimers as well. A C2-symmetrical hetero-trimer with six intermolecular hydrogen bonds is the global minimum at the B3LYP-D3/def2-TZVP level of computation (see Fig. 8 for the ED counterpart). It is named het6 in analogy to the dimer nomenclature and has a predicted dipole moment of about 1 D, making it potentially observable by rotational spectroscopy. The hydrogen bond arrangement is structurally related to a prism and can be found in all het6/hom6 structures. The het6 trimer bares structural similarities with the S4-symmetric het4 building block. It can be obtained by inserting two monomer OH groups into the hydrogen bonded ring at opposite sides, thus releasing some of the strain (for an interactive visual representation see ESI† Fig. S1.3 and S1.3a for a static variant). Less stable hetero-trimers follow with an energetic penalty of about 7 kJ mol−1. The most stable homo-trimer is predicted more than 8 kJ mol−1 above the global minimum, reminiscent of the CD hom dimers at the same level of computation. Again, the four most stable homo-trimers can be found within 2 kJ mol−1 of each other. Calculations with larger basis sets were omitted for CD because of the computational cost and because BSSE is expected to be less conformation dependent for the overall quite compact structures with 5–6 hydrogen bonds. The expected spectral dominance of het6 due to the structural diversity of the hom counterparts is further enhanced by a 3-fold combinatorial advantage of het trimers over hom trimers. Jesus and Redinha also report one cyclic (4 intermolecular hydrogen bonds) and one open (2 intermolecular hydrogen bonds) homo trimer.19 These are also found to not be competitive to the homo trimers found in our conformational search. Reasons for and implications of this mismatch have already been discussed when dealing with the dimers.The het-hom energy gap increases further to about 10 kJ mol−1 when switching to ED. Fig. 8 also shows that in marked contrast to CD, there is no structural competition on the hom side within the first 3 kJ mol−1. The cyclohexyl backbone is seen to provide a much stronger perturbation in trimers than in dimers. For ED, quadruple zeta calculations (see ESI† Fig. S3.8) also confirm less BSSE and other basis set incompleteness effects in trimers. In general the influence of basis set extension on relative energies stays within 1 kJ mol−1. All electronic and ZPE corrected energy values can be found in the ESI† (see Table S2.7).
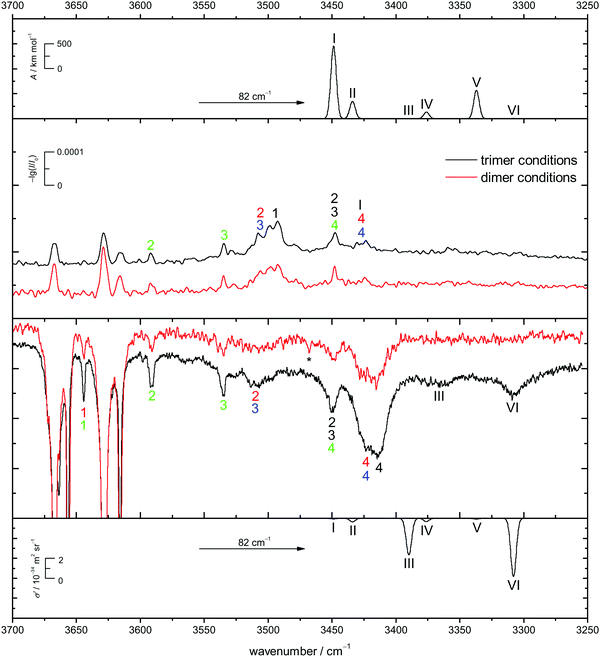
In Fig. 9 the B3LYP-D3/def2-TZVP simulated CD spectra of het6 are contrasted with experimental IR and Raman spectra with different clustering extent. Due to the large energetic separation of het6 to the other hetero-trimers, the limited signal-to-noise ratio and in particular the statistical disadvantage of individual homo-trimers, only het6 is considered. To avoid confusion with the dimers Roman numerals are used to name the trimer bands. By comparing the two Raman spectra with each other the new trimer bands immediately become apparent. The simulated spectra are in acceptable agreement with the experiment after matching the strongest trimer signal with the most cooperative and Raman active harmonic prediction (band VI). As is usually the case for DFT calculations the splitting of bands III and VI due to different cooperativity is overestimated. The IR-spectra are less conclusive but given the overestimation of the cooperativity splitting, an overlap with bands 4/4 of the hom3′ and hom2′′ dimers seems likely. This is further indicated by the fact that this band does not increase as much when measuring the enantiopure compound (see Fig. 7), indicative of a het6 fraction which is removed in the homochiral gas mixture.
In case of the Raman spectrum of ED a very prominent band at lower wavenumbers can be observed (T in Fig. 7). The simulated spectra show a similar pattern as for CD and fit well to the experimental data. Furthermore some overlap with bands 4/4 of the hom3′ and hom3a dimers is remotely possible. IR spectra of ED at higher concentrations show no evidence of distinct trimer signals but rather unspecific large cluster contributions (see ESI† Fig. S4.7).
5 Conclusions
The present work was enabled by improved nozzle designs for supersonic jet FTIR spectroscopy which remove some of the sensitivity limitations of previous designs.73,74 By introducing wedge-shaped slit nozzles adapted to the focussed beam profile and by liquid injection into a premixing chamber, this technological limitation was significantly attenuated. The synergy with spontaneous Raman scattering tools using heatable nozzles40 was thus enhanced.An important scientific goal of this work was to identify the main reason for the apparent dominance of heterochiral dimer vibrations in 1,2-ethanediol (ED) expansions. Based on analogous experiments for racemic and enantiopure trans-1,2-cyclohexanediol (CD), a previously suggested interconversion mechanism via transient heterochiral trimer formation12 could be ruled out with high probability, because it should lead to a more than two-fold homochiral dimer enhancement upon removal of the other enantiomer. The identification of at least three homochiral dimers in enantiopure CD expansions and their similarly strong counterparts in ED further ruled out major contributions from an intramolecular racemisation mechanism triggered by the dimerisation energy.75,76 Computations suggested that the visibility of most homochiral dimer isomers is also not significantly inferior to that of the heterochiral global minimum structure. What remains as an explanation is the spreading of homochiral spectral transition intensity over at least three conformations in combination with partial overlap with the heterochiral bands. This is indeed confirmed by the homology experiments and the simulation shows that all experimental spectra are consistent with a largely statistical formation of homo- and heterochiral dimers under jet conditions. This is supported by very similar spectra obtained in three different jet-FTIR setups with widely different nozzle temperatures and stagnation pressures. On the other hand, it is clear from the robustly calculated energy gap that heating the homochiral dimers up to room temperature will convert them almost quantitatively to S4-symmetric heterochiral dimers, until dissociation takes over. Chirality synchronisation12 is thus suppressed in favour of chirality discrimination under helium jet expansion conditions, whereas it must occur after suitable equilibration of the formed dimers. The latter might be realisable in shock wave experiments after the zone of silence.
The switch from ethanediol to cyclohexanediol has also given first indications about the use of chemical design elements in controlling the aggregation structure. CD brings homochiral dimers with only two intermolecular hydrogen bonds into play. They compete with hom3 conformations, by allowing for secondary and still distant dispersion interactions between the rings and by reducing monomer distortion. It is conceivable that further chemical design can even turn 1,2-diols into test cases for the chirality-induced spin-selectivity effect.
In summary, the heterochiral dimerisation energy preference in 1,2-diols is pronounced and robust, but it does not lead to preferential heterochiral aggregation in supersonic jets when seeding the diols into helium, because the barriers for all conceivable racemisation pathways involving 1–3 molecules are too high in the limited collisional relaxation regime which is characteristic for such experiments. The tentatively assigned experimental signature of a heterochiral trimer for ED and CD indicates that chirality effects may persist in even larger aggregates and they are clearly showing a heterochiral preference, at least in terms of energy and spectral visibility.
The pronounced heterochiral stability predicted for ED dimers and trimers is in stark contrast to the solid state structure, which consists of homochiral monomer units with the same conformation as in the gas phase.8,77 Solid ED is thus an elementary representative of the rare class6 of conglomerate formers, but somewhat surprisingly and very interestingly it still prefers heterochiral aggregation on the nanometer scale.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455 and 271107160/SPP1807 – and further supported by the BMBF (DAAD project-ID 57315059) and MEAE (PHC Procope, Grant 37586TL). We thank the mechanics and electronics workshops for their excellent support in the design and construction of the new jet chambers and Maxim Gawrilow for some preliminary Raman studies and help with the spectral acquisition and calibration.References
- A. Kühnle, T. R. Linderoth, B. Hammer and F. Besenbacher, Chiral Recognition in Dimerization of Adsorbed Cysteine Observed by Scanning Tunnelling Microscopy, Nature, 2002, 415(6874), 891–893 CrossRef PubMed.
- A. Zehnacker and M. A. Suhm, Chirality Recognition between Neutral Molecules in the Gas Phase, Angew. Chem., Int. Ed., 2008, 47(37), 6970–6992 CrossRef CAS PubMed.
- R. Naaman and D. H. Waldeck, Chiral-Induced Spin Selectivity Effect, J. Phys. Chem. Lett., 2012, 3(16), 2178–2187 CrossRef CAS PubMed.
- A. Kumar, E. Capua, M. K. Kesharwani, J. M. L. Martin, E. Sitbon, D. H. Waldeck and R. Naaman, Chirality-Induced Spin Polarization Places Symmetry Constraints on Biomolecular Interactions, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(10), 2474–2478 CrossRef CAS PubMed.
- R. Medel, C. Stelbrink and M. A. Suhm, Vibrational Signatures of Chirality Recognition Between α-Pinene and Alcohols for Theory Benchmarking, Angew. Chem., Int. Ed., 2019, 58(24), 8177–8181 CrossRef CAS PubMed.
- J. Jacques, A. Collet and S. H. Wilen, Enantiomers, Racemates, and Resolutions, Wiley, New York, 1981 Search PubMed.
- A. Otero de-la Roza, J. E. Hein and E. R. Johnson., Reevaluating the Stability and Prevalence of Conglomerates: Implications for Preferential Crystallization, Cryst. Growth Des., 2016, 16(10), 6055–6059 CrossRef CAS.
- A. D. Fortes and E. Suard, Crystal Structures of Ethylene Glycol and Ethylene Glycol Monohydrate, J. Chem. Phys., 2011, 135(23), 234501 CrossRef PubMed.
- K. Le Barbu, V. Brenner, P. Millié, F. Lahmani and A. Zehnacker-Rentien, An Experimental and Theoretical Study of Jet-Cooled Complexes of Chiral Molecules: The Role of Dispersive Forces in Chiral Discrimination, J. Phys. Chem. A, 1998, 102(1), 128–137 CrossRef CAS.
- J. P. Wagner and P. R. Schreiner, London Dispersion in Molecular Chemistry Reconsidering Steric Effects, Angew. Chem., Int. Ed., 2015, 54(42), 12274–12296 CrossRef CAS PubMed.
- A. Poblotzki, H. C. Gottschalk and M. A. Suhm, Tipping the Scales: Spectroscopic Tools for Intermolecular Energy Balances, J. Phys. Chem. Lett., 2017, 8(22), 5656–5665 CrossRef CAS PubMed.
- F. Kollipost, K. E. Otto and M. A. Suhm, A Symmetric Recognition Motif between Vicinal Diols: The Fourfold Grip in Ethylene Glycol Dimer, Angew. Chem., Int. Ed., 2016, 55(14), 4591–4595 CrossRef CAS PubMed.
- C. P. Brock, Crystal Packing in Vicinal Diols CnHm(OH)2, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58(6), 1025–1031 CrossRef PubMed.
- L. Meca, D. Řeha and Z. Havlas, Racemization Barriers of 1,1′-Binaphthyl and 1,1′-Binaphthalene-2,2′-diol: A DFT Study, J. Org. Chem., 2003, 68(14), 5677–5680 CrossRef CAS PubMed.
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, Relaxation of Conformers and Isomers in Seeded Supersonic Jets of Inert Gases, J. Chem. Phys., 1990, 93(5), 3142–3150 CrossRef CAS.
- P. Asselin, B. Madebne, P. Soulard, R. Georges, M. Goubet, T. R. Huet, O. Pirali and A. Zehnacker-Rentien, Competition between inter- and intra-molecular hydrogen bonding: An infrared spectroscopic study of jet-cooled amino-ethanol and its dimer, J. Chem. Phys., 2016, 145(22), 224313 CrossRef PubMed.
- M. A. Lloyd, G. E. Patterson, G. H. Simpson, L. L. Duncan, D. P. King, Y. Fu, B. O. Patrick, S. Parkin and C. P. Brock, Solid-State Compounds of Stereoisomers: cis and trans Isomers of 1,2-Cyclohexanediol and 2,3-Tetralindiol, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63(3), 433–447 CrossRef CAS PubMed.
- J. F. Bacon, J. H. van der Maas, J. R. Dixon, W. O. George and P. S. McIntyre, Structural Information from OH Stretching Frequencies Conformations of Cyclohexanol and Cyclohexandiols, Spectrochim. Acta, Part A, 1989, 45(12), 1313–1318 CrossRef.
- A. J. Lopes Jesus and J. S. Redinha, Self-Association of 1,2-Cyclohexanediols: A Spectroscopic and Computational Study, J. Mol. Struct., 2014, 1067(1), 104–111 CrossRef CAS.
- L. P. Kuhn, The Hydrogen Bond. I. Intra- and Intermolecular Hydrogen Bonds in Alcohols, J. Am. Chem. Soc., 1952, 74(10), 2492–2499 CrossRef CAS.
- C. W. Davey, E. L. McGinnis, J. M. McKeown, G. D. Meakins, M. W. Pemberton and R. N. Young, Hydroxy-Steroids. Part XI. The Preparation and Infrared Spectra of Vicinal Cholestanediols, J. Chem. Soc. C, 1968, 2674–2682 RSC.
- F. A. J. Singelenberg and J. H. Van Der Maas, Fourier Transform Infrared Study of Hydrogen-Bonding between an OH-Donor and a Vicinal Oxygen Acceptor, J. Mol. Struct., 1990, 240, 213–223 CrossRef CAS.
- K. Yamamoto, Y. Nakao, Y. Kyogoku and H. Sugeta, Vibrational Circular Dichroism in Hydrogen Bond Systems: Part III. Vibrational Circular Dichroism of the OH Stretching Vibrations of 1,2-Diols and β-Methoxyalcohols, J. Mol. Struct., 1991, 242, 75–86 CrossRef CAS.
- A. Allerhand and P. von R. Schleyer, Solvent Effects in Infrared Spectroscopic Studies of Hydrogen Bonding, J. Am. Chem. Soc., 1963, 85(4), 371–380 CrossRef CAS.
- A. J. Lopes Jesus, M. T. S. Rosado, I. Reva, R. Fausto, M. E. Eusébio and J. S. Redinha., Conformational Study of Monomeric 2,3-Butanediols by Matrix-Isolation Infrared Spectroscopy and DFT Calculations, J. Phys. Chem. A, 2006, 110(12), 4169–4179 CrossRef CAS PubMed.
- M. Gerhards, C. Unterberg and K. Kleinermanns, Structures of Catechol(H2O)1,3 Clusters in the S0 and D0 states, Phys. Chem. Chem. Phys., 2000, 2, 5538–5544 RSC.
- R. A. Jockusch, R. T. Kroemer, F. O. Talbot, L. C. Snoek, P. Çarçabal, J. P. Simons, M. Havenith, J. M. Bakker, I. Compagnon, G. Meijer and G. von Helden, Probing the Glycosidic Linkage: UV and IR Ion-Dip Spectroscopy of a Lactoside, J. Am. Chem. Soc., 2004, 126(18), 5709–5714 CrossRef CAS PubMed.
- T. J. L. Lockley, J. P. I. Hearn, A. K. King and B. J. Howard, Detection and Analysis of a New Conformational Isomer of Propan-1,2-diol by Fourier Transform Microwave Spectroscopy, J. Mol. Struct., 2002, 612(2), 199–206 CrossRef CAS.
- Z. Su, N. Borho and Y. Xu, Chiral Self-Recognition: Direct Spectroscopic Detection of the Homochiral and Heterochiral Dimers of Propylene Oxide in the Gas Phase, J. Am. Chem. Soc., 2006, 128(51), 17126–17131 CrossRef CAS PubMed.
- A. Amirav, U. Even and J. Jortner, Absorption Spectroscopy of Ultracold Large Molecules in Planar Supersonic Expansions, Chem. Phys. Lett., 1981, 83(1), 1–4 CrossRef CAS.
- C. M. Lovejoy and D. J. Nesbitt, Slit Pulsed Valve for Generation of Long-Path-Length Supersonic Expansions, Rev. Sci. Instrum., 1987, 58(5), 807–811 CrossRef CAS.
- K. Liu, R. S. Fellers, M. R. Viant, R. P. McLaughlin, M. G. Brown and R. J. Saykally, A Long Path Length Pulsed Slit Valve Appropriate for High Temperature Operation: Infrared Spectroscopy of Jet-Cooled Large Water Clusters and Nucleotide Bases, Rev. Sci. Instrum., 1996, 67(2), 410–416 CrossRef CAS.
- M. Hepp, F. Herregodts and M. Herman, Fourier Transform Infrared Jet Spectroscopy Using a Heated Slit Source, Chem. Phys. Lett., 1998, 294(6), 528–532 CrossRef CAS.
- M. Herman, R. Georges, M. Hepp and D. Hurtmans, High Resolution Fourier Transform Spectroscopy of Jet-Cooled Molecules, Int. Rev. Phys. Chem., 2000, 19(2), 277–325 Search PubMed.
- A. Moudens, R. Georges, M. Goubet, J. Makarewicz, S. E. Lokshtanov and A. A. Vigasin, Direct Absorption Spectroscopy of Water Clusters Formed in a Continuous Slit Nozzle Expansion, J. Chem. Phys., 2009, 131(20), 204312 CrossRef CAS PubMed.
- M. Cirtog, P. Asselin, P. Soulard, B. Tremblay, B. Madebène, M. E. Alikhani, R. Georges, A. Moudens, M. Goubet, T. R. Huet, O. Pirali and P. Roy, The (CH2)2O–H2O Hydrogen Bonded Complex. Ab Initio Calculations and Fourier Transform Infrared Spectroscopy from Neon Matrix and a New Supersonic Jet Experiment Coupled to the Infrared AILES Beamline of Synchrotron SOLEIL, J. Phys. Chem. A, 2011, 115(12), 2523–2532 CrossRef CAS PubMed.
- J. Altnöder, J. J. Lee, K. E. Otto and M. A. Suhm, Molecular Recognition in Glycolaldehyde, the Simplest Sugar: Two Isolated Hydrogen Bonds Win Over One Cooperative Pair, ChemistryOpen, 2012, 1(6), 269–275 CrossRef PubMed.
- D. Bernhard, M. Fatima, A. Poblotzki, A. L. Steber, C. Pérez, M. A. Suhm, M. Schnell and M. Gerhards, Dispersion-controlled docking preference: multi-spectroscopic study on complexes of dibenzofuran with alcohols and water, Phys. Chem. Chem. Phys., 2019, 21, 16032–16046 RSC.
- R. Wugt Larsen, P. Zielke and M. A. Suhm., Hydrogen-Bonded OH Stretching Modes of Methanol Clusters: A Combined IR and Raman Isotopomer Study, J. Chem. Phys., 2007, 126(19), 194307 CrossRef PubMed.
- T. Forsting, H. C. Gottschalk, B. Hartwig, M. Mons and M. A. Suhm, Correcting the Record: The Dimers and Trimers of trans-N-Methylacetamide, Phys. Chem. Chem. Phys., 2017, 19, 10727–10737 RSC.
- National Institute of Standards and Technology, http://physics.nist.gov/PhysRefData/ASD/lines_form.html. retrieved 12.09.2018.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS.
- F. Neese, Software Update: The ORCA Program System, Version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8(1), e1327 Search PubMed.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- L. A. Burns, Á. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, Density-Functional Approaches to Noncovalent Interactions: A Comparison of Dispersion Corrections (DFT-D), Exchange-Hole Dipole Moment (XDM) Theory, and Specialized Functionals, J. Chem. Phys., 2011, 134(8), 084107 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals, Mol. Phys., 2017, 115(19), 2315–2372 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, Approximate and Parallel Hartree Fock and Hybrid DFT Calculations. A Chain-of-Spheres Algorithm for the Hartree Fock Exchange, Chem. Phys., 2009, 356(1), 98–109 CrossRef CAS.
- F. Weigend, Accurate Coulomb-Fitting Basis Sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057 RSC.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, B97-3c: A Revised Low-Cost Variant of the B97-D Density Functional Method, J. Chem. Phys., 2018, 148(6), 064104 CrossRef PubMed.
- N. O. B. Lüttschwager and M. A. Suhm, Stretching and Folding of 2-Nanometer Hydrocarbon Rods, Soft Matter, 2014, 10, 4885–4901 RSC.
- M. Gawrilow, personal communication and to be published.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671 CrossRef CAS PubMed.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15(5), 2847–2862 CrossRef CAS PubMed.
- TURBOMOLE V7. 02015, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Yu. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability, J. Chem. Theory Comput., 2017, 13(7), 3185–3197 CrossRef CAS PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, Levels of Symmetry Adapted Perturbation Theory (SAPT). I. Efficiency and Performance for Interaction Energies, J. Chem. Phys., 2014, 140(9), 094106 CrossRef PubMed.
- J. S. Lomas, 1H NMR Spectra of Ethane-1,2-diol and other Vicinal Diols in Benzene: GIAO/DFT Shift Calculations, Magn. Reson. Chem., 2013, 51(1), 32–41 CrossRef CAS PubMed.
- N. Seurre, K. Le Barbu-Debus, F. Lahmani, A. Zehnacker, N. Borho and M. A. Suhm, Chiral recognition between lactic acid derivatives and an aromatic alcohol in a supersonic expansion: electronic and vibrational spectroscopy, Phys. Chem. Chem. Phys., 2006, 8, 1007–1016 RSC.
- N. Borho, M. A. Suhm, K. Le Barbu-Debus and A. Zehnacker, Intra- vs. intermolecular hydrogen bonding: dimers of alpha-hydroxyesters with methanol, Phys. Chem. Chem. Phys., 2006, 8, 4449–4460 RSC.
- K. Le Barbu-Debus. The Role of Deformation Energy of Bifunctional Entities on the Formation of Diastereoisomers. in Chiral Recognition in the Gas Phase, ed. A. Zehnacker, CRC Press, 2010, ch. 4, pp. 47–59 Search PubMed.
- R. Sillanpää, M. Leskelä, L. Hiltunen, A. Dorfman, W. B. Upholt and C. R. Enzell, Crystal and Molecular Structures of (±)trans- and cis-1,2-Cyclohexanediols, Acta Chem. Scand. Ser. B, 1984, 38, 249–254 CrossRef.
- P. G. Jones, M. R. Edwards and A. J. Kirby, Bond Length and Reactivity. The Pinacol Rearrangement. 1. Redetermination of the Structure of trans-Cyclohexane-1,2-diol, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45(2), 244–247 CrossRef.
- J. R. Maple, U. Dinur and A. T. Hagler, Derivation of Force Fields for Molecular Mechanics and Dynamics from Ab Initio Energy Surfaces, Proc. Natl. Acad. Sci. U. S. A., 1988, 85(15), 5350–5354 CrossRef CAS PubMed.
- M. J. Hwang, T. P. Stockfisch and A. T. Hagler, Derivation of Class II Force Fields. 2. Derivation and Characterization of a Class II Force Field, CFF93, for the Alkyl Functional Group and Alkane Molecules, J. Am. Chem. Soc., 1994, 116(6), 2515–2525 CrossRef CAS.
- P. Das, P. K. Das and E. Arunan, Conformational Stability and Intramolecular Hydrogen Bonding in 1,2-Ethanediol and 1,4-Butanediol, J. Phys. Chem. A, 2015, 119(16), 3710–3720 CrossRef CAS PubMed.
- D. L. Howard, P. Jørgensen and H. G. Kjaergaard, Weak Intramolecular Interactions in Ethylene Glycol Identified by Vapor Phase OH-Stretching Overtone Spectroscopy, J. Am. Chem. Soc., 2005, 127(48), 17096–17103 CrossRef CAS PubMed.
- G. Avila, J. M. Fernández, G. Tejeda and S. Montero, The Raman Spectra and Cross-Sections of H2O, D2O, and HDO in the OH/OD Stretching Regions, J. Mol. Spectrosc., 2004, 228(1), 38–65 CrossRef CAS.
- M. Albrecht, C. A. Rice and M. A. Suhm, Elementary Peptide Motifs in the Gas Phase: FTIR Aggregation Study of Formamide, Acetamide, N-Methylformamide, and N-Methylacetamide, J. Phys. Chem. A, 2008, 112(33), 7530–7542 CrossRef CAS PubMed.
- D. Bernhard, F. Dietrich, M. Fatima, C. Perez, A. Poblotzki, G. Jansen, M. A. Suhm, M. Schnell and M. Gerhards, Multi-Spectroscopic and Theoretical Analyses on the Diphenyl Ether–tert-Butyl Alcohol Complex in the Electronic Ground and Electronically Excited State, Phys. Chem. Chem. Phys., 2017, 19(27), 18076–18088 RSC.
- W. Y. Sohn, M. Kim, S.-S. Kim, Y. D. Park and H. Kang, Solvent-assisted conformational isomerization and the conformationally-pure REMPI spectrum of 3-aminophenol, Phys. Chem. Chem. Phys., 2011, 13, 7037–7042 RSC.
- W. Y. Sohn, K.-J. Cho, S. Y. Lee, S. S. Kang, Y. D. Park and H. Kang, Solvent-assisted conformational isomerization (SACI) of meta-substituted phenols: Tuning relative stability, isomerization barrier, and IVR rate, Chem. Phys. Lett., 2012, 525–526, 37–43 CrossRef CAS.
- D. Chopra, T. N. Guru Row, E. Arunan and R. A. Klein, Crystalline Ethane-1,2-diol does not have Intra-Molecular Hydrogen Bonding: Experimental and Theoretical Charge Density Studies, J. Mol. Struct., 2010, 964(1), 126–133 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Interactive and static structures, tables of experimental and computational details, energy diagrams for different levels of calculation, and additional experimental spectra. See DOI: 10.1039/c9cp04943f |
| This journal is © the Owner Societies 2020 |