Open Access Article
Open Access ArticleAttosecond transient absorption spooktroscopy: a ghost imaging approach to ultrafast absorption spectroscopy
Taran
Driver†
 abc,
Siqi
Li†
abc,
Siqi
Li†
 bd,
Elio G.
Champenois
a,
Joseph
Duris
b,
Daniel
Ratner
b,
Thomas J.
Lane
b,
Philipp
Rosenberger
aef,
Andre
Al-Haddad
g,
Vitali
Averbukh
c,
Toby
Barnard
c,
Nora
Berrah
bd,
Elio G.
Champenois
a,
Joseph
Duris
b,
Daniel
Ratner
b,
Thomas J.
Lane
b,
Philipp
Rosenberger
aef,
Andre
Al-Haddad
g,
Vitali
Averbukh
c,
Toby
Barnard
c,
Nora
Berrah
 h,
Christoph
Bostedt
gi,
Philip H.
Bucksbaum
adj,
Ryan
Coffee
ab,
Louis F.
DiMauro
k,
Li
Fang
k,
Douglas
Garratt
c,
Averell
Gatton
b,
Zhaoheng
Guo
ad,
Gregor
Hartmann
lo,
Daniel
Haxton
m,
Wolfram
Helml
h,
Christoph
Bostedt
gi,
Philip H.
Bucksbaum
adj,
Ryan
Coffee
ab,
Louis F.
DiMauro
k,
Li
Fang
k,
Douglas
Garratt
c,
Averell
Gatton
b,
Zhaoheng
Guo
ad,
Gregor
Hartmann
lo,
Daniel
Haxton
m,
Wolfram
Helml
 n,
Zhirong
Huang
bd,
Aaron
LaForge
n,
Zhirong
Huang
bd,
Aaron
LaForge
 h,
Andrei
Kamalov
ad,
Matthias F.
Kling
h,
Andrei
Kamalov
ad,
Matthias F.
Kling
 aef,
Jonas
Knurr
a,
Ming-Fu
Lin
b,
Alberto A.
Lutman
b,
James P.
MacArthur
bd,
Jon P.
Marangos
c,
Megan
Nantel
bd,
Adi
Natan
a,
Razib
Obaid
aef,
Jonas
Knurr
a,
Ming-Fu
Lin
b,
Alberto A.
Lutman
b,
James P.
MacArthur
bd,
Jon P.
Marangos
c,
Megan
Nantel
bd,
Adi
Natan
a,
Razib
Obaid
 h,
Jordan T.
O'Neal
ad,
Niranjan H.
Shivaram
h,
Jordan T.
O'Neal
ad,
Niranjan H.
Shivaram
 b,
Aviad
Schori
a,
Peter
Walter
b,
Anna
Li Wang
aj,
Thomas J. A.
Wolf
b,
Aviad
Schori
a,
Peter
Walter
b,
Anna
Li Wang
aj,
Thomas J. A.
Wolf
 a,
Agostino
Marinelli
*b and
James P.
Cryan
a,
Agostino
Marinelli
*b and
James P.
Cryan
 *ab
*ab
aStanford PULSE Institute, SLAC National Accelerator Laboratory, USA. E-mail: jcryan@slac.stanford.edu
bSLAC National Accelerator Laboratory, USA. E-mail: marinelli@slac.stanford.edu
cThe Blackett Laboratory, Department of Physics, Imperial College London, UK
dDepartment of Physics, Stanford University, USA
eMax-Planck-Institut für Quantenoptik, Germany
fPhysik Department, Ludwig-Maximilians-Universität Munich, Germany
gPaul Scherrer Institut, Switzerland
hPhysics Department, University of Connecticut, USA
iLUXS Laboratory for Ultrafast X-ray Sciences, École Polytechnique Fédérale de Lausanne, Switzerland
jDepartment of Applied Physics, Stanford University, USA
kDepartment of Physics, The Ohio State University, USA
lInstitut für Physik und CINSaT, Universität Kassel, Germany
mKLA Tencor Corporation, USA
nZentrum für Synchrotronstrahlung, Technische Universität Dortmund, Germany
oHelmholtz-Zentrum Berlin, Germany
First published on 26th November 2019
Abstract
The recent demonstration of isolated attosecond pulses from an X-ray free-electron laser (XFEL) opens the possibility for probing ultrafast electron dynamics at X-ray wavelengths. An established experimental method for probing ultrafast dynamics is X-ray transient absorption spectroscopy, where the X-ray absorption spectrum is measured by scanning the central photon energy and recording the resultant photoproducts. The spectral bandwidth inherent to attosecond pulses is wide compared to the resonant features typically probed, which generally precludes the application of this technique in the attosecond regime. In this paper we propose and demonstrate a new technique to conduct transient absorption spectroscopy with broad bandwidth attosecond pulses with the aid of ghost imaging, recovering sub-bandwidth resolution in photoproduct-based absorption measurements.
Introduction
The rearrangement of electrons is the first step in all photochemical reactions. The ability to produce pulses with a time duration shorter than a femtosecond has enabled the probing of electron dynamics on its natural timescale.1–4 This attosecond revolution has been led by the development of sources based on high harmonic generation (HHG).5 These technological developments have enabled the study of autoionisation,6 Auger decay,7 and charge migration8 in the time-domain. The extension of attosecond pulses to soft X-ray wavelengths should enable the study of coherent electronic phenomena with atomic site specificity. One particular class of attosecond spectroscopy commonly used with attosecond sources is attosecond transient absorption spectroscopy (ATAS).9–12 ATAS measures the spectral response of a sample to sequential interaction with a pump pulse and a broadband attosecond probe pulse. Using photon energies in the soft X-ray regime, ATAS can probe resonant transitions between inner valence or core electrons and unoccupied states in the valence shell.13 The spatial localisation of the core orbitals means excitation of electrons from these orbitals to valence electronic states provides an atomic-site specific probe of transient valence electronic structure. The recent demonstration of isolated attosecond pulses from an X-ray free-electron laser (XFEL), with photon energies tunable across the soft X-ray regime and spectral brightness six orders of magnitude greater than HHG sources,14 enables numerous previously unfeasible attosecond measurements. However, the implementation of ATAS with an attosecond XFEL source presents a number of challenges. Here, we introduce and demonstrate a new experimental implementation to perform ATAS at an XFEL.ATAS is an extension of X-ray transient absorption spectroscopy (TAS), which is itself a time domain implementation of X-ray absorption spectroscopy. Traditional X-ray absorption spectroscopy of a target is performed by scanning the central photon energy of a narrow linewidth X-ray source. For each photon energy the total number of photons absorbed by the target is measured, either by directly measuring a depletion in the transmitted photons13 or by measuring the total ion or electron (photoproducts) yield produced from the target following interaction with the incident light. The latter serves as a direct indicator of the number of absorbed photons. In X-ray TAS, a pump laser pulse first creates an excited state in the system being probed. The time evolution of this excited state is mapped out by measuring the X-ray absorption spectrum as a function of delay between the pump and X-ray pulses. This technique has proved successful in measuring the ultrafast evolution of excited systems. For example, Wolf et al. employed this technique at an XFEL by scanning a narrow bandwidth X-ray pulse over the near-edge features of gas phase thymine in order to observe the molecular deactivation process following ultraviolet excitation.15
Probing dynamics that evolve on the femtosecond or sub-femtosecond timescale requires probe pulses with a broad bandwidth (a Fourier transform limited light pulse with 0.5 fs duration has a spectral bandwidth of 3.2 eV). Therefore, the Fourier limit fundamentally restricts the application of traditional photoproduct-based TAS measurements on the attosecond timescale. Simply scanning the central wavelength of a sub-femtosecond X-ray pulse will yield an X-ray absorption spectrum with poor resolution due to the large spectral bandwidth covered by each attosecond pulse.
To resolve this issue, ATAS was developed to measure the attosecond transient absorption spectrum of excited samples. In ATAS, transient absorption spectra are obtained by spectrally resolving the depletion in the number of probe pulse photons transmitted through the sample under analysis.16 The transmitted light is dispersed with a grating and measured on a spatially resolving detector. Measurement of the transient absorption spectrum at a specific pump–probe delay involves acquiring a reference spectrum without the sample or without the pump pulse, and comparing this to the absorption spectrum taken at the pump–probe delay in question. The advantage of this technique is that the spectral resolution of the measurement is dictated by the spectrometer resolution, and not by the bandwidth of the incident pulse. This breaks the requirement for narrow bandwidth pulses to maintain practical spectral resolution. The broad success of such measurements in resolving ultrafast dynamics in molecules and solids is the topic of recent reviews.17,18
X-ray free electron lasers (XFELs) are an emerging source of ultrafast soft X-ray pulses with few-femtosecond to sub-femtosecond duration.19 The tunability and unprecedented brightness of XFEL sources provides a powerful tool for the experimental investigation of ultrafast molecular dynamics.20 Recently, GW-scale soft X-ray isolated attosecond pulses (IAPs) were demonstrated at the Linac Coherent Light Source (LCLS), using an implementation of the enhanced self amplified spontaneous emission (ESASE) technique.14 The spectral brightness of this attosecond source is six orders of magnitude greater than any tabletop HHG-based source of IAPs, facilitating non-linear spectroscopies. The inherent spectral bandwidth of attosecond pulses greatly limits the spectral resolution of traditional photoproduct-based absorption measurements. However, the inevitable instabilities associated with XFEL operation make implementing standard ATAS difficult. A photon depletion-based measurement benefits from a highly stable spectrum: since the number of absorbed photons is determined by taking the difference between transmitted spectra with and without the target, variation in the spectrum of the source produces differences between reference and measurement spectra. This adds noise to the transient absorption measurement. The signal-to-noise of an ATAS measurement also places stringent requirements on the density and absorption cross section of the sample under analysis. For a good quality measurement, the spectrum must be stable and the photon depletion must be sufficient to be both measurable, and significant compared to the spectral instabilities.
So while it is possible to implement a photon depletion-based measurement at an XFEL, a photoproduct-based scheme is desirable for a number of reasons. Electrons or ions produced by photoemission can be detected with very high efficiency, even permitting detection of the absorption of a single X-ray photon. Additionally, the information content of a photoproduct-based scheme surpasses that of photon-depletion spectroscopy if a differential measurement of the photoproducts (e.g. in energy, mass, momentum or angular distribution) can also be performed. In this work, we demonstrate how correlation techniques can be used to recover a high resolution absorption spectrum from a photoproduct-based measurement when the probing X-ray pulse has a bandwidth larger than the absorption features being measured. The photoproduct yield can be correlated with shot-to-shot changes in the incident X-ray spectrum. Absorption spectra may be derived from these correlations using an algorithm that is related to so-called ‘ghost imaging’ methods.
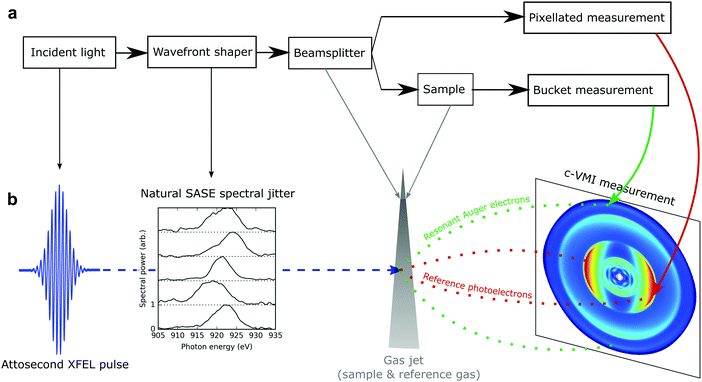
Ghost imaging
Classical ghost imaging is an experimental technique which can retrieve spatially resolved information about a sample using only a single pixel camera (or “bucket” detector) and knowledge of the spatial structure of the source which illuminates the sample. A classical ghost imaging experiment (detailed in Fig. 1) typically consists of a beamsplitter that separates the incident wavefront into two replicas. One arm is used to analyse the wavefront with some form of pixellated detector. For every exposure i, the detector records the wavefront Ai. The other arm passes through the sample under analysis, and the total transmission, bi, is measured by the bucket detector. The coincident measurement of the two arms is repeated many times. By correlating the shot-to-shot variation in the patterned wavefront with the measured bucket intensity that each wavefront produces, the structure of the sample can be inferred without directly detecting it, hence the term “ghost imaging”.The classical ghost imaging problem can be formulated mathematically, across n different measurements with a pixellated detector of m pixels, as a linear matrix multiplication:
| b = Ax. | (1) |
In this work, we exploit the natural fluctuations in the spectral profile of ESASE pulses and apply ghost imaging in the spectral domain to recover sub-bandwidth resolution photoproduct-based absorption spectra using attosecond X-ray pulses from an XFEL. Our demonstration enables attosecond-resolution transient absorption experiments using information-rich photoproduct measurements, and with spectral resolution limited only by the properties of the photon spectrometer and the variation in the X-ray spectrum.
Experimental demonstration
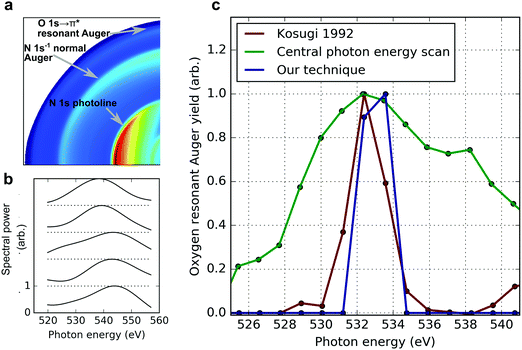
To demonstrate our technique, we have performed an experiment at the LCLS using a static absorption measurement at the oxygen K-edge of nitric oxide (NO). The attosecond X-ray pulses used to excite the system are generated by the ESASE method.14 The attosecond X-ray pulse is tuned near the 1s → 2π* resonance of the oxygen atom in NO, at 532.7 eV.37 At this photon energy, the attosecond ESASE pulses have a median bandwidth of ∼5.5 eV.14 Using a co-axial velocity map imaging spectrometer (c-VMI),38 which projects the charged particle momentum distribution along the propagation axis of the X-rays, we measure photoelectrons with kinetic energies up to ∼600 eV. This enables measurement of the resonant Auger electrons produced following relaxation of the resonant core excitation. In the c-VMI, the momentum of the ionised electron in the plane perpendicular to the direction of the laser propagation maps linearly to the position at which it arrives at the detector plane. The detector is a microchannel plate coupled to a phosphor screen, which is imaged using a CCD camera.38 Given the cylindrical symmetry present in our measurement, it is possible to reconstruct the full three-dimensional momentum distribution of the emitted electrons from the measured two-dimensional distribution using an inverse Abel transformation. This has been performed on our measured data using the pBasex algorithm,39 and the c-VMI images shown in panel b of Fig. 1 and panel a of Fig. 2 are a two-dimensional slice through the center of the three-dimensional reconstruction of the momentum distribution. A threshold is applied to the raw images (1024 × 1024 pixels) before the data is convolved with a Gaussian kernel (σ = 25) to remove noise before Abel inversion. The inverted one-dimensional spectra are Gaussian filtered (σ = 5) to remove high-frequency artefacts associated with the inverse Abel transformation process. Some functional imperfections at the high operating voltages of the c-VMI in this mode of operation contribute to the measured angular anisotropy of the normal and resonant Auger in panel a of Fig. 2. The energy resolution of the c-VMI spectrometer is ∼5–10% ΔE/E (for the set of measurements performed here this is reduced by counting noise), which precludes a spectrally resolved measurement of the high energy resonant Auger electron spectrum, but is sufficient to measure the total resonant Auger yield. This provides a direct measurement of the 1s → 2π* absorption cross section: the number of photons on resonance with this transition maps linearly to the number of resonant Auger electrons produced.As described above, a standard measurement of the near-edge absorption spectrum involves scanning the central photon energy and measuring the yield of resultant photoproducts at each energy. This was performed by Kosugi et al.37 who used narrow bandwidth synchrotron radiation to obtain a high-resolution measurement of the oxygen 1s → 2π* resonance, and this data is reproduced in red in panel c of Fig. 2. At the LCLS, this measurement involves scanning the energy of the lasing electron beam, which changes the wavelength of the X-ray radiation according to the well-known FEL resonance condition.40 Performing this measurement using the broad bandwidth attosecond ESASE pulses produces the absorption spectrum plotted in green in Fig. 2. The measurement of this absorption feature has extremely low resolution because it involves the convolution of the resonant feature with both the broad bandwidth of the attosecond pulses and additional photon energy jitter.14 The asymmetry in the measured absorption spectrum is due to contamination by high-lying Rydberg states, converging to the oxygen K-edge. Both these excitation channels result in a high-energy electron which we are unable to spectrally separate from the oxygen resonant Auger electron. A combination of the broad bandwidth of the attosecond pulses, and the shot-to-shot jitter of the central photon energy for a given electron beam energy, ensures there is already a substantial probability to excite the pre-edge Rydberg series, or ionise the K-shell electrons directly, when the central photon energy is set below these values.
Using the correlations present in the data set, we can increase the resolution of the absorption measurement and obtain sub-bandwidth resolution. Casting the problem in the form of eqn (1), we consider 4060 individual measurements, corresponding to the same number of single XFEL shots each at pulse energy 70 μJ or higher. The yield of resonant Auger electrons is used as the bucket detector reading, b, and the single-shot nitrogen photoelectron spectrum is used as the pixellated detection, A. The unknown vector x now represents the target absorption spectrum. The nitrogen K-shell photoline serves as an approximate measurement for the X-ray spectrum, and is recorded by the c-VMI in coincidence with the Auger electron yield on a shot-to-shot basis, as shown in panel a of Fig. 2. Thus in our implementation we use as the “beamsplitter” the excitation of two independent channels in the gas atoms; i.e. K-shell photoionisation to produce the pixellated measurement of the incoming spectrum and resonant O 1s → 2π* excitation to produce the bucket measurement of the number of photons absorbed. Some example shot-to-shot photon spectra taken from the c-VMI measurement are shown in panel b. The limited resolution of the c-VMI for high energy operations results in lower than expected resolution for an X-ray photon spectrometer. We use a standard optimisation tool known as the alternating direction method of multipliers (ADMM41), to solve eqn (1). This enables regularisation of the retrieved solution according to expected non-negativity, sparseness, and smoothness. We also account for a pulse energy-dependent electron background (primarily due to valence ionisation by the incident X-ray pulse) by introducing an extra term to allow the algorithm to separate the signal from background-related contributions. So eqn (1) becomes:
| b =Ax + Px0, | (2) |
We performed a comparison to characterise the signal-to-noise in our experimental measurement. For the measured spectrum and pulse energy of each of the 4060 shots, we use the retrieved values of x and x0 to calculate the predicted value which we would expect to measure in the bucket detector for that shot. We compare this expected value to the actual measured value in the bucket detector for each shot. This is not perfectly equivalent to extracting the signal-to-noise of the overall measurement, because there is noise in the spectral measurement as well as the bucket measurement. Nonetheless, it serves as a useful approximation to the overall fidelity of the experimental measurement. We find that the actual bucket measurement deviates from the expected bucket measurement by ∼40% of the expected measurement yield, on average. The noise in our experimental measurement has been overcome by significantly overdetermining eqn (2) using a large number of single shot measurements. To check the validity of our reconstruction, we performed one hundred separate randomisations of the order of the bucket detector while maintaining the original order of the spectral measurements, and repeated the reconstruction for each randomisation. The algorithm did not retrieve the correct absorption spectrum on any iteration. Our experimental results indicate that the variation inherent to ESASE operation provides sufficient shot-to-shot spectral differences to successfully reconstruct the sub-bandwidth absorption spectrum.
Discussion
For our technique to work, it is critical to have sufficient variation in the measurement matrix A, which corresponds to sufficient shot-to-shot variation in the X-ray spectrum for our measurements. Moreover, the variation has to be detectable within the instrument resolution. We explore the spectral variation necessary for our correlation analysis using two different metrics.First, we consider the different modes of variation in our experimental spectral measurements. Each of the 4060 c-VMI measured spectra (representative examples in panel b of Fig. 2) can be well-approximated by the Gram–Charlier expansion of a Gaussian curve, up to the fourth moment. We plot the shot-to-shot variation of the first moment (mean), second central moment (standard deviation), third standardised moment (skew) and excess fourth standardised moment (kurtosis) of the measured X-ray spectra in panels a–d of Fig. 3. The measured standard deviation corresponds to a significantly larger spectral bandwidth than the ∼5.5 eV14 measured for ESASE pulses at these photon energies, which is a direct result of the reduced resolution of the c-VMI spectrometer when collecting high energy electrons. Using this moment-based expansion allows us to isolate the variation of each of the spectral moments to explore the dependence of the correlation method on each of these parameters. The traditional method of scanning the central photon energy corresponds to the limit of changing only the first moment. From these moment distributions, we construct different sets of 4060 simulated X-ray spectra to test the performance of ADMM in simulation. First, we artificially narrow the variation in the second, third and fourth moments by a factor of two, while allowing the first moment to vary according to the measured experimental distribution. We then create additional sets of simulated spectra where each higher-order moment is consecutively allowed to vary fully according to its measured distribution, sequentially increasing the contribution to the spectral variation from higher-order moments. We also perform this simulation using our 4060 experimentally measured single-shot spectra.
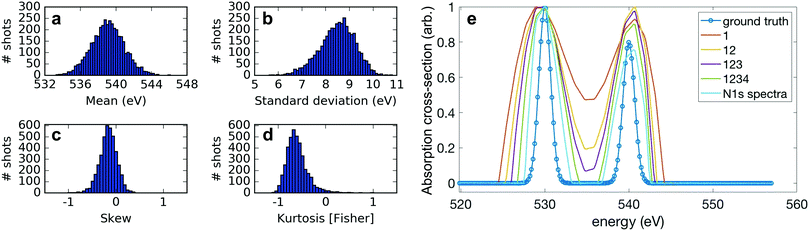 | ||
| Fig. 3 (a–d) Shot-to-shot variation of the four normalised central moments of the spectra used in Fig. 2. (e) Performance of ADMM as the full variation of each moment is added. Using the measured variation in each of the four moments as shown in panels a–d, we simulated different sets of 4060 random spectra where some moments were allowed to vary as measured (these are indicated in the figure legend) and the variation of some moments was artificially restricted. The absorption spectra retrieved for each of these different sets of spectra is plotted against the ground truth used, showing the importance of variation in higher order moments to our technique. “N1s spectra” labels the actual experimental data measured by the c-VMI. | ||
To test the reconstruction using these simulated data sets, we simulate a ground-truth absorption spectrum of two Gaussian peaks separated by 10 eV with root-mean-square (rms) width of 0.7 eV. The simulated bucket detector reading is generated by multiplying the simulated spectra with the ground truth. The results of the different reconstructions are shown in Fig. 3. Including higher moments in the spectra captures more spectral variation and therefore improves the resolution of the reconstruction. The highly similar performance of the reconstruction where all four moments may vary fully and the experimental data indicates that all the experimental variation is well captured by the four moments. Therefore in our ghost imaging technique, we exploit higher moments of variation in the spectra to retrieve sub-bandwidth structures in the absorption spectrum.
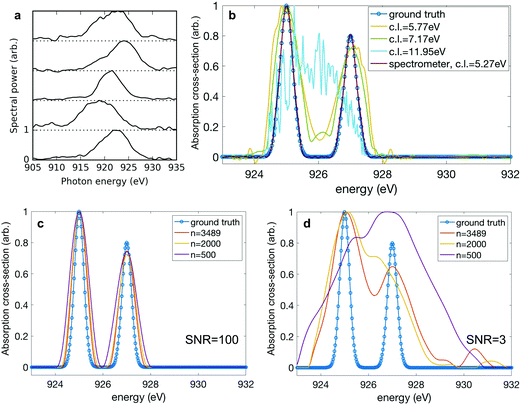
While the variation of the spectral moments serves as a useful and intuitive guide to assess the variation in our data, fundamentally the resolution of our technique is determined by the degree of correlation between neighbouring pixels in the detector. This pixel-to-pixel correlation contains information about the inherent variation in the spectra as well as the spectrometer resolution. In the limiting case where there is no correlation between spectrometer pixels, the resolution is limited simply by the detector resolution. As mentioned above, when configured to collect high energy Auger electrons, the resolution of the c-VMI spectrometer (i.e. the measurement of the nitrogen 1s photoelectrons) is significantly diminished compared to what would be available from a typical X-ray photon spectrometer or electron spectrometer under standard operating parameters. For this reason, in order to further explore the limitations of the correlation absorption spectroscopy technique, we include another set of spectral measurements taken by a photon spectrometer. The single-shot spectra shown in panel a of Fig. 4 are representative examples from a set of 3489 X-ray pulses generated using the ESASE technique at the LCLS.14 To characterise this pixel-to-pixel correlation, we define the correlation length to be the distance between two pixels where the correlation coefficient falls from 1 to 1/e. To extract a single correlation length from a set of different spectra, we select the pixels where the averaged spectral intensity is above half maximum, and we average the correlation lengths over the selected pixels. The correlation length for the measured experimental spectra is 5.27 eV. To explore the effect of changing correlation length, we start with the experimental data and convolve it with a Gaussian filter of successively increasing width to artificially increase the correlation length of the spectra. Again, we simulate a ground truth absorption spectrum. This time we use two Gaussian peaks of rms width 0.2 eV separated by 2 eV, and the simulated bucket is again constructed by multiplying the convolved spectra with the ground truth. The effect of increasing the correlation length is shown in panel b of Fig. 4. When the correlation length is below 6 eV, we see that the reconstruction captures the thin width of the ground truth. As the correlation length increases, the quality of the reconstruction worsens, as expected. At a correlation length of 11.95 eV, the reconstruction fails to capture any elements of the spectral shape.
The performance of the matrix inversion is also dependent on the number of shots across which the measurement was taken, particularly in the case of a noisy measurement. In Fig. 2, we are able to overcome experimental noise by greatly overdetermining our ghost imaging problem. Analogous to averaging over many shots in a simple spectral measurement, this reduces the overall effect of noise on the measurement. To explore this limit, we randomly select a subset of the full 3489 spectra and use these to produce simulated bucket measurements, to which we randomly add measurement noise on a shot-to-shot basis according to a Gaussian distribution. The noise distribution is centred on zero and for a given signal-to-noise ratio (SNR) has width σ = signal/SNR. We test the sensitivity of the reconstruction using ADMM to the number of shots used in the reconstruction, at low (SNR = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and high (SNR = 100
1) and high (SNR = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) signal-to-noise regimes for the bucket measurement. Panel c of Fig. 4 shows that at high signal-to-noise in the bucket, it is possible to faithfully reconstruct the absorption spectrum even at low numbers of shots. In future experiments the counting of electrons or ions could be performed at very high fidelity, with high signal-to-noise and good quantum efficiency. Panel d shows that in the scenario where the bucket measurement is noisier, the reconstruction fails to capture the correct width of the absorption features and the quality of the recovered spectrum significantly degrades at a lower number of shots.
1) signal-to-noise regimes for the bucket measurement. Panel c of Fig. 4 shows that at high signal-to-noise in the bucket, it is possible to faithfully reconstruct the absorption spectrum even at low numbers of shots. In future experiments the counting of electrons or ions could be performed at very high fidelity, with high signal-to-noise and good quantum efficiency. Panel d shows that in the scenario where the bucket measurement is noisier, the reconstruction fails to capture the correct width of the absorption features and the quality of the recovered spectrum significantly degrades at a lower number of shots.
We note that noise in the bucket measurement is not equivalent to noise in the spectral measurement A. In a typical linear regression-type problem, it is only the dependent variable (i.e. the bucket measurement) which is assumed to have measurement noise. The independent variable (or pixellated measurement) is usually assumed to be measured with zero error. As a result, measurement noise in the dependent variable (or bucket measurement) results in uncertainty in the retrieved result, whereas noise in the independent variable leads to a biasing of the retrieved result towards a structureless result. This biasing is a well-known phenomenon and has been dubbed regression dilution.42 In Fig. 2 we investigate the effect of noise in the yield of Auger electrons (the dependent variable) only. We have also investigated the effect of measurement noise in the independent variable A, i.e. the spectral measurement. We found that at high numbers of shots our reconstruction method is robust in simulation up to a significant degree (∼10%) of random noise in the spectral measurement (A).
Conclusions
In this paper, we have proposed and demonstrated a correlation-based analysis to conduct attosecond transient absorption spectrum (ATAS) measurements at an XFEL facility. With the development of attosecond pulses from XFELs, attosecond time resolution measurements at an XFEL have become possible. However, the standard implementation of transient absorption measurements at XFELs will suffer from low spectral resolution due to the wide bandwidth of such short pulses. The correlation-based technique introduced in this paper solves this problem by exploiting the inherent shot-to-shot spectral jitter of the X-ray pulses from an XFEL. We have experimentally demonstrated this technique using an experiment where the X-ray spectrum and the photoproduct (i.e. resonant Auger electron) yield are measured in coincidence, with a single velocity map imaging spectrometer. This measurement demonstrates good agreement with previous high-resolution measurements. The fundamental limit of the correlation-based analysis is no longer the spectral bandwidth of the X-ray source, but rather the spectrometer resolution and the variation in the spectrum of the X-ray pulse. We have explored the effects of variation in the X-ray spectrum as quantified by the variation in different spectral moments and by the correlation length. It is worth noting that we found in further simulation that the quality of the reconstruction is more sensitive to decreasing spectrometer resolution than to decreasing variation in the spectra, in the regime where are not dominated by noise. Practically, this means that high spectrometer resolution should be prioritised in experimental implementations, without introducing additional measurement noise. As we have shown, an optimally designed experiment should take into account spectrometer resolution, available variation in the spectra, and the noise level of the measurements. For retrieving time-resolved absorption spectra the data would first have to be sorted on pump–probe delay, an operation that will be more feasible for the high shot rates anticipated in future high rep-rate machines.It is possible to extend our method beyond X-ray absorption spectroscopy. Provided a differential measurement of the photoproducts (e.g. in energy, mass, momentum or angular distribution), it is possible to reconstruct the photon energy-dependent photoproduct measurement. Eqn (1) can be easily adapted to include multiple bucket detectors. In the case of the experimental implementation considered here, this could correspond to a measurement of the energy-dependent resonant Auger spectrum. Each pixel of the Auger electron kinetic energy spectrum would be an independent bucket measurement. Then b becomes a matrix of size n × p, where n is the number of XFEL shots as defined above, and p is the number of pixels in the Auger electron kinetic energy spectrum. With this change, x becomes an m × p matrix, where m remains the number of pixels in the absorption spectrum. This new map, x, is then the photon energy-dependent resonant Auger spectrum. Such a map is extremely powerful because it provides information not only about the unoccupied electronic orbitals involved in the absorption process, but also on the occupied electronic orbitals that are involved in the Auger process. Recording these maps as a function of time-delay would give an even more precise probe of attosecond charge dynamics, similar to the information given in a resonant inelastic X-ray scattering (RIXS) measurement.43
Author contributions
J. P. C., S. L., A. M., and T. D. conceived the research. S. L. and T. D. realised the method. A. M. and J. D. developed the attosecond XFEL source. All authors contributed to collection of the experimental data and writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The contributions from TD, PHB, AK, AN, JTO, TJAW, ALW, and JPC were supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Chemical Sciences, Geosciences, and Biosciences Division (CSGB); Support for SL, JD, JPMac, and AM was provided by DOE, BES Scientific User Facilities Division Field Work Proposal 100317; EGC was supported by the DOE Laboratory Directed Research and Development program at SLAC National Accelerator Laboratory, under contract DE-AC02-76SF00515. P. R. and M. F. K. acknowledge additional support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) via KL-1439/10, and the Max Planck Society. G. H. acknowledges the DFG Projektnummer 328961117 SFB 1319 ELCH. N. B., R. O. and A. L. acknowledge support of DOE-BES-CSGB grant No. DE-SC0012376. T. D. and J. P. Mar. were partially supported by UK EPSRC grant EP/R019509/1. D. G. acknowledges support of UK EPSRC grant EP/L016524/1. L. F. D. acknowledges support from NSF grant No. PHY-1605042. L. F. acknowledges support from DOE-BES-CSGB grant No. DE-FG02-04ER15614. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.References
- F. Krausz and M. Ivanov., Attosecond physics, Rev. Mod. Phys., 2009, 81(1), 163–234 CrossRef.
- S. R. Leone, C. W. McCurdy, J. Burgdörfer, L. S. Cederbaum, Z. Chang, N. Dudovich, J. Feist, C. H. Greene, M. Ivanov, R. Kienberger, U. Keller, M. F. Kling, Z.-H. Loh, T. Pfeifer, A. N. Pfeiffer, R. Santra, K. Schafer, A. Stolow, U. Thumm and M. J. J. Vrakking, What will it take to observe processes in ‘real time’?, Nat. Photonics, 2014, 8(3), 162–166 CrossRef CAS.
- F. Lépine, M. Y. Ivanov and M. J. J. Vrakking, Attosecond molecular dynamics: fact or fiction?, Nat. Photonics, 2014, 8(3), 195–204 CrossRef.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Attosecond Electron Dynamics in Molecules, Chem. Rev., 2017, 10760–10825 CrossRef CAS.
- M. Chini, K. Zhao and Z. Chang, The generation, characterization and applications of broadband isolated attosecond pulses, Nat. Photonics, 2014, 8(3), 178–186 CrossRef CAS.
- H. Wang, M. Chini, S. Chen, C.-H. Zhang, F. He, Y. Cheng, Y. Wu, U. Thumm and Z. Chang, Attosecond time-resolved autoionization of argon, Phys. Rev. Lett., 2010, 105(14), 143002 CrossRef.
- M. Drescher, M. Hentschel, R. Kienberger, M. Uiberacker, V. Yakovlev, A. Scrinzi, T. Westerwalbesloh, U. Kleineberg, U. Heinzmann and F. Krausz, Time-resolved atomic inner-shell spectroscopy, Nature, 2002, 419(6909), 803–807 CrossRef CAS.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses, Science, 2014, 346(6207), 336–339 CrossRef CAS.
- E. Goulielmakis, V. S. Yakovlev, A. L. Cavalieri, M. Uiberacker, V. Pervak, A. Apolonski, R. Kienberger, U. Kleineberg and F. Krausz, Attosecond Control and Measurement: Lightwave Electronics, Science, 2007, 317(5839), 769–775 CrossRef CAS.
- G. Sansone, T. Pfeifer, K. Simeonidis and A. I. Kuleff, Electron Correlation in Real Time, ChemPhysChem, 2012, 13(3), 661–680 CrossRef CAS.
- A. R. Attar, A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, K. D. Closser, D. Prendergast and S. R. Leone, Femtosecond X-ray spectroscopy of an electrocyclic ring-opening reaction, Science, 2017, 356(6333), 54–59 CrossRef CAS.
- Y. Pertot, C. Schmidt, M. Matthews, A. Chauvet, M. Huppert, V. Svoboda, A. von Conta, A. Tehlar, D. Baykusheva, J.-P. Wolf and H. J. Wörner, Time-resolved X-ray absorption spectroscopy with a water window high-harmonic source, Science, 2017, 355(6322), 264–267 CrossRef CAS.
- C. Bressler and M. Chergui, Ultrafast X-ray Absorption Spectroscopy, Chem. Rev., 2004, 104(4), 1781–1812 CrossRef CAS.
- J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, Z. Zhang, P. Rosenberger, J. W. Aldrich and R. Coffee, et al., Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser, Nat. Photonics, 2019 DOI:10.1038/s41566-019-0549-5.
- T. J. A. Wolf, R. H. Myhre, J. P. Cryan, S. Coriani, R. J. Squibb, A. Battistoni, N. Berrah, C. Bostedt, P. Bucksbaum, G. Coslovich, R. Feifel, K. J. Gaffney, J. Grilj, T. J. Martinez, S. Miyabe, S. P. Moeller, M. Mucke, A. Natan, R. Obaid, T. Osipov, O. Plekan, S. Wang, H. Koch and M. Gühr, Probing ultrafast ππ*/nπ* internal conversion in organic chromophores via K-edge resonant absorption, Nat. Commun., 2017, 8(1), 29 CrossRef CAS PubMed.
- A. R. Beck, D. M. Neumark and S. R. Leone, Probing ultrafast dynamics with attosecond transient absorption, Chem. Phys. Lett., 2015, 624, 119–130 CrossRef CAS.
- R. Geneaux, H. J. B. Marroux, A. Guggenmos, D. M. Neumark and S. R. Leone, Transient absorption spectroscopy using high harmonic generation: a review of ultrafast X-ray dynamics in molecules and solids, Philos. Trans. R. Soc., A, 2019, 377(2145), 20170463 CrossRef CAS.
- K. Ramasesha, S. R. Leone and D. M. Neumark, Real-Time Probing of Electron Dynamics Using Attosecond Time-Resolved Spectroscopy, Annu. Rev. Phys. Chem., 2016, 67(1), 41–63 CrossRef CAS.
- R. N. Coffee, J. P. Cryan, J. Duris, W. Helml, S. Li and A. Marinelli, Development of ultrafast capabilities for X-ray free-electron lasers at the linac coherent light source, Philos. Trans. R. Soc., A, 2019, 377(2145), 20180386 CrossRef CAS.
- N. Berrah, A perspective for investigation photo-induced molecular dynamics from within with femtosecond free electron lasers, Phys. Chem. Chem. Phys., 2017, 19, 19536 RSC.
- B. I. Erkmen and J. H. Shapiro, Ghost imaging: from quantum to classical to computational, Adv. Opt. Photonics, 2010, 2, 405 CrossRef CAS.
- M. Duarte, M. Davenport, D. Takhar, J. Laska, T. Sun, K. Kelly and R. Baraniuk, Single-pixel imaging via compressive sampling, IEEE Signal Proc. Mag., 2008, 25, 83 Search PubMed.
- D. Pelliccia, A. Rack, M. Scheel, V. Cantelli and D. M. Paganin, Experimental X-ray ghost imaging, Phys. Rev. Lett., 2016, 117, 113902 CrossRef.
- H. Yu, R. Lu, S. Han, H. Xie, G. Du, T. Xiao and D. Zhu, Fourier-transform ghost imaging with hard x rays, Phys. Rev. Lett., 2016, 117, 113901 CrossRef.
- A.-X. Zhang, Y.-H. He, L.-A. Wu, L.-M. Chen and B.-B. Wang, Tabletop X-ray ghost imaging with ultra-low radiation, Optica, 2018, 5, 374 CrossRef CAS.
- R. I. Khakimov, B. M. Henson, D. K. Shin, S. S. Hodgman, R. G. Dall, K. G. H. Baldwin and A. G. Truscott, Ghost imaging with atoms, Nature, 2016, 540, 100–103 CrossRef CAS.
- S. Li, F. Cropp, K. Kabra, T. J. Lane, G. Wetzstein, P. Musumeci and D. Ratner, Electron ghost imaging, Phys. Rev. Lett., 2018, 121(11), 114801 CrossRef CAS.
- A. Schori and S. Shwartz, X-ray ghost imaging with a laboratory source, Opt. Express, 2017, 25(13), 14822–14828 CrossRef CAS.
- A. Schori, D. Borodin, K. Tamasaku and S. Shwartz, Ghost imaging with paired X-ray photons, Phys. Rev. A, 2018, 97(6), 063804 CrossRef CAS.
- Y. Klein, A. Schori, I. P. Dolbnya, K. Sawhney and S. Shwartz, X-ray computational ghost imaging with single-pixel detector, Opt. Express, 2019, 27(3), 3284–3293 CrossRef CAS PubMed.
- C. Amiot, P. Ryczkowski, A. T. Friberg, J. M. Dudley and G. Genty, Supercontinuum spectral-domain ghost imaging, Opt. Lett., 2018, 43(20), 5025–5028 CrossRef CAS PubMed.
- P. Janassek, S. Blumenstein and W. Elsäßer, Ghost spectroscopy with classical thermal light emitted by a superluminescent diode, Phys. Rev. Appl., 2018, 9(2), 021001 CrossRef CAS.
- D. A. Kalashnikov, A. V. Paterova, S. P. Kulik and L. A. Krivitsky, Infrared spectroscopy with visible light, Nat. Photonics, 2016, 10(2), 98 CrossRef CAS.
- G. Scarcelli, A. Valencia, S. Gompers and Y. Shih, Remote spectral measurement using entangled photons, Appl. Phys. Lett., 2003, 83(26), 5560–5562 CrossRef CAS.
- P. Ryczkowski, M. Barbier, A. T. Friberg, J. M. Dudley and G. Genty, Ghost imaging in the time domain, Nat. Photonics, 2016, 10(3), 167 CrossRef CAS.
- D. Ratner, J. P. Cryan, T. J. Lane, S. Li and G. Stupakov, Pump-probe ghost imaging with SASE FELs, Phys. Rev. X, 2019, 9(1), 011045 CAS.
- N. Kosugi, J-i. Adachi, E. Shigemasa and A. Yagishita, High-resolution and symmetry-resolved N and O K-edge absorption spectra of NO, J. Chem. Phys., 1992, 97(12), 8842–8849 CrossRef CAS.
- S. Li, E. G. Champenois, R. Coffee, Z. Guo, K. Hegazy, A. Kamalov, A. Natan, J. O'Neal, T. Osipov, M. Owens, D. Ray, D. Rich, P. Walter, A. Marinelli and J. P. Cryan, A co-axial velocity map imaging spectrometer for electrons, AIP Adv., 2018, 8(11), 115308 CrossRef.
- E. G. Champenois, pBASEX Abel transform inversion without polar rebinning, 2017, https://github.com/e-champenois/CPBASEX.
- C. Pellegrini, A. Marinelli and S. Reiche, The physics of X-ray free-electron lasers, Rev. Mod. Phys., 2016, 88(1), 015006 CrossRef.
- S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein, Distributed optimization and statistical learning via the alternating direction method of multipliers, Found. Trends Mach. Learn., 2011, 3, 1–122 Search PubMed.
- N. R. Draper and H. Smith. Applied Regression Analysis, John Wiley, 2011 Search PubMed.
- M. L. Baker, M. W. Mara, J. J. Yan, K. O. Hodgson, B. Hedman and E. I. Solomon, K-and L-edge X-ray absorption spectroscopy (XAS) and resonant inelastic X-ray scattering (RIXS) determination of differential orbital covalency (DOC) of transition metal sites, Coord. Chem. Rev., 2017, 345, 182–208 CrossRef CAS.
Footnote |
| † Authors contributed equally. |
| This journal is © the Owner Societies 2020 |