Two-dimensional halogen-bonded organic frameworks based on the tetrabromobenzene-1,4-dicarboxylic acid building molecule†
Nucharee
Chongboriboon
a,
Kodchakorn
Samakun
a,
Thitirat
Inprasit
 a,
Filip
Kielar
a,
Filip
Kielar
 b,
Winya
Dungkaew
b,
Winya
Dungkaew
 c,
Lawrence W.-Y.
Wong
c,
Lawrence W.-Y.
Wong
 d,
Herman H.-Y.
Sung
d,
Herman H.-Y.
Sung
 d,
Dragan B.
Ninković
d,
Dragan B.
Ninković
 e,
Snežana D.
Zarić
e,
Snežana D.
Zarić
 fg and
Kittipong
Chainok
fg and
Kittipong
Chainok
 *a
*a
aMaterials and Textile Technology, Faculty of Science and Technology, Thammasat University, Pathum Thani 12121, Thailand. E-mail: kc@tu.ac.th; Fax: +66 2 654 4548; Tel: +66 86 339 5079
bDepartment of Chemistry, Faculty of Science, Naresuan University, Phitsanulok 65000, Thailand
cDepartment of Chemistry, Faculty of Science, Mahasarakham University, Maha Sarakham 44150, Thailand
dDepartment of Chemistry, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
eInnovation Center, Faculty of Chemistry, Studentski trg 12-16, 11000 Belgrade, Serbia
fFaculty of Chemistry, University of Belgrade, Studentski trg 12-16, Belgrade, 11000, Serbia
gScience Program, Texas A&M University at Qatar, Education City, Doha, Qatar
First published on 28th October 2019
Abstract
Two-dimensional (2D) halogen-bonded organic frameworks were readily engineered by strong and directional effects of the primary Br⋯O and the secondary Br⋯π halogen bonding interactions from the tetrabromobenzene-1,4-dicarboxylic acid (H2Br4BDC) building molecule involving 100% supramolecular yields. The 2D assembly can function as a host layered framework for the intercalation of various guest solvents including acetone (ATN), ethanol (EtOH), dimethyl sulfoxide (DMSO), and ethylene glycol (EG) resulting in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host
2 host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guest complexation stoichiometry viz. H2Br4BDC·2S (S = ATN (1ATN), EtOH (2EtOH), DMSO (3DMSO), and EG (4EG)). All the solvates show remarkable similarities in their 2D layered sheets and the bilayer distance significantly responds to the size, shape, molecular conformation, and strength of the hydrogen bonding capability of the intercalated solvent molecules. The transition between solvate formation and desolvation was found to be facile and reversible upon the desolvation–resolvation process. The estimated Br⋯O halogen bonding energy of the solvates is in the −0.6 to −1.7 kcal mol−1 range, which was determined by quantum-mechanical calculations based on density functional theory (DFT) calculations. Furthermore, to quantitatively identify the host–guest intermolecular interactions of these solvates, they were visually compared by Hirshfeld surface analysis.
guest complexation stoichiometry viz. H2Br4BDC·2S (S = ATN (1ATN), EtOH (2EtOH), DMSO (3DMSO), and EG (4EG)). All the solvates show remarkable similarities in their 2D layered sheets and the bilayer distance significantly responds to the size, shape, molecular conformation, and strength of the hydrogen bonding capability of the intercalated solvent molecules. The transition between solvate formation and desolvation was found to be facile and reversible upon the desolvation–resolvation process. The estimated Br⋯O halogen bonding energy of the solvates is in the −0.6 to −1.7 kcal mol−1 range, which was determined by quantum-mechanical calculations based on density functional theory (DFT) calculations. Furthermore, to quantitatively identify the host–guest intermolecular interactions of these solvates, they were visually compared by Hirshfeld surface analysis.
Introduction
Noncovalent interactions such as hydrogen bonding, halogen bonding, π–π stacking, and van der Waals force are the fundamental interactions for molecular recognition and self-assembly of discrete molecules to form crystalline solids.1 These interactions have been widely used in crystal engineering and many aspects of supramolecular chemistry. In particular, the relatively high directionality and strength of hydrogen bonds (up to 40 kJ mol−1) make the prediction and control of molecular orientation in organic solids and discrete coordination complexes feasible.2 Over the past few years, hydrogen bonding (HB) has been utilized for the construction of a new class of potentially porous crystalline materials, named hydrogen-bonded organic frameworks (HOFs), through the self-assembly of pure organic building molecules such as guanidinium and sulfonate groups.3 The extended supramolecular framework architectures of HOFs are generally considered as semi-rigid with high flexibility compared to the frameworks created by strong covalent and coordination bonds like covalent organic frameworks (COFs)4 and metal–organic frameworks (MOFs).5 This is considered as an advantage since guest molecules can be fitted to the highly flexible networks by molecular recognition with supramolecular interactions. This is why research on HOF chemistry has recently been gaining great attention and they are considered as emerging functional materials for a wide range of practical applications such as gas separation, chemical sensing, and proton conduction.6 In comparison to COFs and MOFs, HOF materials also offer a number of unique features such as easy recrystallization, low density, potentially high thermal stability, and straightforward characterization in both solution and solid state.Halogen bonding (XB) occurs between a nucleophile and the σ-hole of a polarized halogen atom.7 This kind of intermolecular interaction is highly directional and the interaction energies are comparable to HB in which the strength of XB increases in the order F ≪ Cl < Br < I.8 Over the last few decades, XB has appeared as a promising crystal engineering tool in the design and synthesis of new functional supramolecular materials including the so-called halogen-bonded organic frameworks (XBOFs).9 In this regard, the most commonly used di-, inter-, and pseudohalogens are known as good halogen bond donors to achieve controlled assembly with halide and aromatic amines as halogen bond acceptors, providing potential applications in ion recognition and light-responsive materials.10 Related to XB, the so-called halogen–π bond is also an attractive intermolecular interaction between the σ-hole of a highly polarized halogen atom and electron-rich aromatic π-systems.11 The interaction energy of halogen–π interactions is about 50–60% in comparison to the strength of a hydrogen bond.12 Thus, such interactions are also important and should have a strong effect on the packing and the physical properties of crystalline solids. Intermolecular bonding interactions among molecular organic building blocks in HOFs and XBOFs are much weaker than coordination and covalent bonds in COFs. The control of the organization of the supramolecular arrangement and the accurate prediction of functional properties such as porosities of the resultant supramolecular networks are still very challenging tasks. Furthermore, it is still also very challenging to stabilize HOF and XBOF materials, in which most of the frameworks exhibit an irreversible structural change after the loss of guest molecules or the frameworks collapse during the activations.
On the other hand, the emerging class of two-dimensional (2D) materials such as graphene, silicate clays, and transition metal dichalcogenides has attracted great interest due to their intriguing structural architectures and high surface area to volume ratio, as well as their diverse applications in optoelectronic, energy conversion and storage.13 Although the syntheses of HOFs and XBOFs have been well-documented, to date, only a few reported works deal with 2D supramolecular halogen-bonded networks, especially for materials having reversible desolvation/solvation properties.14 Herein we present novel 2D XBOF assembled materials made from tetrabromobenzene-1,4-dicarboxylicacid (H2Br4BDC) building molecules through strong and directional Br⋯O halogen bonding. The 2D frameworks can act as hosts for the intercalation of various guest solvents including acetone (ATN), ethanol (EtOH), dimethyl sulfoxide (DMSO), and ethylene glycol (EG), resulting in the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host
2 host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guest complexation stoichiometry viz. H2Br4BDC·2S, where S = ATN (1ATN), EtOH (2EtOH), DMSO (3DMSO), and EG (4EG). Interestingly, the host frameworks are sufficiently flexible to permit reversible release and adsorption of guest solvent molecules with retention of their crystallinity. All their crystal structures have been determined by single crystal X-ray diffraction analysis at 100(2) and 296(2) K using graphite-monochromatic Cu-Kα (λ = 1.5418 Å) and Mo-Kα (λ = 0.7107 Å) radiation. Their physiochemical properties were also characterized by thermogravimetric analysis (TGA), infrared (FT-IR) spectroscopy, and powder X-ray diffraction (PXRD). Quantum-mechanical calculations based on density functional theory (DFT) calculations were performed for the determination of the energies of halogen bonding. In addition, to quantitatively identify the host–guest intermolecular interactions these solvates were visually compared with the use of Hirshfeld surface analysis.
guest complexation stoichiometry viz. H2Br4BDC·2S, where S = ATN (1ATN), EtOH (2EtOH), DMSO (3DMSO), and EG (4EG). Interestingly, the host frameworks are sufficiently flexible to permit reversible release and adsorption of guest solvent molecules with retention of their crystallinity. All their crystal structures have been determined by single crystal X-ray diffraction analysis at 100(2) and 296(2) K using graphite-monochromatic Cu-Kα (λ = 1.5418 Å) and Mo-Kα (λ = 0.7107 Å) radiation. Their physiochemical properties were also characterized by thermogravimetric analysis (TGA), infrared (FT-IR) spectroscopy, and powder X-ray diffraction (PXRD). Quantum-mechanical calculations based on density functional theory (DFT) calculations were performed for the determination of the energies of halogen bonding. In addition, to quantitatively identify the host–guest intermolecular interactions these solvates were visually compared with the use of Hirshfeld surface analysis.
Experimental
Materials and physical measurement
All chemicals and solvents of analytical grade were purchased from commercial sources and used without further purification. Elemental (C H N) analysis was conducted with a LECO CHNS 932 elemental analyser. IR spectra were recorded on a Perkin-Elmer model Spectrum 100 spectrometer using the ATR mode, in the range of 650–4000 cm−1. Powder X-ray diffraction (PXRD) measurements were carried out on a Bruker D8 ADVANCE X-ray powder diffractometer using Cu Kα (λ = 1.5418 Å) at room temperature. Variable temperature PXRD measurements were collected on a PanAlytical X'Pert PRO diffractometer with a 1D X'celerator detector strip using Cu Kα (λ = 1.5418 Å) with a heating rate of 3 °C min−1 and measuring a complete diffractogram every 20 °C up to 400 °C. The simulated PXRD patterns were calculated from single crystal X-ray diffraction data and processed by the free Mercury program provided by the Cambridge Crystallographic Data Centre.15 Thermogravimetric analyses (TGA) were carried out using a Mettler Toledo TGA/DSC3+ from ambient temperature to 500 °C with a heating rate of 10 °C min−1, under a N2 atmosphere. The solid-state photoluminescence spectra were measured at room temperature using a Horiba Scientific model FluoroMax-4 spectrofluorometer. The solid-state ultraviolet-visible (UV-vis) diffuse reflectance spectra were recorded at room temperature on a U-4100 Spectrometer (Hitachi Corporation, Tokyo, Japan) in the wavelength range of 200–1100 nm.Crystallization of the solvate forms
H2Br4BDC·2ATN (1ATN). A mixture of H2Br4BDC (5 mg) and ATN (2 mL) was added into a 15 mL Teflon lined reactor, sealed in a stainless steel autoclave and placed in an oven. The mixture was heated to 110 °C under autogenous pressure for 1 h, and then cooled down to room temperature. Colourless block shaped crystals of 1ATN were obtained. IR (νmax/cm−1, s for strong, m medium, w weak): 3376s, 2870m, 2556s, 1750s, 1712s, 1515m, 1084s, 779s.H2Br4BDC·2EtOH (2EtOH). The procedure was the same as that used for the synthesis of 1ATN, except that EtOH was used instead of ATN. Colourless block shaped crystals of 2EtOH were obtained. IR (νmax/cm−1): 3409m, 2986s, 1694s, 1003s, 787s.
H2Br4BDC·2DMSO (3DMSO). The procedure was the same as that used for the synthesis of 1ATN, except that DMSO was used instead of ATN. IR (νmax/cm−1): 3021s, 1671s, 1024s, 793s.
H2Br4BDC·2EG (4EG). The procedure was the same as that used for the synthesis of 1ATN, except that EG was used instead of ATN. IR (νmax/cm−1): 3409s, 2878m, 1688m, 1036s, 782s.
Crystallographic data collection and structure refinement
X-ray diffraction data were collected using a Rigaku Oxford-Diffraction SuperNova diffractometer equipped with a multilayer mirror for Cu-Kα (λ = 1.54184 Å) radiation at 100(2) K. Data reduction was performed using CrysAlisPro software16 and the SCALE3 ABSPACK scaling algorithm was used for absorption correction. The structure was solved with the ShelXT structure solution program using combined Patterson and dual-space recycling methods.17 The structure was refined by least squares using ShelXL.18 All non-H atoms were refined anisotropically. The H atoms of solvent molecules were positioned geometrically with C–H = 0.93–0.97 Å and refined using a riding model (AFIX23, AFIX43 and AFIX137 for methine, methylene, and methyl H atoms, respectively in the ShelXL program) with fixed displacement parameters Uiso(H) = 1.5Ueq(C) for methyl groups and 1.2Ueq(C) for the other groups. The O–H hydrogen atoms were located in difference Fourier maps but refined with O–H = 0.84 ± 0.02 Å. For structure 1ATN, the solvent acetone molecule was found to be disordered with refined occupancy ratios of 0.493(4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.507(4). The crystallographic details for the solvates are summarized in Table 1. Crystallographic data for the solvates at 296(2) K are also provided in the ESI† (Table S1). CCDC-1941497–19414504 contain the supplementary crystallographic data for this paper.
0.507(4). The crystallographic details for the solvates are summarized in Table 1. Crystallographic data for the solvates at 296(2) K are also provided in the ESI† (Table S1). CCDC-1941497–19414504 contain the supplementary crystallographic data for this paper.
| 1 ATN | 2 EtOH | 3 DMSO | 4 EG | |
|---|---|---|---|---|
| Formula | C14H14Br4O6 | C12H14Br4O6 | C12H14Br4O6S2 | C12H14Br4O8 |
| Formula weight | 597.89 | 573.87 | 637.99 | 605.87 |
| Crystal system | Monoclinic | Orthorhombic | Orthorhombic | Orthorhombic |
| Space group | C2/c | Pnma | Pnma | Pbca |
| a (Å) | 24.9223(4) | 9.27849(19) | 9.24933(17) | 7.96170(10) |
| b (Å) | 9.0196(2) | 23.5754(5) | 25.7601(6) | 9.93120(10) |
| c (Å) | 8.88690(10) | 8.6023(2) | 8.66218(18) | 23.5837(3) |
| β (°) | 93.248(2) | 90 | 90 | 90 |
| V (Å3) | 1994.47(6) | 1881.71(7) | 2063.88(7) | 1864.75(4) |
| D calc (g cm−3) | 1.991 | 2.026 | 2.053 | 2.158 |
| Z | 4 | 4 | 4 | 4 |
| μ (mm−1) | 10.086 | 10.652 | 11.639 | 10.880 |
| F(000) | 1144 | 1096 | 1224 | 1160 |
| λ (Å) | 1.54184 (Cu-Kα) | 1.54184 (Cu-Kα) | 1.54184 (Cu-Kα) | 1.54184 (Cu-Kα) |
| θ range (°) | 5.2–73.5 | 5.4–73.5 | 5.4–73.5 | 3.8–73.8 |
| Reflections collected | 5459 | 9416 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378 378 |
9715 |
| Unique reflections | 1977 | 1747 | 1901 | 1875 |
| Parameters | 155 | 109 | 115 | 121 |
| R int, Rsigma | 0.016, 0.016 | 0.045, 0.024 | 0.034, 0.019 | 0.022, 0.014 |
| R 1, wR2 (I > 2σ(I)) | 0.017, 0.043 | 0.029, 0.079 | 0.045, 0.109 | 0.019, 0.049 |
| R 1, wR2 (all data) | 0.018, 0.044 | 0.032, 0.081 | 0.047, 0.109 | 0.023, 0.052 |
| GOF on F2, S | 1.096 | 1.057 | 1.121 | 1.058 |
| Δρmax, Δρmin (e Å−3) | 0.37, −0.29 | 1.01, −0.65 | 1.71, −1.15 | 0.36, −0.33 |
Theoretical calculations
All calculations were performed by using the Gaussian 09 (version D.01) program package.19 All the geometries were extracted from crystal structures type I and type II. For all the calculations of the interaction energies, the ωB97X-D method20 with the def2-TZVPP basis set21 was used. Electrostatic potential maps were used to explain the difference between two types of interactions. These maps were calculated from wB97Xd/def2-TZVPP wave functions obtained with Gaussian 09, and visualized with the gOpenMol v3.0 program.22 The surface was defined by the 0.004 a.u. contour of electron density.Results and discussion
Synthesis and characterization
Crystallization of H2Br4BDC from the polar solvents ATN, EtOH, DMSO, and EG at 110 °C for 1 h in stainless-steel autoclaves with Teflon liners yielded the corresponding solvates of H2Br4BDC, Scheme 1. Alternatively, single crystals of these solvates can also be grown by refluxing H2Br4BDC in the corresponding solvents at 110 °C for 6 h, filtering the solution, and allowing it to stand undisturbed at ambient temperature for 24 h. However, the crystallization process takes quite a long time compared with the former method. Attempts to get crystals of H2Br4BDC alone by reacting H2Br4BDC with either polar or non-polar solvents at different temperatures (such as 40, 60, 80, 100, and 120 °C) were unsuccessful. It should be noted that if the reaction temperature was raised above 120 °C, the H2Br4BDC molecules underwent an in situ decarboxylation reaction to form tetrabromobenzene. The phase purity of all the solvates was confirmed by matching the PXRD pattern with the simulated pattern obtained based on the SCXRD data (Fig. S1†). FT-IR spectroscopy was also used to investigate the possibility of intermolecular HB and XB interactions between the donor and acceptor in the solvates. The IR spectra of the starting materials and the solvates have been measured and compared (Fig. S2†). The spectra exhibit several significant shifts of a number of key bands. Apparently, the free H2Br4BDC shows strong absorption bands at 1725 cm−1 and 1390 cm−1, which are characteristic of the asymmetric and symmetric stretching vibrations of the carboxylic groups.23 These bands are ∼15 cm−1 red shifted in all the solvates, suggesting that the simultaneous formation of HB and XB resulted in a reduced electron density on the carbonyl group with respect to the free H2Br4BDC. The broad bands in the region 3450–3446 cm−1 are attributed to the O–H stretching of the carboxylic and hydroxy groups with ∼10 cm−1 red shift due to the strong hydrogen bonds involving the hydroxy groups. Notice that the strong C–Br stretching for the free H2Br4BDC at 690 cm−1 is also red shifted to ∼25 cm−1 for all the solvates upon XB formation. | ||
| Scheme 1 Molecular structure of the host H2Br4BDC molecule and four organic solvent molecules (ATN, EtOH, EG, and DMSO) used in this study. | ||
Description of crystal structures
Single crystal X-ray structural analyses revealed that all the solvates form similar centrosymmetric crystals with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
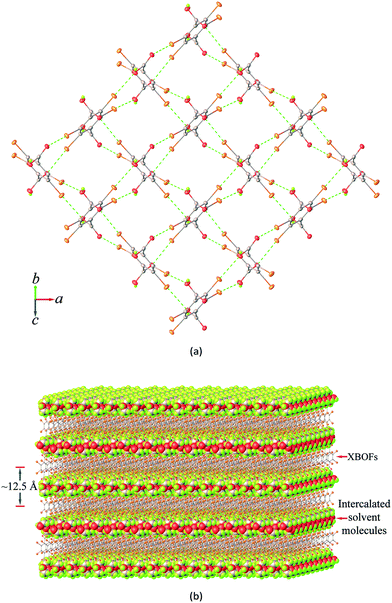
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometric ratio of the host H2Br4BDC and guest solvent molecules. As can be seen in Fig. 1a, the host molecules form a 2D layered framework containing a rectangular grid with dimensions of ca. 6.3 × 6.5 Å2. The vacancy of the grids is not large enough to accommodate the guest solvent molecules inside the cavity. Instead, the solvent molecules can be intercalated between two stacks of layers. It should be noted that the carboxyl groups in the single layer are alternatively pointed up and down with respect to the horizontal mean plane defined by the central phenyl rings of the building molecules and they can behave as either hydrogen bond donors or acceptors for the solvent molecules.
2 stoichiometric ratio of the host H2Br4BDC and guest solvent molecules. As can be seen in Fig. 1a, the host molecules form a 2D layered framework containing a rectangular grid with dimensions of ca. 6.3 × 6.5 Å2. The vacancy of the grids is not large enough to accommodate the guest solvent molecules inside the cavity. Instead, the solvent molecules can be intercalated between two stacks of layers. It should be noted that the carboxyl groups in the single layer are alternatively pointed up and down with respect to the horizontal mean plane defined by the central phenyl rings of the building molecules and they can behave as either hydrogen bond donors or acceptors for the solvent molecules.
It is very interesting that adjacent H2Br4BDC molecules, within the layered framework, are oriented almost perpendicular to and interact with each other through the Br⋯O halogen bonds between the bromine atoms and the oxygen carbonyl or hydroxyl atoms from the carboxyl groups, giving rise to a 2D halogen-bonded framework. Notably, such 2D supramolecular organization is present in all of the four solvates and it involves six Br⋯O contacts per building molecule, thus showing a 100% supramolecular yield. A careful inspection of the structures of these solvates suggests that two types of different supramolecular synthons are observed viz. Br⋯Ocarbonyl and Br⋯Ohydroxyl (Fig. S3†) and in both cases the distances between the Br and O atoms are closely comparable.
The observed XB interactions are considered strong as indicated by the short Br⋯O distances (2.944(1)–3.114(3) Å), Table 2, in which the experimental values are ∼10% shorter than the sum of the Bondi van der Waals radii of the Br and O atoms (3.37 Å),24 and the C–Br⋯O bond angles (170.2(1)–175.6(1)°) are almost linear. These facts strongly suggest that the σ-hole of the halogen atom is a key element for the formation of such intermolecular interactions. An interesting feature observed in the structures of these solvates is an apparent auxiliary Br⋯π contact in which the bromide atom lies above the C–C bond of the phenyl ring. The shortest Br⋯C contact of about 3.5 Å is slightly larger than the sum of Bondi van der Waals radii, implying weak Br⋯π interactions11a in these solvates. It should be noted that stronger interactions are known to be less affected by temperature;25 in all cases decreasing temperature down to 100(2) K does not have a strong influence on the Br⋯O and Br⋯π distances.
| C–Br⋯O | d[Br⋯O] (Å) | ∠[C–Br⋯O] (°) | ||
|---|---|---|---|---|
| 100(2) K | 296(2) K | 100(2) K | 296(2) K | |
| Symmetry codes: (i) x, 1 − y, 0.5 + z; (ii) 1.5 − x, −0.5 + y, 1.5 − z; (iii) −0.5 + x, y, 0.5 − z; (iv) 0.5 + x, y, 1.5 − z; (v) 0.5 − x, 0.5 + y, z; (vi) −0.5 + x, 1.5 − y, 1 − z. | ||||
| 1 ATN | ||||
| C3–Br1⋯O2i | 2.944(1) | 3.007(2) | 174.8(1) | 175.6(1) |
| C4–Br2⋯O1ii | 3.044(1) | 3.132(2) | 174.2(1) | 175.3(1) |
| 2 EtOH | ||||
| C3–Br1⋯O2iii | 2.997(1) | 3.062(2) | 174.1(1) | 174.5(1) |
| C4–Br2⋯O1iv | 2.988(1) | 3.093(2) | 174.6(1) | 175.2(1) |
| 3 DMSO | ||||
| C3–Br1⋯O2iii | 3.024(3) | 3.098(3) | 174.4(1) | 175.1(1) |
| C4–Br2⋯O1iv | 2.977(3) | 3.050(3) | 175.1(1) | 175.5(1) |
| 4 EG | ||||
| C3–Br1⋯O1v | 3.071(1) | 3.114(3) | 172.9(1) | 175.4(1) |
| C4–Br2⋯O2vi | 2.999(1) | 3.075(3) | 170.2(1) | 170.6(1) |
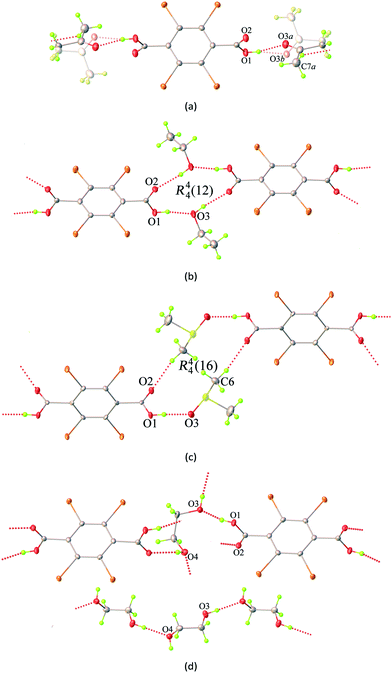
As shown in Fig. 1b, the 2D layers of the host molecules are then held together into a 3D supramolecular structure by host–guest hydrogen bonding. Despite the fact that these solvates show remarkable similarities in their layered frameworks, the geometric features of the hydrogen bonding for host–guest interactions are quite different due to the differences in relative orientation of the solvent molecules confined within the layers. This can be seen from the asymmetric units of each solvate (Fig. S4†), which contain half of a H2Br4BDC molecule located on the inversion centre and one complete solvent molecule in a general position. Furthermore, it can be seen that the molecules of the H2Br4BDC building unit in these solvates are not planar since the dihedral angles between the carboxylic groups and the tetrabromobenzene moieties are close to 90°. Finally, it is well-known that changes in molecular conformations due to strong and weak intermolecular interactions are very common in molecular host–guest and solvate systems.26 Close inspection of the crystal packing of these solvates reveals that the solvent molecules can function as both hydrogen bond donor and acceptor sites, Fig. 2.
In the case of 1ATN, the ATN molecule is found to exhibit positional disorder around a pseudo-glide plane symmetry at 296(2) and 100(2) K. The guest solvent molecule participates in strong O–H⋯O and weak C–H⋯O hydrogen bonding interactions (Fig. 2a), in which the carbonyl and the methyl function as a hydrogen bond acceptor and donor to the respective hydroxy donor and a carbonyl acceptor from the host molecules, giving rise to the R22(8) eight-membered ring motif according to the graph-set analysis.27 For 2EtOH, it is apparent that the orientation of the EtOH molecule is capable of acting as both a hydrogen bond donor and acceptor, which strongly influences the formation of strong O–H⋯O hydrogen bonds across a centre of inversion. The final supramolecular synthon for 2EtOH can be described by the R44(12) graph set twelve-membered ring motif (Fig. 2b). For 3DMSO, the DMSO solvate molecule can also behave as both a hydrogen bond donor and acceptor, participating in symmetry-related O–H⋯O and C–H⋯O hydrogen bonding interactions with carbonyl and hydroxyl oxygen atoms from the host molecules. These interactions give rise to a supramolecular macrocycle similar to that in the case of 2EtOH and can be described by the R44(16) graph set sixteen-membered ring motif (Fig. 2c). In the case of 4EG, the EG solvate molecule can adopt a gauche conformation with respect to the rotation of the central C–C bond and functions as two donors and two acceptors of the hydrogen bonds simultaneously (Fig. 2d). A noteworthy feature of 4EG is that the orientation of the EG molecules facilitates the formation of the head-to-tail O–H⋯O hydrogen bonds within the layers. It is noted that a carboxyl oxygen atom of the host molecule can act as a bifurcated hydrogen bond and halogen bond acceptor, while a hydroxyl oxygen atom possesses both hydrogen bond donor and halogen bond acceptor properties. As indicated above, stronger intermolecular interactions are known to be less affected by temperature. In this study, lowering the temperatures from 296(2) K to 100(2) K does not lead to any significant differences in the interactions (Table S2†).
Furthermore, a detailed structural inspection of these solvates shows the absence of intermolecular Br⋯Br halogen bonding and π–π stacking interactions between the phenyl–phenyl aromatic rings. Hence, it is evident that the Br⋯O/π halogen bonding and O/C–H⋯O hydrogen bonding interactions are largely responsible for the observed molecular arrangement and contribute to the stabilization in the formation of these solvates. It should be pointed out that the molecular size, shape, conformation, and hydrogen bonding capability of the solvents could affect the bilayer distances of these solvates. On comparing the distance between adjacent mean planes of the layers defined by the central phenyl rings (100(2) K), the corresponding distances decrease in the order 3DMSO (13.60 Å) > 1ATN (13.12 Å) > 4EG (12.45 Å) > 2EtOH (11.87 Å). Despite this, the total solvent-accessible volume28 of these crystals after removal of guest solvent molecules was estimated to be about 50% per unit cell volume, in which 3DMSO has the largest potential molecular void of 51% (1049 Å3 of the 2064 Å3 unit cell volume).
Hirshfeld surface analysis
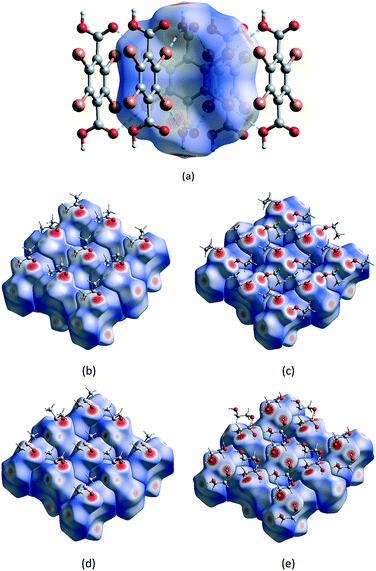
Hirshfeld surface analysis and the 2D fingerprint plot are very useful tools for the visualization of intermolecular interactions using different colours and colour intensities, representing short or long contacts and indicating the relative strength of the interactions in crystal structures relative to the van der Waals radii.29 The molecular Hirshfeld surface plots were generated using CrystalExplorer 17 with the 3D dnorm surfaces mapped over a fixed colour scale of −0.7606 (red) to 1.7819 (blue) Å. The red and blue colours are used for shorter and longer contacts, respectively, while white highlights for contacts around the van der Waals separations. It should be noted that the bond lengths to hydrogen atoms are set to typical neutron values (C–H = 1.083 Å, O–H = 0.983 Å).30Hirshfeld surface analysis and the total area of the molecular surface for the H2Br4BDC host molecule with all of the solvates are highly comparable. With the aid of decomposed 2D fingerprint plots (Fig. S5†), the most important contributions to the stabilization of the packing of the host molecules in these solvates come from the Br⋯H/H⋯Br, Br⋯C/C⋯Br, and Br⋯O/Br⋯O contacts (Table S3†). According to the structural analysis results from SCXRD studies in the preceding section, the formation of 2D XBOFs was mainly driven by molecular self-assembly through the Br⋯O and Br⋯π halogen bonding interactions involving the host molecules. As shown in Fig. 3a, the dominant interactions between Br and O atoms, corresponding to the Br⋯O halogen bonds, can be clearly seen in the Hirshfeld surface as the red spots. The relative contributions of these contacts to the total dnorm surfaces are 12.7%, 15.4%, 13.8%, and 13.0% for 1ATN, 2EtOH, 3DMSO, and 4EG, respectively, and appear as symmetrical sharp spikes centred near a (de + di) sum of ∼2.9 Å in the 2D fingerprint plots (Fig. S6†), where de is the distance from a point on the Hirshfeld surface to the nearest external atom and di is the distance from the same point on the Hirshfeld surface to the nearest atom internal to the surface. The white spots represent the self-complementary weak Br⋯C/C⋯Br contacts resulting from the Br⋯π halogen bonding interactions. The proportions of these contacts are comparable in all independent H2Br4BDC molecules, comprising ∼25% of the contribution with a symmetrical sharp spike in the fingerprint plot having (de + di) ∼3.4 Å. Other visible spots in the Hirshfeld surfaces correspond to Br⋯H/H⋯Br and Br⋯Br contacts (Table S3†), shown as white areas. These contacts are over 15% longer than the sum of Bondi van der Walls radii. Evidently, it was observed that the contribution from the C⋯C contact on the Hirshfeld surfaces for the host molecules in all the solvates is equal to zero. This confirms the absence of intermolecular π⋯π stacking interactions, which is qualitatively consistent with experimental SCXRD analysis. Hence, it can be concluded that the primary Br⋯O and the secondary Br⋯π halogen bonding interactions play a central role in stabilizing the formation of the supramolecular XBOFs among all the solvates reported here.
Furthermore, the intermolecular host–guest interactions have also been visualized via Hirshfeld surface analysis. By selecting the host molecules as the object, the vivid red spots are clearly visible on the dnorm surfaces, Fig. 3b–e, attributed to the H⋯O/O⋯H contacts, which correspond to strong (host)O–H⋯O(guest) hydrogen bonds involving the acidic hydrogen atoms. These contacts are represented by two unsymmetrical narrow pointed areas with a de + di sum range from ∼1.5 Å to ∼1.7 Å (Fig. S7†), meaning that the host molecules can act as hydrogen bond donors and also constitute the acceptor counterpart. On the other hand, by selecting only the solvent molecule as the object, the strong (guest)O–H⋯O(host) and (guest)O–H⋯O(guest) interactions are evident on the Hirshfeld surfaces with the contribution of H⋯O/O⋯H contacts varying from 27.7% in 1ATN to 49.6% in 4EG. The contacts appear as wings having a de + di sum range from ∼1.5 Å to ∼2.2 Å in the 2D fingerprint plot (Fig. S8†). There are, however, some differences between these solvents due to the differences in packing motifs and intermolecular arrangements in the solid state. For 1ATN and 2EtOH, the most significant contribution to the dnorm surface of the solvents comes from H⋯H contacts, which comprise about half of the total Hirshfeld surfaces. Meanwhile the H⋯O/O⋯H contacts are the main contributors in 3DMSO and 4EG (Table S3†), which suggest that solvent DMSO and EG molecules have stronger intermolecular interaction.
DFT calculations
The interaction energies between Br and O atoms in the crystal structures of these solvates have also been investigated by performing quantum chemical calculations. The type I crystal structure has a network of interactions between the H2Br4BDC molecules that consist of two different interactions between these molecules (Fig. S3a†). The first consists of two Br atoms interacting with two O atoms of the carbonyl groups, and the other one is where two Br atoms interact with two O atoms of the hydroxyl groups. Since attraction between two molecules in crystal structures is not only caused by the interactions of Br and O atoms, but also by the van der Waals attraction, we made model systems to evaluate these two contributions. To get the energy of Br⋯O interactions, we made two model systems, one with molecules as in the crystal structure and a second model system in which we have replaced the interacting COOH group with hydrogen atoms to get the interaction energy between these molecules without the Br⋯O interactions. The difference between these two interaction energies is the interaction energy of Br atoms with the COOH groups. For the Br⋯O–H contacts, the interaction energy in the model system with COOH groups (Fig. S9a†) is −4.66 kcal mol−1, while the interaction energy in the model system without COOH groups (Fig. S9b†) is −3.55 kcal mol−1. Hence, the interaction energy of two Br⋯O–H group contacts is −1.11 (−4.66 − (−3.55)) kcal mol−1, whereas the interaction energy for one Br⋯O–H group contact is −0.55 kcal mol−1. For the Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contacts, the interaction energy in the model system with COOH groups (Fig. S10a†) is −6.96 kcal mol−1, while the interaction energy in the model system without COOH groups (Fig. S10b†) is −3.55 kcal mol−1. Thus, the interaction energy of two Br⋯O
C contacts, the interaction energy in the model system with COOH groups (Fig. S10a†) is −6.96 kcal mol−1, while the interaction energy in the model system without COOH groups (Fig. S10b†) is −3.55 kcal mol−1. Thus, the interaction energy of two Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contacts is −3.41 (−6.96 − (−3.55)) kcal mol−1, and the interaction energy for one Br⋯O
C contacts is −3.41 (−6.96 − (−3.55)) kcal mol−1, and the interaction energy for one Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contact is −1.71 kcal mol−1.
C contact is −1.71 kcal mol−1.
The type II crystal structure has a network of Br⋯O interactions that consist of two equivalent contacts between the H2Br4BDC molecules; in each contact, there is one interaction of the Br atom with the O atom of the carbonyl group, and a second interaction of the Br atom with the O atom of the hydroxy group (Fig. S3b†). In a similar manner to the type I structure, to investigate the energies of the particular interactions three models were used. One as in the crystal structure and the other two are models in which we replaced an interacting COOH group with a H atom to get the interaction energy between only one Br and O pair. The model system with Br–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction (Fig. S11a†) has an interaction energy of −5.82 kcal mol−1, while the model system without Br⋯O
C interaction (Fig. S11a†) has an interaction energy of −5.82 kcal mol−1, while the model system without Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction (Fig. S11b†) has an energy of −4.04 kcal mol−1. Thus, the Br⋯O
C interaction (Fig. S11b†) has an energy of −4.04 kcal mol−1. Thus, the Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction energy is the difference, −1.78 kcal mol−1. The model system without Br⋯O–H interaction (Fig. S11c†) has an energy of −5.23 kcal mol−1. Therefore, the Br⋯O–H interaction energy is equal to −0.59 (−5.82 − (−5.23)) kcal mol−1. The calculated interaction energies of Br⋯O
C interaction energy is the difference, −1.78 kcal mol−1. The model system without Br⋯O–H interaction (Fig. S11c†) has an energy of −5.23 kcal mol−1. Therefore, the Br⋯O–H interaction energy is equal to −0.59 (−5.82 − (−5.23)) kcal mol−1. The calculated interaction energies of Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Br⋯O–H interactions are very similar in type I and type II structures (Table S4†), and these results also indicate that Br⋯O
C and Br⋯O–H interactions are very similar in type I and type II structures (Table S4†), and these results also indicate that Br⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions are significantly stronger.
C interactions are significantly stronger.
To investigate the influence of the type of halogen element in these systems, we have calculated the interaction energies of the model systems in which we have replaced the Br atoms with Cl atoms. Model systems based on the type-I crystal structure were used as the starting point and after replacement of Br atoms with Cl atoms, these model systems were optimized at the ωB97X-D/def2-SVPP level of theory. The bond length for the optimized Cl–C bond of 1.73 Å is shorter than the Br–C bond with 1.89 Å, which is consistent with the difference of their van der Waals radii. Optimized model systems and model systems where COOH groups were replaced with H atoms were used to derive the Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H interaction energies, as was previously done for Br/O
C and Cl/O–H interaction energies, as was previously done for Br/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Br/O–H interaction energies. Cl/O
C and Br/O–H interaction energies. Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H interaction energies (−1.05 and −0.43 kcal mol−1, respectively) were less attractive than Br/O
C and Cl/O–H interaction energies (−1.05 and −0.43 kcal mol−1, respectively) were less attractive than Br/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Br/O–H interaction energies (−1.71 and −0.55 kcal mol−1, respectively). This was expected since the sigma hole interaction of the Br atom should be stronger than that of the Cl atom, as is well known and can be observed in the electrostatic potential map in Fig. 4. Our attempt to optimize the model system with the Cl halogen atom that is based on the type-II crystal structure was not successful, since the optimized structure had a completely different geometry with different interactions. Hence, we optimized the dimer with hydrogen bonds between COOH groups and parallel planes of the aromatic rings (without Cl/O
C and Br/O–H interaction energies (−1.71 and −0.55 kcal mol−1, respectively). This was expected since the sigma hole interaction of the Br atom should be stronger than that of the Cl atom, as is well known and can be observed in the electrostatic potential map in Fig. 4. Our attempt to optimize the model system with the Cl halogen atom that is based on the type-II crystal structure was not successful, since the optimized structure had a completely different geometry with different interactions. Hence, we optimized the dimer with hydrogen bonds between COOH groups and parallel planes of the aromatic rings (without Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H interactions). Based on the optimized structure of the H2Cl4BDC molecule and Cl/O
C and Cl/O–H interactions). Based on the optimized structure of the H2Cl4BDC molecule and Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H distances from previous calculations, we have constructed a reasonable model system based on the type-II crystal structure. This model system and the model systems where the COOH group was replaced with a H atom were used to evaluate the Cl/O
C and Cl/O–H distances from previous calculations, we have constructed a reasonable model system based on the type-II crystal structure. This model system and the model systems where the COOH group was replaced with a H atom were used to evaluate the Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H interaction energies, as was previously done for Br/O
C and Cl/O–H interaction energies, as was previously done for Br/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Br/O–H interactions. The interaction energies were similar to the interaction energies that were previously obtained for Cl/O
C and Br/O–H interactions. The interaction energies were similar to the interaction energies that were previously obtained for Cl/O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Cl/O–H interaction energies (−0.98 and −0.32 kcal mol−1, respectively).
C and Cl/O–H interaction energies (−0.98 and −0.32 kcal mol−1, respectively).
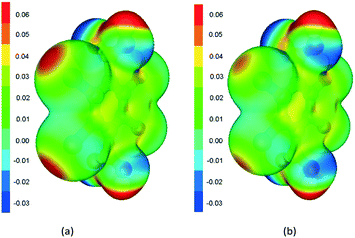
Furthermore, the calculated electrostatic potential map of the H2Br4BDC and H2Cl4BDC molecules can explain the calculated interaction energies. As shown in Fig. 4b, the potential is slightly positive above the ring, and the potential of the Br atoms is negative, with a positive sigma hole in the plane of the ring, opposite to the Br–C bond.31 This positive potential forms the electrostatic interaction with negative potential on oxygen atoms of the other molecule. The electrostatic potential shows significantly stronger negative potential on C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygen than on O–H oxygen, which is in accordance with the calculated interaction energies. The calculated electrostatic potential map of the H2Cl4BDC molecule is very similar to the map of the H2Br4BDC molecule with the exception of the smaller σ-hole on the Cl atoms than that on the Br atoms. This explains the weaker interaction energies calculated for the H2Cl4BDC molecule.
O oxygen than on O–H oxygen, which is in accordance with the calculated interaction energies. The calculated electrostatic potential map of the H2Cl4BDC molecule is very similar to the map of the H2Br4BDC molecule with the exception of the smaller σ-hole on the Cl atoms than that on the Br atoms. This explains the weaker interaction energies calculated for the H2Cl4BDC molecule.
Solvate stability and structural reversibility
To determine the thermal behaviour and to probe the solvate stoichiometry, thermogravimetric (TG) analysis was performed for all the solvates and the H2Br4BDC molecule. As can be seen in Fig. 5a, the TG curve of the H2Br4BDC building molecule shows that there is no weight loss before the sample was melted (275 °C), confirming that the sample of H2Br4BDC did not contain any solvent. Meanwhile the TG curves of the solvates of H2Br4BDC merely undergo two steps of weight loss. For all the solvates, the initial weight loss is in the range 50–215 °C and is due to the release of the exclusion of solvate molecules. The second weight loss is attributed to the decomposition of the H2Br4BDC molecules. It was observed that the loss of solvent molecules from the solvates follows the order 3DMSO > 4EG > 2EtOH > 1ATN. These trends may be attributed to the melting points of the solvents and the appearance of the stronger intermolecular hydrogen bonding interactions as discussed above. It should be noted that the TG curves show no significant difference between the melting points of the solvates and the pure H2Br4BDC. Furthermore, from the weight loss seen in the TG curves of these solvates the stoichiometry of the H2Br4BDC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent was calculated to be 1
solvent was calculated to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, which is in reasonably good agreement with the experimental X-ray crystallographic analysis.
2, which is in reasonably good agreement with the experimental X-ray crystallographic analysis.
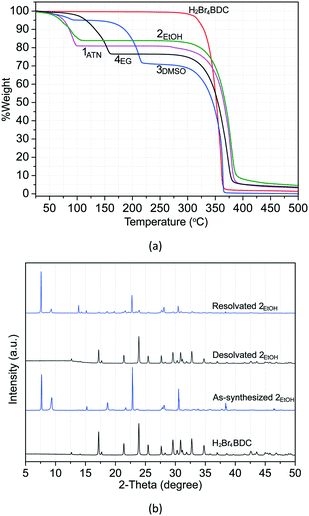 | ||
| Fig. 5 TG curves of H2Br4BDC and all the solvates (a) and PXRD patterns (bottom to top) of H2Br4BDC, as synthesized 2EtOH, desolvated 2EtOH, and resolvated 2EtOH (b). | ||
Moreover, an interesting feature is that structural reversibility was observed through the desolvation–resolvation process. As observed above, the TG results indicate that all the solvates show similar thermal stability in which all the solvates convert to the desolvated forms before melting. Thus, the study of desolvation–resolvation of the ethanol solvate 2EtOH is described in detail as a representative example. When the ethanol molecules were removed by heating at 40 °C under vacuum (∼10 mbar pressure) for 1 h, the solvate form indeed changes to the H2Br4BDC phase. The original solvate form can be easily recovered by adding the ethanol solvent into the desolvated phase and subsequent heating at 110 °C for 1 h in an autoclave. As can be seen from the PXRD patterns in Fig. 5b, the positions of the diffraction peaks for the desolvated and reabsorbed solvent phases are perfectly in accordance with those in original H2Br4BDC and as-synthesized 2EtOH, respectively, showing that the crystal structure remains essentially unchanged in each case. More interestingly, this reversibility of the desolvation–resolvation process for this solvate 2EtOH could be repeated at least ten times. In addition, variable temperature PXRD was also carried out to monitor the structural changes after the solvent leaves (Fig. S12†). It was verified that after removal of lattice solvent molecules at ∼100 °C, the molecules rearranged to the original H2Br4BDC, which was followed by the decomposition of the sample at ∼250 °C.
Photochemical properties
In addition, the photochemical properties of the synthesized solvates, as well as the parent H2Br4BDC molecule were investigated. Both UV-vis and photoluminescence spectra were recorded for the samples (Fig. S13†). The UV-vis spectra of all of the compounds show strong absorption below 320 nm. Inspection of this part of the spectrum reveals slight differences. Compounds H2Br4BDC, 1ATN, and 2EtOH exhibit a trough around 300 nm and shoulders around 245 nm. On the other hand, the spectra of 3DMSO and 4EG have a minimum in this part at 230 nm followed by a gradual increase towards the peak at 300 nm. Furthermore, a small shoulder is observed in these spectra at 358 nm. This feature is most prominent in the spectrum of 4EG. Upon excitation at 300 nm, weak emission spectra can be observed for these compounds. Once again, the spectra of H2Br4BDC, 1ATN, and 2EtOH are somewhat similar, exhibiting fairly broad peaks between 320 and 390 nm. The spectra of the solvates are slightly red shifted and structured in comparison to the starting material. In contrast the emission spectra of 3DMSO and 4EG are narrower and blue shifted in comparison to the previous ones. Meanwhile the spectrum of 4EG exhibits a distinct peak at 325 nm; the peak for 3DMSO merges with the tail of the scattered excitation light. The spectral differences observed in both methods, especially for the solvate samples, are likely to be a reflection of the different hydrogen bond strengths discussed above.Conclusions
In summary, halogen bonding has been shown to be a useful and reliable crystal engineering tool for the formation of solvate crystals. In this work, the construction of 2D halogen-bonded organic frameworks in the crystalline state was readily controlled through the strong and directional Br⋯O halogen bonding interactions (−0.6 to −1.7 kcal mol−1) between H2Br4BDC molecules, involving 100% supramolecular yields. These 2D assemblies are considered as host frameworks; meanwhile the carboxylic groups of the H2Br4BDC building molecules with both hydrogen bond donor and acceptor sites can also form hydrogen bonding with various guest solvents (i.e. ATN, EtOH, DMSO, and EG), and subsequently solvates with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host
2 host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guest stoichiometry are formed. These solvates show interesting facile and reversible crystalline-to-crystalline transformation upon a desolvation–resolvation process and this reversible process of such transformation could be repeated at least ten times as monitored by PXRD. Such studies give some insight into the requirements for the elaboration of layered frameworks, which is necessary in order to ultimately engineer such an emerging class of 2D supramolecular materials for the adsorption of solvent organic molecules. Currently, we are investigating the effects of different solvents and anions on the XB interactions in such systems.
guest stoichiometry are formed. These solvates show interesting facile and reversible crystalline-to-crystalline transformation upon a desolvation–resolvation process and this reversible process of such transformation could be repeated at least ten times as monitored by PXRD. Such studies give some insight into the requirements for the elaboration of layered frameworks, which is necessary in order to ultimately engineer such an emerging class of 2D supramolecular materials for the adsorption of solvent organic molecules. Currently, we are investigating the effects of different solvents and anions on the XB interactions in such systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a research career development grant from the Thailand Research Fund (RSA5780056). S. D. Z. thanks the Serbian Ministry of Education, Science and Technological Development (Grant 172065). The authors thank the Faculty of Science and Technology, Thammasat University, for funds to purchase the X-ray diffractometer and also thank the Science Lab Centre, Faculty of Science, Naresuan University, for the use of equipment.Notes and references
- (a) Crystal Design: Structure and Function, ed. G. R. Desiraju, Wiley, New York, 2003 Search PubMed; (b) Frontiers in Crystal Engineering, ed. E. R. T. Tiekink and J. J. Vittal, John Wiley & Sons, Ltd, Sussex, 2006 Search PubMed.
- (a) C. B. Aakeröy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397–407 RSC; (b) G. R. Desiraju, Acc. Chem. Res., 2002, 35, 565–573 CrossRef CAS PubMed; (c) T. Adachi and M. D. Ward, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef PubMed.
- (a) J. Luo, J.-W. Wang, J.-H. Zhang, S. Lai and D.-C. Zhong, CrystEngComm, 2018, 20, 5884–5898 RSC; (b) R.-B. Lin, Y. He, P. Li, H. Wang, W. Zhou and B. Chen, Chem. Soc. Rev., 2019, 48, 1362–1389 RSC.
- (a) A. P. Côté, A. I. Benin, N. W. Ockwig, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed; (b) S. Yuan, X. Li, J. Zhu, G. Zhang, P. V. Puyvelde and B. V. D. Bruggen, Chem. Soc. Rev., 2019, 48, 2665–2681 RSC.
- (a) S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS; (b) H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS; (c) O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- (a) Y. He, S. Xiang and B. Chen, J. Am. Chem. Soc., 2011, 133, 14570–14573 CrossRef CAS; (b) A. Karmakar, R. Illathvalappil, B. Anothumakkool, A. Sen, P. Samanta, A. V. Desai, S. Kurungot and S. K. Ghosh, Angew. Chem., Int. Ed., 2016, 55, 10667–10671 CrossRef CAS PubMed; (c) D.-D. Zhou, Y.-T. Xu, R.-B. Lin, Z.-W. Mo, W.-X. Zhang and J.-P. Zhang, Chem. Commun., 2016, 52, 4991–4994 RSC; (d) I. Hisaki, Y. Suzuki, E. Gomez, Q. Ji, N. Tohnai, T. Nakamura and T. Nakamura, J. Am. Chem. Soc., 2019, 141, 2111–2121 CrossRef CAS PubMed; (e) X.-T. He, Y.-H. Luo, D.-L. Hong, F.-H. Chen, Z.-Y. Zheng, C. Wang, J.-Y. Wang, C. Chen and B.-W. Sun, ACS Appl. Nano Mater., 2019, 2, 2437–2445 CrossRef CAS.
- (a) P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS; (b) C. B. Aakeröy, M. Baldrighi, J. Desper, P. Metrangolo and G. Resnati, Chem. – Eur. J., 2013, 19, 16240–16247 CrossRef; (c) P. Metrangolo and G. Resnati, Chem. Commun., 2013, 49, 1783–1785 RSC; (d) A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS; (e) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS; (f) D. Bulfield and S. M. Huber, Chem. – Eur. J., 2016, 22, 14434–14450 CrossRef CAS PubMed.
- (a) T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 1992, 44, 57–64 CrossRef; (b) A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714 CrossRef; (c) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS; (d) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS.
- (a) V. I. Nikolayenko, D. C. Castell, D. P. van Heerden and L. J. Barbour, Angew. Chem., Int. Ed., 2018, 57, 12086–12091 CrossRef CAS; (b) S. Shankar, O. Chovnik, L. J. W. Shimon, M. Lahav and M. E. van der Boom, Cryst. Growth Des., 2018, 184, 1967–1977 CrossRef.
- (a) G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati, M. Sansotera and G. Terraneo, Chem. Soc. Rev., 2010, 39, 3772–3783 RSC; (b) A. Brown and P. D. Beer, Chem. Commun., 2016, 52, 8645–8658 RSC.
- (a) A. N. M. M. Rahman, R. Bishop, D. C. Craig and M. L. Scudder, CrystEngComm, 2003, 5, 422–428 RSC; (b) H. Matter, M. Nazar and S. Güssregen, The importance of π-interactions in crystal engineering, ed. E. R. T. Tiekink and J. Zukerman-Schpector, Wiley, Chichester, 2012, pp. 187–132 Search PubMed; (c) H. Zhuo, Q. Li, W. Lia and J. Cheng, Phys. Chem. Chem. Phys., 2014, 16, 159–165 RSC; (d) M. Giese, M. Albrecht and K. Rissanen, Chem. Commun., 2016, 52, 1778–1795 RSC.
- (a) H. G. Wallnoefer, T. Fox, K. R. Liedl and C. S. Tautermann, Phys. Chem. Chem. Phys., 2010, 12, 14941–14949 RSC; (b) K. E. Riley, C. L. Ford Jr. and K. Demouchet, Chem. Phys. Lett., 2015, 621, 165–170 CrossRef CAS; (c) A. Bauzá and A. Frontera, Theor. Chem. Acc., 2017, 136, 1–8 Search PubMed; (d) M. Bujak, H.-G. Stammler, S. Blomeyer and N. W. Mitzel, Chem. Commun., 2019, 55, 175–178 RSC.
- (a) F. Ghahari, D. Walkup, C. Gutiérrez, J. F. Rodriguez-Nieva, Y. Zhao, J. Wyrick, F. D. Natterer, W. G. Cullen, K. Watanabe, T. Taniguchi, L. S. Levitov, N. B. Zhitenev and J. A. Stroscio, Science, 2017, 356, 845–849 CrossRef CAS; (b) S. Mukherjee and G. Singh, ACS Appl. Energy Mater., 2019, 22, 932–955 CrossRef.
- (a) P. Metrangolo, Y. Carcenac, M. Lahtinen, T. Pilati, K. Rissanen, A. Vij and G. Resnati, Science, 2009, 323, 1461–1464 CrossRef CAS; (b) J. Martí-Rujas, L. Colombo, J. Lü, A. Dey, G. Terraneo, P. Metrangolo, T. Pilati and G. Resnati, Chem. Commun., 2012, 48, 8207–8209 RSC.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- CrysAlis CCD and CrysAlis RED, version 1.171.37.35, Oxford Diffraction Ltd, Yarnton, Oxfordshire, U.K., 2014 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revis. D.01, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. L. Bergman, L. Laaksonen and A. Laaksonen, J. Mol. Graphics Modell., 1997, 15, 301–306 CrossRef CAS.
- (a) U. H. F. Bunz, Chem. Rev., 2000, 100, 1605–1644 CrossRef CAS PubMed; (b) P.-Y. Du, W. Gu and X. Liu, CrystEngComm, 2016, 18, 5140–5148 RSC.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- B. K. Saha, J. Indian Inst. Sci., 2017, 97, 177–191 CrossRef.
- (a) F.-G. Klärner and B. Kahlert, Acc. Chem. Res., 2003, 36, 919–932 CrossRef; (b) J. Wang, Y. Gao, J. Xiang, M. Wang and A. Wu, CrystEngComm, 2015, 17, 2245–2249 RSC.
- M. C. Etter and J. C. MacDonal, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262 CrossRef.
- A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18 CrossRef CAS.
- (a) M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC; (b) J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC; (c) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19 RSC.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional structural and finger plot figures, tables, IR spectra, XRD patterns, and luminescence and UV-vis spectra. CCDC 1941497–1941504. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce01140d |
| This journal is © The Royal Society of Chemistry 2020 |