Open Access Article
Open Access ArticleReversible switching from a three- to a nine-fold degenerate dynamic slider-on-deck through catenation†
Vishnu Verman
Rajasekaran
 ,
Indrajit
Paul
,
Indrajit
Paul
 and
Michael
Schmittel
and
Michael
Schmittel
 *
*
Center of Micro and Nanochemistry and Engineering, Organische Chemie I, Universität Siegen, Adolf-Reichwein-Str. 2, D-57068, Germany. E-mail: schmittel@chemie.uni-siegen.de; Tel: +49(0) 2717404356
First published on 17th September 2020
Abstract
Two dynamic slider-on-deck assemblies, i.e. a two-component threefold degenerate (k298 = 34.9 kHz) and a catenated three-component ninefold degenerate (k298 = 27.9 kHz) system, were quantitatively interconverted. Inspection of their computed structures revealed an allosteric effect on the sliding rates due to the spatial interaction between the components.
Since the first breathtaking demonstration of their preparation by simple self-assembly, catenanes1 have assumed an outstanding importance in the arena of synthetic molecular machines.2–4 These mechanically interlocked molecules have been the basis for constructing motors,5 switches,6 solid-state electronics,7 and DNA-based architectures8 mainly capitalizing on the relative translational and/or rotational dynamics between the rings. The inherent dynamics has been studied in much detail, as reported initially in Sauvage's ground-breaking [2]catenane paper,9 followed by many studies on electrochemically,10 light-,11 and chemically12 induced motion.13
To date, a lot of impressive examples of coordination-driven multicomponent dynamic catenanes have been reported,14 but dynamics has been usually limited to the relative motion between rings.15 In contrast, the concept of a multicomponent dynamic catenate exhibiting nanomechanical motion other than dynamics between rings has been a relatively unexplored facet.16 Moreover, to the best of our knowledge, the allosteric adjustment of nanomechanical motion in multicomponent17 dynamic catenanes adds new prospects for the field of catenate-based machines.
In this report, we elaborate on aspects of dual dynamics in catenate DS2, with the interconversion between topological structures (catenate → 2 × macrocycles) being only one facet (Scheme 1). A similar system developed by Sauvage and Heitz on the basis of homoleptic [Cu(phen)2]+ and Npy → ZnPor (zinc porphyrin) interactions, has emphasized the effect of geometric parameters (distance and angles) in coordination-based catenate assemblies.18 The second facet of dynamics encompasses the feature that each macrocyclic unit of catenate DS2 and of DS1 is a highly dynamic slider-on-deck system in itself (e.g.DS1, Scheme 1). In more detail, the dynamic two-component slider-on-deck DS1 constitutes a macrocyclic system with three degenerate states that reversibly and quantitatively converts into the three-component dynamic slider-on-deck catenate DS2 with 3 × 3 degenerate states. Interconversion is accomplished by addition/removal of Cu+ ions. Moreover, the intrasupramolecular dynamics, the rate-determining step of which requires Npy → ZnPor bond cleavage, is affected by an allosteric effect originating at the remote metal-phenanthroline coordination site.
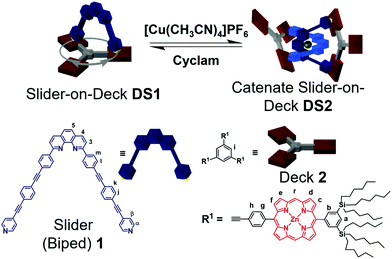 | ||
| Scheme 1 Reversible interconversion between the slider-on-deck DS1 and the dynamic catenate slider DS2. Sliding motion shown for DS1. | ||
Synthesis and characterization of biped 1 and deck 2 are described in the ESI.† At first, we decided to separately prepare the multicomponent dynamic slider-on-deck systems DS1 and DS2 capitalizing on homoleptic [Cu(phenAr2)2]+ complexation and/or Npy → ZnPor interactions, i.e. two binding motifs that are known to be orthogonal.19 Biped 1 and deck 2 were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
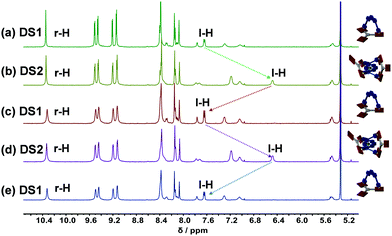
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio quantitatively furnishing DS1 (Fig. 1b). Complex DS1 was fully characterized by 1H, 1H–1H COSY, 1H–1H NOESY, 1H DOSY NMR studies and elemental analysis (ESI,† Fig. S17–S19, S25). The slider assembly was identified by the changes in the 1H-NMR signals of protons α-H, β-H of the biped 1 and r-H of the deck 2 (Fig. 1b, c and e). There are stark changes in the signals of protons α-H and β-H of 1 as they experience the porphyrin's shielding ring current upon axial Npy → ZnPor coordination thus shifting the r-H signals of 2 slightly upfield.
1 ratio quantitatively furnishing DS1 (Fig. 1b). Complex DS1 was fully characterized by 1H, 1H–1H COSY, 1H–1H NOESY, 1H DOSY NMR studies and elemental analysis (ESI,† Fig. S17–S19, S25). The slider assembly was identified by the changes in the 1H-NMR signals of protons α-H, β-H of the biped 1 and r-H of the deck 2 (Fig. 1b, c and e). There are stark changes in the signals of protons α-H and β-H of 1 as they experience the porphyrin's shielding ring current upon axial Npy → ZnPor coordination thus shifting the r-H signals of 2 slightly upfield.
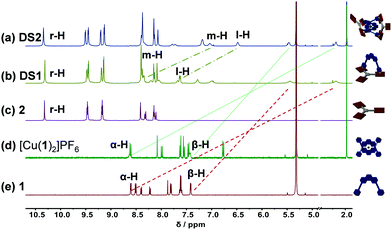 | ||
| Fig. 1 Comparison of partial 1H-NMR (500 MHz, CD2Cl2, 298 K) of (a) catenate slider-on-deck DS2 = [Cu(1)2·(2)2]PF6; (b) slider-on-deck DS1 = [1·2]; (c) free deck 2; (d) [Cu(1)2]PF6; (e) slider 1. | ||
Similarly, 1, 2 and Cu+ were mixed in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to quantitatively assemble DS2. The complex DS2 was fully characterized by 1H NMR, 1H–1H COSY, 1H–1H NOESY NMR, 1H DOSY (ESI,† Fig. S20–S22, S24), and elemental analysis. Formation of the dynamic catenate DS2 was ascertained by changes in the 1H-NMR signature of protons m-H, l-H, α-H, β-H of 1 and r-H of 2. Signals of protons α-H and β-H significantly shifted upfield, while those of m-H and l-H from the [Cu(1)2]+ unit broadened and shifted slightly upfield upon catenation and axial coordination with 2 (Fig. 1a and d). The broadening is a strong indication of dynamic exchange rates faster than the NMR timescale.
1 ratio to quantitatively assemble DS2. The complex DS2 was fully characterized by 1H NMR, 1H–1H COSY, 1H–1H NOESY NMR, 1H DOSY (ESI,† Fig. S20–S22, S24), and elemental analysis. Formation of the dynamic catenate DS2 was ascertained by changes in the 1H-NMR signature of protons m-H, l-H, α-H, β-H of 1 and r-H of 2. Signals of protons α-H and β-H significantly shifted upfield, while those of m-H and l-H from the [Cu(1)2]+ unit broadened and shifted slightly upfield upon catenation and axial coordination with 2 (Fig. 1a and d). The broadening is a strong indication of dynamic exchange rates faster than the NMR timescale.
Finally, we were interested in reversibly interconverting the two slider-on-deck systems and thus first assembled DS1 in solution as described above. Follow-up addition of 0.5 equiv. of [Cu(CH3CN)4]PF6 quantitatively furnished DS2. Sequential addition and removal of Cu+ (using cyclam followed by sonication at 50 °C for 30 min) led to quantitative interconversion between the two assemblies DS1 and DS2 (Fig. 2a–e). The transformation DS1 → DS2 was confirmed by drastic upfield shifts of the 1H-NMR signals of protons m-H and l-H attributed to the shielding by the proximal second phenanthroline. These findings were further corroborated by 1H-DOSY NMR studies (ESI,† Fig. S24 and S25) which indicated a hydrodynamic radius change proportionate to the larger catenate slider-on-deck DS2 (D = 3.30 × 10−10 m2 s−1, rs = 16.1 Å) when compared to DS1 (D = 3.82 × 10−10 m2 s−1, rs = 13.9 Å).
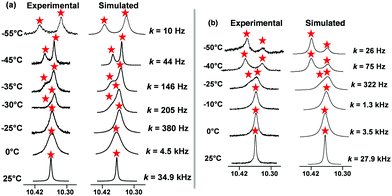
To quantify the sliding exchange dynamics, we analyzed the 1H-NMR signals of DS1 at various temperatures. The diagnostic proton r-H signal of the ZnPor units in DS1 was chosen because it appears as a sharp singlet (10.34 ppm) at 298 K. VT 1H-NMR studies20 confirmed the dynamic coordination of both pyridine terminals of the slider biped 1 to the three degenerate ZnPor stations of deck 2. Diagnostically, the sharp singlet at 298 K separated at 228 K into two singlets (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 10.32 and 10.40 ppm. While the rather sharp signal at 10.32 ppm was assigned to both pyridine-coordinated zinc porphyrins, the freely rotating second zinc porphyrin furnished a broader signal at 10.40 ppm. A kinetic analysis provided the frequency (k) for exchange at different temperatures (Fig. 3a) with k = 34.9 kHz s−1 at 298 K. The activation parameters are ΔH‡ = 52.2 ± 0.7 kJ mol−1 and ΔS‡ = 17.2 ± 2.8 J mol−1 K−1 furnishing the free energy of activation for exchange at 298 K as
1) at 10.32 and 10.40 ppm. While the rather sharp signal at 10.32 ppm was assigned to both pyridine-coordinated zinc porphyrins, the freely rotating second zinc porphyrin furnished a broader signal at 10.40 ppm. A kinetic analysis provided the frequency (k) for exchange at different temperatures (Fig. 3a) with k = 34.9 kHz s−1 at 298 K. The activation parameters are ΔH‡ = 52.2 ± 0.7 kJ mol−1 and ΔS‡ = 17.2 ± 2.8 J mol−1 K−1 furnishing the free energy of activation for exchange at 298 K as 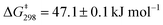 (ESI,† Fig. S28 and S29).
(ESI,† Fig. S28 and S29).
Analogously, the proton r-H signal was chosen as the diagnostic parameter in the VT 1H-NMR for determining the dynamics of the catenate slider-on-deck DS2. At 298 K, the r-H signal showed up as a sharp singlet (10.34 ppm). The VT 1H-NMR data thus confirmed the dynamic coordination of the tetratopic [Cu(1)2]PF6 with its four pyridine terminals to the altogether 2 × 3 degenerate porphyrins from both identical decks 2. At 233 K, the sharp singlet of proton r-H at 298 K separated into two singlets (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 10.40 and 10.32 ppm. Whereas the quite sharp signal at 10.40 ppm was ascribed to the four pyridine-coordinated zinc porphyrins, the two freely rotating zinc porphyrin(s) displayed a broader signal at 10.32 ppm. A kinetic analysis provided the frequency (k) for exchange at different temperatures (Fig. 3b) with k298 = 27.9 kHz at 298 K. The activation parameters are ΔH‡ = 48.9 ± 0.7 kJ mol−1 and ΔS‡ = 3.2 ± 2.6 J mol−1 K−1 furnishing the free energy of activation for exchange at 298 K as ΔG‡ = 47.9 ± 0.1 kJ mol−1 (ESI,† Fig. S26 and S27).
1) at 10.40 and 10.32 ppm. Whereas the quite sharp signal at 10.40 ppm was ascribed to the four pyridine-coordinated zinc porphyrins, the two freely rotating zinc porphyrin(s) displayed a broader signal at 10.32 ppm. A kinetic analysis provided the frequency (k) for exchange at different temperatures (Fig. 3b) with k298 = 27.9 kHz at 298 K. The activation parameters are ΔH‡ = 48.9 ± 0.7 kJ mol−1 and ΔS‡ = 3.2 ± 2.6 J mol−1 K−1 furnishing the free energy of activation for exchange at 298 K as ΔG‡ = 47.9 ± 0.1 kJ mol−1 (ESI,† Fig. S26 and S27).
For similar slider-on-deck systems,21,22 we recently discus-sed various mechanistic options, but only one scenario agreed with the kinetic data. Alike, in both DS1 and DS2 the exchange could occur through complete dissociation followed by re-association of 1 and 2 (intermolecular hopping) or a single Npy → ZnPor bond dissociation-rotation-association (sliding) mechanism. Since the barrier in a rotor23 operating via a well-defined single Npy → ZnPor dissociation amounted to ΔG‡ = 47.6 ± 0.1 kJ mol−1, the pathway involving complete dissociation is rigorously ruled out for DS1 and DS2 as their barriers are almost identical to that of the rotor: ΔG‡ (DS1) = 47.1 ± 0.1 kJ mol−1 and ΔG‡ (DS2) = 47.9 ± 0.1 kJ mol−1.
Comparing the kinetic data of both slider-on-deck systems leads us to interesting mechanistic corollaries. Specifically, one could hypothesize that the exchange motion at both ZnPor decks of DS2 could be either coupled or decoupled. If the exchange would be decoupled, i.e. the motion at both decks is fully independent, then the frequency should be identical to that of DS1. If it were coupled, positions at deck A and B would communicate and then a full exchange would require that all combinations be passed through equally. As a result, the frequency could be derived from the exchange rate at the single site in DS1 and a statistical correction. In principle, this constitutes a case of multiplicative constrained probabilities as P(total) = P(event 1) × P(event 2; given event 1 has happened). In the coupled case one would expect P(total) = (1/3) × (1) = 1/3. However, the observed rate of DS2 is not 1/3 that of DS1; the frequency at DS2 is only slower by 10–15%. On the other hand, the two rates are not identical, as expected for the decoupled case. Rather they remain different even considering the error range (k298 = 34.9 ± 1.8 kHz for DS1 and k298 = 27.9 ± 1.4 kHz for DS2). Nevertheless, it is obvious to postulate for DS2 that the motion at both decks is decoupled. But why is the observed frequency lower? We can exclude metal coordination at the remote phenanthroline to be responsible for this effect. Actually, metal coordination should lower the donor quality of the pyridine feet in the Npy → ZnPor interaction. As a net effect, in such case, exchange in DS2 should be faster than in DS1, contrary to our findings.
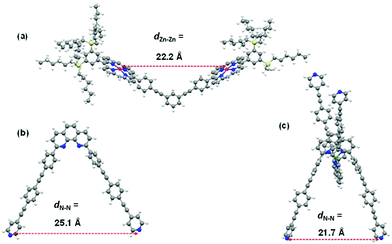
Ultimately, an inspection of the DFT-computed slider-on-deck structures provides a convincing reason for the rate differences. The data suggest that biped 1 in DS1 (ESI,† Fig. S35) is strained once axial Npy → ZnPor coordination at both ZnPor units is realized. The strain is indirectly visible from the intramolecular pyridine–pyridine distance when one compares the d(Npy–Npy′) of the free biped 1 in its unstrained state with the one enforced for 1 when combining with deck 2 in DS1, i.e. 25.1 vs. 22.2 Å, respectively (Fig. 4a and b). Consequently, some release of strain energy is expected to promote the Npy → ZnPor dissociation step in DS1. On the other hand, the computed [Cu(1)2]+ fragment in DS2 (ESI,† Fig. S36) has an intramolecular pyridine–pyridine distance d(Npy–N′py) = 21.7 Å that almost exactly matches that of the unstrained free deck 2 {d(Zn–Zn) = 22.2 Å} (Fig. 4a and c) leading to a possibly strain-free axial Npy → ZnPor coordination in DS2. The reduced Npy–N′py distance in the [Cu(1)2]+ unit as compared to that in 1 indicates a long-range effect of the Cu+ coordination on the biped's spatial arrangement. This finding points to an allosteric effect originating from the four-fold π–π stacking between the 2,9-phenyl groups with the opposite phenanthroline's π cloud in the homoleptic complex [Cu(1)2]PF6.
Finally, due to the reduced strain release in the transition state of the exchange in DS2 as compared to that in DS1, the slower sliding speed of 27.9 ± 1.4 kHz in DS2 is readily understood (cf.DS1, k = 34.9 ± 1.8 kHz).
In summary, we have demonstrated two dynamic slider-on-deck systems that are quantitatively and reversibly toggled through catenation/decatenation. The interconversion between the two-component macrocyclic and the three-component slider-on-deck catenate is accomplished by addition and removal of Cu+ ions. A rigorous kinetic analysis of the three- vs. nine-fold degenerate rearrangement indicates that allosteric effects are switched off/on in the DS1 ⇆ DS2 transformation. The fine tuning of dynamic allosteric effects in switchable multicomponent assemblies opens new routes for the modulation of molecular machine processes.
We are indebted to the University of Siegen, Dr Thomas Paululat (Siegen) and the Deutsche Forschungsgemeinschaft (Schm 647/20-2) for continued support.
Conflicts of interest
There are no conflicts to declare.Notes and references
- S.-L. Huang, T. S. A. Hor and G.-X. Jin, Coord. Chem. Rev., 2017, 333, 1–26 Search PubMed.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 Search PubMed.
- J.-P. Sauvage, Angew. Chem., Int. Ed., 2017, 56, 11080–11093 Search PubMed.
- J. F. Stoddart, Angew. Chem., Int. Ed., 2017, 56, 11094–11125 Search PubMed.
- M. R. Wilson, J. Solà, A. Carlone, S. M. Goldup, N. Lebrasseur and D. A. Leigh, Nature, 2016, 534, 235–240 Search PubMed.
- S. Grunder, P. L. McGrier, A. C. Whalley, M. M. Boyle, C. Stern and J. F. Stoddart, J. Am. Chem. Soc., 2013, 135, 17691–17694 Search PubMed.
- C. P. Collier, G. Mattersteig, E. W. Wong, Y. Luo, K. Beverly, J. Sampaio, F. M. Raymo, J. F. Stoddart and J. R. Heath, Science, 2000, 289, 1172–1175 Search PubMed.
- (a) Y. Liu, A. Kuzuya, R. Sha, J. Guillaume, R. Wang, J. W. Canary and N. C. Seeman, J. Am. Chem. Soc., 2008, 130, 10882–10883 Search PubMed; (b) J. Elbaz, Z.-G. Wang, F. Wang and I. Willner, Angew. Chem., Int. Ed., 2012, 51, 2349–2353 Search PubMed.
- M. Cesario, C. O. Dietrich-Buchecker, J. Guilhem, C. Pascard and J. P. Sauvage, J. Chem. Soc., Chem. Commun., 1985, 244–247 Search PubMed.
- B. Korybut-Daszkiewicz, A. Więckowska, R. Bilewicz, S. Domagała and K. Woźniak, Angew. Chem., Int. Ed., 2004, 43, 1668–1672 Search PubMed.
- P. Mobian, J.-M. Kern and J.-P. Sauvage, Angew. Chem., Int. Ed., 2004, 43, 2392–2395 Search PubMed.
- N. H. Evans, C. J. Serpell and P. D. Beer, Chem. – Eur. J., 2011, 17, 7734–7738 Search PubMed.
- A. Goswami and M. Schmittel, Coord. Chem. Rev., 2018, 376, 478–505 Search PubMed.
- (a) M. Fujita and K. Ogura, Coord. Chem. Rev., 1996, 148, 249–264 Search PubMed; (b) C. Dietrich-Buchecker, B. Colasson, M. Fujita, A. Hori, N. Geum, S. Sakamoto, K. Yamaguchi and J.-P. Sauvage, J. Am. Chem. Soc., 2003, 125, 5717–5725 Search PubMed; (c) S. Prusty, S. Krishnaswamy, S. Bandi, B. Chandrika, J. Luo, J. S. McIndoe, G. S. Hanan and D. K. Chand, Chem. – Eur. J., 2015, 21, 15174–15187 Search PubMed; (d) T. Sawada, M. Yamagami, K. Ohara, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2016, 55, 4519–4522 Search PubMed.
- N. H. Evans and P. D. Beer, Chem. Soc. Rev., 2014, 43, 4658–4683 Search PubMed.
- J. Valero, N. Pal, S. Dhakal, N. G. Walter and M. Famulok, Nat. Nanotechnol., 2018, 13, 496–503 Search PubMed.
- A. Goswami, S. Saha, P. K. Biswas and M. Schmittel, Chem. Rev., 2020, 120, 125–199 Search PubMed.
- M. Beyler, V. Heitz and J.-P. Sauvage, J. Am. Chem. Soc., 2010, 132, 4409–4417 Search PubMed.
- (a) N. Mittal, M. L. Saha and M. Schmittel, Chem. Commun., 2015, 51, 15514–15517 Search PubMed; (b) S. De, S. Pramanik and M. Schmittel, Angew. Chem., Int. Ed., 2014, 53, 14255–14259 Search PubMed.
- (a) A. Goswami and M. Schmittel, Angew. Chem., Int. Ed., 2020, 59, 12362–12366 Search PubMed; (b) S. Saha, P. K. Biswas, I. Paul and M. Schmittel, Chem. Commun., 2019, 55, 14733–14736 Search PubMed; (c) A. Goswami, S. Pramanik and M. Schmittel, Chem. Commun., 2018, 54, 3955–3958 Search PubMed.
- I. Paul, A. Goswami, N. Mittal and M. Schmittel, Angew. Chem., Int. Ed., 2018, 57, 354–358 Search PubMed.
- A. Ghosh, I. Paul, S. Saha, T. Paululat and M. Schmittel, Org. Lett., 2018, 20, 7973–7976 Search PubMed.
- A. Goswami, I. Paul and M. Schmittel, Chem. Commun., 2017, 53, 5186–5189 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc05578f |
| This journal is © The Royal Society of Chemistry 2020 |