Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ionicity-dependent proton-coupled electron transfer of supramolecular self-assembled electroactive heterocycles†
Kendrick K. L.
Ng
,
Reema
Devlia
,
Nichola L.
Foss
,
Luke S.
Alesbrook
 ,
Jennifer R.
Hiscock
,
Jennifer R.
Hiscock
 * and
Alexander T.
Murray
* and
Alexander T.
Murray
 *
*
University of Kent, Park Wood Road, Canterbury, Kent, CT2 7NH, UK. E-mail: j.r.hiscock@kent.ac.uk; a.t.murray@kent.ac.uk
First published on 27th August 2020
Abstract
Herein, we investigate the electrochemical properties of a class of Supramolecular Self-associated Amphiphilic salts (SSAs). We show that varying ionic strength of an SSA solution can cause a switching of the thermodynamics and kinetics of electron transfer. The effect of self-assembly on proton-coupled electron transfer has implications for the understanding of electron transfer kinetics in aqueous organic redox flow batteries, especially at high concentration where organic–organic intermolecular interactions become dominant even for highly soluble organic species.
The electrochemical behaviour of self-assembled systems is challenging both to model and to explore experimentally. Generally, the prime consideration in electron transfer from an external circuit to and from a given supramolecular system is attributed to a change in molecular self-assembly, which is mediated by alteration in coulombic attraction/repulsion upon one-electron redox.1 These considerations have been shown to be appropriate for most electron transfer events that occur in aprotic organic solvents, including the behaviour of host–guest systems (ferrocene-crown ether2 and ferrocene-cyclodextrin3 complex formation) and switchable rotaxane systems.4
However, work to establish the effects of self-association events on proton-coupled electron transfer (PCET) reactions in polar solvents, has seen a lesser amount of experimental exploration despite the ubiquity of proton-coupled processes in biological and abiotic redox systems, such as water oxidation and oxygen reduction.5 One plausible reason for this is that PCET events tend to occur with molecules that are inherently water-soluble and non-amphiphilic, therefore resist incorporation into extended aggregate structures.
Quinones are among the most well-studied of electroactive organic molecules, both in the context of biological and synthetic products.6 These molecular constructs have been used in many diverse contexts, from catalysis, redox flow batteries, to dyes and antimicrobials.7–11 Quinones in water possess a complex proton-coupled electron transfer process which is still challenging to fully understand despite decades of electrochemical study. This is because the aqueous redox chemistry of quinones can be affected to such a large extent by pH, both in the bulk solution and especially at the non-equilibrium conditions of the electrochemical double layer.12–15 A further confounding factor, albeit one with applications in quinone catalysis, is the strong effect of specific proton donors on the rate of electron transfer to quinones, which is itself dependent on the quinone electronics.16
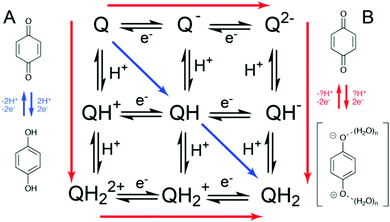
The large variation in redox potential observed at the electrochemical double layer can be further explained by the change in local pH and thus proton activity under reducing and oxidising conditions at the electrochemical boundary layer, in the absence of compensation from a reservoir of buffer solution. This means that quinone reduction is a relatively well-defined 2H+, 2e− process under buffered conditions (Fig. 1, path A). However, in unbuffered electrolyte at a similar pH a partially proton-coupled process occurs with ill-defined hydrogen bonded anions (Fig. 1, path B).7–11 This has implications for the electrochemical behaviour of quinones under buffered and unbuffered conditions.
The two divergent mechanisms delineated in Fig. 1 counterintuitively lead to reduction B being thermodynamically harder due to the formation of the higher energy reduced product Q2−(H2O)n, but kinetically more facile. This can be qualitatively explained by the work of Laviron, who depicted the reduction and oxidation of pH-dependent reactions by a square scheme, whereby “diagonal” movement through a square yields a lower overall rate.12–15 This is because proton transfer alters the equilibrium potential, meaning that in cases such as the reduction of quinones where electron transfer (ET) is not inherently fast, current does not flow until the electrode potential is significantly past the overall half-wave potential E1/2. This is explained by rapid proton equilibration effectively increasing the effects of the inherent kinetic limitations of ET (Fig. 1).17
This complex mechanistic behaviour can be further complicated by the presence of non-covalent complex formation events within the quinone containing system, especially at the high concentrations where quinones would be expected to provide utility e.g. in organic redox flow batteries. For instance, there have been reports of self-association of sulfonated anthraquinones in solution being responsible for the inhibition of complete two-electron reduction at high concentrations, preventing the desired deep charge/discharges in redox flow batteries.18 Additionally, ‘self-association’ has been attributed to a decrease in rate of electron transfer, corresponding to lower peak power densities.19 Finally, a lack of efficiency or degradation in quinone-based systems is often attributed to bimolecular reactions between oxidised and reduced quinone species,20 including the oligomerisation reactions of high-potential quinones.21 However, a mechanistic picture of PCET in species which self-associate has, to the best of our knowledge, not been disclosed.
SSAs are a novel class of Supramolecular Self-associating Amphiphilic salt, the anionic component of which contains a hydrogen bond donor–acceptor thio/urea group, covalently linked through an alkyl spacer, to the anion.20–23 The uneven number of hydrogen bond donating and accepting functionalities contained within the anionic component of an SSA means this unit is able to adopt a number of different hydrogen bonding modes simultaneously. This includes the formation of thio/urea-anion dimers, thio/urea-anion tapes and thio/urea-thio/urea stacks, all of which have been observed in the solid state.22 In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 EtOH
19 EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O solutions these SSAs have shown the propensity towards the formation of spherical aggregates ≈150–350 nm in hydrodynamic diameter.23–25
H2O solutions these SSAs have shown the propensity towards the formation of spherical aggregates ≈150–350 nm in hydrodynamic diameter.23–25
Herein, we explore the use of the SSA construct to produce switchable electroactive quinone containing species (Fig. 2). We establish the influence of the self-associated structures formed, elucidating molecular structure–electroactivity–physicochemical property relationships. We demonstrate that addition of simple salts can influence the self-associated structures formed, and therefore the PCET, switching between buffered and unbuffered-like manifolds.
In strongly acidic medium (pH 0), [Q-SSA][TBA] was found to behave as a ‘typical’ aqueous quinone, with E1/2 = 84 mV vs. standard hydrogen electrode (SHE), consistent with an electron rich quinone as expected from the influence of the donor urea group (Fig. S1, ESI†). The redox couple gave 50 mV peak-to-peak separation (ΔEpp) at a scan rate of 50 mV s−1, suggesting a quasireversible two-electron process. Upon variation of pH in 0.1 M acetate buffer, we observed typical ∼60 mV per pH variation of E1/2 with pH (Fig. S2, ESI†).
We then investigated whether changing the solution ionic strength might affect the electrochemical behaviour. We were surprised to discover that upon titration of increasing [NaCl], E1/2 decreases and ΔEpp increases just as observed by Smith et al. upon changing between buffered and unbuffered solutions (Fig. 3a).17 Systematic addition of NaCl to a solution of pH-adjusted 0.3 mM [Q-SSA][TBA] in 0.1 M NaOAc/HOAc solution (pH 4) showed a decrease in E1/2 in addition to a relatively linear decrease in ΔEpp by approximately 50 mV across the range of concentrations studied, regardless of scan rate (Fig. 3b). This variation in [NaCl] demonstrated a concurrent effect on the thermodynamics of electron transfer, making the redox couple more reducing (Fig. 3c). A gradual decrease of 25 mV in redox potential was observed across the range of ionic strengths probed, showing a greater electrochemical potential must be applied to reduce [Q-SSA][TBA] in the presence of NaCl. This gives approximately 30 mV dec−1 [NaCl] suggesting a possible sodium association to the as-reduced quinones, or that the process could plausibly be first-order in [Na+]. These trends demonstrated the increase in electron transfer rate which would be expected for a Q → Q2− → QH2/QH− pathway around the Laviron square scheme. Real currents were low (<10 μA) and iR (uncompensated resistance) correction with positive feedback was used in all cases, suggesting a change in uncompensated resistance was not a major confounding factor.
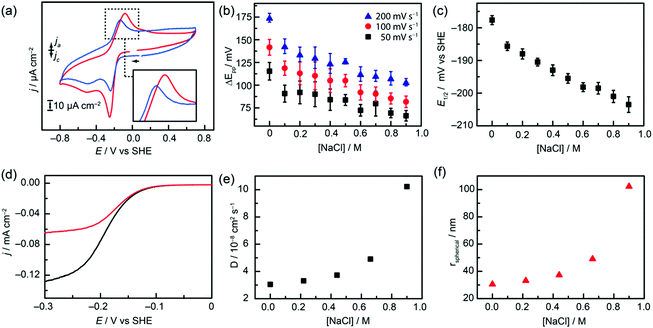 | ||
| Fig. 3 (a) cyclic voltammetry (CV) of [Q-SSA][TBA] taken at 50 mV s−1 in 0.1 M NaOAc (red) and 0.1 M NaOAc/0.9 M NaCl (blue). (b) Plot of [NaCl] vs. ΔEpp at 50, 100 and 200 mV s−1. (c) Plot of [NaCl] vs. E1/2 (d) LSV (50 mV s−1) of [Q-SSA][TBA] rotated at 2000 rpm for 0.1 M NaOAc (black) and 0.1 M NaOAc/0.9 M NaCl (red). (e) Diffusion coefficients calculated from Levich plots (Fig. S4, ESI†) plotted against [NaCl]. (f) Estimated average particle sizes derived from (e), plotted against [NaCl] | ||
Together, these data are consistent with ‘buffered-like’ electrochemical behaviour in the absence of excess ionic species and ‘unbuffered-like’ trends observed upon addition of simple inorganic electrolytes. The application of Randles-Sevcik plots showed linearity for √ν vs. ip (Fig. S3, ESI†), and the use of rotating disk voltammetry (RDE) showed clear changes in limiting current (iL) over all [NaCl] regimes, both demonstrating that a sluggish, surface-bound process was not responsible for the observed electrochemical features (Fig. S4, ESI†). Furthermore, for a range of [NaCl] concentrations a corresponding diffusion coefficient D, for [Q-SSA][TBA] could be determined (Fig. 3d), showing the diffusion becomes slower with increasing [NaCl], suggesting an increase in aggregation state to form, in net, larger nanostructures (Fig. 3e). This can be used in conjunction with the Stokes–Einstein equation (Fig. 3f) to estimate the average size of these self-associated SSA aggregate structures under this range of experimental conditions. An aggregate diameter of 31 nm was calculated at [NaCl] = 0.0 M, this was found to increase to 105 nm at [NaCl] = 0.9 M.
Given these results, we postulate the barrier to proton transfer is caused by a greater degree of [Q-SSA][TBA] self-association. This can be considered as a kind of salting-out effect, with a higher ionic strength electrolyte promoting the greater degree of particle association. Therefore, at high [NaCl] we propose the development of a greater proton gradient into the self-associated aggregates formed, and thus a more ill-defined electrochemical process with a greater kinetic reversibility but also a thermodynamically less facile reductive process (Fig. 3c). However, it is important to note that these bulk measurements may not be strongly indicative of the non-equilibrium electrochemistry observed at the electrode surface. Indeed, given the large electrolyte concentrations adjacent to the electrode, we expect these effects may be even more prominent in the electrochemical double layer.26,27
Previously in the analysis of self-association in PCET systems, varying concentration has been an entry into the analysis of the interactions.18 However, given the relatively low solubility of [Q-SSA][TBA], we turned to the less lipophilic analogue [Q-SSA][TMA]. This did not in fact possess higher solubility, but electrochemical studies of this compound yielded the same thermodynamic trend as for [Q-SSA][TBA] (Fig. S5, ESI†). However, there was not a clear trend in ΔEpp (Fig. S6, ESI†). This suggests that while an overall net change in the electrochemical process from Q → QH2 at low [NaCl] to Q → Q2−(H2O)n at high [NaCl] may still be occurring, there is no systematic change in the path taken through the individual PT and ET steps (Fig. 1).
A tentative rationale was provided using complementary measurements of the nanostructures formed. Dynamic light scattering (DLS) measurements for solutions of [Q-SSA][TBA] were broadly similar to those of [Q-SSA][TMA], though smaller initial particles were observed for [Q-SSA][TMA]. However, zeta-potential measurements showed while the nanostructures were metastable in all cases, the stability of [Q-SSA][TMA] at low [NaCl] was significantly lower than the TBA analogue (Table 1). This suggests that it is possible that the fluxional nature of the self-associative binding in this case means that the kinetic trend is convoluted. Indeed, the difficulties of measuring weak- or highly metastable interactions electrochemically are a common problem in non-aqueous supramolecular electrochemistry.1 Given the bias of DLS measurements towards larger particles, the reported nanostructure sizes (Table 1) are relatively close at the low end to the electrochemically-measured sizes (Fig. 3f). Attempts to observe these trends directly by SEM were convoluted by the presence of excess inorganic salts, nevertheless we observed relatively larger organic-containing particles in the presence of NaCl (Fig. S15, ESI†).
| SSA | [NaCl]/M | E 0/mV | ΔEpp/mV SR 50 | Z/mV | DLS data | |
|---|---|---|---|---|---|---|
| Peak spread/nm | PDI/% | |||||
| [Q-SSA][TBA] | 0 | −178 | 130 | −37 | 34–307 | 22 |
| [Q-SSA][TMA] | 0 | −174 | 135 | −26 | 4–45 | 25 |
| [Q-SSA][TBA] | 0.9 | −208 | 80 | −15 | 21–107 | 36 |
| 107–880 | ||||||
880–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||||
| [Q-SSA][TMA] | 0.9 | −205 | 120 | −32 | 32–56 | 33 |
| 56–391 | ||||||
953–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||||
Drawing on the previously collected data obtained for similar systems, it has been observed that the critical micelle concentration (CMC) typically increases by two orders of magnitude from TMA to TBA counterions.24 Therefore, while we cannot determine the exact morphology of these aggregates, for [Q-SSA][TBA] we would expect a higher proportion of aggregates at all [NaCl], so additionally expect a greater change in overall structure with system perturbation (through the addition of salt). Our DLS and zeta potential measurements tentatively concord with this hypothesis. Indeed, it is possible that Na+ replaces TBA with increasing [NaCl], providing a barrier to proton transfer by increased ion pairing and thus shifting the reaction to the outside of the Laviron square scheme. TMA being more coordinating to the SSA anion would be more competitive to the presence of the sodium ion at high [Na+].
Significantly, our analysis of the electrochemical behaviour of [Q-SSA][TBA] suggests that deviations of the kinetics of quinone redox reactions from ideal behaviour is unlikely to be caused by quinone non-covalent dimerization, or quinhydrone (quinone-hydroquinone dimer)28 formation, as the magnitude of the effect would be low relative to the moderate effects described herein for much larger aggregates. We rule out the formation of quinhydrone dimers being responsible for this effect by the fact we observe neither of the trends in Fig. 3b and c for anthraquinone 2,7-disulfonic acid (Fig. S16, ESI†). Notably, ΔEpp for AQDS exceeds the value for the SSAs at all [NaCl], indicating highly ‘buffered’ kinetics under a wide range of ionic strengths as would be expected for a non-associating small molecule.
Intriguingly, these data show faster electron transfer upon greater quinone self-association. Where sluggish electron transfer has been proposed to be due to dimerization, we would instead suggest it is more likely that a surface interaction occurs between anionic water-solubilising groups and the carbon-based electrodes typically used in ORFB systems.18
In conclusion, we report that the voltammetric electrochemical response of a self-assembled structure has dependence on the supramolecular structure generated in the electrolyte. This demonstrates the sensitivity of PCET processes to changes in solution dynamics. We also show that the choice of amphiphile is critical, but the complex interplay with these solutions under electrochemical conditions makes prediction of behaviour challenging. Ongoing work is being undertaken to understand the more subtle trends in ORFB-related quinones such as AQDS, where we tentatively observe (Fig. S16, ESI†) an opposite trend of increased ΔE1/2 with increased [NaCl].
We thank the Royal Society (RGS\R2\180271) and the University of Kent for funding a summer internship (RD). We thank Dr Megan Jackson and Dr Marcel Schreier for helpful discussions.
Conflicts of interest
There are no conflicts to declare.Notes and references
- A. Kaifer and M. Gómez-Kaifer, Supramolecular Electrochemistry, John Wiley & Sons, Ltd, 2007, pp. 1–10 Search PubMed.
- P. D. Beer, C. Blackburn, J. F. McAleer and H. Sikanyika, Inorg. Chem., 1990, 29, 378–381 CrossRef CAS.
- J. M. Casas-Solvas, E. Ortiz-Salmerón, I. Fernández, L. García-Fuentes, F. Santoyo-González and A. Vargas-Berenguel, Chem. – Eur. J., 2009, 15, 8146–8162 CrossRef CAS.
- M. Horie, Y. Suzaki and K. Osakada, J. Am. Chem. Soc., 2004, 126, 3684–3685 CrossRef CAS.
- M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS.
- E. J. Son, J. H. Kim, K. Kim and C. B. Park, J. Mater. Chem. A, 2016, 4, 11179–11202 RSC.
- P. J. Krause, T. Lepore, V. K. Sikand, J. Gadbaw, G. Burke, S. R. Telford, P. Brassard, D. Pearl, J. Azlanzadeh, D. Christianson, D. McGrath and A. Spielman, N. Engl. J. Med., 2000, 343, 1454–1458 CrossRef CAS.
- H.-S. Bien, J. Stawitz and K. Wunderlich, Ullmann's Encyclopedia of Industrial Chemistry, American Cancer Society, 2000 Search PubMed.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef CAS.
- A. E. Wendlandt and S. S. Stahl, Angew. Chem., Int. Ed., 2015, 54, 14638–14658 CrossRef CAS.
- A. T. Murray, S. Voskian, M. Schreier, T. A. Hatton and Y. Surendranath, Joule, 2019, 3, 2942–2954 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1981, 124, 1–7 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1981, 124, 9–17 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1983, 146, 1–13 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1983, 146, 15–36 CrossRef CAS.
- A. K. Turek, D. J. Hardee, A. M. Ullman, D. G. Nocera and E. N. Jacobsen, Angew. Chem., Int. Ed., 2016, 55, 539–544 CrossRef CAS.
- M. Quan, D. Sanchez, M. F. Wasylkiw and D. K. Smith, J. Am. Chem. Soc., 2007, 129, 12847–12856 CrossRef CAS.
- T. J. Carney, S. J. Collins, J. S. Moore and F. R. Brushett, Chem. Mater., 2017, 29, 4801–4810 CrossRef CAS.
- A. Orita, M. G. Verde, M. Sakai and Y. S. Meng, Nat. Commun., 2016, 7, 13230 CrossRef CAS.
- B. Wermeckes and F. Beck, Denki Kagaku, 1994, 62, 1202–1205 CrossRef CAS.
- B. Rausch, M. D. Symes and L. Cronin, J. Am. Chem. Soc., 2013, 135, 13656–13659 CrossRef CAS.
- L. R. Blackholly, H. J. Shepherd and J. R. Hiscock, CrystEngComm, 2016, 18, 7021–7028 RSC.
- L. J. White, N. J. Wells, L. R. Blackholly, H. J. Shepherd, B. Wilson, G. P. Bustone, T. J. Runacres and J. R. Hiscock, Chem. Sci., 2017, 8, 7620–7630 RSC.
- L. J. White, S. N. Tyuleva, B. Wilson, H. J. Shepherd, K. K. L. Ng, S. J. Holder, E. R. Clark and J. R. Hiscock, Chem. – Eur. J., 2018, 24, 7761–7773 CrossRef CAS.
- S. N. Tyuleva, N. Allen, L. J. White, A. Pépés, H. J. Shepherd, P. J. Saines, R. J. Ellaby, D. P. Mulvihill and J. R. Hiscock, Chem. Commun., 2019, 55, 95–98 RSC.
- J. Ryu, A. Wuttig and Y. Surendranath, Angew. Chem., Int. Ed., 2018, 57, 9300–9304 CrossRef CAS.
- J. Ryu and Y. Surendranath, J. Am. Chem. Soc., 2019, 141, 15524–15531 CrossRef CAS.
- L. Tong, Q. Chen, A. A. Wong, R. Gómez-Bombarelli, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Phys. Chem. Chem. Phys., 2017, 19, 31684–31691 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc05017b |
| This journal is © The Royal Society of Chemistry 2020 |