Electric-field-induced supramolecular phase transitions at the liquid/solid interface: cat-assembly from solvent additives

Abstract

We demonstrate by using scanning tunneling microscopy that a series of trace organic solvent additives can efficiently promote the electrically triggered phase transition of trimesic acid (TMA), which would otherwise occur rather sporadically. DFT simulations taking into account the electric field effect elucidate such tailored phase transformations, based on the Gibbs activation and free energies of the deprotonation reactions of TMA.

---

Oriented external electric fields (OEEFs) as ‘smart reagents’ are no longer a theoretical dream, especially in synthetic chemistry. Such a concept has recently been verified to be efficient in promoting Diels–Alder reactions, where an OEEF of scanning tunneling microscopy (STM) acts as an enzyme with a catalyzing function.¹ In this context, STM not only visualizes the topological changes of surface materials, but also simultaneously determines the orientation of an externally applied electric field at the interface, where the material self-assembly occurs.^2–4 The catalytic effect in chemical reactions has been a well-received concept in synthetic chemistry for more than 100 years. For molecular self-assembly occurring in an environment-controlled manner, a new term has been introduced, that is, “cat-assembly” that comes from “catalysis” and “assembly”, referring to an increase in the rate and the advanced control of molecular assembly.⁵

Conceptually, cat-assembly in molecular assembly is analogous to catalysis in chemical synthesis. Extending such a concept, we recently demonstrated a synergic effect in a supramolecular phase transition using trimesic acid (TMA) as an example.⁶ In general, under the OEEF provided by STM, modulating environmental temperature,^7–10 solution pH,¹¹ solvents,¹² substrates,¹³ or additives^11,14,15 can lead to preferred outcomes. Recently, we experimentally showed that using water as the solvent for TMA can efficiently promote its electrically triggered phase transitions by STM.¹⁶ Here, we explored the effect of highly polar organic solvents. A small amount of the solvents referred to as “additives” was used in this work, as they can cause large leakage currents. The novelty of the present work is that we explore the “additive effect” rather than the “solvent effect” reported abundantly in the literature.¹⁷

Here, we systematically examined a series of organic solvent additives with their polarity index ranging from 2.4 to 7.2 (Fig. 1). The highly polar solvents, namely the additives, have a concentration of only 0.5 vol% in an OA (octanoic acid)-based sample solution. Our experiments found that the trace amount of a highly polar organic solvent (e.g., 0.5 vol% propylene carbonate PC) is efficient for promoting the electric-field-induced TMA phase transitions, which would otherwise occur rather sporadically at the OA/HOPG (highly oriented pyrolytic graphite) interface. DFT simulations considering the electric field effect were performed to elucidate the mechanism of the tailored phase transformations. Such transitions were studied in terms of the Gibbs activation and free energies of the deprotonation reactions of TMA taking place at the interface. For comprehensive comparisons, other factors such as dielectric constant and polarity of additives were also discussed.

Fig. 1 Chemical structures of OA, TMA, BTB, and the additives used in this study. Molecular structures used in this study: 1,3,5-tricarboxylic benzoic acid (trimesic acid, TMA), octanoic acid (OA), toluene, dichloromethane (DCM), tetrahydrofuran (THF), chloroform, acetone, methanol, propylene carbonate (PC), dimethylformamide (DMF), dimethyl sulfoxide (DMSO), and water. R=COOH.

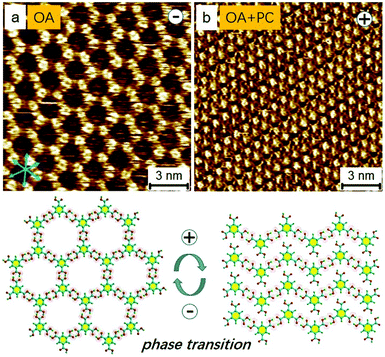
It is well known that the chicken-wire and zigzag motifs of TMA can be formed at the OA/HOPG interface. The detailed information of both phases was previously reported in the literature.⁶ The phase transition from the chicken-wire to the zigzag can occur, however, rather sporadically by merely altering the polarity of substrate bias from negative to positive (sample bias). We recently reported that the zigzag pattern of TMA appears under a positive STM bias with elevated temperatures (e.g., more than 68 °C). We found experimentally that such field-induced phase transitions took place efficiently if water exists on the surface.¹⁶ In this context, we hypothesized that water can accept a proton such that the occurrence of the deprotonation of TMA can be “catalyzed”, thereby promoting the phase transformation.

However, it remains difficult to employ such experimental tactics to achieve full control over the occurrence of the phase transition and its mechanism remains elusive. Besides the ability to accept a proton, water is a highly polar solvent. To further explore this topic, a series of solvents with different polarities was used. Only some of them can accept a proton (Fig. 1). Note however that because these highly polar solvents can cause a large leakage current during STM operations, we only add some small amount of them (e.g., 0.5 vol%) in the OA-based solution. We thus refer them to “additives” in the present study.

Fig. 2a and b shows the typical chicken-wire and zigzag motifs of TMA, formed at the OA/HOPG interface under the negative and positive STM bias, respectively. The fully protonated models were used because the departing protons remain in the vicinity of the COO⁻ groups and move back and forth, as reported in the literature.⁶ As mentioned previously, the phase transition can take place rather sporadically by changing the polarity of STM from negative to positive. After a careful investigation of the additive (solvent) effect on this system, we found that the fast phase transition from chicken-wire to zigzag took place only for the water and PC cases (Fig. S1, ESI†).

Fig. 2 STM images and corresponding models of TMA. The STM images are obtained from the STM-polarity-related experiments on the chicken-wire and zigzag assembly of TMA obtained at the OA/HOPG and OA-PC/HOPG interfaces, respectively. Imaging conditions (E_bias and i_tunneling) are ±0.9 V and 100 pA. The voltage polarity of the substrate in STM experiments is noted on the images. The blue arrows indicate the lattice-structure direction of graphite.

It is expected that the higher polar additives can lead to higher efficiency in the electric-field-induced phase transitions. Our experimental results revealed that only the PC case exhibits a promising ability to readily induce the phase transition. Fig. 3 presents the representative results implying that although some additives can accept a proton (e.g., DCM, toluene, and methanol), they cannot guarantee the promotion of electrically driven phase transitions. Fig. S2 (ESI†) shows that the phase transition did not happen when THF was used as the additive. Qualitatively, besides water, PC is the best “catalyzer”, followed by DMSO (or DMF) and the others are not able to promote the phase transitions.

Fig. 3 STM images of the STM-polarity-related experiment of TMA assembly using different additives. The STM images are obtained from bias-related experiments on the chicken-wire and zigzag assembly of TMA obtained at the OA/HOPG and OA-additive/HOPG interfaces, respectively. Imaging conditions (E_bias and i_tunneling) are ±0.9 V and 100 pA. The voltage polarity of the substrate in STM experiments is noted on the images. The blue arrows indicate the lattice-structure direction of graphite.

For the cases of DMF and DMSO, which are solvents with polarity higher than that of PC, it is found that besides the chicken-wire structure, a flower pattern is also obtained at the negative substrate bias of STM (Fig. S3 in ESI†). The result is similar to that obtained using hexanoic acid (HA) as the solvent, reminiscent of an increase in the environmental polarity after introducing these additives into the system. Quantitatively, we found that the percentage of DMSO (or DMF) can affect the outcomes. Specifically, 0.5% DMSO (or DMF) led to the chicken-wire structure transitioning into the flower one after switching STM polarity from negative to positive, whereas the zigzag pattern only was obtained when the concentration of the additives was higher than 10% (v/v) in the sample solution (Fig. S4, ESI†). For the PC scenario, the minimal percentage of the additive was 0.25% for the phase transition from chicken-wire to zigzag. Occasionally, the use of 0.1% PC (or less) resulted in the flower at a positive bias. Such quantitative tests are consistent with our qualitative conclusion that PC is the best “catalyzer” for the present topic (see the histogram in Fig. S5 in the ESI†). Moreover, Table S1 (ESI†) and Fig. 4 present the calculated quantitative results of Gibbs activation (ΔG^‡) and free energies of the deprotonation reactions. An interesting result for the cases of PC, DMSO, and DMF is that if the substrate bias is changed from −0.5 V to 0.5 V and later to 0.9 V, the chicken-wire motif can transform into the flower and later the zigzag. This was not found for the water system (Fig. S6, ESI†).

Fig. 4 The plot of Gibbs activation energy (ΔG^‡) in red and Gibbs free energy of the reactions (Δ_rG) in black colour for the deprotonation reaction of TMA by different additives. The hollow and filled circles/squares represent the energy values at EF = 0 and EF = 9.0 × 10⁸ V m⁻¹, respectively. Energy values are in kcal mol⁻¹.

It was previously proposed that partial deprotonation of TMA molecules is responsible for the mechanism.^4,16 ppm level water was proposed to induce the deprotonation of TMA and thus promote the transition.^4,16 We also proposed from the simulations that OA plays no role in the deprotonation, while the presence of OH⁻ species in water can cause the deprotonation since the reaction energy barrier was calculated to be the lowest for such a reaction.¹⁶ In the present study, the effect of solvent additives with a wide range of polarity index on the phase transition of TMA was studied by using STM and further verified by DFT simulations. We propose that the phase transition depends on the proton accepting ability of the different additives, which involves numerous factors including polarity, dielectric constant, and thermochemistry, e.g., Gibbs activation energy and free energy of the reaction. The dielectric constant strongly influences the long-range electrostatic interactions, as stated by Coulomb's law. On the other hand, the protic dissociation depends on the free energy of the deprotonation reaction. One part of this free energy is consumed in the electrostatic separation of positive and negative ions, e.g., the products of deprotonation reaction. The higher the free energy, the more difficult the deprotonation. Therefore, a high dielectric constant being proportional to the electrostatic interaction will result in a smaller free energy, making the deprotonation easier.

To provide insights into the deprotonation reactions occurring at the interface, we performed DFT simulations using the functional M062X¹⁸ with the 6-31g(d) basis set.¹⁹ The chosen function and basis set are widely used to calculate transition states and reaction pathways due to their broad applicability.²⁰ The simulations were performed using the Gaussian09 program²¹ to calculate the Gibbs activation (ΔG^‡) and free energy (Δ_rG) for all the additives tested in the experiments, which are presented in Table S1 (ESI†). The simulated reactions and the geometries of stationary points are presented in the ESI.†

The rate of a reaction being proportional to the Gibbs activation energy can be accessed by directly comparing the activation energy values of different reactions. From the results presented in Table S1 (ESI†) and Fig. 4, the activation energy barriers and free energies of reactions are calculated to be higher in the absence of an electric field. However, in the presence of an electric field (0.9 V applied in the STM experiments), the Gibbs activation energy barriers and free energies of reactions decrease significantly. For the PC case, ΔG^‡ and Δ_rG are calculated to be the smallest, followed by those of DMF and DMSO. It is noteworthy that the PC additive has three reaction sites (Fig. S7, ESI†); however, only the PC–O¹ site has the lowest reaction barrier and a small endothermicity to allow a proton transfer reaction. The small endothermicity indicates that the products are less stable than the reactants, however with a small energy difference. The DMSO and DMF cases have reasonably small reaction barriers and reaction free energies even in the absence of EF to allow proton transfer. Nevertheless, the phase transition was not observed. The reason for this may be the presence of EF, which is crucial for the occurrence of the phase transition after the deprotonation of TMA. The dynamics of the products of protic dissociation, i.e. molecules carrying positive and negative charges, are influenced greatly by the EF stimuli. One can use the concept of leakage current while running STM to understand this phenomenon. The presence of the electric field was calculated to affect the Gibbs energies significantly. The impact of the electric field on ΔG^‡ and Δ_rG of the reaction was calculated to be different for various additives.

A plot of the comparison of ΔG^‡ and Δ_rG in the presence and absence of an electric field is presented in Fig. 4. The comparison of the energy values in the presence and absence of EF reveals that the Gibbs activation and free energies of the reaction of PC–O¹ are greatly affected by the EF, making it the lowest among the additives. The activation energy barrier of 2.42 kcal mol⁻¹ is quite small for a rapid deprotonation reaction and hence an immediate phase transition was observed in our experiments. The free energy of 5.84 kcal mol⁻¹ indicates the small endothermicity of the reaction. For the PC case, Gibbs energies are decreased significantly compared to those of methanol, THF, and acetone. To investigate this, we observed the optimized geometry and orientation of the reaction species for PC proton abstraction reaction with TMA. The plane of the PC molecule is parallel to the applied EF both in reactants and in the transition state (Fig. S8, ESI†) and therefore the two electronic structures are greatly influenced by the direction of the electric field. For the methanol, THF and acetone cases, the molecular orientation is parallel to the direction of the applied EF and thus it effects less severely the electron dynamics. DCM, chloroform, and toluene are aprotic solvents; thus they are unable to receive a proton. The solvent with the lowest ΔG^‡ and endothermicity (PC) proceeds with the fastest deprotonation of TMA molecules at the interface, which in turn results in the phase transition, while the solvents with a higher ΔG^‡ are unable to cause an efficient, if any, deprotonation of TMA and hence no phase transition is observed for such solvents (acetone, methanol, and THF).

Table S1 (ESI†) also presents the calculated and experimental values of dielectric constants, and the polarity of the additives tested in experiments. The additives with high dielectric constants are observed to promote the phase transition. A possible explanation for this is the ion-pairing ability of different additives. The additives with high dielectric constants tend to cause a weak ion pairing. In our case, we have neutral TMA reacting with the additives; however, the extent of ion-pairing of the charged product species (e.g., deprotonated TMA and protonated additives) can affect the stability of the products. The calculated free energies show a smaller endothermicity for such additives. Nonetheless, the dielectric constant, polarity and Gibbs activation and free energies of the reactions together determine whether or not the phase transition will occur. A higher polarity or dielectric constant leads to a smaller activation energy barrier and a smaller endothermicity in a faster deprotonation reaction. The phase transition upon the occurrence of the deprotonation of TMA is driven by the polarity of the same additive. High polar additives are hugely influenced by the externally applied EF compared to the less polar additives. The dynamics of the products of dissociation, i.e. additive and TMA ions under the influence of the applied electric field, drive the phase transition. The positively charged additives may move away from the substrate at a positive bias, making the negatively charged TMA molecules closely packed on a surface.

In conclusion, the so-called STM-induced phase transition remains an intriguing phenomenon.^22,23 By using STM and TMA, we have experimentally shown that highly polar solvents can promote the supramolecular phase transitions. Qualitatively, we found that PC is the best “catalyzer” followed by DMSO and DMF, while others are not efficient enough to promote the occurrence of the phase transitions. Quantitatively, the use of 0.25% PC resulted in the phase transition from chicken-wire to zigzag, while a smaller quantity (0.1% or less) only resulted in a flower structure at positive substrate bias. For the DMSO and DMF cases, a lower percentage (0.5%) triggered a transition from chicken-wire to flower upon switching the STM polarity from negative to positive, while only as much as 10% additive can cause the transition to the zigzag pattern. Such quantitative tests also correlate well with our qualitative conclusion: PC is the best “catalyzer” in the present study. The smaller activation energy barrier and the endothermicity of polar solvents and their electric-field dependence obtained from DFT simulations together with the dielectric constant and polarity determine the electric-field-induced phase transitions. Overall, the study presents a combined STM and simulations viewpoint on effective tailoring of supramolecular phase transitions via STM in a controlled environment.

The authors thank NSFC (21972095), Guangdong government (2018A030313467), Shenzhen city (1. the overseas talent set-up funding; 2. JCYJ2018-0305124732178), and 3. Shenzhen University and National Taipei University of Technology joint funding (2019008). S. L. L. thanks Dr Saeed, M. for his experimental help.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091.
2. K. Y. Cheng, C. H. Lin, M. C. Tzeng, A. Mahmood, M. Saeed, C. h. Chen, C. W. Ong and S. L. Lee, Chem. Commun., 2018, 54, 8048.
3. Q. N. Zheng, X. H. Liu, X. R. Liu, T. Chen, H. J. Yan, Y. W. Zhong, D. Wang and L. J. Wan, Angew. Chem., Int. Ed., 2014, 53, 13395.
4. S. L. Lee, Y. Fang, G. Velpula, F. P. Cometto, M. Lingenfelder, K. Mullen, K. S. Mali and S. De Feyter, ACS Nano, 2015, 9, 11608.
5. Y. Wang, H. X. Lin, L. Chen, S. Y. Ding, Z. C. Lei, D. Y. Liu, X. Y. Cao, H. J. Liang, Y. B. Jiang and Z. Q. Tian, Chem. Soc. Rev., 2014, 43, 399.
6. A. Mahmood, M. Saeed, Y. Chan, A. S. Saleemi, J. Guo and S. L. Lee, Langmuir, 2019, 35, 8031.
7. F. Hu, Y. Gong, X. Zhang, J. Xue, B. Liu, T. Lu, K. Deng, W. Duan, Q. Zeng and C. Wang, Nanoscale, 2014, 6, 4243.
8. C. Marie, F. Silly, L. Tortech, K. Müllen and D. Fichou, ACS Nano, 2010, 4, 1288.
9. D. Rohde, C. J. Yan, H. J. Yan and L. J. Wan, Angew. Chem., Int. Ed., 2006, 45, 3996.
10. R. Gutzler, T. Sirtl, J. R. F. Dienstmaier, K. Mahata, W. M. Heckl, M. Schmittel and M. Lackinger, J. Am. Chem. Soc., 2010, 132, 5084.
11. A. Ciesielski, S. Lena, S. Masiero, G. P. Spada and P. Samori, Angew. Chem., Int. Ed., 2010, 49, 1963.
12. L. Kampschulte, M. Lackinger, A. K. Maier, R. S. Kishore, S. Griessl, M. Schmittel and W. M. Heckl, J. Phys. Chem. B, 2006, 110, 10829.
13. T. Balandina, K. Tahara, N. Sandig, M. O. Blunt, J. Adisoejoso, S. Lei, F. Zerbetto, Y. Tobe and S. De Feyter, ACS Nano, 2012, 6, 8381.
14. B. E. Hirsch, K. P. McDonald, B. Qiao, A. H. Flood and S. L. Tait, ACS Nano, 2014, 8, 10858.
15. B. E. Hirsch, S. Lee, B. Qiao, C. H. Chen, K. P. McDonald, S. L. Tait and A. H. Flood, Chem. Commun., 2014, 50, 9827.
16. M. Saeed, A. Mahmood, A. S. Saleemi, X. Zeng and S. L. Lee, J. Phys. Chem. C, 2020, 124, 829.
17. L. Kampschulte, M. Lackinger, A. K. Maier, R. S. Kishore, S. Griessl, M. Schmittel and W. M. Heckl, J. Phys. Chem. B, 2006, 110, 10829.
18. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
19. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724.
20. M. Linder and T. Brinck, Phys. Chem. Chem. Phys., 2013, 15, 5108.
21. M. J. G. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision D.01, 2009.
22. F. P. Cometto, K. Kern and M. Lingenfelder, ACS Nano, 2015, 9, 5544.
23. J. Ubink, M. Enache and M. Stohr, J. Chem. Phys., 2018, 148, 174703.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional STM data and simulation details. See DOI: 10.1039/d0cc01670e

‡ Authors contributed equally to this work.

---