Open Access Article
Open Access ArticleHexanuclear [Cp*Dy]6 single-molecule magnet†
Jianfeng
Wu
ab,
Serhiy
Demeshko
a,
Sebastian
Dechert
a and
Franc
Meyer
 *a
*a
aUniversität Göttingen, Institut für Anorganische Chemie, Tammannstr. 4, D-37077 Göttingen, Germany. E-mail: franc.meyer@chemie.uni-goettingen.de
bSino-German Joint Research Lab for Space Biomaterials and Translational Technology, School of Life Sciences, Northwestern Polytechnical University, Xi’an, 710072, P. R. China
First published on 27th February 2020
Abstract
A hexanuclear cluster [(Cp*Dy)6K4Cl16(THF)6], [Cp*Dy]6, has been constructed from six {Cp*DyIII} synthons in which the strongly coordinating Cp*− caps determine the local anisotropy axes. Structural characterization of [Cp*Dy]6 shows two almost parallel triangular (Cp*Dy)3 fragments that are linked by the K+ and Cl− ions. Magnetic measurements reveal slow thermal relaxation and fast quantum tunneling relaxation in the absence of an external dc field. After applying a weak dc field, the quantum tunneling relaxation is efficiently suppressed, giving a sizable energy barrier of 561 K, which represents the current record energy barrier for high nuclearity organometallic SMMs.
During the past three decades, single-molecule magnets (SMMs) have been in the spotlight of research in the chemical, physical and materials sciences. Their bistable magnetic ground states and phenomena such as quantum tunneling of magnetization (QTM)1 make SMMs interesting for the design of spintronics devices for high-density information storage and quantum computations.2 Building upon the discovery of lanthanide-based SMMs,3 the field has recently received a major boost by exploiting organometallic f-element complexes. Using such systems, the record energy barrier and blocking temperature for magnetic reversal have been raised dramatically during the past few years,4 currently reaching a maximum blocking temperature of 80 K and Ueff = 2217 K.4d
These recent advances towards high performance SMMs are mostly based on the development of mononuclear complexes, mainly because of the relative simplicity of properly adjusting the ligand field and coordination geometry of a single lanthanide ion with a given electron configuration, such as an equatorial ligand field for prolate ErIII![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 or an axial ligand field for oblate DyIII.6 Particularly successful are mononuclear DyIII complexes with ligand fields that approach the axial limit.7 However, the existence of quantum tunneling often shortcuts the thermal relaxation pathway and shuts down any memory effect of the magnetization at zero field.8
5 or an axial ligand field for oblate DyIII.6 Particularly successful are mononuclear DyIII complexes with ligand fields that approach the axial limit.7 However, the existence of quantum tunneling often shortcuts the thermal relaxation pathway and shuts down any memory effect of the magnetization at zero field.8
An efficient way to suppress QTM is to increase interactions between lanthanide ions, e.g. via organic radicals9 or open-shell transition metal ions10 that can mediate strong coupling. Prominent examples are dinuclear complexes bridged by radical ligands such as N23−,4a or Tb2 pairs with a single electron metal–metal bond;11 in these cases any QTM is suppressed.4a,12 Another strategy is to arrange anisotropic metal–ligand subunits in a linear array to control the direction and magnitude of anisotropy.13 Recently, Rinehart and coworkers used [(COT)Er]+ (COT2− is the cyclooctatetraene dianion) as building block and I− and phosphino ligands as weak linkers to achieve a million-fold improvement of the relaxation time by controlling the anisotropy alignment in dinuclear ErIII based SMMs.14 These systems benefit from the COT2− inducing the favorable prolate electron density of ground state ErIII ions. For oblate DyIII ions, a strong axial ligand field is required.
Dysprosium metallocene SMMs exhibit outstanding single-ion anisotropies, and several high performance SMMs composed of two or three {Cp2Dy} subunits have been isolated.15 However, the steric demand of two Cp rings in a sandwich-type structure limits the ability of DyIII ions to accommodate additional linker ligands to construct high nuclearity complexes, in particular for substituted Cp rings such as Cp* (Cp* is pentamethylcyclopentadienyl). As far as we know the nuclearity of {Cp2Dy}-based organometallic complexes showing SMM behavior is still limited to trimers.15d Fragments such as {CpDyIII} containing only a single Cp ligand promise to provide SMMs of higher nuclearity,16 as such fragments have an open coordination half-sphere and have previously served as building blocks for the construction of polynuclear clusters.17 Here we present our strategy to achieve favorable magnetic property by using {Cp*Dy} as a synthon for the assembly of polynuclear SMMs. The large Cp* is anticipated to effectively shield one side of the DyIII and to provide the peripheral shell of the cluster core.
The reaction of KCp* and DyCl3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in THF gives the titled complex [(Cp*Dy)6K4Cl16(THF)6], [Cp*Dy]6, which was isolated as large yellow crystals. X-ray diffraction reveals that [Cp*Dy]6 crystallizes in the triclinic space group P
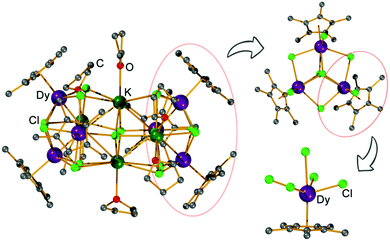
1 ratio in THF gives the titled complex [(Cp*Dy)6K4Cl16(THF)6], [Cp*Dy]6, which was isolated as large yellow crystals. X-ray diffraction reveals that [Cp*Dy]6 crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table S1, ESI†) with 1.5 molecules in the asymmetric unit and three molecules in the unit cell. These molecules are very similar (Fig. S2–S5, ESI†), therefore, only one of these molecules is described hereafter. The cluster-type molecule contains six {Cp*DyIII} units, four K+, 16 Cl−, and six coordinated THF (Fig. 1). Three {Cp*DyIII} fragments and three K+ ions are linked by eight μ3-Cl and one μ6-Cl, forming a distorted heterometallic octahedron. Two of these heterometallic octahedra share a K⋯K edge to form the heterometallic cluster having the overall shape of a curved peanut, whose two ends are encased by the peripheral Cp* ligands. Similar structures, albeit without K+ ions, have previously been observed for some early lanthanide clusters.18 The K+ ions at the central shared edge of [Cp*Dy]6 are each ligated by one THF molecule while the other two K+ ions are coordinated by two THF. All DyIII ions are found in similar coordination environment, capped by a Cp* and bound to five Cl− ligands (Fig. S6, ESI†). Comparison of the atom distances and bond angles (Tables S2 and S3, ESI†) shows that the Dy–Cp* distances (2.34 Å) are much shorter than the Dy–Cl bonds (2.6–2.9 Å), suggesting that the Cp* caps may dominate the anisotropy of the DyIII ions. Three {Cp*Dy} groups are close to each other and linked by the Cl− (Fig. 1) with Dy⋯Dy distances in a narrow range (4.0–4.1 Å), constituting a (Cp*Dy)3 triangle of approximate (non-crystallographic) threefold symmetry (Fig. S3, ESI†). In [Cp*Dy]6, two such (Cp*Dy)3 triangles are arranged almost parallel and are linked by the K+ and Cl− (Fig. S3, ESI†). The Dy⋯Dy distances between the two (Cp*Dy)3 subunits are in the range of 7.9–9.9 Å.
(Table S1, ESI†) with 1.5 molecules in the asymmetric unit and three molecules in the unit cell. These molecules are very similar (Fig. S2–S5, ESI†), therefore, only one of these molecules is described hereafter. The cluster-type molecule contains six {Cp*DyIII} units, four K+, 16 Cl−, and six coordinated THF (Fig. 1). Three {Cp*DyIII} fragments and three K+ ions are linked by eight μ3-Cl and one μ6-Cl, forming a distorted heterometallic octahedron. Two of these heterometallic octahedra share a K⋯K edge to form the heterometallic cluster having the overall shape of a curved peanut, whose two ends are encased by the peripheral Cp* ligands. Similar structures, albeit without K+ ions, have previously been observed for some early lanthanide clusters.18 The K+ ions at the central shared edge of [Cp*Dy]6 are each ligated by one THF molecule while the other two K+ ions are coordinated by two THF. All DyIII ions are found in similar coordination environment, capped by a Cp* and bound to five Cl− ligands (Fig. S6, ESI†). Comparison of the atom distances and bond angles (Tables S2 and S3, ESI†) shows that the Dy–Cp* distances (2.34 Å) are much shorter than the Dy–Cl bonds (2.6–2.9 Å), suggesting that the Cp* caps may dominate the anisotropy of the DyIII ions. Three {Cp*Dy} groups are close to each other and linked by the Cl− (Fig. 1) with Dy⋯Dy distances in a narrow range (4.0–4.1 Å), constituting a (Cp*Dy)3 triangle of approximate (non-crystallographic) threefold symmetry (Fig. S3, ESI†). In [Cp*Dy]6, two such (Cp*Dy)3 triangles are arranged almost parallel and are linked by the K+ and Cl− (Fig. S3, ESI†). The Dy⋯Dy distances between the two (Cp*Dy)3 subunits are in the range of 7.9–9.9 Å.
Direct current (dc) magnetic susceptibility measurements were carried out on polycrystalline samples of [Cp*Dy]6 under an applied field of 5000 Oe in the temperature range 2–210 K. As shown in Fig. S7 (ESI†), the χMT product (χM = molar magnetic susceptibility) at 210 K is 85.4 cm3 K mol−1, close to the value expected for six DyIII ions in the free-ion approximation (85 cm3 K mol−1, 6H15/2, g = 4/3). Upon cooling, the χMT product decreases gradually and reaches 57.6 cm3 K mol−1 at 2 K, which can be attributed to crystal-field effects and/or dominating weak antiferromagnetic interactions.19
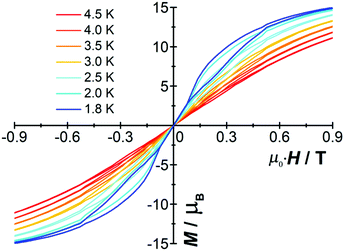
The molar magnetization (M) vs. H plot for [Cp*Dy]6 at 2 K (Fig. S8, ESI†) shows a sharp rise with increasing magnetic field and a further linear increase at high fields without saturation. Butterfly-shaped hysteresis loops were detected at low temperatures (Fig. 2). At H ≠ 0 a loop still appears up to 4.5 K (Fig. S9, ESI†); however, the collapse at zero field indicates quantum tunneling of the magnetization (see below), which is a common phenomenon in most of the reported SMMs.20
To study the magnetization dynamics, alternating current (ac) susceptibility measurements were performed on [Cp*Dy]6 using an oscillating field of 3.0 Oe. The temperature-dependent in-phase (χ′) and out-of-phase (χ′′) susceptibilities show frequency-dependent peaks up to 29 K (1488 Hz). When decreasing the frequency of the ac field, the χ′′ peaks shift towards lower temperatures (Fig. 3). In the absence of a dc field, a significant rise of the χ′′ signal at low temperatures is detected (Fig. 3 top, and Fig. S10, ESI†), indicating the presence of a second relaxation process, probably originating from QTM. The frequency-dependent ac susceptibilities also show two relaxation profiles (Fig. S11, ESI†). The low-frequency χ′′ peaks are temperature-dependent and shift to higher frequency when increasing the temperature. In contrast, the χ′′ peaks at higher frequency are temperature independent, suggestive of quantum tunneling relaxation. In order to suppress the QTM, application of a dc field is necessary, therefore field dependent ac susceptibility measurements were carried out at low temperature (2 K) at a frequency of 1488 Hz to determine the optimum field (Fig. S13, ESI†). The χ′′ signal decreases gradually when increasing the dc field, and above 1500 Oe the χ′′ value is close to zero. This suggests that an applied dc field of 1500 Oe is sufficient to suppress any QTM, hence further ac susceptibility measurements were carried out under such dc field. Compared with the measurements under zero dc field, the temperature-dependent peaks under 1500 Oe shift to higher temperatures (Fig. S12, ESI†) and the rise of the ac signal at low temperatures has disappeared (Fig. 3). As shown in Fig. S15 (ESI†), the frequency-independent region has also disappeared to give a single relaxation process, indicating that the dc field efficiently suppresses the QTM.
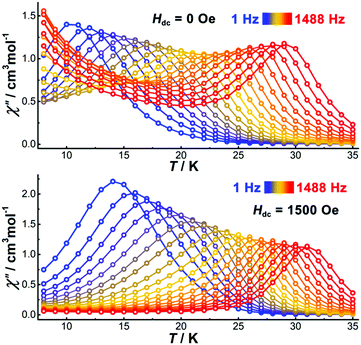 | ||
| Fig. 3 Temperature dependence of the out-of-phase part of the ac susceptibility for [Dy–Cp*]6 under zero (top) and 1500 Oe dc field (bottom). | ||
The Cole–Cole plots represented as χ′′ versus χ′ show two semi-circular profiles at zero dc field (Fig. S16, ESI†), reflecting the presence of two relaxation processes. Extracting the relaxation time from the frequency-dependent measurements using a double relaxation Debye model21 and the CC-FIT program22 gives two relaxation regimes. The slow relaxation phase (SR) has a typical thermal relaxation profile, while the fast relaxation phase (FR) shows almost temperature-independent behavior indicative of zero-field QTM (Fig. 4, top). To examine the mechanism of the relaxation process, the τ versus 1/T data was fitted by using the following equation:23
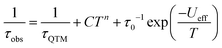 | (1) |
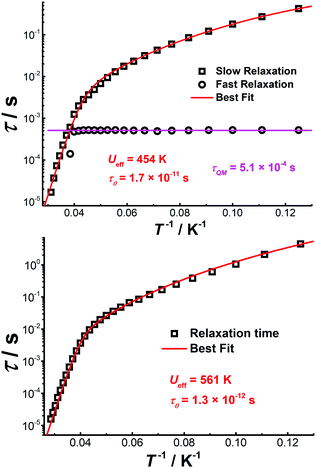 | ||
| Fig. 4 Plot of τ vs. T−1 for [Cp*Dy]6 obtained under zero (top) and 1500 Oe dc fields (bottom). The red lines represent the best fits. | ||
It can be hypothesized that the large anisotropy of [Cp*Dy]6 originates mainly from the individual {Cp*Dy} entities. Cp* provides a relatively strong ligand field if compared with the weak Cl− donors. The anisotropy axes of all DyIII ions were calculated using the Magellan program,26 showing that the main magnetic axes are close to the Cp*–Dy vectors (Fig. S18, ESI†); deviations in the range 11.5–21° are likely caused by the perturbation stemming from the Cl− ions. Calculating the magnetic axes in the entire molecule shows that the anisotropy axis of each DyIII ion is perpendicular to the plane of the respective (Cp*Dy)3 triangle (Fig. S19, ESI†), with all the anisotropy axes being almost parallel to each other (Table S7, ESI†). This result demonstrates that the anisotropy axes can be aligned in a parallel fashion in polynuclear Dy clusters, which is proposed to give rise to the relatively high energy barrier for magnetization relaxation.13 Herein, the {Cp*Dy} units are connected by weak Cl− linkers at Dy⋯Dy distances of around 4.0 Å, likely giving rise to weak magnetic coupling within the (Cp*Dy)3 fragments. While the two triangular (Cp*Dy)3 fragments are linked via Cl− and K+ ions at a distance of more than 7.9 Å, very weak magnetic interaction between these fragments can still be assumed, and such kind of interaction might induce the observed QTM at zero field.19b By the application of a weak dc field the QTM relaxation process can be efficiently suppressed, which is consistent with the ac data under 1500 Oe dc field.
In conclusion, using Cp*− as strongly coordinating capping ligand we have isolated a hexanuclear DyIII cluster, [Cp*Dy]6, that is composed of six (Cp*Dy) units, arranged in two almost parallel (Cp*Dy)3 fragments that are connected by Cl− and K+ ions. In accordance with the short Cp*–Dy distances, the Cp*–Dy vectors define the local anisotropy axes, and magnetic data evidence slow thermal relaxation, yet fast quantum tunneling relaxation, under zero field. After applying a weak dc field, QTM relaxation is suppressed, giving a record energy barrier for hexanuclear SMMs of 561 K. This study suggests that the {Cp*Dy} entities, which favorably combine strong axial anisotropy and an accessible coordination half-sphere, can serve as valuable synthons for constructing polynuclear organometallic SMMs with high blocking temperatures.
J. W. thanks the Alexander von Humboldt Foundation for a postdoctoral fellowship.
Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (b) D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 CrossRef.
- (a) D. Gatteschi, Adv. Mater., 1994, 6, 635 CrossRef CAS; (b) M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed.
- (a) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed; (b) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829 CrossRef CAS; (c) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed; (d) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484 CrossRef CAS PubMed.
- (a) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC; (b) S.-D. Jiang, B.-W. Wang and S. Gao, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, p. 111 Search PubMed.
- (a) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed; (b) L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043 CrossRef CAS PubMed; (c) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431 RSC.
- (a) N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931 CrossRef CAS PubMed; (b) F. Ortu, D. Reta, Y.-S. Ding, C. A. P. Goodwin, M. Gregson, E. J. L. McInnes, R. E. P. Winpenny, Y.-Z. Zheng, S. Liddle, D. P. Mills and N. F. Chilton, Dalton Trans., 2019, 48, 8541 RSC.
- (a) S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289-290, 149 CrossRef CAS; (b) C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, Angew. Chem., Int. Ed., 2017, 56, 10103 CrossRef CAS PubMed.
- (a) S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014 CrossRef CAS PubMed; (b) S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. Sci., 2014, 5, 3246 RSC; (c) K. S. Murray, S. K. Langley, B. Moubaraki and D. Wielechowski, Chem. Commun., 2016, 52, 10976 RSC.
- G. Velkos, D. S. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. M. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp, H. C. Dorn and A. A. Popov, Angew. Chem., Int. Ed., 2019, 58, 5891 CrossRef CAS PubMed.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144 CrossRef PubMed.
- J. D. Hilgar, M. G. Bernbeck and J. D. Rinehart, J. Am. Chem. Soc., 2019, 141, 1913 CrossRef CAS PubMed.
- (a) J. D. Hilgar, B. S. Flores and J. D. Rinehart, Chem. Commun., 2017, 53, 7322 RSC; (b) J. D. Hilgar, M. G. Bernbeck, B. S. Flores and J. D. Rinehart, Chem. Sci., 2018, 9, 7204 RSC.
- (a) F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976 CrossRef CAS PubMed; (b) T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082 CrossRef CAS PubMed; (c) F.-S. Guo and R. Layfield, Chem. Commun., 2017, 53, 3130 RSC; (d) B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880 CrossRef CAS.
- Y.-S. Meng, Y.-S. Qiao, M.-W. Yang, J. Xiong, T. Liu, Y.-Q. Zhang, S.-D. Jiang, B.-W. Wang and S. Gao, Inorg. Chem. Front., 2020, 7, 447 RSC.
- (a) W. J. Evans, T. M. Champagne, B. L. Davis, N. T. Allen, G. W. Nyce, M. A. Johnston, Y.-C. Lin, A. Khvostov and J. W. Ziller, J. Coord. Chem., 2006, 59, 1069 CrossRef; (b) M. E. Burin, M. V. Smirnova, G. K. Fukin, E. V. Baranov and M. N. Bochkarev, Eur. J. Inorg. Chem., 2006, 351 CrossRef CAS.
- (a) F. Bonnet, M. Visseaux, D. Barbier-Baudry, A. Hafid, E. Vigier and M. M. Kubicki, Inorg. Chem., 2004, 43, 3682 CrossRef CAS PubMed; (b) E. Barnea, C. Averbuj, M. Kapon, M. Botoshansky and M. S. Eisen, Eur. J. Inorg. Chem., 2007, 4535 CrossRef CAS.
- (a) J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Chem. Sci., 2017, 8, 1288 RSC; (b) T. Han, Y. Ding, Z.-H. Li, K.-X. Yu, Y.-Q. Zhai, N. F. Chilton and Y.-Z. Zheng, Chem. Commun., 2019, 55, 7930 RSC.
- (a) A. F. R. Kilpatrick, F.-S. Guo, B. M. Day, A. Mansikkamäki, R. A. Layfield and F. G. N. Cloke, Chem. Commun., 2018, 54, 7085 RSC; (b) J. Wu, J. Jung, P. Zhang, H. Zhang, J. Tang and B. Le Guennic, Chem. Sci., 2016, 7, 3632 RSC.
- (a) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538 CrossRef CAS PubMed; (b) Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953 RSC.
- D. Reta and N. F. Chilton, Phys. Chem. Chem. Phys., 2019, 21, 23567 RSC.
- (a) E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648 RSC; (b) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125 RSC; (c) X.-L. Li, J. Wu, L. Zhao, W. Shi, P. Cheng and J. Tang, Chem. Commun., 2017, 53, 3026 RSC.
- (a) R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 485 CrossRef CAS; (b) R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 458 CrossRef CAS.
- T. Pugh, N. F. Chilton and R. Layfield, Chem. Sci., 2017, 8, 2073 RSC.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and additional figures (Tables S1–S7 and Fig. S1–S19). CCDC 1972215. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cc09774k |
| This journal is © The Royal Society of Chemistry 2020 |