Molecular balloon, Pd₆L₈ cages: recognition of alkyl sulfate surfactants

Abstract

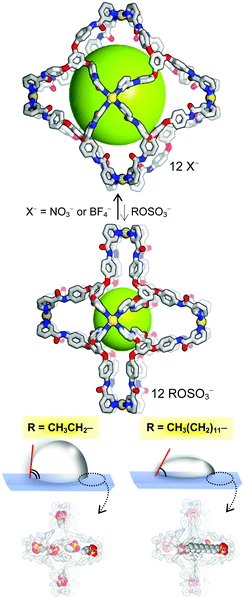
The unique molecular balloon system of [Pd₆L₈](NO₃)₁₂ (an inner cavity of 19 × 21 × 25 ų ⇄ 13 × 13 × 13 ų) was carried out via the anion exchange of nitrate with alkyl sulfates.

---

Reversible molecular encapsulation via the control of a trigger plays a major role in important chemical recognition processes including biological signal transduction and enzyme catalysis.¹ Recently, chemical scientists have attempted to exploit intermolecular interactions as an alternative means of significant control over the threshold of encapsulation.² Such interactions tend to mimic the supramolecular system that brings changes to the encapsulated substrates via the desired hydrophobic/hydrophilic pores.³ The encapsulated substrate can be activated by the influence of weak interactions or external stimuli.⁴ Thus, research on the construction of desirable tailor-made large cages has been a hot issue, owing to diverse task-specific functions such as guest indicators, catalysts, solvent reservoirs, region-selectivity controllers, and drug-delivery systems.⁵ Among various cage compounds, elegant cationic palladium(II) coordination cages have exhibited molecular recognition depending on the counteranionic nature and confined space.⁶ Furthermore, post-modification of coordination cages for control of their physicochemical properties has attracted particular attention for its provision of facile variation of function.⁷ However, to date, it remains difficult to include various guest molecules in coordination cages, due to the fixed size of the cavity. Both the internal space and the functional sites of such coordination cages have been known to be important factors for encapsulation and confinement effects.⁸ A series of alkyl sulfate salts of C_nH_2n+1OSO₃⁻ have been used in ubiquitous detergents for dish-washing liquids, shower gels, shampoos, hair conditioners, fabric softeners, cosmetics, medicines, toothpaste emulsifiers, and fire-extinguishing agents.⁹ Thus, recognition of and analytical techniques for alkyl sulfate surfactants are significant issues, owing to their widespread use.¹⁰

Herein we present an unprecedented novel approach to the control of the uptake of alkyl sulfate surfactants based on flexible host–guest interaction between alkyl sulfates and large coordination cages. For the aggregates encapsulated via hydrogen bonds between sulfate groups and cage skeletons, the contact angles were measured according to the length of the alkyl sulfates. Electrostatic interaction between Pd²⁺⋯⁻OSO₃R (3.92(1)–4.23(2) Å) forced to face to each other inside cage (Table S2, ESI†). A new C₃-symmetric N-donor ligand, 1,3,5-tris(4-nicotinamide-phenoxy)benzene (L), was synthesized in three steps in a reasonable yield starting from phloroglucinol. The L was employed in the self-assembly of palladium(II) ions for the coordination cages [Pd₆L₈]¹²⁺(X⁻)₁₂ (X⁻ = NO₃⁻, 1·12NO₃; X⁻ = BF₄⁻, 1·12BF₄) (Scheme 1). The reaction was monitored by ¹H NMR spectra that showed a significant downfield shift compared with that of the free L (Fig. S1–S5 and S8–S11, ESI†). High-resolution ESI-mass data at 1711.2797 ([1·12NO₃–4NO₃]⁴⁺, calcd 1711.276), 1356.6252 ([1·12NO₃–5NO₃]⁵⁺, calcd 1356.623) for 1·12NO₃ and at 1761.2153 ([1·12BF₄–4BF₄]⁴⁺, calcd 1761.306), 1391.6473 ([1·12BF₄–5BF₄]⁵⁺, calcd 1391.661), 1145.2067 ([1·12BF₄–6BF₄]⁶⁺, calcd 1145.203) for 1·12BF₄ were consistent with the formation of the coordination cages. Their crystal structures were investigated via single-crystal X-ray structure determination. The crystalline solids of the cages are insoluble in common organic solvents such as chloroform, acetonitrile, and tetrahydrofuran, but are soluble in Me₂SO. Subsequent reactions with the addition of tetrabutylammonium alkyl sulfates (ROSO₃⁻NBu₄⁺, R = ethyl-, octyl-, decyl-, dodecyl-, and tetradecyl-), [Pd₆(ROSO₃)₆L₈](ROSO₃)₆ (2·12ROSO₃) were attempted. It is noteworthy that the crystalline solid of 2·12ROSO₃ has a much lower solubility in common organic solvents including N,N-dimethylformamide and Me₂SO. In a trial entailing X-ray diffraction data collection, we could calculate unit cell parameters for 2·12C₂H₅OSO₃ and 2·12C₁₄H₂₉OSO₃ that were similar to those of 2·12C₈H₁₇OSO₃ and 2·12C₁₂H₂₅OSO₃, due to weak diffraction. The IR spectra for 2·12ROSO₃ showed the S–O vibrational frequencies of the sulfate group (1361 and 1064 cm⁻¹) and C–H from the aliphatic chains (1925–2852 cm⁻¹) (Fig. S15, ESI†). Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) results showed that the coordinate cages of 1·12NO₃ were stable up to 367 °C and that the solvate molecules were evaporated at 350 °C (two-step weight loss for solvate molecules: found, 4.7%; calcd, 9.3%, found, 24%; calcd, 27%). 1·12BF₄ decomposed at 297 °C, up to the point, the solvate molecules were evaporated (two-step weight loss for solvate molecules: found, 8.1%; calcd, 7.9%, found, 20%; calcd, 25%). 2·12C₁₂H₂₅OSO₃ started to be decomposed at temperatures above 420 °C, and the solvate molecules were fully evaporated by 300 °C (found, 23%; calcd, 22%).

Scheme 1 Encapsulation of ROSO₃⁻ (R = ethyl-, octyl-, decyl-, dodecyl-, and tetradecyl-) within present spherical coordination cages and different surface tensions depending on included alkyl chains of surfactant.

In the crystal structures of the Pd₆L₈ cages, the geometry of the palladium(II) ion was a typical square-planar arrangement with four N-donors from four L (Pd–N = 1.97(2)–2.048(6) Å). The diameter of all of the present cages was ∼4 nm. However, the dimensions of the inner cavity for each cage were significantly different depending on the anions (19 × 21 × 25 ų and 13 × 13 × 13 ų for 1·12NO₃ and 2·12C₁₂H₂₅OSO₃, respectively) (Scheme 1 and Fig. S19, ESI†). The encapsulated alkyl sulfates were bound with skeletal cages via hydrogen bonds (RO₃S–O⋯H–NCO = 2.11(1)–2.66(6) Å) for 2·12C₈H₁₇OSO₃ and 1.98(2)–2.38(1) Å for 2·12C₁₂H₂₅OSO₃ following the conformational change in the amide bonds, which was a driving force of the cage contraction (Fig. S19, ESI†). The solvent-accessible void volume was calculated as 63.0% (11695.6/18556.0 ų) for 1·12NO₃, 50.2% (26491.5/52684.0 ų) for 2·12C₈H₁₇OSO₃, and 45.3% (23932.4/52813.0 ų) for 2·12C₁₂H₂₅OSO₃ based on PLATON.¹¹ For the 2·12C₈H₁₇OSO₃ and 2·12C₁₂H₂₅OSO₃ structures, a half amount of alkyl sulfates were found on the electron density map, which showed them to exist at the apical position of the palladium(II) inside the cages (Fig. 1b), whereas the opposite position was occupied by the Me₂SO solvate molecules (Me₂S = O⋯Pd(II) = 2.96(2) Å for 2·12C₈H₁₇OSO₃ and 2.88(3) Å for 2·12C₁₂H₂₅OSO₃).

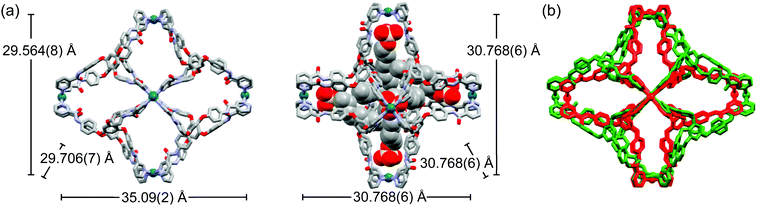Fig. 1 Crystal structures and Pd⋯Pd distances for 1·12NO₃ (a, left) and 2·C₈H₁₅OSO₃ (a, right). Overlay (b) of 1·12NO₃ (green) and 2·C₈H₁₅OSO₃ (red).

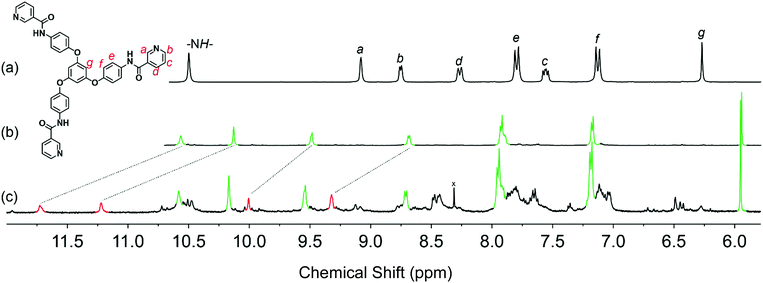
In ¹H NMR spectra, the addition of sodium dodecyl sulfate to the Me₂SO-d₆ solution of 1·12NO₃ produced significant chemical shifts in the protons of the amide and pyridyl moieties, indicating the contracted cages’ strong hydrogen bonds between the sulfate groups and the cage-skeletal structures (Fig. 2c). That is, the intermolecular interactions between the coordination cages and alkyl sulfates resulted in downfield shifts. The gradual addition up to 12 equiv. of alkyl sulfate to the 1·12NO₃ solution attained the equilibrium state with a 2 : 3 integral ratio of contracted and expanded cages in the solution state along with a small amount of free L owing to partial dissociation of the cages in the Me₂SO solution. However, either addition of an excessive amount of alkyl sulfate or rapid addition results in precipitation from the solution, owing to the low solubility. Of course, crystalline solids of 2·12ROSO₃ are rarely soluble in common organic solvents. The significant solubility difference seems to come from low solvation energy between cage and solvent molecules, presumably owing to suitable interactions between cages and alkyl sulfates. The present IR spectra support our hypothesis that the anion exchange is reversible between NO₃⁻ and alkyl sulfate (Fig. S21, ESI†).

Fig. 2 ¹H NMR spectra for L (a), 1·12NO₃ (b), and after addition of 12 equiv. of NaC₁₂H₂₅OSO₃ into 1·12NO₃ (c) in Me₂SO-d₆. The 1·12NO₃ and 2·12C₁₂H₂₅OSO₃ resonances are indicated by the green and red signals, respectively.

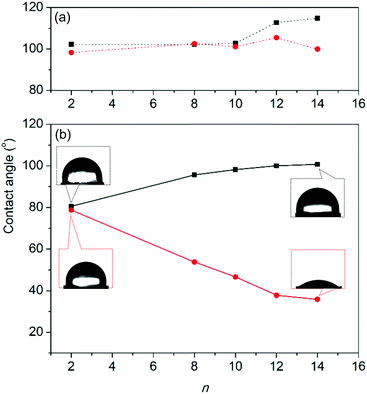
In order to investigate the recognition and adsorption properties of the flexible cages, the contact angles of a droplet on the surface of fine-ground microcrystals (20–40 μm) were measured (Fig. S22, ESI†). The crystalline surface was prepared by spreading the ground microcrystals on a glass tape and subsequently flattening them onto slide glass. As shown in Fig. 3 and Table S3 (ESI†), the contact angles for a drop of water to 2·12C₁₄H₂₉OSO₃ (114.87°) were larger than those of cages containing 2·12C₂H₅OSO₃ with ethyl analog (102.20°). Furthermore, contact angles increase according to the carbon number (n) of alkyl sulfates, thus indicating that the surface of the long chain crystals is more hydrophobic. In the present experimentation, the contact angles slightly decreased to 80.54° (n = 2) ∼100.80° (n = 14) after 10 min. By contrast, for a drop of 20% ethanol aqueous solution, the contact angles drastically decreased (from 99.94° to 35.84° on 2·12C₁₄H₂₉OSO₃) after 10 min, as depicted in Fig. 3. The alcohol aqueous drop induced water adsorption into the void of the microcrystalline structure, as caused by hydrophilic structure transformation.¹² Furthermore, the reason it takes several minutes to wet the surface is that adsorption occurs in the heterogeneous phase. This process is an advanced method for surface modification of crystals via anion exchange by alkyl sulfate surfactants. Furthermore, the wettability of 2 crystals can be utilized as a molecular ruler for measurement of the length of alkyl sulfate chains.

Fig. 3 Surfactant responsive contact angles on fine-ground crystal surface of 2·12C_nH_2n+1OSO₃ at 0 min (a) and after 10 min (b) (black line: drop of H₂O; red line: mixture solution of water and ethanol (4 : 1)).

In conclusion, we demonstrated an unusual system for contraction and expansion of flexible Pd₆L₈ cages via inclusion and release of alkyl sulfate surfactants. Hydrogen bonds between surfactants and cage structures are the main driving force of cage transformation. Furthermore, the microcrystal surface of the Pd₆L₈ cages presents the opportunity for tremendous modification of physical properties according to the chain length of sulfate anions. In particular, the relationship between surfactant recognition and hydrophobic properties has been demonstrated by dynamic contact angles showing surfactant-enhanced spread. That is, these cages can be an unprecedented recognizer for C_nH_2n+1OSO₃⁻ surfactants as well as a unique molecular ruler of alkyl chains via contact angles. This strategy, which involves an uncommon synergic cage effect, might find important applications for spatial and chain-length control entailing the release and retention of molecules.

This work was supported by National Research Foundation of Korea (NRF) grants funded by the Korean Government [MEST] (2016R1A2B3009532 and 2016R1A5A1009405). X-ray crystallography at the PLS-II 2D-SMC beamline was supported in part by MSIP and POSTECH.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) C. Edlinger, T. Einfalt, M. Spulber, A. Car, W. Meier and C. G. Palivan, Nano Lett., 2017, 17, 5790; (b) G. Grossi, M. D. E. Jepsen, J. Kjems and E. S. Andersen, Nat. Commun., 2017, 8, 1.
2. (a) V. H. Pérez-Luna and O. González-Reynoso, Gels, 2018, 4, 61; (b) E. M. M. D. Valle, Process Biochem., 2004, 39, 1033; (c) J. Rebek, Jr., Angew. Chem., Int. Ed., 2005, 44, 2068.
3. (a) D. K. Singh, B. V. V. S. P. Kumar and M. Eswaramoorthy, Nanoscale, 2015, 7, 13358; (b) Y. Jang, R. Natarajan, Y. H. Ko and K. Kim, Angew. Chem., Int. Ed., 2014, 53, 1003; (c) D. Prochowicz, A. Kornowicz and J. Lewiński, Chem. Rev., 2017, 117, 13461.
4. (a) A. J. Harnoy, I. Rosenbaum, E. Tirosh, Y. Ebenstein, R. Shaharabani, R. Beck and R. J. Amir, J. Am. Chem. Soc., 2014, 136, 7531; (b) I. K. Jeong, G. H. Gao, Y. Li, S. W. Kang and D. S. Lee, Macromol. Biosci., 2013, 13, 946; (c) Y. Y. Xu, G. Li, W. Zhuang, H. C. Yu, Y. Hu and Y. Wang, J. Mater. Chem. B, 2018, 6, 7495.
5. (a) D. Shetty, et al. , ACS Appl. Mater. Interfaces, 2018, 10, 17359; (b) M. Hatano, T. Sakamoto, T. Mizuno, Y. Goto and K. Ishihara, J. Am. Chem. Soc., 2018, 140, 16253; (c) S. Kawano, T. Fukushima and K. Tanaka, Angew. Chem., Int. Ed., 2018, 130, 15043; (d) J. Guo, Y.-W. Xu, K. Li, L.-M. Xiao, S. Chen, K. Wu, X.-D. Chen, Y.-Z. Fan, J.-M. Liu and C.-Y. Su, Angew. Chem., Int. Ed., 2017, 56, 3852; (e) I. Ortiz-Rivera, M. Mathesh and D. A. Wilson, Acc. Chem. Res., 2018, 51, 1891.
6. (a) T. Murase, Y. Nishijima and M. Fujita, J. Am. Chem. Soc., 2012, 134, 162; (b) W. Cullen, M. C. Misuraca, C. A. Hunter, N. H. Williams and M. D. Ward, Nat. Chem., 2016, 8, 231; (c) S. Löffler, J. Lübben, L. Krause, D. Stalke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2015, 137, 1060; (d) Y. Nishioka, T. Yamaguchi, M. Yoshizawa and M. Fujita, J. Am. Chem. Soc., 2007, 129, 7000; (e) T. Y. Kim, R. A. S. Vasdev, D. Preston and J. D. Crowley, Chem. – Eur. J., 2018, 24, 14878; (f) A. M. Castilla, T. K. Ronson and J. R. Nitschke, J. Am. Chem. Soc., 2016, 138, 2342; (g) J. E. M. Lewis, A. B. S. Elliott, C. J. McAdam, K. C. Gordon and J. D. Crowley, Chem. Sci., 2014, 5, 1833.
7. (a) M. Han, R. Michel, B. He, Y.-S. Chen, D. Stalke, M. John and G. H. Clever, Angew. Chem., Int. Ed., 2013, 52, 1319; (b) R. Custelcean, Chem. Soc. Rev., 2014, 43, 1813; (c) J. Mosquera, S. Zarra and J. R. Nitschke, Angew. Chem., Int. Ed., 2014, 53, 1556; (d) L. M. Mesquita, J. Anhäuser, D. Bellaire, S. Becker, A. Lützen and S. Kubik, Org. Lett., 2019, 21(16), 6442; (e) L. Escobar, D. Villarón, E. C. Escudero-Adán and P. Ballester, Chem. Commun., 2019, 55, 604.
8. C. M. Hong, D. M. Kaphan, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2017, 139, 8013.
9. (a) M. Tsumadori, CD Proceedings 6th World Surfactant Congress CESIO, 2004, 196; (b) D. A. Korolchenko, E. N. Degaev and A. F. Sharovarnikov, ICMEA 2015, 2015, 23; (c) R. Vanyúr, L. Biczók and Z. Miskolczy, Colloids Surf., A, 2007, 299, 256.
10. (a) K. M. Ko, B. H. Chon, S. B. Jang and H. Y. Jang, J. Ind. Eng. Chem., 2014, 20, 228; (b) J. Huang. and H. R. Matthews, Anal. Biochem., 1990, 188, 114.
11. A. L. Spek, Acta Crystallogr., 2009, D65, 148.
12. (a) J. F. Wall and C. F. Zukoski, Langmuir, 1999, 15, 7432; (b) Y. Yuan and T. R. Lee, Surface Sciences, Springer, New York, 2013, vol. 51, p. 3; (c) X. Wang, J. Venzmer and E. Bonaccurso, Langmuir, 2016, 32, 8322.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details and crystal structure determination. CCDC 1888048–1888051. HR-ESI-TOF-Mass spectra, TGA/DSC curves, NMR spectra, IR spectra and SEM images. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cc09742b

‡ Haeri Lee and Dongwon Kim contributed equally to this work.

---