Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the characteristics of conducting polymer-redox biopolymer supercapacitors†
Musbaudeen O.
Bamgbopa
 ab,
Jesper
Edberg
ab,
Jesper
Edberg
 c,
Isak
Engquist
c,
Isak
Engquist
 ab,
Magnus
Berggren
*ab and
Klas
Tybrandt
ab,
Magnus
Berggren
*ab and
Klas
Tybrandt
 *ab
*ab
aLaboratory of Organic Electronics, Department of Science and Technology, Linköping University, 601 74 Norrköping, Sweden. E-mail: klas.tybrandt@liu.se; magnus.berggren@liu.se
bWallenberg Wood Science Center, Laboratory of Organic Electronics, Linköping University, 601 74 Norrköping, Sweden
cRISE Acreo, SE-601 74 Norrköping, Sweden
First published on 31st July 2019
Abstract
The growth of renewable energy production has sparked a huge demand for cheap and large-scale electrical storage solutions. Organic supercapacitors and batteries are envisioned as one, among several, candidates for this task due to the great abundance of their constituent materials. In particular, the class of supercapacitors based on conjugated polymer-redox biopolymer composites are of great interest, since they combine the benefit of high electrical conductivity of the conducting polymers with the low cost and high specific capacitance of redox biopolymers. The optimization of such complex systems is a grand challenge and until now there have been a lack of models available to ease that task. Here, we present a novel model that combines the charge transport and impedance properties of conducting polymers with the electrochemical characteristics of redox polymers. The model reproduces a wide range of experimental data and elucidates the coupling of several critical processes within these supercapacitors, such as the double-layer capacitance, redox kinetics and dissolution/release of the redox polymer to the electrolyte. Further, the model also predicts the dependencies of the power and energy densities on the electrode composition. The developed model shows how organic supercapacitors can be analyzed beyond archetypical equivalent circuit models and thus constitutes a promising tool for further advancements and optimization within the field of research of green energy storage technology.
Introduction
The ongoing transition from fossil fuels to renewable energy sources is creating a huge demand for cheap and large-scale electrical energy storage solutions. Organic supercapacitors and batteries have been suggested as a crucial part of the solution, as they are made up of abundant materials that can be processed with low energy consumption.1,2 Conducting polymers (CPs) have been thoroughly studied for supercapacitors, with reported specific capacitances reaching beyond 500 F g−1 for polypyrrole3 and polyaniline.4 Unfortunately, these polymers are unstable with a typical degrading performance during cycling, rendering them unsuitable for may applications. PEDOT (poly(3,4-ethylenedioxythiophene)) is currently the most widely used conducting polymers due to its high conductivity, long-term stability, and processability from water dispersions.5 However, the relatively large monomer size of PEDOT gives a relatively lower specific capacitance, typically reaching the 80–90 F g−1 range,6 which is insufficient for many energy storage applications. Also, the cost of synthesizing and producing CPs, even at large volumes, is still too high for large scale energy storage applications.One route to partly circumvent the issue of low specific capacitance and high production costs is to amalgamate the CP phase with cheaper redox-active polymers/molecules.6–8 Here, biopolymers from the forest are certainly of special interest due to their abundance, cheapness and sustainability. By assembling a thin layer of PEDOT:PSS (poly(styrene sulfonate)) onto cellulose nanofibrils (CNF), highly porous and conductive papers can be achieved.9 Recently, the redox-active polymer lignosulfonate (LS) was incorporated into such paper electrodes, creating supercapacitor positrodes with specific capacitances reaching up to 230 F g−1.10 LS can be directly derived from lignin, being a waste product from wood pulp manufacturing, and represents the 2nd most prevalent biopolymer on earth. This combination of CPs with redox active biopolymers constitutes a highly attractive concept, as it combines the outstanding electrical properties of PEDOT with the high specific capacitance and cheapness of LS. Devices based on this concept generate new challenges from a theoretical and characterization perspective, as both the structural and reaction complexity increase drastically in comparison to pure CP-based supercapacitors. Therefore, careful modelling is necessary to better understand the dynamics and energetics of these devices and to enable further optimization.
A common approach to model supercapacitors is to fit an equivalent circuit model to electrochemical impedance spectroscopy measurements.11–13 This approach might be adequate for system-level integration of (super)capacitors, but is often insufficient when applied at the device level and more so; such a modelling approach fails in describing the crucial parameters of supercapacitors including redox-active molecules/polymers with complex redox reaction pathways. Such models typically also fail to account for the coupled mass transport of various species within the electrode/electrolyte.
Most early models of CPs were built around the classic Butler–Volmer equations describing them as solely redox electrochemical reactions.14–16 This approach does not capture the capacitive-like charging behaviour commonly observed in CPs, which sometimes was incorporated as an additional phenomenological term. More recently, models based on the drift-diffusion equations have been developed to properly describe the dynamics of CPs,17–19 however also these models tend to fail with respect to the volumetric capacitive behaviour,20 most likely because electrons and ions were assumed to co-exist within the same material phase. Indeed, by explicitly implementing 2D CP nanopores, the capacitive behaviour of CPs can be reproduced qualitatively.21 To quantitatively reproduce both the dynamics and charging characteristics of CPs, a modified drift-diffusion model was recently developed.22 By coupling the Fermi level in the semiconductor to the electric double layer residing between the electronic and ionic phases, the full charging and transport characteristics of PEDOT:PSS can be reproduced.22
Here, we extend this model to address the complexity of CP redox-enhanced supercapacitors. By coupling the electrochemical redox reactions of LS to the Fermi level of the conducting polymer, the electrode characteristics are reproduced and analysed. When modelling sequences of charging cycles, our model did not only properly describe the charging characteristics, but it also elucidates the interplay between dissolution and mass transport of LS along with its redox reaction kinetics. We apply our developed model to predict the electrode performance of a variety of charge storage device configurations, providing crucial insights in the trade-off between specific power and energy density.
Experimental
Numerical simulations
Simulations were executed in COMSOL Multiphysics software version 5.3a; coupling both the Electrostatics and Transport of Species modules. The models were executed in 1D, where the meshing included finer meshing at the electrode–electrolyte interface and coarser meshing elsewhere. The bulk electrolyte domain has 1000 elements with an element ratio of 0.0001 in an arithmetic sequence distribution, while the electrode mesh has maximums of both element size and growth rate of 1 μm and 1.1, respectively. The galvanostatic charge–discharge cycling was implemented using the Events module given cut-off potentials. Modelling operating parameters are included in the ESI.†Sample preparation
Lignosulfonic acid sodium salt (MW ∼52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), glycerol, perchloric acid, and dimethyl sulfoxide (DMSO) was purchased from Sigma Aldrich. PEDOT:PSS (Clevios PH 1000) was purchased from Heraeus. Conductive carbon paste (7102) was purchased from DuPont. Wet proofed Toray carbon paper was purchased from FuelCellStore. All materials were used without further modifications. Cellulose nanofibrils (CNF) were prepared by RISE Bioeconomy. A mixture of water and cellulose fibres were passed 10 times through a microfluidic system at 1700 bars to obtain a suspension of nanofibrils (0.5 wt%). The paper electrodes were prepared by adding 35 mg of lignosulfonate to 2 mL deionised water and stirring using a Vortex mixer until fully dissolved. 4.7 g of PEDOT:PSS solution was then added followed by stirring and sonication for 5 minutes in an ultrasonic bath. 4.42 g of CNF solution, 36 mg glycerol and 258 mg DMSO was subsequently added followed by mixing using a T-10 basic ultra Turrax (IKA) at medium rotation speed for 5 minutes. The mixture was poured into plastic Petri dishes followed by degassing for 1 hour in a vacuum desiccator. The samples were then dried at 60 °C in an oven over night. Reference samples without lignosulfonate were also prepared following the same procedure. The paper samples were cut into circular discs (7 mm diameter) using a hole punching tool and were then subsequently glued onto carbon paper current collectors using carbon paste. The samples were baked on a hotplate for at 60 °C for 15 minutes to dry the paste.
000), glycerol, perchloric acid, and dimethyl sulfoxide (DMSO) was purchased from Sigma Aldrich. PEDOT:PSS (Clevios PH 1000) was purchased from Heraeus. Conductive carbon paste (7102) was purchased from DuPont. Wet proofed Toray carbon paper was purchased from FuelCellStore. All materials were used without further modifications. Cellulose nanofibrils (CNF) were prepared by RISE Bioeconomy. A mixture of water and cellulose fibres were passed 10 times through a microfluidic system at 1700 bars to obtain a suspension of nanofibrils (0.5 wt%). The paper electrodes were prepared by adding 35 mg of lignosulfonate to 2 mL deionised water and stirring using a Vortex mixer until fully dissolved. 4.7 g of PEDOT:PSS solution was then added followed by stirring and sonication for 5 minutes in an ultrasonic bath. 4.42 g of CNF solution, 36 mg glycerol and 258 mg DMSO was subsequently added followed by mixing using a T-10 basic ultra Turrax (IKA) at medium rotation speed for 5 minutes. The mixture was poured into plastic Petri dishes followed by degassing for 1 hour in a vacuum desiccator. The samples were then dried at 60 °C in an oven over night. Reference samples without lignosulfonate were also prepared following the same procedure. The paper samples were cut into circular discs (7 mm diameter) using a hole punching tool and were then subsequently glued onto carbon paper current collectors using carbon paste. The samples were baked on a hotplate for at 60 °C for 15 minutes to dry the paste.
Characterization
Electrochemical measurements were performed on a potentiostat (SP-200 BioLogic Science Instruments) in a three-electrode setup using a Pt mesh counter electrode, Ag/AgCl reference electrode and 0.1 M HClO4 electrolyte. The choice of electrolyte was based on previous work on PEDOT:LS electrodes.6,10 Galvanostatic charge–discharge measurements were performed at 1 or 2 A g−1 (based on PEDOT + LS mass) between 0–0.7 V.Results and discussion
Electrode system
PEDOT:PSS + CNF + LS electrodes of varying LS content were fabricated and characterized according to the experimental details above (Fig. 1a). The different kinds of electrodes are denoted according to the PEDOT:LS mass ratio, with 1_0 having no LS and 1_2 having 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mass ratio. The 1
2 mass ratio. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
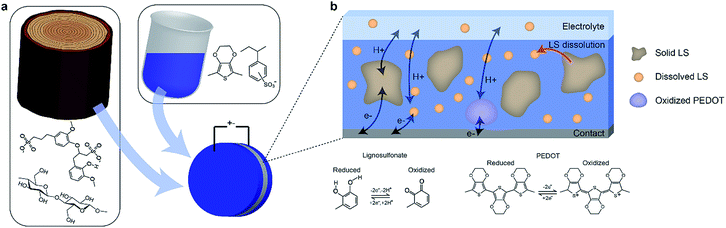
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mass ratio was chosen based on a previous study,10 where that ratio produced the highest specific capacitance. Positrodes were characterized in electrolytes containing various concentrations of LS in order to verify the impact of the mass transport of LS between the electrode and the electrolyte on the electrical performance. Fig. 1b gives an overview of the various constituents and processes within the system. As the electrodes initially contain a solid phase of LS, the characteristics of the electrode change over time as the solid LS gradually dissolves into its dissolved form, which then can diffuse within the positrode-electrolyte system. The charging dynamics of the system will include three contributions; the capacitive charging of the PEDOT and the redox reactions of the solid and dissolved LS.
2 mass ratio was chosen based on a previous study,10 where that ratio produced the highest specific capacitance. Positrodes were characterized in electrolytes containing various concentrations of LS in order to verify the impact of the mass transport of LS between the electrode and the electrolyte on the electrical performance. Fig. 1b gives an overview of the various constituents and processes within the system. As the electrodes initially contain a solid phase of LS, the characteristics of the electrode change over time as the solid LS gradually dissolves into its dissolved form, which then can diffuse within the positrode-electrolyte system. The charging dynamics of the system will include three contributions; the capacitive charging of the PEDOT and the redox reactions of the solid and dissolved LS.
Model
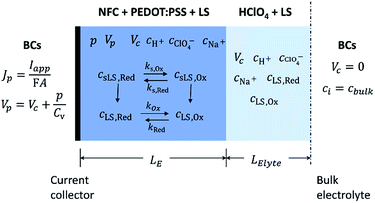
To capture the dynamic characteristics of the supercapacitor, the model must account for the coupling between many different quantities and processes, including electrostatic potential, conducting polymer doping level, concentrations of included matter and charged species, mass transport and electrochemical reaction rates. The experimental three-electrode setup is approximated by the 1D model geometry shown in Fig. 2, where the electrode comprises an electronic phase and an ionic phase, while the electrolyte only conducts ions. At galvanostatic test conditions the ensuing boundary conditions are also depicted in Fig. 2.Within the model, ionic transport is described by the Nernst–Planck–Poisson (NPP) equations throughout the whole system:
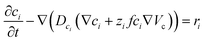 | (1) |
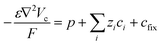 | (2) |
The hole transport within the PEDOT phase is described by modified NPP equations which take into accounts the shift in Fermi level due to the density of states:22
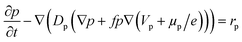 | (3) |
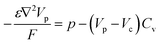 | (4) |
Assuming a Gaussian density of states in the PEDOT:22
μp = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p) + eB ln(p) + eB | (5) |
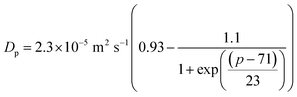 | (6) |
| r = −kr(csat − cLS); (csat − cLS) ≥ 0 | (7) |
Given the quinone reduction mechanism in acidic media detailed in earlier studies,24 the redox reaction rate of LS (solid or dissolved) is described by the concentration dependent Butler–Volmer type kinetics in eqn (8):25
r = kOxcOxcH+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(αOxfη) − kRedcRed2 exp(αOxfη) − kRedcRed2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(αRedfη) exp(αRedfη) | (8) |
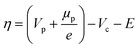 | (9) |
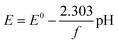 | (10) |
In implementing the model as described by the eqn (1)–(10), the following assumptions and initial conditions were made:
(i) The modelled electrodes are homogeneous in the initial distribution of species and morphology, with assigned single effective diffusivities for Dci in the electrode domain (see ESI†).
(ii) kr is considered being constant, with an estimated value obtained by fitting to experimental leakage tests (see ESI† and later discussions).
(iii) Cv (in mol (m−3 V−1)) is calculated from a specific capacitance of 21 F g−1, which was obtained from cyclic voltammetry in our previous article.10
(iv) A steady state solution at zero applied voltage was used as the initial condition for all transient simulations. When LS is involved, the redox reactions are turned off for this initial condition since E0 = 0.52 V is far away from the applied 0 V.10
(v) The influence of cycling-induced (electro)chemical instability of LS is not considered.
PEDOT:PSS + NFC electrodes
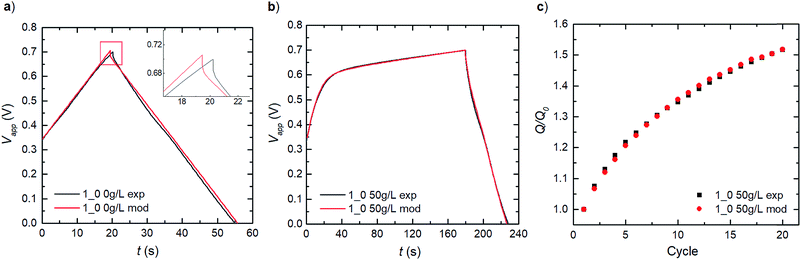
We establish consistency in our modelling by first capturing the double-layer capacitance that ensues in a PEDOT:LS 1_0 electrode, thereby decoupling the influence of LS. Given that Dci for the supporting electrolyte ions ClO4− and H+ in the bulk electrolyte, can be obtained from previous experimental studies,27 the effective Dci for these ions in the electrode domain can be obtained by fitting the experimental charge–discharge data as show in Fig. 3a. The good fit to the experimental data shows that the model can reproduce the ohmic potential drop during discharge, seen in the inset of Fig. 3a.By applying these obtained parameters, we further deduce the redox behaviour of the free LS species in the electrode by matching the experimental charge–discharge data for a similar PEDOT:LS 1_0 electrode but with 50 g L−1 of LS added to the bulk electrolyte (Fig. 3b). This provides the redox transfer coefficients (αLS,Ox and αLS,Red) and reaction rate constants (kLS,Ox and kLS,Red) for dissolved LS. Fig. 3b shows a comparison of the model with experimental data for the first cycle; thereafter, the capacity increases with cycling as more LS is transported into the electrode, see Fig. 3c (given an initial state without LS loading at the electrode preparation). This diffusive transport is dictated by the diffusivities of LS species in both the electrolyte and the electrode domains. Given that DLS,Red in the electrolyte can be obtained from a previous study,28 we adopted the same value for its reduced form (DLS,Ox) herein. Then, their effective values within the electrode domain can be estimated via fitting to experimental relative discharge capacity data (Fig. 3c).
PEDOT:PSS + NFC + LS electrodes
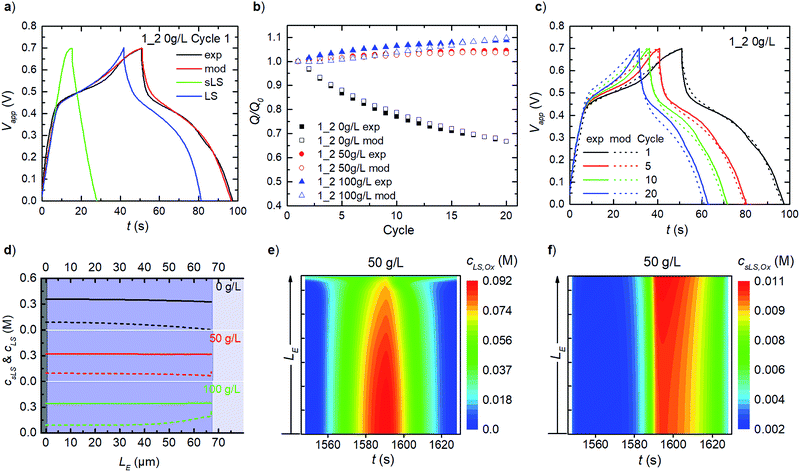
For PEDOT:LS 1_2 electrodes, i.e. with LS loaded during preparation, the charging response includes contributions from both solid and dissolved LS species (Fig. 4a). To avoid numerical artefacts and for a consistent transient solution, we select the second experimental cycle as our cycle 1 herein. This also helps estimate the initial concentrations of both solid and dissolved LS in all cases (Fig. S1†), by varying both while targeting the best-fit with experimental data, after the initial LS mass at electrode preparation is discounted by first cycle coulombic efficiency. Given that the effective diffusivity of solid LS species is negligible compared to that of the dissolved LS species in the electrode, the solid LS redox (csLS,Red ↔ csLS,Ox) contributes minimally to the capacity compared to the dissolved LS redox (cLS,Red ↔ cLS,Ox). This is also reflected in the model with their respective reaction rate constants (see eqn (8)). The rate constants for dissolved LS species are orders of magnitude greater than for the solid LS, which is expected since – in reality, only the outermost surface of a static lump of solid LS contacts the electrolyte. As cycling continues, relative discharge capacity decreases with time as solid LS dissolves and simultaneously diffuses out into the electrolyte (Fig. 4b). We verified that this capacity decay is primarily dissolution/diffusion driven, by comparing the capacity decay with another experiment where the electrode is cycled only twice, then left to rest for 20 minutes before continuing cycling (see Fig. S2†).As described in our previous work, the relative discharge capacity of the electrode can be stabilized by the addition of LS to the electrolyte.10 The model reproduces the trends in relative discharge capacity for 20 cycles of 1_2 0 g L−1 LS, 1_2 50 g L−1 and 1_2 100 g L−1 (Fig. 4b). For 1_2 0 g L−1, Fig. 4c shows the corresponding evolution of the galvanostatic charge–discharge response with cycle number. Note that the higher charging voltage plateau (at ∼0.6 V) from csLS,Red ↔ csLS,Ox fades as the cycle number increases, since LS gradually dissolves and diffuse out of the electrode over time. Hence, a transition from a battery-like to a supercapacitor-like behaviour is observed for the system. Fig. S3† presents the respective charge–discharge responses for both 1_2 50 g L−1 and 1_2 100 g L−1. The concentration profiles for fixed and dissolved LS within the electrodes after 20 cycles are shown in Fig. 4d. The addition of LS to the electrolyte decrease the diffusional leakage out from the electrode, thereby maintaining a higher concentration of dissolved LS within the electrode. This in turn slows down the dissolution of solid LS (see eqn (7)). The stabilization of discharge capacity is thus caused by maintaining/increasing both dissolved and solid LS within the electrode. The relative increase in discharge capacity for 50 g L−1 in Fig. 4b can be explained by the dissolution of solid LS into the more reactive dissolved LS within the electrode. For 100 g L−1 LS, the concentration is high enough for LS to diffuse in from the electrolyte into the electrode.
As concentrations and mass transport vary throughout the electrode, it is of interest to analyse the spatial distribution of the redox reactions in the model. Time-varying heat maps of cLS,Ox and csLS,Ox in the electrode domain during cycle 20 for 1_2 50 g L−1 are shown in Fig. 4e and f. The oxidation of dissolved LS occurs throughout the whole electrode, with the highest concentrations of oxidized LS found close to the contact, reflecting the concentration profile of dissolved LS (Fig. 4e). At the electrode–electrolyte interface, oxidized LS is present during the whole cycle as a result of diffusional exchange with the electrolyte. For solid LS (Fig. 4f), the highest concentration of oxidized species is found close to the electrolyte interface. Since the electronic transport is faster than the ionic transport within the electrode, this behaviour is expected as the ionic transport causes ohmic losses within the electrode. Note that the solid oxidized LS concentration is substantially lower than the dissolved one.
In the previous sections we have demonstrated that the model quantitatively captures the major characteristics in galvanostatic charge–discharge cycling. Cyclic voltammetry (CV) is another frequently used method for supercapacitor characterization. In Fig. S4,† the model is compared to previously reported CVs of PEDOT:LS electrodes.10 The CV is reproduced well for 1_0 electrodes, although some minor side reactions seem to be present, which are not accounted for in the model. For the 1_2 electrode, the CV is reproduced fairly well, but some deviations, especially for the cathodic reaction, are present. This indicates that a more complex reaction model would be needed to reproduce the second cathodic peak in the CV.
Ideal system behaviour and device design directions
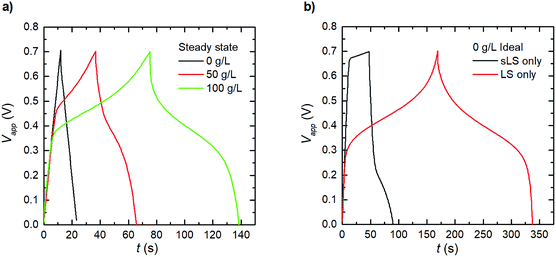
The results and discussion so far have shown the behaviours of the electrode systems during short cycling (20 cycles), with the model being capable of reproducing transient experimental results. However, reliable electrochemical energy storage systems are expected to be able to undergo several thousand charge–discharge–rest cycles within their lifetime.29 Therefore, Fig. 5a shows the expected charge–discharge response of the three scenarios from Fig. 4b at steady operation by cycling the steady state concentration profile results for the same three electrode testing setup. We calculate from our model that the three cases (1_2 0 g L−1, 1_2 50 g L−1 and 1_2 100 g L−1) reach this steady state at 2, 5 and 44 hours respectively. It was observed in Fig. 4b that the relative discharge capacity increases within 20 cycles for both the 1_2 50 g L−1 and 1_2 100 g L−1 electrodes. At steady state, the discharge capacity has increased even further for the 1_2 100 g L−1 electrode. Interestingly, for the 1_2 50 g L−1 electrode the discharge capacity instead decreases from cycle 20 to steady state. The initial increase can be understood by considering the dissolution of solid LS, which temporarily increases the concentration of dissolved LS within the electrode.Based on the developed model, we explore two ideal cases; when the LS is confined in the electrode domain as either only solid, or only dissolved forms – without release to the bulk electrolyte (Fig. 5b). The solid LS case can be achieved by making LS insoluble in the solvent/electrolyte, and the dissolved case can be derived when a perfect separator or a capping membrane suppresses the electrode domain from releasing LS into the bulk electrolyte. From the galvanostatic charge–discharge curves it is evident that the case with dissolved LS is superior and provides the highest capacity and discharging voltage. Thus, the model indicates that the best performance of the PEDOT:PSS + NFC + LS electrodes will be obtained by using a good solvent for LS and coatings which encapsulate the electrodes to prevent leakage of LS out from the electrodes.
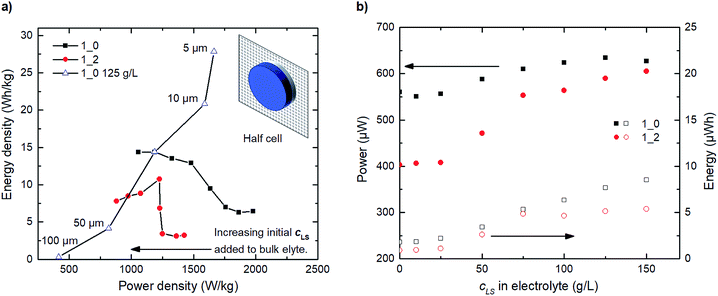
Furthermore, we proceed to simulate the steady-state operation of hypothetical half-cells assembled of both 1_0 and 1_2 electrodes (electrodes and 30 μm electrolyte). This investigation emphasizes the compromise between energy and power with increasing initial LS added to the bulk electrolyte. The Ragone plot in Fig. 6a shows that, as the amount of added initial LS to the bulk electrolyte increases, we sacrifice some power density to improve energy density. The trend for the 1_0 electrode is monotone; the more LS the lower power density and the higher energy density. For the 1_2 electrode the trend is more complex with an energy density maximum occurring around 75 g L−1 LS in the electrolyte. The decrease in energy density after the maximum is related to increasing amount of low-contributing solid LS within the electrode. The charge–discharge profiles used to construct Fig. 6a and b can be seen in Fig. S5.† We also studied the influence of the electrolyte thickness in the half-cell for the 1_0 125 g L−1 LS configuration. Both energy and power density decrease with thickness, as LS far out in the electrolyte is inaccessible to the electrode. One should keep in mind that these results are valid for the steady-state operation. For short term usage and operation, it can still be beneficial to preload LS within the electrodes. Also, preloading of LS can be a convenient way of setting the final concentration of dissolved LS within a closed cell configuration from a production point of view.
Fig. 6b shows that small amounts of initially added LS in the bulk electrolyte (<50 g L−1) appear to be inadequate to influence power or energy to a large extent, therefore leading to initially stable power and energy densities, see Fig. 6a. At concentrations greater than 50 g L−1, LS redox reactions start contributing significantly to the overall capacitance, thereby increasing power and energy, until a flat in energy is observed starting at ≈125 g L−1. Beyond this optimal point, the amount of initially added LS in the bulk electrolyte becomes excessive and adversely affects the coulombic efficiency, in which case not all oxidized dissolved LS during charging can be returned to their previous reduced forms after discharge.
Conclusions
A novel modelling approach to describe the power and energy densities of CP redox-enhanced supercapacitors has been developed based on the Nernst–Planck–Poisson equations and concentration-dependent Butler–Volmer type kinetics. The model reproduces a wide range of experimental data including transient device trends. A major benefit of the model over the commonly employed equivalent circuit models is that each introduced quantity has a well-defined physical denotation. The model can also capture complex coupled nonlinear processes such as dissolution/release of active species, a necessity to model these complex supercapacitor systems adequately. Our model provides several fundamental insights on the connection between device performance and transport processes within the supercapacitors. The model is further used to suggest a direction for optimal design based on the extracted parameters from experimental data. Although the model accounts for the major processes within the studied redox-enhanced supercapacitors, it can still be further refined. The current model assumes homogeneous electrodes, neglecting microscopic or macroscopic inhomogeneities. By incorporating such aspects, in combination with detailed morphological studies of the electrodes, the description of the mass transport can be further improved. Also, as indicated by the CVs, the current reaction model needs to be refined to capture side reactions and more details of the LS redox reactions. Altogether, this work demonstrate how complex CP-based supercapacitors can be analysed at high detail far beyond what can be achieved using equivalent circuit models, thereby providing additional insights and tools for further development of the field.Conflicts of interest
A spin-out company, LIGNA Energy AB, has recently been established that aims at commercializing electrical energy storage technology in part based on forest-based biopolymers. The results from this work may be of importance for the work and development of that company. LIGNA Energy is in part owned by Linköping University (LiU Invest), RISE and researchers (e.g. Isak Engquist, Magnus Berggren, Jesper Edberg) of LiU and RISE.Acknowledgements
This work was financially supported by the Knut and Alice Wallenberg foundation, Linköping University and industry through the Wallenberg Wood Science Center and Wallenberg Scholar, the Swedish Government Strategic Research Area in Materials Science on Advanced Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971), and the Swedish Foundation for Strategic Research.References
- M. M. Pérez-Madrigal, M. G. Edo and C. Alemán, Green Chem., 2016, 18, 5930–5956 RSC.
- I. Shown, A. Ganguly, L.-C. Chen and K.-H. Chen, Energy Sci. Eng., 2015, 3, 2–26 CrossRef CAS.
- D. P. Dubal, S. H. Lee, J. G. Kim, W. B. Kim and C. D. Lokhande, J. Mater. Chem., 2012, 22, 3044–3052 RSC.
- T. C. Girija and M. V. Sangaranarayanan, Synth. Met., 2006, 156, 244–250 CrossRef CAS.
- A. Elschner, PEDOT: principles and applications of an intrinsically conductive polymer, CRC Press, Boca Raton, FL, 2011 Search PubMed.
- F. N. Ajjan, N. Casado, T. Rębiś, A. Elfwing, N. Solin, D. Mecerreyes and O. Inganäs, J. Mater. Chem. A, 2016, 4, 1838–1847 RSC.
- G. Milczarek and O. Inganäs, Science, 2012, 335, 1468–1471 CrossRef CAS PubMed.
- J. Edberg, R. Brooke, H. Granberg, I. Engquist and M. Berggren, Adv. Sustainable Syst., 2019, 1900050 CrossRef.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed.
- J. Edberg, O. Inganäs, I. Engquist and M. Berggren, J. Mater. Chem. A, 2018, 6, 145–152 RSC.
- K. Ma, C. Zhang, C. E. Woodward and X. Wang, Electrochim. Acta, 2018, 289, 29–38 CrossRef CAS.
- F. Barzegar, L. Zhang, A. Bello, N. Manyala and X. Xia, J. Mater. Chem. A, 2018, 6, 17481–17487 RSC.
- H. M. Fellows, M. Forghani, O. Crosnier and S. W. Donne, J. Power Sources, 2019, 417, 193–206 CrossRef CAS.
- S. W. Feldberg, J. Am. Chem. Soc., 1984, 106, 4671–4674 CrossRef CAS.
- T. W. Yeu, K. M. Yin, J. Carbajal and R. E. White, J. Electrochem. Soc., 1991, 138, 2869–2877 CrossRef CAS.
- T. W. Yeu, T. V. Nguyen and R. E. White, J. Electrochem. Soc., 1988, 135, 1971–1976 CrossRef CAS.
- X. Z. Wang, B. Shapiro and E. Smela, J. Phys. Chem. C, 2009, 113, 382–401 CrossRef CAS.
- M. Modestov, V. Bychkov, D. Valiev and M. Marklund, J. Phys. Chem. C, 2011, 115, 21915–21926 CrossRef CAS.
- V. N. Prigodin, F. C. Hsu, J. H. Park, O. Waldmann and A. J. Epstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035203 CrossRef.
- J. Rivnay, P. Leleux, M. Ferro, M. Sessolo, A. Williamson, D. A. Koutsouras, D. Khodagholy, M. Ramuz, X. Strakosas, R. M. Owens, C. Benar, J.-M. Badier, C. Bernard and G. G. Malliaras, Sci. Adv., 2015, 1, e1400251 CrossRef PubMed.
- A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Adv. Funct. Mater., 2017, 27, 1700329 CrossRef.
- K. Tybrandt, I. V. Zozoulenko and M. Berggren, Sci. Adv., 2017, 3, eaao3659 CrossRef PubMed.
- J. Siepmann and F. Siepmann, Int. J. Pharm., 2013, 453, 12–24 CrossRef CAS PubMed.
- P. S. Guin, S. Das and P. C. Mandal, Int. J. Electrochem., 2011, 2011, 22 Search PubMed.
- M. Nandanwar and S. Kumar, J. Power Sources, 2019, 412, 536–544 CrossRef CAS.
- T. Rębiś and G. Milczarek, Electrochim. Acta, 2016, 204, 108–117 CrossRef.
- R. K. Malhotra and L. A. Woolf, J. Solution Chem., 1993, 22, 351–360 CrossRef CAS.
- A.-K. Kontturi and K. Kontturi, J. Colloid Interface Sci., 1987, 120, 256–262 CrossRef CAS.
- M. O. Bamgbopa, S. Almheiri and H. Sun, Renewable Sustainable Energy Rev., 2017, 70, 506–518 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta07030c |
| This journal is © The Royal Society of Chemistry 2019 |