Band-gap engineering in AB(O_xS_1−x)₃ perovskite oxysulfides: a route to strongly polar materials for photocatalytic water splitting

Abstract

Polarity in heterogeneous photocatalysts was shown to enhance charge-carrier separation, resulting in superior efficiency for example for photocatalytic water splitting. Oxynitrides are promising photocatalysts due to their small band gaps and can be rendered polar by epitaxial strain. However, while the low electronegativity of nitrogen results in small band gaps in non-polar oxynitrides, it is also responsible for a large increase in band gap with increasing polar distortion amplitude. This suggests a trade-off between small band gaps and polar distortions – both being crucial for the catalyst's performance. Due to the even lower electronegativity of sulfur, sulfides normally have band gaps that are too small for water splitting but polar distortions could shift their band gap to a suitable range. In this paper we investigate, using density functional theory calculations, the suitability of polar AB(O_xS_1−x)₃ perovskites for photocatalytic water splitting. We find that polar distortions – induced by epitaxial strain or substitution of sulfur by oxygen – can indeed increase the band gap to a suitable range. In particular, our calculations predict compressively strained BaZr_yTi_1−yO₂S compounds to be highly promising for photocatalytic water splitting.

---

1 Introduction

Efficient electron–hole separation is a key requirement for high-performing photocatalysts for example for photocatalytic water splitting. Charge-carrier separation can be enhanced in polar materials such as ferroelectrics, where the compensation of the internal dipolar field results in preferential migration of electrons and holes in opposite directions.^1,2 Ferroelectric materials, which traditionally are d⁰ perovskite oxides (ABO₃),^3,4 typically have band gaps above 3 eV. Optimal band gaps for photocatalytic water splitting, however, are much lower: while very small band gaps would lead to absorption of a large fraction of the solar spectrum, the condition that the valence and conduction band edges have to straddle the oxygen and hydrogen evolution potential respectively, imposes a minimal band gap of 1.23 eV. After considering theoretical minimum overpotentials⁵ for the oxygen and hydrogen evolution reaction, this minimum increases to 1.7 eV and since in practice there are always energy losses associated for example with interfacial charge transfer, band gaps should be larger than approximately 2 eV.⁶ One possibility to reduce the band gap of oxides is by substituting oxygen with nitrogen, which has a lower electronegativity (η = 3.04 on the Pauling scale) than oxygen (η = 3.44) resulting in materials with higher valence band edges and band gaps just above 2 eV.⁷

Bulk oxynitrides are not ferroelectric but out-of-plane ferroelectricity can be induced using compressive biaxial strain,^8,9 applied for example by lattice matching during coherent epitaxial growth by pulsed layer deposition or molecular beam epitaxy. Whereas the in-plane lattice parameters shorten with increasing compressive strain, the out-of-plane lattice parameter expands due to Poisson's effect. This elongation affects the balance between coulombic and covalent interactions and eventually leads to ferroelectric distortions along the elongated direction.^10,11 Ferroelectric distortions in oxides and oxynitrides however also increase the band gap due to a stabilizing effect on the O 2p respectively N 2p orbitals forming the valence-band edge together with a destabilization of the transition-metal t_2g π* orbitals forming the conduction-band edge.^12,13 The band gap in strained oxide and oxynitride materials hence depends on the strain-dependent existence and amplitude of the ferroelectric distortion as illustrated in Fig. 1(a) and (b). While this effect is rather small in oxides,¹⁴ we have shown it to be much more pronounced in oxynitrides, where the reduced electronegativity of nitrogen leads to stronger bonds and hence larger ferroelectric distortions that increase the band gap by up to 1.5 eV, effectively disabling visible light absorption.¹³ More details on the physical mechanisms behind band-gap changes as a function of strain, ferroelectric distortions and octahedral rotations in oxides and oxynitrides can be found elsewhere.^13,14

Fig. 1 Schematic representation of changes in band energies and resulting band gaps for increasing ferroelectric distortion amplitudes. The band gap increases from (a) small to (b) intermediate distortion amplitudes and (c) remains constant above a certain amplitude. Blue and grey boxes represent bands that are affected (2p/3p and t_2g π*) respectively not affected by the ferroelectric distortion and the darker/lighter shade distinguishes occupied/empty states respectively.

In search for polar materials with suitable band gaps, we investigate in this study perovskite (oxy)sulfides. Due to band gaps below 2 eV resulting from the low electronegativity of sulfur (η = 2.58), this class of materials has so far mainly been investigated for photovoltaics^15,16 or for Z-scheme water splitting.^17,18 A polar distortion, induced for example by epitaxial strain or anisotropic chemical strain, could however increase the band gap to slightly above 2 eV and yield materials suitable for photocatalytic water splitting.

Besides the smaller electronegativity, sulfur also has a much larger ionic radius¹⁹ (r = 1.84 Å) compared to oxygen (r = 1.40 Å) and nitrogen (r = 1.46 Å). Considering the tolerance factor²⁰ and Pauling's first rule,²¹ this leads to a limited number of possible elements on the A and B site in the perovskite ABS₃ structure. Indeed only compounds with A = Ca, Sr, Ba, Eu and B = Zr, Hf, U have been reported in the GdFeO₃ perovskite structure²². Mixed-anion materials with both sulfur and oxygen were reported to be difficult to synthesize and mainly crystallize in Ruddlesden-Popper structures with different coordination environments for apical and equatorial anion sites.²³

We therefore start our density functional theory (DFT) investigation of the AB(O_xS_1−x)₃ system with BaZrS₃, which is one of the most investigated perovskite sulfides^24–28 and for which sulfur was partially substituted with oxygen.²⁴ We then systematically investigate polarity and band gaps in related compounds obtained by partial substitution of sulfur by oxygen as well as by changing the A site (Ca, Sr, Ba) and the B site (Ti, Zr, Hf). We find the BaZr_yTi_1−yO₂S system to be most promising in terms of a simultaneous polarization and small band gaps (E_g = 2.8 eV at the HSE level of theory for BaZr_0.625Ti_0.375O₂S under 3% compressive strain). The actual band gap could even be significantly lower as experiments for BaZrO₂S (ref. 24) indicate that the measured band gap is systematically lower (ΔE_g ≈ 1 eV) than HSE predictions, which could be related to a small degree of anion disorder. These materials also have a strong out-of-plane polarization but are unlikely to be ferroelectric due to their large theoretical coercive fields.

2 Computational methods

DFT calculations were performed with Quantum ESPRESSO²⁹ at the PBE+U level of theory.^30,31 Hubbard U was calculated self-consistently^32,33 for the different transition metal B sites resulting in 3.1 eV for Ti, 1.8 eV for Zr and 1.5 eV for Hf. While computationally affordable PBE+U band gaps severely underestimate experiment, they were shown to follow the same relative strain-dependence as quasiparticle GW band gaps¹⁴, which are known for their good accuracy but also their high computational cost. In order to compare band gaps between different compositions, we selectively performed hybrid functional calculations using HSE (α = 0.18) on structures relaxed at the PBE+U level of theory. HSE is known to yield reasonable band gaps at a lower computational cost than GW.

Calculations were performed in a 40 atom 2 × 2 × 2 supercell of the 5-atom perovskite unit cell. Reciprocal space was sampled with a 4 × 4 × 4 Monkhorst–Pack grid.³⁴ All atoms are represented by ultrasoft pseudopotentials³⁵ with Ca(3s, 3p, 4s, 3d), Sr(4s, 4p, 5s), Ba(5s, 5p, 5d, 6s, 6p), Ti(3s, 3p, 3d, 4s), Zr(4s, 4p, 5s, 5p, 4d), Hf(5s, 6s, 5p, 6p, 5d), O(2s, 2p) and S(3s, 3p, 3d) valence electrons. The cutoff for the plane-wave basis set was 40 Ry for the kinetic energy combined with 400 Ry for the augmented density.

The convergence criteria for geometry relaxations were 0.05 eV Å⁻¹ for forces and 1.4 × 10⁻⁵ eV for the total energy. Atomic positions, cell shape and volume were fully relaxed for unstrained structures. For known compounds such as pure sulfides and oxides we use experimental structures as the starting point for the structural relaxations. For the ABX₂Y compositions (X and Y being either sulfur or oxygen) we search the most stable unstrained 2D cis (Fig. 3(a)) and 1D trans (Fig. 3(b)) structures by starting the geometry relaxation from a slightly expanded unit cell with small random atomic displacements with respect to the high-symmetry structure to allow for relaxation into the preferred octahedral rotation patterns. For low-energy (i.e. trans) structures we further tested different octahedral rotation patterns, previously observed in oxynitrides^9,13 and identified the same low-energy structures as with the first method. For polar trans structures with the polarization along c we test the a⁰b⁰c⁰, a⁰b⁰c⁺ and a⁰b⁰c⁻ rotation patterns (in Glazer notation³⁶). The occurrence of only these three patterns is compatible with the usual competition between polar distortions and octahedral rotations along the same axis.^37,38 For zirconium substituted BaZr_yTi_1−yO₂S compounds we used the most stable BaZrO₂S structure as the starting point for structural optimizations. The most important crystal structures can be found in the ESI Section S3.†

Epitaxial strain imposed by the (001) facet of a cubic substrate is modeled by setting the in-plane lattice parameters to equal lengths and orthogonal to each other. Strain was applied in all three {001} planes and defined with respect to the average in-plane lattice constant of the unstrained structure. In strained calculations only the atomic positions and the out-of-plane lattice vector were relaxed. Strain was applied to all unstrained structures to test for strain induced phase changes. We used climbing-image nudged elastic band (cNEB) calculations³⁹ to obtain the energy profile along the ferroelectric switching pathway. Paths in cNEB calculations were relaxed until the norm of the force orthogonal to the path was smaller than 0.05 eV Å⁻¹ for all images. The electric polarization was calculated using the Berry phase method^40–42 with 6 k-points along the symmetry-reduced string. Crystal orbital Hamilton population (COHP) analysis^43,44 was performed with LOBSTER^45–47 and atomic structures were visualized using VESTA.⁴⁸

3 Results and discussion

3.1 BaZr(O_xS_1−x)₃

We start our exploration of the AB(O_xS_1−x)₃ system with the perovskite BaZrS₃, which was reported to have large octahedral rotations and antiferroelectric distortions characterized by large displacements of the Ba atoms.²⁶ Lattice parameters of the fully relaxed unstrained structures compare well with available experimental values (Table 1) having deviations less than 1.4%.

Table 1 Lattice constants of unstrained fully relaxed Pnma ABS₃ structures obtained from PBE+U calculations compared to experimental values

Materials		a [Å]	b [Å]	c [Å]
BaZrS3	Calc.	6.98	7.16	9.98
	Exp.^22	7.03	7.06	9.98
BaHfS3	Calc.	6.92	7.04	9.89
	Exp.^22	7.00	7.00	9.92

---

We induce ferroelectricity in BaZrS₃ by applying epitaxial strain. We show the strain-dependent energy for different polar and non-polar phases in the ESI Section S1† and monitor octahedral rotations and the polar distortion as these two distortions were shown to often compete with each other.^37,38 We characterise the former by the deviation of the out-of-plane Zr–S–Zr bond angle from 180°, while the latter is measured via the deviation from 1 of the ratio of two consecutive S–Zr bonds along a given direction

A = d_D/d_N − 1 (1)

where d_D and d_N are the bond lengths of the longer and shorter S–Zr bond respectively as shown in Fig. 2(a). As such A is zero for a non-polar structure and increases with increasing polar distortion amplitude. As shown in Fig. 2(b), we observe a gradual decrease of the out-of-plane octahedral rotations with increasing compressive strain. The polar distortion only appears once the octahedral rotations have changed to a⁰b⁰c⁻ at a compressive strain between 4% and 5%. Such large strains are unlikely to be experimentally accessible. However, given the usual competition between polar distortions and octahedral rotations, it is likely that a reduction of the latter will promote polarity at smaller compressive strains. Interestingly, the band gap of the polar structure is only slightly larger (DFT+U E_g = 1.2 eV) compared to the non-polar structure (DFT+U E_g = 1.1 eV). This suggests that not only a reduced anionic electronegativity¹³ but also the structural anisotropy in mixed anion perovskites significantly amplifies the polar distortion and hence increases the band gap. This is confirmed later when we analyze the band gap of polar oxysulfides that increases substantially in presence of a polar distortion. Thus, it might be interesting in future studies to compare single anion and mixed anion compounds in more detail.

Fig. 2 (a) Definition of bond lengths used to describe the ferroelectric distortion and (b) amplitude of the polar distortion and out-of-plane octahedral rotations in BaZrS₃ as a function of epitaxial strain.

The tolerance factor²⁰ is a good descriptor for structural distortions such as octahedral rotations or ferroelectric distortion in oxides. It is defined as

where r_A and r_B are the ionic radii of the A and B site and r_X is the radius of the anion. A tolerance factor t > 1 implies an instability of the perovskite structure compared to hexagonal phases, a t close to one suggests ferroelectricity, while for t < 1 octahedral rotations become increasingly more favorable up to the point where the perovskite structure is no longer stable. For BaZrS₃ (r_Ba = 1.61 Å, r_Zr = 0.72 Å, r_S = 1.84 Å),¹⁹ the large radius of sulfur results in t = 0.95, indeed suggesting large octahedral rotations. A partial substitution of sulfur by oxygen will increase the tolerance factor and should therefore also decrease octahedral rotations. We calculate the composition-dependent tolerance factor for a mixed-anion oxysulfide using the arithmetic average of the two anion radii

r_X: = x·r_O + (1 − x)·r_S (3)

with x the fraction of oxygen and r_O = 1.40 Å the ionic radius of oxygen.¹⁹ For the BaZr(O_xS_1−x)₃ series we obtain tolerance factors of 0.97, 0.99 and 1.00 for BaZrOS₂, BaZrO₂S and BaZrO₃ respectively, showing indeed an increase of t and suggesting a reduction of the octahedral rotations with increasing oxygen content.

In these mixed-anion compounds the anion order represents a further degree of freedom. In BaZrOS₂ and BaZrO₂S, the oxygen and sulfur anions within one BX₆ octahedron can order either in cis or trans configuration shown in Fig. 3(a) and (b). We refer here to the anion configuration with respect to the minority anion species (O in BaZrOS₂ and S in BaZrO₂S). While the cis configuration is preferred in many mixed-anion perovskites such as oxynitrides,⁴⁹ the trans configuration is generally rare,²³ one example being SrVO₂H, for which the hydride ions fully order on apical sites.⁵⁰ For both BaZrOS₂ and BaZrO₂S we find the energetically most stable trans order to be energetically much more favorable than the energetically most stable cis order (by 0.23 eV f.u.⁻¹ and 0.33 eV f.u.⁻¹ respectively). This preference stems from the large mismatch the radii of oxygen and sulfur that result in very different ideal Zr–S and Zr–O bond lengths. A trans order is optimal as the presence of either only Zr–S or Zr–O bonds along each pseudocubic direction leads to the smallest deviations from the optimal bond lengths. These large energy differences also indicate that the synthesis of perovskite oxysulfides with anion stoichiometries different from X₂Y might be difficult.

Fig. 3 Schematic representation of the anion orders in a BX₄Y₂ mixed-anion octahedron (a) cis and (b) trans. Relaxed structures of unstrained (c) BaZrOS₂ and (d) BaZrO₂S. Color code: Ba = purple, Zr = cyan, O = red, S = yellow.

The relaxed structure of the mixed-anion compounds are shown in Fig. 3(c) and (d). While BaZrOS₂ still has large octahedral rotations in the bc plane (a⁻b⁰c⁰), they completely vanish in BaZrO₂S (a⁰b⁰c⁰) and the structure develops a strong polar distortion along the Zr–S bond. This distortion is so large that it changes the local B-site coordination from octahedral to tetrahedral. We confirm the weak bond strength of the elongated Zr–S bond by COHP analysis, which shows strong bonding contributions only for the short Zr–S bond; the integrated COHP up to the Fermi level revealing that the shorter Zr–S bond is one order of magnitude stronger than the longer Zr–S bond.

As oxysulfides are known to be difficult to synthesize due to the large mismatch in anionic radii, we assess the thermodynamic stability of BaZrO₂S and BaZrOS₂ by calculating different decomposition pathways. We calculate the decomposition energy E_d with respect to possible binary phases E_d(B), ternary phases E_d(T) as well different reasonable decomposition pathways for mixed binary and ternary phases E_d(B + T) (see ESI Section S2† for details). The smallest decomposition energy for each pathway is reported in Table 2, negative values indicating an instability of the perovskite structure. We find BaZrO₂S to be unstable with respect to binary phases (E_d = −0.367 eV f.u.⁻¹) and BaZrOS₂ to be slightly unstable with respect to ternary phases (E_d = −0.063 eV f.u.⁻¹). While these results suggest that these oxysulfides – especially BaZrO₂S – might be difficult to synthesize, they also suggest that thin-film growth on a structure-imposing perovskite substrate could be easier than powder synthesis. We note however that both materials were recently synthesized as powders,²⁴ which is in agreement with a small metastability (0.2 eV per atom) that is usually tolerated in high-throughput studies.⁵¹

Table 2 Decomposition energies of BaZrO₂S and BaZrOS₂ with respect to binary (B), ternary (T) and mixed binary and ternary (B + T) phases

Materials	T [eV f.u.^−1]	B [eV f.u.^−1]	B + T [eV f.u.^−1]
BaZrO2S	0.017	−0.367	0.123
BaZrOS2	−0.063	1.69	0.287

---

Having established the preferred anion order of the mixed-anion members as well as their structural distortions, we now turn to the electronic properties of the BaZr(O_xS_1−x)₃ series. The conduction-band edge is Zr 4d dominated in all compounds. The valence-band edge in the pure oxide is O 2p dominated, but due to the smaller electronegativity of sulfur it is formed by S 3p states in the oxysulfides and the sulfide. We show the projected density of states (PDOS) for BaZrOS₂ in Fig. 4(a). Fig. 4(b), shows the evolution of the DFT+U and HSE band gaps as a function of the oxygen content. Due to the S 3p dominated valence band-edge we expect no marked change in band gap for sulfur-containing compounds. This is indeed observed for BaZrS₃ and BaZrOS₂ but for BaZrO₂S the band gap increases markedly. We can relate this to the emergence of the polar distortion shown in Fig. 2(d), which was shown to drastically increase the band gap for compounds with low-electronegativity anions such as nitrogen in oxynitrides.¹³ The same behavior was also observed experimentally, but not further investigated.²⁴ While our HSE band gaps agree well with experiment for BaZrS₃ and BaZrOS₂, the value predicted for BaZrO₂S (3.4 eV) is much larger than the experimental value of 2.5 eV.²⁴ This mismatch could stem from a small anion disorder in experiment that would reduce the polar distortion and hence the band gap. Calculating the band edge positions with respect to the normal hydrogen electrode using the Mulliken electronegativities of the pure chemical elements as well as the experimental band gap⁵² we further find that both valence (E_VB = 1.8 eV) and conduction band (E_CB = −0.7 eV) should straddle with the oxygen and hydrogen evolution potential respectively.

Fig. 4 (a) Partial density of states of BaZrOS₂ at the PBE+U level of theory and (b) PBE+U and HSE band gaps in the BaZr(O_xS_1−x)₃ series.

The band gap of BaZrO₂S (HSE: 3.4 eV, experiment: 2.5 eV)²⁴ should be further reduced to improve the photocatalytic activity. BaZrOS₂ on the other hand, has a band gap that is too small (HSE: 1.66 eV, experiment: 1.8 eV)²⁴ to promote photocatalytic water splitting. We therefore apply epitaxial strain to both materials with the goal of changing the amplitude of the polar distortion and tune their band gaps (which in absence of octahedral rotations were shown to be linearly affected by strain^13,14) to values suitable for photocatalytic water splitting. We consider only orientations of the 1D trans chains along the film normal as preliminary test for other orientations (not shown) were energetically significantly less favorable due to the very different length of Zr–O and Zr–S bonds. As shown by the green background in Fig. 5, we find that both large compressive and tensile strain induce polar distortion in BaZrOS₂. For compressive strain the distortion is oriented along the out-of-plane direction (along Zr–O bonds) and for tensile strain along the in-plane direction (along Zr–S bonds), which is not relevant for applications in photocatalysis. Looking at the band gap (green curve in Fig. 5), we observe in the intermediate strain range, where the structure is non-polar, a continuous decrease in the band gap with increasing compressive strain that stems from increased bandwidths with decreased volume. While we see an increase in band gap when the out-of-plane polar distortion appears beyond 3% compressive strain, there is no overall increase in band gap for compressively strained BaZrO₂S and the band gap is therefore still too small for photocatalytic water splitting.

Fig. 5 Relative change in band gap for BaZrOS₂ and BaZrO₂S. The green coloured background indicates the appearance of polar distortions for BaZrOS₂. BaZrO₂S shows polar distortions at all investigated strains.

BaZrO₂S has a polar distortion already without strain and we would expect strong changes in band gaps due to the strain-dependent modulation of the distortion amplitude. The blue curve in Fig. 5 however shows only small changes comparable to the volume-induced ones discussed above for BaZrOS₂. We believe this to stem from the fact that a very large polar distortion as shown in Fig. 3(d) leads to changes in the band-edge forming orbitals as shown in Fig. 1(c). While strain does modulate the amplitude of the polar distortion, this has no longer an effect on the band gap. Strain engineering of the oxysulfides BaZrOS₂ and BaZrO₂S can thus not yield band gaps in the suitable range for photocatalytic water splitting.

3.2 Changing the conduction-band edge by B site alloying: BaHfOS₂ and BaZr_yTi_1−yO₂S

Given that band gaps for strained BaZrOS₂ and BaZrO₂S are still too small respectively too large for photocatalytic water splitting, we substitute the B site with isovalent elements with slightly different electronegativities to further engineer the band gap. Since BaZrOS₂ has a too small band gap, we substitute Zr (η = 1.33) by Hf (η = 1.30) in order to increase the band gap. As expected, BaHfOS₂ has a higher-lying conduction-band edge but we do not find the emergence of polar distortions for experimentally accessible strains (not shown). For BaZrO₂S on the other hand, we try to decrease the conduction-band edge and hence the band gap by substituting Zr with Ti (η = 1.54). A full substitution of Zr by Ti leads to a large decrease in the conduction-band edge and hence in band gap (ΔE_g,HSE = 1.3 eV) while the structure preserves its strong polar distortion. We observe, however, structural instabilities of the fully substituted structure and hence investigate also partial substitution of Zr by Ti by computing all symmetrically distinct Zr/Ti arrangements on the 8 B sites in the 40 atom unit cell for different Ti content. The band gap of the most stable structure for each BaZr_yTi_1−yO₂S composition is shown by the green squares in Fig. 6. While the band gap generally decreases with increasing titanium content, this trend is broken for 1 − y = 0.500 and 0.625. For these structures we find large rotations of the tetrahedra (see structure (3) in Fig. 7) that we characterize by the deviation of the B–S bond from the c axis (blue triangles in Fig. 6). This is in agreement with the fact that rotations of the coordination polyhedra, like polar distortions, lead to an increased band gap in perovskite oxides.¹⁴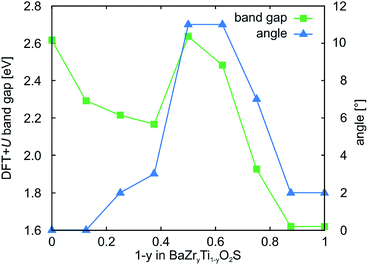

Fig. 6 DFT+U band gaps and tetrahedral rotation angles for the most stable BaZr_yTi_1−yO₂S structures.

Fig. 7 Relative energy of different low energy structures of BaZr_0.625Ti_0.375O₂S: (1) no Ti clustering or polyhedra rotations, lowest energy for compressive strain larger than 3%, (2) Ti clustering but no polyhedra rotations, lowest energy between 3 and 2.2% compressive strain and (3) Ti clustering and polyhedra rotations, lowest energy above 2.2% compressive strain. Color code: Ba = purple, Zr = cyan, Ti = white, O = red, S = yellow.

The observed tetrahedral rotations indicate a potential instability of the perovskite structure for 1 − y > 0.2, which is supported by two additional observations: first, we observe that in the energetically most favorable structures B sites of the same element tend to cluster and second, we see a bond-length asymmetry of O–Ti–O bonds as shown for structure (2) in Fig. 7. We further investigate the potential to stabilize the perovskite-like BaZr_yTi_1−yO₂S structure by strain. This is motivated by previous findings for BaZr_yTi_1−yS₃, where BaTiS₃ was found to be unstable in the perovskite structure but the substitution of Ti by Zr and compressive biaxial strain both lead to a stabilization of the perovskite structure.^27,53 As shown for BaZr_0.625Ti_0.375O₂S in Fig. 7, we find indeed that compressive strain strongly destabilises structure (3), which has tetrahedral rotations and Ti-clustering. For compressive strain around 2.2% first a structure without tetrahedral rotations becomes stable, while beyond 3% compressive strain also the Ti-clustering vanishes. These findings are general for 1 − y ≤ 0.375, whereas for larger Ti content the perovskite-like structure is unstable for all investigated strains. Compressive strain also reduces the band gap and for 3% compressive strained BaZr_0.675Ti_0.325O₂S we predict a HSE band gap of 2.8 eV. We want to stress again that anion disorder could further reduce the band gap by a reduction of the polar distortion.

We also investigate the stability of various unstrained and fully relaxed BaZr_yTi_1−yO₂S compositions via their decomposition energy with respect to ternary phases (see ESI Section S2† for details). As shown in Fig. 8 we find that while compositions with small Ti content are slightly metastable, the stability first increases for the strongly distorted (non-perovskite) structures at intermediate composition before becoming unstable at high Ti content.

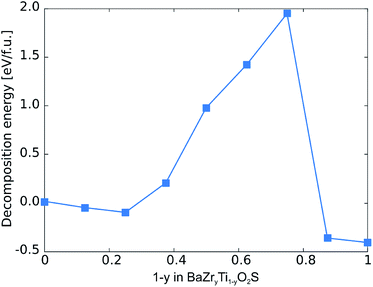Fig. 8 Decomposition energies with respect to ternary phases for different BaZr_yTi_1−yO₂S compositions.

3.3 Electric polarization and coercive field

Finally, we determine the coercive field of BaZrO₂S, which is defined aswhere E is the switching barrier per formula unit between the two oppositely polarized states, P the electric polarization at the bottom of the double well potential normalized per area perpendicular to the polarization direction and V the volume per formula unit.⁵⁴ We determine the switching barrier to be 1.5 eV per formula unit (see Fig. 9) via a nudged elastic band calculation and the polarisation to be 0.88 C m⁻²via the Berry phase method, using the transition state as a non-polar reference to determine the quantum of polarization. While the polarization is slightly larger compared to traditional ferroelectrics such as PbTiO₃,⁵⁴ the switching energy is significantly larger and results in a coercive field of 2143 MV m⁻¹, one order of magnitude larger than in PbTiO₃.⁵⁴ Substitution of the A site with Ca and Zr as well as the B site with Ti do not result in significantly smaller coercive fields (not shown). We therefore conclude that sulfides and oxysulfides, where the polarisation occurs along S–B–S bonds, are only polar but not ferroelectric due to their prohibitively large coercive fields.

Fig. 9 Energy profile for polarization switching in BaZrO₂S.

4 Conclusion

We investigated the AB(O_xS_1−x)₃ system as polar photocatalysts for water splitting. We find that oxysulfides strongly prefer a trans anion configuration due to the large size mismatch of oxygen and sulfur, which is contrary to most mixed-anion perovskites that favor a cis configuration. The trans anion configuration in ABO₂S oxysulfide thin films is directly related to the appearance of a strong polar distortion along the technologically relevant out-of-plane direction. Due to the high switching barrier, these materials are however only polar and not ferroelectric.

Increasing the Ti content in the BaZr_yTi_1−yO₂S series lowers the band gap but also leads to structural instabilities that can be stabilized by compressive strain up to 1 − y = 0.375. We find 3% compressively strained BaZr_0.625Ti_0.375O₂S to have the most promising 2.8 eV HSE band gap for photocatalytic water splitting. Comparison with experiment for the BaZr(O_xS_1−x)₃ series suggests that band gaps could be smaller than our HSE estimates (e.g. due to anion disorder). Mixed cation oxysulfides are therefore promising candidates for highly efficient water-splitting photocatalysts that combine strong polarity with small band gaps.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the SNF Professorship Grant PP00P2_157615. Calculations were performed on UBELIX (http://www.id.unibe.ch/hpc), the HPC cluster at the University of Bern as well as the Swiss National Supercomputing Centre (CSCS) under project ID 766 and SuperMUC at GCS@LRZ, Germany, for which we acknowledge PRACE for awarding us access.

Notes and references

1. J. L. Giocondi and G. S. Rohrer, J. Phys. Chem. B, 2001, 105, 8275–8277.
2. L. Li, P. A. Salvador and G. S. Rohrer, Nanoscale, 2014, 6, 24–42.
3. B. Matthias, Phys. Rev., 1949, 75, 1771.
4. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694–6709.
5. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
6. J. R. Bolton, S. J. Strickler and J. S. Connolly, Nature, 1985, 316, 495.
7. A. Kasahara, K. Nukumizu, G. Hitoki, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. A, 2002, 106, 6750–6753.
8. D. Oka, Y. Hirose, H. Kamisaka, T. Fukumura, K. Sasa, S. Ishii, H. Matsuzaki, Y. Sato, Y. Ikuhara and T. Hasegawa, Sci. Rep., 2014, 4, 4987.
9. N. Vonrüti and U. Aschauer, Phys. Rev. Lett., 2018, 120, 046001.
10. I. B. Bersuker, Chem. Rev., 2013, 113, 1351–1390.
11. J. M. Rondinelli, A. S. Eidelson and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205119.
12. R. A. Wheeler, M. H. Whangbo, T. Hughbanks, R. Hoffmann, J. K. Burdett and T. A. Albright, J. Am. Chem. Soc., 1986, 108, 2222–2236.
13. N. Vonrüti and U. Aschauer, Phys. Rev. Mater., 2018, 2, 105401.
14. R. F. Berger, C. J. Fennie and J. B. Neaton, Phys. Rev. Lett., 2011, 107, 146804.
15. Y.-Y. Sun, M. L. Agiorgousis, P. Zhang and S. Zhang, Nano Lett., 2015, 15, 581–585.
16. M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, Adv. Energy Mater., 2017, 7, 1700216.
17. S. Sun, T. Hisatomi, Q. Wang, S. Chen, G. Ma, J. Liu, S. Nandy, T. Minegishi, M. Katayama and K. Domen, ACS Catal., 2018, 8, 1690–1696.
18. G. Ma, S. Chen, Y. Kuang, S. Akiyama, T. Hisatomi, M. Nakabayashi, N. Shibata, M. Katayama, T. Minegishi and K. Domen, J. Phys. Chem. Lett., 2016, 7, 3892–3896.
19. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
20. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
21. L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026.
22. R. Lelieveld and D. Ijdo, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2223–2226.
23. Y. Kobayashi, Y. Tsujimoto and H. Kageyama, Annu. Rev. Mater. Res., 2018, 48, 303–326.
24. S. Perera, H. Hui, C. Zhao, H. Xue, F. Sun, C. Deng, N. Gross, C. Milleville, X. Xu and D. F. Watson, et al. , Nano Energy, 2016, 22, 129–135.
25. S. Niu, H. Huyan, Y. Liu, M. Yeung, K. Ye, L. Blankemeier, T. Orvis, D. Sarkar, D. J. Singh and R. Kapadia, et al. , Adv. Mater., 2017, 29, 1604733.
26. J. W. Bennett, I. Grinberg and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235115.
27. W. Meng, B. Saparov, F. Hong, J. Wang, D. B. Mitzi and Y. Yan, Chem. Mater., 2016, 28, 821–829.
28. J. A. Brehm, J. W. Bennett, M. R. Schoenberg, I. Grinberg and A. M. Rappe, J. Chem. Phys., 2014, 140, 224703.
29. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
31. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
32. H. Hsu, K. Umemoto, M. Cococcioni and R. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125124.
33. I. Timrov, N. Marzari and M. Cococcioni, Phys. Rev. B, 2018, 98, 085127.
34. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
35. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
36. A. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
37. N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349.
38. U. Aschauer and N. A. Spaldin, J. Phys.: Condens. Matter, 2014, 26, 122203.
39. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
40. R. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651.
41. R. Resta, Europhys. Lett., 1993, 22, 133.
42. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4442.
43. R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624.
44. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
45. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
46. S. Maintz, M. Esser and R. Dronskowski, Acta Phys. Pol., B, 2016, 47, 1165–1175.
47. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
48. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
49. J. P. Attfield, Cryst. Growth Des., 2013, 13, 4623–4629.
50. F. Denis Romero, A. Leach, J. S. Möller, F. Foronda, S. J. Blundell and M. A. Hayward, Angew. Chem., Int. Ed., 2014, 53, 7556–7559.
51. I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 5814–5819.
52. I. E. Castelli, J. M. García-Lastra, F. HÃser, K. S. Thygesen and K. W. Jacobsen, New J. Phys., 2013, 15, 105026.
53. J. Huster, Z. Naturforsch., B, 1980, 35, 775.
54. S. Beckman, X. Wang, K. M. Rabe and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 144124.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta03116b

---