Design of organic structure directing agents for polymorph A zeolite beta

Abstract

Zeolite beta is a crystalline material with layer-type faulting. The two end members with perfect crystalline order are beta A and beta B. While zeolite beta in faulted form is a widely used industrial catalyst, additional applications may be possible with the perfect crystalline forms. We here computationally design chemically synthesizable organic structure directing agents that may aid the nucleation and growth of pure zeolite beta A, excluding the competing product zeolite beta B.

---

Introduction

Zeolites are nanoporous metastable crystal forms of Si/Al oxides with the general chemical formula Si_1–xAl_xO₂. Their nanoporous nature allows the adsorption of guest molecules in the void space between the composing metal and oxygen atoms. The presence of charge centers at the position of the Al atoms induces catalytic activity towards adsorbed species.¹ The building blocks of zeolites are tetrahedral TO₄ units, where T is Si or Al. The structure and volume of the zeolite pores are determined by the spatial ordering of these TO₄ building blocks. Different TO₄ orderings lead to different zeolite structures, and as of today 239 zeolite structures, both naturally occurring and man-made, have been identified.^2,3

Of these 239 known zeolites, 17 are of industrial interest.⁴ One of these is zeolite beta, which finds application as a catalyst for benzene alkylation and separation of aromatic compounds from aqueous phases.^5,6 As with many zeolites,⁷ zeolite beta is synthesized by an hydro-thermal process in the presence of tetra-ethyl ammonium as structure directing agent.⁸ The structure of zeolite beta thus obtained is a closely inter-grown mixture of 2 polymorphs, polymorph A (BEA) and polymorph B (BEB). Of these, BEA consists of an enantiomorphic pair.^9,10 While syntheses of BEA-enriched zeolite beta have been reported,^11–15 the synthesis of pure BEA has until now remained elusive. More uniformly structured zeolites have the potential to be cleaner and catalytically more efficient.¹⁶ Synthesis of pure BEA would be a breakthrough in catalytic applications of zeolite beta. Synthesis of the pure BEA polymorph would also be a first step towards the enantiomerically pure or enriched substance, which would open possibilities for chiral separation and catalysis.

The use of organic structure directing agents (OSDAs) in zeolite synthesis is well established.¹⁷ Moreover, it has been shown that the structure-directing ability of an OSDA is governed by its non-bonded interaction energy with the zeolite pores.¹⁸ In previous work we have used this principle to successfully design novel OSDAs for a number of zeolites.^19–22 In the present study, we build upon this experience to design OSDAs for pure BEA. We seek OSDAs that stabilize BEA but not BEB. To design selective, synthesizable OSDAs for zeolite BEA we used de novo design, virtual screening, exhaustive virtual combinatorial screening, and stochastic virtual combinatorial screening. The scoring function evaluates the stabilization energy of a putative OSDA in both the BEA and BEB forms of zeolite beta. Pareto optimization is used to design molecules that bind strongly to BEA but bind weakly to BEB.

Methods

Scoring function

We evaluated putative OSDAs with a vector scoring function. The computational protocol calculated several molecular properties of increasing computational complexity. This score vector is summarized in Table 1. The score vector was evaluated in a step-wise manner. Initially, the easy-to-calculate properties were calculated and used as filters. If one of these properties did not pass a threshold value, the scoring function was aborted, and the more computationally expensive calculations were skipped. As a first filter, the amenability of a molecule to calculation with the force field used was checked. Next, several properties that can be obtained in a trivial way from the molecular connectivity table were evaluated. A successful OSDA must not be too flexible.²³ Therefore, both the total number of rotatable bonds and the number of consecutive sp³–sp³ bonds were restricted. For stability under zeolite synthesis conditions, only molecules containing C, N and H were allowed, and no triply bound C atoms were allowed. It has been observed that successful OSDAs contain at least one quaternary ammonium functionality, and that the ratio of C atoms to the number of quaternary N atoms is not larger than 18.²³ These restraints were imposed by the scoring function vector. For ease of synthesis and to avoid issues with racemic or partially racemic mixtures, no chiral centers were allowed in the present work. When these properties were within their respective thresholds, a molecular mechanics minimization was carried out to generate a local minimum energy conformation of the molecule. This conformation was used to calculate the molecular volume, which must be small enough for the molecule to fit into the cavities of the zeolite.

Table 1 Vector score function that evaluates the binding energy of a putative OSDA in BEA and BEB. The score type indicates how the score vector is used to sort the molecules that are input into the score function

score	score type	threshold
Force field compatibility	Binary
Number of rotatable bonds	≤	6
Longest sp^3–sp^3 chain	≤	3
Non-C, –N or –H atoms	≤	0
Triply bonded C	≤	0
C to charged N ratio	≤	18
Chiral centers	≤	0
Molecular volume	≤	800 Å^3
Fit in BEA	Binary
MD stabilization energy in BEA	Minimize
Energy gap MD stabilization energy in BEB	Maximize

---

If the molecular volume filter was passed, an estimate for the global minimum energy conformation of the molecule was determined using a genetic algorithm²⁴ for conformational search (Gacs). Gacs operates on a set of conformations encoded by chromosomes with the decimal encoded values of the torsion angles of the rotatable bonds in the molecule. Initially, a population of conformations with randomly chosen torsion angles between 0° and 360° is generated. The default population size is 20 × N, where N is the number of rotatable bonds. The fitness of each conformation is the molecular mechanics energy obtained by initializing the torsion angles of the molecule with the values coded by the chromosome and performing a local gradient optimization of the molecule. The force field used for the molecular mechanics minimization is the Merck molecular force field (MMFF).²⁵ After the local optimization, the torsion angle values in the molecule are replaced by the torsion angles in the local optimal conformation. After the population is initiated, mutation and selection occur. Child conformations are generated from parent conformations by recombination and random mutation. The parent conformations are selected by tournament selection: two different conformations are selected randomly, and the one with the highest fitness is chosen as the parent. At each fitness evaluation, the torsion angles are optimized. The new conformation replaces the worst scoring conformation in the population if it has a higher fitness. If the fitness of the new conformation is worse than the worst conformation in the population, or if it is already present in the population, it is discarded. The algorithm finishes after a fixed number of fitness evaluations, by default 50 × N. The search for the global potential energy minimum of flexible molecules is a challenging problem, and only deterministic search methods can offer some guarantee that this minimum will be found. These methods, such as the interval analysis algorithm in ref. 26, are time consuming and limited to relatively small molecules. They are therefore not suitable for high-throughput applications. As Gacs is a stochastic algorithm, we cannot guarantee that the lowest energy conformation found is the global potential energy minimum. However, it has been our experience that for molecules with up to 10 rotatable bonds the same lowest energy conformer is reproducibly generated in repeated runs of the algorithm. We therefore assume that this is the global potential energy minimum. The CPU time consumed by a Gacs run is typically between 1 and 10 minutes, depending on the number of flexible bonds and the number of atoms in the molecule.

In the next step of the scoring function, a number of copies of the lowest energy conformation of the molecule obtained by the Gacs program was fitted into the unit cell of the zeolite using an optimized grid procedure.²⁷ The number of OSDA copies fitted into the zeolite is fixed and depends on the zeolite species. It must be determined by geometric evaluation before subsequent screening and searching for promising molecules. The optimal translation of the molecule was determined by fast Fourier transform from the optimal convolution shift. The optimal rotation was obtained by repeating this procedure for 100 random orientations of the molecule. The optimal number of copies for both BEA and BEB has been determined to be eight for small ‘monomer’ molecules, and four for ‘dimer’ molecules.

When the desired number of copies of the putative OSDA had been fitted into the zeolite without large steric clashes, the stabilization energy of the OSDA in the zeolite was calculated using a molecular dynamics (MD) procedure as in ref. 27. The stabilization energy was obtained from the non-bonded Lennard-Jones interaction of the OSDA with the zeolite and the other OSDA copies in the unit cell. It is defined as E = E_system − E_zeolite − nE_OSDA where the energies are calculated as averages from molecular dynamics runs. E_system is the energy of the zeolite with n copies of OSDAs in the unit cell, E_zeolite is the energy of the zeolite, and E_OSDA is the energy of a single OSDA. After fitting the OSDA copies into the zeolite, four rounds of energy minimization were carried out. The minimized structures were used as starting points for three MD runs of 0.1, 1 and 30 ps respectively, at a temperature of 70 °C. Average energies were obtained from the last 5 ps of the production run of the third MD run. While the initial positioning of the OSDA copies uses a single, rigid conformer, the subsequent multiple rounds of MD simulation with various time steps allow the ODSA to adjust this initial conformation to the shape of the zeolite. The stabilization energy was obtained in units of kilojoule per mol Si (kJ per (mol Si)), allowing comparison of different OSDAs in the zeolite. The MD calculations were carried out with the GULP program²⁸ using the Dreiding force field.

In a first MD calculation, the stabilization energy of the molecule in the BEA polymorph was calculated. If this stabilization energy was below the threshold of −15 kJ per (mol Si), the stabilization energy in the BEB energy was calculated, and the energy gap between the two energies was obtained. Due to the stochastic nature of the scoring protocol, there may exist computational errors in the calculation of the stabilization energies. Therefore, when molecules with a stabilization energy gap between BEA and BEB greater than 2 kJ per (mol Si) were generated in the various design runs, we a posteriori recalculated the stabilization energy in BEB of these molecules in six independent runs. We then took the lowest values of the BEB stabilization energies and used these to recalculate the gaps.

We seek to design OSDAs that bind favorably to BEA and less favorably to BEB. We used the above scoring function to design molecules that have a low binding energy to BEA and a large positive energy gap with respect to BEB. We have adopted 4 strategies in our design effort: de novo design, virtual screening of commercially available compounds, exhaustive virtual combinatorial chemistry, and stochastic virtual combinatorial chemistry.

De novo design

The de novo design algorithm we used differs from other de novo design algorithms in that it directly addresses the synthetic accessibility of the designed compounds and can be used in combination with any externally-provided scoring function. The synthetic accessibility was addressed by generating molecular structures via well-documented organic chemistry synthesis routes with commercially available building blocks.^27,29 The search space of the algorithm was the set of molecules that can be generated by applying one or multiple chemical transformations to a set of reagents. We used a Pareto-driven genetic algorithm (GA) to search this space. Full details of the algorithm can be found in ref. 30. We here give a brief overview. The chromosomes of the GA encoded a single or a succession of virtual organic chemistry reactions that were applied to chemicals in a user provided reagent database. At the start of the GA, an initial population of 100 such synthesis routes was generated, and the fitness of each resulting molecule was calculated. In the present study, the fitness was the score vector generated by the scoring function in Table 1. When the initial population had been generated, it was evolved by applying six genetic operators:

(1) Add a reaction step to a parent synthesis route.

(2) Delete a reaction step from a parent synthesis route.

(3) Replace a reagent in a parent synthesis route by a randomly chosen different reagent.

(4) Replace a reagent in a parent synthesis route by a similar reagent.

(5) Combine two parent synthesis routes.

(6) Generate a new synthesis route from scratch.

The parent synthesis routes needed by the genetic operators were chosen by tournament selection. As child molecules were individually generated, if their fitness was better than the worst molecule in the population, they were inserted in the population by replacing the worst molecule. This generation process allowed an efficient parallelization of the GA, because no synchronization was needed in contrast to a traditional generational replacement GA. Asynchronous operation was especially important with the step-wise scoring function used in this study, as the molecules that did not pass the threshold values of the property vector were evaluated in a very short time. Conversely, molecules that required MD evaluation of their stabilization energies in both BEA and BEB required a large amount of CPU time. Parallelization was implemented using a master-worker paradigm. The master program was responsible for structure generation and optimization. Several score function daemons were run as separate stand-alone programs that calculated the fitness of the molecules generated by the de novo design algorithm. Communication between the main program and the score function daemons was through disk file semaphores. Multiple copies of the score function daemons were run on different machines with communication through NFS. For molecules that passed the threshold values of the property vector, a two-dimensional fitness needed to be optimized: the stabilization energy in BEA must be minimized, and the stabilization energy in BEB must be maximized. To allow simultaneous optimization of these two, often conflicting, fitness values, the molecules of the GA were Pareto sorted, and the de novo design produced a set of molecules that are Pareto optimal with respect to the BEA stabilization energy and the stabilization energy gap with BEB. Within this Pareto optimal set, no molecule dominated another molecule: if a molecule within the Pareto optimal set had a better stabilization energy in BEA than another molecule in the Pareto optimal set, its energy gap with BEB was worse. We have shown that the application of Pareto sorting not only allows simultaneous optimization of multiple fitness criteria, but also makes the GA more efficient.³⁰ At present, 100 organic chemistry reactions are implemented in the de novo design program. As reagent database we have used a set of 39 500 commercially available chemical building blocks. With these reagents, a synthesis route comprising a single reaction step can generate 118 × 10³ zero-order and 203 × 10⁶ first-order reaction products. Assuming a constant expansion factor, the number of compounds generated in a synthesis route comprising N reaction steps can be estimated as 39 520 × [(118 × 10³ + 203 × 10⁶)/39 520]^N. To limit synthetic complexity, the number of reactions in a reaction scheme was limited to three. With this limitation, the available chemical search space consists of an estimated 5.3 × 10¹⁵ compounds.

Virtual screening

In addition to searching molecular space using de novo design, we have screened manually selected molecules. The molecules selected were commercially available compounds that were close analogs to the molecules produced by the de novo design runs (cf. the Results section below). The screening was carried out in parallel using a master program that serves a set of molecules to multiple copies of the identical score daemon program as used by the de novo design algorithm. In this way a list of putative OSDAs can be evaluated in parallel.

Exhaustive virtual combinatorial chemistry

In virtual combinatorial chemistry, several reagents are virtually combined using a fixed reaction scheme to generate a set of reaction products. All possible unique compounds that could be generated by the fixed reactions and reagents were examined. Our virtual combinatorial chemistry program used the same organic chemistry reactions set as the de novo design program and a user provided set of reagents. The reaction products generated were scored using the virtual screening protocol described above.

Stochastic virtual combinatorial chemistry

The number of reaction products generated exhaustively by virtual combinatorial chemistry becomes intractable for large numbers of reagents or extended reaction schemes. We have therefore devised a stochastic virtual combinatorial chemistry program. This program searches for the optimal set of reagents from a user supplied database of chemical building blocks with a fixed sequence of reactions to generate reaction products that score well on the vector scoring function. It is comparable to the de novo program, except that the reaction scheme is user-provided, and only reagent space is searched. It uses a GA as an optimizer, and it applies Pareto sorting to allow multi-objective optimization of the molecules to be designed. It uses the same master-worker paradigm to allow efficient parallelization over multiple CPUs and machines. Full details of the program can be found in ref. 31.

Principal coordinate analysis

To visualize sets of molecules generated in the design runs with the different design methods, principal coordinate analysis (PCOA)³² was applied to distance matrices obtained from the 2-D similarity indices of the molecules. Molecules were represented by a binary fingerprint of size 2115 based upon the patterns of up to 4 atoms bound to a central atom, using the MMFF forcefield²⁵ atom types as atom descriptors. From these fingerprints, a Tanimoto similarity coefficient³³T was obtained, and the quantity 1 − T was used as a distance metric for input into the PCOA.

Results

Preliminary experiments using the scoring function from Table 1 revealed that the structure of BEA can accommodate 8 smaller or 4 larger guest molecules that can act as OSDAs. As in our previous work on STW zeolite, we proceeded by first designing good scoring small ‘monomer’ OSDAs that, in a second stage, could be coupled to form larger dimers according to the reaction Scheme 1. Some of the most effective OSDA for BEA have a stabilization energy near −14 kJ per (mol Si).^{11,14,15,34,36} To be conservative we designed molecules that bind to BEA with a stabilization energy equal to or below −15 kJ per (mol Si).

Scheme 1 Dimerization of a monomer ODSA. ArN is an aromatic 5- or 6- membered N-heterocycle. N may or may not be bound to H, X is a halogen, L is a linker with 1 up to 6 C atoms between the halogens.

Monomers

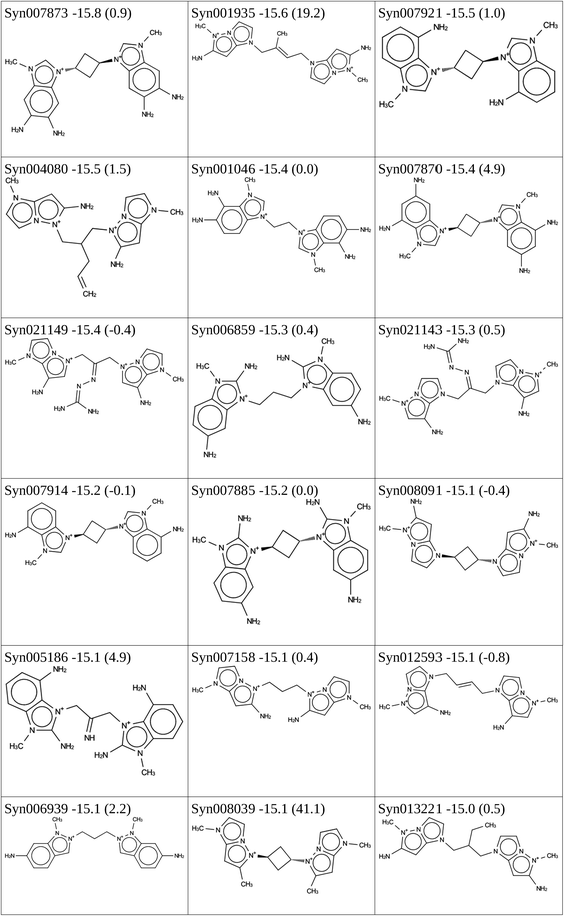
Two de novo design runs were carried out to design a starting set of monomers. This led to a total of 158 putative OSDAs that fitted with an occupancy of eight in the BEA structure with stabilization energy lower than −15 kJ per (mol Si). Some typical de novo designed molecules are presented in Schemes 2 through 5.

Scheme 2 De novo design of monomers: Syn069824. The predicted stabilization energy in BEA is −16.2 kJ per (mol Si).

Scheme 3 De novo design of monomers: Syn304344. The predicted stabilization energy in BEA is −17.0 kJ per (mol Si).

Scheme 4 De novo design of monomers: Syn074355. The predicted stabilization energy in BEA is −15.3 kJ per (mol Si).

Scheme 5 De novo design of monomers: Syn189538. The predicted stabilization energy in BEA is −15.6 kJ per (mol Si).

The putative monomer OSDAs obtained by the de novo design runs were derivatized in two ways. First, compounds formed from reactants containing a pyridine functionality were replaced by their phenyl analogues, as exemplified in Scheme 6. Second, molecules with alkylatable aromatic nitrogen atoms were virtually methylated as exemplified in Scheme 7. In addition to extending the number of compounds, this latter modification ensures that upon dimerization with a dihalogen linker the resulting dimers will have a quaternary ammonium functionality that is typical of effective OSDAs. Subsequent combinations of the two virtual derivatizations led to a total of 2988 molecules that were scored. Of these, 170 compounds were predicted to have a stabilization energy in BEA equal to or below −15 kJ per (mol Si).

Scheme 6 Replacement of a pyridine functionality by the corresponding commercially available phenyl analog.

Scheme 7 Methylation of aromatic nitrogen positions.

We also examined the tetra-hydro indazole ‘THI’ shown in Table 2. It was found to have a stabilization energy of −17.9 kJ per (mol Si). Therefore, the eMolecules building block database³⁵ was searched for analogues of these structures through the substructure search functionality. A set of 122 of these were directly scored, and 18 were found to have a stabilization energy equal to or below −15 kJ per (mol Si) threshold. The 3 top scoring tetra-hydro indazole analogs are also shown in Table 2.

Table 2 A favorable scoring tetra-hydro indazole and 3 commercially available analogs

---

The result of the 3 design routes above is a set of 346 putative monomer OSDAs that have a stabilization energy below −15 kJ per (mol Si). Of these, 271 have an aromatic N functionality suited for dimerization with a dihalide linker.

Dimers

To virtually dimerize the monomer OSDAs we found, a set of linker molecules consisting of 78 achiral dichlorides separated by up to six C atoms were downloaded from the eMolecules building block database.³⁵ In combination with the 271 monomers, these linkers can be used to virtually synthesize 271 × 78 = 21 138 symmetric dimers, i.e. dimers consisting of a linker and two identical copies of a monomer. These compounds were screened, a total number of 20 229 dimers in total. This number is less than the theoretical 21 138 because some of the intermediates in the reaction scheme contain functional groups that are incompatible with a second addition of a monomer molecule. Of these 21 138 molecules, 11 260 passed the easy-to-calculate filters in the scoring function and were subjected to the MD calculation. Of these, 18 were predicted to have a stabilization energy in BEA lower than −15 kJ per (mol Si). They are listed in Table 3.

Table 3 Symmetric dimers generated by exhaustive virtual combinatorial chemistry with a stabilization energy in BEA lower than −15 kJ per (mol Si). The numbers are the stabilization energy in BEA and, in parentheses, the gap in stabilization energy with respect to BEB. The values for the energy gaps larger than 2 kJ per (mol Si) have been a posteriori recalculated. The energies are in kJ per (mol Si)

---

In addition, 271 × 271 × 78 = 5 728 398 asymmetric dimers can be formed consisting of a linker and two different monomer OSDAs. This number is no longer amenable to an exhaustive MD calculation. Instead, the stochastic virtual combinatorial screening protocol was used to search the asymmetric dimer molecular space. As it has been our experience that this protocol is quite effective in searching very large chemical spaces, we extended the molecular space by including monomers identified in the de novo design that pass the simple molecular filters of the scoring function in Table 1, even if they had a stabilization energy above −15 kJ per (mol Si). As there are 2996 of these, the chemical space to be searched contains 2996 × 2996 × 78 ≈ 700 × 10⁶ molecules. We performed two runs to search this molecular space, one that was allowed to evaluate a total of 20 000 molecules, and one that was allowed to evaluate a total of 100 000 molecules. The first run produced 166 dimers with a stabilization energy in BEA below −15 kJ per (mol Si), the second run produced 564 dimers with a stabilization energy in BEA below −15 kJ per (mol Si). The molecules forming the Pareto front are shown Tables 4 and 5.

Table 4 Molecules in the final Pareto front of the first stochastic virtual chemistry run. Within the Pareto front, the molecules have been sorted according to their predicted stabilization energy in BEA. The numbers are the stabilization energy in BEA and, in parentheses, the gap in stabilization energy with respect to BEB. The values for the energy gaps larger than 2 kJ per (mol Si) have been a posteriori recalculated. The energies are in kJ per (mol Si)

---

Table 5 Molecules in the final Pareto front of the second stochastic virtual chemistry run. Within the Pareto front, the molecules have been sorted according to their predicted stabilization energy in BEA. The numbers are the stabilization energy in BEA and, in parentheses, the gap in stabilization energy with respect to BEB. The values for the energy gaps larger than 2 kJ per (mol Si) have been a posteriori recalculated. The energies are in kJ per (mol Si)

---

De Novo design

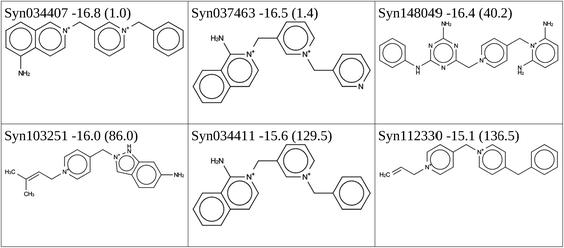
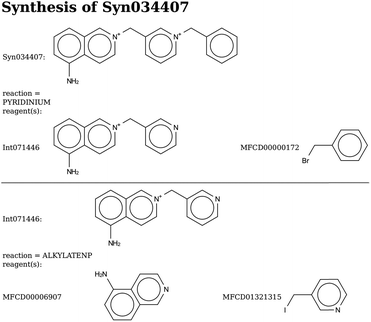
In addition, we performed two de novo design runs to design large OSDAs from scratch by searching the chemical space covered by the set of reactions and reagents. This led to two series of good scoring compounds, one with 402 and one with 430 that have a predicted BEA stabilization energy below −15 kJ per (mol Si). The molecules forming the Pareto fronts are shown in Tables 6 and 7. The synthesis routes to the molecules with the lowest stabilization energy in BEA in both Pareto fronts are shown in Schemes 8 and 9.

Table 6 Molecules in the final Pareto front of the first de novo design run. Within the Pareto front, the molecules have been sorted according to their predicted stabilization energy in BEA. The numbers are the stabilization energy in BEA and, in parentheses, the gap in stabilization energy with respect to BEB. The values for the energy gaps larger than 2 kJ per (mol Si) have been a posteriori recalculated. The energies are in kJ per (mol Si)

---

Table 7 Molecules in the final Pareto front of the second de novo design run. Within the Pareto front, the molecules have been sorted according to their predicted stabilization energy in BEA. The numbers are the stabilization energy in BEA and, in parentheses, the gap in stabilization energy with respect to BEB. The values for the energy gaps larger than 2 kJ per (mol Si) have been a posteriori recalculated. The energies are in kJ per (mol Si)

---

Scheme 8 De novo design of dimers: Syn034407, the highest scoring molecule in the first de novo design run. The predicted stabilization energy for BEA is −16.8 kJ per (mol Si), the gap with respect to the stabilization energy in BEB is 1.0 kJ per (mol Si).

Scheme 9 De novo design of dimers: Syn025304, the highest scoring molecule in the second de novo design run. The predicted stabilization energy for BEA is −17.5 kJ per (mol Si), the gap with respect to the stabilization energy in BEB is 1.5 kJ per (mol Si).

Final selection

To design OSDAs that efficiently form BEA, we have decided to design molecules that have a stabilization energy in BEA below or equal to the threshold of −15 kJ per (mol Si). Additionally, we have established that differences in stabilization energy larger or equal to 2 kJ per (mol Si) distinguish well-fitting OSDA-zeolite pairs from ineffective ones.¹⁹ We therefore have selected from the results of the different design runs those putative OSDAs that have a stabilization energy in BEA equal to or below −15 kJ per (mol Si) and a stabilization energy in BEB that is at least 2 kJ per (mol Si) higher. After re-calculating the stabilization energies, we obtained a total of 212 putative ODSAs with a stabilization energy lower than or equal to −15 kJ per (mol Si) and an energy gap with respect to BEB larger than or equal to 2 kJ per (mol Si). The numbers of compounds with a BEA stabilization energy ≤ −15 kJ per (mol Si) and an energy gap with respect to BEB ≥ 2 kJ per (mol Si) found in each run are shown in Table 8. The last column of this table lists the number of Pareto optimal compounds found in each run.

Table 8 Designed OSDAs with a BEA stabilization energy ≤ −15 kJ per (mol Si) and an energy gap with respect to BEB ≥ 2 kJ per (mol Si). The second column lists the total number of molecular dynamics calculations in each run. Columns three and four list the number of molecules found with a BEA stabilization energy ≤ −15 kJ per (mol Si), and the number of molecules with a BEA stabilization energy ≤ −15 kJ per (mol Si) and an energy gap with respect to BEB ≥ 2 kJ per (mol Si), respectively. Column five is the number listed in column four divided by the number in column two multiplied by 1000. Column six lists the number of Pareto optimal compounds found in each run

run	MD runs	BEA ≤ −15 kJ	BEA ≤ −15 kJ and gap ≥ 2 kJ	BEA ≤ −15 kJ and gap ≥ 2 kJ per 1000 MD runs	Pareto
Exhaustive dimers	11 260	18	5	0.44	3
Stochastic dimers 1	5493	169	17	3.09	5
Stochastic dimers 2	18 962	571	95	5.01	4
de novo 1 molecules	5731	405	38	6.63	7
de novo 2 molecules	8122	436	57	7.02	9

---

Discussion

Promising compounds are compounds that have a predicted stabilization energy equal to or below −15 kJ per (mol Si) for BEA, and at the same time have an energy gap of at least 2 kJ per (mol Si) with respect to their score in BEB. We have identified a total of 212 of these compounds. Table 8 lists the number of such compound found in each of the five design runs. Column five of this table lists the number of promising compounds found per 1000 molecular dynamics calculations, which can be interpreted as a measure of effectiveness of the design method used. From these numbers, it can be seen that the stochastic virtual chemistry and de novo design protocols are more effective than the virtual screening. As stated in the methods section, the chemical search space of the de novo design algorithm covers an estimated 5.3 × 10¹⁵ compounds. The combinatorial chemistry algorithms explore a very limited subspace of this de novo design space. They use the same reagents database, but act on a single, manually selected synthesis route comprising a single reaction or a reaction sequence that is inspired by chemical intuition or, as in the present study, based upon experience. Even then, exhaustive combinatorial chemistry screening becomes intractable for all but very limited combinations of reagents and reactants. The exhaustive virtual combinatorial chemistry run we performed was not very effective in comparison with the heuristic runs, given that only 5 favorable OSDAs were found in 11 260 MD runs (Table 8). This is not surprising, as this algorithm is basically a random search. The motivation for performing exhaustive screening is ease of synthesis: dimerization using a single monomer previously determined to have a favorable zeolite stabilization energy was used to bias the random search towards good scoring dimers.

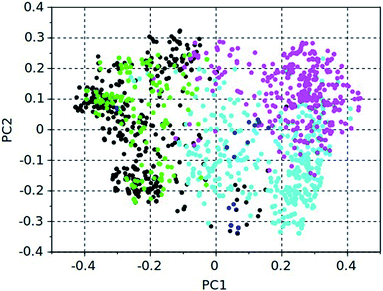
Both algorithms are multi-objective genetic algorithms that seek to generate a front of Pareto-optimal molecules, i.e. molecules that have both a low stabilization energy in BEA, and a large energy gap with respect to BEB. This is illustrated in Fig. 1. The color-coded dots in this figure represent all molecules with a stabilization energy below or equal to −15 kJ per (mol Si) found by the 5 design runs, and the solid lines represent the Pareto fronts for each run.

Fig. 1 BEA stabilization energies and BEA/BEB energy gaps of the molecules with a stabilization energy lower than or equal to −15 kJ per (mol Si) generated in the five design runs. The solid lines represent the Pareto fronts. Blue = exhaustive dimers run, green = stochastic dimers run 1, black = stochastic dimers run 2, magenta = de novo molecule run 1, cyan = de novo molecule run 2.

Table 8 also lists the numbers of compounds with a stabilization energy equal to or below −15 kJ per (mol Si) in BEA found in each run. Except for 23 compounds that were found in the two stochastic dimers runs, no overlap between these sets of compounds was found. This indicates that in each run, different parts of the chemical space were searched. A total of 1579 unique molecules were found that stabilize BEA with a stabilization energy equal to or below −15 kJ per (mol Si) BEA. How these cover the chemical space is illustrated in Fig. 2, which shows the first and second principal coordinates of the molecules as obtained from a Tanimoto similarity matrix. The compounds generated by the two stochastic dimers runs occupy the same region of the chemical space, which can be ascribed to the smaller search space of the stochastic algorithm, and which explains the overlap of 23 molecules between the search results. The two de novo design runs occupy relatively different regions of the chemical space.

Fig. 2 Principal coordinates of the Tanimoto similarity distance matrix of 1579 designed BEA OSDAs with stabilization energy below −15 kJ per (mol Si). Blue = exhaustive dimers run, green = stochastic dimers run 1, black = stochastic dimers run 2, magenta = de novo molecule run 1, cyan = de novo molecule run 2. The fractions of the variance captured in PC1 and PC2 are 0.26 and 0.11, respectively.

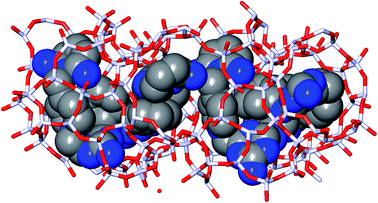
In the 5 design runs, the molecule with the lowest stabilization energy for BEA with an energy gap with respect to BEB larger than 2 kJ per (mol Si) is the third molecule listed in Table 6, with identifier Syn148049, which was generated in the first de novo design run. The stabilization energy in BEA is −16.4 kJ per (mol Si), and the energy gap with respect to BEB is 40.2 kJ per (mol Si). Fig. 3 shows the Van der Waals surface renderings of the unit cell of Syn148049 inside BEA and BEB. This figure shows in a qualitative way how the shape of the designed OSDA is highly complementary to the shape of BEA. In contrast, the channels of the BEB zeolite are not fully occupied by the guest molecule. Fig. 4 shows the position of the 4 distinct copies of Syn148049 in BEA in atomic detail.

Fig. 3 Van der Waals surface rendering of the unit cell of Syn148049 inside BEA (left) and BEB (right). The OSDA surfaces are in blue, the zeolite surfaces are in red. Both views are in the plane of the a and c crystallographic axes. The coordinates of both complexes are taken from the final MD runs used to calculate the stabilization energies.

Fig. 4 Syn148049 inside BEA. Four distinct copies of the designed OSDA are shown in CPK rendering with carbon atoms in gray and nitrogen atoms in blue. Of the zeolite, atoms within 5 Å from the selected OSDA copies are shown as sticks, with Si in white and O in red. The view is in the a-c place, with the chiral channel of BEA along the X-axis. The coordinates the complex are taken from the final MD run used to calculate the stabilization energy.

In efforts to synthesize BEA enriched zeolite beta, a number of ODSAs have been investigated.^{11,14,15,34,36} From these references, we selected those OSDAs reported to be effective in BEA formation and calculated their stabilization energies. These were obtained by fitting 4, 6, and 8 copies of the OSDAs in BEA and performing the MD simulation. The lowest stabilization energies obtained for the OSDAs as well as the corresponding number of copies in BEA are listed in Table 9. The lowest stabilization energy is −14.1 kJ per (mol Si) for compound B82, with 6 OSDA copies in BEA. The lowest stabilization energy for a compound with 4 OSDA copies in BEA is −13.3 kJ per (mol Si) for compound E96. Both compounds are shown in Fig. 5. It may be appreciated that the stabilization energies of the compounds designed in this work are significantly lower than the stabilization energies of the existing OSDAs.

Table 9 Stabilization energies of documented BEA forming OSDAs

Compound	Reference	Stabilization energy (kJ per (mol Si))	Copies in BEA
B82	34	−14.1	6
iPenMP	36	−13.6	6
iProMP	36	−13.5	8
B71	34	−13.4	6
E96	34	−13.3	4
EDMCHOH	11	−13.3	6
iButMP	36	−13.2	6
E95	34	−13.1	4
B204	34	−13.1	4
A07	34	−12.9	6
B75	34	−12.7	6
TMCHOH	11	−12.7	6
B108	34	−12.6	4
A61	34	−12.6	6
B172	34	−12.5	6
E32	34	−12.1	4
B203	34	−12.0	6
E39	34	−11.6	4
B27	34	−11.6	6
B130	34	−11.6	6
B08	34	−11.6	4
DMDPOH	11	−11.4	8
A69	34	−11.4	4
B81	34	−11.3	4
A60	34	−11.2	6
E51	34	−11.0	4
B125	34	−10.8	4
A70	34	−10.7	4
TEA	14 and 15	−10.7	6
G101	34	−10.0	4
DMPOH	11	−10.0	6

---

Fig. 5 Best scoring OSDAs from ref. 11, 14, 15, 34 and 36, their stabilization energy in BEA, and the corresponding number of copies in BEA.

In the studies described in ref. 34, 36, both BEA forming and non-BEA forming OSDAs are reported. We computed that the BEA-forming OSDAs have an average stabilization energy of −12.1 ± 1.0 kJ per (mol Si). The average stabilization energy of the non-BEA forming OSDAS is −10.8 ± 1.7 kJ per (mol Si). While the formation of BEA does not solely depend on the OSDA used but also on the specific reaction parameters and the stabilization energy in other zeolite structures, the observation that the experimentally BEA forming OSDAs have lower calculated stabilization energies lends support to our scoring protocol.

In the present study, we have used all-silica models of the zeolites BEA and BEB. The use of zeolites as catalysts depends on the presence of charge centers that act as Lewis acids and that are provided by replacement of Si atoms by metals such as Al and Cu. As more detailed studies on the reaction mechanisms become available from quantum mechanical studies, e.g. (ref. 37), it will become interesting to influence and steer the siting of these metallic sites with the aid of computational design strategies such as detailed in the present study. This would require, to begin with, the inclusion of a Coulomb energy term in the calculation of the OSDA-zeolite stabilization energies in addition to the currently used Van der Waals potential. We will address this problem in future research.

While zeolite beta consists of a close intergrowth of the BEA and BEB polymorphs, in our design model we consider the interaction of putative OSDAs with perfect BEA and BEB structures. Increase of BEA content of zeolite beta can be achieved either by an increase in the occurrence of small BEA domains, or the presence of larger BEA domains. Structural characterization of BEA-enriched zeolite beta has shown that the enrichment involves the presence of larger BEA domains in this material.¹¹ We can therefore assume that OSDAs interacting favorably with pure BEA can effectively lead to BEA enriched zeolite beta.

Our de novo design program generates not only chemically correct molecular structures, but also virtual synthesis routes from well-established organic chemistry reactions and available building blocks. While the proposed synthesis routes may not be the most efficient ones to produce their outcome, it has been shown that on average approximately two thirds of the routes are feasible with reasonable effort.²⁹ Our method to computationally design OSDAs has been validated in previous studies. In a first study, as a proof of principle, a novel OSDA for STW zeolite was designed, synthesized and successfully used to produce the target zeolite.²¹ Next, a novel OSDA was designed, synthesized and successfully used to produce zeolite SSZ-39 under highly variable reaction conditions.²⁰ Also, an alternative, cheaper OSDA that produced zeolite SSZ-52, a zeolite that has potential application in engine exhaust clean-up, was designed.¹⁹ Finally, using the Pareto based multi-objective approach also deployed in the present study, a chiral OSDA to generate, for the first time, enantiomerically enriched STW zeolite was discovered.²² In the present study, a large but tractable number of putative OSDAs to selectively guide the synthesis of BEA were obtained using the combined methods of de novo design, virtual screening, exhaustive combinatorial chemistry and stochastic combinatorial chemistry. From these compounds, those that can be synthesized with the least effort and cost can be chosen for synthesis and zeolite formation.

Conclusion

We have designed several putative OSDAs that have the potential to form zeolite beta enriched in the BEA polymorph. The in silico design approaches we have used consider the synthetic accessibility of the proposed molecules. In total, we have found 212 OSDAs with a stabilization energy in zeolite beta A lower than −15 kJ per (mol Si) and an energy gap greater than 2 kJ per (mol Si) with respect to zeolite beta B. These compounds are promising putative OSDAs for nucleation and growth of the zeolite beta A polymorph.

Conflicts of interest

MWD consults for the petrochemical industry on zeolites; this relationship had no impact on these results. FD also works for FD Computing BVBA; this relationship had no impact on these results.

Acknowledgements

This work was supported by the US Department of Energy Basic Sciences Separation Sciences by grant number DE-SC0019324 and by the Welch Foundation by grant number C-1917-20170325.

References

1. D. W. Breck, Zeolite molecular sieves: structure, chemistry and use, Wiley, NewYork, 1973, ISBN 0471099856.
2. C. Baerlocher and L. B. McCusker, Database of Zeolite Structures, htttp://www.iza-structure.org/databases/.
3. Y. Li and J. Yu, New Stories of Zeolite Structures: Their Descriptions, Determinations, Predictions, and Evaluations, Chem. Rev., 2014, 114(14), 7268–7316.
4. Introduction to Zeolite Science and Practice, ed. J. Cejka, H. van Bekkum, A. Corma and F. Schuth, Elsevier, New York, 3rd edn, 2007, vol. 168.
5. W. Vermeiren and J. P. Gilson, Impact of Zeolites on the Petroleum and Petrochemical Industry, Top. Catal., 2009, 52, 1131–1161.
6. Zeolites in Industrial Separation and Catalysis, ed. S. Kulprathipanja, 2010, ISBN: 978-3-527-32505-4.
7. B. M. Lok, T. R. Cannan and C. A. Messina, The Role of Organic Molecules in Molecular Sieve Synthesis, Zeolites, 1993, 3(4), 282–291.
8. R. L. Wadlinger, G. T. Kerr and E. J. Rosinski, Catalytic composition of a crystalline zeolite, US Pat. no. 3,308,069, 1967.
9. J. M. Newsam, M. M. J. Treacy, W. T. Koetsier and C. B. de Gruyter, Structural Characterization of Zeolite Beta, Proc. R. Soc. A, 1988, 420, 375–408.
10. J. B. Higgins, R. B. LaPierre, J. L. Schlenker, A. C. Rohrman, J. D. Wood, G. T. Kerr and W. J. Rohrbaugh, The framework topology of zeolite-Beta, Zeolites, 1988, 8, 446–452.
11. M. Tong, D. Zhang, W. Fan, J. Xu, L. Zhu, W. Guo, W. Yan, J. Yu, S. Qiu, J. Wang, F. Deng and R. Xu, Synthesis of polymorph A-enriched zeolite Beta with an extremely concentrated fluoride route, Sci. Rep., 2015, 5, 11521.
12. T. Lu, R. Xu and W. Yan, Co-templated synthesis of polymorph A-enriched zeolite beta, Microporous Mesoporous Mater., 2016, 226, 19–24.
13. T. Lu, L. Zhu, X. Wang, W. Yan, W. Shi and R. Xu, A green route for the crystallization of a chiral polymorph A-enriched zeolite beta, Inorg. Chem. Front., 2018, 5, 802–805.
14. T. Lu, L. Zhu, W. Yan, W. Shi and R. Xu, Identification of the key factor promoting the enrichment of chiral polymorph A in zeolite beta and the synthesis of chiral polymorph A highly enriched zeolite beta, Inorg. Chem. Front., 2018, 7, 1640–1645.
15. G. Zhang, B. Wang, W. Zhang, M. Li and Z. Tian, Synthesis of polymorph A-enriched beta zeolites in a HF-concentrated system, Dalton Trans., 2016, 45, 6634–6640.
16. C. Perego and P. Ingallina, Recent advances in the industrial alkylation of aromatics: new catalysts and new processes, Catal. Today, 2002, 73, 3–22.
17. M. E. Davis and R. F. Lobo, Zeolite and molecular sieve synthesis, Chem. Mater., 1992, 4, 756–768.
18. D. W. Lewis, C. M. Freeman and C. R. A. Catlow, Predicting the Templating Ability of Organic Additives for the Synthesis of Microporous Materials, J. Phys. Chem., 1995, 99(28), 11194–11202.
19. T. M. Davis, A. T. Liu, C. Lew, D. Xie, A. Benin, S. Elomari, S. I. Zones and M. W. Deem, Computationally-Guided Synthesis of SSZ-52, a Zeolite for Engine Exhaust Clean-up, Chem. Mater., 2016, 28, 708–711.
20. J. E. Schmidt, M. W. Deem, C. M. Lew and T. M. Davis, Computationally-Guided Synthesis of the 8-Ring Zeolite AEI, Top. Catal., 2015, 58, 410–415.
21. J. E. Schmidt, M. W. Deem and M. E. Davis, Synthesis of a Specified, Silica Molecular Sieve using Computationally Predicted Organic Structure Directing Agents, Angew. Chem., Int. Ed., 2014, 53, 8372–8374.
22. S. K. Brand, J. E. Schmidt, M. W. Deem, F. Daeyaert, Y. Ma, O. Terasaki, M. Orazova and M. E. Davis, Enantiomerically Enriched, Polycrystalline Molecular Sieves, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5101–5106.
23. Y. Kubota, M. M. Helmkamp, S. I. Zones and M. E. Davis, Properties of organic cations that lead to the structure-direction of high-silica molecular sieves, Microporous Mater., 1996, 6, 213–229.
24. W. E. Hart, T. E. Kammeyer and R. K. Belew, Foundations of Genetic Algorithms III, Morgan Kauffman, San Francisco CA, 1994.
25. T. A. Halgren, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17, 490–519.
26. Y. Lin and M. A. Stadtherr, Deterministic global optimization of molecular structures using interval analysis, J. Comput. Chem., 2005, 26, 1413–1420.
27. R. Pophale, F. Daeyaert and M. W. Deem, Computational prediction of chemically synthesizable organic structure directing agents for zeolites, J. Mater. Chem. A, 2013, 1, 6750–6760.
28. J. D. Gale, GULP – a computer program for the symmetry adapted simulation of solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637.
29. H. M. Vinkers, M. R. de Jonge, F. F. Daeyaert, J. Heeres, L. M. Koymans, J. H. van Lenthe, P. J. Lewi, H. Timmerman, K. Van Aken and P. A. Janssen, SYNOPSIS: SYNthesize and OPtimize System in Silico, J. Med. Chem., 2003, 46, 2765–2773.
30. F. Daeyaert and M. W. Deem, A Pareto Algorithm for Efficient De Novo Design of Multi-Functional Molecules, Mol. Inf., 2017, 36, 1600044.
31. F. Daeyaert and M. W. Deem, In silico design of chiral dimers to direct the synthesis of a chiral zeolite, Mol. Phys., 2018, 116, 2836–2855.
32. J. C. Gower, Some distance properties of latent root and vector methods used in multivariate analysis, Biometrika, 1966, 53, 325–338.
33. T. Tanimoto, An Elementary Mathematical theory of Classification and Prediction, IBM Internal Report, 1958.
34. S. I. Zones, S.-J. Hwang, S. Elomari, I. Ogino, M. E. Davis and A. W. Burton, The fluoride-based route to all-silica molecular sieves: a strategy for synthesis of new materials based upon close-packing of guest–host products, C. R. Chim., 2005, 8, 267–282.
35. https://reaxys.emolecules.com .
36. F. Taborda, T. Wilhammar, Z. Wang, C. Montes and X. Zou, Synthesis and characterization of pure silica zeolite beta obtained by an aging–drying method, Microporous Mesoporous Mater., 2011, 143(1), 196–205.
37. Y. Horbatenko, J. P. Perez, P. Hernandez, M. Swart and M. Sola, Reaction mechanisms for the formation of mono- and dipropylene glycol from the propylene oxide hydrolysis over ZSM-5 zeolite, J. Phys. Chem., 2014, 118, 21852–21962.

---

Footnote

† Electronic supplementary information (ESI) available: A .sdf file containing the 212 compounds with a stabilization energy in zeolite beta A lower than −15 kJ per (mol Si) and an energy gap greater than 2 kJ per (mol Si) with respect to zeolite beta B. See DOI: 10.1039/c8ta11913a

---