Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Droplet leaping governs microstructured surface wetting†
Susumu
Yada
a,
Shervin
Bagheri
 *a,
Jonas
Hansson
b,
Minh
Do-Quang
a,
Fredrik
Lundell
a,
Wouter
van der Wijngaart
b and
Gustav
Amberg
ac
*a,
Jonas
Hansson
b,
Minh
Do-Quang
a,
Fredrik
Lundell
a,
Wouter
van der Wijngaart
b and
Gustav
Amberg
ac
aDepartment of Mechanics, KTH Royal Institute of Technology, 100 44 Stockholm, Sweden. E-mail: shervin@mech.kth.se
bDivision of Micro and Nanosystems, KTH Royal Institute of Technology, 100 44 Stockholm, Sweden
cSödertorn University, Stockholm, Sweden
First published on 5th November 2019
Abstract
Microstructured surfaces that control the direction of liquid transport are not only ubiquitous in nature, but they are also central to technological processes such as fog/water harvesting, oil–water separation, and surface lubrication. However, a fundamental understanding of the initial wetting dynamics of liquids spreading on such surfaces is lacking. Here, we show that three regimes govern microstructured surface wetting on short time scales: spread, stick, and contact line leaping. The latter involves establishing a new contact line downstream of the wetting front as the liquid leaps over specific sections of the solid surface. Experimental and numerical investigations reveal how different regimes emerge in different flow directions during wetting of periodic asymmetrically microstructured surfaces. These insights improve our understanding of rapid wetting in droplet impact, splashing, and wetting of vibrating surfaces and may contribute to advances in designing structured surfaces for the mentioned applications.
1 Introduction
Natural surfaces with texture provide organisms the ability to control liquid transport in fascinating ways. For example, lotus leaves have hierarchically structured surfaces that ease droplet removal.1,2 The “pitcher plant” Nepenthes alata has wettable asymmetric microridges on their peristomes that make the surface slippery and aid in catching insects efficiently.3,4 Ryegrass leaves have inclined protrusions which help them to shed water unidirectionally.5 Cacti in deserts gather water through thorns with surface structures that collect fog effectively.6Understanding how liquids act on non-smooth surfaces has also become increasingly important in technological processes, such as printing, coating, adhesion, mixing, and sorting.7 In particular, natural surfaces have inspired the fabrication of micro- and nanoscopic topographies where asymmetric structures are introduced to enable capillary-driven directional liquid transport.8–10 Chu et al.8 first demonstrated that droplets can spread unidirectionally on arrays of asymmetric nanorods. Various applications of asymmetric-structured surfaces have been reported since, including mixing in microreactors,11 oil–water separation,12 and transport in microfluidic channels.13
The spreading of a liquid droplet over a textured surface has thus far been analyzed in the slow late spreading regime (≈100 ms to few seconds).8,11,14–16 The details and mechanisms of such spreading have been described in terms of contact-line pinning,3,16 Laplace pressure,11,16,17 and gradients in surface energy.18,19 Also, numerical simulations have provided valuable insights into the spreading mechanisms in the late regime.20,21 However, the rapid wetting that precedes this late spreading is not well understood. Rapid wetting is crucial for droplet impact on solid surfaces,22,23 or in situations where time scales are imposed externally, such as wetting phenomena in the presence of vibrations.24
Here, we theoretically, experimentally and numerically investigate rapid wetting on microstructures. We consider the dynamics of the leading contact line on slanted ridges in a two dimensional plane. We elucidate how the contact line follows the microstructures and explain and predict the effect of the geometry on the spreading speed.
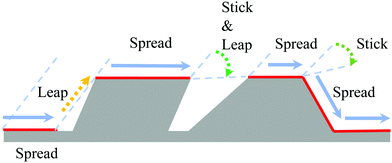
We hypothesize that three wetting regimes determine the contact line velocity and that wetting can be understood from the succession of these regimes as the contact line travels over the surface (Fig. 1). The first regime, called spread, is the movement of the contact line on a homogeneous surface with a velocity determined by surface chemistry and liquid–gas properties.25,26 The second regime, called stick, refers to the pinning of the contact line on surface corners, resulting in a temporarily stationary contact line.27 Both spread and stick regimes are well understood15,27,28 in contrast to the third phenomenon we observed and that we call leap. Contact line leaping involves the establishment of a new contact line downstream of the wetting front when the liquid leaps over specific sections of the solid surface, trapping gas between the solid and the liquid. As the surface wets, the wetting regimes can follow each other in any order, as illustrated in Fig. 1.
2 Experiments and methods
2.1 Experimental set-up
Spontaneous droplet spreading is recorded using a high-speed camera (DANTEK dynamics Speedsense M) at a frame rate of 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044 per second. A water droplet develops from a needle with an outer diameter of 0.31 mm (Hamilton, gauge 30, point style 3) and starts to spread spontaneously immediately after it touches a substrate. Water is pumped by a syringe pump (Cetoni, neMESYS 1000N) at a flow rate 0.04 μl s−1. The flow rate is so small that a static state is assumed before the droplet touches the surface. The initial radius of the droplet R0 is determined by the distance between the needle and the surface and fixed to 0.4 mm. The scope is composed of 128 × 128 pixels, which leads to a spatial resolution of ≈8 μm. As seen in Fig. 3(c), owing to the limited spatial resolution, the observed droplet has a finite spreading radius even before it actually touches the substrate. In order to estimate the initial time t0 in which the droplet starts to spread, a power-law curve r = C(t − t0)γ is fitted to the time history of the observed spreading radius where C, γ, and t0 are scalar parameters. The initial time is then determined by shifting the original spreading time by t0.
044 per second. A water droplet develops from a needle with an outer diameter of 0.31 mm (Hamilton, gauge 30, point style 3) and starts to spread spontaneously immediately after it touches a substrate. Water is pumped by a syringe pump (Cetoni, neMESYS 1000N) at a flow rate 0.04 μl s−1. The flow rate is so small that a static state is assumed before the droplet touches the surface. The initial radius of the droplet R0 is determined by the distance between the needle and the surface and fixed to 0.4 mm. The scope is composed of 128 × 128 pixels, which leads to a spatial resolution of ≈8 μm. As seen in Fig. 3(c), owing to the limited spatial resolution, the observed droplet has a finite spreading radius even before it actually touches the substrate. In order to estimate the initial time t0 in which the droplet starts to spread, a power-law curve r = C(t − t0)γ is fitted to the time history of the observed spreading radius where C, γ, and t0 are scalar parameters. The initial time is then determined by shifting the original spreading time by t0.
2.2 Sample preparation
The microstructured surfaces are made from Ostemer 220 (Mercene Labs, Stockholm, Sweden), a UV-curing Off-Stoichiometry-Thiol–Ene (OSTE) resin, with excellent lithographic patterning, previously used to create complex slanted structures.29 The samples are manufactured as follows. First, a flat Ostemer layer is manufactured on a smooth plastic film. Second, slanted Ostemer ridges are patterned on the base layer by exposing slanted UV light through a patterned photomask. After rinsing the surfaces in an Acetone bath to remove uncured OSTE, surface modification is performed to hydrophilize the surface (equilibrium contact angle θe ≈ 50° on a flat substrate) in order to achieve partial wetting. The surface structures are characterized by scanning electron microscopy as shown in Fig. S1 (ESI†). The inclination of the ridges β is 60° for all the structures. The samples used in this work are labeled as (W, P) where W and P are the width and pitch of the ridge in micrometers, respectively (see the inset in Fig. 3(a) for definition), and listed in Table 1.| Label | W | P | H | S against | S with |
|---|---|---|---|---|---|
| (10, 15) | 10 | 15 | 14 | 1.39 ± 0.10 | 1.21 ± 0.06 |
| (10, 20) | 10 | 20 | 14 | 1.61 ± 0.15 | 1.30 ± 0.11 |
| (10, 30) | 10 | 30 | 14 | 3.07 ± 0.50 | 4.66 ± 0.71 |
| (15, 23) | 15 | 23 | 14 | 1.30 ± 0.12 | 1.13 ± 0.07 |
| (15, 30) | 15 | 30 | 14 | 1.43 ± 0.11 | 4.12 ± 0.58 |
| (15, 45) | 15 | 45 | 14 | 3.11 ± 0.67 | 6.3 ± 1.4 |
| (20, 30) | 20 | 30 | 15 | 1.99 ± 0.33 | 5.19 ± 0.84 |
| (20, 40) | 20 | 40 | 17 | 3.77 ± 0.44 | 5.5 ± 1.7 |
| (20, 60) | 20 | 60 | 17 | 1.80 ± 0.36 | 5.06 ± 0.62 |
2.3 Navier–Stokes–Cahn–Hilliard equations
The Navier–Stokes equations combined with the phase-field approach (the Cahn–Hilliard equation) are solved to simulate the droplet wetting on a comparable geometry to the experiments. The incompressible Navier–Stokes equations are given by | (1) |
| ∇·u = 0. | (2) |
The Cahn–Hilliard equation is given by
 | (3) |
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200. The surface tension σ is fixed to 0.073 N m−1, which gives a capillary speed σ/μ = 73 m s−1 employed as the characteristic velocity U, and leads to Ca = 1. The mass diffusivity D in the Peclet number is set to 5.7 × 10−6 m2 s−1, which leads to Pe = 5120. The interface thickness ε is set to 2 μm, and results in Cn = 5 × 10−3. The interface is thicker than the actual physical interface but it is sufficiently thin compared to the structures in order not to influence the simulated results. The choices of the Peclet number and the Cahn number do not influence the results for sufficiently thin interface and small mass diffusivity.32 The line friction parameter μf is obtained by fitting25,31 the simulated spreading radius with the experiments on a smooth substrate and found to be μf = 0.10 Pa s (see Fig. S2, ESI†).
200. The surface tension σ is fixed to 0.073 N m−1, which gives a capillary speed σ/μ = 73 m s−1 employed as the characteristic velocity U, and leads to Ca = 1. The mass diffusivity D in the Peclet number is set to 5.7 × 10−6 m2 s−1, which leads to Pe = 5120. The interface thickness ε is set to 2 μm, and results in Cn = 5 × 10−3. The interface is thicker than the actual physical interface but it is sufficiently thin compared to the structures in order not to influence the simulated results. The choices of the Peclet number and the Cahn number do not influence the results for sufficiently thin interface and small mass diffusivity.32 The line friction parameter μf is obtained by fitting25,31 the simulated spreading radius with the experiments on a smooth substrate and found to be μf = 0.10 Pa s (see Fig. S2, ESI†).
3 Wetting mechanism
3.1 Wetting regimes
For wetting of structured surfaces, the combination of spread, stick and leap that ultimately determines the contact-line speed depends on the relation between the globally observed apparent dynamic contact angle θg, and the corner angle of the surface, α (Fig. 2). The former angle is the apparent angle between the solid and the liquid–gas interface measured from the wetted side in the vicinity of the contact line. The corner angle defines the local corner of the surface structure that is approached by a moving contact line (see the insets in Fig. 2). For the rapid wetting considered here, the contact line movement is driven by Young's force per unit length of a contact line FY ∼ σ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe − cos
θe − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θg). During spontaneous spreading, we have θe < θg < π.
θg). During spontaneous spreading, we have θe < θg < π.
Three different spreading mechanisms can be distinguished (Fig. 2): (i) a spread-and-leap behavior of the contact line when θg > α; (ii) a stick-and-leap behavior of the contact line when θg < α − π + θe, and; (iii) continuous spreading driven by FY for intermediate corner angles α − π + θe < θg < α. For spread-and-leap, the moving contact line leaps from the valley to the nearest ridge, leaving behind some dry surface. For stick-and-leap, the contact line is held pinned33 at the corner while the liquid–air interface above the pinning site bulges due to inertial forces. If there exists a rise of the surface sufficiently nearby, the interface eventually makes contact with the next rise in the texture, resulting in a leap that leaves dry the entire valley between the pinning position and the new contact line. For intermediate angles, where no leaping occurs and the liquid wets the dry solid, the contact line speed varies with the slope of the surface. In particular, a reduced speed is expected in downward-sloping sections of the surface, compared to flat sections, due to a reduced Young's force FY.
3.2 Experimental and numerical observations
We experimentally investigated wetting of asymmetric ridges by depositing a water drop of radius 0.4 mm on the surfaces and recording the first 1.2 ms of wetting using a high-speed video camera (Fig. 3(a)). We also numerically simulated spreading of droplets on axisymmetric textured surfaces with the same height, pitch and angle as in our experiments using a phase-field approach.30,34Fig. 3(c) shows a time sequence of a water drop spreading on a surface with W = 20 μm, P = 60 μm, and H = 17 μm. The experiments reveal the asymmetric evolution of the droplet spreading on the structure; the contact line travels faster against the inclination (passing five ridges in 0.5 ms) than with the inclination (passing two ridges in 0.5 ms). Our numerical simulations reproduce the experimental droplet shapes and the apparent contact line velocity with respect to the spreading radius (see Fig. S3 and Movie S1, ESI†). This agreement between the experiment and the numerical model allows us to rely on the simulations for understanding the detailed contact line movement across the textured surface.
The difference between the wetting dynamics in the two directions results from the difference in the wetting regimes. Fig. 3(b) shows a time sequence of the liquid–gas interface as the droplet travels against the direction of inclination over one ridge. Fig. 3(e) shows how the corresponding contact line velocity varies during the same time interval. Note that our optical resolution leads to experimental errors in the order of 0.1 m s−1. The fluctuations of the simulated velocities in Fig. 3(e and f) arise from post-processing.
We observe a fast spread on ridge tips (A1 → A2), slower spread while descending into the valley (A2 → A3), and finally an increase in speed with a spread-and-leap to the next ridge (A3 → A4 → A5). During the process of moving from A1 to A5, the simulation-predicted apparent dynamic contact angle is in the range of θg = 140° to θg = 120° (Fig. S4, ESI†), whereas the corner angles encountered by the moving contact line have the values α = 180° (A1), 240° (A2), 120° (A3), and 60° (A4–A5). The velocity between A3–A4 is lower than that between A1–A2, since the contact line must be accelerated to reach spreading velocity on a flat surface. Thus, our numerical observations conform with the kinematic map in Fig. 2, explaining the mechanisms behind the peaks and troughs of the contact line speed.
Fig. 3(d) shows spreading in the direction with the inclination over one periodic structure. The corresponding contact line speed (Fig. 3(f)) has a distinct slow–fast–slow spreading velocity going from point W1 to point W4. This velocity profile corresponds to the stick-and-leap (W1 → W2) at the corner W1, followed by fast spread on the flat top of the ridge (W2 → W3) and then again followed by the stick-and-leap (W3 → W4). As the liquid front moves from W1 to W3, the apparent dynamic contact angle varies from θg = 160° to θg = 130° (Fig. S4, ESI†). The stick-and-leap follows from θg < α − π + θe = 170° at the corners W1 and W3.
Further insight into the contact-line speed can be obtained by characterizing the driving and resisting forces during initial wetting. The Young's force driving the contact line can be balanced by an inertial force FI ∼ ρUflat2R or a contact line friction force Ff ∼ μfUflat, where Uflat is a characteristic contact line speed on a smooth surface. The contact line friction is related to non-hydrodynamic energy dissipation at the contact line, connected to molecular scale processes represented by the line friction parameter, μf.30,35 The viscous resistance associated with bulk liquid viscosity (μ) can be neglected in the early stages of wetting since μf ≫ μ.26
The Ohnesorge number based on the line friction parameter,  , expresses the relative importance of line friction and fluid inertia. For a water droplet of radius R0 = 0.4 mm, Ohf ≈ 0.6, where we computed the contact line friction to μf = 0.10 Pa s by combining experiments and numerical simulations (see Section 2 and Fig. S2, ESI† for details). Since Ohf is of order one, both inertia and contact line friction may be involved in resisting the spreading. However, they play very different roles during spread-and-leap compared to stick-and-leap. As we will show in the following, in the former regime line friction dominates, whereas, in the latter, inertial forces determine the contact-line speed.
, expresses the relative importance of line friction and fluid inertia. For a water droplet of radius R0 = 0.4 mm, Ohf ≈ 0.6, where we computed the contact line friction to μf = 0.10 Pa s by combining experiments and numerical simulations (see Section 2 and Fig. S2, ESI† for details). Since Ohf is of order one, both inertia and contact line friction may be involved in resisting the spreading. However, they play very different roles during spread-and-leap compared to stick-and-leap. As we will show in the following, in the former regime line friction dominates, whereas, in the latter, inertial forces determine the contact-line speed.
4 Influence of the pitch on spreading speed
4.1 Passage time ratio
Fig. 4(a) shows the experimental spreading radius evolution in the direction against the inclination for surfaces with different widths (W) and pitches (P). We observe that the spread on structured surfaces is always slower compared to that on a smooth surface (solid line). To characterize the spread-and-leap regime quantitatively, we define the passage time ratio, | (5) |
4.2 Model and scaling analysis
The non-monotonic behavior in Fig. 4(b) for W = 20 μm can be explained by characterizing leaping over the microstructures in more detail. For a smooth flat surface, the passage time over a distance P can be estimated as Tflat ∼ P/Uflat, where Uflat is the average contact-line velocity. For a surface with ridges, the wetted distance Ws per period can be estimated as Ws ≈ 2r1H + r2P + (1 − r2)W. Here, r1 and r2 represent the wetted portions of the vertical walls of the ridge and the valley between the ridges, respectively (see Fig. 5(a)). The time it takes for the contact line to move a distance P is Ts ∼ Ws/Us, where Us is the pitch-averaged contact-line velocity. By inserting the scaling estimates for Ts and Tflat in eqn (5), we obtain,
 | (6) |
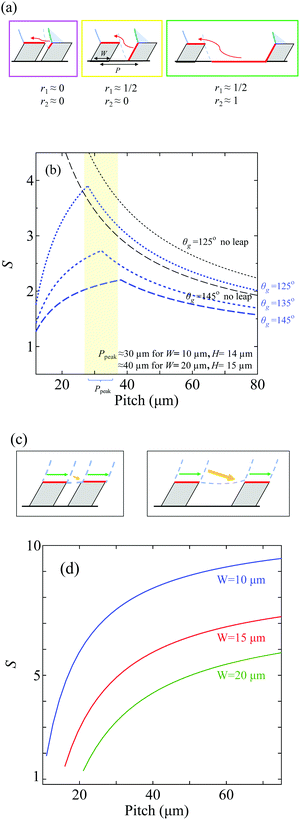 | ||
| Fig. 5 (a) Sketches illustrating wetting situation in the direction against the inclination for small (left, r1 ≈ r2 ≈ 0), intermediate (center, r1 ≈ 1/2, r2 ≈ 0) and large (right, r1 ≈ 1/2, r2 ≈ 1) pitch. The wetted sections are colored red. (b) The passage time ratio S in the direction against the inclination based on eqn (9) for W = 10 μm as a function of surface pitch. The blue lines correspond to S obtain from the theoretical model for different apparent dynamic contact angles (θg = 125°, 135°, and 145°). The black line corresponds to passage times S that would exist without leaping, i.e. assuming that the structured surface is wetted everywhere. Without leaping, spreading becomes very slow for a small pitch, which contradicts the experimental observations where leaping will significantly increase the spreading speed. (c) Sketches illustrating the wetting situation in the direction with the inclination for small (left) and large (right) pitches. (d) The passage time ratio S in the direction with the inclination based on eqn (13) for surface ridges of different widths as a function of surface pitch. | ||
To be more quantitative, we consider the local contact line velocity based on phase field theory. As discussed in Section 3.1, the spreading in the direction against the inclination is in spread-and-leap regime. In this regime, we assume that Young's force is driving the contact line and the line friction is the resistive force. Assuming that wetting resistance for spread-and-leap is dominated by line friction, we can develop a theoretical model of the contact-line velocity based on the Navier–Stokes–Cahn–Hilliard equations,36,37
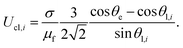 | (7) |
 | (8) |
 | (9) |
Fig. 5(b) shows the dependence of S on the pitch obtained from the model for three different local dynamic contact angles. We observe that the model captures the trend of the resistance due to surface texture relatively well, confirming that line-friction is the dominating physical resistance for the spreading. The spread-and-leap model explains the – perhaps counter-intuitive – fast spreading for small pitch. Without taking into account the leaping, a spreading model where all solid is wetted will overestimate S significantly (Fig. 5(b)). The model also predicts the pitch that gives the maximum S, Ppeak. For W = 10 μm, Ppeak is 32 μm, for W = 15 μm, Ppeak is 39 μm and for W = 20 μm (obtained assuming θg = 135°) Ppeak is 43 μm. The estimate of Ppeak explains why the non-monotonic behaviour is observed only for W = 20 μm. For W = 10 μm and 15 μm, each P is below Ppeak. However for W = 20 μm, Ppeak is close to the intermediate pitch 40 μm, and therefore the non-monotonic behavior is observed. The existence of the peak for surfaces W = 10 μm and W = 15 μm can be confirmed from two observations: (i) S > 1 for small values of the pitch (Fig. 4(b)) and (ii) S → 1 with increasing pitch (since an extremely large pitch is approximately a smooth surface, S ≈ 1).
4.3 Scaling analysis for the stick-and-leap regime
The spreading in the direction with the inclination is in the stick-and-leap regime. The contact line travels on the tip of the ridges and is pinned on the corner intermittently, and the interface bulges by the liquid inertia until it makes a new contact with the next structure. To understand the role of pinning, we perform a simple scaling analysis. In the direction with the inclination, Young's force is balanced both by inertia and line friction. Here, Young's force accelerates the spreading motion when the contact line is pulled over the structure (W2 → W3 in Fig. 3(f)) and then adds to the droplet inertia. When the contact line reaches the acute corner at W3, it is momentarily pinned there. The contact line remains pinned until the inertia in the droplet brings the local dynamic contact angle out of equilibrium such that the droplet interface can make contact with the solid in the forward direction. Here, we note that the change of dynamic contact angle is driven by the inertial force, since the contact line is pinned at the corner and other forces are required to move the interface outwards. Therefore, we assume that the interface is driven by the inertia of the droplet and do not take the influence of the dynamic contact angle into consideration.Assuming the work done by Young's force at the contact line (F ∼ 2πR0σ) is distributed as kinetic energy over a whole droplet during the spreading on the top of the ridge, we have
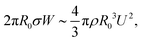 | (10) |
 | (11) |
 in eqn (11) can be neglected for simplicity.
in eqn (11) can be neglected for simplicity.
Based on this physical insight as depicted in Fig. 5(c), we can model the passage time for stick-and-leap as
 | (12) |
 | (13) |
 . In our scaling analysis, we have assumed that this saturation value is reached when the liquid–gas interface remains pinned at the acute corner infinitely long.
. In our scaling analysis, we have assumed that this saturation value is reached when the liquid–gas interface remains pinned at the acute corner infinitely long.
Fig. 5(d) presents S obtained from eqn (13) for different ridge widths. We observe that the scaling estimates for stick-and-slip correctly capture the trend of increasing passage time with increasing pitch. The scaling analysis shows that inertia plays a central role in the stick-and-leap regime, in contrast to spread-and-leap in the direction against inclination. The surface energy is converted to the kinetic energy of the droplet (∼inertia) while the contact line spreads on the top of the ridge, and inertia drives the liquid front to reach the next rise of the surface during the stick-and-leap at the corners (W2 in Fig. 3(f)).
We note that the advancement of the contact line is primarily determined by the line friction and the geometrical details of the structure when moving against the inclination, but that it is inertial when moving with the inclination.
5 Conclusions
We have presented a comprehensive study of rapid wetting on complex asymmetric microstructures. We identified three wetting regimes, denoted as spread, stick, and leap. By coordinated simulations and experiments we can follow the passage of the contact line over the microstructure in detail and formulate a model and scaling estimates that explain how the geometrical features determine the macroscopic wetting speed. We showed that when wetting proceeds against the inclination of the ridges, a spread-and-leap behavior underpins the wetting and the driving Young's force is primarily balanced by the contact line friction. In contrast, when the spreading direction is with the inclination, a stick-and-leap behavior is observed, and it is the liquid inertia that limits the wetting speed. Our experiments and theory show that the leaping phenomenon plays a central role in increasing the spreading speed compared to a surface textured without leaping. We believe that this newly identified spreading mechanism forms the foundation to design surface structures for controlling wetting in realistic unsteady environments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swedish Research Council (VR 2015-04019). S. B. acknowledges the support of the Swedish Foundation of Strategic Research (SSF-FFL6). We thank Calvin J. Brett at KTH for his kind help for SEM measurements.References
- M. Liu, S. Wang and L. Jiang, Nat. Rev. Mater., 2017, 2, 17036 CrossRef CAS.
- Z. Guo and W. Liu, Plant Sci., 2007, 172, 1103–1112 CrossRef CAS.
- H. Chen, P. Zhang, L. Zhang, H. Liu, Y. Jiang, D. Zhang, Z. Han and L. Jiang, Nature, 2016, 532, 85 CrossRef CAS PubMed.
- H. F. Bohn and W. Federle, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14138–14143 CrossRef CAS PubMed.
- P. Guo, Y. Zheng, C. Liu, J. Ju and L. Jiang, Soft Matter, 2012, 8, 1770 RSC.
- J. Ju, H. Bai, Y. Zheng, T. Zhao, R. Fang and L. Jiang, Nat. Commun., 2012, 3, 1247 CrossRef PubMed.
- E. D. Cohen and E. B. Gutoff, Modern Coating and Drying Technology, John Wiley and Sons, Inc., New York, 1992 Search PubMed.
- K. H. Chu, R. Xiao and E. N. Wang, Nat. Mater., 2010, 9, 413–417 CrossRef CAS PubMed.
- H. R. Holmes and K. F. Böhringer, Microsyst. Nanoeng., 2015, 1, 15022 CrossRef CAS.
- N. A. Malvadkar, M. J. Hancock, K. Sekeroglu, W. J. Dressick and M. C. Demirel, Nat. Mater., 2010, 9, 1023 CrossRef CAS PubMed.
- Y. Lin, Z. Hu, C. Gao, Z. Guo, C. Li and Y. Zheng, Adv. Mater. Interfaces, 2018, 5, 1800962 CrossRef.
- C. Li, N. Li, X. Zhang, Z. Dong, H. Chen and L. Jiang, Angew. Chem., Int. Ed., 2016, 55, 14988–14992 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, H. Chen, Z. Dong and D. Zhang, Adv. Mater., 2017, 29, 1702995 CrossRef PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS.
- L. H. Tanner, J. Phys. D: Appl. Phys., 1979, 12, 1473–1484 CrossRef CAS.
- C. Yu, C. Li, C. Gao, Z. Dong, L. Wu and L. Jiang, ACS Nano, 2018, 12, 5149–5157 CrossRef CAS PubMed.
- Y. Si, T. Wang, C. Li, C. Yu, N. Li, C. Gao, Z. Dong and L. Jiang, ACS Nano, 2018, 12, 9214–9222 CrossRef CAS PubMed.
- A. Shastry, M. J. Case and K. F. Böhringer, Langmuir, 2006, 22, 6161–6167 CrossRef CAS PubMed.
- C. Liu, J. Sun, J. Li, C. Xiang, L. Che, Z. Wang and X. Zhou, Sci. Rep., 2017, 7, 1–8 CrossRef PubMed.
- A. Cavalli, M. L. Blow and J. M. Yeomans, Soft Matter, 2013, 9, 6862 RSC.
- N. T. Chamakos, G. Karapetsas and A. G. Papathanasiou, Colloids Surf., A, 2016, 511, 180 CrossRef CAS.
- J. Li, Y. Hou, Y. Liu, C. Hao, M. Li, M. K. Chaudhury, S. Yao and Z. Wang, Nat. Phys., 2016, 12, 606–612 Search PubMed.
- R. L. Agapov, J. B. Boreyko, D. P. Briggs, B. R. Srijanto, S. T. Retterer, C. P. Collier and N. V. Lavrik, Adv. Mater. Interfaces, 2014, 1, 1 Search PubMed.
- M. Habibi, M. Eslamian, F. Soltani-Kordshuli and F. Zabihi, J. Coat. Technol. Res., 2016, 13, 211–225 Search PubMed.
- Q. Vo and T. Tran, Phys. Rev. E, 2018, 97, 063101 CrossRef CAS PubMed.
- M. Do-Quang, J. Shiomi and G. Amberg, Europhys. Lett., 2015, 110, 46002 CrossRef.
- Y. Mori, T. van de Ven and S. Mason, Colloids Surf., 1982, 4, 1–15 CrossRef CAS.
- J. C. Bird, S. Mandre and H. A. Stone, Phys. Rev. Lett., 2008, 100, 1 CrossRef PubMed.
- J. Hansson, H. Yasuga, T. Haraldsson and W. van der Wijngaart, Lab Chip, 2016, 16, 298 RSC.
- A. Carlson, M. Do-Quang and G. Amberg, Phys. Fluids, 2009, 21, 1 Search PubMed.
- A. Carlson, G. Bellani and G. Amberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 1 Search PubMed.
- A. Carlson, M. Do-Quang and G. Amberg, J. Fluid Mech., 2011, 682, 213–240 CrossRef.
- D. Quéré, Annu. Rev. Mater. Res., 2008, 38, 71–99 CrossRef.
- J. Wang, M. Do-Quang, J. J. Cannon, F. Yue, Y. Suzuki, G. Amberg and J. Shiomi, Sci. Rep., 2015, 5, 8474 CrossRef CAS PubMed.
- P. Johansson and B. Hess, Phys. Rev. Fluids, 2018, 3, 074201 CrossRef.
- P. Yue and J. J. Feng, Phys. Fluids, 2011, 23, 012106 CrossRef.
- Y. Lee, N. Matsushima, S. Yada, S. Nita, T. Kodama, G. Amberg and J. Shiomi, Sci. Rep., 2019, 9, 7787 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01854a |
| This journal is © The Royal Society of Chemistry 2019 |