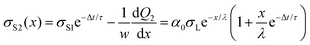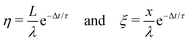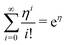Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Slide electrification: charging of surfaces by moving water drops
Amy Z.
Stetten
a,
Dmytro S.
Golovko
a,
Stefan A. L.
Weber
 ab and
Hans-Jürgen
Butt
ab and
Hans-Jürgen
Butt
 *a
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: butt@mpip-mainz.mpg.de
bDepartment of Physics, Johannes Gutenberg University, Staudingerweg 10, 55128 Mainz, Germany
First published on 17th September 2019
Abstract
We investigate the charge separation caused by the motion of a water drop across a hydrophobic, insulating solid surface. Although the phenomenon of liquid charging has been consistently reported, these reports are primarily observational, results are difficult to reproduce, and no quantitative theory has been developed. In this work, we address both the experimental and theoretical sides of this problem. We reproducibly measure the charge gained by water drops sliding down a substrate, and we outline an analytical theory to describe this charging process. As an experimental system, we choose water drops moving down an inclined plane of glass hydrophobized with perfluoro octadecyltrichlorosilane (PFOTS). On this surface, sliding drops gain a positive charge. We observe charge saturation in three variables: increasing drop number, increasing interval between drops, and increasing drop-sliding length. These charge saturations indicate a limited “storage capacity” of the system, as well as a gradual discharging of the surface. To explain these results, we theorize that some fraction of the charge in the Debye layer is transferred to the surface rather than being neutralized as the drop passes. This fraction, or “transfer coefficient”, is dependent on the electric potentials of surface and drop. All of our experimental charge saturation results can be interpreted based on the proposed theory. Given that nearly every surface in our lives comes in contact with water, this water-dependent surface charging may be a ubiquitous process that we can begin to understand through the proposed theory.
1 Introduction
Here, we analyze the charging of aqueous drops sliding down hydrophobic surfaces. This study is motivated by both applied and fundamental research. With respect to applications, the motivation is to convert the kinetic energy of a flowing liquid directly to electrical energy.1–16 To this end, much literature has focused on how charging affects the dynamic wetting of surfaces, the movement of drops, and contact angle hysteresis.17–20 However, the efficiency of charge separation by flowing liquids is still much lower than that of conventional electric generators. Attempts to design more efficient energy converters are hindered by a lack of fundamental understanding. It seems likely that the fundamental mechanism behind this charge separation would involve the electric double layer. However, the fact that drops become charged violates the paradigm of electroneutrality assumed in electric double layer theory. This seeming paradox has yet to be resolved.Resolving this paradox could also have broader implications. A few authors have suggested that the charge separation in water could be at the heart of solid/solid contact electrification.21–23 At very low humidity, the effect of contact electrification decreases, suggesting that water plays an important role. Thus, the study of charging in aqueous drops could be essential, not only to the design of efficient energy converters, but also to a full comprehension of general contact electrification.
Electric charging phenomena in connection with flowing water have been described for more than 150 years. A prominent example of charge separation by breaking streams of water is the Kelvin dropper.24,25 Examples from nature include the negative charge around waterfalls,26 and the generation of charge in clouds leading to lightning.27,28 Water drops impacting and rebounding off of solids usually acquire a charge, although they carry no charge before the impact.26,29–32 They leave a negative charge on the solid. Electrowetting experiments revealed charge deposition on hydrophobic surfaces.33 Drops that condense on a surface will also “jump” from this surface with a net charge.34,35 Furthermore, water drops ejected from a nozzle are usually charged, leaving behind the opposite charge in the nozzle.6,8,27,36–38 The charge of ejected water drops depends on the surface chemistry of the tube and nozzle,39 the flow rate,40 the pH,41 the salt concentration,11 and the potential bias on the nozzle.42
Here we are concerned with drops moving on solid surfaces, i.e., drops with moving three-phase contact lines. Water drops sliding down a hydrophobic tilted plane often acquire a charge and deposit a surface charge of opposite sign.18,43–45 In 1994, Yatsuzuka, Mizuno, and Asano introduced the term “slide electrification” for this process.18 They dripped drops of distilled water from a grounded pipette onto a tilted polytetrafluoroethylene (PTFE) plate. After sliding down the plate, the drops were collected in a Faraday cup to measure their charge. In addition, the authors measured the Kelvin potential of the PTFE after electrification. The drops collected were positively charged, while a net negative charge was deposited on the PTFE. The charge on the PTFE was strongly negative at the impact point, then decreased with distance, and even became slightly positive at the end of the path. The net drop charge increased with path length up to at least 15 cm. The charge per drop saturated with increasing drop rate.7 Other hydrophobic surfaces such as poly(methyl methacrylate) (PMMA)10 or silicon oxide hydrophobized with monolayers of octadecyltrichlorosilane also induced charging.43 The fact that charging depends on the chemical nature of the substrate was confirmed by measuring charges of drops flowing out of tubes.11,37,39 Polycarbonate,18 nylon, polyethylene, polyvinyl chloride,11 polystyrene, and even copper or steel tubes39 have all been observed to release positively charged drops.
These observational studies give clear evidence for charge separation, but leave the separation processes surrounding three-phase contact lines poorly understood. Explanations that have been proposed for solid tribocharging46–48 are problematic to generalize to liquids. When two solids are rubbed against each other, real contact is only established at few asperities due to omnipresent roughness. At these asperities, extremely high shear stresses can occur and are a likely candidate for a tribocharging mechanism. For liquids, high shear stress cannot occur. There is, therefore, no theory to describe slide electrification in liquids. In addition to a lack of theory on slide electrification, there is also difficulty performing reproducible experiments. Measured charges seem to depend critically on the surface chemistry, the detailed design of the experimental setup, and how the experiment is carried out.
Here, we address both of these issues: we reproducibly measure the charge gained by drops of water sliding down a substrate, and we outline an analytical theory that quantitatively describes slide electrification. The degree of charging seems to be highest for perfluorinated surfaces, so we choose to use a glass plate coated with perfluoro octadecyltrichlorosilane (PFOTS) as our substrate. While a water drop is in contact with this substrate, surface charges form spontaneously. When the rear of a drop dewets, some fraction of this spontaneously-formed charge is left on the surface. We call this fraction the transfer coefficient. Since the deposition of charge is a non-equilibrium process, the transfer coefficient may depend on the process itself, not only on conditions such as temperature and humidity. By comparing the experimental results with theory, we are able to fit all of our theoretical parameters for drop charging.
2 Experimental
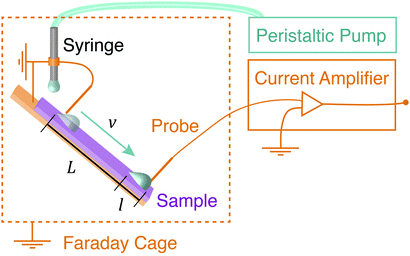
Glass microscope slides (6 × 2 cm2, 1 mm thick) were silanated with perfluoro octadecyltrichlorosilane (PFOTS) by chemical vapor deposition. Before silanization, the glass slides were first cleaned with acetone and ethanol, and then plasma treated for 10 minutes at 100% power (Diener Electronic Plasma Surface Technology: Femto BLS, Ebhausen, Germany). Next, the slides were placed in a vacuum desiccator containing a vial with 1 mL of trichloroperfluorooctylsilane. A magnetic stir bar was added to the vial for airflow. The desiccator was evacuated to less than 100 mbar. Then the desiccator became filled with a saturated vapor of the fluorosilane, which was allowed to coat the samples for thirty minutes. Samples had advancing and receding contact angles, as measured with a sessile drop, of (113 ± 3)° and (75 ± 6)°, respectively. Samples were only used within the first 10 days after preparation. We used them for several days until at some point the charge, contact angle and sliding speed decreased markedly. Samples were not used past this point.The sample surface was mounted on a grounded tilting stage within a grounded Faraday cage (Fig. 1) at a default tilt angle of 40°. A grounded syringe needle (stainless steel Hamilton syringe needle, 2 mm diameter, point style 3 – blunt) was mounted above the sample and was connected to a peristaltic pump (Gilson Minipuls 3, Wisconson, USA). The peristaltic pump produced water drops at variable drop rate between 0.01 and 1 s−1. These water drops were deposited on the tilted sample surface. As the drops slid down the surface, they briefly contacted a series of two, variably-spaced electrodes (loops of 0.025 mm tungsten wire – thin enough to minimize altering the shape of the drop). The first electrode grounded the drop, and the second electrode measured the drop current via a low noise current amplifier (response time: 5 μs, FEMTO DLPCA-200, Berlin, Germany). Both the pump and the current amplifier were kept outside of the Faraday cage. Both electrodes sat just above and perpendicular to the surface such that the drop was in contact with both surface and electrode as it moved by. Care was taken so that the drop disconnected from the electrode before rolling over the end of the sample and into a collection dish. Data was collected and recorded using a National Instruments data acquisition card (NI USB-6366 X-Series) and the accompanying LabVIEW software.
Before every experiment, an Ionizing Air Blower (Simco-Ion, Aerostat PC Ionizing Air Blower, Pennsylvania, USA) was blown over the surface for 5 minutes in order to neutralize the surface. Drops were run successively over the surface and a current spike was recorded when each drop touched the probe. In all experiments, V = 45 μL drops of deionized water (Sartorius Arium Pro VF, 18.2 MΩ cm resistivity, Germany) were used. The drops fell approximately 0.5 cm (just far enough so that they broke from the syringe before touching the surface), and then slid approximately 1 cm before touching the grounding electrode.
The velocity was measured by viewing drop motion from the side using a high speed camera (Photron Fastcam Mini AX-100, Photron Deutschland GmbH). This was not done during experiments where charge was recorded due to the sensitivity of the charge measurements and the high noise that the camera caused.
3 Results
In this section, we will discuss experimental results from series of multiple drops that are moving down a tilted PFOTS substrate. We start by describing the current signal detected from a moving drop. This signal is integrated to obtain the total charge on the drop. The charges accumulated by successive drops in a given trial are not identical, therefore we always analyze a series of drops. We will discuss the effects on charge of increasing drop number, increasing interval between drops, and increasing drop slide distance. In each of these variables, we observe charge saturation. Each of these saturation behaviors yields information about the charging process that we will use in our drop charging theory.Current generated by a moving drop
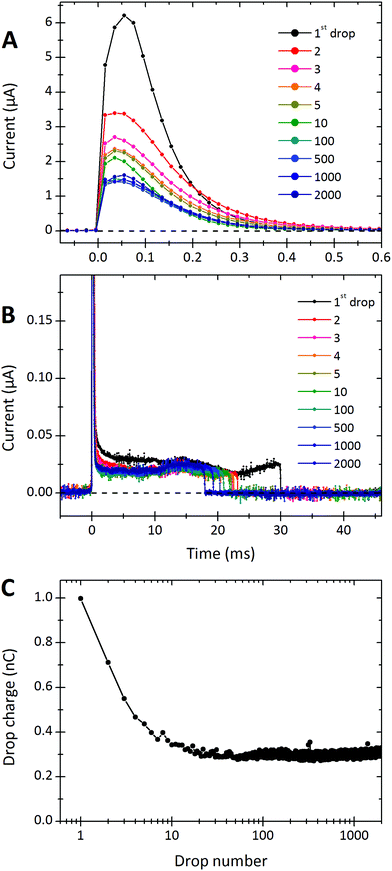
A typical sequence of current signals detected from a series of water drops is shown in Fig. 2. When the first drop touches the detection electrode, it discharges within ≈0.2 ms, reaching a maximal current of 6 μA. A positive current implies that the drop is positively charged and electrons flow from the electrode into the drop. After the peak, there is a low positive current of ≈20 nA until the rear of the drop detaches from the electrode roughly 30 ms later. This low positive current is presumed to be from the continued deposition of negative charges on the surface as the drop moves while still in contact with the electrode.The drop charge was calculated by integrating the current signal over the first 1 ms. In this particular example (Fig. 2) it was 0.99 nC for the first drop. To calculate the average deposited surface charge density, we need to know the free sliding distance of the drop, L. This is the distance the drop slides while not being discharged by either electrode (see Fig. 1). From videos we determine the free sliding distance to be the electrode spacing of 20 mm minus the drop length of 6.7 mm. Assuming the initial peak is equal to the accumulated charge over a sliding distance of 13.3 mm, and that the drop is w = 5 mm wide, the average deposited surface charge density is estimated to be σS ≈ 0.99 nC/(5 × 13.3 mm2) = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μC m−2.
μC m−2.
While the sliding drop is in contact with the electrode, a current of ≈23 nA is detected for 30 ms. Assuming a drop width of 5 mm and a length of 6.7 mm the surface charge deposited by the drop while being in contact with the detection electrode is σS0 ≈ 23 nA × 30 ms/(5 × 6.7 mm2) = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μC m−2. We added the index “0” to indicate that σS0 is the charge density deposited by an electrically neutral drop onto a neutral solid surface. Note that σS0 is higher than σS. We think that this is because the drop's continued contact with the electrode keeps it neutral, thereby allowing it to deposit more charge.
μC m−2. We added the index “0” to indicate that σS0 is the charge density deposited by an electrically neutral drop onto a neutral solid surface. Note that σS0 is higher than σS. We think that this is because the drop's continued contact with the electrode keeps it neutral, thereby allowing it to deposit more charge.
With the bare eye, we did not observe discharging effects, as have been described by Matsui et al.,49 not even when doing the experiment in the dark.
Charging of series of drops
After the first drop, the integrated charge of successive drops decreases. After 10–100 drops, the charge per drop saturates to a steady state. To demonstrate this effect, we plot the accumulated charge of each drop (that is the current peak integrated over the first 1 ms) versus the drop number (Fig. 2C). The first drop on this particular sample carried a charge of Q1 = 0.99 nC. Then the charge per drop decreased. After 10–100 drops it reached a constant steady-state value. We denote this steady-state charge per drop by Q∞. In Fig. 2C, the steady state charge was Q∞ = 0.28 nC.Dependence on time interval
This observed steady-state charge depends on drop rate. In the particular experiment shown in Fig. 3A, we decreased the interval between drops from 4.11 s to 2.77 s after 500 drops (enough drops to reach steady-state). This decrease in drop interval reduced the steady-state drop charge, Q∞. Further decreases in drop interval after 1000, 1500, and 2000 drops showed similar decreases in the steady-state charge. The reverse order was observed when starting with the short time intervals and increasing (Fig. 3B). In this case, the steady-state charge increased with increasing drop interval. This dependence indicates that the recovery time of the surface is important. With greater time between drops, the surface is given longer to discharge before the next drop passes. Thus, successive drops are able to deposit greater charge at greater drop intervals.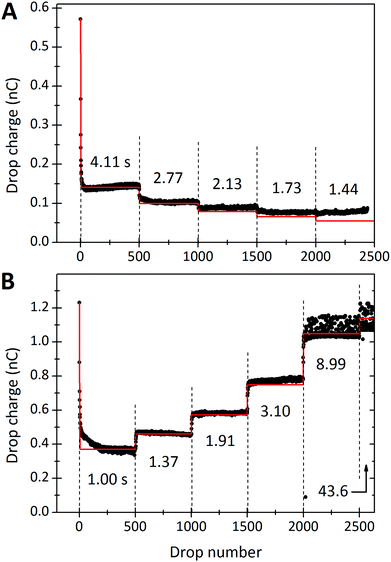 | ||
| Fig. 3 Charge of a drop versus the drop number. In (A) the drop rate was increased every 500 drops. Time intervals between subsequent drops were reduced from initially Δt = 4.11 s to 2.77, 2.13, 1.73 and 1.44 s. The red curves were calculated with the proposed model (eqn (7) and (21)) using λ = 8.2 mm, τ = 28 s, and α0σL = 17.4 μC m−2. 19.9 °C, 28% humidity. In (B) the order was reversed and we used a different sample. For the first 500 drops the interval was 1.00 s. Then it increased to 1.37, 1.91, 3.10, and 8.99 s for the next 500 drops, respectively. Finally we used a time interval of 43.6 s for the last 163 drops. The red curve was calculated with λ = 5.8 mm, τ = 6.3 s and α0σL = 44 μC m−2. 24.7 °C, 64% humidity. The error on all drop intervals is blow 5%, except for the longest two intervals, which have 10% error. | ||
In the limit of very long drop intervals, the surface fully recovers between drops. This surface recovery time can be seen in the plot of steady-state charge, Q∞, versus the time interval between two subsequent drops (Fig. 4). Q∞ first increases, and then saturates after Δt ≈ 10 s. In this particular experiment, the first drop carried a charge of Q1 = 1.23 nC (shown as red circle). The steady-state charge at very long time intervals approaches the charge carried by the first drop, indicating nearly full surface recovery.
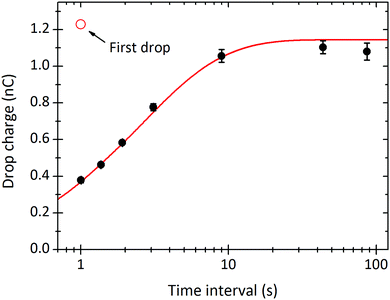 | ||
Fig. 4 Steady-state charge of a drop, Q∞, versus the time interval between subsequent drops Δt. The curves were fitted with eqn (21) to obtain λ = 5.8 mm, τ = 6.3 s, and α0σL = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μC m−2. 24.7 °C, 64% humidity. Black points are averages of the plateaus in Fig. 3B. μC m−2. 24.7 °C, 64% humidity. Black points are averages of the plateaus in Fig. 3B. | ||
For time intervals longer than ≈5 s we systematically observed a higher scatter of drop charges than for shorter time intervals (Fig. 3B). Errors were 2–6%; the higher errors were detected for long time intervals (Fig. 4) and long sliding distance. We attribute this scatter to slight fluctuations in the sliding path. It seems that once a drop has chosen a certain path, the next takes the same path unless there is enough time to “forget” the old path. In rare cases (not shown) the drops spontaneously changed their sliding path visibly. In these cases, the drop charge jumped up and then fell back to the same-steady state charge after 10–100 further drops.
Dependence on sliding distance
Measurements of drop charge for different sliding distances (at fixed time interval) show a monotonic increase (Fig. 5). This result agrees with previous reports of sliding drops18 or water flowing out of a tube.11 The drop charge saturates with sliding distance. The saturation distance depends on the drop number: ≈40 mm for the first drops, and ≈80 mm for the drops in steady-state. The saturations in both drop interval and sliding distance indicate some limiting charge storage capacity of the drop/surface system.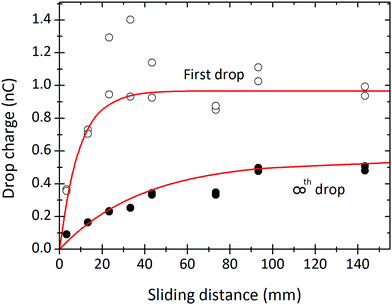 | ||
| Fig. 5 Charge of the first drop (open symbols) and steady state charge (filled symbols) of a drop versus the sliding length. The sliding length is the electrode spacing minus the drop length of 6.7 mm. The curves were fitted with eqn (7) and (21) to obtain, λ = 9 mm and τ = 8 s. 24.7 °C, 64% humidity. In order to be able to also fit a complete set of results as shown in Fig. 8 we varied the charge density; it was α0σL = 21 μC m−2 for the first drops and α0σL = 12 μC m−2 for the drops in steady state. Results were obtained from the same experiment as in Fig. 8. | ||
Potential of drops and capacitance
In order to complete our model of charge deposition, we must have an idea of the capacitance of our drops. To measure capacitance, we first measured the electric potential of sliding drops by connecting our electrode to an oscilloscope. Electric potentials were typically 2–2.5 V. Combining this value with our measured current data yields an effective drop capacitance of Cd ≈ 1 nC/2.5 V = 0.3 nF. We have no good explanation for the high capacitance yet. Even if we consider the whole glass plate as one plate capacitor of dielectric permittivity εS = 10, at an area of 2 × 6 cm2 and a thickness of d = 1 mm we only calculate a capacitance of Cd = εSε0A/d ≈ 0.1 nF.4 Theory
Drop charging mechanism
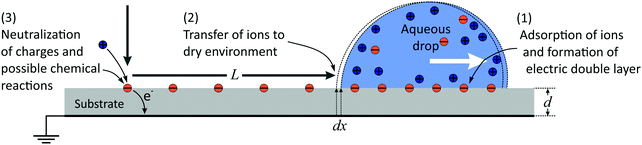
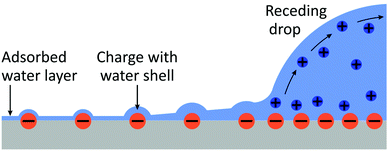
In the following, we propose a model for a quantitative description of charging effects of moving drops. We follow an earlier proposal that surface charges, which form spontaneously in water, do not fully recombine when the rear side of the drop passes over them.10,11,18,37 As a result, some charge is left on the substrate and the counter-charge remains in the drop. The surface charge density in liquid can be large, but the charge density remaining on the substrate is only a fraction of the total charge density. We define this fraction as the transfer coefficient, α.The whole charging process can be divided into three steps (Fig. 6): (1) spontaneous charge formation in the aqueous electrolyte, (2) transfer of charge to the surface, and (3) neutralization of the charges e.g., by flow of electrons through the grounded substrate, or by ions in the air.11,48,50 When a hydrophobic surface is immersed in water it charges negatively, most likely due to the adsorption of hydroxyl ions.51–53 Therefore, in the following we use charging by adsorption of hydroxyl groups as an example.
To describe the deposition of charge behind the drop, we use our transfer coefficient, α, to link the charge density left behind on the substrate, σS, to the charge density within the tail of the drop, σL:
| σS = ασL | (1) |
As the drop deposits charge, it becomes oppositely charged. With increasing sliding distance, the drop becomes more and more charged. This process, however, cannot go on forever. We suggest that an accumulation of charge within a drop is limited by the self-induced growth of electric potential. The total charge of the drop and its potential are proportional, Q = Cdψd. The capacitance of the drop, Cd, is the proportionality constant. The likelihood of a charge to remain on the solid surface decreases with increasing drop potential. To describe this effect, we introduce a potential-dependence in the transfer coefficient. Thus, the transfer coefficient may be approximated by a series expansion in potential. As a first approximation, we only consider the first term, which leads to a linear dependence:
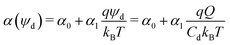 | (2) |
The deposited charge density behind the drop, σS, and the charge density in the liquid at the rear of the drop, σL, are now linked by:
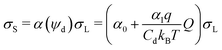 | (3) |
Single drop
In eqn (2) and (3) we did not yet specify the charge or potential. Now we assume that the drop potential is entirely generated by the deposited charge. As the drop moves, more and more hydroxyl ions are left on the surface. As a result, positive charge accumulates in the drop and its potential increases. With increasing potential it becomes more and more unfavorable for hydroxyl ions to leave the drop and remain on the surface. The charge density behind the drop and the transfer coefficient α gradually decrease. Counting from the initial rear side of the drop, the charge density decreases along its path. The deposited charge of the drop at every distance step dx is wσS(x)dx. Here, w is the width of the drop and x is the coordinate along the sliding path (Fig. 6). With σS = ασL (eqn (1)), the charge of the drop correspondingly changes by| dQ1(x) = −αwσLdx | (4) |
Inserting eqn (2), we obtain a differential equation for the charge of the drop:
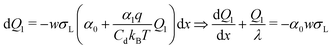 | (5) |
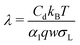 | (6) |
| Q1(L) = −α0λwσL(1 − e−L/λ) | (7) |
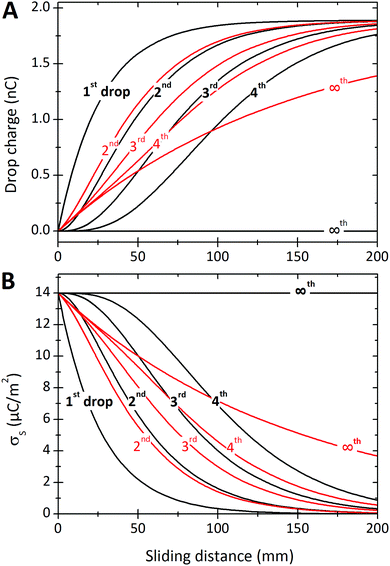 | ||
| Fig. 7 (A) Charge of the first four drops and Q∞versus sliding distance. (B) Surface charge density deposited by the first four drops and σS∞versus position. The black curves were calculated assuming that discharging is negligible, Δt/τ = 0. Drop charges were calculated with eqn (7), (19) and (21). To calculate the surface charge density we used eqn (8), (20) and (22). Red curves were calculated allowing for a charge neutralization with Δt/τ = 0.2. Parameters were σL = 0.28 × 10−3 C m−2, Cd = 0.3 nF, α0 = 0.05, α1 = 0.0002, w = 5 mm, and λ = 2.7 cm. | ||
Applying eqn (4), we obtain the corresponding charge density along the path of the first drop:
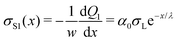 | (8) |
We formally distinguish the coordinate x form the sliding distance L. x starts at the same position, but it describes the surface charge density along the path for a given sliding distance (Fig. 6).
Series of drops
As subsequent drops slide down the same path as the first drop, the initially uncharged drops encounter a charged surface. The time between two subsequent drops is assumed to be constant and denoted by Δt. For simplicity, we further assume that the time required by the drop to move along its own length is much faster than the interval between drops. To distinguish the charge of different drops and the surface charge densities left by different drops, we index using the drop-number as a subscript. For the charges of individual drops, we write: Q1(L), Q2(L), Q3(L), etc. For the surface charge densities left by individual drops, we write σS1(x), σS2(x), σS3(x), etc.Here we also take charge neutralization into account. We describe charge neutralization by an exponential function with a relaxation time, τ:
| σS(t) = σS(0)e−t/τ | (9) |
• A flow of electrons through the substrate to the grounded electrode on its back side. The corresponding time constant is given by the capacitance of the substrate, εSε0A/d, multiplied with its resistance, ρed/A, leading to an electric discharge time constant of τe = εSε0ρe. Here, ρe is the specific resistivity of the substrate material. A is the area over which the surface charge is distributed. The relaxation time only depends on material properties. For glass, which makes up the majority of our substrate, (εS = 5–10, ρe = 1011–1015 Ω m) it ranges from τe = 4 s up to 1 day. For reference, Teflon (εS = 2.1, ρe ≥ 1016 Ω m) has a much longer relaxation time of τe ≥ 105 s.
• Discharging via free ions in air. Ions in air are for example generated by cosmic rays. At sea level, air has a typical conductivity of 10−14 S m−1.54–56 Though discharging in air may be slow, it is the only option for substrates like Teflon. If we denote the relaxation time for discharging through air by τa, the total relaxation time for discharging is 1/τ = 1/τe + 1/τa.
• Discharging via the surface. It is known that silicon oxide or glass show significant surface conduction at a humidity above ≈40%.57–59 This surface conduction may lead to discharging via the back electrode, or at least to a diffusion of charge away from the area where the charges were deposited. As a result, the charge may be distributed over the whole glass surface.
At a time, Δt, after the first drop has passed, the surface charge density has decreased by a factor e−Δt/τ. Because the surface is already partially charged, when the second drop slides a distance dx, fewer ions go from the bulk water to the solid/liquid interface. At the front of the second drop, the charge balance will be the difference between the charge that would have been deposited if the surface were neutral, and the charge that is already present on the surface: w(σL − σS1e−Δt/τ)dx. At the rear of the second drop, a charge w(1 − α)σLdx is taken up again. Equivalent to eqn (4), we find the incremental charge on the second drop:
| dQ2(x) = w(σS1e−Δt/τ − ασL)dx | (10) |
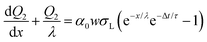 | (11) |
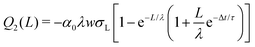 | (12) |
We repeat the calculation for the third, fourth, and nth drops. The general differential equations for drop charge and surface charge density are:
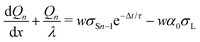 | (13) |
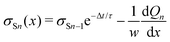 | (14) |
The following are solutions to eqn (13) and (14) for the 3rd, 4th, and nth drops:
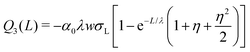 | (15) |
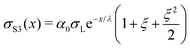 | (16) |
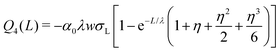 | (17) |
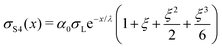 | (18) |
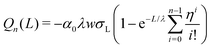 | (19) |
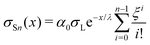 | (20) |
which yields the solution for the drop charge and surface charge density at steady-state:
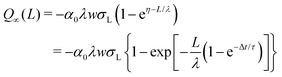 | (21) |
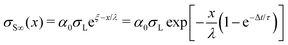 | (22) |
Predictions
We will begin by considering our solutions for the special case of negligible charge neutralization, Δt ≪ τ (black curves in Fig. 7). If discharging is negligible, the reduced sliding distance and coordinate become η = L/λ and ξ = x/λ. For the second drop sliding down the surface, the exponential factor, e−L/λ, is modified by the factor (1 + L/λ). It causes a delayed charge uptake of the drop. The second drop needs to slide a longer distance to acquire the same charge as the first drop. Following drops require longer and longer distances to charge. Reason: they deposit less charge when passing an area that has already been charged by previous drops. After many drops, indicated by “∞th”, the drops do not charge at all anymore, Q∞ = 0. Correspondingly, for multiple drops running along the same path, the charges on the surface extend further and further along the sliding direction (black curves Fig. 7B). After an infinite number of drops, the whole surface along the path of the drop bears a homogeneous surface charge density of α0σL.Neutralization of surface charges (red curves in Fig. 7A) increases the charge picked up by the sliding drops. Even after a large number of drops, subsequent drops still acquire a charge (red curve with “∞”). Correspondingly, the surface does not reach a homogeneous surface charge density when discharging is included (Fig. 7B). The red curve σ∞(x) starts with a initial descent. For a series of drops, the charge density decays exponentially with a modified decay length λ/(1 − e−Δt/τ).
5 Discussion
Comparison between theory and experiment
To determine the three independent parameters α0σL, λ, and τ from the experimental results, one needs to fit all of the presented data simultaneously. Specifically, we fit Qn-vs.-n with eqn (19), Q1-vs.-L with eqn (7), Q∞-vs.-L with eqn (21), and Q∞-vs.-Δt also with eqn (21).To facilitate the fitting procedure, good starting values are helpful. To obtain good starting values we use eqn (12), (15) and (17) and write:
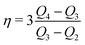 | (23) |
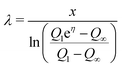 | (24) |
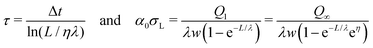 | (25) |
When comparing the modeled curves to the experimental results, we found overall good agreement. The whole set of curves could be fitted with only three parameters (Fig. 3). For the two examples shown in Fig. 3 we found ασL = 17.4 μC m−2, λ = 8.2 mm, and τ = 28 s for Fig. 3A, and ασL = 44 μC m−2, λ = 5.8 mm, and τ = 6.3 s for Fig. 3B. It is not yet clear whether the differences are caused by the fact that the samples were different, or that experiments were carried out at different temperature and humidity. The surface charge density deposited, α0σL, agrees with the previously estimated value of σS0 = 21 μC m−2 (from Fig. 2).
There is, however, one small, but systematic deviation. For the first few drops, theoretical drop charges decrease slightly faster than experimental observations. We hypothesize, that this may be caused by slight deviations in drop path or drop width. In the theory, we assume that each drop follows precisely the same path as the first drop, which may not be the case in reality. Additionally, our procedure of using an ionizing air blower to discharge the surface before experiments might result in some excess ions in the air, and thus a slightly higher surface discharge rate for the first few drops. This could manifest as a slightly slower decrease in charge for the first few drops.
Fig. 8 shows a comparison between theory and experiment for a full set of drops measured at different sliding lengths. Charges for the first, second, fifth, and steady-state drops are plotted. The whole set of results can be fitted with one decay length, λ = 9 mm, and one relaxation time, τ = 8 s. We only had to slightly adjust the deposited surface charge ranging from α0σL = 21 μC m−2 for the first drop to α0σL = 12 μC m−2 for Q∞. We cannot yet explain this gradual decrease in the deposited charge, but suggest that other variables such as changing drop velocity or changing humidity may play a role. It may also reflect an increased hydration of the glass surface underneath the silane monolayer. In most experiments, the first drops show greater variability compared to subsequent drops.
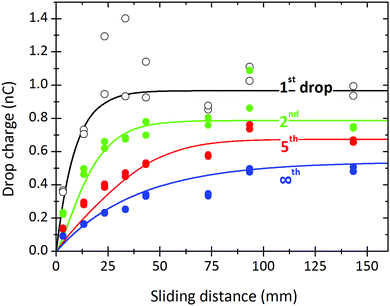 | ||
| Fig. 8 Charge of the first, second, fifth drop and drops in saturation measured at different sliding lengths (symbols). Continuous lines were calculated with eqn (7), (19) and (21) using λ = 9 mm, τ = 8 s, and α0σL = 21, 17.5, 15, and 12 μC m−2 for the first, second, fifth and the steady state drop, respectively. 24.7 °C, 64% relative humidity. w = 5 mm, Δt = 2.13 s. This is the same experiment as in Fig. 5. | ||
Estimation of the transfer coefficient
In water, hydrophobic surfaces charge negatively, most likely due to the adsorption of hydroxyl ions.51–53,60–64 In pure water at pH 6, typical surface potentials of PDMS and PTFE are −70 and −90 mV. For simplicity, we take the zeta potential as the surface potential, φ0, and convert it via the Grahame equation to a surface charge density:65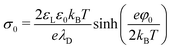 | (26) |
The Debye length,
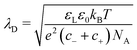 | (27) |
In the following, we assume that the surface charge in water forms quickly. To verify the validity of this assumption, we estimate the formation time of the electric double layer. It is limited by the diffusion of ions towards and away from the interface, and can be estimated by the Debye time:66–68τEDL = λD2/(D+ + D−). Here, D+ and D− are the diffusion coefficients of the cations and anions. In pure water, we consider hydronium and hydroxyl ions with D+ = 9.31 × 10−9 m2 s−1 and D− = 5.27 × 10−9 m2 s−1 at 25 °C, respectively. With a typical Debye length in Millipore water of 300 nm, we obtain τEDL = 6 μs. This is much faster than the typical time a drop is in contact with a specific surface area, which is tens of milliseconds, even at high velocity.
Taking our estimated σL = 0.28 mC m−2, and α0σL = 20 × 10−6 C m−2 (from the experiment in Fig. 3A) or α0σL = 44 × 10−6 C m−2 (from Fig. 3B) we obtain a transfer coefficient at zero drop potential of α0 = 0.062 or 0.16, respectively. Thus, our results indicate that approximately 6–16% of the charges at the solid/water interface are left behind on the surface.
The potential-dependence of the transfer coefficient can be estimated with eqn (6):
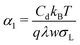 | (28) |
These estimations of the transfer coefficient α0 and in particular of the linear correction α1 should only be taken as a first estimate. Possible sources of error are: (1) we took σL from the literature and did not measure it for this particular interface. (2) The capacitance is only measured with a large error of ≈30%. (3) We only considered linear terms in eqn (2). This may only be a good approximation for small deviations of α from α0.
At this point, it is instructive to address one issue with respect to the definition of the transfer coefficient. One may argue that it is σL, and not the transfer coefficient that is changing with electric potential. In fact, if the drop is charged, one expects all of the charge to collect in an interfacial layer of thickness λD (like a charged conductor). Inside the drop, no electric field is present because of the mobility of ions. Thus, the surface charge density, σL, inside the drop (more than λD away from the contact line) should not be affected by the drop potential. Close to the contact line, however, countercharges are enriched. This increased concentration of counterions may indeed change the surface charge. For our theory, this effect poses no problem. In eqn (7), (8) and (11)–(22)α and σL appear as a product. This allows for two interpretations:
• Either we define σL as the equilibrium surface charge at the solid/liquid interface, and we attribute any change in the number of transferred ions to the transfer coefficient. (We adopt this interpretation.)
• Or we take σL as the local surface charge at the solid/liquid interface, which indeed depends on potential. In this case the transfer coefficient relates the number of charges within the drop, near the contact line to the number of charges left on the surface once the liquid has receded.
Energy penalty for charge deposition in air
One may argue that it is highly unlikely that charges are not neutralized when the liquid recedes, because it is energetically highly unfavorable. A charge e of radius a on a solid surface has a different energy depending on whether it is in a liquid or dry. This energy difference is the self-charging energy of a spherical charge with its center at the interface between the two respective media (solid/air in the first term and solid/liquid in the second):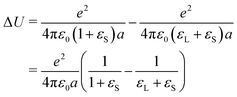 | (29) |
Such a large ΔU makes it statistically unlikely to leave charges on a dry surface. However, this value will be substantially reduced by two effects (Fig. 9):
• At the rear of the drop, we have a vapor pressure close to saturation. It is well known that a shell of liquid molecules will remain around the ion. The presence of the charge will diminish the tendency of a drop to evaporate. On the contrary, a charge would even induce condensation of liquid molecules around it. This effect of ion-induced condensation is the basis for the Wilson cloud chamber,69 and it is one cause for drop formation in the atmosphere.28,70–73 For free ions, the condensation from a saturated water vapor reduces the self-charging energy by more than a factor of two. This suggests that the surface charges may even be surrounded by tiny droplets which gradually evaporate.
• A layer of water will physisorb to the surface attracted by e.g., van der Waals forces.74 The thickness of the layer depends on the vapor pressure and can be several monolayers for a vapor pressure close to saturation.
The combined effect of ion-induced condensation (or prevention of water evaporation) and physisorption of water will provide a mainly aqueous environment for charges on solid surfaces. This means that the energy penalty for leaving ions behind could be significantly reduced as compared to leaving ions on a dry surface.
6 Conclusions
When a water drop moves down a hydrophobic inclined plane, it deposits a negative charge on the substrate. The total charge density deposited is roughly 6–16% of the surface charge density in water. Accordingly, drops charge positively. When series of drops slide down the surface, the charge per drop decreases and reaches a steady-state charge. The charge per drop increases with sliding length and with drop interval.The transfer of charge at the rear of the drop can be described by a transfer coefficient. To describe experimental results accurately, we assume that the transfer coefficient decreases with increasing drop potential. In addition, we allow for a gradual neutralization of surface charges. Neutralization is characterized by a relaxation time constant. Using three independent parameters, the charge of drops can be fitted, and the deposited charge distribution can be predicted. In agreement with experiments, we predict a steady-state charge from series of drops, a saturation of the drop charge with sliding length, and a saturation of the steady-state charge with the time interval between drops.
These results also indicate why measurements of slide electrification are often difficult to reproduce. The deposited charge depends critically on many factors. It depends on the surface chemistry via the surface charge and the transfer coefficient. It depends on the specific experimental design via the decay length, and thus the capacitance of the drop. It depends on the neutralization time, which in turn may be determined by the conductivity of air or of the sample.
Contact charging of water may be much more ubiquitous than previously realized. It is very likely not to be limited to hydrophobic surfaces, but to extend to hydrophilic and conducting surfaces as well. The effect may go unnoticed because the relaxation time for neutralization is shorter in these cases. Thus far, charging has primarily been observed when the charges remained for more than a few seconds. However, even short-term charging may influence wetting dynamics and drop behavior. Additionally, water's ability to acquire charge on a wide range of materials could allow it to act as a charge-transfer bridge between surfaces. Two solid surfaces with a water bridge between them could violate electroneutrality when that bridge is quickly broken, leaving the solid surfaces charged, as in contact electrification. A thin layer of water exists on nearly every surface in our lives, revealing a diverse, uncharted field of research in water charging and slide electrification.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Alfons Becker, Alexander Saal, Simon Silge, and Andreas Best for aiding in experiments, and Diego Diaz, William Wong, and David van Duinen for helpful discussions. Open Access funding provided by the Max Planck Society.References
- S. H. Kwon, J. Park, W. K. Kim, Y. J. Yang, E. Lee and C. J. Han, et al., An effective energy harvesting method from a natural water motion active transducer, Energy Environ. Sci., 2014, 7, 3279–3283 RSC.
- T. Krupenkin and J. A. Taylor, Reverse electrowetting as a new approach to high-power energy harvesting, Nat. Commun., 2011, 2, 448 CrossRef PubMed.
- Z. Yang, E. Halvorsen and T. Dong, Power generation from conductive droplet sliding on electret film, Appl. Phys. Lett., 2012, 100, 213905 CrossRef.
- J. K. Moon, J. Jeong, D. Lee and H. K. Pak, Electrical power generation by mechanically modulating electrical double layers, Nat. Commun., 2013, 4, 1487 CrossRef PubMed.
- Z. H. Lin, G. Cheng, L. Lin, S. Lee and Z. L. Wang, Water-solid surface contact electrification and its use for harvesting liquid-wave energy, Angew. Chem., Int. Ed., 2013, 52, 12545–12549 CrossRef CAS PubMed.
- Y. B. Xie, D. Bos, L. J. de Vreede, H. L. de Boer, M. J. van der Meulen and M. Versluis, et al., High-efficiency ballistic electrostatic generator using microdroplets, Nat. Commun., 2014, 5, 3575 CrossRef PubMed.
- L. Zheng, Z. H. Lin, G. Cheng, W. Z. Wu, X. N. Wen and S. M. Lee, et al., Silicon-based hybrid cell for harvesting solar energy and raindrop electrostatic energy, Nano Energy, 2014, 9, 291–300 CrossRef CAS.
- A. M. Duffin and R. J. Saykally, Electrokinetic power generation from liquid water microjets, J. Phys. Chem. C, 2008, 112, 17018–17022 CrossRef CAS.
- Q. J. Liang, X. Q. Yan, Y. S. Gu, K. Zhang, M. Y. Liang and S. N. Lu, et al., Highly transparent triboelectric nanogenerator for harvesting water-related energy reinforced by antireflection coating, Sci. Rep., 2015, 5, 9080 CrossRef CAS PubMed.
- L. E. Helseth, Electrical energy harvesting from water droplets passing a hydrophobic polymer with a metal film on its back side, J. Electrost., 2016, 81, 64–70 CrossRef CAS.
- Y. J. Sun, X. Huang and S. Soh, Using the gravitational energy of water to generate power by separation of charge at interfaces, Chem. Sci., 2015, 6, 3347–3353 RSC.
- J. Park, Y. J. Yang, S. H. Kwon and Y. S. Kim, Influences of surface and ionic properties on electricity generation of an active transducer driven by water motion, J. Phys. Chem. Lett., 2015, 6, 745–749 CrossRef CAS PubMed.
- T. H. Hsu, S. Manakasettharn, J. A. Taylor and T. Krupenkin, Bubbler: a novel ultra-high power density energy harvesting method based on reverse Electrowetting, Sci. Rep., 2015, 5, 16537 CrossRef CAS PubMed.
- J. Yin, X. M. Li, J. Yu, Z. H. Zhang, J. X. Zhou and W. L. Guo, Generating electricity by moving a droplet of ionic liquid along graphene, Nat. Nanotechnol., 2014, 9, 378–383 CrossRef CAS PubMed.
- J. Park, S. Song, C. Shin, Y. Yang, S. A. L. Weber and E. Sim, et al., Ion specificity on electric energy generated by flowing water droplets, Angew. Chem., Int. Ed., 2018, 57, 2091–2095 CrossRef CAS PubMed.
- L. E. Helseth and X. D. Guo, Contact electrification and energy harvesting using periodically contacted and squeezed water droplets, Langmuir, 2015, 31, 3269–3276 CrossRef CAS PubMed.
- I. Langmuir, Surface electrification due to the recession of aqueous solutions from hydrophobic surfaces, J. Am. Chem. Soc., 1938, 60, 1190–1194 CrossRef CAS.
- K. Yatsuzuka, Y. Mizuno and K. Asano, Electrification phenomena of pure water droplets dripping and sliding on a polymer surface, J. Electrost., 1994, 32, 157–171 CrossRef.
- Q. Sun, W. Wang, Y. Li, J. Zhang, S. Ye and J. Cui, et al., Surface charge printing for programmed droplet transport, Nat. Mater., 2019, 18, 936–941 CrossRef CAS PubMed.
- R. Digilov, Charge-induced modification of contact angle: the secondary electrocapillary effect, Langmuir, 2000, 16, 6719–6723 CrossRef CAS.
- Z. L. Gu, W. Wei, J. W. Su and C. W. Yu, The role of water content in triboelectric charging of wind-blown sand, Sci. Rep., 2013, 3, 1337 CrossRef CAS PubMed.
- H. T. Baytekin, B. Baytekin, S. Soh and B. A. Grzybowski, Is water necessary for contact electrification?, Angew. Chem., Int. Ed., 2011, 50, 6766–6770 CrossRef CAS PubMed.
- S. Pence, V. J. Novotny and A. F. Diaz, Effect of surface moisture on contact charge of polymers containing ions, Langmuir, 1994, 10, 592–596 CrossRef CAS.
- W. Thomson, On a self-acting apparatus for multiplying and maintaining electric charges, with applications to illustrate the Voltaic theory, Proc. R. Soc. London, 1867, 16, 67–72 Search PubMed.
- S. Desmet, F. Orban and F. Grandjean, On the Kelvin electrostatic generator, Eur. J. Phys., 1989, 10, 118–123 CrossRef.
- P. Lenard, Ueber die Electricität der Wasserfälle, Ann. Phys., 1892, 46, 584–636 CrossRef.
- J. J. Nolan and J. Enright, Experiments on the electrification produced by breaking up water, with special application to Simpson's theory of the electricity of thunderstorms, Sci. Proc. R. Dublin Soc., 1922, 17, 1–11 Search PubMed.
- A. Hirsikko, T. Nieminen, S. Gagne, K. Lehtipalo, H. E. Manninen and M. Ehn, et al., Atmospheric ions and nucleation: a review of observations, Atmos. Chem. Phys., 2011, 11, 767–798 CrossRef CAS.
- J. J. Thomson, On the electricity of drops, Philos. Mag., 1894, 37, 341–358 Search PubMed.
- K. Kaehler, Über die durch Wasserfälle erzeugte Leitfähigkeit der Luft, Ann. Phys., 1903, 12, 1119–1141 CrossRef.
- Z. Levin and P. V. Hobbs, Splashing of water drops on solid and wetted surfaces – hydrodynamics and charge separation, Philos. Trans. R. Soc., A, 1971, 269, 555–585 CrossRef CAS.
- D. M. Chate and A. K. Kamra, Charge separation associated with splashing of water drops on solid surfaces, Atmos. Res., 1993, 29, 115–128 CrossRef.
- A. G. Banpurkar, Y. Sawane, S. M. Wadhai, C. U. Murade, I. Siretanu and D. van den Ende, et al., Spontaneous electrification of fluoropolymer–water interfaces probed by electrowetting, Faraday Discuss., 2017, 199, 29–47 RSC.
- N. Miljkovic, D. J. Preston, R. Enright and E. N. Wang, Electrostatic charging of jumping droplets, Nat. Commun., 2013, 4, 2517 CrossRef PubMed.
- N. Miljkovic, D. J. Preston, R. Enright and E. N. Wang, Jumping-droplet electrostatic energy harvesting, Appl. Phys. Lett., 2014, 105, 013111 CrossRef.
- J. J. Nolan, Electrification of water by splashing and spraying, Proc. R. Soc. London, Ser. A, 1914, 90, 531–543 CrossRef.
- D. Choi, H. Lee, D. J. Im, I. S. Kang, G. Lim and D. S. Kim, et al., Spontaneous electrical charging of droplets by conventional pipetting, Sci. Rep., 2013, 3, 2037 CrossRef PubMed.
- P. C. L. Kwok, S. J. Trietsch, M. Kumon and H. K. Chan, Electrostatic charge characteristics of jet nebulized aerosols, J. Aerosol Med. Pulm. Drug Delivery, 2010, 23, 149–159 CrossRef CAS PubMed.
- T. A. L. Burgo, F. Galembeck and G. H. Pollack, Where is water in the triboelectric series?, J. Electrost., 2016, 80, 30–33 CrossRef.
- N. Schwierz, R. K. Lam, Z. Gamlieli, J. J. Tills, A. Leung and P. L. Geissler, et al., Hydrogen and electric power generation from liquid microjets: design principles for optimizing conversion efficiency, J. Phys. Chem. C, 2016, 120, 14513–14521 CrossRef CAS.
- M. Faubel and B. Steiner, Strong bipolar electrokinetic charging of thin liquid jets emerging from 10 μm PtIr nozzles, Ber. Bunsenges Phys. Chem., 1992, 96, 1167–1172 CrossRef CAS.
- L. P. Santos, T. R. D. Ducati, L. B. S. Balestrin and F. Galembeck, Water with excess electric charge, J. Phys. Chem. C, 2011, 115, 11226–11232 CrossRef CAS.
- A. Shahzad, K. R. Wijewardhana and J. K. Song, Contact electrification efficiency dependence on surface energy at the water–solid interface, Appl. Phys. Lett., 2018, 113, 023901 CrossRef.
- L. E. Helseth and H. Z. Wen, Visualisation of charge dynamics when water droplets move off a hydrophobic surface, Eur. J. Phys., 2017, 38, 055804 CrossRef.
- L. E. Helseth, The influence of micro-scale surface roughness on water–droplet contact electrification, Langmuir, 2019, 35, 8268–8275 CAS.
- F. Galembeck and T. A. L. Burgo, Chemical Electrostatics, Springer International, Cham, 2017 Search PubMed.
- L. S. McCarty and G. M. Whitesides, Electrostatic charging due to separation of ions at interfaces: contact electrification of ionic electrets, Angew. Chem., Int. Ed., 2008, 47, 2188–2207 CrossRef CAS PubMed.
- W. R. Harper, Contact and Frictional Electrification. Monographs on the Physics and Chemistry of Materials, Clarendon Press, Oxford, 1967 Search PubMed.
- M. Matsui, N. Murasaki, K. Fujibayashi, P. Y. Bao and Y. Kishimoto, Electrification of pure water flowing down a trough set up with a resin sheet, J. Electrost., 1993, 31, 1–10 CrossRef CAS.
- S. Soh, S. W. Kwok, H. Liu and G. M. Whitesides, Contact de-electrification of electrostatically charged polymers, J. Am. Chem. Soc., 2012, 134, 20151–20159 CrossRef CAS PubMed.
- V. Tandon, S. K. Bhagavatula, W. C. Nelson and B. J. Kirby, Zeta potential and electroosmotic mobility in microfluidic devices fabricated from hydrophobic polymers: 1. The origins of charge, Electrophoresis, 2008, 29, 1092–1101 CrossRef CAS PubMed.
- T. Preocanin, A. Selmani, P. Lindqvist-Reis, F. Heberling, N. Kallay and J. Luetzenkirchen, Surface charge at Teflon/aqueous solution of potassium chloride interfaces, Colloids Surf., A, 2012, 412, 120–128 CrossRef CAS.
- C. S. Tian and Y. R. Shen, Structure and charging of hydrophobic material/water interfaces studied by phase-sensitive sum-frequency vibrational spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15148–15153 CrossRef CAS PubMed.
- S. D. Pawar, P. Murugavel and D. M. Lal, Effect of relative humidity and sea level pressure on electrical conductivity of air over Indian Ocean, J. Geophys. Res., 2009, 114, D02205 Search PubMed.
- E. Seran, M. Godefroy, E. Pili, N. Michielsen and S. Bondiguel, What we can learn from measurements of air electric conductivity in 222Rn-rich atmosphere, Earth and Space Science, 2017, 4, 91–106 CrossRef.
- C. B. Moore and B. Vonnegut, Measurements of the electrical conductivities of air over hot water, J. Atmos. Sci., 1988, 45, 885–890 CrossRef.
- V. T. C. Paiva, L. P. Santos, D. S. da Silva, T. A. L. Burgo and F. Galembeck, Electric conduction and excess charge in silicate glass/air interfaces, Langmuir, 2019, 35, 7703–7712 CrossRef CAS PubMed.
- A. Soffer and M. Folman, Surface conductivity and conduction mechanisms on adsorption of vapours on silica, Trans. Faraday Soc., 1966, 62, 3559–3569 RSC.
- R. Umezawa, M. Katsura and S. Nakashima, Electrical conductivity at surfaces of silica nanoparticles with adsorbed water at various relative humidities, e-J. Surf. Sci. Nanotechnol., 2018, 16, 376–381 CrossRef CAS.
- J. K. Beattie, The intrinsic charge on hydrophobic microfluidic substrates, Lab Chip, 2006, 6, 1409–1411 RSC.
- R. Zimmermann, U. Freudenberg, R. Schweiss, D. Küttner and C. Werner, Hydroxide and hydronium ion adsorption – a survey, Curr. Opin. Colloid Interface Sci., 2010, 15, 196–202 CrossRef CAS.
- R. Zimmermann, N. Rein and C. Werner, Water ion adsorption dominates charging at nonpolar polymer surfaces in multivalent electrolytes, Phys. Chem. Chem. Phys., 2009, 11, 4360–4364 RSC.
- K. N. Kudin and R. Car, Why are water–hydrophobic interfaces charged?, J. Am. Chem. Soc., 2008, 130, 3915–3919 CrossRef CAS PubMed.
- T. W. Healy and D. W. Fuerstenau, The isoelectric point/point-of zero-charge of interfaces formed by aqueous solutions and nonpolar solids, liquids, and gases, J. Colloid Interface Sci., 2007, 309, 183–188 CrossRef CAS PubMed.
- D. C. Grahame, The electric double layer and the theory of electrocapillarity, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- R. J. Hunter, Foundations of Colloid Science II, Clarendon Press, Oxford, 1995, vol. 2 Search PubMed.
- R. W. O'Brien, The high-frequency dielectric dispersion of a colloid, J. Colloid Interface Sci., 1986, 113, 81–93 CrossRef.
- L. Collins, S. Jesse, J. I. Kilpatrick, A. Tselev, O. Varenyk and M. B. Okatan, et al., Probing charge screening dynamics and electrochemical processes at the solid–liquid interface with electrochemical force microscopy, Nat. Commun., 2014, 5, 3871 CrossRef CAS PubMed.
- C. T. R. Wilson, On the comparative efficiency as condensation nuclei of positively and negatively charged ions, Philos. Trans. R. Soc., A, 1900, 193, 289–308 CrossRef.
- J. J. Thomson, Conduction of Electricity through Gases, At the University Press, Cambridge, 1903 Search PubMed.
- A. Laaksonen, V. Talanquer and D. W. Oxtoby, Nucleation: measurements, theory, and atmospheric applications, Annu. Rev. Phys. Chem., 1995, 46, 489–524 CrossRef CAS PubMed.
- J. Curtius, E. R. Lovejoy and K. D. Froyd, Atmospheric ion-induced aerosol nucleation, Space Sci. Rev., 2006, 125, 159–167 CrossRef CAS.
- S. Heiles, R. J. Cooper, M. J. DiTucci and E. R. Williams, Sequential water molecule binding enthalpies for aqueous nanodrops containing a mono-, di- or trivalent ion and between 20 and 500 water molecules, Chem. Sci., 2017, 8, 2973–2982 RSC.
- H. J. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley-VCH, Berlin, 2003 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |