Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemically active nanodroplets in a multi-component fluid†
Dino
Osmanović
 *a and
Yitzhak
Rabin
b
*a and
Yitzhak
Rabin
b
aCenter for the Physics of Living Systems, Department of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: dinoo@mit.edu
bDepartment of Physics, and Institute of Nanotechnology and Advanced Materials, Bar-Ilan University, Ramat Gan 52900, Israel
First published on 4th July 2019
Abstract
We introduce a model of chemically active particles of a multi-component fluid that can change their interactions with other particles depending on their state. Since such switching of interactions can only be maintained by the input of chemical energy, the system is inherently non-equilibrium. Focusing on a scenario where the equilibrium interactions would lead to condensation into a liquid droplet, and despite the relative simplicity of the interaction rules, these systems display a wealth of interesting and novel behaviors such as oscillations of droplet size and molecular sorting, and raise the possibility of spatio-temporal control of chemical reactions on the nanoscale.
1 Introduction
A particularly salient attribute of biological complexity is the highly multi-component nature of living cells. A normal cell contains thousands of different proteins which all exist in multiple copy numbers1 that can range over many orders of magnitude, even for the same protein in different cells.2 Since live cells operate as chemical reactors, for a cell to be functional it is necessary for all of these proteins to find and bind their specific targets that can be other proteins, small molecules or specific DNA (RNA) sequences.3 These specific interactions have to be realized in a sea of non-specific interactions which can, in principle, interfere with the ability of proteins to find and bind their targets. Surprisingly, the presence of non-specific interactions does not necessarily impede the formation of specific complexes; in fact, such “non-functional” interactions can help the diffusion-limited search by reducing the effective search space for specific partners through condensation and formation of membraneless compartments.4 The realization that liquid–liquid phase separation on the nanoscale may play an important role in biology has received considerable attention recently.5–10 However, as is well known from studies of microemulsions (e.g., oil droplets in water), in order to prevent coagulation and growth (Ostwald ripening) and eventual separation into macroscopic phases, one has to reduce the surface tension by adding surfactants or to maintain the microemulsion in a non-equilibrium steady state by the input of mechanical energy (stirring). Another possibility that is perhaps more relevant to biology is that droplet size may be controlled by the input of chemical energy, e.g., through hydrolysis of ATP.11 A particular example of the latter has been explored by Zwicker et al.,12 in what they deemed chemically active droplets (see also ref. 13). By considering a system where a chemical energy source converts one kind of chemical species to another, with different solubility properties, they have observed life-like splitting of droplets.In order to gain qualitative insight about nanoscale separation in real biological systems, in this work we introduce and simulate a microscopic model of a multi-component fluid in which non-specific interactions between particles promote aggregation and formation of droplets while specific interactions lead to the formation of bound pairs. Once a bound pair is formed, the interaction of its constituents with other particles changes (reminiscent of allosteric transitions in proteins following binding of ligands and ATP hydrolysis14,15) and this affects the stability of droplets. We find that such systems display new and unexpected non-equilibrium phenomena, such as oscillations between states of aggregation (i.e., size and number of droplets) that depend on the number of different chemical components and the copy number of each component. We would like to emphasize that in this work we define as different chemical components as particles that interact only non-specifically with each other. Particles that can interact specifically with each other are deemed to be copy numbers of the same component. Our results point to the possibility of spatio-temporal control over chemical reactions in multi-component systems that are driven by input of chemical energy.
2 Model
Consider a dilute gas of N particles (volume fraction η ≪ 1) that consists of N/M different sets (components) of M particles each, where different sets represent chemically different species. All particles i and j within each set (i, j ∈ M) are identical in the sense that they interact with pair interaction parameter εij = εS (“specific” interaction), while particles k and l that belong to different sets (k ∈ M, l ∈ M′) interact with pair interaction parameter εkl = εNS (“non-specific” interaction) such that εS ≫ εNS. We assume that the interaction between particles i and j separated by a distance r is given by the Lennard-Jones potential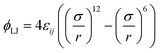 | (1) |
3 Results
We begin our analysis with a system of N = 500 particles and M = 2, i.e., with 250 sets of 2 particles in each set. We choose the interaction parameters to be εS = 6 and εNS = 2.2 (this choice guarantees that the non-specific interactions are sufficiently strong to form liquid droplets4). We take η = 0.01 since a low volume fraction is necessary in order to observe condensation into droplets. Though the only difference from our previous model is the change in the non-specific interactions once a bound pair is formed (this step requires input of chemical energy), the new model gives rise to strikingly different phenomena.3.1 Dynamic steady state
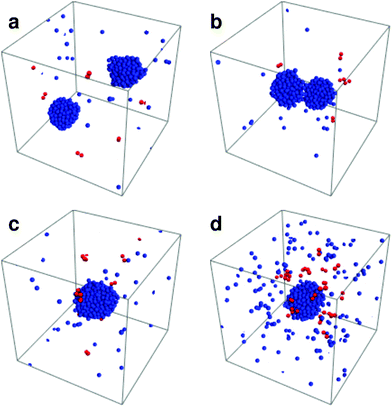
The most striking feature in this system is that instead of the system evolving towards a single equilibrium state, it now settles into a dynamic steady state in which it oscillates between different states. These states are observed in Fig. 1 and are summarized below (also see Movie M1 in ESI†):• Coexistence of two droplets: as can be seen from the figure, the system quickly separates into two clusters of roughly equal size, which coexist for relatively long periods of time.
• Fusion of droplets: the two separate droplets diffuse and, upon encountering each other, they undergo a fusion event leading to the formation of a large droplet which contains most of the particles in the system. This fusion is why the forwards and backwards traces of the time trace of droplet size are different. Fusion events only require two droplets to find each other, then as soon as the droplets are close they count as being part of the same droplet, leading to a very sharp (instantaneous) increase.
• Decay of the large droplet: the fusion of the two smaller droplets is associated with increase in the number of bound pairs that form inside the large droplet. These bound pairs are rapidly ejected from the droplet leading to fast initial decay. Subsequent to this fast decay, the droplet enters into a metastable state where the influx of particles from the gas is balanced by emission of bound pairs. This metastable equilibrium persists until a second droplet is nucleated (see ESI,† Fig. S1).
• Nucleation of a second droplet: bound pairs dissociate in the gas phase and isolated particles aggregate and form another droplet of similar size. In order for this to occur particles, after dissociation, need to find another non-specific partner in the gas phase as the density of the gas phase is even lower than of the system this step may require some time. This non specific pair then needs to stay together long enough for another gas particle to find it and get attached to it (aggregation by non-specific interactions). This process repeats itself until a stable second droplet is formed. Eventually the first step is repeated.
The steps outlined above can be quantified by tracing the number of particles Nc in the largest and the second largest droplets against time in Fig. 2. For the same plot in terms of radial size see ESI,† Fig. S2.
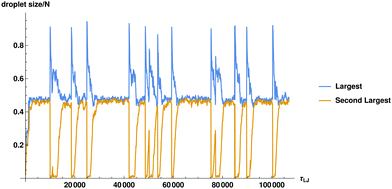 | ||
| Fig. 2 The fraction of particles in the largest and the second largest droplets in the system is plotted as a function of time. The size in terms of particle diameters will be related to spatial size by approximately R ≈ σN1/3. For precise measurement of the radius of the cluster see ESI,† Fig. S2. | ||
3.2 Pair formation
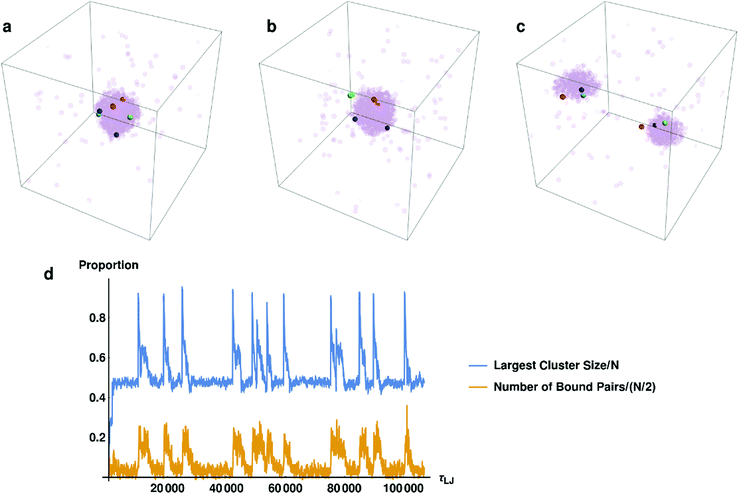
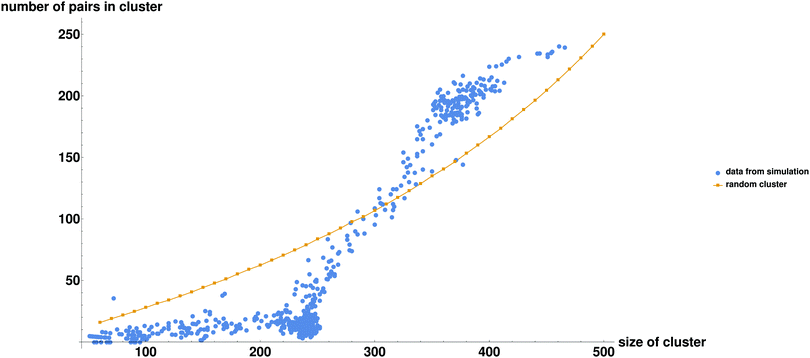
In the previous subsection, we elucidated what happens to the system on a large scale. Now we will discuss the connection between droplet dynamics and the formation of specific complexes (bound pairs). In Fig. 3a–c we present several typical snapshots of the system, with 3 randomly chosen potential pairs (i.e., particles that interact specifically with each other and can form a bound pair upon close approach) shown in different colors. In Fig. 3d we track the fraction of bound pairs (number of bound pairs divided by the total number of pairs N/2 = 250) and the fraction of particles in the largest droplet, as a function of time. It can clearly be seen from Fig. 3d that the proportion of pairs is strongly correlated with the size of the largest droplet. The moment at which the two droplets fuse to form a larger droplet corresponds to an explosion in the number of bound pairs. These pairs then change their non-specific interactions with the surrounding particles in the droplet from attractive to repulsive, causing them to be ejected from the droplet (see ESI,† Fig. S3). Formation of bound pairs is directly correlated with the decrease in the size of the droplet as pairs continue to be ejected from it. Ejected bound pairs dissociate in the gas phase outside the droplet, and the released particles interact attractively with other particles in the gas. Eventually the ejected material nucleates a second droplet that grows until its size approaches that of the first droplet and the process repeats itself.In order to get additional insight into the interplay between droplet dynamics and formation of bound pairs, we consider the total number of particle pairs (both potential and bound pairs) np, contained in droplets of various sizes. Fig. 4 shows in a striking way how the simulation values differ from those calculated for a random system (a droplet made of randomly chosen particles). While in the random case the number of pairs increases roughly quadratically with Nc, the simulation results deviate from this curve. Thus, for droplets larger than about 300 there is overabundance of pairs compared to the random value, and for droplets smaller than 300 the number of pairs is below that for a randomly composed droplet. In order to understand what is going on we first focus on the small clusters with Nc < 250, in which the average number of pairs per cluster np is very small and nearly independent of cluster size Nc. Clearly, we are observing the phenomenon of active sorting in which the only one of the two complementary particles of each set is found in the small cluster while the other particle is found either in another small cluster (or in the remaining gas phase). As the binding occurs within sets and particles of the same set are found in different droplets, this drastically reduces the production of complexes. To understand this phenomenon note that as bound pairs are ejected from the decaying droplet, the number of pairs in this droplet decreases. The emitted bound pairs dissociate in the gas phase and, eventually, another droplet is nucleated somewhere in the system. This droplet grows mostly by absorbing single particles, with a tendency to eject any bound pair that forms. Such pairs break up in the gas phase and their constituents are reabsorbed by the two droplets. This leads to effective “sorting” where the two complementary particles of each set have the tendency to be found in different droplets, each of which is roughly of half the system size. This explains why the number of the potential pairs is so much lower than the random result for droplets of size Nc < 250, and also provides intuition for why the size of each of the two coexisting droplets is stabilized somewhat below Nc = 250 (recall that some particles remain in the gas phase). Note that the condition for this mechanism to be valid is that the diffusion controlled encounter time between two members of the pair in a droplet should be much shorter than the time between the nucleation of the second droplet and the coalescence of the two droplets. This condition is indeed satisfied in our simulation (see Table 1 for the relevant timescales in this simulation).
| Timescale | Mean value (τLJ) |
|---|---|
| Bond lifetime | 23 |
| Pair search time | 1619 |
| Pair search time in cluster | 247 |
| Cluster decay time | 2313 |
| Cluster rejoining time | 8992 |
Now lets return to Fig. 4 and consider large droplets of size Nc > 250. Clearly such droplets correspond to the time intervals during which a single large droplet exists (see Table 1). Since this large droplet is formed by coalescence of two small clusters that are enriched in complementary members of all pairs, the average number of potential pairs within it exceeds that expected for a randomly composed droplet. The broad crossover region corresponds to time intervals (Fig. 2) in which a single large droplet decays by emission of bound pairs.
We would like to also briefly mention the origin on the various timescales presented in Table 1. Obviously these parameters arise from the confluence of the parameters we initialize our system with. The bond lifetime strongly depends on the strength of the specific attraction. Most of the other timescales are diffusion-limited, the average encounter time for the objects in question in a given volume. One timescale is however more complicated, which is the decay time of the large droplet. One can see from the time traces that this first involves a rapid decay followed by a much slower decay, which is related to continuous exchange of particles with the gas and to the nucleation of the second droplet. After this there is a “sorting” process by which complementary pairs are separated into different clusters. The confluence of all these factors leads to the decay timescale. The longest timescale in the problem is the rejoining time of the two independent droplets. This rejoining time will depend on the diffusion constant of the droplet, which goes down as the number of particles in the droplet increases. As the governing physics of this diffusion will only weakly be affected by the formation of pairs (pair production is low in the two droplet phase), this distribution will be the same as that of two ideal droplets (without internal dynamics) diffusing within the same volume, we plot these distributions in ESI,† Fig. S4 for different starting distances of the droplets.
3.3 Large sets
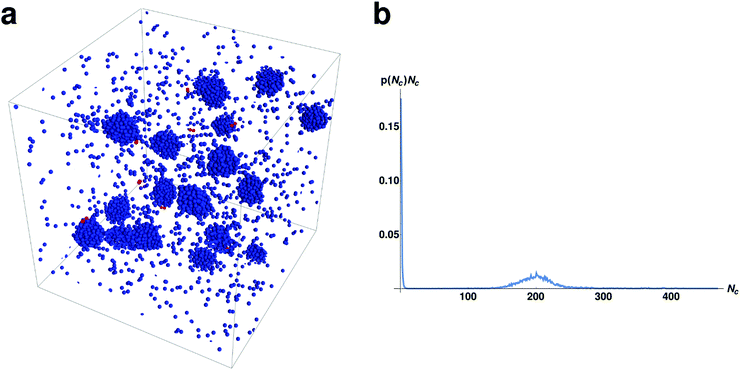
We now consider what occurs as we increase the number of particles per set M (recall that all M particles within a set can form bound pairs with each other) while keeping the same number of sets (250) as in the previous sections. This is a more realistic representation of a chemically heterogeneous fluid where multiple particles can interact specifically with each other. The interaction rules are the same as presented in the “Model” section. The behavior of a system with M = 15 and N = 3750 can be seen in Fig. 5.Inspection of Fig. 5 shows that in the larger system there are many droplets rather than just the two observed in the smaller system. The average size of a droplet in this system is slightly lower than in the M = 2 case. Beyond this the droplets have similar dynamics including coalescence events of two droplets, followed by decay of the resulting droplet by emission of bound pairs (see Movie M2 in ESI†), as seen in the previous sections.
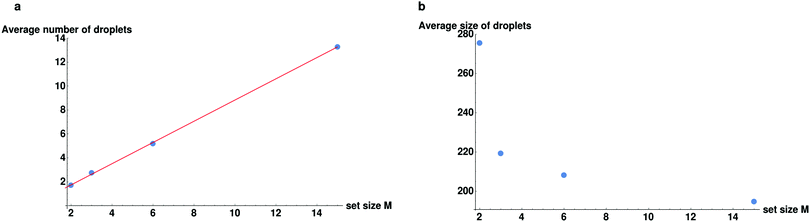
We proceed to explore the full range of behaviors as we keep the number of sets fixed and change the amount of particles per set M. We plot the trends for set sizes of M = 2, 3, 6, 15 in Fig. 6. As can be seen in Fig. 6, the number of droplets increases linearly with the set size. From these plots we can identify a rule of thumb for these chemically active, multi-copy systems, both in terms of the number and the average size of droplets. It would appear that the number of droplets is approximately equal to the size of the set and the average size of the droplet is approximately equal to the total number of sets N/M. This accords with our previous observations that the members of a set will tend to sort themselves into different droplets. Obviously this rule of thumb does not entirely rule true and deviations from it can be understood by considering how many of all the possible pairings in the system (N(N − 1)/2) can form bound pairs, ((N/M)M(M − 1)/2). Since the fraction of pairs goes as (M − 1)/(N − 1), it grows when we keep N/M fixed while increasing M. This means that the “latent” proportion of possible specific chemical bonds increases as the set size M increases (though it saturates quickly as M becomes large). This increased probability of encountering a member of the set means that droplets are slightly smaller, up to the saturation threshold.
4 Discussion
While the model we have presented is fairly simple, it captures a range of complex behaviors that arise from the fact that non-specific interactions between particles can change as the result of binding between specific partners. In this section we go over some of the consequences that could have some relevance for real systems.4.1 Non-equilibrium chemical reactions
The way the interaction rules have been implemented defines the system as a non-equilibrium one. The changing interaction of the non-specific bonds requires an implicit input of energy in order to form specific bonds. In the simulation, this energy cost is effectively paid for immediately by removing the attractive part of the non-specific interactions upon the length of the specific bond being less than 1.5σ, thus increasing the total energy of the system. We would here like to comment on several aspects of this and how it relates to real systems.The nature of the defined interaction rules can be understood as a particular form of a three body potential V(r1,r2,r3), by this we mean that the state of randomly chosen particles 1 and 2 in a set (their separation |r1 − r2|) will affect their interaction with any other particle 3. A more realistic formulation of this three body potential would introduce a barrier for the formation of a specific bond were the particles under consideration already bound non-specifically. The difference in energy between the situation where there is a specific bond and that where the particles are bound to non-specific neighbors would have to be either supplied from the bath or by an non-equilibrium energy input. In addition to this, the traversal over the barrier could be helped by catalysts present in the system.
In the ESI,† we show a figure of how the total energy of the system changes during its cycle (see ESI,† Fig. S5). The process of switching off the non-specific attractions as a bound pair is formed raises the energy of the particles by approximately 15kbT. As observed in Fig. S4 (ESI†), the entire fusion-decay process raises the potential energy of the system by approximately 1000kbT, this energy has many different contributions, as the process does increase the production of energetically favorable specific pairs, but at the cost of non-specific interactions. We could imagine this scenario in various different ways. In the case where the system is quantum mechanical: the energy (with kbT replaced by electron volts) could be provided through excitations by photons. In a biological settings this would correspond to shape changes in a protein provided by the hydrolysis of ATP.
An alternative scenario which would have similar physics but be more challenging to simulate would involve the energy of the specific interactions being orders of magnitude larger than the non-specific interaction. In this case the formation of specific bonds would be very energetically favored, and they would also be expelled from the droplet. However, in such a system the thermal energy would not be sufficient to dissociate the specific bonds, thus favoring the formation of a diatomic gas. Yet, if we were to provide an energy input in the gas phase to break apart the specific bonds, we would anticipate seeing similar results to the current work. In order to put the present work in a proper context we would like to mention that our system belongs to a broader class of chemical reactions that give rise to non-equilibrium spatio-temporal patterning (see, e.g., the Belousov–Zhabotinskii reaction17).
4.2 Storage and production modes
Of particular interest is the spatio-temporal organization of the multitude of different chemical components in the system. It is apparent from the results that combination of (a) weak non-specific interactions between particles in different sets that leads to phase separation and formation of droplets (b) bound pair formation due to strong attractive interaction between particles within a set that changes the interaction between the constituents of these pairs and all other particles to repulsive and (c) the dissociation of these bound pairs, results in oscillations between “storage” and “production” modes. In the storage phase, there is effective sorting (segregation) of the different members of each set into different droplets that act as “storage tanks” whose number and size depends on the size and number of sets M and N/M, respectively. The number of complexes (bound pairs) formed in the storage phase is low since complex formation is greatly suppressed through members of the set being found in different droplets. The duration of the storage phase depends on the concentration of droplets that increases with increasing set size M. Coalescence of these droplets gives rise to the appearance of larger droplets that act as “chemical reactors” in which complementary members of the sets present combine to form bound pairs, a production mode that requires the input of chemical energy. These bound pairs are then ejected from the large droplets and diffuse in the surrounding gas phase until they finally dissociate (the energy released in the process is dissipated) and are absorbed by the droplets, and the system returns to the storage phase. The duration of the period between production and storage phases increases with the lifetime of the bound pairs and it is during this intermediate phase that metastable complexes exist in the gas phase and may play a functional role (e.g., as catalysts/enzymes) in biological or in artificially engineered systems.As one goes to larger, more realistic, systems, the same features are present but there is no longer a global temporal separation between production and storage. Instead droplets exist relatively stably until they encounter another droplet, in the same way as is seen in the smaller system, but now there are many droplets in the system. Therefore the production of complexes is tied to the dynamics of all the droplets.
4.3 Nanoemulsions of chemically heterogeneous fluid systems
Phase separation has been a topic of recent interest in biological systems.9 However, some of its observed features suggest that such phase separated systems are not at equilibrium. Recall that a normal liquid–liquid phase separation leads to macroscopically segregated phases, rather than to many small droplets immersed in the surrounding medium (the classic oil and water example would have small droplets of oil in upon immediate mixing, but were the system to be left for a while the droplets would coalesce and two macroscopically separated phases would be observed). The current scheme provides a microscopic basis for how phase separation on the nanoscale might occur in a fluid, the necessary requirements being that the fluid is chemically heterogeneous and that the microscopic interactions can change upon binding.In reality the chemical composition of the system would probably not have the symmetries included here. Different components would exist in different copy numbers. In addition, there would be different degrees of attraction or binding amongst components. However, in the case that there are binding events that modify interactions, there would still be an effective flux out of the droplet, despite the greater complexity.
The system selects a length scale of the droplets based on the degree of chemical heterogeneity. As can be seen in Section 3.3 the degree of chemical heterogeneity, represented in our case by the number of different sets N/M, will determine the subsequent size of the nanodroplets. While the precise mechanism in real systems might differ in details, especially with regards to the interactions within sets, it is clear that microphase separation requires a way to suppress Ostwald ripening. In the case studied in the present work, droplets above a certain size have a tendency to form bound pairs that are expelled from the droplet, thus suppressing the formation of very large droplets.
5 Conclusions
In this paper we have explored the behavior of a chemically heterogeneous system in which the interactions between various particles in the system depends on the particular spatial configuration of the particles. In particular, we introduce a scheme whereby the system is divided into sets such that when any two members of a set encounter each other, they change their interactions with all the other particles in the system. This scheme was introduced to mimic real chemical bonds, but many different schemes where there are state-dependent interactions also exist in a variety of settings, leading to potentially many differing kinds of behaviors. For example, the attractive interaction might be simply reduced instead of completely switched off, or there might be an energetic barrier to binding. One could also imagine scenarios where the set size was different for different sets.We have observed a number of physically interesting and potentially biologically-relevant phenomena. The system is maintained in a non-equilibrium state by the input of chemical energy required to change the way in which particles that form bound pairs, interact non-specifically with other particles in the system. Despite the fact that the energy input is on the molecular scale (change of the local interactions), its effects are manifested on a much larger scale than this. One immediate observation is that very large droplets become unstable because they contain too many particles which can form bound pairs that are ejected from the droplet. This naturally leads to the formation of smaller droplets in which the number of particles that can form bound pairs is drastically reduced. Of course, such smaller droplets are unstable with respect to coalescence and therefore a dynamic steady state in which the system oscillates between larger and smaller droplet states, is established. While this droplet dynamics is the most striking large-scale feature of the system, other facets of its behavior become apparent if we focus our attention on the chemical composition of the droplets. In the regimes studied here the molecules that form specific bonds have a tendency to sort themselves into different droplets. Therefore the system becomes organized not only in the sense that multiple liquid droplets of similar size form, but also in terms of the highly non-random chemical makeup of those droplets. This makes these smaller droplets quasi-stable, but upon encountering another droplet, the high degree of chemical compatibility will lead to an explosion in production of chemical compounds (bound pairs), which are immediately expelled from the larger droplet. This is a possible method of controlling the output of chemical compounds on the nanoscale in real systems. Whether similar mechanisms play a role in the functioning of living cells, remains an open question.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
DO would like to thank the Gordon and Betty Moore foundation for funding. YR's work was supported by grants from the Israel Science Foundation and from the Israeli Centers for Research Excellence program of the Planning and Budgeting Committee.References
- M. Beck, A. Schmidt, J. Malmstroem, M. Claassen, A. Ori, A. Szymborska, F. Herzog, O. Rinner, J. Ellenberg and R. Aebersold, Mol. Syst. Biol., 2011, 7, 549 CrossRef PubMed.
- N. Maheshri and E. K. O'Shea, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 413–434 CrossRef CAS.
- S. J. Wodak, J. Vlasblom, A. L. Turinsky and S. Pu, Curr. Opin. Struct. Biol., 2013, 23, 941–953 CrossRef CAS.
- D. Osmanović and Y. Rabin, J. Chem. Phys., 2016, 144, 205104 CrossRef.
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732 CrossRef CAS PubMed.
- C. P. Brangwynne, Soft Matter, 2011, 7, 3052 RSC.
- A. A. Hyman and K. Simons, Science, 2012, 337, 1047–1049 CrossRef CAS.
- Y. Lin, D. S. W. Protter, M. K. Rosen and R. Parker, Mol. Cell, 2015, 60, 208–219 CrossRef CAS.
- S. Boeynaems, S. Alberti, N. L. Fawzi, T. Mittag, M. Polymenidou, F. Rousseau, J. Schymkowitz, J. Shorter, B. Wolozin, L. V. D. Bosch, P. Tompa and M. Fuxreiter, Trends Cell Biol., 2018, 28, 420–435 CrossRef CAS.
- S. Elbaum-Garfinkle, Y. Kim, K. Szczepaniak, C. C.-H. Chen, C. R. Eckmann, S. Myong and C. P. Brangwynne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7189–7194 CrossRef CAS.
- C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Reports on progress in physics, Physical Society, Great Britain, 2019 Search PubMed.
- D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Jülicher, Nat. Phys., 2016, 13, 408–413 Search PubMed.
- R. Seyboldt and F. Jülicher, New J. Phys., 2018, 20, 105010 CrossRef.
- J. Liu and R. Nussinov, PLoS Comput. Biol., 2016, 12, e1004966 CrossRef.
- S. J. Wodak, E. Paci, N. V. Dokholyan, I. N. Berezovsky, A. Horovitz, J. Li, V. J. Hilser, I. Bahar, J. Karanicolas, G. Stock, P. Hamm, R. H. Stote, J. Eberhardt, Y. Chebaro, A. Dejaegere, M. Cecchini, J.-P. Changeux, P. G. Bolhuis, J. Vreede, P. Faccioli, S. Orioli, R. Ravasio, L. Yan, C. Brito, M. Wyart, P. Gkeka, I. Rivalta, G. Palermo, J. A. McCammon, J. Panecka-Hofman, R. C. Wade, A. D. Pizio, M. Y. Niv, R. Nussinov, C.-J. Tsai, H. Jang, D. Padhorny, D. Kozakov and T. McLeish, Structure, 2019, 27(4), 566–578 CrossRef CAS.
- J. D. Weeks, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- J. D. Murray, BZ Oscillating Reactions, Springer New York, New York, NY, 2002, pp. 257–277 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00826h |
| This journal is © The Royal Society of Chemistry 2019 |