Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic optical rectification and delivery of active particles†
Nick
Koumakis
 *,
Aidan T.
Brown
*,
Aidan T.
Brown
 ,
Jochen
Arlt
,
Jochen
Arlt
 ,
Samuel E.
Griffiths
,
Vincent A.
Martinez
and
Wilson C. K.
Poon
,
Samuel E.
Griffiths
,
Vincent A.
Martinez
and
Wilson C. K.
Poon
SUPA and School of Physics & Astronomy, The University of Edinburgh, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh EH9 3FD, Scotland, UK. E-mail: nick.koumakis@ed.ac.uk
First published on 5th August 2019
Abstract
We use moving light patterns to control the motion of Escherichia coli bacteria whose motility is photo-activated. Varying the pattern speed controls the magnitude and direction of the bacterial flux, and therefore the accumulation of cells in up- and down-stream reservoirs. We validate our results with two-dimensional simulations and a 1-dimensional analytic model, and use these to explore parameter space. We find that cell accumulation is controlled by a competition between directed flux and undirected, stochastic transport. Our results point to a number of design principles for using moving light patterns and light-activated micro-swimmers in a range of practical applications.
1 Introduction
Active colloids1 are fundamentally interesting, exhibiting phenomena not found in equilibrium systems such as currents and unique kinds of pattern formation.2 Such phenomena have been applied, e.g., to concentrate particles3 or separate them by size, actuate micro-machines,4 or self-assemble microstructures. For example, V-shaped ‘funnel gates’ fabricated using soft lithography can rectify the motion of randomly-swimming bacteria,3 producing steady currents or spatial patterns. Similar effects can be achieved by applying a spatial light pattern to bacteria or other active colloids whose speed v depends on the intensity of incident light, I. If dv/dI > 0, bacteria in illuminated regions swim until they encounter a darker region, where they are slowed down. Cells then accumulate in the dark regions because they swim out of the light regions and stop in the dark. Quantitatively, this leads to the relationship ρv = constant5,6 where ρ is the spatially varying bacterial concentration.This technique for ‘painting patterns with bacteria’ has been demonstrated using Escherichia coli in which the proton motive force (PMF) driving swimming is generated by light-powered proteorhodopsin (PR).6–8 Potential applications include directing swimmers into compartments3,9 to actuate micro-mechanical components.4 Such ‘bacterial painting’ becomes significantly more versatile if the template is dynamic. Thus, globally time-varying light fields projected onto PR-driven E. coli can ‘erase’ and ‘re-paint’ patterns.7 Here, we study the response of PR-driven E. coli to spatio-temporally varying light fields, specifically, wave-like propagating periodic patterns of illumination. By using a combination of experiments, theory and simulations we uncover a rich array of often counter-intuitive phenomena.
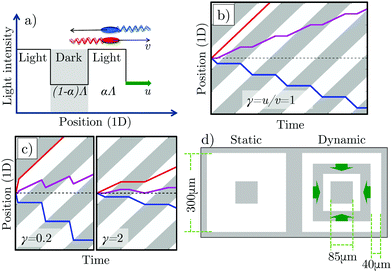
To motivate our work, consider a 1D model solvable by inspection. Bacteria swim right 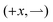 or left
or left 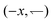 at speed v when illuminated, and stop completely in the dark; the (equal)
at speed v when illuminated, and stop completely in the dark; the (equal)  and
and  populations do not exchange. Now impose and translate at speed u > 0 a square-wave light pattern, Fig. 1a. If γ = u/v = 1,
populations do not exchange. Now impose and translate at speed u > 0 a square-wave light pattern, Fig. 1a. If γ = u/v = 1, 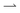 cells keep up with the moving light field in steady state, and so maintain their speed v, whereas
cells keep up with the moving light field in steady state, and so maintain their speed v, whereas  cells spend only some of their time in the light, determined by the duty cycle (fractional on time) of the pattern, α. This results in a net positive cell flux, i.e., a light pattern translating at γ = 1 rectifies the cells' motion and transports them with the pattern. We can represent this behaviour in a space-time plot (kymograph), Fig. 1b.
cells spend only some of their time in the light, determined by the duty cycle (fractional on time) of the pattern, α. This results in a net positive cell flux, i.e., a light pattern translating at γ = 1 rectifies the cells' motion and transports them with the pattern. We can represent this behaviour in a space-time plot (kymograph), Fig. 1b.
Optimal rectification is obtained for γ ≈ 1: for γ ≪ 1, 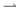 cells remain trapped at the slowly-moving light–dark interface, while the
cells remain trapped at the slowly-moving light–dark interface, while the  cells move faster through the light regions; for γ ≫ 1, the light field moves much faster than the cells, so both
cells move faster through the light regions; for γ ≫ 1, the light field moves much faster than the cells, so both 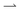 and
and  cells spend ≈50% time in the dark and the light. Either way, the net flux falls, Fig. 1c. This qualitative picture has been quantified previously in simulations and theoretically.10,11 Counter-intuitively, these works also predicted that a reversal of the flux direction is possible for γ ≪ 1, and showed that this was dependent on other parameters such as the bacterial tumbling rate10 or the speed of bacteria in the dark.11
cells spend ≈50% time in the dark and the light. Either way, the net flux falls, Fig. 1c. This qualitative picture has been quantified previously in simulations and theoretically.10,11 Counter-intuitively, these works also predicted that a reversal of the flux direction is possible for γ ≪ 1, and showed that this was dependent on other parameters such as the bacterial tumbling rate10 or the speed of bacteria in the dark.11
In this paper, we first perform bacterial experiments designed to quantitatively test these theoretical predictions. Our experiments reproduce the optimal rectification suggested by the intuitive picture, and identify flux reversal at low pattern speeds. Simulations of our system quantitatively reproduce our experimental results, but only when we include a biological delay in the bacterial response to light, and translational thermal diffusion of the bacteria. We go on to explore the wider parameter space using a one-dimensional analytical theory. This allows us to explain various mechanisms for flux reversal, controlled, e.g., by rotational diffusion or the duty cycle of the pattern. Further, we show that the parameter dependence of the steady-state downstream accumulation of bacteria, i.e., their ability to form patterns, can be quite different, and even reversed, from the parameter dependence of the flux in periodic boundary conditions, which theoretical studies generally discuss.10,11 Based on these findings, we articulate design principles for the transport of light-activated swimmers using moving patterns of illumination.
2 Materials and methods
The bodies of E. coli bacteria12 are ≈2 μm × 1 μm × 1 μm spherocylinders. They swim by using their PMF (of ≈−150 mV) to power membrane-embedded rotary motors which rotate ≈7–10 μm helical flagella. Unusually for bacteria, E. coli can generate a PMF without external nutrients13 by using internal resources and O2 to pump protons out of the cell. Without O2, swimming ceases12 unless there is another source of PMF, as in cells expressing PR,14 a photon-driven proton pump. Thus, under anaerobic conditions, PR-expressing E. coli cells swim only when illuminated, which is analogous to synthetic light-activated swimmers.15,16We inserted a PR-bearing plasmid into E. coli AB1157, and deleted the cheY gene and the unc operon encoding the ATP synthase complex to give strain AD10.7 The former deletion turns wild-type run-and-tumblers into smooth swimmers, while the latter gives fast stopping whenever illumination ceases.7
Overnight cultures were grown aerobically in 10 ml Luria–Bertani broth at 30 °C. A fresh culture was inoculated at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 dilution of the pre-grown cells in 35 ml tryptone broth and grown for 4 h. The production of PR was induced by adding arabinose to a concentration of 1 mM, as well as the necessary cofactor all-trans-retinal to 10 μM in the growth medium. Cells were incubated under the same conditions for a further hour to allow protein expression to take place and then transferred to motility buffer. A single filtration was used to prepare high density stock solutions (optical density ≈ 10) which were diluted with phosphate motility buffer (MB, pH 7.0, 6.2 mM K2HPO4, 3.8 mM KH2PO4, 67 mM NaCl and 0.1 mM EDTA) to an optical density ≈6 at 600 nm (≈0.8 vol% cell bodies12). 2 μL aliquots sealed into 20 μm-thick, ≈10 mm wide, flat glass capillaries were observed in phase contrast under red illumination using a PF 10×/0.3 NA objective on a Nikon TE2000 microscope. Movies were recorded with a high speed CMOS MC1462 Mikrotron camera. Swimming stopped a few minutes after sealing due to O2 depletion.
100 dilution of the pre-grown cells in 35 ml tryptone broth and grown for 4 h. The production of PR was induced by adding arabinose to a concentration of 1 mM, as well as the necessary cofactor all-trans-retinal to 10 μM in the growth medium. Cells were incubated under the same conditions for a further hour to allow protein expression to take place and then transferred to motility buffer. A single filtration was used to prepare high density stock solutions (optical density ≈ 10) which were diluted with phosphate motility buffer (MB, pH 7.0, 6.2 mM K2HPO4, 3.8 mM KH2PO4, 67 mM NaCl and 0.1 mM EDTA) to an optical density ≈6 at 600 nm (≈0.8 vol% cell bodies12). 2 μL aliquots sealed into 20 μm-thick, ≈10 mm wide, flat glass capillaries were observed in phase contrast under red illumination using a PF 10×/0.3 NA objective on a Nikon TE2000 microscope. Movies were recorded with a high speed CMOS MC1462 Mikrotron camera. Swimming stopped a few minutes after sealing due to O2 depletion.
After leaving these cells in the dark for a further 10 min, uniform green illumination was turned on (510–560 nm, corresponding to peak PR absorption; ≈5 mW cm−2 at the sample). Differential dynamic microscopy (DDM)17,18 returned an increasing mean swimming speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , saturating at ≈6.5 μm s−1, with standard deviation ≈2.5 μm s−1 and a typical fraction β ≈ 25% of non-motile bacteria (
, saturating at ≈6.5 μm s−1, with standard deviation ≈2.5 μm s−1 and a typical fraction β ≈ 25% of non-motile bacteria (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is averaged over the motile bacteria only). The non-motile bacteria have diffusivity DT ≈ 0.15 μm2 s−1. In this work, we use the terms ‘motile/non-motile’ to refer to cells that are able/unable to swim in the presence of green light, while the descriptors ‘swimmers/non-swimmers’ are reserved for those motile cells that are transiently powered/not-powered by external illumination.
is averaged over the motile bacteria only). The non-motile bacteria have diffusivity DT ≈ 0.15 μm2 s−1. In this work, we use the terms ‘motile/non-motile’ to refer to cells that are able/unable to swim in the presence of green light, while the descriptors ‘swimmers/non-swimmers’ are reserved for those motile cells that are transiently powered/not-powered by external illumination.
A spatial light modulator projected a 4 × 4 array of static and dynamic patterns onto this initially uniform field of swimmers and non-motile cells. Each pattern featured a central dark square (side l = 85 μm) inside an outer square (side L = 300 μm), Fig. 1d. In the static pattern, the square annulus was uniformly illuminated. The dynamic pattern comprised concentric square annuli of equal width Λ/2 = 40 μm (α = 0.5) propagating inwards at speed u. The area outside the patterns was dark in all cases. We chose a square-wave intensity pattern because its predicted flux is higher than other waveforms previously considered, e.g., sinusoidal.11 Moreover, the fact that the swimming speed is non-linearly dependent on the light intensity7 means that any pattern apart from a square-wave pattern will be distorted, complicating the experiment and analysis.
In our setup, the local intensity variance in the microscopy image, σ2, has previously been found to be proportional to the local cell density7 (see ESI† for details). Here, we are interested in the density ρin(t) of motile cells in the central square of the pattern
| ρin(t) = fσin2(t)[1 − βin(t)], | (1) |
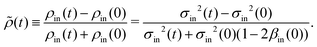 | (2) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) also corresponds to the contrast between the inside and outside of the pattern, i.e.,
(t) also corresponds to the contrast between the inside and outside of the pattern, i.e., ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) = (ρin(t) − ρout(t))/(ρin(t) + ρout(t)). Our choice of normalization means that
(t) = (ρin(t) − ρout(t))/(ρin(t) + ρout(t)). Our choice of normalization means that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = ±1 for complete rectification in the inwards or outwards directions respectively.
= ±1 for complete rectification in the inwards or outwards directions respectively.
3 Results
3.1 Rectification in 2D experiments and simulations
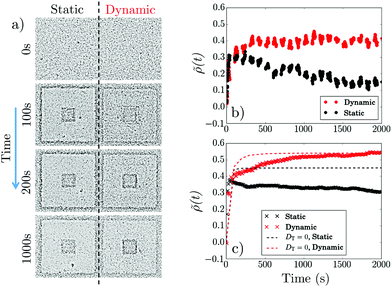
Fig. 2 shows data for u = 2.25 μm s−1, corresponding to γ = 0.35. Imposing a static pattern ‘paints’ a central dark square and the outer square acquires a dark edge, Fig. 2a, as previously,7 because cells in the bright (B) annulus swim into the dark (D) central square and outer regions in roughly equal numbers and stop upon arrival. Because the central square is much smaller than the outer region this initial influx of swimmers from the bright annulus gives a sharp increase in ρin and therefore![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , Fig. 2b (•). Thereafter,
, Fig. 2b (•). Thereafter, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) decreases slowly as accumulated non-swimmers diffuse back out into the bright annulus and swim to the outside of the annulus. Presumably, at long times, a steady state obtains where the B → D active flux balances the D → B diffusive flux, so that we expect ρin(t → ∞) ≈ ρout(t → ∞) = ρ0, and
decreases slowly as accumulated non-swimmers diffuse back out into the bright annulus and swim to the outside of the annulus. Presumably, at long times, a steady state obtains where the B → D active flux balances the D → B diffusive flux, so that we expect ρin(t → ∞) ≈ ρout(t → ∞) = ρ0, and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t → ∞) = 0. However, we cannot reach this limit experimentally because bacteria slow down and begin to aggregate with time, possibly due to accumulated photo-damage. The contrast in the steady-state ‘static painting’ is due to the annulus, inhabited by a small amount of non-motile cells and few swimmers in transit, so that ρann ≪ ρ0.
(t → ∞) = 0. However, we cannot reach this limit experimentally because bacteria slow down and begin to aggregate with time, possibly due to accumulated photo-damage. The contrast in the steady-state ‘static painting’ is due to the annulus, inhabited by a small amount of non-motile cells and few swimmers in transit, so that ρann ≪ ρ0.
The dynamic light pattern also accumulates cells in the central square, Fig. 2a. The difference from the static case, already visible in the snapshots but highlighted in Fig. 2b, is that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) does not decay after the initial increase, but reaches instead a finite steady-state value. This enhancement of accumulation depends non-monotonically on γ = u/v, Fig. 3a, and, counter-intuitively, it reverses sign at γ ≪ 1: cells are swept out of the central region (
(t) does not decay after the initial increase, but reaches instead a finite steady-state value. This enhancement of accumulation depends non-monotonically on γ = u/v, Fig. 3a, and, counter-intuitively, it reverses sign at γ ≪ 1: cells are swept out of the central region (![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) < 0). Both of these features are clearly illustrated in Fig. 3c, which shows that at both t = 500 s and t = 4000 s,
< 0). Both of these features are clearly illustrated in Fig. 3c, which shows that at both t = 500 s and t = 4000 s, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is peaked as a function of γ, and that at the later time
is peaked as a function of γ, and that at the later time ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) < 0 when γ ≲ 0.05 (see ESI,† Movie 1).
< 0 when γ ≲ 0.05 (see ESI,† Movie 1).
To explore these features, we simulated 2 × 104 non-interacting swimmers in a 600 × 600 μm2 periodic box. Particle speeds vi are drawn from an experimental Schultz distribution for our bacteria17,18 (mean = 6.5 μm s−1, 40% standard deviation). The dynamics of particle i obeys
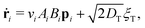 | (3) |
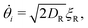 | (4) |
| Ȧi = (I(ri) − Ai)/τA, | (5) |
| Ḃi = (I(ri) − Bi)/τB, | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi, sin
θi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi) its position and propulsion direction respectively. ξT is a two- and ξR is a one-dimensional unit-variance temporally-uncorellated Gaussian noise term (in each direction for ξT). Translational, DT = 0.15 μm2 s−1, and rotational, DR = 0.05 s−1, diffusivities reflect experimental values (see ESI†). The normalized light intensity, I(ri,t) = 1 for bright and 0 for dark. The two dynamical variables A and B reflect the observation7 that two independent, internal processes control the response of our cells to changes in the intensity of external illumination. We independently measured τA = 1.6 s and τB = 100 s (see ESI†). Note that in the instant-response limit (τA = τB = 0) this model reduces to the popular 2-dimensional active-Brownian-particle (ABP) model that was previously used to study the effect of translating light patterns.10,11
θi) its position and propulsion direction respectively. ξT is a two- and ξR is a one-dimensional unit-variance temporally-uncorellated Gaussian noise term (in each direction for ξT). Translational, DT = 0.15 μm2 s−1, and rotational, DR = 0.05 s−1, diffusivities reflect experimental values (see ESI†). The normalized light intensity, I(ri,t) = 1 for bright and 0 for dark. The two dynamical variables A and B reflect the observation7 that two independent, internal processes control the response of our cells to changes in the intensity of external illumination. We independently measured τA = 1.6 s and τB = 100 s (see ESI†). Note that in the instant-response limit (τA = τB = 0) this model reduces to the popular 2-dimensional active-Brownian-particle (ABP) model that was previously used to study the effect of translating light patterns.10,11
Our simulations reproduce the observed rise and decay in ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) for the static pattern, Fig. 2c (×). The saturation behavior for the dynamic pattern is also reproduced, Fig. 2c (
(t) for the static pattern, Fig. 2c (×). The saturation behavior for the dynamic pattern is also reproduced, Fig. 2c ( ). Most visibly in the decay of the static case, the simulated dynamics is slower than experiments, by a factor of ≈2, possibly due to our neglect of cell–cell interactions, which are expected to lead to an increased apparent diffusivity.19 Even so, the semi-quantitative agreement is gratifying given the simplicity of our model.
). Most visibly in the decay of the static case, the simulated dynamics is slower than experiments, by a factor of ≈2, possibly due to our neglect of cell–cell interactions, which are expected to lead to an increased apparent diffusivity.19 Even so, the semi-quantitative agreement is gratifying given the simplicity of our model.
We also claimed that the diffusion of cells that had stopped swimming in the dark was responsible for the observed non-monotonicity in ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) of the static pattern, Fig. 2b (•). Simulations confirm this: setting DT = 0 removes the drop in
(t) of the static pattern, Fig. 2b (•). Simulations confirm this: setting DT = 0 removes the drop in ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t), Fig. 2c (- - -). The effect of removing diffusion on the dynamic pattern is to render the rise to saturation significantly more rapid, Fig. 2c (
(t), Fig. 2c (- - -). The effect of removing diffusion on the dynamic pattern is to render the rise to saturation significantly more rapid, Fig. 2c ( ). Thus, a dynamic pattern has to work against translational thermal diffusion, as identified previously10 (see ESI,† Movies 2–4).
). Thus, a dynamic pattern has to work against translational thermal diffusion, as identified previously10 (see ESI,† Movies 2–4).
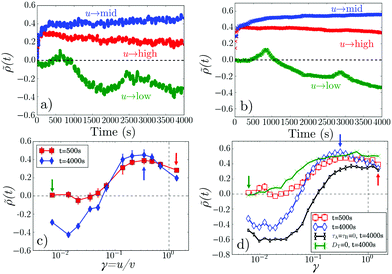
The simulations account well for the dynamics of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) at our selected experimental u values, Fig. 3b, including the oscillations at low u with a characteristic time = Λ/u ∼ 2 × 103 s. These oscillations occur because as the band of light approaches the dark centre, swimmers in the band are able to ‘tunnel through’ and stop in the centre, increasing the accumulation transiently, until the leading edge of the light band reaches the outer edge of the dark centre. Now, thermal diffusion can transport cells from the darkness to the light, whereupon they swim outwards, reducing ρ in the central dark area (see ESI,† Movies 5 and 6).
(t) at our selected experimental u values, Fig. 3b, including the oscillations at low u with a characteristic time = Λ/u ∼ 2 × 103 s. These oscillations occur because as the band of light approaches the dark centre, swimmers in the band are able to ‘tunnel through’ and stop in the centre, increasing the accumulation transiently, until the leading edge of the light band reaches the outer edge of the dark centre. Now, thermal diffusion can transport cells from the darkness to the light, whereupon they swim outwards, reducing ρ in the central dark area (see ESI,† Movies 5 and 6).
Similarly, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (γ) is well reproduced over two orders of magnitude in γ, for both t = 500 s and 4000 s, see Fig. 3c and d. In both cases γ ≈ 0.3 is optimal for accumulation, and flux reversal (drainage of the central square) occurs if γ ≲ 0.1. Importantly, with DT = 0, Fig. 3d (green), simulations show no flux reversal: bacteria transported inwards cannot escape the inner square (see ESI,† Movie 7). Nor does taking the instant-response limit τA,B = 0 give quantitative agreement, Fig. 3d (black).
(γ) is well reproduced over two orders of magnitude in γ, for both t = 500 s and 4000 s, see Fig. 3c and d. In both cases γ ≈ 0.3 is optimal for accumulation, and flux reversal (drainage of the central square) occurs if γ ≲ 0.1. Importantly, with DT = 0, Fig. 3d (green), simulations show no flux reversal: bacteria transported inwards cannot escape the inner square (see ESI,† Movie 7). Nor does taking the instant-response limit τA,B = 0 give quantitative agreement, Fig. 3d (black).
3.2 Exploring parameter space with a 1D analytic model
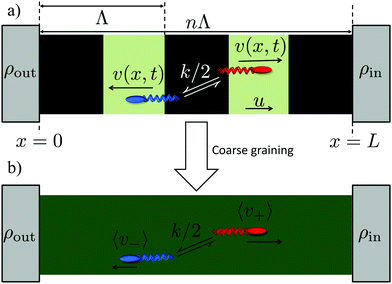
So far we have studied the effect of varying one parameter, the pattern speed u = γv using 2D experiments and simulations. We now turn away from experiments to construct an idealized 1D analytic model, which will allow us to explore the wider parameter space. Our calculations are based on recent analytical results for light-activated particles in a 1D periodic moving light field,11 which is the one-dimensional version of our 2-dimensional simulation model, but with instant bacterial response, no translational diffusion, and rotational diffusion replaced by tumbling (the only possibility in 1D). The 1-dimensional model was originally solved for a square wave in periodic boundary conditions, and used to show that flux inversion can occur if the bacteria have a finite swimming speed in the dark. Here, our bacteria do not swim in the dark, so we look at other mechanisms for flux inversion, notably caused by the pattern's duty cycle, α, or by the tumbling rate of the bacteria. We also extend the analysis to account for the non-periodic boundaries in our 2D experiments, which permit accumulation.In the original theory,11 active point particles move right or left at speed v in the light and v′ in the dark, but we set v′ = 0 here. Particles reorient independently at rate k, which can be viewed as a tumbling or rotational diffusion rate, non-dimensionalised as κ ≡ kΛ/u (tumbling and rotational diffusion are indistinguishable in 1D). A periodic, square light pattern is imposed, moving at speed u > 0, in whose comoving frame are periodic boundary conditions (BCs) at x = 0 and x = Λ, with [0,αΛ) light and [αΛ,Λ) dark. The Fokker–Planck equation (FPE) for this system with α = 0.5 was solved11 to yield the average transport velocity, 〈v〉 (equivalently, the flux), in periodic boundary conditons.
In our experiments, we do not have periodic boundary conditions, and we do not measure flux: instead we probe the density difference between different regions, which is also the relevant variable for pattern formation. We therefore extend the results of ref. 11 (see ESI†) into a coarse-grained theory to predict density differences. In detail, we calculate the concentration difference between either end of a finite square-wave illumination pattern of n (not necessarily integer) periods moving from an ‘outer’ reservoir at x = 0 to an ‘inner’ reservoir at x = L = Λn, see Fig. 4a. In the moving region, 0 < x < L, we coarse-grain over the periodic dynamics by approximating all the bacteria in this region as having uniform speeds given by the mean speeds 〈v+〉 and 〈v−〉 that 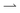 and
and  bacteria, respectively, would have in the equivalent periodic pattern, see Fig. 4. This approximation should be valid as long as there are a sufficient number n of periods in the moving pattern. The mean speeds 〈v+〉 and 〈v−〉 are obtained in the same way as the overall mean speed 〈v〉 = (〈v+〉 − 〈v−〉)/2 was in ref. 11. We give expressions for and outline the calculation of these quantitities in the ESI.†
bacteria, respectively, would have in the equivalent periodic pattern, see Fig. 4. This approximation should be valid as long as there are a sufficient number n of periods in the moving pattern. The mean speeds 〈v+〉 and 〈v−〉 are obtained in the same way as the overall mean speed 〈v〉 = (〈v+〉 − 〈v−〉)/2 was in ref. 11. We give expressions for and outline the calculation of these quantitities in the ESI.†
We are interested in concentration differences in steady state, so we write down the resulting FPE for the time-invariant (coarse grained) probability densities ϕ± in the lab frame
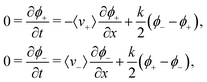 | (7) |
 particles into the light-pattern at x = 0 is
particles into the light-pattern at x = 0 is| j+(0) = ϕ+〈v+〉 = Cρout, | (8) |
 particles out of the x = L reservoir is
particles out of the x = L reservoir is| j−(L) = −ϕ−〈v−〉 = −Cρin. | (9) |
Solving eqn (7) subject to these conditions yields an exponential density distribution across the moving part of the light-field
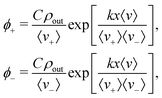 | (10) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ∞ =
∞ = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t → ∞) (see eqn (2))
(t → ∞) (see eqn (2))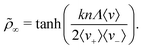 | (11) |
This result can be understood as a balance between the persistent particle flux, 〈v〉, and stochastic events where individual particles traverse the pattern against the flux. This can be seen most clearly in the case where the flux is strong in one direction, with bacteria only occasionally moving against the flow, e.g., if 〈v−〉 ≪ 〈v+〉. In this case, the probability of a bacterium which leaves the outer reservoir reaching the inner reservoir is p+ ∼ 1, whereas the probability p− of a bacterium passing in the opposite direction without returning to the inner reservoir is much smaller, and is approximately equal to the probability that zero left-to-right tumbles occur within the time τ− = nΛ/〈v−〉 taken for the bacterium to traverse this distance, i.e., p− ∼ exp(−kτ−/2). The steady state requirement then gives ρin/ρout = p+/p− ∼ exp[knΛ/(2〈v−〉)], yielding ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ∞ ∼ tanh[knΛ/(4〈v−〉)], which is in fact the limiting form of eqn (11) for 〈v−〉 ≪ 〈v+〉.
∞ ∼ tanh[knΛ/(4〈v−〉)], which is in fact the limiting form of eqn (11) for 〈v−〉 ≪ 〈v+〉.
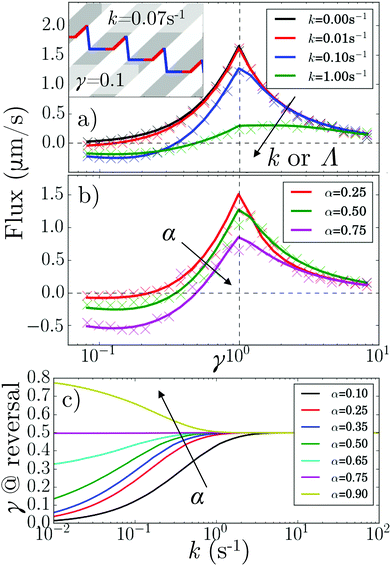
These theoretical results predict what happens when we vary α and κ (by changing k or Λ or both), Fig. 5. In particular, the flux reverses at a critical γ* < 1, Fig. 5a and b, that is k and α-dependent, Fig. 5c. Under our v′ = 0 conditions, such reversal requires a finite k (whereas for v′ > 0, reversal can occur at k = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ).11
).11
The speed reversal at k > 0 occurs, Fig. 5a, because of an asymmetry in the effect of tumbling on the  parts of the trajectory, which is illustrated in the inset for regular (period 1/k) tumbling. Tumbling effectively retards particles more during
parts of the trajectory, which is illustrated in the inset for regular (period 1/k) tumbling. Tumbling effectively retards particles more during  (red) periods because they then become un-trapped from the moving interface and so spend significant amounts of time static in the dark. The effect on the
(red) periods because they then become un-trapped from the moving interface and so spend significant amounts of time static in the dark. The effect on the  (blue) part of the trajectory is weaker because this part of the trajectory is already significantly in the dark even without tumbles, so tumbling will not disturb the relatively rapid runs through the light, lasting τlight = Λα/(u + v) until the tumbling rate increases above the rate of this process, i.e., when kτlight ≳ 1.
(blue) part of the trajectory is weaker because this part of the trajectory is already significantly in the dark even without tumbles, so tumbling will not disturb the relatively rapid runs through the light, lasting τlight = Λα/(u + v) until the tumbling rate increases above the rate of this process, i.e., when kτlight ≳ 1.
How the duty cycle α affects reversal, Fig. 5b, is illustrated by the kymographs in Fig. 6a. For increasing α,  particles spend longer in the light (so the blue curve becomes steeper), whereas
particles spend longer in the light (so the blue curve becomes steeper), whereas  particles trapped at the boundary are unaffected (the red curve stays the same); hence the reversal point γ* shifts to higher values with increasing α.
particles trapped at the boundary are unaffected (the red curve stays the same); hence the reversal point γ* shifts to higher values with increasing α.
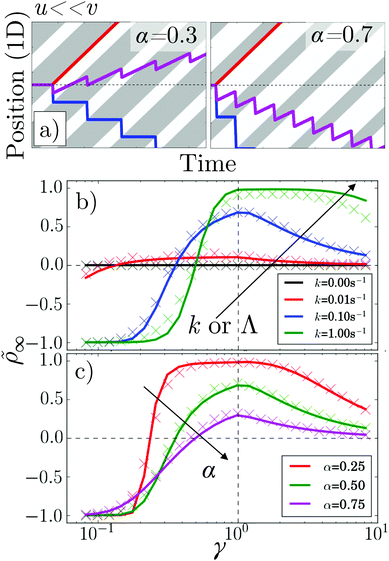 | ||
Fig. 6 (a) Kymographs for α = 0.3 and α = 0.7 with traces of non-tumbling particles moving left (blue) and right (red) for γ ≪ 1. Magenta: the average of the two tracks. (b) 1D simulation and theory of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) vs. pattern speed for α = 0.5 and k = 0, 0.01, 0.1 s−1 and 1 s−1. (c) As in (b) but for k = 0.01 s−1 and α = 0.25, 0.5 and 0.75. The colour coding of (b) follows that of Fig. 5a, while (c) follows that of Fig. 5b and c. vs. pattern speed for α = 0.5 and k = 0, 0.01, 0.1 s−1 and 1 s−1. (c) As in (b) but for k = 0.01 s−1 and α = 0.25, 0.5 and 0.75. The colour coding of (b) follows that of Fig. 5a, while (c) follows that of Fig. 5b and c. | ||
Perhaps counter-intuitively, the accumulation ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ∞, Fig. 6b and c, is not trivially related to the behavior of the flux, Fig. 5a and b. The case of α = 0.5 is striking: the accumulation generally increases with increasing k even though the flux decreases. This is mainly because as the tumbling rate increases, the probability of a bacterium moving from one reservoir to the other, without tumbling, decreases; hence, the number of events where bacteria ‘hop’ back over the moving light field against the net flow also decreases. As the tumbling rate rises, it thus becomes easier to maintain a concentration gradient, and this effect turns out to be stronger than the simultaneous decrease of the flux.
∞, Fig. 6b and c, is not trivially related to the behavior of the flux, Fig. 5a and b. The case of α = 0.5 is striking: the accumulation generally increases with increasing k even though the flux decreases. This is mainly because as the tumbling rate increases, the probability of a bacterium moving from one reservoir to the other, without tumbling, decreases; hence, the number of events where bacteria ‘hop’ back over the moving light field against the net flow also decreases. As the tumbling rate rises, it thus becomes easier to maintain a concentration gradient, and this effect turns out to be stronger than the simultaneous decrease of the flux.
To validate our analytics, we simulated a 1D system obeying the same dynamical equations already used for 2D, but with the reorientation, eqn (4), replaced by a Poissonian tumbling process, and with instant bacterial response, τA = τB = 0. This reproduced the predicted fluxes exactly, Fig. 5a and b, as before.11 To extract ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , we used simulations of a finite system, adding a small DT = 0.01 μm2 s−1 to allow the particles to escape 20 μm-long reservoirs. These simulations only approximately reproduced the theory, Fig. 6b and c. This is reasonable, as the theory itself is an approximation and we expect it to be exact only in the limit of (i) many periods, i.e., n ≫ 1, where the BCs become less important, and (ii) for limited accumulation each period, i.e., for kΛ〈v〉/(〈v+〉〈v−〉) ≪ 1, where it is valid to use a periodic approximation for the cell density distribution.
, we used simulations of a finite system, adding a small DT = 0.01 μm2 s−1 to allow the particles to escape 20 μm-long reservoirs. These simulations only approximately reproduced the theory, Fig. 6b and c. This is reasonable, as the theory itself is an approximation and we expect it to be exact only in the limit of (i) many periods, i.e., n ≫ 1, where the BCs become less important, and (ii) for limited accumulation each period, i.e., for kΛ〈v〉/(〈v+〉〈v−〉) ≪ 1, where it is valid to use a periodic approximation for the cell density distribution.
These results suggest that by tuning α and κ, it should be possible to exercise a great deal of control over how the accumulation and flux vary with γ. This is significant because polydispersity in e.g., speed and rotational diffusion rates are unavoidable, so that one will be dealing with a wide γ distribution in practice, and the ideal pattern design will depend on the goal. For example, concentrating all bacteria in a single target region requires bacteria with a wide range of speeds to be strongly rectified in the same direction, corresponding to the wide γ plateau seen at low α or high Λ in Fig. 6b and c. Alternatively, to separate a sample on the basis of speed when there is also polydispersity in tumbling or rotational diffusion, the value of α = 0.75 would be ideal, as the reversal point is then independent of k, see Fig. 5c.
4 Summary and conclusions
Recent numerical10 and analytical work11 has explored the effect of moving patterns of light–dark illumination on light-activated swimmers, and predicted the rectification of the random motion of swimmers in the direction of the moving light pattern, and a counter-intuitive regime of reverse rectification at low pattern speeds. We have performed experiments and simulations in 2D to verify that rectification in both directions does indeed occur. The simulations included a finite bacterial response time with two timescales accounting for distinct biological processes, which we found was necessary to faithfully reproduce the experimental results.We have also generalized the recent 1-dimensional analytic theory11 to predict not only the swimmer flux, but differences in swimmer densities for different spatial regions, the latter being a more natural experimental variable, and the variable directly relevant to pattern formation. We used this 1D theory to explore a wide parameter range and considered in detail two mechanisms of flux inversion: via bacterial tumbling, and via asymmetry in the waveform (i.e. the duty cycle α). To the best of our knowledge, the effects of waveform asymmetry have not been previously considered in the theoretical or simulation literature.10,11 We expect that the ability to achieve precise control of bacterial flux by several means will allow for crucial flexibility in future studies.
Indeed, our results point to a number of design principles for particle transport using moving light fields. If the target application requires accumulation, γ ≈ 1 is a necessity, however any light control delays, i.e. deviations from τA = τB = 0 are expected to shift the γ of optimum accumulation. Maximal accumulation is also achieved by minimizing the tumble rate and regulating α. Additionally, e.g., if the possibility of flux reversal is important, it will be necessary to use Brownian particles, because setting DT = 0 produced no reversal in our simulations. It is likely that some, if not all, of these principles will be applicable more widely to the control of active particles in other kinds of spatiotemporally-varying fields, e.g., electrical20 or ultrasound.21 Spatiotemporally-varying fields, in turn, may become a standard component in developing applications such as the separation of polydisperse mixtures, the directed-assembly of active particles, and the dynamic actuation and control of microscopic machines.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Teun Vissers and Mike Cates for discussions. NK was part-funded by the EU (H2020-MSCA-IF-2014, ActiDoC No. 654688). AB received funding from UK EPSRC (EP/S001255/1). All except SEG received funding from UK EPSRC (EP/J007404/1) and ERC (Advanced Grant ERC-2013-AdG 340877-PHYSAP). SEG held an EPSRC studentship. The raw microscopy images are available on the University of Edinburgh DataShare open access data repository at https://doi.org/10.7488/ds/2603.Notes and references
- W. C. K. Poon, in Physics of Complex Colloids, ed. C. Bechinger, F. Sciortino and P. Ziherl, IOS Press, Amsterdam, 2013, pp. 317–386 Search PubMed.
- M. E. Cates, Rep. Prog. Phys., 2012, 75, 042601 CrossRef CAS PubMed.
- P. Galajda, J. Keymer, P. Chaikin and R. Austin, J. Bacteriol., 2007, 189, 8704–8707 CrossRef CAS PubMed.
- R. Di Leonardo, L. Angelani, D. Dell’Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541–9545 CrossRef CAS PubMed.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- J. Arlt, V. A. Martinez, A. Dawson, T. Pilizota and W. C. K. Poon, Nat. Commun., 2019, 10, 2321 CrossRef PubMed.
- J. Arlt, V. A. Martinez, A. Dawson, T. Pilizota and W. C. K. Poon, Nat. Commun., 2018, 9, 768 CrossRef PubMed.
- G. Frangipane, D. Dell'Arciprete, S. Petracchini, C. Maggi, F. Saglimbeni, S. Bianchi, G. Vizsnyiczai, M. L. Bernardini and R. Di Leonardo, eLife, 2018, 7, e36608 CrossRef PubMed.
- N. Koumakis, A. Lepore, C. Maggi and R. Di Leonardo, Nat. Commun., 2013, 4, 2588 CrossRef CAS PubMed.
- A. Geiseler, P. Hänggi, F. Marchesoni, C. Mulhern and S. Savel'ev, Phys. Rev. E, 2016, 94, 012613 CrossRef PubMed.
- C. Maggi, L. Angelani, G. Frangipane and R. Di Leonardo, Soft Matter, 2018, 4958–4962 RSC.
- J. Schwarz-Linek, J. Arlt, A. Jepson, A. Dawson, T. Vissers, D. Miroli, T. Pilizota, V. A. Martinez and W. C. K. Poon, Colloids Surf., B, 2016, 137, 2–16 CrossRef CAS PubMed.
- J. Adler and B. Templeton, J. Gen. Microbiol., 1967, 46, 175–184 CrossRef CAS PubMed.
- J. M. Walter, D. Greenfield, C. Bustamante and J. Liphardt, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2408–2412 CrossRef CAS PubMed.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Tailleur, G. Bryant, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 2011, 106, 018101 CrossRef CAS PubMed.
- V. A. Martinez, R. Besseling, O. A. Croze, J. Tailleur, M. Reufer, J. Schwarz-Linek, L. G. Wilson, M. A. Bees and W. C. K. Poon, Biophys. J., 2012, 103, 1637–1647 CrossRef CAS PubMed.
- A. Jepson, V. A. Martinez, J. Schwarz-Linek, A. Morozov and W. C. K. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 041002 CrossRef PubMed.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- K. J. Rao, F. Li, L. Meng, H. Zheng, F. Cai and W. Wang, Small, 2015, 11, 2836–2846 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00799g |
| This journal is © The Royal Society of Chemistry 2019 |