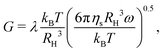Open Access Article
Open Access ArticleSurface heterogeneity affects percolation and gelation of colloids: dynamic simulations with random patchy spheres†
Gang
Wang
 and
James W.
Swan
and
James W.
Swan
 *
*
Massachusetts Institute of Technology, Department of Chemical Engineering, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: jswan@mit.edu
First published on 5th June 2019
Abstract
Surface heterogeneity of colloidal particles has a significant impact on their structure in solution and their rheological properties. During particle synthesis, heterogeneous chemical functionalization, processes of self-assembly, or phase separation, can all lead to heterogeneous colloidal surfaces which impart anisotropic interactions to suspended particles. Additionally, an important class of colloids, biological macromolecules, exhibit similar localized, short-ranged, anisotropic interactions, which have a significant impact on their solution properties. Therefore, understanding the assembly and rheology of such colloids can provide insight into a wide variety of relevant physical systems. In this computational study, we investigate dispersions of particles having surface patches with randomized functionality as a model for heterogeneous colloids. We use Brownian dynamics simulations with hydrodynamic interactions to explore the differences between these random patchy particles and homogeneous (or isotropic) particles. The common basis used for comparing dispersions of particles with different surface functionality is equality of the second virial coefficient, so that dispersions of particles with different patterns of surface heterogeneity are similar thermodynamically at low particle concentrations. We show that at modest particle concentrations, significant deviations from the isotropic model are evident in the dispersion micro-structure, giving drastically different percolation transition points depending on the degree of surface heterogeneity. However, these deviations can be rationalized and a universal percolation criteria derived in terms of the osmotic pressure of the dispersion. Heterogeneous interactions also impose extra constraints on the relative translation and rotation between neighboring particles, which increase the viscosity and elastic modulus of aggregated dispersions and gels built from heterogeneous colloids and shifts the gel point measurably.
1 Introduction
Colloidal particles with short-range interactions are ubiquitous in functional materials and pharmaceuticals. Versatile physical properties can be achieved by different synthetic routes, which make them useful for a variety of applications.1–9 The ability to understand and predict the behavior of dispersions of these particles from the microscopic properties of individual particles will enable rational design of colloidal materials for specific applications. Inter-colloid interactions are commonly treated as isotropic,10–12 which for many materials can be a useful approximation for interpreting experiments.13–16 However, heterogeneities in the inter-particle interaction are common at the colloidal scale, and can have significant impact on micro-structure and rheology of colloidal dispersions. Anisotropic inter-particle interactions are usually caused by heterogeneous chemical functionalization,17,18 self-assembly,19,20 or phase separation21 during particle synthesis. Anisotropic interactions are also common between proteins and other biological macromolecules.22–25 A fundamental understanding of the impact of surface heterogeneity on the micro-structure and rheology of colloidal particles will aid in the rational design of their functionalities.One important effect of surface heterogeneity is a constraint on the relative translation and rotation of neighboring particles. This extra constraint can potentially change the dynamics and rheology of attractive colloidal dispersions. This is illustrated schematically in Fig. 1, where dispersions of spherical particles having homogeneous or heterogeneous surfaces are assumed to have identical percolated micro-structure. The homogeneous surface allows neighboring particles to freely rotate relative to each other. The rotational constraint between heterogeneous colloids generates additional bending moments that resist deformation. This changes the complex modulus and the gel point of the heterogeneous suspension relative to the homogeneous suspension.
Colloidal gels are important soft material for their unique mechanical properties. They are widely applied in paints,5 cosmetics,6 and food products,7 and are being developed for new applications such as tissue engineering8 and 3D printing.9 Despite the numerous applications of colloidal gels, the location of the gel point is not well understood. The gel transition, or critical gel point, is commonly defined as the condition at which the power law scaling with respect to frequency of both storage modulus G′ and loss modulus G′′ coincide for a broad range frequencies,26,27 and is typically determined using small amplitude oscillatory shear (SAOS) experiments. However, other definitions of the critical gel point have been used.28,29 For example, “percolation”, which is defined as the appearance of an infinitely spanning network in the suspension, is sometimes used interchangeably with term “gelation”.30 Percolation, a structural criterion, does not necessarily ensure gelation, a rheological criterion. Eberle and coworkers31,32 found that the critical gel point overlapped perfectly with the percolation transition for polymer brush grafted nanoparticles. However, other works16,28 have shown that spinodal decomposition, which requires much stronger inter-particle attractions than exhibited at the percolation transition, is necessary for some colloidal dispersions to form gels. These diverse experimental results from previous works suggest there are different physical attributes of the particles critical for understanding their gelation. Surface heterogeneity is a candidate, which will be investigated in this work.
Understanding the influence of surface heterogeneity has an especial implication for protein solution rheology. Protein molecules are highly heterogeneous colloidal particles having a widely varied surface charge distribution and hydrophobic patches.15,24,33 Protein surface functionalities significantly impact the solution micro-structure and viscosity,23,34 which is a phenomenology that is not explained by isotropic liquid theories22,35 based on spherically averaged attractions and lumped charges. Our recent work36 has shown that constraint on relative motion between nearly touching proteins explains the high viscosity observed in concentrated solutions of monoclonal antibodies.
The patchy particle model is one of the simplest and most flexible models that can capture heterogeneity. Many different types of patchy particles have been synthesized with regular arrangements of surface patches, and their phase behavior22,37–39 and self-assembly40,41 has been extensively studied. However, these studies primarily focus on particles with geometrically ordered patch architectures.42,43 For colloidal dispersions and biomacromolecules in general, a disordered, or random distribution of patches is more representative. In the present work, we develop a flexible random patchy sphere model and use Brownian dynamics simulations with hydrodynamic interactions to investigate the micro-structure, thermodynamic properties, and rheology of concentrated dispersions. Patchy particles are compared with uniform particles to elucidate the effect of surface heterogeneity on percolation and gelation. Recent work by Blanco and Shen (2016),70 has analyzed spherical particles with a small number of symmetrically positioned patches reflecting different dipolar and quadrupolar charge distributions that could be correlated with phase behavior and percolation.
2 Methods
2.1 Random patchy sphere model
We utilized a model colloidal particle similar to that proposed by Van Lehn and Alexander-Katz for nanoparticle–lipid bilayer simulations,44 and apply this model to study dispersions. We allow that the surface of our model spherical particle can be occupied by two types of patches, as shown in (Fig. 2a). The patches are identified on the surface of the particle with beads whose positioning is determined by a geodesic decomposition of the particle surface into a Goldberg polyhedron. Beginning with an initial icosahedral tessellation, the edges of the polyhedron are iteratively bisected to generate a new set of vertices on which the beads centers are positioned. Each bead on the polyhedron is randomly assigned one of two states, +1 (red) or −1 (blue), as shown in (Fig. 2a). To control the spatial characteristics of this assignment process, a Monte Carlo simulation of the Ising model on the tessellated spherical surface is applied to randomly assign the states to the beads. The energy of the Ising model is defined as: | (1) |
The force and torque acting on these particles can be obtained by summing up the site–site interactions. In addition to a stiff quadratic repulsive interaction representing excluded volume effects, beads interact via pairwise attractive or repulsive interactions, depending on the site types in the pair, to model heterogeneous surface effects. Throughout the main text, sites of the same type repel while sites of opposite type attract, as shown in (Fig. 2c). The appendix considers the implications of an inverted set of interactions. The Yukawa potential is used for the functional form of the site–site interactions because of its simplicity and applicability to modeling screened electrostatics:
 | (2) |
2.2 Brownian Dynamics of rigid composite-bead particles
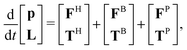 | (3) |
For a micrometer or nanometer sized particle in a viscous fluid, the characteristic time scale for momentum relaxation, or the inertial time scale is approximately τI = ρRH2/ηs, where ρ is the density of the particle, RH is the hydrodynamic radius of the particle, and ηs is the viscosity of the solvent. This time scale about 10−6 seconds for micron-sized colloids in water. However, the diffusion time scale τD = 6πηsRH3/kBT which describes the characteristic time for Brownian motion, is approximately 1 second in the same scenario. Thus, changes in the momenta occur much faster than all other dynamic processes, and the left hand side of the Langevin eqn (3) is approximately zero in this over-damped regime.
Hydrodynamic forces and torques (FH and TH) are long-ranged interactions due to the flow field perturbation caused by particle motion in a viscous fluid. They greatly affect the dynamics of colloidal dispersions, and including them in computational models is crucial to accurately explain kinetic phenomena such as gelation,13,14 and quantify transport properties such as diffusivity and viscosity.36,45 The hydrodynamic force FH and torque TH in the over-damped regime are linear in the particles' translational velocity U and angular velocity Ω:46
 | (4) |
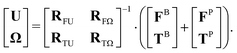 | (5) |
Our previous works36,45 efficiently evaluated the dynamics of such assemblies by describing bead–bead hydrodynamic interactions with the Rotne–Prager–Yamakawa (RPY) mobility tensor47 ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) RPYαβ, which is a far-field approximation for velocity-force couplings between spherical beads:
RPYαβ, which is a far-field approximation for velocity-force couplings between spherical beads:
 | (6) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) RPYαβ is the block at row α, column β of the grand mobility matrix
RPYαβ is the block at row α, column β of the grand mobility matrix ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) :
: | (7) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) and r are the unit vector and distance between the centers of beads α and β, respectively. We choose to set a = aB for this work. Other choices yield similar hydrodynamic interactions among the particles.
and r are the unit vector and distance between the centers of beads α and β, respectively. We choose to set a = aB for this work. Other choices yield similar hydrodynamic interactions among the particles.
The force on any bead fα = fEα + fCα can be divided into an external force fEα, representing the force from other particles or external fields, and a constraint force fCα, which is the internal force necessary to enforce rigid body motion of the particles. The external force is known, but the constraint force cannot be directly expressed. However, there are relationships that fEα and fCα must satisfy: (i) the summation and total moment of fEα on a composite-bead particle i must be equal to the total force and torque on that particle; and (ii) the summation and total moment of fCα on any particle i must be zero. Therefore, bead force fα satisfies:
 | (8) |
 | (9) |
| uα = Ui + HTi,α·Ωi, | (10) |
 | (11) |
 | (12) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1·ΣT acting as the resistance tensor in (5).
−1·ΣT acting as the resistance tensor in (5).
According to the fluctuation–dissipation theorem, the mean value and the autocorrelation function of the Brownian stochastic force on the beads fB can be characterized by:46
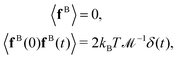 | (13) |
An efficient implementation of this algorithm is described in further detail in the ESI,† as well as other works on immersed boundary simulations.52,53 It is important to note that when samples fully equilibrate, thermodynamic properties can be computed using other, simple simulation methods such as Markov-chain Monte Carlo, molecular dynamics, or freely-draining Brownian dynamics, which neglect the hydrodynamic interactions among the particles. For transport properties such as diffusion and viscoelasticity, the hydrodynamic interactions are critical to quantitative modeling.
 | (14) |
 | (15) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) xy,
xy, | (16) |
 | (17) |
The bulk stress, σ in a dispersion deformed at rate of strain e is given by:48
| σ = −pfI + 2ηse − nkBTI + σH + σP + σB, | (18) |
In the dilute limit, the hydrodynamic contribution is given by the familiar Einstein's expression σH = 5ηsϕe. However, in solutions with higher concentrations, the stress coupling with particle motion and strain field gives higher order terms and cannot be simplified by this expression. In addition to the stresslet SHe contribution, the relative motion to the fluid also contributes to the hydrodynamic stress σH linearly through the stresslet coupling resistance tensors RSU and RSΩ. The total stress contributed hydrodynamically is:49
 | (19) |
The 5 new resistance tensors RFE, RTE, RSE, RSU, and RSΩ can be evaluated using the same approach to derive (12). For a rigid particle i consisting of beads α, its stresslet S is:
 | (20) |
| uα = Ui + HTi,α·Ωi + e·(xα − xi). | (21) |
 | (22) |
 | (23) |
The contribution from deterministic inter-particle interactions σP can be expressed as:49
 | (24) |
The Brownian contribution to the stress σB is:49
 | (25) |
A high-performance algorithm for dynamic simulation of rigid composite-bead particles has been developed that combines a newly developed integration scheme52,53 with the computation of bead mobility tensor is powered by a fast algorithm for evaluating the RPY mobility, named the Positively Split Ewald (PSE) method.54 The implementation is built as a plugin to HOOMD-blue,55,56 a molecular dynamics suite optimized for massively parallel processing on GPUs, and can be downloaded from a publicly accessible domain: http://web.mit.edu/swangroup/software.shtml.
2.3 Ramped-frequency sweep method
To obtain linear viscoelastic properties G′(ω) and G′′(ω) under small amplitude oscillatory shear (SAOS), a ramped-frequency sweep (“chirp”) method57,58 is used to investigate the rheology at a range of frequencies with a single simulation run. A wide bandwidth oscillatory strain γxy signal is imposed: | (26) |
 | (27) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) xy(ω) and
xy(ω) and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) xy(ω) are Fourier transform of shear stress and strain, respectively.
xy(ω) are Fourier transform of shear stress and strain, respectively.
Abrupt start-up and cessation of the shear rate often introduce noise into the Fourier transform. To resolve this issue, we apply the Optimally Windowed Chrip (OWCh)59 method using a Tukey window function w to modulate the strain (γwxy = γxyw) and smooth the initial and final stages of the oscillatory shear:
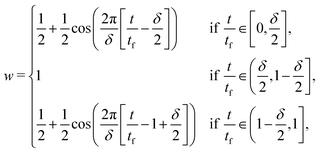 | (28) |
2.4 Adhesive hard sphere model
Baxter's adhesive hard sphere (AHS) model is the most widely used theory describing colloidal dispersions with short-ranged attractions60 and serves as the standard reference for comparison of experiments and simulations with different types of particles. In this model, the range of attraction potential is assumed to be infinitesimally small, and the attraction strength is characterized by a single parameter, the Baxter temperature τ, which can be obtained from the second virial coefficient B22:64 | (29) |
 | ||
| Fig. 4 Phase diagram for Baxter's adhesive hard sphere (AHS) model.60–63 | ||
To compare suspensions of patchy particles and isotropic particles, we compute Baxter temperature τ as a measurement of the averaged interaction strength between particles. This also allows us to directly compare our patchy particles to Baxter's AHS model. The Baxter temperature can be computed from the second virial coefficient B22 by (29). For particles with isotropic interactions, the pair potential, E, is only a function of distance r, so B22 is obtained by a simple integration:
 | (30) |
 | (31) |
3 Results and discussion
Brownian dynamics simulations with hydrodynamic interactions have been performed on suspensions of random patchy particles with different βJ value from −0.3 to 1.0 (unconstrained and balanced), isotropically attractive particles (particles composed of the same type of attractive sites), and Janus particles (particles with two types of sites occupying the two hemispheres) within a volume fraction range of 0.10 to 0.30. For each βJ value, 5 unconstrained and 5 balanced random patchiness patterns are generated from the Monte Carlo method, and separate simulations are performed on single particle types. 500 identical composite-bead particles are included in the simulation box, and each particle is composed of 42 beads.For each different Baxter temperature τ, a random hard-sphere configuration of composite-bead particles is generated first, and the suspension is quenched to the corresponding target interaction strength immediately. Solution micro-structure, percolation transition, thermodynamics, and rheology are then investigated. It should be noted that the volume fraction used in this work is based on the hydrodynamic radius of composite-bead particles. The hydrodynamic radius is found by computing the translational drag coefficient of a single composite bead particle and dividing by 6πηs. As shown in the ESI,† the equivalent volume fraction obtained by fitting the osmotic pressure to the equation of state for hard-sphere suspensions is approximately 20% larger. This represents a 6% difference between the hydrodynamic radius and the “thermodynamic” radius of the particles. Any micro-structural models depending on the hard sphere volume fraction are appropriately scaled to represent the model in terms of the hydrodynamic volume fraction.
3.1 Micro-structure and percolation transition
At high Baxter temperature or low interaction strength, Brownian motion dominates over the site–site interactions, and the micro-structure of any particle type is similar to that of hard-sphere suspensions. As the Baxter temperature decreases, both isotropic particles and patchy particles form bonds due to the attractive Yukawa potential and aggregate to form clusters. However, the structure of the clusters formed from isotropic particles is different from the structure of the clusters formed from patchy particles. Because of the anisotropic inter-particle interactions due to heterogeneity, the energy profile between a pair of approaching patchy particles is rough and has strong angular dependency. The roughness of the energy profile creates a barrier preventing rotations that would allow a patchy particle pair traverse between states with local energy minima. This anisotropic effect limits the number of potential configurations accessible when anisotropic particles approach each other, and arrests them from further relaxation. Isotropic particles, on the other hand, do not have the same rough energy landscape and rotate freely within clusters.Simulation snapshots of different types of particles quenched well below their percolation transition (τ = 0.05) at ϕ = 0.30 are shown in Fig. 5. All of the suspensions percolate, but the micro-structure is different despite having the same Baxter temperature. Because isotropically attractive particles can form bonds with each other from any orientation, and neighbors can freely rotate among different configurations, the isotropic particles form compact clusters. Patchy particles form more clusters because only limited orientations are allowed for bonding, and the constraint due to heterogeneity creates a barrier to further structural relaxation. Close packed clusters are seldom observed in patchy particle solutions.
Fig. 6 shows the average number of bonds (or number of nearest neighbors) of each particle 〈Nb〉 at ϕ = 0.30 plotted against the Baxter temperature τ. The number of bonds for all types of particle is approximately the same at τ values larger than 10. However, for τ below 0.01, isotropically attractive particles have more than 6 nearest neighbors, indicating the formation of closely packed clusters, while all the patchy particles have about 4 nearest neighbors regardless of patchiness type within the same τ regime. The number of bonds in suspensions of patchy particles with finer patches (higher βJ values) starts to increase at a higher τ value than particles with coarser patches (lower βJ values), Janus particles, and isotropically attractive particles. This indicates that particles with the same second virial coefficient exhibit different structures at higher concentrations depending on the surface patchiness. With finer patchiness, patchy particles form clusters at higher τ values where isotropic particles are still well dispersed. The number of bonds is determined by identifying all particle pairs within a cut-off set by the range of the inter-bead interaction, which decays exponentially. Alternative nearest neighbor schemes varying the cut-off by fifteen percent or using the first nearest neighbor shell in the radial distribution function gave quantitatively indistinguishable results.
Because the number of nearest neighbors Nb is an indicator of percolation,61,65 the shift of the 〈Nb〉–τ curves implies that surface heterogeneity will shift the percolation transition. Typically, the percolation transition is defined as the appearance of an infinitely spanning network in the suspension.66 Our simulations define a suspension to be percolated when more than 50% of particle configurations sampled over time have a cluster that connects with its periodic images in all three directions of the simulation box. The percolation transition for different types of particles with volume fractions from 0.10 to 0.30 is shown in Fig. 7. The theoretical prediction from Percus–Yevick theory for adhesive hard-spheres61 is also included in the plot as a reference. For every particle type, the percolation transition τ increases with volume fraction ϕ, which qualitatively agrees with the theoretical prediction. With finer patchiness, the suspension percolates at higher τ values, and the percolation boundary moves away from the theoretical prediction. For example, the finest patchy particles with the highest βJ = 1 percolate at around τ = 4 with ϕ = 0.30, while the theory predicts the percolation Baxter temperature to be approximately τ = 0.6.
 | ||
| Fig. 7 State diagram showing the percolation transition, τ, of different types of particles as a function of volume fraction. Closed circles represent percolated suspensions, and open circles represent un-percolated suspensions. The solid line is the percolation line predicted from Percus–Yevick theory.61 | ||
For isotropic particles with short-ranged attractions in the dilute limit, the Baxter temperature is the only determining factor for structure and percolation. For patchy particles, even at low concentrations, there are differences arising from many-body effects. The highly localized attractive interactions of patchy particles bind them together and form a network, which prevents the particles from exploring all phase space. This rough energy landscape explains the variation in averaged number of bonds 〈Nb〉 and Baxter temperature τ beyond the percolation transition.
3.2 Osmotic pressure
Surface heterogeneity greatly affects the thermodynamic properties of the dispersions. Fig. 8 shows the osmotic pressure P, normalized by nkBT where n is the particle number density, plotted as a function of Baxter temperature τ. As τ decreases, the attraction between particles reduces the osmotic pressure of the suspension. The theoretical prediction from Percus–Yevick theory by Baxter60 is also included to compare with our simulation results. | ||
| Fig. 8 Osmotic pressure P normalized by nkBT, where n is the particle number density, as a function of Baxter temperature τ. The prediction from Percus–Yevick theory by Baxter60 is shown as the black curve. | ||
The isotropically attractive particle suspensions agree with the theoretically predicted osmotic pressure. As the surface patchiness becomes finer, however, the pressure deviates from the theory. At the same τ value, suspensions of particles with finer patches have lower osmotic pressure than those of particles with coarser patches. This is another example where the Baxter temperature, or averaged pair interaction strength cannot give a successful prediction of the thermodynamic properties of heterogeneous particles.
Osmotic pressure P is plotted as a function of averaged number of nearest neighbors 〈Nb〉 as shown in Fig. 9. The data for all types of particles collapse into a single master curve, which seems to indicate there exists a common, coarse-grained thermodynamic model from which to analyze the structure and percolation of diverse sets of patchy particles. In Fig. 9, the osmotic pressure decreases with increasing attraction strength, while the number of bonds increases. The only perceived difference between particle types in the P–〈Nb〉 curves occurs at very negative osmotic pressures, where isotropic particles have six bonds on average while patchy particles have four. These bond numbers agree with the isostatic contact numbers of frictionless spheres (ziso = 6) and perfect frictional spheres (ziso = 4), respectively. This indicates the constraint due to surface heterogeneity is similar to that from surface friction. Negative osmotic pressure indicates that the dispersion would undergo syneresis if it were not attached to the boundaries. Such a condition is common in dispersions of attractive particles.
 | ||
| Fig. 9 Normalized osmotic pressure P/nkBT as a function of average number of bonds 〈Nb〉. The solid line is the theoretical percolation osmotic pressure using Percus–Yevick theory. | ||
Because of the universal correlation between micro-structure and osmotic pressure regardless of particle type, osmotic pressure P may be more useful than τ to describe the percolation transition. The percolation transition is shown on the ϕ–P plane instead of the ϕ–τ plane in Fig. 10(a). The solid curve is the percolation pressure predicted by Percus–Yevick theory, which is obtained by calculating the percolation transition τ value61 and using Baxter's equation of state60 to compute the corresponding pressure. Unlike the ϕ–τ diagram in Fig. 7, the theoretical percolation curve clearly separates percolated and unpercolated samples for all types of particles. The only exception is at ϕ = 0.10, where fluid–fluid phase separation competes with the percolation transition. The agreement between theory and simulation when adopting osmotic pressure P instead of Baxter temperature τ indicates that heterogeneous particles at the same pressure have the same micro-structure. This is in contrast to Fig. 5 where the influence of heterogeneity on packing structure at the same τ is evident. At the percolation transition point, there appears to be a universal critical mechanical load, or pressure, for any particle patchiness.
 | ||
| Fig. 10 Osmotic pressure, determines the percolation transition regardless of surface heterogeneity. (a) Phase diagram in the pressure–volume fraction (P–ϕ) plane, where closed circles represent percolated suspensions, and open circles represent unpercolated suspensions. The percolation transition has a universal osmotic pressure regardless of particle surface heterogeneity that agrees with Percus–Yevick theory. (b) P–τ–ϕ surfaces for different particle types. The percolation transition can also be represented by a surface perpendicular to the P–ϕ plane, because of the universal percolation pressure. The projections of the intersections between equation of state surfaces and the percolation surface into the τ–ϕ plane are the different percolation τ values as shown in Fig. 7. | ||
Fig. 10(b) shows a schematic of the percolation transition in P–τ–ϕ space for different patchy particles. For a given particle type, the osmotic pressure P is a single-valued function of volume fraction ϕ and Baxter temperature τ. Therefore, the equations of state for different particle types can be represented as different two-dimensional surfaces (“particle surfaces”) in P–τ–ϕ space. The percolation transition can also be represented by a surface. Because of the universal percolation pressure which is only a function of ϕ, this surface is perpendicular to the P–ϕ plane. The intersecting curve between a particle surface and the percolation surface can be used to compute the percolation transition as a function of τ for that particle type. Because different particle surfaces intersect the percolation surface in different places, the projections of the intersections into the τ–ϕ plane are different. Therefore, heterogeneity strongly affects the values of τ at which percolation occurs, as shown in Fig. 7. Finally, the osmotic pressure and number of nearest neighbors at lower volume fractions are depicted in the ESI† and are consistent with the observations at ϕ = 0.3. This collapse in terms of the osmotic pressure is reminiscent of the use of the compressibility factor to collapse dynamics in hard sphere systems.67
3.3 Gelation
Multiple definitions of gelation are commonly used in literature. In this work, gelation is defined as described in the seminal work by Chambon and Winter (1987).26 A colloidal dispersion is at the critical gel point if the tangent of the loss angle, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, is independent of the oscillation angular frequency ω:
δ, is independent of the oscillation angular frequency ω: | (32) |
Fig. 11 shows G′ and G′′ of a suspension at ϕ = 0.30 in simulations of SAOS with a ramped-frequency sweep (26). The complex modulus is normalized by the pressure scale of the system kBT/RH3, and angular frequency is normalized by the diffusion time scale of the system τD = 6πηsRH3/kBT. Linear viscoelastic responses of 4 types of particles are shown at Baxter temperatures above, below, and at the critical gel point.
The Baxter temperature τ at the critical gel point differs among suspensions with different particle types. Similar to observations of τ at the percolation transition, the gel point τ increases for finer patchiness. A similar trend with respect to the percolation transition volume fraction is also observed at the gel transition: τ increases with the volume fraction ϕ. The critical gel point for different particle types and volume fractions ϕ can be found in Table 1. Some patchy particles gel above the AHS percolation transition, τ, which again confirms that τ cannot be used to predict phase behavior of heterogeneous particle suspensions at moderate concentrations.
| Type | ϕ = 0.10 | ϕ = 0.20 | ϕ = 0.30 |
|---|---|---|---|
| Isotropic | 0.01 | 0.02 | 0.02 |
| Janus | 0.02 | 0.03 | 0.05 |
| βJ = −0.2 | 0.1 | 0.3 | 0.5 |
| βJ = 1 | 0.3 | 0.8 | 1 |
The solid black lines in Fig. 11 show the modulus:
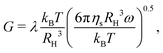 | (33) |
As shown for percolation, the osmotic pressure P instead of Baxter temperature τ is more useful for predicting the micro-structure and thermodynamic properties for heterogeneous particle dispersions. The percolation transition pressure is independent of particle type, and it is interesting to ask whether the osmotic pressure is also predictive of the gel point for different particle types. After all, there is a universal viscoelastic scaling at this point. We performed equilibrium Brownian dynamics simulations at the critical gel point to obtain the osmotic pressures for suspensions of different particle types. Fig. 12 shows the osmotic pressure at the critical gel point with volume fractions from 0.10 to 0.30 overlaid with the percolation transition data in the P–ϕ plane. Compared with the universal percolation transition pressure line, the osmotic pressure P at the critical gel point is not universal. The gel point with respect to pressure increases with patch fineness. Suspensions of particles with finer patchiness have higher osmotic pressure at the critical gel point, while suspensions of Janus particles and isotropically attractive particles only reach critical gel point at very low osmotic pressure, presumably after phase separating.
 | ||
| Fig. 12 State diagram in the pressure–volume fraction (P–ϕ) plane comparing percolation transition and gel point. In addition to the comparison of percolation transition between simulation and theory (as in Fig. 10), osmotic pressures at critical gel point (closed squares) of 4 types of particles are also included in the plot. The dashed line represents the osmotic pressure at fluid–fluid phase separation predicted by Baxter's AHS model.60 Despite the universal percolation transition pressure, the corresponding pressure at the observed gel point differs due to the surface heterogeneity. | ||
Below the gel point, particles in the dispersion are dynamically arrested in a network from reaching the thermodynamic equilibrium state. Therefore, it is not surprising that almost all types of particles have an osmotic pressure below that of fluid–fluid phase separation by AHS model60 (except random patchy spheres at ϕ = 0.30), but without phase separating micro-structure. The different osmotic pressure for each type of particles partially explains the previous discrepancies in literature over the relationship among percolation, gelation, and phase separation.16,28,31,32
The percolation transition and the gel point are controlled by osmotic pressure P and complex modulus G*, respectively, which are mechanical properties with distinct physical origins. The universality of one does not necessarily ensure universality of the other. The micro-structure and percolation are dependent on the normal mechanical load among particles, which is embodied in the osmotic pressure. Rheology, on the other hand, is also influenced by the bending moments and frictions between neighboring particles, which is still quite sensitive to surface heterogeneity. Therefore, in experiments we may expect to observe critical gelation anywhere from the percolation line to below the spinodal, due to varied surface characteristics of the dispersed particles.
Fig. 13 shows two dynamic properties, mean squared displacement (MSD) 〈Δr2〉 and intermediate scattering function (ISF) F(q,Δt), for dispersions of different particle types at ϕ = 0.30.
The mean squared displacement (MSD) is a measurement of the tracer diffusion rate of individual particles. Fig. 13(a) shows the MSD slightly above the percolation transition (“dispersed”) and at the critical gel point (“gel”). For dispersed particles, the MSD curves are identical for all types of particles in both the short-time and long-time limits. Without a percolated network structure, the freely moving particles have similar diffusive motion on all time scales, and the MSD is almost linear in the whole range of lag time Δt. At the critical gel point, however, the MSD curves differ for different types of particles. In the short-time limit, the MSD of patchy particle suspensions are linear in time and lay on the same curve. The isotropic particle suspensions, on the other hand, forms compact clusters and thus has a slightly lower MSD than the patchy particles do. As the lag time increases, the MSD becomes sublinear with lag time and the curves of patchy particles also start to diverge. In the long-time limit, the MSD is linear again. The Janus particle suspension has the highest MSD value in the long lag time regime, while the random patchy particle with βJ = 1 diffuses the slowest.
The intermediate scattering function characterizes the relaxation processes across many length scales, represented by the various wave vector q values. In Fig. 13(b), the ISF of particle suspensions at ϕ = 0.30 is shown as a function of lag time Δt. Three q values are selected to probe the dynamics at various length scales. Like the MSD results, the decay of ISF is similar for all types of particles at short-time limit, but differs at longer times. The ISF of the isotropically attractive particle suspension cannot be directly compared with those of the patchy particle suspensions because the micro-structures are quite different. For the heterogeneous particles, the Janus particle suspension decays the most rapidly and thus has the fastest relaxation rate. The random patchy particle suspension with the finest patchiness (βJ = 1) relaxation the slowest. This trend agrees with the MSD results.
The different long-time dynamics among particles with different heterogeneity demonstrates the constraining effects imposed by patch–patch interactions. Although all the patchy particles form slowly relaxing clusters that give equal averaged bond number, they have different rates of relaxation due to different energy landscape roughness.
4 Conclusions
Using simulations of model dispersions of random patchy spheres, we have elucidated the differences between heterogeneous and isotropic particles. Isotropic particles with short-ranged attractions having the same second virial coefficient B22 are thermodynamically indistinguishable in the dilute limit. We showed that particles having fine patches and the same second virial coefficient can exhibit significant deviations in micro-structure compared to isotropic models, leading to different percolation transition points at modest particle concentrations. Surface heterogeneity can prevent particles from forming compact clusters which shifts the percolation transition away from the theoretical prediction of Baxter's isotropic AHS model.Baxter temperature τ, which is determined by the second virial coefficient B22, is a measurement of averaged attraction strength between two particles. From measurement of the number of nearest neighbors and the osmotic pressure, we found that τ alone is not suitable for characterizing the state of a dispersion of heterogeneous particles. Different sized patches on the particle surface lead to different τ values at the percolation transition. Instead, the micro-structure is universally controlled by mechanics, and correlated strongly with the osmotic pressure. The percolation transition pressure is the same for all particle types and agrees with the theoretical prediction. In addition to its impact on thermodynamics, heterogeneity on particle surfaces impose extra constraints on relative rotations between neighboring particles, resulting in higher elastic modulus and slower long-time diffusion dynamics. This heterogeneity effect on dynamics and rheology of particles at their critical gel point could account for previous discrepancies in literature over the relationship among percolation, gelation, and phase separation.
To further understand the effect of heterogeneity on colloidal dispersions, future investigation should focus on developing equations of state for random patchy particles as a function of surface patch size. In addition to patchiness, surface roughness, friction, and steric effect due to anisotropic shapes can all constrain particle motion when particles approach each other. Therefore, further quantitative understanding in the local interactions between particles at contact is required to understand the nature of gelation and the location of gel point. A quantitative description of the strength of rotational hindrance due to heterogeneity, friction, or anisotropic shape is necessary to predict the gel points of different colloidal systems based on individual particle properties. The typical bending moment could be a critical quantity to measure and characterize its contribution to complex modulus.69 Lastly, the effects of anisotropic shape are not covered in the present work, but it impacts solution micro-structure and rheology. Understanding the properties of heterogeneous non-spherical particle suspensions, which are exemplified by protein drugs in the biopharmaceutical industry, is critical for their applications.
Conflicts of interest
There are no conflicts to declare.Appendix: thermodynamics of patchy particles with inverted site–site interactions
Sites interact with each other via pairwise attractive or repulsive interactions depending on there types in our random patchy sphere model. Sites of the same type repel while sites of opposite types attract. In this section, we investigate another form of pairwise interactions: sites of the same type attract while sites of opposite types repel. Fig. 14 shows the comparison between the original model and this inverted model of the short-ranged interaction. As shown in Fig. 14(a), regardless of the two different interaction forms, the osmotic pressure only depends on τ value and βJ value. The original model and the inverse model with the same patch size share the same trend in the plot. Fig. 14(b) shows the osmotic pressure P as a function of averaged number of nearest neighbors 〈Nb〉. All types of particles collapse into a single curve. The universal correlation between micro-structure and osmotic pressure is not affected by either the patch size or the form of interactions. In conclusion, the thermodynamics of composite-bead patchy particle suspensions with attractive/repulsive site–site interactions is only determined by the patch size and not the site model. | ||
| Fig. 14 Comparison of thermodynamic properties between the original interaction model (circles: sites of the same type repel while sites of opposite types attract) and the inverse model (crosses: sites of the same type attract while sites of opposite types repel). Without loss of generality, only balanced patchy spheres are used. (a) Osmotic pressure P normalized by nkBT, where n is the particle number density, as a function of Baxter temperature τ. The prediction from Percus–Yevick theory by Baxter60 is shown as the black curve. (b) Normalized osmotic pressure P/nkBT as a function of average number of bonds 〈Nb〉. | ||
Acknowledgements
This work was supported by Genentech Inc., the MIT Portugal Program, and NSF CBET award 1554398. We gratefully thank Zsigmond Varga for useful discussions on oscillatory shear simulations and Gareth McKinley and Thibaut Divoux for insightful discussions on gelation.Notes and references
- Y. Xia, B. Gates, Y. Yin and Y. Lu, Adv. Mater., 2000, 12, 693–713 CrossRef CAS.
- L. Di Michele, F. Varrato, J. Kotar, S. H. Nathan, G. Foffi and E. Eiser, Nat. Commun., 2013, 4, 2007 CrossRef PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S. Kim, D. J. Pine and G. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- Y. S. Lee, E. D. Wetzel and N. J. Wagner, J. Mater. Sci., 2003, 38, 2825–2833 CrossRef CAS.
- T. Gibaud, D. Frelat and S. Manneville, Heterogeneous yielding dynamics in a colloidal gel, Soft Matter, 2010, 6, 3482–3488 RSC.
- S. Schnittger and M. Sinha, MRS Bull., 2007, 32, 760–769 CrossRef CAS.
- D. B. Genovese, J. E. Lozano and M. A. Rao, J. Food Sci., 2007, 72, R11–R20 CrossRef CAS PubMed.
- B. Xie, R. L. Parkhill, W. L. Warren and J. E. Smay, Adv. Funct. Mater., 2006, 16, 1685–1693 CrossRef CAS.
- J. A. Lewis, Adv. Funct. Mater., 2006, 16, 2193–2204 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Polym. Sci. A, 1958, 33, 183–192 CAS.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, 1989 Search PubMed.
- Z. Varga, G. Wang and J. W. Swan, Soft Matter, 2015, 11, 9009–9019 RSC.
- Z. Varga and J. W. Swan, Soft Matter, 2016, 12, 7670–7681 RSC.
- D. Arzenšek, D. Kuzman and R. Podgornik, J. Colloid Interface Sci., 2012, 384, 207–216 CrossRef PubMed.
- Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360–6370 RSC.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- A. M. Jackson, J. W. Myerson and F. Stellacci, Nat. Mater., 2004, 3, 330–336 CrossRef CAS.
- A. B. E. Attia, Z. Y. Ong, J. L. Hedrick, P. P. Lee, P. L. R. Ee, P. T. Hammond and Y. Yang, Curr. Opin. Colloid Interface Sci., 2011, 16, 182–194 CrossRef.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed.
- I. Cho and K. Lee, J. Appl. Polym. Sci., 1985, 30, 1903–1926 CrossRef CAS.
- A. Lomakin, N. Asherie and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9465–9468 CrossRef CAS.
- S. Yadav, T. M. Laue, D. S. Kalonia, S. N. Singh and S. J. Shire, Mol. Pharmaceutics, 2012, 9, 791–802 CrossRef CAS PubMed.
- J. J. McManus, P. Charbonneau, E. Zaccarelli and N. Asherie, Curr. Opin. Colloid Interface Sci., 2016, 22, 73–79 CrossRef CAS.
- S. Bucciarelli, J. S. Myung, B. Farago, S. Das, G. A. Vliegenthart, O. Holderer, R. G. Winkler, P. Schurtenberger, G. Gompper and A. Stradner, Sci. Adv., 2016, 2, e1601432 CrossRef PubMed.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697 CrossRef CAS.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS PubMed.
- H. Verduin and J. K. G. Dhont, J. Colloid Interface Sci., 1995, 172, 425–437 CrossRef CAS.
- A. Coniglio, L. De Arcangelis, E. Del Gado, A. Fierro and N. Sator, J. Phys.: Condens. Matter, 2004, 16, S4831–S4839 CrossRef CAS.
- A. P. R. Eberle, N. J. Wagner and R. Castañeda-Priego, Phys. Rev. Lett., 2011, 106, 105704 CrossRef PubMed.
- A. P. R. Eberle, R. Castañeda-Priego, J. M. Kim and N. J. Wagner, Langmuir, 2012, 28, 1866–1878 CrossRef CAS PubMed.
- C. J. Roberts and M. A. Blanco, J. Phys. Chem. B, 2014, 118, 12599–12611 CrossRef CAS PubMed.
- A. Kurut, B. A. Persson, T. Åkesson, J. Forsman and M. Lund, J. Phys. Chem. Lett., 2012, 3, 731–734 CrossRef CAS.
- E. J. Yearley, I. E. Zarraga, S. J. Shire, T. M. Scherer, Y. Gokarn, N. J. Wagner and Y. Liu, Biophys. J., 2013, 105, 720–731 CrossRef CAS.
- G. Wang, Zs. Varga, J. Hofmann, I. E. Zarraga and J. W. Swan, J. Phys. Chem. B, 2018, 122, 2867–2880 CrossRef CAS PubMed.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801 CrossRef PubMed.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed.
- R. P. Sear, J. Chem. Phys., 1999, 111, 4800–4806 CrossRef CAS.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- M. Grünwald and P. L. Geissler, ACS Nano, 2014, 8, 5891–5897 CrossRef PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- G. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101 CrossRef PubMed.
- R. C. Van Lehn and A. Alexander-Katz, Soft Matter, 2011, 7, 11392–11404 RSC.
- J. W. Swan and G. Wang, Phys. Fluids, 2016, 28, 011902 CrossRef.
- J. F. Brady and G. Bossis, Stokesian dynamics, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- D. R. Foss and J. F. Brady, J. Fluid Mech., 2000, 407, 167–200 CrossRef CAS.
- G. Bossis and J. F. Brady, J. Chem. Phys., 1989, 91, 1866–1874 CrossRef CAS.
- T. N. Phung, J. F. Brady and G. Bossis, J. Fluid Mech., 1996, 313, 181–207 CrossRef CAS.
- A. J. Banchio and J. F. Brady, J. Chem. Phys., 2003, 118, 10323–10332 CrossRef CAS.
- S. Delong, F. Balboa Usabiaga, R. Delgado-Buscalioni, B. E. Griffith and A. Donev, J. Chem. Phys., 2014, 140, 134110 CrossRef PubMed.
- S. Delong, F. Balboa Usabiaga and A. Donev, J. Chem. Phys., 2015, 143, 144107 CrossRef PubMed.
- A. M. Fiore, F. Balboa Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 2017, 146, 124116 CrossRef PubMed.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- HOOMD-blue, https://codeblue.umich.edu/hoomd-blue, 2017.
- E. Ghiringhelli, D. Roux, D. Bleses, H. Galliard and F. Caton, Rheol. Acta, 2012, 51, 413–420 CrossRef CAS.
- D. J. Curtis, A. Holder, N. Badiei, J. Claypole, M. Walters, B. Thomas, M. Barrow, D. Deganello, M. R. Brown, P. R. Williams and K. Hawkins, J. Non-Newtonian Fluid Mech., 2015, 222, 253–259 CrossRef CAS.
- M. Geri, B. Keshavarz, T. Divoux, C. Clasen, D. J. Curtis and G. H. McKinley, Phys. Rev. X, 2018, 8(4), 041042 CAS.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770–2774 CrossRef CAS.
- Y. C. Chiew and E. D. Glandt, J. Phys. A, 1983, 16, 2599–2608 CrossRef.
- D. W. Marr and A. P. Gast, J. Chem. Phys., 1993, 99, 2024–2031 CrossRef CAS.
- M. A. Miller and D. Frenkel, J. Chem. Phys., 2004, 121, 535–545 CrossRef CAS PubMed.
- C. G. De Kruif, P. W. Rouw, W. J. Briels, M. H. G. Duits, A. Vrij and R. P. May, Langmuir, 1989, 5, 422–428 CrossRef CAS.
- N. E. Valadez-Pérez, Y. Liu, A. P. R. Eberle, N. J. Wagner and R. Castañeda-Priego, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 060302 CrossRef PubMed.
- S. A. Safran, I. Webman and G. S. Grest, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 506–511 CrossRef CAS.
- J. Mittal, J. Phys. Chem. B, 2009, 113(42), 13800–13804 CrossRef CAS PubMed.
- J. W. Swan, E. M. Furst and N. J. Wagner, J. Rheol., 2014, 58, 307–337 CrossRef CAS.
- E. M. Furst and J. P. Pantina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 050402 CrossRef PubMed.
- M. A. Blanco and V. K. Shen, J. Chem. Phys., 2016, 145, 155102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00607a |
| This journal is © The Royal Society of Chemistry 2019 |