Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dry active turbulence in a model for microtubule–motor mixtures†
Ivan
Maryshev
 a,
Andrew B.
Goryachev
a,
Andrew B.
Goryachev
 a,
Davide
Marenduzzo
a,
Davide
Marenduzzo
 b and
Alexander
Morozov
b and
Alexander
Morozov
 *b
*b
aCentre for Synthetic and Systems Biology, Institute of Cell Biology, School of Biological Sciences, The University of Edinburgh, Max Born Crescent, Edinburgh EH9 3BF, UK. E-mail: Ivan.Maryshev@ed.ac.uk; Andrew.Goryachev@ed.ac.uk
bSUPA, School of Physics and Astronomy, The University of Edinburgh, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK. E-mail: Alexander.Morozov@ed.ac.uk; dmarendu@ph.ed.ac.uk
First published on 8th July 2019
Abstract
We study the dynamics and phase behaviour of a dry suspension of microtubules and molecular motors. We obtain a set of continuum equations by rigorously coarse graining a microscopic model where motor-induced interactions lead to parallel or antiparallel ordering. Through numerical simulations, we show that this model generically creates either stable stripes, or a never-settling pattern where stripes periodically form, rotate and then split up. We derive a minimal model which displays the same instability as the full model, and clarifies the underlying physical mechanism. The necessary ingredients are an extensile flux arising from microtubule sliding and an interfacial torque favouring ordering along density gradients. We argue that our minimal model unifies various previous observations of chaotic behaviour in dry active matter into a general universality class.
Recent studies of active matter, comprising particles that convert internal energy to relative motion – exerting force or torque dipoles on the surrounding medium as they do so – reveal that these systems generally function far from equilibrium and possess no passive analogues.1 Instead, their microscopic models can sometimes be grouped into unique “universality” classes, and identifying the corresponding continuous equations is currently an area of active research.1–6 For systems with orientational order (i.e., active liquid crystals), two important classes of models that emerged in the process are momentum-conserving (“wet”) incompressible systems1,7 and non-momentum conserving (“dry”) compressible ones,1,8–10 with the vast majority of work dedicated to the former class.
Here we propose a new universality class of dry active systems defined by the following continuum equations‡
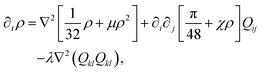 | (1) |
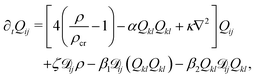 | (2) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ij = ∂i∂j − (1/2)δij∂k∂k. We demonstrate that these equations arise naturally from a microscopic kinetic theory of model mixtures of microtubules (MTs) and molecular motors (MMs).1,11 While wet incompressible active gels are generically unstable to orientational fluctuations ultimately resulting in “active turbulence”,7,12,13 we show that compressible dry MT–MM mixtures undergo seemingly similar chaotic dynamics, which we name dry active turbulence. The underlying mechanism is, however, completely different and we use eqn (1) and (2) to elucidate it: importantly, in our case concentration inhomogenenities play a central role. We note that similar dynamical patterns were observed, mainly at the level of a kinetic theory, for a very different physical system, a suspension of flocking self-propelled particles with nematic alignment.8,14–16 We therefore argue that dry active turbulence unifies various previous observations of chaotic behaviour in nematically ordered microtubules and flocking self-propelled particles.
ij = ∂i∂j − (1/2)δij∂k∂k. We demonstrate that these equations arise naturally from a microscopic kinetic theory of model mixtures of microtubules (MTs) and molecular motors (MMs).1,11 While wet incompressible active gels are generically unstable to orientational fluctuations ultimately resulting in “active turbulence”,7,12,13 we show that compressible dry MT–MM mixtures undergo seemingly similar chaotic dynamics, which we name dry active turbulence. The underlying mechanism is, however, completely different and we use eqn (1) and (2) to elucidate it: importantly, in our case concentration inhomogenenities play a central role. We note that similar dynamical patterns were observed, mainly at the level of a kinetic theory, for a very different physical system, a suspension of flocking self-propelled particles with nematic alignment.8,14–16 We therefore argue that dry active turbulence unifies various previous observations of chaotic behaviour in nematically ordered microtubules and flocking self-propelled particles.
Here, we consider the dynamics of pattern formation in model MT–MM mixtures that have actively been studied as biological and synthetic instances of active matter.1,11,17–20 On the one hand, they incorporate the essential ingredients of the mitotic spindle,21–23 on the other hand, they closely mirror the so-called “hierarchical active matter”, which can be self-assembled in the lab from MTs and MMs, in the presence of polyethylene glycol.24–26 Whilst the continuous description of the overdamped active biofilaments can be postulated on symmetry grounds,9,27 it can also be derived by rigorously coarse-graining a specific underlying microscopic model.28–35 This avenue – which has also been often used for systems of self-propelled particles36 – is useful as it allows one to determine the effective parameters of the continuum theory in terms of the geometrical and physical quantities appearing in the microscopic model. Here, we follow this approach and consider a caricature model of a MT–MM mixture, inspired by actin–myosin37,38 and MT–kinesin/dynein24,25,39–42 systems. While missing many specific biological ingredients, our model instead focuses on the symmetries of the microscopic interactions that, ultimately, define the universality class of eqn (1) and (2). Since most of the experiments either studied MT–MM mixtures directly on surfaces24,37–41 or observed spontaneous clustering of bulk systems unto interfaces,25 we consider our model in 2D.
We treat MTs as rigid rods of fixed length l with distinct ends, denoted as “+” and “−”, and consider “+”-directed MMs, which are described by their distribution along individual MTs, as detailed below. Unlike in MT motility assays43 (where MTs are self-propelled), in MT–MM mixtures microtubular rods possess no constant velocity. Instead, filaments can only change position and orientation due to either thermal diffusion, or motor-mediated interactions.
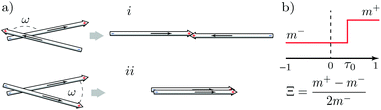
The nature of motor-mediated interactions between filaments depends on the underlying microscopic detail. For instance, it was demonstrated that MMs able to associate with two filaments simultaneously can either cluster MTs, or actively separate them, depending on the initial configuration (Fig. 1). Importantly, our dynamics captures both possible outcomes – consistent with the current view of most kinesin motors,41,44 and unlike previous work,34 which solely focused on the case of polar clustering. Specifically, our interaction rule is the following. If the initial relative angle between rods exceeds some critical value (in our case π/2) then MTs first align in an anti-parallel way and then slide apart. Otherwise, MTs cluster to acquire the same position and orientation (Fig. 1a).
Within our model, MTs are covered by a steady-state static distribution of motors. Motor coverage may either be homogeneous or inhomogeneous,45,46 and is parametrized by two geometrical quantities: Ξ = (m+ − m−)/(2m−), and τ0 (m+ and m− denote motor concentrations at the two ends of a MT, Fig. 1b). Hereafter, we refer to Ξ = 0 and Ξ ≠ 0 as the isotropic and anisotropic cases, respectively.
In what follows, we work in two-dimensional Cartesian coordinates. Assuming that motor-induced rearrangements of MTs are fast with respect to diffusion, we treat them as instantaneous collisions. The probability distribution function, P(r,ϕ), for a MT to be at a position r with an orientation n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), given by the angle ϕ, obeys the following Boltzmann-like kinetic equation
ϕ), given by the angle ϕ, obeys the following Boltzmann-like kinetic equation
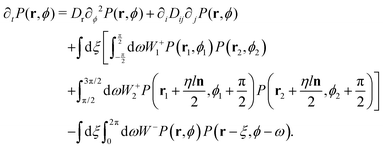 | (3) |
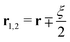 , while their orientations are defined by the angles
, while their orientations are defined by the angles 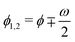 ; ξ and ω parametrise separations between MT centres and their orientations, respectively. The parameter η determines the final relative displacement of MTs after sliding – henceforth we consider η = 1, corresponding to full separation. For needle-like MTs considered here, the collision rates W+1, W+2, W− only differ from zero when two MTs intersect in 2D; see ref. 34 and 48 for their explicit dependence on ξ, ω, Ξ, and τ0. Also, we note here that while the value π/2 of the critical angle separating clustering and sliding dynamics of MTs is hard-wired into our theory, some idea of phase behaviour corresponding to different values of that angle can be obtained by using η ≠ 1. We performed exploratory simulations with η in the range between 1 and 0.5 and found no qualitative difference with the phase behaviour reported below.
; ξ and ω parametrise separations between MT centres and their orientations, respectively. The parameter η determines the final relative displacement of MTs after sliding – henceforth we consider η = 1, corresponding to full separation. For needle-like MTs considered here, the collision rates W+1, W+2, W− only differ from zero when two MTs intersect in 2D; see ref. 34 and 48 for their explicit dependence on ξ, ω, Ξ, and τ0. Also, we note here that while the value π/2 of the critical angle separating clustering and sliding dynamics of MTs is hard-wired into our theory, some idea of phase behaviour corresponding to different values of that angle can be obtained by using η ≠ 1. We performed exploratory simulations with η in the range between 1 and 0.5 and found no qualitative difference with the phase behaviour reported below.
We proceed by applying a rigorous coarse-graining procedure developed in ref. 34 to eqn (3) to derive a system of mean-field equations for the density of filaments ρ, their mean orientation pi, and the nematic tensorial field Qij. These variables are defined as the first three moments of P(r,ϕ):
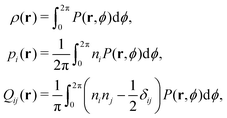 | (4) |
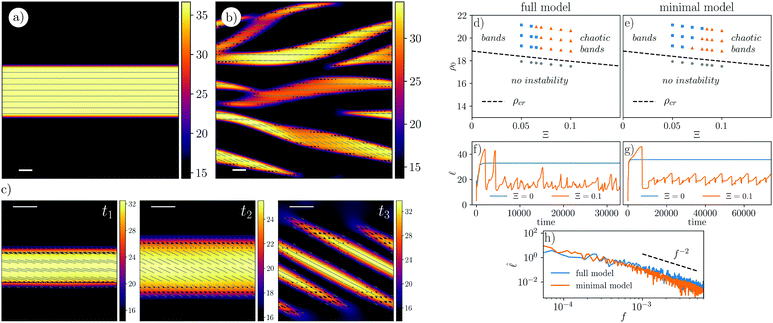 | ||
Fig. 2 (a–c) Numerical simulations of the full model. (a) Formation of a stable stripe in the isotropic case (Ξ = 0, ρ0 = 1.1ρcr, system size L = 150). (b) Chaotic dynamics for Ξ ≠ 0 (Ξ = 0.1,τ0 = 0.5, ρ0 = 1.1ρcr, L = 150). (c) Same as (b), but for L = 50; snapshots t1 − t2 − t3 show the evolution of a nematic band. In (a–c) colormaps represent the MT density, black arrows denote the polar order field, and gray segments illustrate the largest eigenvector of the nematic alignment tensor Qij. Scale bar: 10 l. (d and e) Phase diagram for the full (d) and minimal (e) model. Note that ρN is much above the density range plotted.48 (f and g) Domain size ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) versus time for the full (f) and minimal (g) model. (h) Fourier transform of versus time for the full (f) and minimal (g) model. (h) Fourier transform of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) versus frequency, for the full and minimal model. versus frequency, for the full and minimal model. | ||
A linear stability analysis48 shows that the uniform isotropic state is linearly unstable towards the emergence of a globally-ordered nematic state, when ρ0 > ρcr = 6π/(1 + Ξ(1 − τ0)). Additionally, for ρcr < ρ0 < ρN, this nematic state is itself unstable. Simulations demonstrate that the latter instability leads to co-existence between high-density, nematically-ordered elongated domains and a low-density isotropic background (Fig. 2a and Movie S1, ESI†). The outcome of this phase separation at late times depends on the value of the anisotropy parameter, Ξ. For small Ξ, domains coarsen to leave a single static band, whose size scales with the system size (Fig. 2a). Inside the band, MTs are ordered nematically, with residual polar order confined at the interface with the isotropic phase. For large enough Ξ, we instead observe an ever-evolving pattern (Fig. 2b and Movie S2, ESI†), superficially reminiscent of “active turbulence”49 in wet active gels. To characterise the properties of this spatiotemporal pattern, which we call dry active turbulence, we plot the time evolution of the domain size, computed via the first moment of the structure factor,48 and its Fourier transform (Fig. 2f and h respectively). It is apparent that there is a selected lengthscale in the isotropic case, while the dynamics in the anisotropic case appear to be chaotic (as the Fourier transform in Fig. 2h contains all frequencies). Our findings are summarised in the phase diagram in Fig. 2d.
The kinetic pathway associated with dry active turbulence becomes apparent in simulations with smaller domains (Fig. 2c and Movie S3, ESI†). These shows that the self-assembled nematically ordered MT bands undergo a cyclic process where they stretch perpendicular to their long direction, rotate, stretch and split, to reform later on. This process is quasi-periodic in smaller system, but appears to be chaotic in larger ones.
To identify the fundamental mechanism leading to pattern formation in our system, we now search for a minimal model. We define the latter as a set of simple equations, which simultaneously satisfies two conditions. First, it needs to have qualitatively similar dynamics as the full model (Fig. 2a and b): it should retain both a transition between a uniform and a phase separated nematic state, as well as a regime with chaotic dynamics; in small domains, it should exhibit features similar to Fig. 2c. Second, we require that the location of the phase boundaries in the minimal and full models (Fig. 2d and e), is quantitatively similar. As a first step, we exploit the observation that polar order plays a minor role (Fig. 2c), and adiabatically eliminate pi in favour of ∂iρ and ∂jQij, keeping only the lowest order terms in spatial gradients (as in a hydrodynamic expansion50). Then, we systematically switch off each term individually in the resulting equations, and compute the phase diagram; the term is only reinstated if its exclusion leads to a substantial change in the phase boundary location.
This procedure yields the minimal model defined in eqn (1) and (2), and its phase diagram is presented in Fig. 2e. The eight constants – μ, χ, λ, α, κ, ζ, β1, β2 – are not arbitrary, and are explicitly derived in terms of the microscopic parameters ρ0, Ξ, τ0 and η (see ESI† for details48). Within this set, ζ is the only parameter that can change sign – the others are always positive.
We now discuss the physical meaning of each term in eqn (1) and (2). First, μ and λ determine the non-equilibrium chemical potential of our mixture: their main role is to set the values of the densities in the isotropic and nematic phases. Next, α is a non-equilibrium Landau coefficient setting the magnitude of order in the bulk (together with the term 4(ρ/ρcr − 1)Qij), while κ is the nematic elastic constant. Similar terms are also present in a purely passive Model C51 describing, for instance, phase separation in passive liquid crystals.§ The key qualitative ingredients that produce chaotic behaviour in our model are the terms proportional to χ, ζ, β1 and β2. Among them, χ is an “extensile flux”, whose role is similar to that of an extensile stress in active gels.1,7,52 This term enhances diffusion along the direction of the local nematic order (i.e., the eigenvector of Qij corresponding to its positive eigenvalue), and decreases it along the perpendicular direction. Second, ζ creates an effective torque at the interface, as the associated term depends on density gradients, which are largest at the interface. When ζ is positive (negative), it tends to orient MTs parallel (perpendicular) to an isotropic–nematic interface. Finally, β1 and β2 create modulation of the nematic ordering (i.e., the positive eigenvalue of Qij). These terms promote activity-induced disorder, and act similarly to a negative elastic constant.10 Additionally, they contribute to the interfacial torque at the boundary of a nematic band, where QklQkl drops sharply to zero, following the density field. While similar terms could in principle be derived from an effective free energy, a thermodynamic framework would lead to additional constraints between the values of β1 and β2.
The minimal model is now simple enough for us to dissect the mechanisms underlying pattern formation. The kinetic pathway leading to non-equilibrium phase separation proceeds as follows. Starting from a uniform disordered solution with ρ > ρcr, MTs rapidly acquire orientational order, through the Landau coupling in eqn (2). At this point, the extensile active flux, arising from MT sliding, enhances diffusion along the nematic direction, and hinders it perpendicularly. When this effect is strong enough, the perpendicular diffusion becomes effectively negative, causing MT bundling and the formation of one or more nematically ordered high-density bands (see Fig. 2 and Movies S1, S4, ESI†). Notably, although the phase separation is driven by a non-equilibrium phenomenon (MM activity), the kinetic growth laws resemble canonical Model C phase separation in passive mixtures of liquid crystalline and isotropic fluids.48,51,53
Second, when Ξ is sufficiently large, the β1,2 terms dominate over both the restoring elastic constant κ and the ζ term: the associated torque rotates the MTs at the nematic–isotropic interface, so that they tend to orient perpendicular to the band border. This interfacial alignment conflicts with the direction of the nematic order within the bulk of the band; it couples to the extensile flux to yield locally synchronous rotation (and stretching) of nematic bands as observed in our simulations. This cycle repeats, creating a never-settling pattern, as seen in our simulations in the dry active turbulent regime (Fig. 2 and 3a, and Movies S3 and S5, ESI†). As the sense of the emerging band rotation (clockwise or anticlockwise) is selected by spontaneous symmetry breaking, it may be different in different regions of our simulation domain, yielding a chaotic pattern (Fig. 3b, Movies S2 and S6, ESI†). Measuring the time evolution of the domain size in this regime yields statistically the same results as for the full model (Fig. 2g and h).
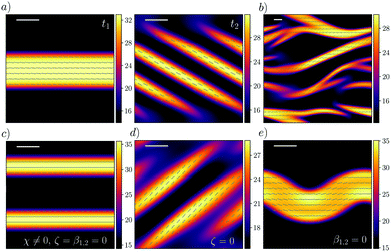 | ||
| Fig. 3 Pattern formation within the minimal model. (a) Chaotic dynamics similar to Fig. 2b (Ξ = 0.1, τ0 = 0.5). (b) Chaotic dynamics for larger system size and anisotropy (Ξ = 0.3, τ0 = 0.5). (c) Non-equilibrium phase separation with β1,2 = ζ = 0 (Ξ = 0). (d) Chaotic dynamics with ζ = 0 (Ξ = 0). (e) Interfacial undulation and chaos with β1,2 = 0 (Ξ = 0). For all plots ρ0 = 1.1ρcr, scale bar: 10l. | ||
There is also a second mechanism that can destabilise a homogeneous nematic state, again dependent on β1,2. A linear stability analysis starting from the uniform nematic phase48 shows that when these terms are large enough, they trigger the development of a modulation in Qij – in the direction parallel to that of the nematic order, for β1,2 > 0. This instability is independent of density fluctuations and ultimately fragments the nematic phase into infinitely small microdomains. This pathway to chaos is related to that identified in ref. 9 and 10 for dry active matter with near-uniform density. However, in our model this instability is only relevant for ρ0 ≫ ρcr, and for lower ρ0 is superseded by the turbulent phase separation dynamics discussed above.
While our minimal model is the result of a systematic coarse-graining, we can view eqn (1) and (2), more generally, as a phenomenological model that contains the lowest terms of the correct tensorial nature.54 Upon coarse-graining, a microscopic model within the same universality class as the one studied here would, therefore, provide the expressions for the parameters in eqn (1) and (2), but would not generate extra terms. Indeed, setting β1,2 = λ = μ = 0 shows that our equations, in this limit, reduce to the minimal model for flocking of self-propelled particles with nematic order.8,14–16 We, therefore, propose eqn (1) and (2) as a unifying model for dry active systems with nematic order. Recently, similar arguments were used to propose active versions of Models B and H4,5 in Hohenberg–Halperin classification.51 We follow this analogy and refer to eqn (1) and (2) as active Model C. This model is in a different universality class with respect to active gel theory,1 which exhibits instabilities in an active nematic fluid with constant density, whereas in our case patterns are always associated with a non-equilibrium phase separation. We want to stress that while previous work reported types of chaotic behaviour similar to the limiting cases of our model, either based on hydrodynamic8,14 or kinetic theories,15,55 active model C unifies all this into a general universality class.
Analysis of active Model C with phenomenological coefficients re-enforces our physical interpretation of the instability modes. First, nematic–isotropic phase separation also occurs with ζ = β1,2= 0, confirming that this phenomenon relies solely on a non-zero extensile flux, χ ≠ 0 (Fig. 3c and Movie S7, ESI†). Second, setting χ = 0 whilst retaining β1,2 and ζ only leads to a uniform nematic phase, confirming that χ is necessary for any patterning (Movie S8, ESI†). Third, switching off only ζ leads to chaotic dynamics for a much wider parameter range, including Ξ = 0 (Fig. 3d and Movie S9, ESI†), as now β1,2 only need to compete with the elastic constant κ. Fourth, switching off only β1,2 whilst retaining ζ > 0 does not lead to chaotic dynamics as in Fig. 2b and 3a, b, as there is no competition between the orientational order in the bulk and at the interface (see ref. 48). This case however, yields another interesting instability associated with interfacial undulations and an elastic bend deformation in the nematic order (Fig. 3e and Movie S10, ESI†). The ensuing patterns may also be chaotic for sufficiently large ζ (Movies S11 and S12, ESI†), and are similar to the structures seen experimentally in microtubule–kinesin mixtures.25
For various values of its parameters, active Model C serves as a catalogue of patterns in dry active systems. As mentioned above, a sub-set of terms in eqn (1) and (2) was obtained in models of flocking of self-propelled particles with nematic order.8,14–16 Within those models, rigorous coarse-graining shows that χ and ζ are both positive, and, accordingly, the generic outcome found by numerical simulations8,14–16 is non-equilibrium phase separation and chaos through band undulations (as in Fig. 3e). Based on our phenomenological model and interpretation, we also expect dry active turbulence with contractile active flux, χ < 0, and interfacial torques favouring parallel alignment at the interface, as would occur when ζ, or β1,2 are positive. This scenario may be relevant for pattern formation in MT–MM mixtures where the underlying microscopic collision rules differ from those in Fig. 1. Further work is required to identify the criteria for a microscopic model to belong to the universality class of our active Model C.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Discussions with Hugues Chaté are kindly acknowledged. AG acknowledges funding from the Biotechnology and Biological Sciences Research Council of UK (BB/P01190X, BB/P006507). DM acknowledges support from ERC CoG 648050 (THREEDCELLPHYSICS).References
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- J. Toner and Y. Tu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 4828 CrossRef CAS.
- J. Toner, Y. Tu and S. Ramaswamy, Ann. Phys., 2005, 318, 170–244 CAS.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef.
- A. Tiribocchi, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 115, 188302 CrossRef.
- E. Tjhung, C. Nardini and M. E. Cates, Phys. Rev. X, 2018, 8, 031080 CAS.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef.
- A. Peshkov, I. S. Aranson, E. Bertin, H. Chaté and F. Ginelli, Phys. Rev. Lett., 2012, 109, 268701 CrossRef.
- E. Putzig, G. S. Redner, A. Baskaran and A. Baskaran, Soft Matter, 2016, 12, 3854–3859 RSC.
- P. Srivastava, P. Mishra and M. C. Marchetti, Soft Matter, 2016, 12, 8214–8225 RSC.
- D. Needleman and Z. Dogic, Nat. Rev. Mater., 2017, 2, 17048 CrossRef CAS.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- S. Ngo, A. Peshkov, I. S. Aranson, E. Bertin, F. Ginelli and H. Chaté, Phys. Rev. Lett., 2014, 113, 038302 CrossRef PubMed.
- X.-Q. Shi, H. Chaté and Y.-Q. Ma, New J. Phys., 2014, 16, 035003 CrossRef.
- R. Großmann, F. Peruani and M. Bär, Phys. Rev. E, 2016, 94, 050602 CrossRef.
- S. Wang and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15184–15189 CrossRef CAS.
- S. Wang and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6446–6451 CrossRef CAS.
- T. Gao, R. Blackwell, M. A. Glaser, M. D. Betterton and M. J. Shelley, Phys. Rev. Lett., 2015, 114, 048101 CrossRef PubMed.
- M. J. Shelley, Annu. Rev. Fluid Mech., 2016, 48, 487–506 CrossRef.
- A. Mogilner and E. Craig, J. Cell Sci., 2010, 123, 3435–3445 CrossRef CAS.
- K. S. Burbank, T. J. Mitchison and D. S. Fisher, Curr. Biol., 2007, 17, 1373–1383 CrossRef CAS.
- J. Brugués and D. Needleman, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18496–18500 CrossRef.
- T. Sanchez, D. Welch, D. Nicastro and Z. Dogic, Science, 2011, 333, 456–459 CrossRef CAS.
- T. Sanchez, D. T. N. Chen, S. J. Decamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 1–5 CrossRef.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5498–5502 CrossRef CAS.
- H. Y. Lee and M. Kardar, Phys. Rev. E, 2001, 64, 056113 CrossRef CAS.
- K. Kruse and F. Jülicher, Phys. Rev. Lett., 2000, 85, 1778 CrossRef CAS.
- T. B. Liverpool and M. C. Marchetti, Phys. Rev. Lett., 2003, 90, 138102 CrossRef.
- I. S. Aranson and L. S. Tsimring, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 050901 CrossRef.
- F. Ziebert and W. Zimmermann, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 18, 41–54 CrossRef CAS PubMed.
- I. S. Aranson and L. S. Tsimring, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031915 CrossRef PubMed.
- D. Johann, D. Goswami and K. Kruse, Phys. Rev. E, 2016, 93, 062415 CrossRef CAS.
- I. Maryshev, D. Marenduzzo, A. B. Goryachev and A. Morozov, Phys. Rev. E, 2018, 97, 022412 CrossRef CAS.
- E. Bertin, A. Baskaran, H. Chaté and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042141 CrossRef.
- E. Bertin, H. Chaté, F. Ginelli, S. Mishra, A. Peshkov and S. Ramaswamy, New J. Phys., 2013, 15, 085032 CrossRef.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73 CrossRef CAS.
- T. Butt, T. Mufti, A. Humayun, P. B. Rosenthal, S. Khan, S. Khan and J. E. Molloy, J. Biol. Chem., 2010, 285, 4964–4974 CrossRef CAS.
- F. J. Nédélec, T. Surrey, A. C. Maggs and S. Leibler, Nature, 1997, 389, 305–308 CrossRef.
- T. Surrey, F. Nédélec, S. Leibler and E. Karsenti, Science, 2001, 292, 1167–1171 CrossRef CAS.
- L. C. Kapitein, E. J. Peterman, B. H. Kwok, J. H. Kim, T. M. Kapoor and C. F. Schmidt, Nature, 2005, 435, 114 CrossRef CAS.
- P. J. Foster, S. Fürthauer, M. J. Shelley and D. J. Needleman, eLife, 2015, 4, e10837 CrossRef.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448 CrossRef CAS.
- G. Fink, L. Hajdo, K. J. Skowronek, C. Reuther, A. A. Kasprzak and S. Diez, Nat. Cell Biol., 2009, 11, 717–723 CrossRef CAS.
- C. Leduc, K. Padberg-Gehle, V. Varga, D. Helbing, S. Diez and J. Howard, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6100–6105 CrossRef CAS.
- A. Parmeggiani, T. Franosch and E. Frey, Phys. Rev. Lett., 2003, 90, 086601 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1986 Search PubMed.
- See ESI†.
- L. Giomi, T. B. Liverpool and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051908 CrossRef.
- D. A. Wolf-Gladrow, Lattice-gas cellular automata and lattice Boltzmann models: an introduction, Springer, 2004 Search PubMed.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435 CrossRef CAS.
- S. Ramaswamy, R. Aditi Simha and J. Toner, Europhys. Lett., 2003, 62, 196–202 CrossRef CAS.
- M. Mata, C. J. Garca-Cervera and H. D. Ceniceros, J. Non-Newton. Fluid Mech., 2014, 212, 18–27 CrossRef CAS.
- A. Beris and B. Edwards, Thermodynamics of Flowing Systems: with Internal Microstructure, Oxford University Press, 1994 Search PubMed.
- L.-B. Cai, H. Chaté, Y.-Q. Ma and X.-Q. Shi, Phys. Rev. E, 2019, 99, 010601 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00558g |
| ‡ All coefficients of eqn (1) and (2) will be defined below. |
| § Here we generically use the term “model C” to describe a set of equations coupling the dynamics of a conserved field to that of a non-conserved one. |
| This journal is © The Royal Society of Chemistry 2019 |