DOI:
10.1039/C9SM00262F
(Paper)
Soft Matter, 2019,
15, 4098-4108
Physics-based prediction of biopolymer degradation
Received
5th February 2019
, Accepted 30th April 2019
First published on 2nd May 2019
Abstract
In the natural environment, insoluble biomatter provides a preeminent source of carbon for bacteria. Its degradation by microbial communities thus plays a major role in the global carbon-cycle. The prediction of degradation processes and their sensitivity to changes in environmental conditions can therefore provide critical insights into globally occurring environmental adaptations. To elucidate and quantify this macro-scale phenomenon, we conduct micro-scale experiments that examine the degradation of isolated biopolymer particles and observe highly nonlinear degradation kinetics. Since conventional scaling arguments fail to explain these observations, it is inferred that the coupled influence of both the physical and biochemical processes must be considered. Hence, we develop a theoretical model that accounts for the bio-chemo-mechanically coupled kinetics of polymer degradation, by considering the production of bio-degraders and their ability to both dissociate the material from its external boundaries and to penetrate it to degrade its internal mechanical properties. This change in mechanical properties combined with the intake of solvent or moisture from the environment leads to chemo-mechanically coupled swelling of the material and, in-turn, influences the degradation kinetics. We show that the model quantitatively captures our experimental results and reveals distinct signatures of different bacteria that are independent of the specific experimental conditions (i.e. particle volume and initial concentrations). Finally, after validating our model against the experimental data we extend our predictions for degradation processes across various length and time scales that are inaccessible in a laboratory setting.
1 Introduction
Understanding degradation of biopolymers by bacteria can elucidate key processes that occur in the environment. In fact, the global rate of carbon turnover is dependent upon degradation of insoluble biopolymers, that encapsulate a large portion of the carbon stock in the environment.1 These biopolymers can be found in the form of exopolysaccharides that are secreted by algae and corals, or in other organic aggregates of animal and plant detritus.2 In the ocean, particulate organic matter provides hot-spots of biological activity in an otherwise nutrient poor landscape.3,4 Attached to particle surfaces, marine bacteria degrade and consume biopolymers, thus recycling essential nutrients and closing the loop of the global carbon cycle.5–8 The degradation of biopolymers in particulate organic matter is mediated by the action of hydrolytic enzymes, secreted by bacteria, which cleave biopolymer bonds releasing soluble oligosaccharides into the local environment. Understanding and predicting the consumption dynamics at the level of a single particle on the micro-scale can provide insights into the fundamental principles that govern the global function of microbial ecosystems.9
While the consumption kinetics of dissolved resources is well understood, the dynamics of particulate organic matter degradation remain poorly explained. One of the main reasons is the complexity that arises from the coupling between physical, chemical, biological and mechanical processes, namely diffusion of enzymes, hydrolysis, bacterial growth and changes in the mechanical properties, respectively.
In this study we address this challenge using a hybrid experimental and theoretical approach. We take advantage of our ability to study particle degradation kinetics in a controlled and quantitative fashion in the laboratory, obtaining measurements of particle volume and bacterial density over time.10 Although observations in the laboratory setting are limited to a specific range of length scales and time scales, a theoretical model, which captures the observed degradation process, can be extended to predict degradation dynamics and their sensitivity to varying environmental conditions. Moreover, by accounting for the complexity of the multiphysics phenomenon that is at the interface of biology, chemistry and mechanics, a theoretical model can complement the experimental approach by determining the prominent mechanisms and parameters behind the rate of carbon release through microbial activity.
To develop our model of particle degradation we employ theoretical tools to examine the coupling of biochemical and mechanical effects. We account for the action of enzymes that are gradually produced at the surface of the particle and can penetrate into its interior, contributing to both dissociation of material from the particle surface, and degradation of mechanical properties in its bulk. Building on recent continuum models11–14 and incorporating enzyme effects on the mechanical properties, we investigate the sensitivity of the degradation process to material parameters and to kinetic parameters that are associated with different types of bacteria and their concentrations in the local environment.
In the next section we will start by presenting our experimental observations. Then, in Section 3, we develop a continuum mechanics framework. In Section 4, we show that our model captures the experimental results and that the kinetic parameters provide a signature of the degrading bacterial species. Then, by extending the model predictions beyond the experimental scale, we analyze the sensitivity of the degradation process. Finally, in Section 5 we discuss the conclusions of this analysis.
2 Observations
To understand degradation dynamics of insoluble organic matter by microorganisms such as bacteria, we use model particles made of chitin hydrogel. Chitin is the second most abundant biopolymer in the planet after cellulose,15–17 and therefore represents a relevant substrate to study the degradation of organic materials. Model chitin particles have an average radius of ∼50 μm and are incubated with marine bacteria capable of secreting chitinolytic enzymes and growing on hydrolysis products.
We use three different bacterial strains with different degradation capacities, which were incubated at known initial concentration with ∼100 chitin beads in a 200 mm3 volume. Using high resolution time-lapse microscopy we then track changes in particle volume over a period of 240 hours to capture the kinetics of particle volume change. More details on the experimental protocol and methods can be found in ref. 10.
Surprisingly, as shown in Fig. 1, the kinetics of particle volume change are strongly nonlinear. Rather than a monotonic decrease in particle volume, we observed a long waiting phase at the end of which an expansion of the particle volume (of roughly 10%) was observed, before the onset of a relatively fast collapsing phase during which the particle is fully degraded. Depending on the bacterial strain identity, waiting phases can persist for over 100 hours. Importantly, these long waiting phases are not caused by lag phases in bacterial growth, since experimental data shows an exponential increase in bacterial concentration during the waiting phase.10
 |
| | Fig. 1 Normalized particle volume evolution under the action of primary degrader vsple1A01 of initial concentration 4 cells per mm3. Orange crosses labelled with a letter correspond to the images on the top. | |
Fig. 2 summarizes the experimental volume measurements over time for chitin particles exposed to three different bacterial strains and incubated at different initial bacterial concentrations. This data shows that the durations of the waiting and the collapsing phases depend on the type of bacterial strain and its initial concentration, and that the volume expansions seems to be more pronounced for particles of higher initial volumes. It is worth noting that the particle volume after the collapsing phase does not completely vanish; this is due to the presence of a preexisting fraction of non-degradable material. The puzzling absence of apparent particle degradation during the waiting phase and the fact that particles expand before collapsing, raise a number of questions regarding the interplay between bacterial growth, enzyme secretion rates and polymer degradation. We hypothesize that these nonlinear kinetics are due to a strong coupling between the biological process and the chemo-mechanical response of the particle. In the following, we develop a mechanistic model which shows that the kinetics of particle consumption can be explained by accounting for the bio-chemo-mechanically coupled nature of biopolymer degradation and bacterial growth.
 |
| | Fig. 2 Time evolution of the chitin particle volume, under the action of three different types of bacteria indicated in the beginning of each line, and different initial concentration of bacteria, specified on the top of each column. Psych6C06 corresponds to a strain of the genus Psychromonas, palte3D05 to a member of the genus Pseudoalteromonas and vsple1A01 to a Vibrio splendidus, all of which were described in ref. 10. The crosses represent experimental points while the line represents the model prediction. Different colors are used to distinguish between repeated experiments with different initial particle volumes. | |
3 Theoretical model
To develop a predictive theoretical model, we first need to quantify the dominant mechanisms at play. As a first step, we focus on the mechanical response of the biopolymer particle. We notice that throughout the waiting phase, volume expansion is necessarily associated with intake of solvent from the surrounding bath. This chemo-mechanically induced swelling is associated with finite stretching of the polymer backbone and thus nonlinearity should be accounted for in modeling its mechanical response. As a second step, we turn to consider the degradation kinetics. The particle degrades upon the activity of enzymes that are secreted by the bacteria and diffuse through the bulk of the particle. These enzymes dissociate the polymeric network both on the free surface of the particle and within its interior; they are simultaneously responsible for freeing monomers from the particle at its boundary surface, and for splitting polymer chains in the bulk of the particle. The latter mechanism leads to the degradation of elastic properties and, in-turn, promotes swelling of the particle.18–21 The former mechanism is ultimately responsible for the release of monomers to the environment and is assumed to occur at much longer time scales in comparison with the swelling. Finally, our observations indicate that the concentration of enzymes increases throughout the process, thus accelerating the degradation kinetics. All of these mechanisms will be account for in our theoretical model.†
3.1 Problem setting and governing equations
The chitin particle is assumed to be perfectly spherical and is composed of two species: a solid polymeric matrix and an impregnating solvent.‡ The solvent can contain, in addition to solvent molecules, dissolved monomers and enzymes secreted by bacteria living on the surface of the particle and in its bulk. The evolution of the spherical particle is assumed to be quasi-static, i.e. it remains in both swelling and mechanical equilibrium. To capture this response, we employ the general continuum mechanics framework for kinetics of surface growth coupled with solvent diffusion, developed in ref. 11, and specialize it here to the spherical problem while introducing the effect of degradation of elastic properties (in Section 3.2). The response of the material system in the bulk accounts for large deformation and swelling as in ref. 12–14.
Kinematics.
In the (true) current configuration of the particle, a spatial point is described using spherical coordinates (r,θ,φ). The swollen particle is a sphere of radius a = a(t). At its boundary, surface dissociation takes place. In the reference configuration, the polymer matrix is in its stress-free state, which will be taken to be the dry state (i.e. without any solvent). The dry particle is a sphere of radius A = A(t) and a material point is described using spherical coordinates (R,Θ,Φ).
The region occupied by the particle in the current configuration and its image region in the reference configuration are time dependent as they continuously evolve due to the reorganization of constituents (Fig. 3) as a result of swelling changes in the bulk of the particle and dissociation occurring at the boundary. Hence, the deformation field defined by the spherically symmetric mapping ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t) is inhomogeneous. Nevertheless, each material point sustains its location in the reference configuration as long as it is attached to the body.
(R,t) is inhomogeneous. Nevertheless, each material point sustains its location in the reference configuration as long as it is attached to the body.
 |
| | Fig. 3 Schematic of the spherical chitin particle in its dry reference configuration (left) and current swollen configuration (right). Surface degradation is represented by the molecular scissors. Degradation of elastic properties by enzymes that penetrate into the bulk is represented by the color gradient. | |
A material point in the reference configuration, can be mapped into a spatial point in the current configuration by the time dependent transformation
| | r = ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), θ = Θ, φ = Φ. (R,t), θ = Θ, φ = Φ. | (1) |
In the absence of rigid body motion, we require
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (0,t) = 0. (0,t) = 0. | (2) |
In the present spherically symmetric setting, the principal stretch components (
λR,
λΘ,
λΦ) can be written as
| |  | (3) |
and the volume ratio
J reads
| |  | (4) |
Assuming that either species (
i.e. polymer network and solvent) are separately incompressible, the change in volume with respect to the dry state is solely due to swelling. Hence the volume ratio
J will also be referred to as the swelling ratio. It relates to the solvent volume fraction
ω in the current configuration, and the corresponding referential field
Ω =
Jω, by
| |  | (5) |
Due to spherical symmetry, the material velocity
v(
R,
t) is along the radial direction and can be written as
| |  | (6) |
The velocity
Ȧ of the boundary in the reference space, which represents the rate of monomer dissociation, and the true velocity
ȧ of the boundary in the current configuration are also along the radial direction and are related to the material velocity by
The system is ultimately fully described by the dry radius A(t) and the mapping function ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), R ∈ [0,A].
(R,t), R ∈ [0,A].
Constitutive response.
The free energy of a unit volume of polymer is due to stretching of the elastic network (represented by the stretches λR, λΘ and λΦ) and mixing of the polymer network with the solvent (represented by the field Ω). Following22 the Helmholtz free energy can be represented as the summation of the two contributions| | | ψ(λR,λΘ,λΦ,Ω) = ψe(λR,λΘ,λΦ) + ψs(Ω), | (8) |
where ψe denotes the elastic free energy of the solid matrix and ψs denotes the free energy of the solvent mixing.
The constitutive relations are then derived using the dissipation inequality§ as in ref. 11. Accordingly, the radial and circumferential components SR(R,t) and SΘ(R,t) of the first Piola stress tensor read
| |  | (9) |
where
p is the hydrostatic pressure that arises as a reaction to the constrain
(5) and is constitutively indeterminate.
The chemical potential per unit reference volume is given by
| |  | (10) |
Equilibrium requirements.
Mechanical equilibrium in spherical symmetry and in the absence of body forces requires that| |  | (11) |
In the considered fluid permeated polymer, diffusion of solvent is generated by gradients of chemical potential. Considering degradation processes that take several of hours, in comparison with the diffusion process that occurs over significantly shorter timescales (of the order of minutes12), it is reasonable to assume swelling equilibrated states (no flux). Hence, we require a spatially homogeneous chemical potential such that
| |  | (12) |
Boundary conditions.
In the absence of pressure in the surrounding solvent, the stresses vanish on the outer boundary of the particle. Hence we can write the boundary conditionAccording to (12) and requiring the chemical potential to be in equilibrium with the surrounding solvent we can writewhere μ0 is the chemical potential of the surrounding solvent. Combining (10) and (14) yields an expression for the hydrostatic pressure| |  | (15) |
Specific response functions.
As in ref. 11–14, we employ the Helmholtz free energy function proposed by Flory and Rehner,22 to account for both finite stretching of the polymer network and for species migration. The free energy due to elastic deformation of the solid matrix is thus| |  | (16) |
where G = NkT and the free energy of solvent mixing is| |  | (17) |
which depends on the fraction of solvent within a unit reference volume. The later free energy density can be rewritten as a function of the volume ratio J using eqn (5) as| |  | (18) |
In the previous relations, G is the elastic shear modulus, N represents the number of solid chains per unit volume of the body, k is the Boltzmann's constant, T is the temperature, ψ0 is the free energy of a unit volume of unmixed solvent (which, due to species incompressibility, is equal to the constant chemical potential μ0 of the unmixed surrounding solvent), χ is the Flory–Huggins interaction parameter, and η the volume of a solvent unit.
By substituting the Helmholtz free energy given by combination of (8) with (16) and (18), in the constitutive relation (9), we can write the stress components
| |  | (19) |
and similarly from
(15) we can write the hydrostatic pressure
| |  | (20) |
In this section we have established a framework that describes the coupled chemo-mechanical behavior of the spherical particle. In the next section, we will couple the chemo-mechanical response to the biologically driven degradation kinetics.
3.2 Degradation kinetics
The enzymes produced by the bacteria diffuse through the particle and are responsible for a twofold degradation mechanism: (i) degradation of the polymer network within the bulk of the particle leading to reduction of cross-links,18,19,21 and (ii) monomer release on the free surface of the particle. These two degradation mechanisms are dependent upon local enzyme concentration. We thus start by examining the enzyme diffusion, then we elaborate on degradation kinetics.
Enzyme diffusion.
Enzymes are gradually secreted by the bacteria and carried by the solvent through which they can diffuse. Let u(r,t) denote the volumetric concentration of enzymes (per unit volume in the current configuration). On the outer surface of the particle, bacteria generate an enzyme concentration ua(t). The diffusion of enzymes through the solvent can be modeled using a modified Feynman diffusion law that accounts for the local fraction of solvent and the decay of enzymes| |  | (21) |
where D and Q denote the diffusion coefficient and the rate of decay of the enzymes, respectively. Notice that the diffusion of enzymes is highly dependent on the presence of solvent through the term ω (for highly swollen particles ω → 1).
Since the concentration of enzymes must be positive, we require
at all times
t. Additionally, the particle is assumed to sit in a well-mixed bath of enzymes, so that the concentration on the outer surface is
The concentration of enzymes on the particle surface is highly dependent on the local concentration of bacteria. In ref. 10 it was shown that the number of bacteria increases exponentially with time. For simplicity, we assume that each bacteria secretes enzymes at a constant rate. Hence, we can write ![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) a(t) ∝ eγt, where γ denotes the characteristic rate of bacteria multiplication (that depends on the type of bacteria). By integration, we can thus write
a(t) ∝ eγt, where γ denotes the characteristic rate of bacteria multiplication (that depends on the type of bacteria). By integration, we can thus write
where we have applied initial conditions such that
ua(0) = 0 and
![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) a
a(0) =
γuc, with
uc representing a characteristic level of enzyme concentration. The initial rate of bacteria multiplication
γ is dependent upon the initial bacteria concentration [B]
0.
¶
Degradation of elastic properties.
Enzymes that penetrate the particle cut the polymer chains, thus effectively reducing the number of cross-links. To account for this effect and its dependence on the local concentration of enzymes, we employ a degradation law of the form| |  | (25) |
where the kinetic parameter α depends on the specific bacterial strain. According to (25), if u(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t),t) is not homogeneous, it can result in inhomogeneous mechanical properties and therefore to an inhomogeneous stress state.
(R,t),t) is not homogeneous, it can result in inhomogeneous mechanical properties and therefore to an inhomogeneous stress state.
The change in N(R,t) entails a change in the chemo-mechanical equilibrium solution ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), and consequently a change in the volume ratio through (4). In other words, the changes in elasticity of the polymer network induce changes in volume of the particle.
(R,t), and consequently a change in the volume ratio through (4). In other words, the changes in elasticity of the polymer network induce changes in volume of the particle.
Surface dissociation.
By employing the dissipation inequality,11 it has been shown that the driving force of dissociation on the boundary of the body (per unit reference surface area), specified to the present geometry, has the formwhereis the latent energy of dissociation, and the fields ψ and J are evaluated at the boundary R = A(t). Using (8), (16), (18), (14) and (4) the driving force of degradation f can be expressed in terms of A, ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (A,t), ∂
(A,t), ∂![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (A,t)/∂R and N(A,t). The degradation rate of the solid network is the thermodynamic conjugate of the driving force and is considered here to obey a kinetic law of Arrhenius form
(A,t)/∂R and N(A,t). The degradation rate of the solid network is the thermodynamic conjugate of the driving force and is considered here to obey a kinetic law of Arrhenius form| |  | (28) |
where the kinetic parameter β depends on the specific bacterial strain. Note that the dissipation rate per unit surface on the dissociation boundary can be expressed as fȦ and has to be positive for all t. For the degradation process, Ȧ(t) ≤ 0, and therefore the driving force must obey f(t) ≤ 0.
Volume change.
A volume element dv of the current configuration can be expressed in terms of the reference configuration viaeqn (4) by dv = 4πr2dr = 4πJR2dR. Hence, the volume of the entire particle can be written in the integral form| |  | (29) |
Taking the time derivative of the above integral, we can write| |  | (30) |
The first term corresponds to a volume increase, that can be attributed to the degradation of the elastic properties; the second term corresponds to a volume decrease due to surface dissociation as ∀t, Ȧ(t) ≤ 0.
While v represents the particle volume in the current configuration, that depends on both swelling and surface dissociation, the volume of the particle in the reference frame, that we denote V, changes only due to dissociation at the surface. The rate of change of V can thus be written as
| | ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 4πA2Ȧ, = 4πA2Ȧ, | (31) |
which is monotonic since
Ȧ(
t) ≤ 0. By integration of the total volume of released monomers reads
| |  | (32) |
where
V0 is the initial dry volume of the particle in the reference configuration. In other words,
V0 −
V corresponds to the organic matter that is detached from the particle.
The two competing terms in (30) may lead to a negligible volume variation rate ![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) that characterize the waiting phase, or even a positive
that characterize the waiting phase, or even a positive ![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) that captures the experimentally observed volume expansion. This non-monotonic evolution of the swollen particle volume ‘hides’ a monotonic variation of the dry volume given by (31). This agrees qualitatively with the observations by ref. 19–21 and 23. Released monomers feed the bacteria that are thus able to grow and multiply during the waiting phase in which no apparent change in the particle happens. However, changes are happening: monomers are released, feeding the bacteria growth, while swelling is compensating this volume loss, making the system seem unchanged.
that captures the experimentally observed volume expansion. This non-monotonic evolution of the swollen particle volume ‘hides’ a monotonic variation of the dry volume given by (31). This agrees qualitatively with the observations by ref. 19–21 and 23. Released monomers feed the bacteria that are thus able to grow and multiply during the waiting phase in which no apparent change in the particle happens. However, changes are happening: monomers are released, feeding the bacteria growth, while swelling is compensating this volume loss, making the system seem unchanged.
3.3 Solution procedure and dimensionless formulation
By combining the kinetic relations (3) and (4) and the constitutive relations (19) and (20), and inserting them into the requirement for mechanical equilibrium (11) the problem can be restated as a second order nonlinear differential equation in space for r(R,t), for a known N(R,t).
The solution to this differential equation, along with boundary conditions (2) and (13), provides the chemo-mechanically equilibrated mapping ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), R ∈ [0,A(t)] at a given time. There remains the determination of N(R,t) and A(t). The number of solid chains per unit volume of the body N is altered both spatially and temporally by the enzymatic action following (25), and the time evolution of A is given by (28) with the driving force and latent energy specified in (26) and (27). Both degradations depend on the concentration of enzymes u obtained by solving (21) with conditions (22) and (23). The resolution requires initial conditions on the evolving N and A in the form
(R,t), R ∈ [0,A(t)] at a given time. There remains the determination of N(R,t) and A(t). The number of solid chains per unit volume of the body N is altered both spatially and temporally by the enzymatic action following (25), and the time evolution of A is given by (28) with the driving force and latent energy specified in (26) and (27). Both degradations depend on the concentration of enzymes u obtained by solving (21) with conditions (22) and (23). The resolution requires initial conditions on the evolving N and A in the form
| | | N(R,0) = N0, A(0) = A0, | (33) |
where
A0 and
N0 denote the initial dry radius of the particle in the reference configuration and the initial homogeneous number of solid chains per unit volume of the polymer network, respectively. We denote by
a0 and
v0 the corresponding initial radius and volume of the particle in the current configuration.
Finally, to compare with experimental data, the evolution of volume with respect to time can be determined using (30).
Dimensionless formulation.
To better understand the underlying parameters of this coupled degradation process, we write the kinetic equations in dimensionless forms.
Introducing the dimensionless quantities r* = r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, t* = t/t0 and u* = u/uc, where
0, t* = t/t0 and u* = u/uc, where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 denotes a length scale of the particle dimension (
0 denotes a length scale of the particle dimension (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ a0), and t0 a time scale of the process, we re-rewrite eqn (21) in the dimensionless form
0 ∼ a0), and t0 a time scale of the process, we re-rewrite eqn (21) in the dimensionless form
| | 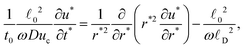 | (34) |
where

is the characteristic length scale of enzyme diffusion within the particle. Considering problems in which the characteristic time scale
t0 is large enough such that
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02
02/(
ωDuc) ≪
t0, namely, diffusion of enzymes happens much faster than degradation,
eqn (34) yields
| |  | (35) |
Note that with typical values of
Duc ∼ 10
−8 m
2 s
−1 and with
ω ∼ 1, this simplification holds for systems with
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02
02/
t0 ≪ 10
−8 m
2 s
−1 which covers a broad range of degradation processes.
Integrating the latter equation with conditions (22)–(24), yields an integral form of the enzyme concentration
| |  | (36) |
where the dimensionless
γ* =
γt0. Note that in
(36),
a*(
t*) is time dependent, and that
γ* and
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D
D are the only two parameters that characterize
u*. In particular, if we neglect enzyme decay, the diffusion length scale is much greater than the particle dimension
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D
D ≫
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0, the enzymes diffuse through the entire particle with a homogeneous concentration.
Now introducing A* = A/L0 and N* = N/N0, where L0 denotes a length scale of the dry particle, we re-write (25) and (28) in the dimensionless forms
| |  | (37) |
and
| |  | (38) |
respectively, where the dimensionless parameters
α* and
β* are such that
α* =
t0αuc and
β* =
t0βuc/
L0.
Model parameters.
The exhaustive set of model parameters is k, T, η, ψ0, N0, χ, γ, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D, α, β. At room temperature, k and T are known: kT = 4 × 10−21 J. Parameters η and ψ0 characterize the solvent, N0 and χ describe the initial elasticity and swelling of the polymer hydrogel, γ and
D, α, β. At room temperature, k and T are known: kT = 4 × 10−21 J. Parameters η and ψ0 characterize the solvent, N0 and χ describe the initial elasticity and swelling of the polymer hydrogel, γ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D describe the enzyme secretion and diffusion, and kinetic parameters α and β describe the degradation.
D describe the enzyme secretion and diffusion, and kinetic parameters α and β describe the degradation.
Regarding the polymer network constitutive response, common values of material parameters (η, ψ0, N0, χ) are taken from the literature for the specific case of chitin particles swollen by water (97% water):11–13,24,25η = 10−28 m3, ψ0 = −4 × 106 J m−3, χ = 0.2 and an initially homogeneous N0 = 1025 m−3. In the present framework, the free energy in (16) and (18) can be normalized by kT/η, thus reducing the number of model parameters needed to determine the bulk response of the swollen polymer to three: ηψ0/(kT), ηN0 and χ.
In summary, our problem has four unknown parameters α, β, γ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D. Due to the small length scale of the particles in the considered experiments and the apparent homogeneous swelling response, we assume that enzyme diffusion occurs much faster than decay, leading to a diffusion length scale such that
D. Due to the small length scale of the particles in the considered experiments and the apparent homogeneous swelling response, we assume that enzyme diffusion occurs much faster than decay, leading to a diffusion length scale such that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≫
D ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, thus removing
0, thus removing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D from the set of parameters and leading to a homogeneous enzyme concentration throughout the particle. There remains three model parameters, α, β and γ, that need to be determined, or alternatively, their dimensionless counterparts α*, β* and γ*. The normalization time scale and dry length scale will be taken to be of the order of magnitudes experimentally observed: t0 = 100 h and L0 = 10 μm. These scales only serve for normalization and do not impact the numerical results. After determining α*, β* and γ*, we can consider the influence of
D from the set of parameters and leading to a homogeneous enzyme concentration throughout the particle. There remains three model parameters, α, β and γ, that need to be determined, or alternatively, their dimensionless counterparts α*, β* and γ*. The normalization time scale and dry length scale will be taken to be of the order of magnitudes experimentally observed: t0 = 100 h and L0 = 10 μm. These scales only serve for normalization and do not impact the numerical results. After determining α*, β* and γ*, we can consider the influence of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D that may become important for larger particles.
D that may become important for larger particles.
4 Results and discussion
In this section we aim to verify that the theoretical model developed in the previous section can explain the experimental observations and be consistently applied to all of our data. By determining the three unknown model parameters α*, β* and γ*, we can possibly learn and quantitatively distinguish between degradation behaviors of different bacteria. In other words, the experiments will serve as a validation of the pertinence of the physical basis on which the theoretical model is built.
Beyond our specific experimental setting, the theoretical model involves parameters that can be tuned to predict situations that are not experimentally feasible, such as the material initial density and the particle initial volume, that can vary significantly in the natural environment. Hence, after using the experimental results to validate the model, we can apply it to shortcut more complex experimental procedures to study the influence of different factors on the degradation process.
4.1 Agreement between theory and experiments
We now make use of the solution procedure described in the previous section, providing the initial condition on the bead radius that is optically measured via time-lapse microscopy, for each bacterial strain. We optimize parameters α*, β* and γ* to fit one of the experiments with a certain initial volume, and apply the optimized set of parameters to predict other experiments with different initial volumes (recall that γ* is a function of the initial concentration of bacteria). In Fig. 2 we compare experimental observations to the model predictions. It is shown that the predicted curves agree well with the experimental measurements for the different volumes and for all three bacteria strains. In Table 1 we summarize the model parameters obtained for the different bacterial types. While allowing for γ* to vary with [B]0, we find it to have a logarithmic dependence on [B]0. This result agrees with the general trend in the dependence of the experimentally measured degradation half-time|| on [B]0.10 Notice that the presence of material that cannot be degradable by enzymes is accounted for in numerical integrations.
Table 1 Calibrated parameters α*, β* and γ* for each of three tested bacteria strains
| Bacterial strain |
α* |
β* |
γ* |
| vsple1A01 |
1.2 |
0.023 |
0.69 + 0.04 ln[B]0 |
| palte3D05 |
2.0 |
0.11 |
1.93 + 0.30 ln[B]0 |
| psych6C06 |
3.4 |
0.17 |
1.34 + 0.50 ln[B]0 |
As shown in Fig. 2, the model captures the different characteristics of the observation (i.e. the waiting phase, the expansion and the collapsing phase). The collapsing phase is ultimately due to the surface degradation that ends up prevailing over the swelling, while the expansion is a consequence of the competition between elasticity degradation (α*) and surface dissociation (β*). The waiting phase is conditioned by the characteristic rate γ*, and the absence of significant relative volume variation during the waiting phase is due to the compensation of surface degradation by particle swelling.
As shown in Table 1, each of the bacterial strains is characterized by a specific signature defined by parameters α*, β* and γ*. Hence, fitting the parameters cannot be arbitrary. Increase in both α* and β* enhances the polymer degradation and accelerate it. However, the two parameters have competing effects leading to different levels of volume expansion during the waiting phase: when α* prevails over β*, cross-link reduction is more dominant than surface dissociation, thus resulting in more volume expansion; when β* prevails over α* changes in swelling are less noticeable. As for the characteristic rate of enzyme secretion – γ*, is directly related to the degradation half-time.
4.2 Predictions beyond the scope of the experimental setting
The confrontation of the theoretical model and the experimental measurements shows the validity of the physics-based prediction that the model provides. Beyond the range of the experimentally accessible time and length scales, we can use this model to predict degradation behaviors of biopolymer particles, with different properties that can be observed in the natural environment. For instance, we can consider different initial volumes by several orders of magnitude, we can tune their initial solvent to solid ratio, and we can explore different regimes of enzyme diffusion.
Initial volume.
In Fig. 4, we represent the sensitivity of the degradation process to the initial volume of the particle. The particles studied in our experimental set-up have volumes of the order of 10−3 mm3. As we consider larger particles, the waiting phase becomes longer and the volume expansion more pronounced. This is a consequence of the ratio between surface area and particle volume which dictates that for larger particles the bulk response plays a more dominant role. In Fig. 5, we represent the sensitivity of the degradation half-time and the expansion amplitude, to α*, β* and γ* for different initial volumes. In all cases, both the degradation half-time and the expansion amplitude undergo an increase with respect to the initial volume. We note that a higher γ* leads to a higher degradation time, but doesn't affect the expansion.
 |
| | Fig. 4 Evolution of normalized particle volume variation for various values of initial particle volume (expressed in 10−3 mm3) containing 97% of solvent initially. Kinetic parameters are kept constant α* = 1.1, β* = 0.036 and γ* = 0.77. | |
 |
| | Fig. 5 (a) Degradation half-time and (b) expansion amplitude as a function of particle volume for different sets of material parameters specified in the legend. | |
Initial swelling.
In Fig. 6 we represent the effect of initial swelling of the particle on the evolution. We vary the initial solvent volume fraction, while keeping the dry volume constant. As expected, it is shown that denser particles take longer to degrade, and undergo a more pronounced expansion. It is worth noting that the significant expansion that appears for some of the curves in Fig. 4 and in Fig. 6, could lead to fracturing. Fracturing can expose more surface and can thus lead to accelerated degradation that should be accounted for in determining the degradation time, however is beyond the scope of the present work.
 |
| | Fig. 6 Normalized volume evolution for particles with different initial solvent volume fraction, indicated on the curves. Initial volume and kinetic parameters are kept constant v0 = 10−3 mm3, α* = 1.1, β* = 0.036 and γ* = 0.77. | |
Diffusion length.
In Fig. 7, we examine the effect of the diffusion length on the particle response.** For diffusion lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D that are considerably smaller than the particle initial radius a0, enzymes only diffuse through a thin peripheral layer in the vicinity of the particle boundary surface. Changes in elasticity become less significant as enzymes don't reach deep into the particle to cut cross-links, and the volume expansion does not occur. On the other hand, when the diffusion length is sufficiently larger than the particle radius (
D that are considerably smaller than the particle initial radius a0, enzymes only diffuse through a thin peripheral layer in the vicinity of the particle boundary surface. Changes in elasticity become less significant as enzymes don't reach deep into the particle to cut cross-links, and the volume expansion does not occur. On the other hand, when the diffusion length is sufficiently larger than the particle radius (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≫ a0), the solution converges to the solution of the problem with homogeneous enzyme concentration throughout the particle.
D ≫ a0), the solution converges to the solution of the problem with homogeneous enzyme concentration throughout the particle.
 |
| | Fig. 7 Normalized volume evolution for different values of diffusion length. Dashed line represents the limit where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D/a0 → ∞. Initial volume and kinetic parameters are kept constant v0 = 10−3 mm3, α* = 1.1, β* = 0.036 and γ* = 0.77. D/a0 → ∞. Initial volume and kinetic parameters are kept constant v0 = 10−3 mm3, α* = 1.1, β* = 0.036 and γ* = 0.77. | |
5 Conclusions
At the interface between microbiology and continuum mechanics, this work brings deeper understanding into the degradation kinetics of biomatter; a process that determines the fate of carbon in the oceans and plays a significant role in the marine ecosystem. Based on controlled experimental observations of the degradation of isolated chitin particles, by an isogenic bacterial colony, we determine that the two primary mechanisms at play are degradation of the internal mechanical properties, and dissociation of material from the surface of the particle. To capture the chemo-mechanical coupling associated with swelling of fluid permeated polymeric particles at large deformations, as well as the kinetics of dissociation on their surface, we have extended recent continuum models. We consider spherical particles that are composed of two interacting species (i.e. a polymer network and a permeating solvent) and account for the influence of bacterial concentrations on the degradation and dissociation kinetics. For each bacterial strain, we determine the associated kinetic parameters by comparing the theoretical predictions with our experimental observations. We also examine the influence of varying initial volume and initial swelling of the particles on the degradation process and study the sensitivity to the kinetic parameters.
Three main conclusions come out of this work:
(i) The bio-physical processes incorporated in our model are sufficient to predict the observed degradation kinetics for particles of various initial volumes, degraded by different bacterial strains at different initial concentrations, and explain the non-monotonic behavior that has been observed experimentally.
(ii) The kinetic parameters of the degradation response reveal distinct signatures of the different bacterial strains. This result may be useful in the future to better understand interactions within bacterial communities that involve several strains.
(iii) Being validated against experimental results, this model provides means for prediction of degradation under varying environmental conditions that are not experimentally feasible. Thus, the model can both guide the interpretation of the experimental results and be extended to formulate conclusions for more complex systems.
Beyond the considered example, mechanical behavior of hydrogels, coupling swelling and large deformation, have continuously been subject to unique interest from a constitutive point of view,12–14,25 due to their wide range of applications, such as, but not restricted to, drug delivery,26,27 soft machines,28 sensors and actuators.29–31 Motivated by the rich variety of medical applications, several works attempted to understand the correlation between polymer degradation, and mechanical swelling properties.18–21,23 Due to clear analogies that can be established between the experiments presented here and hydrogel degradation in different contexts, the current work can be extended to formulate predictive models for other degradation processes.
Conflicts of interest
There are no conflicts to declare.
Appendix A – nomenclature
|
t
| Time variable |
|
r, θ, ϕ | Spherical coordinates in the current configuration |
|
R, Θ, Φ | Spherical coordinates in the reference configuration |
|
a
| Particle radius in the current configuration |
|
A
| Particle radius in the reference configuration |
|
v
| Particle volume in the current configuration |
|
V
| Particle volume in the reference configuration |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
| Mapping from reference to current configuration |
| v | Radial particle velocity in the current configuration |
|
λ
R
, λΘ, λΦ | Principal stretch components |
|
J
| Volume ratio |
|
ω
| Current volume fraction of solvent |
|
Ω
| Reference volume fraction of solvent |
|
ψ
| Helmholtz free energy of the body |
|
ψ
e
| Elastic free energy of the solid matrix |
|
ψ
s
| Free energy of the solvent |
|
S
| Piola stress tensor |
|
p
| Hydrostatic pressure |
|
μ
| Chemical potential of the solvent |
|
f
| Driving force on the boundary |
| Δψ | Latent energy of growth |
|
k
| Boltzmann constant |
|
T
| Temperature |
|
N
| Number of polymer chains per unit volume |
|
η
| Volume of a solvent unit |
|
χ
| Flory–Huggins interaction parameter |
| [B] | Concentration of bacteria |
|
u
| Volumetric concentration of enzymes |
|
D
| Enzyme diffusion coefficient |
|
Q
| Enzyme decay rate |
|
α
| Kinetic parameter of cross-links reduction |
|
β
| Kinetic parameter of surface dissociation |
|
γ
| Characteristic rate of bacteria multiplication |
|
u
c
| Characteristic level of bacteria concentration |
|
L
0
| Length scale of the dry particle |
|
t
0
| Time scale of the process |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D D | Characteristic length scale of enzyme diffusion |
Acknowledgements
The authors wish to acknowledge the financial support of the MIT Civil and Environmental Engineering cross disciplinary seed fund award. Thanks to Ali Ebrahimi and Gabriel E. Leventhal for valuable discussions.
References
- N. Jiao, G. J. Herndl, D. A. Hansell, R. Benner, G. Kattner, S. W. Wilhelm, D. L. Kirchman, M. G. Weinbauer, T. Luo and F. Chen,
et al., Microbial production of recalcitrant dissolved organic matter: long-term carbon storage in the global ocean, Nat. Rev. Microbiol., 2010, 8(8), 593 CrossRef CAS PubMed
 .
.
-
D. L. Kirchman, A primer on dissolved organic material and heterotrophic prokaryotes in the oceans, The Ocean Carbon Cycle and Climate, Springer, 2004, pp. 31–63 Search PubMed
 .
.
- F. Azam, D. C. Smith, G. F. Steward and Å. Hagström, Bacteria–organic matter coupling and its significance for oceanic carbon cycling, Microb. Ecol., 1994, 28(2), 167–179 CrossRef CAS
 .
.
- F. Azam and F. Malfatti, Microbial structuring of marine ecosystems, Nat. Rev. Microbiol., 2007, 5(10), 782 CrossRef CAS
 .
.
- A. L. Alldredge and M. W. Silver, Characteristics, dynamics and significance of marine snow, Prog. Oceanogr., 1988, 20(1), 41–82 CrossRef
 .
.
- J. K. Volkman and E. Tanoue, Chemical and biological studies of particulate organic matter in the ocean, J. Oceanogr., 2002, 58(2), 265–279 CrossRef CAS
 .
.
- U. Passow, Transparent exopolymer particles (tep) in aquatic environments, Prog. Oceanogr., 2002, 55(3–4), 287–333 CrossRef
 .
.
- A. Engel, S. Thoms, U. Riebesell, E. Rochelle-Newall and I. Zondervan, Polysaccharide aggregation as a potential sink of marine dissolved organic carbon, Nature, 2004, 428(6986), 929 CrossRef CAS PubMed
 .
.
- O. X. Cordero and R. Stocker, A particularly useful system to study the ecology of microbes, Environ. Microbiol. Rep., 2017, 9(1), 16–17 CrossRef PubMed
 .
.
- T. N. Enke, G. E. Leventhal, M. Metzger, J. T. Saavedra and O. X. Cordero, Microscale ecology regulates particulate organic matter turnover in model marine microbial communities, Nat. Commun., 2018, 9(2018), 2743 CrossRef PubMed
 .
.
- R. Abi-Akl, R. Abeyaratne and T. Cohen, Kinetics of surface growth with coupled diffusion and the emergence of a universal growth path, Proc. R. Soc. A, 2019, 475(2221), 20180465 CrossRef PubMed
 .
.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, A theory of coupled diffusion and large deformation in polymeric gels, J. Mech. Phys. Solids, 2008, 56(5), 1779–1793 CrossRef CAS
 .
.
- S. A. Chester and L. Anand, A coupled theory of fluid permeation and large deformations for elastomeric materials, J. Mech. Phys. Solids, 2010, 58(11), 1879–1906 CrossRef CAS
 .
.
- F. P. Duda, A. C. Souza and E. Fried, A theory for species migration in a finitely strained solid with application to polymer network swelling, J. Mech. Phys. Solids, 2010, 58(4), 515–529 CrossRef CAS
 .
.
- N. O. Keyhani and S. Roseman, Physiological aspects of chitin catabolism in marine bacteria1, Biochim. Biophys. Acta, Gen. Subj., 1999, 1473(1), 108–122 CrossRef CAS
 .
.
- B. Sara and S. Bertilsson, Bacterial chitin degradation-mechanisms and ecophysiological strategies, Front. Microbiol., 2013, 4, 149 Search PubMed
 .
.
- C. Jeuniaux and M. F. Voss-Foucart, Chitin biomass and production in the marine environment, Biochem. Syst. Ecol., 1991, 19(5), 347–356 CrossRef CAS
 .
.
- T. K. L. Meyvis, S. C. D. Smedt, J. Demeester and W. E. Hennink, Influence of the degradation mechanism of hydrogels on their elastic and swelling properties during degradation, Macromolecules, 2000, 33(13), 4717–4725 CrossRef CAS
 .
.
- B. G. Stubbe, K. Braeckmans, F. Horkay, W. E. Hennink, S. C. De Smedt and J. Demeester, Swelling pressure observations on degrading dex-hema hydrogels, Macromolecules, 2002, 35(7), 2501–2505 CrossRef CAS
 .
.
- B. G. Stubbe, W. E. Hennink, S. C. De Smedt and J. Demeester, Swelling pressure of hydrogels that degrade through different mechanisms, Macromolecules, 2004, 37(23), 8739–8744 CrossRef CAS
 .
.
- K. Yong Lee, K. H. Bouhadir and D. J. Mooney, Controlled degradation of hydrogels using multi-functional cross-linking molecules, Biomaterials, 2004, 25(13), 2461–2466 CrossRef
 .
.
- P. J. Flory and J. Rehner Jr., Statistical mechanics of cross-linked polymer networks ii. swelling, J. Chem. Phys., 1943, 11(11), 521–526 CrossRef CAS
 .
.
- D. F. Coutinho, S. V. Sant, H. Shin, J. T. Oliveira, M. E. Gomes, N. M. Neves, A. Khademhosseini and R. L. Reis, Modified gellan gum hydrogels with tunable physical and mechanical properties, Biomaterials, 2010, 31(29), 7494–7502 CrossRef CAS PubMed
 .
.
- P. Hassanzadeh, W. Sun, J. P. de Silva, J. Jin, K. Makhnejia, G. L. W. Cross and M. Rolandi, Mechanical properties of self-assembled chitin nanofiber networks, J. Mater. Chem. B, 2014, 2(17), 2461–2466 RSC
 .
.
- Y. Lai and Y. Hu, Probing the swelling-dependent mechanical and transport properties of polyacrylamide hydrogels through afm-based dynamic nanoindentation, Soft Matter, 2018, 14(14), 2619–2627 RSC
 .
.
- B. V. Slaughter, S. S. Khurshid, O. Z. Fisher, A. Khademhosseini and N. A. Peppas, Hydrogels in regenerative medicine, Adv. Mater., 2009, 21(32–33), 3307–3329 CrossRef CAS PubMed
 .
.
- J. Li and D. J. Mooney, Designing hydrogels for controlled drug delivery, Nat. Rev. Mater., 2016, 1(12), 16071 CrossRef CAS
 .
.
- P. Calvert, Hydrogels for soft machines, Adv. Mater., 2009, 21(7), 743–756 CrossRef CAS
 .
.
- D. Buenger, F. Topuz and J. Groll, Hydrogels in sensing applications, Prog. Polym. Sci., 2012, 37(12), 1678–1719 CrossRef CAS
 .
.
- A. Richter, G. Paschew, S. Klatt, J. Lienig, K.-F. Arndt and H.-J. P. Adler, Review on hydrogel-based ph sensors and microsensors, Sensors, 2008, 8(1), 561–581 CrossRef CAS PubMed
 .
.
- G. Gerlach, M. Guenther, J. Sorber, G. Suchaneck, K.-F. Arndt and A. Richter, Chemical and ph sensors based on the swelling behavior of hydrogels, Sens. Actuators, B, 2005, 111, 555–561 CrossRef
 .
.
Footnotes |
| † A comprehensive nomenclature can be found in Appendix A. |
| ‡ Also referred to as the bacterial growth media. |
| § The derivation of constitutive relations applies the Coleman-Noll methodology on the dissipation rate in a material subregion. |
| ¶ Note that in absence of models that determine the coupling between bacterial metabolism and production of enzymes, we employ here a first order approximation that is based on the experimental evidence. |
| || The degradation half-time is defined as the time it takes to reduce the particle volume by half. |
| ** Note that an important environmental factor that can affect the diffusion length, and therefore the degradation rate, is the temperature (through the diffusion coefficient). |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab

![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t) is inhomogeneous. Nevertheless, each material point sustains its location in the reference configuration as long as it is attached to the body.
(R,t) is inhomogeneous. Nevertheless, each material point sustains its location in the reference configuration as long as it is attached to the body.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), θ = Θ, φ = Φ.
(R,t), θ = Θ, φ = Φ.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (0,t) = 0.
(0,t) = 0.



![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), R ∈ [0,A].
(R,t), R ∈ [0,A].










![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) a(t) ∝ eγt, where γ denotes the characteristic rate of bacteria multiplication (that depends on the type of bacteria). By integration, we can thus write
a(t) ∝ eγt, where γ denotes the characteristic rate of bacteria multiplication (that depends on the type of bacteria). By integration, we can thus write![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) a(0) = γuc, with uc representing a characteristic level of enzyme concentration. The initial rate of bacteria multiplication γ is dependent upon the initial bacteria concentration [B]0.¶
a(0) = γuc, with uc representing a characteristic level of enzyme concentration. The initial rate of bacteria multiplication γ is dependent upon the initial bacteria concentration [B]0.¶

![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t),t) is not homogeneous, it can result in inhomogeneous mechanical properties and therefore to an inhomogeneous stress state.
(R,t),t) is not homogeneous, it can result in inhomogeneous mechanical properties and therefore to an inhomogeneous stress state.
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), and consequently a change in the volume ratio through (4). In other words, the changes in elasticity of the polymer network induce changes in volume of the particle.
(R,t), and consequently a change in the volume ratio through (4). In other words, the changes in elasticity of the polymer network induce changes in volume of the particle.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (A,t), ∂
(A,t), ∂![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (A,t)/∂R and N(A,t). The degradation rate of the solid network is the thermodynamic conjugate of the driving force and is considered here to obey a kinetic law of Arrhenius form
(A,t)/∂R and N(A,t). The degradation rate of the solid network is the thermodynamic conjugate of the driving force and is considered here to obey a kinetic law of Arrhenius form


![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 4πA2Ȧ,
= 4πA2Ȧ,
![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) that characterize the waiting phase, or even a positive
that characterize the waiting phase, or even a positive ![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) that captures the experimentally observed volume expansion. This non-monotonic evolution of the swollen particle volume ‘hides’ a monotonic variation of the dry volume given by (31). This agrees qualitatively with the observations by ref. 19–21 and 23. Released monomers feed the bacteria that are thus able to grow and multiply during the waiting phase in which no apparent change in the particle happens. However, changes are happening: monomers are released, feeding the bacteria growth, while swelling is compensating this volume loss, making the system seem unchanged.
that captures the experimentally observed volume expansion. This non-monotonic evolution of the swollen particle volume ‘hides’ a monotonic variation of the dry volume given by (31). This agrees qualitatively with the observations by ref. 19–21 and 23. Released monomers feed the bacteria that are thus able to grow and multiply during the waiting phase in which no apparent change in the particle happens. However, changes are happening: monomers are released, feeding the bacteria growth, while swelling is compensating this volume loss, making the system seem unchanged.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (R,t), R ∈ [0,A(t)] at a given time. There remains the determination of N(R,t) and A(t). The number of solid chains per unit volume of the body N is altered both spatially and temporally by the enzymatic action following (25), and the time evolution of A is given by (28) with the driving force and latent energy specified in (26) and (27). Both degradations depend on the concentration of enzymes u obtained by solving (21) with conditions (22) and (23). The resolution requires initial conditions on the evolving N and A in the form
(R,t), R ∈ [0,A(t)] at a given time. There remains the determination of N(R,t) and A(t). The number of solid chains per unit volume of the body N is altered both spatially and temporally by the enzymatic action following (25), and the time evolution of A is given by (28) with the driving force and latent energy specified in (26) and (27). Both degradations depend on the concentration of enzymes u obtained by solving (21) with conditions (22) and (23). The resolution requires initial conditions on the evolving N and A in the form![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, t* = t/t0 and u* = u/uc, where
0, t* = t/t0 and u* = u/uc, where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 denotes a length scale of the particle dimension (
0 denotes a length scale of the particle dimension (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ a0), and t0 a time scale of the process, we re-rewrite eqn (21) in the dimensionless form
0 ∼ a0), and t0 a time scale of the process, we re-rewrite eqn (21) in the dimensionless form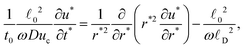
 is the characteristic length scale of enzyme diffusion within the particle. Considering problems in which the characteristic time scale t0 is large enough such that
is the characteristic length scale of enzyme diffusion within the particle. Considering problems in which the characteristic time scale t0 is large enough such that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02/(ωDuc) ≪ t0, namely, diffusion of enzymes happens much faster than degradation, eqn (34) yields
02/(ωDuc) ≪ t0, namely, diffusion of enzymes happens much faster than degradation, eqn (34) yields
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02/t0 ≪ 10−8 m2 s−1 which covers a broad range of degradation processes.
02/t0 ≪ 10−8 m2 s−1 which covers a broad range of degradation processes.

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D are the only two parameters that characterize u*. In particular, if we neglect enzyme decay, the diffusion length scale is much greater than the particle dimension
D are the only two parameters that characterize u*. In particular, if we neglect enzyme decay, the diffusion length scale is much greater than the particle dimension ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≫
D ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, the enzymes diffuse through the entire particle with a homogeneous concentration.
0, the enzymes diffuse through the entire particle with a homogeneous concentration.


![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D, α, β. At room temperature, k and T are known: kT = 4 × 10−21 J. Parameters η and ψ0 characterize the solvent, N0 and χ describe the initial elasticity and swelling of the polymer hydrogel, γ and
D, α, β. At room temperature, k and T are known: kT = 4 × 10−21 J. Parameters η and ψ0 characterize the solvent, N0 and χ describe the initial elasticity and swelling of the polymer hydrogel, γ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D describe the enzyme secretion and diffusion, and kinetic parameters α and β describe the degradation.
D describe the enzyme secretion and diffusion, and kinetic parameters α and β describe the degradation.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D. Due to the small length scale of the particles in the considered experiments and the apparent homogeneous swelling response, we assume that enzyme diffusion occurs much faster than decay, leading to a diffusion length scale such that
D. Due to the small length scale of the particles in the considered experiments and the apparent homogeneous swelling response, we assume that enzyme diffusion occurs much faster than decay, leading to a diffusion length scale such that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≫
D ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, thus removing
0, thus removing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D from the set of parameters and leading to a homogeneous enzyme concentration throughout the particle. There remains three model parameters, α, β and γ, that need to be determined, or alternatively, their dimensionless counterparts α*, β* and γ*. The normalization time scale and dry length scale will be taken to be of the order of magnitudes experimentally observed: t0 = 100 h and L0 = 10 μm. These scales only serve for normalization and do not impact the numerical results. After determining α*, β* and γ*, we can consider the influence of
D from the set of parameters and leading to a homogeneous enzyme concentration throughout the particle. There remains three model parameters, α, β and γ, that need to be determined, or alternatively, their dimensionless counterparts α*, β* and γ*. The normalization time scale and dry length scale will be taken to be of the order of magnitudes experimentally observed: t0 = 100 h and L0 = 10 μm. These scales only serve for normalization and do not impact the numerical results. After determining α*, β* and γ*, we can consider the influence of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D that may become important for larger particles.
D that may become important for larger particles.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D that are considerably smaller than the particle initial radius a0, enzymes only diffuse through a thin peripheral layer in the vicinity of the particle boundary surface. Changes in elasticity become less significant as enzymes don't reach deep into the particle to cut cross-links, and the volume expansion does not occur. On the other hand, when the diffusion length is sufficiently larger than the particle radius (
D that are considerably smaller than the particle initial radius a0, enzymes only diffuse through a thin peripheral layer in the vicinity of the particle boundary surface. Changes in elasticity become less significant as enzymes don't reach deep into the particle to cut cross-links, and the volume expansion does not occur. On the other hand, when the diffusion length is sufficiently larger than the particle radius (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≫ a0), the solution converges to the solution of the problem with homogeneous enzyme concentration throughout the particle.
D ≫ a0), the solution converges to the solution of the problem with homogeneous enzyme concentration throughout the particle.
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D
D.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.






