Open Access Article
Open Access ArticleSelf-organization of gel networks formed by block copolymer stars
Ioana C.
Gârlea
 *,
Diego
Jaramillo-Cano
and
Christos N.
Likos
*,
Diego
Jaramillo-Cano
and
Christos N.
Likos

Faculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: ioana.cristina.garlea@univie.ac.at
First published on 29th March 2019
Abstract
The equilibrium properties of block copolymer star networks (BCS) are studied via computer simulations. We employ both molecular dynamics and multiparticle collisional dynamics simulations to investigate the self-organization of BCS with f = 9 functionalized arms close to their overlap concentrations under conditions of different fractions of functionalization and varying attraction strength. We find three distinct macroscopic self-organized states depending on fraction of attractive end-monomers and the strength of the attraction. At weak attractions, ergodic, diffusive liquids result, with short-lived bonds between the stars. As the attraction strength grows, the whole system forms a percolating cluster, while at the same time the individual molecules are diffusive. Finally, arrested gels emerge when the attractions become strong. The conformation of the BCS in these solutions is found to be strongly affected by the concentration, with the stars assuming typically spherical, open configurations in seeking to maximize inter-star associations as opposed to the inter-star collapse that results at infinite dilution, giving rise to strongly aspherical shapes and reduced sizes.
1 Introduction
Chemically heterogeneous, nano-sized particles have emerged in the last two decades as novel building blocks for steering the self-assembly, structure, dynamics and macroscopic phase behavior in condensed matter and soft materials. A prominent example are patchy colloids,1–6i.e., hard, non-deformable nano- to micron-sized colloidal particles featuring chemically or physically decorated surfaces with selective interactions toward the patched and non-patched sectors of the surfaces of other colloids. The presence of such competing interactions (usually: repulsive between the non-patched and attractive for the patched parts) gives rise to an unprecedented variety of self-assembly scenarios,1,2,7,8 tunable through control of the anisotropy of their interaction patterns. Moreover, the ability to control the number and the (orientational) flexibility of the attractive patches has led to a number of important advances in our understanding of the low-temperature phases and the critical behavior of systems with limited valence,9–12 contributing thereby to our understanding of fundamental questions in statistical mechanics. The variety of ordered and disordered phases grows further when interaction anisotropy becomes combined with shape anisotropy,13,14 which provides a link between patchy colloids and stiff associating polymers, to be discussed below. Further, surface heterogeneities on colloidal particles also arise through the introduction of particles with a heterogeneous surface charge, called inverse patchy colloids (IPCs).15 While conventional patchy particles are realized by adding attractive patches on the surface of otherwise repulsive particles, IPCs have patches that electrostatically repel each other, while they attract the rest of the colloidal surface that is free of patches. The interplay between attraction and repulsion of oppositely and like charged regions leads to a complex effective potential between IPCs,16 and associated, highly nontrivial self-assembly scenarios.17,18A distinct physical framework for intra- and, most importantly, intermolecular assembly driven by competing interactions is offered within the broad field of associating polymers.19–21 Whereas polymer chains are held together via irreversible, covalent bonds, associating polymers contain units that are capable of forming reversible, physical bonds with similar units of other chains. These include van der Waals interactions, π–π stacking, hydrogen bonding and metal–ligand coordination,21,22 and they cover at least two orders of magnitude in terms of binding energy, ranging from one to several hundred kJ mol−1. The reversibility of the bonds leads, at high concentrations, to the formation of reconfigurable, supramolecular networks,19,20 a feature common with the systems that are the subject of the current manuscript. These networks feature a number of unusual and highly interesting properties, such as enhanced resistance to fracture,23–25 self-memory and self-healing.26–28 The dynamics and rheology of concentrated solutions and melts of associating polymers is very rich and complex.21,29–38 A key role in determining the dynamics of networks of associating polymers is played by the ratio between the timescales associated to bond breakage and lifetime on the one hand, and to polymer relaxation on the other.39,40 Particular attention has to be paid to the fact that it is not the bare bond lifetime that is of importance to the dynamics but rather a renormalized lifetime associated with the typical timescale it takes for an associating monomer to find a new partner in the network; indeed, the latter can exceed the former by a large factor.22,40 Recently, the effects of backbone rigidity on the structure and rheology of telechelic associating linear chains have been examined in detail by computer simulations, providing evidence for the existence of an unusual scaffolding structure in equilibrium,41 accompanied by the formation of bundles and thixotropic behavior under steady shear.42,43 Rigid telechelic chains provide thereby a natural physical link between associating polymers and anisotropic patchy colloids.13,14
A third, and least understood, category of nanosized particles with antagonistic interactions and heterogeneous composition is a hybrid between the hard colloids and the flexible block copolymers presented above. Typically, these are polymer-based nanocolloids formed by, e.g., centrally-grafted block copolymers or by surface patterning by polymers of varying solvent quality. Members of this class have been termed soft patchy nanoparticles.44–46 Examples of this class of particles can be mostly found in polymer-based systems: some characteristic examples are Janus-like polymer vesicles,47 micelles based on targeted design of functionalized dendritic polymers,48 patchy nanoparticles with tunable symmetries resulting from the self-aggregation of block copolymer chains45,49 or stars,50 block copolymer nanoparticles with microphase separation structures,51 hydrophobic dendrimers particles with dynamic hydrophobic patches52 or colloids grafted with poor-solvent polymer brushes.45 Most recently, DNA-coated colloids53,54 and emulsions,55 as well as DNA nano-stars12,56–60 have emerged as real systems characterized by fluctuating patches: notice, however, that in the latter case only one bond can be formed between complementary single-DNA strands on different DNA-stars, whereas in the case of bock copolymer stars (BCS) we consider in this work the valence of any bond is only limited by steric constraints, i.e., by the maximum number of neighbors that can pack around a given monomer.
Our stars have polymeric arms made of diblock copolymers with a solvophilic inner block A and a solvophobic terminal block B, the chains grafted on a common center on their A-parts. Concrete experimental realizations of such end-functionalized macromolecules are also zwitterionic polybutadiene star polymers61,62 or polybutadiene/polyisoprene block copolymer stars in selective solvents. At the infinite dilution limit (single particle state diagram), the antagonism between entropic and enthalpic contributions leads to the formation of aggregation regions (patches) for the B-type monomers on the surface of the stars. The single particle properties (patchiness, patch arrangement, angular and radial correlations and extent) can be readily tuned by the number of arms per star, the ratio between solvophobic and solvophilic monomers and the attraction strength.50,63–65 Our model also bears similarities with recently studied experimental systems of amphiphilic conetwork gels66,67 and star block copolymers.68
For finite densities, when the block copolymer stars interact with one another, most of what is known is based on Monte Carlo simulations of lattice models.69–72 It has been shown there that for low functionalities and low fractions of functionalized monomers, the BCSs self-organize into micelles, which, as density grows, interconnect and can form elongated, wormlike aggregates. For intermediate functionalities and attraction strengths, the growth of extended network structures has been seen in lattice Monte Carlo70 but neither the structure of the network nor the conformational and dynamical characteristics of the stars in the network have been analyzed. In addition, the system has not been investigated at all in the continuum and, of course, no information about the dynamics has been gained from the aforementioned Monte Carlo investigations,69–72 which included a number of special moves to accelerate equilibrium sampling that are unphysical from the dynamics point of view. Here we perform detailed molecular dynamics and multiparticle collisional dynamics simulations to analyze the structure and the diffusion dynamics of concentrated solutions of BCSs of intermediate functionalities, f = 9. Since at infinite dilution these soft patchy colloids have the form of dumbbells,65 they do not self-organize into micelles but, rather, they form networks. We find, however, that in forming these networks the BCSs become reconfigured with respect to their infinite-dilution conformation, assuming in concentrated solution rather open, spherical shapes in attempting to maximize inter-star association. Our model system has many similarities with the telechelic star polymers in the recent work of Metri et al.,73 who performed a joint experimental and simulation investigation of the stress-relaxation and rheological properties of the physical networks formed by these molecules. We will comment on these in the appropriate section below.
The rest of the work is organized as follows. In Section 2 we present the model employed for the block copolymer stars, as well as the methods of simulation and analysis. In Section 3 we present and analyze our results on association, network formation and connectivity characteristics, pair correlations and equilibrium diffusion. Finally, in Section 4 we summarize and draw our conclusions.
2 Model and methods
We perform simulations of block copolymer stars (BCS) by modeling the macromolecules as f = 9 linear chains (called arms) consisting of N = 30 spherical monomers of diameter σ, exhibiting steric repulsion which are attached to a core monomer referred to as anchor. The blocks located at the outer ends of each chain are functionalized or chemically diverse from the inner block in such a way that they attract each other, the attraction being short-ranged; typically, these are AB-block copolymers for which the inner, A-block is in good solvent conditions but the B-block finds itself in a Θ-solvent or even poor solvent. The anchor was designed as a non-functionalized monomer but having, for geometrical reasons, a higher diameter than the arm monomers (σanchor = 2σ). We denote the fraction of functionalized monomers by α (i.e., the number of attractive monomers in the outer block over the total number of monomer in an arm).The non-functionalized monomers interact among themselves as well as with the functionalized monomers via a generalized truncated and shifted Lennard-Jones potential of the form:
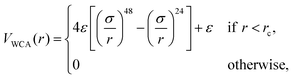 | (1) |
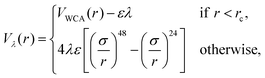 | (2) |
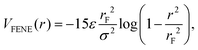 | (3) |
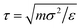 . We employed two simulation approaches: considering the solvent implicit and performing molecular dynamics simulations (MD), and by explicitly representing the solvent using Multi-Particle Collision Dynamics (MPCD). Even if the second approach may seem more realistic, it is also much more demanding computationally. We found that differences between the two approaches are within simulation error bars, as they should, since in equilibrium, hydrodynamics, which is present in the MPCD-MD scheme, has no influence on the system properties.
. We employed two simulation approaches: considering the solvent implicit and performing molecular dynamics simulations (MD), and by explicitly representing the solvent using Multi-Particle Collision Dynamics (MPCD). Even if the second approach may seem more realistic, it is also much more demanding computationally. We found that differences between the two approaches are within simulation error bars, as they should, since in equilibrium, hydrodynamics, which is present in the MPCD-MD scheme, has no influence on the system properties.
2.1 Molecular dynamics simulations
We perform NVT molecular dynamics simulation of BCSs, the solvent being only implicitly taken into account. Throughout our simulation, we keep the temperature fixed at kBT = 0.5 using a Nosé–Hoover thermostat. The strength of the attractive potential was varied from λ = 1 to λ = 1.75. We start each simulation with all BCSs, which are randomly distributed in the simulation box, in an open star configuration i.e., one in which no attractive beads are aggregated; this is equivalent to abruptly lowering the temperature at the beginning of our simulation time. For the single-star simulations, we placed one single star in a cubic box with periodic boundary conditions of side length L = 200σ. For the networks we simulated Ns = 52 BCSs in a box of linear size L = 50σ, which amounts to a monomer volume fraction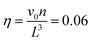 , where
, where 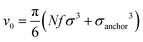 is the volume of one BCS considered as the sum of the monomers forming it. Typical runs consist of 107 molecular dynamics steps with a time-step Δt = 0.002τ. Equilibrium times are in the order of 106 MD steps.
is the volume of one BCS considered as the sum of the monomers forming it. Typical runs consist of 107 molecular dynamics steps with a time-step Δt = 0.002τ. Equilibrium times are in the order of 106 MD steps.
2.2 Hybrid MPCD-MD simulations
Multi-particle collision dynamics (MPCD)74,75 was employed in addition at selected densities, to ascertain that no hydrodynamic effects play a role in the phenomena observed. The solvent is an ideal gas composed of ns particles, each having mass ms = m/5, which interact with each other only in the collision step. In the streaming step, the solvent particles move ballistically for a time step of duration Δtmpcd; at that point, solvent particles are sorted into cubic cells with length a, and the collision consists of rotating their relative velocities with respect to the cell center-of-mass by an angle χ around a random axis,74–76 in which the solvent particles exchange linear momentum. Galilean invariance, is ensured by a random shift of the grid before any collision step. We simulated an average number ρ = 5 of solvent particles per collision cell and we coupled the monomers of the polymer to the collision, while evolving the polymer in parallel with molecular dynamics. As in the pure MD, for the temperature T, we choose the value kBT/ε = 0.5. The remaining MPCD-parameters were set as follows: the time between collisions is Δtmpcd = 0.1τ, the rotation angle is χ = 130°, and the cell size a = σ, making the presence of two monomer centers in the collision cell very unlikely. MPCD-MD simulations have been performed for all combinations of the following parameters: η ∈ {0.01, 0.065, 0.1}, α ∈ {0.3, 0.5}, and λ ∈ {1.0, 1.1}.We used a multi-step protocol to equilibrate our BCSs system. First, a number of 35 completely stretched BCSs were placed in regular pattern in the simulation box. These stars are composed of only repulsive monomers, the attraction of the outer ends of the arms being turned off by setting λ = 0. The system was equilibrated by performing MD simulations, the solvent not being yet considered at this point. In the second step of our protocol, the size of the box is gradually reduced, allowing the stars to equilibrate, until the desired volume fraction was reached. Afterwards the attractive interaction was switched on (λ ≠ 0) and the system was again allowed to reach equilibrium. Finally, the solvent is also introduced and hybrid MPCD-MD simulations are performed, typical runs being in the order of 107 MD steps.
2.3 Shape parameters
To accurately describe the shape of our block copolymer stars we make use of the three eigenvalues λ1 > λ2 > λ3 of the gyration tensor, which reads: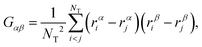 | (4) |
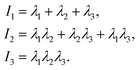 | (5) |
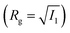 . With the help of these invariants we can define the asphericity δ, the prolateness S, and the acylindricity c as:
. With the help of these invariants we can define the asphericity δ, the prolateness S, and the acylindricity c as: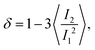 | (6) |
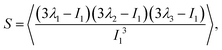 | (7) |
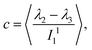 | (8) |
3 Results and discussion
3.1 Network structure and pair correlations
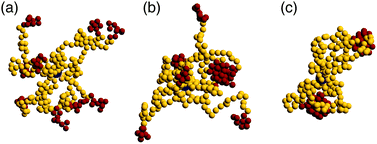
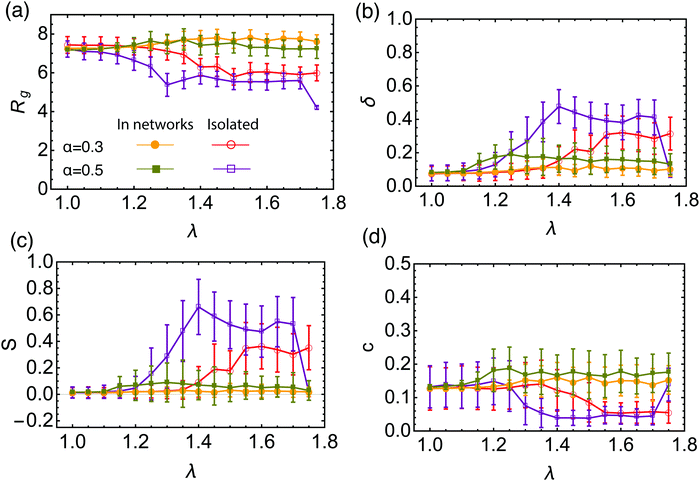
In the very dilute regime, where single BCS's cannot feel each other, these macromolecules have been found to self-assemble by bringing together the attractive part of arm to form monomer aggregates that we call patches. The number and size of these aggregates depends on a few physical parameters such as the number of arms per star, the fraction of functionalized monomers and the strength of the attractive interaction,65i.e., f, α and λ. The number of patches increases with the functionality f of the star for a fixed value of the attraction strength λ. Since our aim is to assemble polymer-based networks, it is wise to choose as building blocks BCSs that do not form one single patch at infinite dilution, the so called watermelon configutation,63 since these stars are likely to only further assemble into micelles upon increasing the concentration.46,69 Even when these micelles open up and form inter-micellar connections as concentration increases,72 the resulting connected networks have the form of assemblies of wormlike micelles80,81 interconnected via individual polymeric arms,82,83 as we also confirmed in the present work. Although the structure and rheology of such (interconnected) solutions of wormlike micelles are very interesting topics in their own right, and they have received considerable attention for linear block terpolymer-based solutions,82–88 these do not lie within the focus of the current work. Nevertheless, we have performed also simulations of low-functionality (f = 4) BCS-solutions to accompany our main results on the intermediate-functionality case studied here, and provide a comparison to it, and we will discuss these differences later on.We are also not interested in probing the regime of high functionality, in which the BCS's would behave like multi-patchy soft colloids. We therefore focus instead on BCS's with a moderately high functionality, f = 9, having N = 30 monomers per arm which is, by considering that our monomers are equivalent to one Kuhn length, realistic in terms of possible experimental realizations such as polyisoprene/polystyrene block copolymers.89 For this functionality, both off- and on-lattice simulations44,70,90 have shown that homogeneous, extended networks form at sufficiently high concentrations. We find that, at functionalization fraction of α = 0.3, the BCSs are, for low attraction strength (λ < 1.25), in an open star configuration, i.e., arms are not usually bound together, see Fig. 1(a). In this type of configuration, even if sometimes two arms bind through their attractive end-blocks, this patch is transient, being relatively fast disassembled and surviving only for ≈10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps. In this regime, even if we are below the Θ-point corresponding to the chosen attractive potential,65 (λΘ = 0.92), the thermal fluctuations are strong enough to overcome the gain in potential energy due to patch assembly. Compared to previous published data,65 where open stars have been observed for λ ≤ 1.0, the increase in λ found here is due to the relative length of the arms: shorter arms (which is the case in the present study) make it harder for the attractive blocks to meet and bind, hence observation of open stars for higher λ. For λ > 1.55 we observe that the BCS self assembles into an aggregate that features two patches, see Fig. 1(c). Each of these patches, containing either 4 or 5 arms, is located at roughly the same distance from the anchor, on opposite sides of the latter. Due to its shape, we refer to this configuration as “dumbbell”. In the region λ ∈ [1.25, 1.55] we find a transition regime between the two previously described configurations. The BCS has typically a few arms assembled into one or more patches, while a number of arms still remain free, as shown in Fig. 1(b). For the case of a longer attractive block, α = 0.5, the trend is similar to the one of lower functionalization: below λ = 1.05 the stars are open; the transition regime can be found in between λ = 1.05 and λ = 1.35, while above this value we find the dumbbell configuration. As opposed to the α = 0.3 case, we find, at the highest values considered for the attraction strength λ = 1.75, watermelon structures. The characterization of the BCS configurations was done on the basis of the shape parameters and will be discussed later on.
000 MD steps. In this regime, even if we are below the Θ-point corresponding to the chosen attractive potential,65 (λΘ = 0.92), the thermal fluctuations are strong enough to overcome the gain in potential energy due to patch assembly. Compared to previous published data,65 where open stars have been observed for λ ≤ 1.0, the increase in λ found here is due to the relative length of the arms: shorter arms (which is the case in the present study) make it harder for the attractive blocks to meet and bind, hence observation of open stars for higher λ. For λ > 1.55 we observe that the BCS self assembles into an aggregate that features two patches, see Fig. 1(c). Each of these patches, containing either 4 or 5 arms, is located at roughly the same distance from the anchor, on opposite sides of the latter. Due to its shape, we refer to this configuration as “dumbbell”. In the region λ ∈ [1.25, 1.55] we find a transition regime between the two previously described configurations. The BCS has typically a few arms assembled into one or more patches, while a number of arms still remain free, as shown in Fig. 1(b). For the case of a longer attractive block, α = 0.5, the trend is similar to the one of lower functionalization: below λ = 1.05 the stars are open; the transition regime can be found in between λ = 1.05 and λ = 1.35, while above this value we find the dumbbell configuration. As opposed to the α = 0.3 case, we find, at the highest values considered for the attraction strength λ = 1.75, watermelon structures. The characterization of the BCS configurations was done on the basis of the shape parameters and will be discussed later on.
We define the volume fraction η occupied by the monomers as η = (Ns/V)v0, with v0 = π(fNσ3 + σanchor3)/6, where Ns the number of stars and V the volume of the simulation box, whilst σ and σanchor are the diameters of the arm monomers and the anchoring point, respectively. Our systems need to be at a volume fraction of the same order of magnitude as the overlap value η*, defined as the monomer packing fraction in the interior of the star, η* = 3v0/(4πRg3), with the gyration radius Rg of the molecule. For the remainder of this subsection, we focus on a monomer volume fraction η = 0.06 which corresponds to 65% of the overlap packing fraction η*, sufficiently high to bring about nontrivial inter-star associations.
Depending on the values of λ and the α, we observe three distinct morphologies of the networks. For low attraction strength, λ ∈ [1.0, 1.2], and for both values of α considered, the attractive terminal blocks of the arms are in close proximity but do not appear to build stable, long-living aggregates, see Fig. 2(a and d). As λ is increased, we observe the formation of well-structured aggregates while at the same time, free arms are still present, as shown in Fig. 2(b and e). The size of the aggregates increases with λ and at the same time the number of free arms decreases with attraction strength. At λ = 1.5 for α = 0.3 and at λ = 1.35 for α = 0.5 all arms are bound, i.e., they are attached through their functionalized part to an aggregate to which multiple arms contribute. For α = 0.5, at the higher attraction strengths, the network formed opens up voids which are on the order of length of the simulated volume. For these parameters, the attraction strength and the number of functionalized monomers is so high that the network contracts, leaving part of the simulation volume unoccupied, as shown in Fig. 2(c and f). This is in agreement with lattice-model simulation results predicting a macroscopic, gas–liquid phase separation70 for attractive monomer fractions α ≥ 0.5.
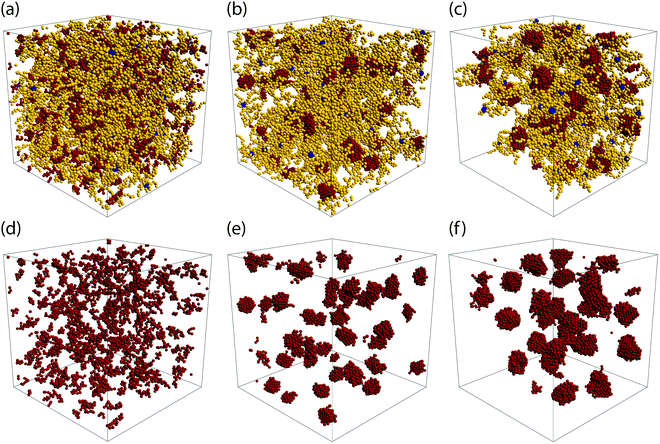 | ||
| Fig. 2 Network architecture types. The upper row shows snapshots of the three types of BCS networks observed. On the lower row, only the attractive part of the BCS's from the upper panels has been drawn, to highlight the structure of the attractive aggregates. Parameters for the three configurations are: (a and d): α = 0.3 and λ = 1.0; (b and e): α = 0.3 and λ = 1.35; (c and f): α = 0.5 and λ = 1.25. Color code of the monomers is the same as in Fig. 1. Results obtained by MD simulations at η = 0.06. | ||
To have a quantitative description for the pair structure of attractive aggregates observed, we first look, in similarity to the case of linear telechelic polymers,41 at the pair-correlation function between the attractive monomers, defined as:
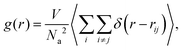 | (9) |
To better quantify the long-range spatial correlations between the attractive aggregates, we make use of the structure factor S(q), which can be obtained from the pair-correlation function via the following relation:41,94
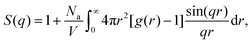 | (10) |
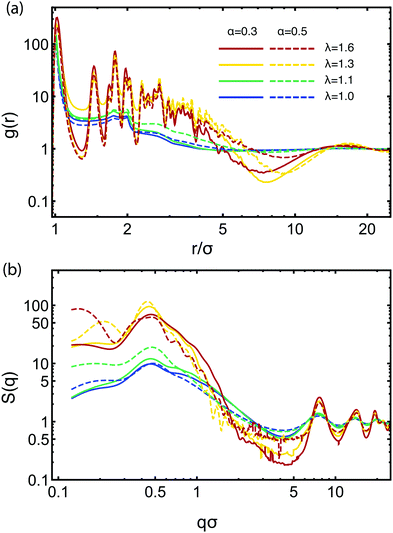
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≅ 2π/q ≅ 14σ associated with this peak is of the order of the diameter of a star, and it expresses the typical inter-cluster separation obtained also with the function g(r) above. For α = 0.5, there is a second, longer-range length scale appearing marked by the peak at qσ ≈ 0.2 for λ = 1.3. This peak signals the growth of larger-scale clusters through the merging of smaller ones at sufficiently strong attractions, and by increasing λ to 1.6, it moves to even lower qσ which reaches the limit of what we can probe considering our chosen simulation volume. It can be considered for higher values of α as a precursor to macroscopic phase separation, q → 0. At high values of q, we see a series of four peaks at qσ ≅ 7.5, 14, 19, and 22 show up, which also become more pronounced with the increase of λ. These peaks correspond to the close-packed structure of the attractive aggregates, i.e., they arise from the internal structure of the self-assembled clusters. Finally, the wavy structure that develops in the interval qσ ∈ [0.6, 1.5] for the higher λ-values at α = 0.5 comes from the scattering on the surface of the attractive aggregates. The slope of the decay of these oscillations is −4, corresponding to Porod's law for scattering from sharp (spherical) surfaces,95 whereas the locations of the oscillatory minima are consistent with the radius of the compact micelle-patches (i.e., 7σ for λ = 1.3 and 7.8σ for λ = 1.6). The structure is visible only on the curves with high λ-values and α = 0.5, since only for this regime the patches are big enough to be approximately spherical. Above qσ = 1.5, the structures appearing have no physical significance, being just an artifact due to numerically performing the integration in eqn (10). Overall, there is striking similarity in both g(r) and S(q) with the corresponding results obtained for stiff, linear telechelic star polymers.41 The pair correlation functions for η = 0.1 look very similar to the ones for η = 0.06, whereas at the very low concentration, η = 0.01, the individual chain structure of the BCS manifests itself in the distribution functions between the various types of monomers (not shown).
≅ 2π/q ≅ 14σ associated with this peak is of the order of the diameter of a star, and it expresses the typical inter-cluster separation obtained also with the function g(r) above. For α = 0.5, there is a second, longer-range length scale appearing marked by the peak at qσ ≈ 0.2 for λ = 1.3. This peak signals the growth of larger-scale clusters through the merging of smaller ones at sufficiently strong attractions, and by increasing λ to 1.6, it moves to even lower qσ which reaches the limit of what we can probe considering our chosen simulation volume. It can be considered for higher values of α as a precursor to macroscopic phase separation, q → 0. At high values of q, we see a series of four peaks at qσ ≅ 7.5, 14, 19, and 22 show up, which also become more pronounced with the increase of λ. These peaks correspond to the close-packed structure of the attractive aggregates, i.e., they arise from the internal structure of the self-assembled clusters. Finally, the wavy structure that develops in the interval qσ ∈ [0.6, 1.5] for the higher λ-values at α = 0.5 comes from the scattering on the surface of the attractive aggregates. The slope of the decay of these oscillations is −4, corresponding to Porod's law for scattering from sharp (spherical) surfaces,95 whereas the locations of the oscillatory minima are consistent with the radius of the compact micelle-patches (i.e., 7σ for λ = 1.3 and 7.8σ for λ = 1.6). The structure is visible only on the curves with high λ-values and α = 0.5, since only for this regime the patches are big enough to be approximately spherical. Above qσ = 1.5, the structures appearing have no physical significance, being just an artifact due to numerically performing the integration in eqn (10). Overall, there is striking similarity in both g(r) and S(q) with the corresponding results obtained for stiff, linear telechelic star polymers.41 The pair correlation functions for η = 0.1 look very similar to the ones for η = 0.06, whereas at the very low concentration, η = 0.01, the individual chain structure of the BCS manifests itself in the distribution functions between the various types of monomers (not shown).
3.2 Patch and network characteristics
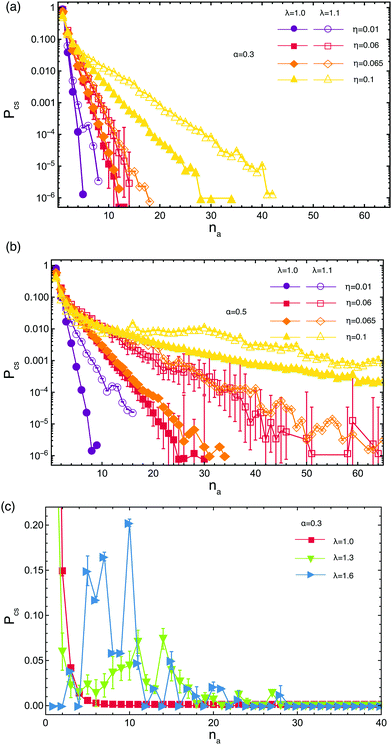
To gain more insight into the architecture of the networks, we look at the size distribution of the clusters in the network formed by the attractive parts of the arms, shown in Fig. 4. We define a cluster as the set of functionalized monomers that have to fulfill the criterion that any monomer in the cluster is placed at a maximum distance d from at least one other monomer in the cluster. Following this definition all attractive monomers in an arm are part of the same cluster. Two monomers (and consequently two arms) do not need to have direct “contact” to be part of the same cluster, but can be both at a distance lower than d to functionalized monomers of another arm or other arms that have contact to each others. We have chosen d = 1.08σ, which corresponds to approximately the distance where our attractive potential reaches half its minimum, for all the λ domain considered. Any choice of d ∈ [rc, rcut] yields almost identical results. The probability Pcs(na) of finding a cluster containing na arms is calculated as Pcs(na) =![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) cs(na)/
cs(na)/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) cs, where
cs, where ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) cs(na) is the number of clusters containing na arms and
cs(na) is the number of clusters containing na arms and 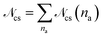 . Here we include also the case na = 1 in gathering statistics, to also account for single-arm clusters or patches formed by the self-association of terminal monomers of a single arm without participation of any other arm in the na = 1-cluster.
. Here we include also the case na = 1 in gathering statistics, to also account for single-arm clusters or patches formed by the self-association of terminal monomers of a single arm without participation of any other arm in the na = 1-cluster.
For low attraction strengths, the distribution of cluster sizes is exponentially falling, most of the arms being unbound, as seen in Fig. 4(a). By increasing either the attraction strength λ or the volume fraction η, the average number of arms 〈na〉 contributing to a cluster also increases. The probability of occurrence of a cluster of a certain size starts to deviate from the exponential decay trend as λ and/or η grow bigger. Increasing the functionalization α has the same effect as increasing λ, i.e., more arms become bound and clusters grow bigger compared to systems with lower density. For values of λ that correspond to the transition regime from open star to dumbbells for the single stars configurations, we see the coexistence of free arms with clusters of various sizes, whereas for λ values for which dumbbells are fully assembled in isolation all arms are bound, see Fig. 4(c). In the latter regime, clusters containing na ≤ 10 arms have higher occurrence probability than in the former one, where cluster with na > 10 arms are more frequent. This is due to the aforementioned possibility that arms detach from clusters and recombine into new ones, leading to the formation of big aggregates, which is present for λ = 1.3 but not for λ = 1.6 where the arms are tightly bound to their clusters and the barrier toward detachment and recombination are much higher. We further draw the reader's attention to the fact that, in the regime in which larger clusters start having non-negligible probabilities, such as the case of (α, λ) = (0.3, 1.3) shown in Fig. 4(c), the number of free arms or arms that participate in small clusters is actually much smaller than the ones in big clusters even if the probability of occurrence of these clusters is higher as consequence of the chosen normalization. Finally, we point out that the results obtained using only molecular dynamics simulations and one obtained by the hybrid Molecular Dynamics-Multiparicle Collision Dynamics (MPCD) method, which explicitly takes into account the hydrodynamics of the solvent, are in excellent agreement with one another, as they should be for equilibrium properties. We therefore only focus, for the remainder of this section, on the intermediate volume fraction regime taking η = 0.06.
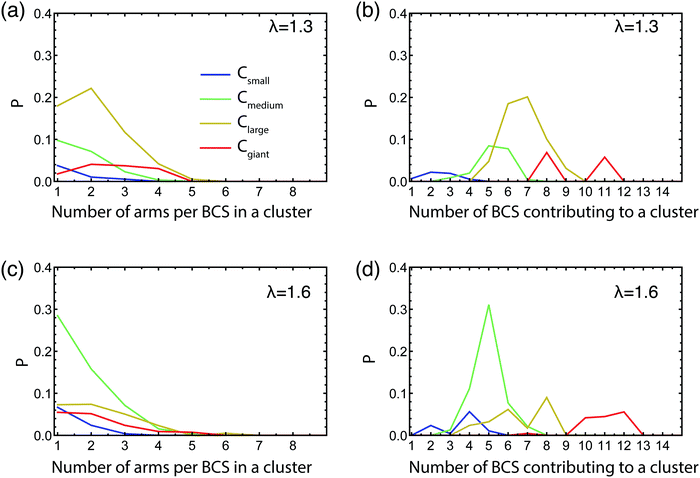
Contrary to hard, colloidal patchy particles5 that carry a fixed pattern of attractive spots on their surface, block copolymer stars are soft and reconfigurable: the patchiness they feature as isolated particles at the infinite dilution limit, where only intra-star arm associations are possible, need not be the same as the one that results at finite concentrations where inter-star associations occur. For tetrahedrally-patched BCS, it has been found that the patchiness is robust with respect to changes in the concentration,50,90 but this is not too surprising since a tetrahedral patch arrangement has a sufficiently high degree of symmetry and it thus offers inter-star association possibilities also within an isotropic liquid. For self-assembling patchy particles that form dumbbells in isolation, as the BCS at hand, it is not a priori clear that the pattern of patchiness will be preserved also at finite concentrations. Accordingly, we need to determine whether the networks that we have let self-assemble are constructed having the single star configuration as building blocks or if there is a reconfiguration of these involved in the network construction. For this purpose, we count the number of arms that one star contributes to a cluster of a certain size as well as to the number of molecules that are contributing to a cluster for a particular size of clusters, all shown in Fig. 5. We normalize these histograms by the total number of arms and also choose to group the attractive aggregates by the number of arms participating in a cluster, into a four size groups as follows: small clusters having 2 ≤ na ≤ 5, medium clusters with 6 ≤ na ≤ 10, large clusters 11 ≤ na ≤ 19, and giant clusters of size na ≥ 20.
We focus on the intermediate volume faction regime taking η = 0.06. For low λ, since the vast majority of the clusters are very small, containing 2 or 3 arms, there are of course very few stars contributing to these aggregates, and, as expected, every BCS contributes with just one or at most two arms to an aggregate (data not shown). However, in the λ-region that corresponds to the transition from open stars to dumbbells for the isolated star, such as λ = 1.3 shown in Fig. 5(a and b), we find that the larger the clusters are, the more stars contribute to them. The number of arms a star puts into one cluster is always lower than 5, with the preferred size being 1 or 2 arms. By going to λ values at which dumbbells are formed in the very dilute regime, we would expect to find that each BCS contributes 4 or 5 arms to a cluster and consequently the number of BCSs contributing to such a cluster is 4–5 times lower than the cluster size. Surprisingly, we observe that, at λ = 1.6, the BCSs have a even stronger preference to contribute just 1 or 2 arms to a cluster, the 4–5-arm contributors being almost nonexistent, see Fig. 5(c). Furthermore, there is a significant number of stars per cluster, approximately 5, as seen in Fig. 5(d). These findings demonstrate that each star contributes with a low number of arms to multiple clusters, thus leading us to the conclusion that stars in the network must be geometrically/conformationally different than the isolated ones. This implies that there must be significant reconfiguration of the BCSs forming the network compared to their one star conformation. In particular, the stars assume an isotropic configuration akin to the non-functionalized molecules for λ = 0, reducing thereby the entropic penalty they would have to pay for having a dumbbell shape; the energetic gain from inter-arm associations is now offered by the neighboring stars present in the concentrated solution.
Further corroboration for the reconfigurable nature of the BCS is offered by an analysis of the geometrical characteristics of the stars in isolation versus the ones that are part of a network. For this purpose, we employ shape parameters computed starting from the gyration tensor (details can be found in the Methods section), and the results are presented in Fig. 6. For isolated stars, we find that the gyration radius Rg, shown in Fig. 6(a), decreases in the transition region toward a dumbbell-shape compared to the open star configuration. This is consistent with some of the arms self-assembling into small clusters, hence reducing the size of the object. The star becomes also less spherical due to intra-star assembly, as can be seen from increased asphericity δ in Fig. 6(b). As dumbbell structures are formed, the radius of gyration further decreases and the star assumes an increasingly prolate shape S > 0, shown in Fig. 6(c) as well as a decreased acylindricity, Fig. 6(d). For α = 0.5 the trend is the same, two differences being worth noting: first, for λ = 1.3 we see a sharp decrease in Rg, the value being lower than the one for the dumbbells. For these parameters the star assembles first into 3 patches, which accounts for this difference. For λ = 1.75, the attraction strength becomes strong enough to overcome the entropic contribution of the non-fuctionalized part of the arms, and the star assembles into a collapsed, watermelon structure,63 characterized by a small gyration radius and high sphericity. On the other hand, the shape of the stars that form the networks do not follow the isolated star trends. The BCSs in the network have a morphology similar with the open star configuration and their geometrical characteristics are essentially independent of λ. They are highly spherical and have a similar gyration radius as the open stars throughout the λ interval considered. The gyration radius is somewhat smaller for α = 0.5 compared to α = 0.3, since in the former case, more attractive beads are available to form clusters which are highly packed objects. On the basis of the measured gyration radius, we estimate the degree of swelling of stars in the network to be of the order 10. These findings, together with the detailed analysis of the attractive aggregates, show that BCSs in networks are not just self-assembled stars that are further bound together but rather each star contributes to multiple attractive aggregates homogeneously distributed around the star. BCSs are not pre-configured units that further self-assemble into larger structures as concentration grows but rather reconfigurable objects that organize themselves into homogeneous networks with well-dispersed inter-star association sites. The reconfiguration of these dumbbell-forming molecules in concentrated solutions is at odds with the behavior of higher-functionality telechelic stars, which form tetrahedrally coordinated soft patchy nanoparticles that are robust in their shape also at high concentrations, at least for temperatures as low as the Θ-temperature of the solvophobic end-blocks.90
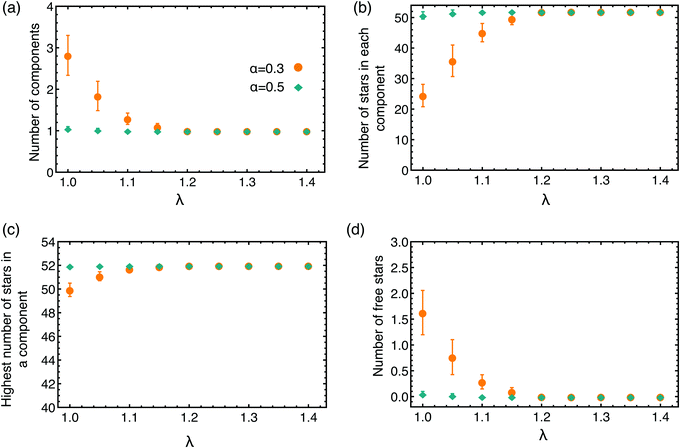
To explore the connectivity of the network, we now focus on the full BCS network, not only on the patches formed by the attractive part of the arms. We look at the number of components present in the network, defining a component as all stars that are connected with each other through a cluster formed by the attractive ends of the arms. To belong to a component, a star only needs to be bound to one other BCS in the same component. We count, at a given α and λ, the average number of components, shown in Fig. 7(a), the average number of stars that contributes to a component, Fig. 7(b), the average number of stars contributing to the biggest component in the system, Fig. 7(c), and the average number of free BCSs that have no connections at all (called free stars), Fig. 7(d). For most of the values of α and λ considered we find that (see Fig. 7) all star are connected among themselves: there is just one component in the network, the number of star in this component is Ns = 52, which equals the total number of BCSs in the simulation volume, and there are no free stars. For the lowest values of λ considered (at α = 0.3) the system appears to contain multiple components. However, by observing the size of the bigger component in the system and the number of free BCSs, we conclude that our systems consists of one very large component containing almost all the star available in the simulation volume and a couple of free stars.
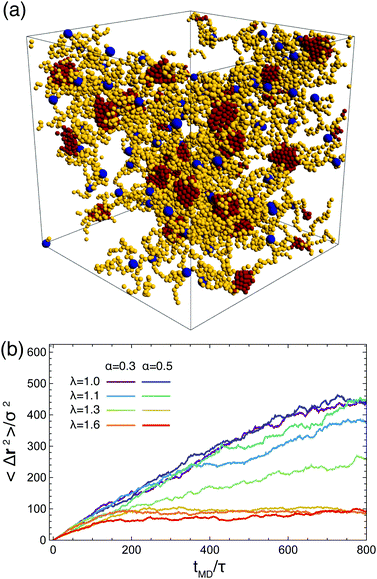
Related to the above considerations is the question whether the networks that have assembled are still reconfigurable: can arms leave one aggregate and re-attach to another one allowing for configuration changes in the networks? Furthermore, it is pertinent to know whether the stars are still mobile, i.e., free to diffuse. To evaluate the mobility of the stars we compute the mean squared displacement of the anchoring point (centers) of the stars as:
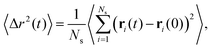 | (11) |
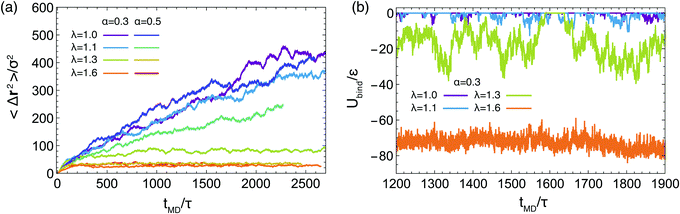
Our analysis up to now has been exclusively for the intermediate-functionality case, f = 9. To provide a brief comparison with the low-functionality case, we have performed simulations at the same star density, η/η* ≅ 0.6, and λ-values, for BCS of functionality f = 4 and fractions of attractive monomers α = 0.3 and α = 0.5; representative results are shown in Fig. 9. We found very different connectivity characteristics between the two functionalities for identical λ-conditions, which physically correspond to fixed temperature. For small λ-values, the f = 4-stars do not form any kind of network, a significant fraction of them being free of connections to other ones. The values of λ for which a percolating network is observed are much higher than for the case of f = 9. The two resulting networks have very different morphologies. For f = 9, we found a homogenous-looking network with patches connected by several arms, whereas for f = 4 we observe regions where patches and their contributing stars alternate with voids, as seen in Fig. 9(a). In other words, in the second case we have micellar patches formed by many stars and a few arms of the latter connect the micelles, leaving at the same time large regions that are populated by stars that share their arms between different micelles. As these regions contain also lots of empty space, the cages that they form are larger than those of the f = 9-stars. Concomitantly, in the resulting arrested networks, the size of the cage in which the anchor is trapped is approximately twice as big for f = 4 in comparison to f = 9. This can be clearly seen in Fig. 9(b) in comparing the height of the MSD-plateau, 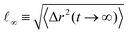 , there, with the corresponding value for f = 9 from Fig. 8(a). Indeed, for f = 4, λ = 1.6 and α = 0.3, we obtain
, there, with the corresponding value for f = 9 from Fig. 8(a). Indeed, for f = 4, λ = 1.6 and α = 0.3, we obtain ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∞2 ≅ 100, whereas for f = 9 and identical λ- and α-values, a plateau-value of
∞2 ≅ 100, whereas for f = 9 and identical λ- and α-values, a plateau-value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∞2 ≅ 25 results, showing the much stronger confinement of the latter stars in their cages.
∞2 ≅ 25 results, showing the much stronger confinement of the latter stars in their cages.
 | ||
| Fig. 9 BSCs with lower functionality (f = 4): (a) snapshot of network formed at α = 0.3 and λ = 1.35. (b) The mean squared displacement of the star cores in the network for different values of α and λ, as indicated in the legend. For details about the quantities on the horizontal axis we refer to Fig. 8. | ||
Recently, Metri et al.73 investigated a system of network-forming telechelic star polymers that bears certain similarities, but also important differences, with the systems we examine here. The experimental system consisted of a cross-linked glycol diacrylate core with an average of f = 13 attached arms made of poly(n-butyl acrylate); at the tip, each arm was functionalized with three bis(2-methacrylooyloxyethyl) disulfide stickers, playing a role analogous to the terminal B-monomers of our system. Contrary to our solvophobic beads, however, the stickers can form a connection to other stickers only once but since each arm carries at its end a sticker with three ‘fingers’, intra- or inter-star association sites with more than two participating arms are still possible. On the other hand, the attractions for the system of Metri et al.73 are so strong that the associations are considered to be irreversible. Accordingly, in the coarse-grained simulations employed there, a certain fraction of stickers, pext, is attached to external stickers from other stars in a quenched, i.e., pre-determined (albeit randomly selected) fashion. Also the simulation technique employed there is a different, hybrid one, employing Rouse dynamics for the chains and an effective potential for the cores,97 with the purpose of accelerating the dynamics to cover a broad range of time scales, reaching up to ∼105 s. Despite these differences, striking similarities with the findings for the systems at hand arise: at a cross-linking fraction pext ≅ 0.25 of stickers, the mean-square displacements of the cores show a plateau, which broadens further for higher values of this parameter, in full analogy with our findings in Fig. 8(a), where the role of the control parameter is now played by the attraction strength λ. This dynamical arrest is accompanied by a long-time plateau of the stress relaxation G(t), signalling the presence of extremely long relaxation processes in the system and the transition to an amorphous rheological solid. Although we have not performed measurements of the stress relaxation (or the viscosity) in this work, and additional coarse-graining would be required also here to reach long-time scales, it is justified to expect that systems that are fully connected and the arms have very large and negative inter-star binding energies such as those shown in Fig. 8(b), will also have the typical rheological response of a solid.
Finally, to probe the fluctuations of the arms of the stars, we focus now on α = 0.3 and look at the values of the sum of the attractive potentials of all the beads in an arm, Ubind, over the course of our simulations. We have excluded from Ubind the contribution arising from same-arm monomers, since we are interested in the interaction with other arms, and thus the participation in the formation of attractive aggregates, and not in the intra-arm self assembly. The quantity computed in this way vanishes for free arms and takes negative values for an arm that is attached (bound) to at least one another arm. Results for different values of λ for one single representative arm are presented in Fig. 8(b). For λ = 1.0 and 1.1, the arm frequently attaches and leaves an aggregate. For the case of λ = 1.3 arms tend to spend more time in a bounded state but they also unbind, allowing for reconfigurations, and the quantity Ubind features very strong fluctuations. At λ = 1.6, and consistently with the existence of an arrested network, the energy barrier to unbind becomes too high and the arms spend their entire time in a bound state, reconfiguration of the network being possible only by cluster merging.
4 Conclusions
We have carried out detailed, monomer-resolved, off-lattice simulations of associating, block copolymer stars of moderate functionality to investigate the structure, equilibrium dynamics and molecular conformations of the building blocks in the resulting macroscopic networks formed by the system at finite concentrations. Though still far away from the melt (and thus also from any considerations regarding entanglements between the chains), the system features the nontrivial characteristics of self-organized networks of associating polymers. The choice of the functionality and the fraction of attractive monomers drives the system into a network configuration rather than toward the formation of micelles. The network is homogeneous, i.e., there exist uniformly distributed physical association sites, which are not broadly polydisperse in size, and these are interconnected through the star arms that are anchored on their centers. We find characteristic spatial correlations and scattering spectra that feature short- and intermediate-range ordering at the monomer- and macromolecule-length scales, in close similarity with findings on telechelic liner chains,41 whereas the patches compactify and internally crystallize at strong attractions, when the temperature drops well below the Θ-point of the terminal groups. A major finding of this work is that within the networks the stars reorganize and reconfigure in order to best take advantage of an isotropic environment of potential association partners: the dumbbell-shape of infinite dilution is lost and the stars recover a spherical shape with their arms reaching out toward association partners in all spatial directions around their cores. In stark contrast to usual stars, this conformational change upon increase of concentration is accompanied by a growth of the overall size, since the stars abandon the relatively compact dumbbell-shape to assume an open, radially-symmetric configuration.The model we adopted is monomer-based but still considerably coarse-grained: in particular, no possible differences in size, Kuhn lengths or rigidities between the A- and B-blocks have been considered and no particular chemistry has been employed. Still, we believe that the approach contains the salient physical characteristics to capture the main mechanisms and properties of network formation. The next step should be toward the investigation of out-of-equilibrium properties, such as the shear-rate-dependent shear viscosity of the system, for which the MPCD-technique is eminently suitable: work along these lines is in progress. Moreover, the stress relaxation at equilibrium, G(t), should be calculated, establishing a link to the typical rheological response of the system, the storage and loss moduli G′(ω) and G′′(ω). This endeavor will require some additional coarse-graining, since the time scale one can cover with the current model is limited and thus insufficient to reach the terminal relaxation of G(t). Work along these lines is also in progress and it will be the subject of a future publication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. J.-C. thanks support by the European Training Network COLLDENSE (H2020-MCSA-ITN-2014, Grant No. 642774). Computer time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.References
- S. C. Glotzer, Science, 2004, 306, 419–420 CrossRef CAS PubMed.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–56 CrossRef CAS PubMed.
- E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397–6410 RSC.
- E. Bianchi, B. Capone, I. Colluzza, L. Rovigatti, P. van Oostrum and L. Rovigatti, Phys. Chem. Chem. Phys., 2017, 19, 19847–19868 RSC.
- W. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–385 CrossRef PubMed.
- Q. Chen, E. Diesel, J. K. Whitmer, S. C. Bae, E. Luijten and S. Granick, J. Am. Chem. Soc., 2011, 133, 7725–7727 CrossRef CAS PubMed.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed.
- F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558 Search PubMed.
- F. Smallenburg, L. Filion and F. Sciortino, Nat. Phys., 2014, 10, 653–657 Search PubMed.
- L. Rovigatti, F. Smallenburg, F. Romano and F. Sciortino, ACS Nano, 2014, 8, 3567–3574 CrossRef CAS PubMed.
- R. Chelakkot, R. Lipowsky and T. Gruhn, Macromolecules, 2007, 39, 7138–7143 CrossRef.
- R. Chelakkot, R. Lipowsky and T. Gruhn, Soft Matter, 2009, 5, 1504–1513 RSC.
- E. Bianchi, P. van Oostrum, C. N. Likos and G. Kahl, Curr. Opin. Colloid Interface Sci., 2017, 30, 8–15 CrossRef CAS.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2013, 7, 8313–8323 RSC.
- E. Bianchi, C. N. Likos and G. Kahl, ACS Nano, 2014, 7, 4657–4667 CrossRef PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, Nano Lett., 2014, 14, 3412–3418 CrossRef CAS PubMed.
- L. Brunsveld, B. Folmer, E. W. Meijer and R. P. Sijbesma, Chem. Rev., 2001, 101, 4071–4097 CrossRef CAS PubMed.
- S. Seiffert and J. Sprakel, Chem. Soc. Rev., 2012, 41, 909–930 RSC.
- E. van Ruymbeke, J. Rheol., 2017, 62, 1099–1102 CrossRef.
- D. Amin, A. E. Likhtman and Z. Wang, Macromolecules, 2016, 49, 7510–7524 CrossRef CAS.
- J.-F. Berret and Y. Séréro, Phys. Rev. Lett., 2001, 87, 048303 CrossRef CAS PubMed.
- G. V. Kolmakov, K. Matyjazewski and A. C. Balazs, ACS Nano, 2009, 3, 885–892 CrossRef CAS PubMed.
- P. J. Skrzeszewska, J. Sprakel, F. A. de Wolf, R. Fokking, M. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 3542–3548 CrossRef CAS.
- P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Nature, 2008, 451, 977–990 CrossRef CAS PubMed.
- E. B. Stukalin, L.-H. Cai, N. Arun Kumar, L. Leibler and M. Rubinstein, Macromolecules, 2013, 46, 7525–7541 CrossRef CAS PubMed.
- W. Schmolke, N. Perner and S. Seiffert, Macromolecules, 2015, 48, 8781–8788 CrossRef CAS.
- F. J. Stadler, W. Pyckhout-Hintzen, J.-M. Schumers, C.-A. Fustin, J.-F. Gohy and C. Bailly, Macromolecules, 2009, 42, 6181–6192 CrossRef CAS.
- E. van Ruymbeke, D. Vlassopoulos, M. Mierzwa, D. Charalabidis, M. Pitsikalis and N. Hadjichristidis, Macromolecules, 2010, 43, 4401–4411 CrossRef CAS.
- S. Suzuki, T. Uneyama, T. Inoue and H. Watanabe, Macromolecules, 2012, 45, 888–898 CrossRef CAS.
- S. Suzuki, T. Uneyama and H. Watanabe, Macromolecules, 2013, 46, 3497–3504 CrossRef CAS.
- T. Uneyama, S. Suzuki and H. Watanabe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031802 CrossRef PubMed.
- M. Ahmadi, L. Hawke, H. Goldansaz and E. van Ruymbeke, Macromolecules, 2015, 48, 7300–7310 CrossRef CAS.
- Q. Chen, C. Huang, R. A. Weiss and R. H. Colby, Macromolecules, 2015, 48, 1221–1230 CrossRef CAS.
- Y. Kwon, Y. Matsumiya and H. Watanabe, Macromolecules, 2016, 49, 3593–3607 CrossRef CAS.
- H. Goldansaz, C.-A. Fustin, M. Wübbenhorst and E. van Ruymbeke, Macromolecules, 2016, 1890–1902 CrossRef CAS.
- Z. Zhang, Q. Chen and R. Colby, Soft Matter, 2018, 14, 2961–2977 RSC.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068 CrossRef CAS.
- J. S. Myung, F. Taslimi, R. G. Winkler and G. Gompper, Macromolecules, 2014, 47, 4118–4125 CrossRef CAS.
- F. Taslimi, G. Gompper and R. G. Winkler, Macromolecules, 2014, 47, 6946–6954 CrossRef CAS.
- J. S. Myung, R. G. Winkler and G. Gompper, J. Chem. Phys., 2015, 143, 243117 CrossRef PubMed.
- E. Bianchi, B. Capone, G. Kahl and C. N. Likos, Faraday Discuss., 2015, 181, 123–138 RSC.
- R. M. Chuoeiri, E. Galati, H. Thérien-Aubin, A. Klinkova, E. M. Larin, A. Quejereta-Fernández, L. Han, H. L. Xin, O. Gang, E. B. Zhulina, M. Rubinstein and E. Kumacheva, Nature, 2016, 538, 79 CrossRef PubMed.
- I. C. Gârlea, E. Bianchi, B. Capone, L. Rovigatti and C. N. Likos, Curr. Opin. Colloid Interface Sci., 2017, 30, 1–7 CrossRef.
- F. Wurm and A. F. M. Kilbinger, Angew. Chem., Int. Ed., 2009, 48, 8412 CrossRef CAS PubMed.
- Z. Poon, S. Chen, A. C. Engler, H. Lee, E. Atas, G. von Maltzahn, S. N. Bhatia and P. T. Hammond, Angew. Chem., Int. Ed., 2010, 49, 7266 CrossRef CAS PubMed.
- J. Zhang, Z.-Y. Lu and Z.-Y. Sun, Soft Matter, 2011, 7, 9944–9950 RSC.
- B. Capone, I. Coluzza, F. Lo Verso, C. N. Likos and R. Blaak, Phys. Rev. Lett., 2012, 109, 238301 CrossRef PubMed.
- T. Higuchi, A. Tajima, K. Motoyoshi, H. Yabu and M. Shimomura, Angew. Chem., Int. Ed., 2008, 47, 8044 CrossRef CAS PubMed.
- M. T. Hermans, M. A. C. Broeren, N. Gomopoulos, P. van der Schoot, M. H. P. van Genderen, N. A. J. M. Sommerdijk, G. Fytas and E. W. Meijer, Nat. Nanotechnol., 2009, 4, 721 CrossRef PubMed.
- B. M. Mladek, J. Fornleitner, F. J. Martinez-Verachoechea, A. Dawid and D. Frenkel, Phys. Rev. Lett., 2012, 108, 268301 CrossRef PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2013, 113, 128303 CrossRef PubMed.
- L. Feng, L.-L. Pontani, R. Dreyfus, P. Chaikin and J. Brujic, Soft Matter, 2013, 9, 9816 RSC.
- S. Biffi, R. Cerbino, F. Bomboi, E. M. Paraboschi, R. Asselta, F. Sciortino and T. Bellini, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15633–15637 CrossRef CAS PubMed.
- E. Locatelli, P. H. Handle, C. N. Likos, F. Sciortino and L. Rovigatti, ACS Nano, 2017, 11, 2094–2102 CrossRef CAS PubMed.
- R. A. Brady, N. J. Brooks, P. Cicuta and L. Di Michele, Nano Lett., 2017, 17, 3276–3281 CrossRef CAS PubMed.
- Z. Xing, A. Caciagli, T. Cao, I. Stoyev, M. Zupkauskas, T. O'Neill, T. Wenzel, R. Lamboll, D. Liu and E. Eiser, Proc. Natl. Acad. Sci. U. S. A., 2018, 32, 8137–8142 CrossRef PubMed.
- J. Fernandez-Castanon, S. Bianchi, F. Saglimbeni, R. Di Leonadro and F. Sciortino, Soft Matter, 2018, 14, 6431–6438 RSC.
- M. Pitsikalis, N. Hadjichristidis and J. W. Mays, Macromolecules, 1996, 29, 179 CrossRef CAS.
- D. Vlassopoulos, T. Pakula, G. Fytas, M. Pitsikalis and N. Hadjichristidis, J. Chem. Phys., 1999, 111, 1760 CrossRef CAS.
- F. Lo Verso, C. N. Likos, C. Mayer and H. Löwen, Phys. Rev. Lett., 2006, 96, 187802 CrossRef PubMed.
- F. Lo Verso, C. N. Likos and H. Löwen, J. Phys. Chem. C, 2007, 111, 15803 CrossRef CAS.
- L. Rovigatti, B. Capone and C. N. Likos, Nanoscale, 2016, 8, 3288–3295 RSC.
- T. Hiroi, S. Kondo, T. Sakai, E. P. Gilbert, Y.-S. Han, T.-H. Kim and M. Shibayama, Macromolecules, 2016, 49, 4940–4947 CrossRef CAS.
- S. Nakagawa, X. Li, M. Shibayama, H. Kamata, T. Sakai and E. P. Gilbert, Macromolecules, 2018, 51, 6645–6652 CrossRef CAS.
- E. J. Kepola, E. Loizou, C. S. Patrickios, E. Leontidis, C. Voutouri, T. Stylianopoulos, R. Schweins, M. Gradzielski, C. Krumm and J. C. Tiller, et al. , ACS Macro Lett., 2015, 4, 1163–1168 CrossRef CAS.
- F. Lo Verso, A. Z. Panagiotopoulos and C. N. Likos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 010401(R) CrossRef PubMed.
- C. Koch, C. N. Likos, A. Z. Panagiotopoulos and F. Lo Verso, Mol. Phys., 2011, 109, 3049–3060 CrossRef CAS.
- C. Koch, A. Z. Panagiotopoulos, F. Lo Verso and C. N. Likos, Soft Matter, 2013, 9, 7424 RSC.
- C. Koch, A. Z. Panagiotopoulos, F. Lo Verso and C. N. Likos, Soft Matter, 2015, 11, 3530–3535 RSC.
- V. Metri, A. Louhichi, J. Yan, G. P. Baeza, K. Matyjazewski, D. Vlassopoulos and W. J. Briels, Macromolecules, 2018, 51, 2872–2886 CrossRef CAS PubMed.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 2000, 112, 7260–7269 CrossRef CAS.
- M. Ripoll, R. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS PubMed.
- M. O. Steinhauser, J. Chem. Phys., 2005, 122, 094901 CrossRef PubMed.
- G. Zifferer and W. Preusser, Macromol. Theory Simul., 2001, 10, 397–407 CrossRef CAS.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478 CrossRef CAS.
- J. T. Padding, E. S. Boek and W. J. Briels, J. Phys.: Condens. Matter, 2005, 17, S3347 CrossRef CAS.
- J. T. Padding, W. J. Briels, M. R. Stukan and E. S. Boek, Soft Matter, 2009, 5, 4367 RSC.
- L. Ramos and C. Ligoure, Macromolecules, 2007, 40, 1248 CrossRef CAS.
- K. Nakaya-Yaegashi, L. Ramos, H. Tabuteau and C. Ligoure, J. Rheol., 2008, 52, 359 CrossRef CAS.
- C. Quellet, H.-F. Eicke and W. Meier, Macromolecules, 1990, 23, 3347 CrossRef CAS.
- M. Odenwald, H.-F. Eicke and W. Meier, Macromolecules, 1995, 28, 5069 CrossRef CAS.
- H. Bagger-Jörgensen, L. Coppola, K. Thuresson, U. Olsson and K. Mortensen, Langmuir, 1997, 13, 4204 CrossRef.
- J. Appell, G. Porte and M. Rawiso, Langmuir, 1998, 14, 4409 CrossRef CAS.
- W. Meier, J. Hotz and S. Günther-Ausborn, Langmuir, 1996, 12, 5028 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003, p. 53 Search PubMed.
- B. Capone, I. Coluzza, R. Blaak, F. Lo Verso and C. N. Likos, New J. Phys., 2013, 15, 095002 CrossRef.
- M. Allen and D. Tildesley, Computer Simulation of Liquids, Clarendon Press, 1987 Search PubMed.
- J. H. Conway and N. J. A. Sloane, Sphere packings, lattices and groups, Springer Science & Business Media, 2013, vol. 290 Search PubMed.
- N. Ashcroft and N. Mermin, Solid State Physics, Holt, Rinehart and Winston, 1976 Search PubMed.
- J. Dhont, An Introduction to Dynamics of Colloids, Elsevier Science, 1996, p. 46 Search PubMed.
- C. Sorensen, Aerosol Sci. Technol., 2001, 35, 648–687 CrossRef CAS.
- I. Wadgaonkar and A. Chatterji, J. Chem. Phys., 2017, 146, 084906 CrossRef PubMed.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |