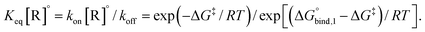Open Access Article
Open Access ArticleHarnessing entropy to enhance toughness in reversibly crosslinked polymer networks†
Nicholas B.
Tito
 *ab,
Costantino
Creton
*ab,
Costantino
Creton
 cde,
Cornelis
Storm
ab and
Wouter G.
Ellenbroek
cde,
Cornelis
Storm
ab and
Wouter G.
Ellenbroek
 ab
ab
aDepartment of Applied Physics, Eindhoven University of Technology, PO Box 513, 5600 MB, Eindhoven, The Netherlands. E-mail: nicholas.b.tito@gmail.com
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, PO Box 513, 5600 MB, Eindhoven, The Netherlands
cÉcole Supérieure de Physique et de Chimie Industrielles de la Ville de Paris (ESPCI) ParisTech, UMR 7615, 10, Rue Vauquelin, 75231 Paris Cédex 05, France
dCNRS, UMR 7615, 10, Rue Vauquelin, 75231 Paris Cédex 05, France
eSorbonne-Universités, Université Pierre et Marie Curie (UPMC) Université Paris 06, UMR 7615, 10, Rue Vauquelin, 75231 Paris Cédex 05, France
First published on 5th February 2019
Abstract
Reversible crosslinking is a design paradigm for polymeric materials, wherein they are microscopically reinforced with chemical species that form transient crosslinks between the polymer chains. Besides the potential for self-healing, recent experimental work suggests that freely diffusing reversible crosslinks in polymer networks, such as gels, can enhance the toughness of the material without substantial change in elasticity. This presents the opportunity for making highly elastic materials that can be strained to a large extent before rupturing. Here, we employ Gaussian chain theory, molecular simulation, and polymer self-consistent field theory for networks to construct an equilibrium picture for how reversible crosslinks can toughen a polymer network without affecting its elasticity. Maximisation of polymer entropy drives the reversible crosslinks to bind preferentially near the permanent crosslinks in the network, leading to local molecular reinforcement without significant alteration of the network topology. In equilibrium conditions, permanent crosslinks share effectively the load with neighbouring reversible crosslinks, forming multi-functional crosslink points. The network is thereby globally toughened, while the linear elasticity is left largely unaltered. Practical guidelines are proposed to optimise this design in experiment, along with a discussion of key kinetic and timescale considerations.
1 Introduction
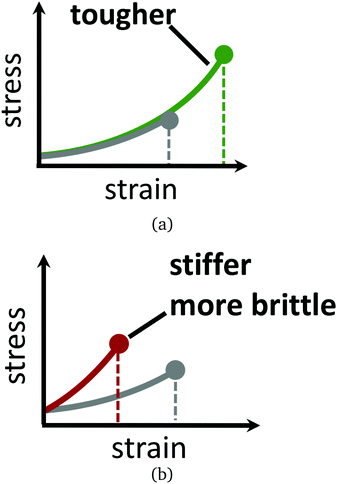
Materials composed of polymers chemically crosslinked into a network, such as in gels and rubbers, eventually break if strained enough.1–5 This is because the polymer chains or crosslinks irreversibly rupture once the local force acting on them becomes too large for their covalent bonds to withstand. Strategies for exploiting reversible bonding and crosslinking for dynamic remodelling, in response to stress or other physical changes, is thus an active focus of study. Recent examples include materials—some biological in nature—that self-heal when damaged,6–10 dynamically adapt to strain by topology change and reversible bonding,2,11–18 or reshape and deform in response to light, temperature, or local chemical environment.19 Polymer networks with reversible crosslinks form the basis for many of these exciting new materials, attracting a variety of recent theoretical modelling efforts into systems exhibiting transient inter-polymer, intra-polymer, and telechelic bonding.20–33Here, attention is focused on how reversible crosslinking can enhance the strength of a network of flexible chains. Our inspiration comes from recent studies that show that reversible crosslinking can be leveraged to separately tune the toughness of a material, independent of its elasticity. For example, in two motivating experimental studies by Kean et al.14 and Mayumi et al.,34 reversible crosslinking agents are added into the solvent phase of a permanently crosslinked polymer gel. While the two studies differ in their underlying chemistry, both find clear regimes where the presence of the reversible crosslinks allows the gel to be stretched to a larger extent before it fails—yet remarkably having the same elasticity before failure—compared to the material without the reversible crosslinks. This notion is illustrated by schematic stress–strain curves in Fig. 1. Salient details and observations from these two studies are now summarised, to motivate our objective.
The experiments by Kean et al. and Mayumi et al. examine gels of permanently crosslinked polymers, comprising poly(4-vinylpyridine)14 and polyvinyl alcohol34 respectively. In Kean et al., the reversible crosslinks are Van Koten-type pincer complexes, composed of two transition metals attached into a small organic scaffold.35 The complex can form one or two coordination bonds, anti-podal to each other, with monomers along the polymer network chains. The complexes are free to diffuse within the solvent phase of the gel, so that they can form and break their coordination bonds at will at any position along the polymer chains. The lifetime of the bonds is controlled by altering the chemical structure of the complexes. In Mayumi et al., borate ions act as the reversible crosslinks, which can form up to four transient bonds with the polyvinyl alcohol chains. Note that both reversible crosslinking paradigms have different underlying physics compared to scenarios where the reversible linking units are fixed along the contour lengths of the polymers.36–38
Judicious choice of the reversible crosslink binding strength (at fixed loading rate and reversible crosslink concentration) in Kean et al. leads to toughening of the gel, without altering its elastic properties.14 In this sense, the reversible crosslinks are mechanically “invisible”, as the authors so put it. When the reversible linkers bind too strongly, then they lead the material to be stiffer and more brittle, with lower toughness. Conversely, if the reversible crosslinks bind too weakly, then their toughening effect decreases. In Mayumi et al., the complementary perspective is taken: the polyvinyl alcohol gel is subjected to different loading rates, all having the same borate ion (reversible crosslinker) concentration and binding strength.34 Here, the largest increase in toughness and smallest change in elasticity, relative to the gel without the reversible crosslinks, occurs in the limit of slow loading rate. Faster loading rates cause the reversible crosslinks to behave more like permanent crosslinks on the timescale of the strain rate, so that the material is apparently stiffer than the native material.
Reversible crosslinking can allow for somewhat independent control over the toughness of a gel, without an influence on its elasticity. Schematic stress–strain curves for hypothetical polymer gels with and without reversible crosslinks are given in Fig. 1. Understanding how reversible crosslinks enact this toughening at the microscale is thus of great value for the development of new gel materials with tailored properties. The subject of this paper is understanding, on theoretical grounds, the optimal design of reversible crosslinks that leads to maximum toughening, with minimal influence on the elasticity of the material.
An oft-discussed suggestion for how free reversible crosslinks invisibly toughen a polymer network is that, through the course of strain, the reversible crosslinks (re-)migrate via diffusion to locations where microscopic damage (rupture) is actively occuring. In doing so, the reversible links are purported to have a significant structural and regenerative influence in ruptured locations, while not having the dynamical longevity to affect the mechanics of undamaged regions. However, a recent theoretical study on a polymer network composed of mobile crosslinks by Mulla et al. (ref. 39 and 40) suggests that the mobile links migrate away from areas of damage over time, particularly when the length scale of the ruptures grows large.41
In this paper, a combination of molecular theory and simulation is used to construct a different argument, based on equilibrium thermodynamics, for how free reversible crosslinks can significantly enhance toughness with minimal change of elasticity.
The starting point for our theory is the classical observation that microscopic topology of a polymer network has a key role in dictating the macroscopic stress–strain behaviour of the material.42–46 Adding crosslinks or chains to a network leads to a stiffer and less extensible material, due to the larger entropic restoring force and shorter average length of the polymers at the molecular scale. On the other hand, more dilute networks of the same material exhibit a lower modulus. If reversible crosslinks can toughen a polymer gel without changing its elasticity, then the microscopic mechanism of toughening must leave the load-supporting part of the molecular topology of the network mostly unaltered.
To construct an explanation for how this feature arises, we first demonstrate that reversible linkers are entropically biased to form transient connections adjacent to permanent crosslinks in the network, when the reversible linker equilibrium binding constant is weak. Forming a transient bond near a permanent crosslink leads to a smaller configurational entropy penalty for the associated polymer strands, relative to forming a transient bond far from a permanent link. The implication of this selective recruitment is that existing permanent crosslinks are less loaded, while the network topology is not changed. Casting our arguments in terms of thermodynamic entropy, rather than structural proximity effects, opens the doorway for explicitly quantifying how this clustering competes with the other thermodynamic factors, e.g. reversible linker binding enthalpy and concentration.
Molecular dynamics simulations are used to verify this hypothesis, and to show that “recruiting” (clustering) reversible crosslinks around permanent crosslinks leads to local load-sharing and reduced chance of failure of the permanent bond when the polymer network is under strain. Coarse-grained modeling of polymer network failure, using a self-consistent field model, demonstrates that local molecular strengthening of permanent crosslinks in the network leads to an amplified toughening of the polymer network as a whole. After a discussion of kinetic considerations around our equilibrium theory, we put forth practical design guidelines with the aim of illuminating future experimental efforts.
2 Entropy & recruitment
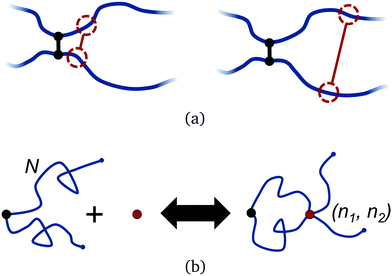
Polymers have an intrinsic entropy, depending upon the number of configurations they can explore at equilibrium.47,48 Free polymers have higher entropy than constrained polymers. When permanently crosslinked into a network, polymers have an inherently smaller entropy, yet the polymers still explore a space of configurations at equilibrium which satisfy the fixed connectivity of the network. Their non-trivial entropy can be further reduced by adding additional constraints, such as transient crosslinks.Adding a transient bond between two polymers in a network imposes a temporary constraint on the network configuration. This entails an entropic penalty that depends on the position of the bond, relative to the existing crosslinks in the network, as shown in Fig. 2(a). Within the approximation of ideal Gaussian polymer chains, we can compute the corresponding free energy change exactly. We examine this by considering two Gaussian polymer chains of finite number of segments N, indexed n1 = 1…N and n2 = 1…N respectively, each attached to a permanent crosslink by their first segment. The permanent crosslink defines the origin of the system, but is otherwise not counted as a segment. For the moment, the other two ends of the chains are left untethered.
It is convenient to write the partition function of each polymer using the normalized Gaussian probability density for the end-to-end vector R of a chain of N segments with Kuhn length b
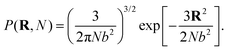 | (1) |
This way, any linear polymer with an unconstrained end-to-end vector (and even any loopless branched polymer with free ends) will have a partition function
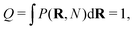 | (2) |
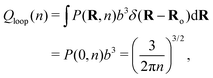 | (3) |
Returning to the event sketched in Fig. 2(b), two Gaussian chains of N segments are connected to each other at the origin. Assuming the other two ends are free, the partition function of this configuration equals unity with our normalization. When a reversible crosslink ties segment n1 from the first chain to segment n2 from the second chain, a loop of n1 + n2 ≡ n segments is formed and the partition function is reduced to Qloop(n). The change in conformational free energy of the two chains is therefore
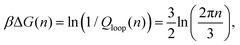 | (4) |
As it stands, eqn (4) tells us that the polymer network pays a free energy of order 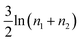 when a reversible crosslink is added that connects site n1 of chain 1 to site n2 of chain 2. In order for this estimate to account for all loops of n polymer segments, the partition function after binding needs to be multiplied by the number of choices one can make for n1 and n2 such that n = n1 + n2, which equals min(n − 1,2N − n + 1). This makes the final change in network free energy due to the creation of a loop of size n through a binding event in Fig. 2b equal to
when a reversible crosslink is added that connects site n1 of chain 1 to site n2 of chain 2. In order for this estimate to account for all loops of n polymer segments, the partition function after binding needs to be multiplied by the number of choices one can make for n1 and n2 such that n = n1 + n2, which equals min(n − 1,2N − n + 1). This makes the final change in network free energy due to the creation of a loop of size n through a binding event in Fig. 2b equal to
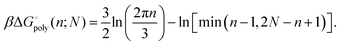 | (5) |
This expression describes the entropy cost for adding one reversible crosslink between two polymers. The degeneracy adds a term that goes like −ln(n − 1), so the overall free energy cost still grows logarithmically with n. The polymer network loses the least entropy when the reversible crosslink binds as close to an existing permanent crosslink as possible. The permanent crosslinks can therefore be said to act as nucleation points for reversible crosslink binding on the polymer network scaffold.
When additional reversible linkers bind to the same two polymers, then the entropy cost depends on the configuration of the linkers that are already bound. In this way, reversible crosslinks can similarly act as nucleation sites for new linkers to bind, so that “stray clusters” of reversible crosslinkers can form far from permanent crosslinks. However, such stray clusters have a low probability of formation when the reversible crosslink binding free energy is small, so that the permanent crosslinks act as the dominant nucleation sites for reversible bonding. We will return to this regime of interest shortly.
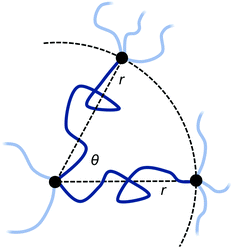
In real networks, chain ends are not usually free, but tied to the rest of the network at other points. As a related scenario, we now turn to the case where the free ends of the two polymers are constrained to two points, both for simplicity at the same distance r from the permanent crosslink and with the same number of segments N. The distance r of the additional attachment points from the permanent crosslink, as well as the angle θ between them, can be varied as illustrated in Fig. 3.
The initial free energy for each chain is identical, since the separation distance r between their endpoints is the same. From the partition function for the chains, the free energy for the two chains combined is two times the standard stretch free energy, i.e. βGpoly,ub(N,r) = 2 × 3r2/2Nb2. Note that this reference state free energy does not depend on the angle θ between the two chains.
The entropic free energy of the two chains is reduced when adding a bond at some combined monomer distance (i.e. loop length) n1 + n2 = n from the shared permanent crosslink. The resulting expression for Gpoly,b(n;N,r,θ) is derived in ESI Section SI.† The entropic free energy loss to the two polymers upon reversible crosslinker binding at position n1 + n2 = n is then
| ΔGpoly(n;N,r,θ) = Gpoly,b(n;N,r,θ) − Gpoly,ub(N,r). | (6) |
Note that this expression now depends on the angle θ between the chains, as this affects how much the chains are perturbed when forming the bond at (n1,n2).
Fig. 4 presents calculations of the entropic free energy change, eqn (6), for adding a bond at combined monomer distance n, for several choices of chain stretches r and angles θ. Results from the untethered chains (eqn (5)) are also shown in each panel. Even for only moderately stretched polymers, such as the green dataset where the stretch ratio is r/Nb = 0.25, the entropy penalty grows very steeply with n. The penalty grows larger, to the order of tens of kT, as the distance between the chain ends grows (panel a) and also as the angle between them increases (panel b).
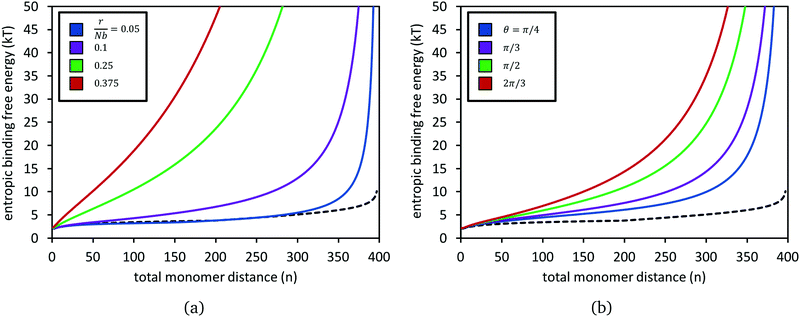 | ||
| Fig. 4 Entropic binding free energy, βΔGpoly(n;N,r,θ), for forming a reversible crosslink at position n1 + n2 = n along two polymers of N = 200 segments each, for different choices of chain stretch r at constant angle θ (panel a), and for different θ at constant stretch r (panel b). In (a), the two chains are at an angle of θ = π/2. In (b), the stretch ratio is set to r/Nb = 0.15. In both panels, the black dashed curve is for when the two polymers have their ends untethered, i.e.eqn (5). | ||
For the polymer gel in contact with a non-depletable reservoir of reversible crosslinks at a fixed bulk concentration, the full binding free energy for binding a reversible crosslink to a position n1 + n2 = n is
| ΔGbind(n;N,r,θ) = 2ΔHbind + ΔGcnf − μ + ΔGpoly(n;N,r,θ) | (7) |
The reversible linker binding strength and concentration are two key parameters that dictate how much of an entropy cost the reversible crosslinks are able to “pay”; that is, how far from the permanent crosslinks the reversible linkers are likely to bind. These two parameters can be manipulated to tune the overall binding equilibrium constant Keq,eff of the linkers to given positions along polymer backbone. For example, assuming the polymer network is in contact with a solution of reversible crosslinkers at concentration [R], then
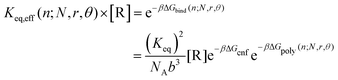 | (8) |
A reversible linker binding strength and concentration that is sufficient to compensate for the entropy penalty of binding near a permanent crosslink, but not much further away, leads to selective clustering around the permanent links. This has two microscopic consequences:
• Permanent crosslinks can share their local stress with adjacent bound transient crosslinks whilst the material is under strain;
• The polymer network topology is not substantially altered, as transient bonds far from permanent crosslinks have a low probability of formation and survival.
At the macroscale these two effects should lead to a material which is tougher, yet responding elastically in a way that is very similar to that without the reversible crosslinks. The remaining discussion is dedicated to demonstrating this connection with molecular simulation and numerical modelling.
On the other hand, very negative and favourable βΔHbind or a very high concentration of reversible linkers will lead to non-selective binding, as the entropy contribution becomes negligible regardless of the binding position n. Reversible crosslink binding will then be non-selective, and long-lived cooperatively-surviving clusters of reversible linkers far from permanent crosslinks have a greater chance of formation. Both of these lead the network topology to be altered, and the macroscopic elasticity to be different than the native material without the reversible crosslinks.
We have thus far cast our theory in terms of thermodynamic entropy. Similar qualitative conclusions could be obtained by arguing that the reversible crosslinks cluster around the permanent crosslinks on the grounds of a structural proximity effect, particularly if the gel is quite dilute. The argument would be that near a permanent crosslink, two polymer strands are by necessity already in close proximity. Therefore, there is a higher likelihood of adding a connecting reversible crosslink in that vicinity compared to elsewhere in a dilute gel.
While conceptually sound, the line of thinking based on proximity effects does not yield an obvious mathematical framework for quantifying the recruitment effect relative to the other key thermodynamic factors involved in reversible crosslinker binding, namely the binding strength, and reversible linker concentration. Casting our argument fundamentally in terms of entropy, on the other hand, gives a clear and quantitative handle (e.g.eqn (7)) for assessing the balance between these thermodynamic factors, so we can justify which choices of microscopic design give rise to the optimal sought-after macroscopic behaviour.
3 Clustering & load sharing around permanent crosslinks
In this section, we use molecular dynamics to examine reversible crosslink recruitment around a permanent crosslink, and to what extent adjacent bound reversible links share stress at a permanent crosslink.Illustrated in Fig. 5(a), the model consists of two polymer chains, each of 100 segments, connected together at their midsection (segment 50). The chains are placed in a simulation box, along with a given number of bivalent reversible crosslinkers. Details of the model are given in ESI Section SII;† what follows is a brief summary of the ingredients. The polymer segments are connected together by strong harmonic bonds. Non-bonded monomers interact via a repulsive inverse power law potential V(r) ∝ r−12 (with r the intermonomer distance). Each monomer has attached to it a binding site. The reversible crosslinkers each consist of a single bead, with two binding sites attached, held at an angle of π relative to each other by a strong three-body angle potential. A fixed number of 1000 reversible crosslinks are put into the simulation box of volume (200![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) )3 (where
)3 (where ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is the length unit in the simulation), such that the reversible crosslinks are at a density of 1.25 × 10−4 particles per
is the length unit in the simulation), such that the reversible crosslinks are at a density of 1.25 × 10−4 particles per ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3. Binding sites on a reversible crosslink interact with binding sites on the polymers via an attractive Gaussian potential, with an effective binding strength εbind,eff. Bonds between reversible crosslinks and the polymer segments are reversible and dynamic during the course of the simulation, while the geometry of the bonding sites and their host beads ensures that the interactions are valence-limited (i.e. only one reversible crosslink may bind to one polymer segment at a given time). Calculations are carried out using the HOOMD-blue molecular dynamics software package.50,51
3. Binding sites on a reversible crosslink interact with binding sites on the polymers via an attractive Gaussian potential, with an effective binding strength εbind,eff. Bonds between reversible crosslinks and the polymer segments are reversible and dynamic during the course of the simulation, while the geometry of the bonding sites and their host beads ensures that the interactions are valence-limited (i.e. only one reversible crosslink may bind to one polymer segment at a given time). Calculations are carried out using the HOOMD-blue molecular dynamics software package.50,51
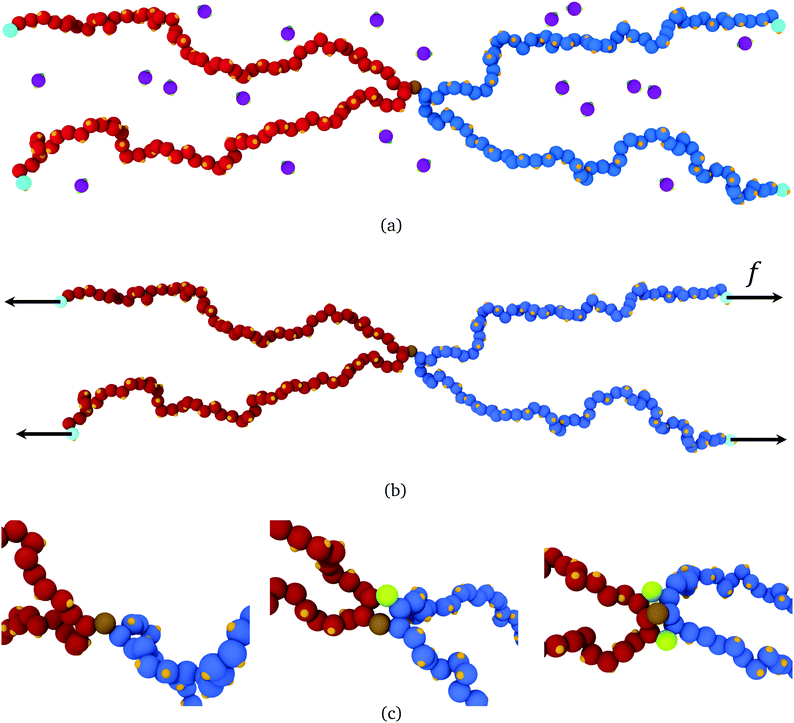 | ||
| Fig. 5 (a) Snapshot of a molecular dynamics simulation of two polymers (blue beads, red beads) each of 100 segments, permanently crosslinked at their midsection (brown bead). Reversible crosslink binding sites are shown in orange, and reversible crosslinking monomers are shown in purple, with green binding sites. (b) A force of strength f can be applied to the light blue beads, with directions indicated by the black vectors. (c) Close-up around the permanent crosslink showing simulations with no helper linkers (left), one helper in green (middle), and two helpers (right) (images generated with OVITO49). | ||
The parameters in this molecular dynamics model correspond to the thermodynamic reversible crosslink binding terms in eqn (7). The reversible crosslink binding enthalpy ΔHbind is dictated by εbind,eff, and the chemical potential μ is set by the bulk concentration of reversible crosslinks in the simulation. Note that a canonical ensemble for the reversible crosslinks in the molecular dynamics model is employed; however, strictly speaking a grand canonical ensemble should be used so that the average concentration of free reversible linkers remains fixed in the simulation regardless of how many bind to the polymer chains. To approximate a grand canonical ensemble and avoid significant reversible linker depletion effects, we use a large simulation box in which the number of reversible crosslinkers is large relative to the number of possible reversible crosslinker binding sites along the two polymer chains. Lastly, since the reversible crosslinkers are simple monomers, then the only notable entropy loss they experience upon binding (besides their translational entropy loss captured in the chemical potential) is rotational entropy, which goes into ΔGcnf. However, this term will be generally independent of the binding position (n1,n2) along the polymers. The remaining term in eqn (7), ΔGpoly, is the non-trivial entropy change of the two polymer network strands when a transient crosslink is formed between them at a given contour position—the subject of the ensuing discussion.
At present, we are interested only in the statistics of reversible crosslink binding between the different polymers (red and blue) in Fig. 5(a). In order to study just the physics of intermolecular reversible crosslink binding, and to prevent binding between segments on the same chain, the model distinguishes between binding sites on the red and blue polymer. The two binding units on a given reversible linker are also distinct, so that one can bind only to binding sites on the red polymer, while the other only to those on the blue polymer.
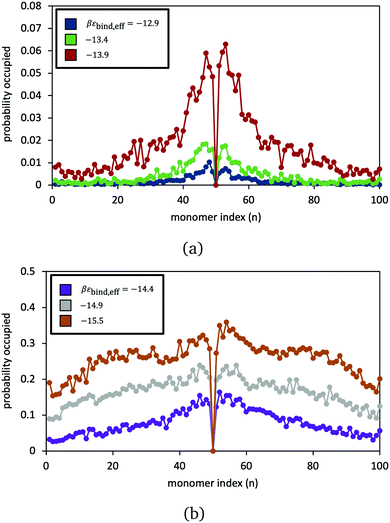
The model is employed to examine the equilibrium statistics of reversible crosslinker binding along the polymer chains. In Fig. 6, we record the simulation-average probability that segment j (from 1 to 100) is bound to a doubly bound reversible crosslink, for six different choices of reversible crosslink binding strength. At low and intermediate binding strength, we see very clear preference for binding near the permanent crosslink j = 50. The reversible crosslinks form a “zipper” domain around the permanent crosslink, resembling what is observed in earlier molecular simulation studies52 (indeed, here the permanent crosslink is acting like a nucleation site for the zipper domain). At larger binding strength, the reversible linkers bind more randomly across the polymers.
We now turn to examining how bound linkers adjacent to the permanent crosslink locally share stress. Our objective is to show within the molecular model: that having one or more reversible crosslinks bound adjacent to a permanent crosslink helps the latter to share stress; and that adding more reversible crosslinks generally leads to a smaller stress along the permanent crosslink.
To do so, the reversible crosslinking units are removed from the system, and one or more linkers are permanently affixed to the polymer segment(s) adjacent to the permanent crosslink as shown in Fig. 5(c). These “helper” linkers remain bound to their respective polymer segments for the duration of the simulation. The four ends of the polymers are then pulled with a constant force f in opposite directions throughout the duration of the simulation. As depicted in Fig. 5(b), the ends of polymer A are pulled along +x, and those of polymer B along −x; they are otherwise free to fluctuate in (x,y,z). This results in an extensional force along the permanent crosslink.
This simulation setup corresponds to a realistic physical scenario in which the bond exchange kinetics of the reversible crosslinkers are slow; that is, the average lifetime for a reversible crosslink to remain attached to its two partners is far longer than the (microscopic) simulation timescale. Indeed, in experiment14 the reversible crosslink bonding half-life spans the order of milliseconds to seconds, clearly far longer than the molecular timescale being examined in our molecular dynamics simulation. As such, fixing the helper linkers in position over the course of our simulation is actually most representative of the experimental regime of interest for mechanical testing at the microscale.
Importantly, as will be discussed in Section 5, reversible bonding exchange kinetics are not necessarily coupled to the thermodynamic linker binding strength. Slow kinetics, with long reversible linker binding lifetimes, can result from large activation barriers (entropic or enthalpic in origin) for binding or unbinding. These barriers can be present and independently tuned even when the linkers have a “weak” thermodynamic binding free energy, as is necessary for entropy to guide recruitment of the linkers around permanent crosslinks. We will argue that this is actually the optimal recipe for toughness-enhancing reversible crosslinks in Section 5.
The average force along the permanent crosslink is obtained from simulation by monitoring the average lengths 〈l〉 of its two bonds, relative to the preferred bond length l0. The bonds follow the harmonic force law 〈F〉 = k(〈l〉 − l0), where the spring constant k = 1000kT/![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2. From 〈l〉 in simulation, 〈F〉 may be calculated. Note that the choice of k for the permanent crosslink bonds is arbitrary, affecting the quantitative result of the simulation but not the qualitative trends we seek.
2. From 〈l〉 in simulation, 〈F〉 may be calculated. Note that the choice of k for the permanent crosslink bonds is arbitrary, affecting the quantitative result of the simulation but not the qualitative trends we seek.
Fig. 7 reports the average force 〈F〉 along the permanent crosslink, as a function of pulling force f, for: the two polymers connected only by the permanent crosslink; with one helper; and with two helpers. The addition of the helpers indeed reduces the average tension along the permanent crosslink bonds. If we suppose that the probability of permanent crosslink failure grows exponentially with its average force according to the Bell model,53,54P(fail) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(B〈F〉/kT), where A and B are constants, then the presence of the helper linkers substantially reduces the probability of bond breakage. Indeed, adding more helpers leads to a mutually lower probability that any one of the linkers or the permanent crosslink will fail at a given pulling force.55
exp(B〈F〉/kT), where A and B are constants, then the presence of the helper linkers substantially reduces the probability of bond breakage. Indeed, adding more helpers leads to a mutually lower probability that any one of the linkers or the permanent crosslink will fail at a given pulling force.55
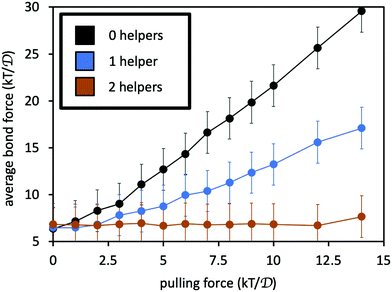 | ||
| Fig. 7 Average force on the permanent crosslink as a function of pulling force f on the four chain ends. Black curve is for system with only the permanent crosslink, blue includes one adjacent helper, and orange includes two adjacent helpers. See Fig. 5(b) for simulation snapshots of the three scenarios. Error bars indicate size of thermal fluctuations in the force, computed as the standard deviation of the force divided by 10 for visual clarity. | ||
4 Amplified toughness enhancement at the network scale
Recruitment of reversible crosslinks around permanent crosslinks implies that the latter are locally reinforced, so that they can bear more force before breaking. In this section, we examine the consequences of locally reinforced crosslinks on the global toughness of a polymer network as it is strained. To be able to apply strain at a timescale that is much longer than the relaxation time of polymer strands in the network, a coarse-grained self-consistent field theory (SCFT) model for polymer networks that we previously developed is utilised.56The model uses lattice SCFT57 to converge on the equilibrium distribution of crosslinks and polymer chain configurations in a microscopically sized volume element of the material, given a fixed local network topology (polymer chain connectivity) and boundary conditions. The network is represented with finitely extensible phantom (i.e. non-interacting non-self-avoiding) lattice polymers, and does not account for chain entanglements. Each polymer is composed of a given number of segments of width b, equal to the width of a single lattice site.
The model allows for easy extraction of the free energy of the network, as a function of strain applied to the boundaries of the system. For simplicity, we perform the calculations in two dimensions. Even though the entropic recruitment of reversible crosslinks near permanent ones is a three-dimensional phenomenon, we expect the effect of crosslink strength on global toughness to be similar in two and three dimensions.
The calculations carried out here consist of defining a square polymer network with an initial width and height within the lattice SCFT model, and then straining along its horizontal axis via a series of strain steps. On each strain step, the SCFT model is used to approximate the equilibrium spatial distribution of polymers and crosslinks for the current system dimensions, obtaining the network free energy for that strain. On the next strain step, the system width is increased by a desired amount, and the process repeated. Thus, the SCFT model represents the limiting scenario of a quasi-equilibrium strain experiment on the polymer network.
In order to examine how effective crosslink strength translates into global toughness, we must microscopically capture when and where connections break within the network as it is strained. Our model from ref. 56 is adapted by adding in the possibility for polymer chains (“bridges” in the model) to irreversibly disconnect from one of its two attachment points (“nodes”) as the network boundaries are strained. The bridge is instantaneously and irreversibly cut when its tension exceeds F*, a tunable threshold tension parameter.
The parameter F* physically represents the effective strength of the crosslinks in the network. It is into this parameter that the physics of reversible crosslinking outlined in the previous two sections can be invested in a coarse-grained way.
We begin by choosing a baseline value of F* = Fo* representing the strength of the permanent crosslinks alone. Increasing the value of F* from this baseline Fo* represents the idea that reversible crosslinks have attached next to these permanent crosslinks, locally enhancing the strength of the connections. In the following calculations, we assume that F* is the same for every connection in the system. This is for simplicity, and implies that the same average number of reversible crosslinks are bound adjacent to each permanent crosslink in the network. In reality, the F* of each permanent crosslink is different depending on the number of reversible crosslinks that recruit around the connection. Any mechanical contributions that would arise from reversible crosslinks binding far from permanent crosslinks, thereby altering the topology of the network, are neglected. Thus, the assumption in this model is that the reversible crosslinks have a weak-binding Keq, and are entropically driven to bind only near permanent crosslinks as discussed in Section II (ESI†).
For the following calculations, a square network initially of 50 × 50 lattice units in size is defined with 283 bridges, and 190 nodes. Details of the network configuration are given in ESI Section SIII.† The network topology and number of crosslinks is the same for all calculations, while only the crosslink strength parameter F* is varied.
Fig. 8 shows a schematic of the polymer network used for calculations. The figure shows the polymer network in its initial state, and at different subsequent strain steps. The polymer bridges (lines) are shaded to indicate whether the force in the bridge is low (black) or high (red). As the network is strained, the tensions in the bridges grow depending on their average end-to-end distance Li. Provided we operate within a regime where bridges are not stretched very near to their finite end-to-end extent (accomplished by choosing an appropriately moderate value of F*), then the force along a bridge can be approximated by the ideal chain model in two dimensions:
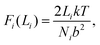 | (9) |
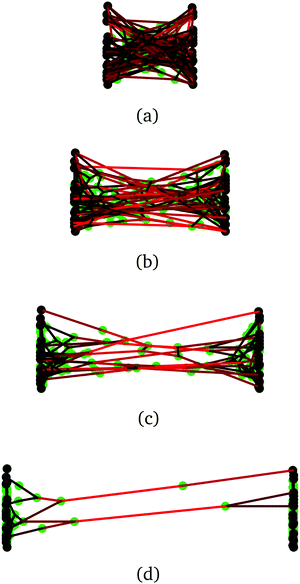 | ||
| Fig. 8 Snapshots of a network strain experiment in the lattice SCFT model, going from low strain (a) to high strain (d). Crosslinks (nodes) are shown as green dots, localised to their most probable position as given by the SCFT calculation, and polymer chains (bridges) are represented by lines. The shading of the line indicates that the polymer is experiencing high (red) or low (black) tension following eqn (9). The network is suspended between two fictitious plates by the solid black points. Polymer bridges disconnect from one of their two attachment nodes when the force on the bridge exceeds F* = 1.25kT/b, in this case. | ||
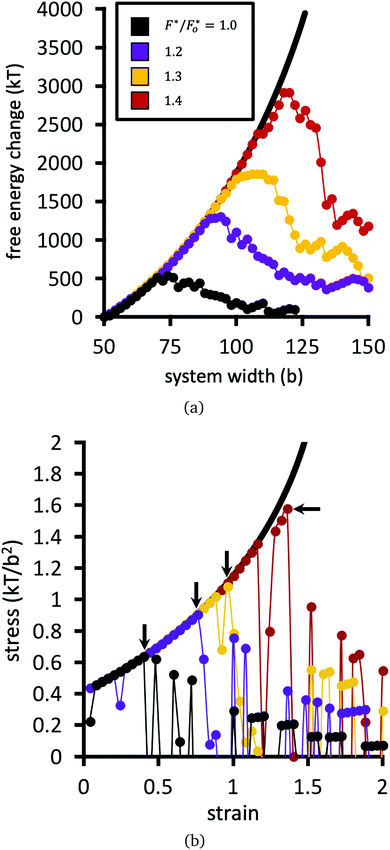
Fig. 9(a) plots the free energy of the network as a function of system width, while Fig. 9(b) shows the stress σ as a function of strain. The strain is defined as the change in system width, divided by its initial width (50b). The stress, in units of kT/b2, is defined as the finite difference derivative of the free energy in Fig. 9(a) divided by the fixed height of the system (50b).
Numerical results for the baseline system are plotted in black points in Fig. 9. The remaining datasets show calculations for the same network, but with larger choices of F* relative to the baseline dataset. The free energy in Fig. 9(a) initially increases with strain; if none of the bridges are allowed to break, then the free energy follows the solid black line. The increase of the free energy with strain is sharper than quadratic in this network, because the model captures the finite extensibility of the polymers.56 The stress as a function of strain for the network therefore increases faster than linearly in Fig. 9(b).
Upon continued strain in Fig. 9, the network reaches a rupture point, defined as the strain where the stress σ in Fig. 9(b) reaches a maximum σrup. At or just before the critical strain, the free energy of the system begins to fluctuate and decrease in a jagged fashion. Each downward plunge in the free energy corresponds to breakage of a bridge/node connection.
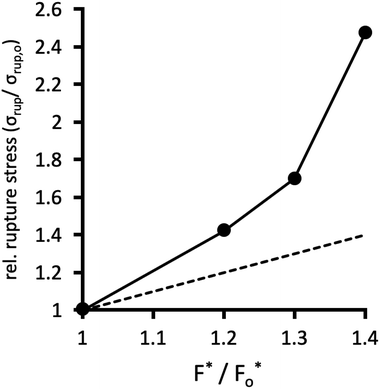
Fig. 10 plots the stress σrup at which the network ruptures (indicated by the black arrows in Fig. 9b), against the factor F*/Fo* by which the crosslinks are locally reinforced relative to the baseline system. The rupture stress for each network is divided by that for the baseline system with F* = Fo*. The dashed line in Fig. 10 is what would be expected if the relative rupture stress were to scale directly with F*/Fo*.
The SCFT results in Fig. 10 demonstrate that the stress the network can bear before rupturing (relative to the baseline system) grows faster than the factor F*/Fo* of local crosslink reinforcement. For example, the red dataset in Fig. 9 uses F*/Fo* = 1.4, i.e. the crosslinks can locally bear 1.4 times more tension before breaking, compared to the baseline system. However, this local enhancement allows the network to globally bear ≈2.5 times more stress relative to the baseline system before rupturing (Fig. 9b). For the yellow dataset, F*/Fo* = 1.3, while that network can bear ≈1.7 times more stress compared to the baseline system.
These calculations suggest that reinforced crosslinks at the molecular scale lead to an even larger factor of strengthening for the whole network. This is likely a cooperative effect, whereby reducing the probability for breaking a single isolated connection translates, in the network context, into an even lower chance of failure of a connection that is bearing stress shared by other nearby connections.54,55,58 Thus, reversible crosslinks that locally reinforce the permanent crosslinks of a polymer network even by a small margin can lead the network to be tougher by a larger factor, at the macroscopic scale.
A polymer bridge breaks when its force, calculated by eqn (9), exceeds the given choice of the breakage force parameter F*. Fig. 11 presents the cumulative number of polymer bridge connections broken in the network as a function of horizontal strain. This provides an assessment for the mechanism by which the network fails when approaching and surpassing its rupture point (indicated by black arrows in the figure). Before the rupture point, polymer bridge failure is rare, and the network remains largely intact. Beyond the rupture point, polymer bridges rapidly (and irreversibly) break away from their permanent crosslinks. In this quasi-equilibrium model, where strain is imagined to happen at an infinitely slow rate, the number of bridge failures per unit strain generally follows the same curve for all choices of crosslink strength F* considered; the choice of F* only shifts the curves horizontally, i.e. the strain at which rupture initiates. Therefore, locally strengthening the crosslinks in the network (i.e. by larger F*) serves only to delay the onset of rupture, while not having an influence on the rate of polymer bridge rupture with respect to strain thereafter.
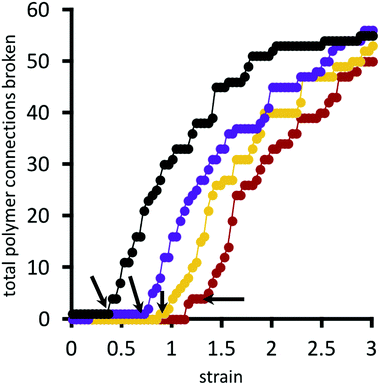 | ||
| Fig. 11 Total number of polymer bridges with broken connections as a function of strain, for different choices of F*/Fo* = 1.0, 1.2, 1.3, 1.4 (see Fig. 9 for colour legend). Arrows indicate the rupture point of the material. Value of Fo* = 1.25kT/b. | ||
The topology of the network, among other factors, dictates to what extent local stress is transferred through the network as it ruptures, which will in turn temper the influence of local crosslink reinforcement on global toughness. A recent simulation study by Nabavi et al.23 considered the work required to stretch a polymer chain to full extent, when reversibly associating monomers are embedded into the polymer chain in a particular sequence. Altering the reversibly bonding monomer sequence, so that the polymer exhibits a different self-associated conformation in the unstretched state, can shift the work required to rupture the links and stretch the polymer by a factor of two to three. This order of magnitude is consistent with the degree of toughening amplification observed for our network in Fig. 8, though a systematic examination of toughness in different network topologies should be carried out to gain better insight into this effect.
5 Experimental guidelines & kinetic considerations
We have developed a microscopic theory for freely diffusing reversible crosslinks in a permanently crosslinked polymer gel. The theory enables us to define clear guidelines for optimal reversible crosslink design in experiment.When the equilibrium constant for reversible crosslink binding to the polymer chains is small, then entropy dictates the ensemble of binding configurations at equilibrium. Entropy favours clustering of the reversible links around permanent crosslinks. This leads to local load sharing of stress around the permanent crosslinks during strain, so that the material has a globally lower probability of rupture at higher stress relative to the native material. This translates into higher material toughness. Moreover, the microscopic topology of the polymer network is not affected by the reversible crosslinks, and so the elasticity of the material is left mostly unaltered compared to the native material.
On the other hand, if the reversible link equilibrium binding constant is large, then the entropic bias becomes negligible. The reversible links are then expected to bind in random locations to the polymer network scaffold. The altered network topology at the microscale results in a different macroscopic elasticity compared to the native material, and the permanent crosslinks are not selectively reinforced at the microscale by reversible links. In this regime, material toughness is not enhanced.
This picture is consistent with the experimental results in Kean et al.14 In their study, relatively weak-binding reversible crosslinks lead to the greatest toughness enhancement, with the smallest change in elasticity. This is in contrast to their strong-binding linker, which causes the material to become stiffer, and more brittle.
Our theory is also in agreement with the recent experimental work by Mayumi et al.34,59 This study examines the behaviour of a permanently crosslinked gel, with a fixed concentration of reversible crosslinks, at different strain rates. In fracture tests of notched samples, the gel exhibits the least change in low-strain modulus and greatest enhancement of intrinsic toughness, compared to the gel without reversible crosslinks, in the limit of slow loading. The sample is also far more extensible before fracture in this case.
In the context of our theory, the slow-strain limit allows the reversible crosslinks sufficient time to equilibrate—to sample a broad ensemble of microscopic configurations—in which reversible crosslinks are localised around the permanent crosslinks as the polymer strands are stretched. While the reversible linkers will be dynamically moving and exchanging binding partners in a slow-strain limit experiment, the macroscopic stress–strain behaviour of the material will be dominated by the thermodynamic ensemble average of reversible crosslink binding. If, on the other hand, the material is strained more rapidly, then the timescale of strain will begin to approach and exceed the timescale of reversible crosslink rearrangement. The material will be more strongly governed by reversible crosslink configurations that are kinetically locked on the timescale of the experiment (for example, see ref. 60).
Reconfigurability below the strain timescale is where reversible crosslinks present their greatest utility in the present case. As a juxtaposed example, consider instead adding new permanent crosslinkers to the native polymer gel. New connections between the polymer scaffold will be formed, but the locations of the new bonds are largely dictated by first-passage kinetics. Once a permanent crosslink finds a partner, it is stuck. Entropy instead acts at the ensemble level, when added crosslinks are allowed to try and re-try many different binding options within the fluctuating polymer network. This provides the opportunity to tune the linker binding strength and concentration, so as to bring them into the entropically governed regime where linkers localise around the permanent crosslinks.
We have thus far argued that entropic recruitment of reversible crosslinks around permanent crosslinks occurs most prominently when the reversible linkers are in a “weak-binding” regime. This corresponds to when the product of the following two quantities is small: the equilibrium constant Keq of reversible linker binding; and the reversible linker concentration [R]. A large value of one quantity can in principle be compensated for by designing a smaller value for the other. However, the reversible crosslinks must also have sufficiently long-lived bonds so that they are useful in sharing local stress near a permanent crosslink. Indeed, in Kean et al., half-lives of binding for the reversible crosslink structures considered are on the order of milliseconds to seconds.14 In microscopic terms, these are very long-lived bonds. We now decipher how to design reversible crosslinks that have long bound lifetimes, yet can still reside in a “weak-binding” regime.
The equilibrium binding constant between a reversible crosslinker, and an arbitrary single polymer segment, is related to the standard binding free energy by the relation 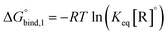 (where R = 8.314 J mol−1 K−1 is the ideal gas constant and [R]° is the reference reversible crosslink concentration taken to be 1 molar). The equilibrium constant can also be expressed by the ratio of the rate constant kon of reversible linker binding to the rate constant koff of unbinding:
(where R = 8.314 J mol−1 K−1 is the ideal gas constant and [R]° is the reference reversible crosslink concentration taken to be 1 molar). The equilibrium constant can also be expressed by the ratio of the rate constant kon of reversible linker binding to the rate constant koff of unbinding:
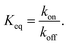 | (10) |
These rate constants can be directly tuned by the binding enthalpy; for example, a stronger bond has a longer bound lifetime, and thus a smaller koff. This can be manipulated by chemical construction, e.g. opting for hydrogen bonding, coordination bonding, or multiple adjacent binding groups located on the same reversible linker. The rate constants also depend on how exquisitely oriented a reversible linker must be, relative to a nearby polymer segment, in order to form a bond. This will depend on the type of chemical interaction they have, as well as steric considerations. The more precisely oriented the reversible linker must be relative to its partner to form a bond, the smaller kon will be. Note that the reversible crosslinker concentration [R] enters only into the true rates of binding/unbinding—e.g. for binding, rate ∝ kon[R]—but it does not alter the intrinsic standard rate constants kon and koff.
The reversible crosslink enthalpy and orientational free energy cost for binding adjust kon and koff, but they also affect the Keq of the interaction. On the other hand, kon and koff can be tuned without altering the intrinsic Keq by introducing an activation barrier ΔG‡ to reversible linker binding and unbinding. For binding, the total barrier is just ΔG‡, while for unbinding it is 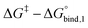 . Thus, the rate constants kon and koff are both shifted by the same factor ∝ exp(−ΔG‡/RT), yet the ratio of kon/koff results in the same Keq as when the activation barriers are absent. We can see this by
. Thus, the rate constants kon and koff are both shifted by the same factor ∝ exp(−ΔG‡/RT), yet the ratio of kon/koff results in the same Keq as when the activation barriers are absent. We can see this by
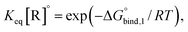 the intrinsic Keq of reversible crosslinkers.
the intrinsic Keq of reversible crosslinkers.
In this way, the timescale for reversible crosslink binding/unbinding can be tuned independently from the equilibrium binding constant Keq. A large activation barrier to binding and unbinding will lead to long-lived and persistent bonds, even if Keq is small. An activation barrier can be manipulated by the chemical composition of the reversible crosslinks. For example, bulky side groups could be added to the reversible linker so that there is an initial steric barrier to binding, overcome only when the side group(s) are configured so as to expose the binding site to the polymer backbone.
Thus, a “weak-binding” reversible linker, i.e. having a small Keq, can be constructed by any choice of ratio kon/koff leading to that Keq. Long reversible linker binding lifetimes (i.e. small koff), such as used in Kean et al. 2014,14 can be offset by comparably small binding rates kon such that the system is in an overall weak-binding (small Keq) regime. We expect that Kean et al. 2014 are sampling that regime in their system exhibiting strong toughness enhancement yet little change in elasticity.14 On the other hand, they likely enter into a large-Keq regime for their strongest reversible linker, and that is why that system exhibits a significantly different modulus relative to the native material.
As a final point, we remark on how actively exchanging reversible crosslinks can still bear mechanical stress during strain. Reversible crosslinks can continuously propagate and exchange binding partners over the timescale of strain, particularly if the strain is slow relative to the binding/unbinding timescale. Suppose we design the reversible crosslinks to have a small Keq that is sufficient to yield, on average, a few reversible crosslinks bound around each permanent crosslink at any given moment during strain. The macroscopic stress/strain curve represents an average over the ensemble of different local molecular environments, having fluctuations from the mean. For example, over a short interval of microscopic time, some localities in the material might be unbinding and rebinding new reversible crosslinks, while other spots have their reversible links fixed during that time interval. However, at the level of a macroscopic average over all such microscopic environments, the strain experiment will “feel” those reversible crosslinks that happen to be bound, and locally reinforcing the material, at any given instant in time. The small Keq effectively biases these bound linkers so that they are more likely to be clustered around the permanent crosslinks, while a binding/unbinding activation barrier can give the bound linkers enough “residence time” to bear some local stress before moving on to a new partner.
6 Conclusions
This work has constructed an equilibrium picture for how reversible crosslinks, allowed to freely diffuse as individual units throughout a polymer network, can toughen the network while maintaining the intrinsic network elasticity. The reversible crosslinks are driven by entropy to recruit to binding positions around the permanent crosslinks in the network, as this leads to the smallest entropy loss for participating polymer chains. The permanent crosslinks are thereby reinforced so that they may bear more local stress before rupturing, leading the network as a whole to be tougher when strained. Since the topology of the polymer network is not significantly altered when the reversible crosslinks recruit around existing permanent links, the material exhibits its original intrinsic elasticity.From the results and discussion presented here, we can define guidelines for optimal reversible crosslink design. The best design is one that
• is in the “weak-binding” regime, defined as when the product of the equilibrium constant Keq and concentration [R] of the reversible crosslinkers is small, so that they selectively cluster to binding positions around permanent crosslinks in the network;
• has sufficiently long-lifetime bonds (i.e. small binding/unbinding rate constants kon and koff) to productively share local stress near a permanent crosslink;
• simultaneously has binding exchange rate constants that are larger than the rate at which the material will be strained in typical use, so that the reversible crosslinks are able to equilibrate and re-equilibrate to positions near permanent crosslinks.
The chemical construction of the reversible linkers establishes the binding equilibrium constant Keq. Adjusting the reversible crosslink concentration [R] is a simple tactic to honing in on the ideal weak-binding regime for a given Keq. The lifetime of bonding (i.e. the binding/unbinding rate constants kon and koff) can be tuned independently of the equilibrium constant Keq by designing an activation barrier to binding/unbinding.
The three optimal design guidelines above are easiest to satisfy when the timescale of strain is very long. This regime allows leeway for designing reversible linkers that have sufficiently long-lived bonds for sharing local stress in the network during strain, yet nevertheless have a rearrangement timescale that is still less than the strain timescale.
A more challenging scenario is a material where strain is occurring on “short” (mesoscopic or microscopic) timescales. Here, the window for making reversible linkers that can bear local stress yet rearrange below the strain timescale becomes narrow. For strain rates larger than the reversible crosslink binding/unbinding rates, the rearrangement kinetics of the reversible linkers will dominate the behaviour of the material—a topic we leave to future study.
A key question arising out of this study is how microscopically enhancing the strength of crosslinks in a polymer network leads the material to be macroscopically tougher by an even larger factor. Our SCFT network model can be used to examine the length scale over which polymer strands break as a network is strained to rupture point, which may play a role in this. This length scale additionally has predictive power for assessing the macroscopic behaviour of the material at the tip of a crack during rupture. A systematic examination of toughness enhancement in different network topologies will also be undertaken.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been performed within the framework of the 4TU. High-Tech Materials research programme ‘New Horizons in designer materials’ (http://www.4tu.nl/htm). We are grateful for compute time obtained from the Netherlands Organisation for Scientific Research (NWO) SURFsara Pilot Program (Grant No. 15582). Additional thanks to Rint Sijbesma, Rob Jack, Yuval Mulla, and Gijsje Koenderink for valuable discussions.Notes and references
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108 CAS.
- C. Ligoure and S. Mora, Rheol. Acta, 2013, 52, 91–114 CrossRef CAS.
- C. Creton, Macromolecules, 2017, 50, 8297–8316 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- G. Linga, P. Ballone and A. Hansen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 1065 CrossRef PubMed.
- Y. H. Kim and R. P. Wool, Macromolecules, 1983, 16, 1115–1120 CrossRef CAS.
- S. v. d. Zwaag and E. Brinkman, Self healing materials, IOS Press, Amsterdam, The Netherlands, 2015 Search PubMed.
- R. P. Wool, Soft Matter, 2008, 4, 400 RSC.
- E. B. Stukalin, L.-H. Cai, N. A. Kumar, L. Leibler and M. Rubinstein, Macromolecules, 2013, 46, 7525–7541 CrossRef CAS PubMed.
- A. J. R. Amaral and G. Pasparakis, Polym. Chem., 2017, 8, 6464–6484 RSC.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173 RSC.
- T. Narita, K. Mayumi, G. Ducouret and P. Hébraud, Macromolecules, 2013, 46, 4174–4183 CrossRef CAS.
- Z. S. Kean, J. L. Hawk, S. Lin, X. Zhao, R. P. Sijbesma and S. L. Craig, Adv. Mater., 2014, 26, 6013–6018 CrossRef CAS PubMed.
- Q. Li, D. G. Barrett, P. B. Messersmith and N. Holten-Andersen, ACS Nano, 2015, 10, 1317–1324 CrossRef PubMed.
- J. A. Neal, D. Mozhdehi and Z. Guan, J. Am. Chem. Soc., 2015, 137, 4846–4850 CrossRef CAS PubMed.
- N. A. Kurniawan, B. E. Vos, A. Biebricher, G. J. L. Wuite, E. J. G. Peterman and G. H. Koenderink, Biophys. J., 2016, 111, 1026–1034 CrossRef CAS PubMed.
- L. Imbernon, S. Norvez and L. Leibler, Macromolecules, 2016, 49, 2172–2178 CrossRef CAS.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed.
- R. S. Hoy and G. H. Fredrickson, J. Chem. Phys., 2009, 131, 224902 CrossRef PubMed.
- J. Sprakel, E. Spruijt, J. van der Gucht, J. T. Padding and W. J. Briels, Soft Matter, 2009, 5, 4748–4749 RSC.
- T. Indei and J.-i. Takimoto, J. Chem. Phys., 2010, 133, 194902 CrossRef PubMed.
- S. S. Nabavi, P. Fratzl and M. A. Hartmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032603 CrossRef PubMed.
- A. West and J. T. Kindt, Macromol. Theory Simul., 2015, 24, 208–217 CrossRef CAS.
- Y. D. Gordievskaya, A. M. Rumyantsev and E. Y. Kramarenko, J. Chem. Phys., 2016, 144, 184902 CrossRef PubMed.
- D. Amin, A. E. Likhtman and Z. Wang, Macromolecules, 2016, 49, 7510–7524 CrossRef CAS.
- F. Meng, R. H. Pritchard and E. M. Terentjev, Macromolecules, 2016, 49, 2843–2852 CrossRef CAS.
- K. Yu, Q. Shi, H. Li, J. Jabour, H. Yang, M. L. Dunn, T. Wang and H. J. Qi, J. Mech. Phys. Solids, 2016, 94, 1–17 CrossRef CAS.
- R. Brighenti and F. J. Vernerey, Composites, Part B, 2017, 115, 257–265 CrossRef PubMed.
- F. J. Vernerey, R. Long and R. Brighenti, J. Mech. Phys. Solids, 2017, 107, 1–20 CrossRef CAS.
- B. Oyarzún and B. M. Mognetti, J. Chem. Phys., 2018, 148, 114110 CrossRef PubMed.
- B. Oyarzún and B. M. Mognetti, Mol. Phys., 2018, 1–18 Search PubMed in press.
- G. A. Parada and X. Zhao, Soft Matter, 2018, 14, 5186–5196 RSC.
- K. Mayumi, J. Guo, T. Narita, C. Y. Hui and C. Creton, Extreme Mech. Lett., 2016, 6, 52–59 CrossRef.
- M. Albrecht and G. van Koten, Angew. Chem., Int. Ed., 2001, 40, 3750–3781 CrossRef CAS PubMed.
- L. G. Baxandall, Macromolecules, 1989, 22, 1982–1988 CrossRef CAS.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- S. Hackelbusch, T. Rossow, P. van Assenbergh and S. Seiffert, Macromolecules, 2013, 46, 6273–6286 CrossRef CAS.
- Y. Mulla and G. H. Koenderink, arXiv:1805.12431v1 [cond-mat.soft], 2018, 1–8.
- Y. Mulla, G. Oliveri, J. T. B. Overvelde and G. H. Koenderink, Phys. Rev. Lett., 2018, 120, 268002 CrossRef PubMed.
- G. Foyart, C. Ligoure, S. Mora and L. Ramos, ACS Macro Lett., 2016, 5, 1080–1083 CrossRef CAS.
- L. R. G. Treloar, Rep. Prog. Phys., 1942, 9, 113 CrossRef.
- H. M. James, J. Chem. Phys., 1947, 15, 651–668 CrossRef CAS.
- S. F. Edwards, J. Phys. C: Solid State Phys., 1969, 2, 1–13 CrossRef.
- P. J. Flory, Polym. J., 1985, 17, 1–12 CrossRef CAS.
- T. Holzl, H. L. Trautenberg and D. Goritz, Phys. Rev. Lett., 1997, 79, 2293–2296 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- J. T. Kindt, J. Chem. Phys., 2005, 123, 144901 CrossRef PubMed.
- G. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- E. Evans, D. Berk and A. Leung, Biophys. J., 1991, 59, 838–848 CrossRef CAS PubMed.
- U. Seifert, Phys. Rev. Lett., 2000, 84, 2750–2753 CrossRef CAS PubMed.
- N. B. Tito, C. Storm and W. G. Ellenbroek, Macromolecules, 2017, 50, 9788–9795 CrossRef CAS PubMed.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- C. Vaca, R. Shlomovitz, Y. Yang, M. T. Valentine and A. J. Levine, Soft Matter, 2015, 11, 4899–4911 RSC.
- K. Mayumi, A. Marcellan, G. Ducouret, C. Creton and T. Narita, ACS Macro Lett., 2013, 2, 1065–1068 CrossRef CAS.
- W. C. Yount, D. M. Loveless and S. L. Craig, Angew. Chem., Int. Ed., 2005, 44, 2746–2748 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical derivations of key equations in main text, molecular dynamics simulation details, and self-consistent field calculation details. See DOI: 10.1039/c8sm02577k |
| This journal is © The Royal Society of Chemistry 2019 |