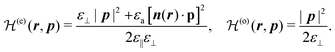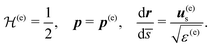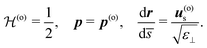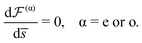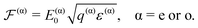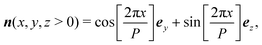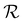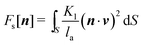Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ray-based optical visualisation of complex birefringent structures including energy transport†
Guilhem
Poy
 * and
Slobodan
Žumer
* and
Slobodan
Žumer

Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia. E-mail: guilhem.poy@fmf.uni-lj.si; Tel: +33 7 86 09 07 39
First published on 11th April 2019
Abstract
We propose an efficient method to simulate light propagation in lossless and non-scattering uniaxial birefringent media, based on a standard ray-tracing technique supplemented by a newly-derived transport equation for the electric field amplitude along a ray and a tailored interpolation algorithm for the reconstruction of the electromagnetic fields. We show that this algorithm is accurate in comparison to a full solution of Maxwell's equations when the permittivity tensor of the birefringent medium typically varies over a length much bigger than the wavelength. We demonstrate the usefulness of our code for soft matter by comparing experimental images of liquid crystal droplets with simulated bright-field optical micrographs, and conclude that our method is more general than the usual Jones method, which is only valid under polarised illumination conditions. We also point out other possible applications of our method, including liquid crystal based flat element design and diffraction pattern calculations for periodic liquid crystal samples.
1 Introduction
Liquid crystal (LC) phases are always associated with an orientational order: the molecules inside a mesoscopic volume are oriented around the same direction n, called the director.1,2 Because of this orientational order, LCs have an anisotropic permittivity tensor at optical frequencies, i.e. they are birefringent fluids. Together with the easy reorientation of n under external electric fields, this fundamental optical property is at the core of the most successful technological applications of LCs3 (LC displays, phase retarders, spatial light modulators…), in which light propagates through simple director fields manipulated with external voltages.In the past ten years, major developments in the field of soft matter have unlocked the possibility to create and control even more complex birefringent structures useful for advanced light applications: without being exhaustive, one can mention tunable LC microresonators,4 laser-directed patterns of cholesteric fingers allowing one to generate optical phase singularities,5 photoaligned chiral superstructures with application to diffraction gratings and lasing,6 and beam shaping using LC micro-optical elements with engineered Pancharatnam–Berry phases.7
Having access to the orientational field of these complex birefringent structures is essential for a better theoretical understanding of these systems and for the design of new optical devices. If the birefringent structure under consideration is quasi two-dimensional (Langmuir layers, smectic films…), one can use standard polarised light microscopy techniques to fully reconstruct the director field:8 by illuminating the sample with polarised light and collecting with a camera the reflected or transmitted light though a lens and an analyser, one can generally find a link between the measured intensity and the local orientation of the director. The images measured with such techniques are called polarised optical micrographs (POMs), a term which also encompasses images measured in other polarised microscopy setups (only one polariser or analyzer, presence of a half-wave or quarter-wave plate…).
If the birefringent structure under consideration is fully three-dimensional, the POMs generally depend on the focal setting of the microscope and one cannot directly measure n using these simple microscopy techniques. To fully reconstruct the three dimensional director field, three possibilities can be envisioned: either a direct experimental measurement using tomography techniques (fluorescence confocal polarised microscopy9 or multiphoton imaging techniques10), a numerical simulation with a minimization of the free energy of the system,11,12 or a hybrid experimental/numerical method recently developed by Posnjak et al.13 The first and third possibilities have the advantage of being in situ measurements, but also have a major limitation: the birefringence of the LC must be very small in order to avoid optical artefacts. The second possibility does not suffer from such a limitation, but necessitates accurate values of the material constants present in the expression of the free energy.
In any case, one should always try to validate the reconstructed director field by simulating what it would look like under a real microscope and comparing the simulated images with the experimental POMs of the structure under consideration. The most widely adopted method to simulate POMs is the Jones method:3 in this method, the polarisation state of light is represented by a vector of size 2 which is propagated in one direction through the birefringent medium using 2-by-2 transfer matrices depending on the given director field. However, this method suffers from two important limitations: first, the sample is assumed to be illuminated by a single plane wave, although this is generally not the case under a real microscope;14 second, light does not propagate in a straight line inside birefringent media, but can be deflected due to the spatial variation of n.15 The first limitation implies that the Jones method is unable to predict the effect of the numerical aperture and focusing optics of the microscope on the POMs, and the second limitation implies that the Jones method cannot simulate bright-field optical micrographs (BFOM) obtained when the sample is observed with unpolarised light without any polariser or analyser.‡
Although the first limitation can be easily addressed by using a generalised Jones method,14 the situation concerning the second issue is more complicated. The finite-difference time-domain method can be used to directly solve Maxwell's equations in a birefringent medium,16 but this approach can be computationally very intensive for large 3D domains. More efficient ray-tracing methods15,17 have been extensively studied in anisotropic media, but all studies in the literature either focus on simple 2D geometries18,19 or do not propose a reconstruction of the electromagnetic field amplitudes.20,21 Beam propagation22 and eikonal methods23 have also been used to fully calculate the electromagnetic fields inside complex 3D birefringent systems, but these approaches are not very efficient if one want to compute light transmission in samples surrounded by thick isotropic layers such as glass plates: since light is deflected by the birefringent medium, one would need a prohibitively large computational domain in order to contain the full extent of the light wave.§ In addition, the eikonal propagation equation becomes highly singular when the deflection effects are too important,24 which complicates the numerical integration.
In this paper, we present a novel numerical method for the propagation of light in uniaxial birefringent samples, with two important features: fast and accurate reconstruction of the electromagnetic fields inside the sample, as well as the possibility to simulate POMs and BFOMs even when the sample is surrounded with thick isotropic layers.
The plan of the paper is as follows. In Section 2, we describe the theoretical framework and numerical implementation of our method, which is based on a ray-tracing technique supplemented by transport equations for the wave amplitudes and an efficient interpolation algorithm to calculate the electromagnetic fields. In Section 3, we validate our method with a comparison against a full solution of Maxwell's equations. In Section 4, we use our method to calculate the BFOM of a LC droplet, which we compare with experimental micrographs of the same droplet. Finally, we draw our conclusions in Section 5.
2 Ray-tracing method including energy transport
In this section, we explicitly describe our ray-tracing method allowing a full reconstruction of the electric and magnetic fields inside the uniaxial birefringent medium. First, we will compute the polarisation basis of each transverse mode of the electric and magnetic fields. Second, we will derive the Hamiltonian ray-tracing equations for each of these modes. Third, we will derive simple equations for the transport of energy and the associated conservation laws allowing the computation of the amplitude of the transverse modes. Finally, we will present the details of our numerical implementation.2.1 WKB expansion and polarisation bases
We use the usual notation for the Maxwell fields: E and B for the electric and magnetic fields, and D = ε0εE for the displacement field. Here, ε0 (resp. μ0) is the permittivity (resp. permeability) of empty space and ε is the tensorial relative permittivity. As we will only consider uniaxial birefringent media, this tensor has the following expression:| ε = ε‖(n⊗n) + ε⊥(I − n⊗n), |
We assume that the fields oscillate at a single angular frequency ω and that the wavelength λ = 2πc/ω is much smaller than the typical length L over which ε varies in the plane orthogonal to the propagation axis.¶ Under these assumptions, the wave equation for the electric field3 can be put into the following form:
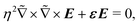 | (1) |
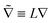 the dimensionless gradient.
the dimensionless gradient.
Since the smallness parameter appears in front of the derivative of highest order, the standard method for solving such an equation is the so-called Wentzel–Kramers–Brillouin (WKB) method.25 More precisely, we use the following asymptotic expansion for the electric field:
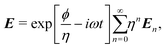 | (2) |
| LpE0 = 0, | (3) |
| LpE1 + DpE0 = 0, | (4) |
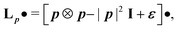 | (5) |
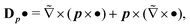 | (6) |
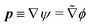 the dimensionless wave vector k/k0. As will become apparent later, eqn (3) allows one to calculate the direction of E0 and eqn (4) allows one to reconstruct the amplitude of E0. Note that eqn (4) also allows one to compute the first-order correction E1, but for simplicity's sake we will only keep the zeroth order term in the reconstructed electric field.
the dimensionless wave vector k/k0. As will become apparent later, eqn (3) allows one to calculate the direction of E0 and eqn (4) allows one to reconstruct the amplitude of E0. Note that eqn (4) also allows one to compute the first-order correction E1, but for simplicity's sake we will only keep the zeroth order term in the reconstructed electric field.
For now, let us examine the zeroth-order eqn (3). This equation admits a non-trivial solution if and only if the determinant of Lp is zero. After some algebra, we find that this condition is equivalent to the following equation:
| (|p|2 − ε⊥)(ε⊥|p|2 + εa[n·p]2 − ε‖ε⊥) = 0, |
We therefore retrieve the well-known eigenvalue equation for the ordinary and extraordinary modes in a uniaxial birefringent medium.1 In the following, we will indicate with an (o) index all quantities associated with the ordinary mode – which must fulfill the condition |p(o)|2 = ε⊥ – and with an (e) index all quantities associated with the extraordinary mode – which must fulfill the condition ε⊥|p(e)|2 + εa[n·p(e)]2 = ε‖ε⊥.
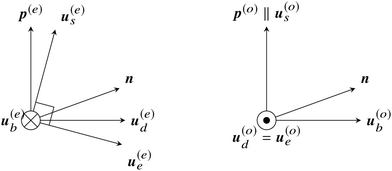
We can now easily obtain for each mode the polarisation states of E0, D0 and B0, as well as the direction of the Poynting vector S0 ≡ μ0E0 × B0. Let us define u(α)x ≡ X(α)0/|X(α)0|, with α = e or o and X0 = E0, D0, B0, or S0. We compute the expressions of the vectors u(α)x by writing that E0 must be in the kernel of Lp (cf.eqn (3)) and by developing the Maxwell equations at the lowest order in η. Since the fully covariant form of these vectors is a bit lengthy, we refer to Section S0 of the ESI† for the final result of this calculation. Here, we will simply mention that the expressions of these vectors only depend on the optical axis n, the dimensionless wave vectors p(e) and p(o), and the effective relative permittivity along the propagation axis ε(α) ≡ [p(α)·u(α)s]2 for the extraordinary (α = e) and ordinary (α = o) modes. The expressions of these effective relative permittivities are ε(o) ≡ ε⊥ and:
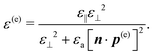 | (7) |
To summarize, we have obtained in this subsection the normalized directions of the electric, displacement, magnetic and Poynting fields in both extraordinary and ordinary eigenmodes. The orientation of these vectors is recapitulated in Fig. 1. Note that to fully reconstruct E, D, B and S at the lowest order in η using eqn (2), we still need to find a method to compute the scalar amplitude of these fields as well as the ψ(e) and ψ(o) fields (from which we can deduce the phase of the Maxwell fields and the renormalised wave vectors p(e) and p(o)). These two points are addressed in the next sections.
2.2 Hamiltonian flow and ray-tracing
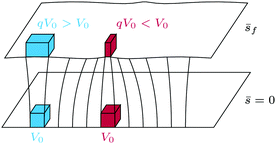
To reconstruct the eikonal functions ψ(e) and ψ(o), let us introduce the concept of a ray, defined as an integral curve (also called a field line) of the vector field u(e)s (extraordinary ray) or u(o)s (ordinary ray) – the directions in which the energy flows, since these vector fields correspond to the renormalised Poynting vector field associated with each eigenmode. Our strategy here is to compute a great number of these rays inside the sample by using ψ(e) (resp., ψ(o)) itself as the natural parametrisation for each extraordinary (resp., ordinary) ray. The trajectory of each ray is computed thanks to a Hamiltonian ray-tracing method|| similar to the method of Sluijter et al.,20 with two small improvements:• All the formulae presented below are in a covariant form, contrary to Sluijter's formulas which are expressed in the principal coordinate system of the birefringent system.
• Sluijter et al. derived the ray-tracing equations directly from the eigenvalue equation for p(e) and p(o), and then showed that these equations have a Hamiltonian form. Here, we prefer to directly derive the Hamiltonian formulation of these equations from the Fermat principle, which has the double advantage of making the link with the century-old theory of Fermat–Grandjean15 and showing that the natural parametrisation for this problem is the optical length ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) – the difference Δψ(α) (α = e or o) between the value of the eikonal function at the considered point and the value of the same function at the starting point of the ray (for simplicity's sake, we do not use an (e) or (o) index for
– the difference Δψ(α) (α = e or o) between the value of the eikonal function at the considered point and the value of the same function at the starting point of the ray (for simplicity's sake, we do not use an (e) or (o) index for ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) since it can be inferred from other terms in each equation).
since it can be inferred from other terms in each equation).
Since this derivation is quite technical, we refer to Section S1 of the ESI† for the full calculation, whose main result is the following expressions for the two Hamiltonian functions associated with extraordinary and ordinary rays:
In these definitions, r corresponds to the spatial position of a virtual bullet propagating along the ray and p is the conjugate moment of dr/d![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) , with
, with ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) the optical length defined above. Tracing a ray (i.e. computing its spatial trajectory) is fully equivalent to propagating the virtual bullet parametrized by r, which we will call the “end point of the ray” in the following.
the optical length defined above. Tracing a ray (i.e. computing its spatial trajectory) is fully equivalent to propagating the virtual bullet parametrized by r, which we will call the “end point of the ray” in the following.
The ray-tracing equations for the extraordinary rays are then simply obtained from the Hamilton equations associated with 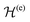 :
:
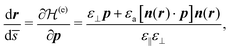 | (8) |
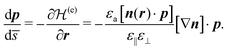 | (9) |
Similarly, the ray-tracing equations for the ordinary rays are obtained from the Hamilton equations associated with 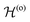 :
:
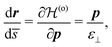 | (10) |
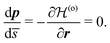 | (11) |
Note that we neglected a possible spatial dependence of the refractive indices in eqn (8)–(11). If taken into account, this dependence leads to additional terms in the equations for dp/d![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) . Although such terms are really not difficult to take into account in the numerical code, we will assume here for simplicity's sake that they are negligible.
. Although such terms are really not difficult to take into account in the numerical code, we will assume here for simplicity's sake that they are negligible.
Since it is shown in Section S1 of the ESI† that ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) can be directly identified with Δψ(e) or Δψ(o) depending on the type of ray, the eikonal functions can be calculated along the rays by directly integrating the ray-tracing equations (8)–(11), on the condition that a suitable set of initial conditions is given – the values of p(α) and ψ(α) (α = e or o) need to be specified on the surface defining the light source (i.e. the object of origin for all rays).
can be directly identified with Δψ(e) or Δψ(o) depending on the type of ray, the eikonal functions can be calculated along the rays by directly integrating the ray-tracing equations (8)–(11), on the condition that a suitable set of initial conditions is given – the values of p(α) and ψ(α) (α = e or o) need to be specified on the surface defining the light source (i.e. the object of origin for all rays).
2.3 Conservation laws along a ray
The last step to fully reconstruct the Maxwell fields is to find a way of computing the amplitudes of these fields at order 0 in the WKB expansion. This can be done by eliminating E1 from the first-order term in the WKB expansion of the wave equation (eqn (4)). To simplify this elimination process, we neglect all energy exchange between the extraordinary and ordinary modes. This corresponds to the so-called adiabatic regime, which in our formalism is equivalent to saying that E(e) and E(o) separately verify eqn (4):| Lp(α)E(α)1 + Dp(α)E(α)0 ≈ 0, α = e or o | (12) |
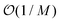 , where we defined the Mauguin number M = k0Δneff/qeff with
, where we defined the Mauguin number M = k0Δneff/qeff with 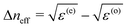 and qeff = {[u(o)s·∇]u(o)e}·u(o)b the effective twist of the polarisation vectors along the propagation axis.26 Neglecting all energy exchange between the extraordinary and ordinary modes is therefore equivalent to the condition M ≫ 1, which we will assume in the following.
and qeff = {[u(o)s·∇]u(o)e}·u(o)b the effective twist of the polarisation vectors along the propagation axis.26 Neglecting all energy exchange between the extraordinary and ordinary modes is therefore equivalent to the condition M ≫ 1, which we will assume in the following.
Using the fact that u(α)e is in the kernel of Lp(α), we can eliminate E(α)1 from eqn (12) by taking the scalar product of this equation with u(α)e. After some simplifications, we then find:
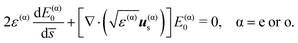 | (13) |
More specifically, we introduce the geometrical spreadings q(α) ≡ det[J(α)] associated with each collection of rays (α = e or o), where we defined the Jacobian matrices J(e) and J(o) as:
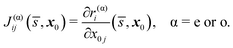 | (14) |
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,x0) and r(o)(
,x0) and r(o)(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,x0) correspond to the Lagrangian trajectories of the extraordinary and ordinary rays starting at x0 and computed from the ray-tracing equations of the previous section.
,x0) correspond to the Lagrangian trajectories of the extraordinary and ordinary rays starting at x0 and computed from the ray-tracing equations of the previous section.
The geometrical spreadings q(e) and q(o) obey the following differential equations:
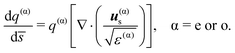 | (15) |
By combining the transport equations for E(α) and q(α) (eqn (13) and (15)) and by using the Leibniz formula for the divergence, we finally find the following conservation laws:
Assuming that the amplitudes E(e)0 and E(o)0 are specified on the reference surface defining the light source, one can directly compute the values of the conserved quantities
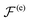 and
and 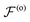 and then deduce E(e)0 and E(o)0 in the rest of the sample using the following equation:
and then deduce E(e)0 and E(o)0 in the rest of the sample using the following equation: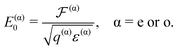 | (16) |
2.4 Details of the numerical implementation
In the last three sections, we presented all the equations necessary to reconstruct the polarisation state (Section 2.1), the eikonal function (Section 2.2) and the amplitude (Section 2.3) of the electric field at the lowest order in the WKB expansion. We now propose a numerical scheme allowing one to efficiently solve these equations.Our target system will consist of two parallel isotropic plates enclosing either a birefringent medium or a suspension of birefringent droplets in an isotropic fluid. Fig. 3 schematizes these two types of system. In each case, the light source corresponds to an incident plane wave below the sample.** The birefringent structure is specified by its orientational field n, which can be obtained from a theoretical model, a numerical simulation or an experiment. The field n is internally represented in our code as a C1 mapping using tricubic interpolation.27 Instead of copying by hand the general formula for the interpolation kernel (>300 lines of code), we automatically generated the associated C code with a symbolic calculation in Mathematica using the centered finite-difference approximation for the derivatives.
To propagate the rays across the sample, we define a target plane containing the current end points of all rays. This target plane is always parallel to the source plane and is moved in the upward direction e3 (see Fig. 3) by small increments. To fully reconstruct the electric and magnetic field in the bulk of the sample, we associate a 2D regular grid with the target plane and we use the following iterative procedure:
(A1) Initial setup of the rays on the source plane; the target plane is initially aligned with the source plane.
(A2) While the target plane has not reached the end of the sample, do the following steps:
(A2.1) Move the target plane with a small vertical increment and propagate the rays until they cross the new position of the target plane.
(A2.2) Reconstruct the electric and magnetic field at the new end points of the rays.
(A2.3) Interpolate the values of the electric and magnetic field on the regular grid associated with the target plane.
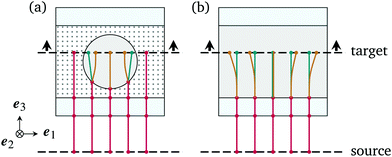
A detailed description of the steps (A1) and (A2.1–2.3) is available in Section S3 of the ESI.† Here, we will only mention two subtleties in our algorithm. First, each interface of discontinuity of the optical index produces reflected and transmitted rays, which means that the number of rays at each point of the sample is theoretically infinite. In our code, we only take into account transmitted rays propagating forward in the sample and apply the full Fresnel boundary conditions at each interface to update the amplitude, polarisation and phase of the rays. Second, the last step (A2.3) of the main loop of our algorithm is more complicated than it appears because the local value of the electric field at a point P of the target plane is obtained by summing all contributions from rays arriving at P. When deflection effects are important, several rays from the same family (extraordinary, ordinary or isotropic) can contribute to the local value of the electric field, as illustrated in Fig. 4. The surface separating the white domain (one-to-one correspondence between the source and target planes) from the red domain (multiple-to-one correspondence between the source and target planes) in Fig. 4 is called a caustic, and the red region itself is called a caustic domain. Reconstructing the full electric and magnetic fields inside caustic domains is challenging, but it can still be done efficiently and accurately when elementary caustic domains do not overlap (see Section S3.4 and Section S4 in the ESI†).
3 Validation of our method on a simple test case
In the previous section, we presented our improved ray-tracing method but did not examine the conditions of validity of such a method. We address this problem here by comparing the solution obtained with our method with a more exact solution obtained directly from Maxwell's equations with the finite-difference time-domain (FDTD) method. We first present the system on which this comparison is made, and then discuss our results.3.1 Numerical setup
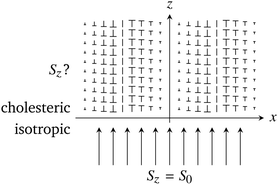
The simple system used in this study consists of an isotropic medium filling the lower half space z < 0 and an undeformed cholesteric helix texture filling the upper half space z > 0, with the helix axis oriented along the axis ex. A schematic representation of this system is visible in Fig. 5. The comparison between our ray-tracing method and FDTD was made on the z-component Sz of the time-averaged Poynting vector ℜ[μ0E × B*] inside the cholesteric domain, when the latter is illuminated from below by a plane-wave of constant intensity Sz = S0. The polarisation of incident light was set to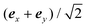 in order to generate both extraordinary and ordinary rays inside the cholesteric domain.
in order to generate both extraordinary and ordinary rays inside the cholesteric domain.
Since we assumed that the cholesteric texture is an undeformed helix oriented along ex, the director field can be expressed as:
| λ | P | n iso | n ⊥ | n ‖ |
|---|---|---|---|---|
| 0.5 μm | 20 μm | 1 | 1.45 | 1.55 |
The FDTD simulation was done with the open-source code Meep developed by MIT,16 which includes support for light propagation in inhomogeneous uniaxial media. We chose a spatial resolution Δf = λ/75 ≈ 6.7 nm and an associated time resolution T = Δf/(2c), which fulfills the Courant condition for FDTD in 3D28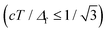 . We used periodic boundary conditions on the vertical boundaries (x = ± P/4) and perfectly-matched layer (PML) absorbing conditions on the top and bottom boundaries. We stopped the simulation after N = 20H/Δf = 6 × 108 integration steps (with H = P the length of the mesh in the z direction), which was sufficient to get good convergence for the time-averaged amplitude of the electric and magnetic fields. Note that the spatial resolution was not chosen randomly but in order to get an accurate solution near the cholesteric/isotropic interface. This was checked by directly comparing the computed solution with an analytical calculation of the Maxwell fields on each side of this interface.
. We used periodic boundary conditions on the vertical boundaries (x = ± P/4) and perfectly-matched layer (PML) absorbing conditions on the top and bottom boundaries. We stopped the simulation after N = 20H/Δf = 6 × 108 integration steps (with H = P the length of the mesh in the z direction), which was sufficient to get good convergence for the time-averaged amplitude of the electric and magnetic fields. Note that the spatial resolution was not chosen randomly but in order to get an accurate solution near the cholesteric/isotropic interface. This was checked by directly comparing the computed solution with an analytical calculation of the Maxwell fields on each side of this interface.
In the ray-tracing method, we used a total of 200 rays and 200 target points to reconstruct the Maxwell fields in the xz-plane. The target plane (which here corresponds to a line parallel to the x-axis, since we neglected the invariance axis y) was moved upward by increments Δr = 50 nm, which also correspond to the spatial resolution along the x axis (200 points over a length P/2 = 10 μm). We emphasize that with our choice of parameters, the rays are never leaving the computational domain, which allows us to easily calculate the Poynting vector everywhere inside the latter without having to resort to periodic boundary conditions on the vertical boundaries.
Finally, note that both methods were parallelised in order to benefit from the multiple CPU cores available on the simulation desktop computer. For the FDTD code Meep, the parallelisation was done using MPI (a distributed model with communication between the parallel processes). For our ray-tracing method, the parallelisation was done using OpenMP (a shared memory model without any communication between the threads) by evolving in parallel multiple rays.
3.2 Results and discussion
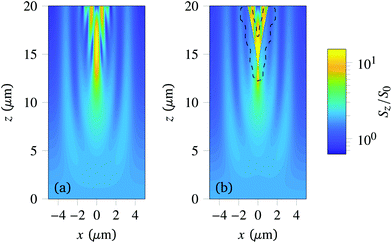
Fig. 6 shows two density plots of Sz/S0 computed with the FDTD method (Fig. 6a) and our ray-tracing method (Fig. 6b). The agreement between the two methods is visually very good, especially for the low-intensity elongated bands near the vertical boundaries of the computational domain. Note that the contrast of these bands is not due to an exchange of energy between the extraordinary and ordinary waves (which we neglected in Section 2.3), but is simply caused by interference between these two waves. This interference is possible because the polarisation of an extraordinary ray at a given point is not orthogonal to the polarisation of the associated ordinary ray at the same point (the directions of the wave vectors associated with both rays are different since we have taken into account ray deflection). Had we neglected the deflection of the extraordinary rays – as in the Jones method – no such interference would have been visible.However, some differences between the ray-tracing and FDTD method can be seen in the small region 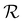 delimited by the black dashed line of Fig. 6. This region was numerically obtained by searching for all points where the relative error between the FDTD solution and ray-tracing solution was more than 25%. In this region, a sharp boundary between low and high intensity regions can be seen in the ray-tracing simulation, while the FDTD simulation is associated with a much smoother solution. This sharp boundary corresponds to a caustic, whose shape is similar to the one described schematically in Fig. 4. The sharp increase of intensity is due to an artificial divergence of the electric and magnetic field on the caustic itself, where the geometrical spreading q can be shown to become zero.24 Since no such divergence is present in the exact solution of Maxwell's equations, this means that our method is highly inaccurate near caustics – a problem which is common to all ray-based methods.24
delimited by the black dashed line of Fig. 6. This region was numerically obtained by searching for all points where the relative error between the FDTD solution and ray-tracing solution was more than 25%. In this region, a sharp boundary between low and high intensity regions can be seen in the ray-tracing simulation, while the FDTD simulation is associated with a much smoother solution. This sharp boundary corresponds to a caustic, whose shape is similar to the one described schematically in Fig. 4. The sharp increase of intensity is due to an artificial divergence of the electric and magnetic field on the caustic itself, where the geometrical spreading q can be shown to become zero.24 Since no such divergence is present in the exact solution of Maxwell's equations, this means that our method is highly inaccurate near caustics – a problem which is common to all ray-based methods.24
Nevertheless, the good agreement between our method and the FDTD method is quickly retrieved outside the domain 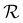 , whose extent is rather limited. This can be directly confirmed by looking at the horizontal and vertical profiles of the Sz/S0 field. Two such profiles are presented in Fig. 7. In these graphs, the intersection between the profile lines and the region
, whose extent is rather limited. This can be directly confirmed by looking at the horizontal and vertical profiles of the Sz/S0 field. Two such profiles are presented in Fig. 7. In these graphs, the intersection between the profile lines and the region 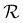 is represented by gray areas. At the center of these gray areas, the divergence of Sz can be clearly seen, while outside these gray areas, the curves associated with the ray-tracing solution quickly converge to the curves associated with the FDTD solution. In particular, good agreement is obtained inside the caustic domain (but sufficiently far from the caustic itself), where multiple extraordinary rays contribute to the local value of the Maxwell fields (as depicted in Fig. 4).
is represented by gray areas. At the center of these gray areas, the divergence of Sz can be clearly seen, while outside these gray areas, the curves associated with the ray-tracing solution quickly converge to the curves associated with the FDTD solution. In particular, good agreement is obtained inside the caustic domain (but sufficiently far from the caustic itself), where multiple extraordinary rays contribute to the local value of the Maxwell fields (as depicted in Fig. 4).
 | ||
Fig. 7 (a) Vertical profile of Sz/S0 over the line x = 0 μm. (b) Horizontal profile of Sz/S0 over the line z = 19.5 μm. The legend of (a) also applies for (b). The gray regions correspond to the intersection of the domain  of Fig. 6b with the profile line. of Fig. 6b with the profile line. | ||
Up until this point, all our results were associated with a transverse periodicity P/2 = 10 μm, as indicated in Table 1. Since this periodicity corresponds to the typical length over which the director field varies, the associated amplitude for the smallness parameter introduced in Section 2.1 is |η| ≡ πλ/P ≈ 0.15. To determine how the accuracy of our method varies with |η|, we reproduced the same numerical experiments as above with different values of pitch, while keeping the other parameters constant and using a scaled mesh of dimensions {P/2,P} in the {x,z} directions.
Whatever the value of the cholesteric pitch, we found that the typical lateral extent of the branches defining the domain  is always around 2λ–4λ, which means that our method allows us to localize the expansion error around the caustics, while keeping good convergence properties far from the caustics. In particular, we get an even better agreement with FDTD than in Fig. 6 and 7 when the cholesteric pitch is greater than 20 μm, because the meshes associated with these systems are much bigger than the wavelength – and therefore much bigger than the typical lateral extent of the high-inaccuracy region
is always around 2λ–4λ, which means that our method allows us to localize the expansion error around the caustics, while keeping good convergence properties far from the caustics. In particular, we get an even better agreement with FDTD than in Fig. 6 and 7 when the cholesteric pitch is greater than 20 μm, because the meshes associated with these systems are much bigger than the wavelength – and therefore much bigger than the typical lateral extent of the high-inaccuracy region 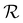 .
.
Conversely, the agreement between FDTD and ray-tracing becomes less satisfactory for small cholesteric pitches: when |η| ≡ πλ/P = 0.3, the mesh size becomes comparable to the lateral extent of the high-inaccuracy region, which means that the convergence error is becoming global. This critical point corresponds to a periodicity length of 5 μm, which corresponds here to ten times the wavelength. For even lower periodicity length, our method is not applicable anymore and a full solution of Maxwell's equations using FDTD must be envisioned.
On a similar line, we also noticed that the caustics were always appearing at a critical vertical position zc scaling linearly with the cholesteric pitch. This scaling can be theoretically explained by directly computing the analytical expression of zc for the system considered here:
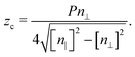 | (17) |
Finally, let us conclude this section by pointing out that our improved ray-tracing method is massively faster than the FDTD method. This can be directly checked by the running times of both methods. As a typical example, the running times associated with the results of Fig. 6 and 7 are 4 s for our method and around 1 h for FDTD. These running times were obtained on a state-of-the-art desktop computer (6 multithreaded cores cadenced at 3.5 GHz). Here, the high computational cost of FDTD is simply explained by the high density of the mesh necessary to get an accurate solution: the wavelength is much smaller than the typical size of our system, which means that a few millions of points are necessary if we impose a ratio of 75 vertices per wavelength. When a third dimension is added to the system (as in the next section), the computational cost of FDTD becomes prohibitive if the considered system is large. Since our method works well for these large systems (small expansion parameter η), it can be adopted as a replacement for FDTD.
4 Application to the visualisation of liquid crystal droplets
In this section, we show how our method is able to predict the bright-field optical micrographs (BFOMs) of liquid crystal droplets as observed under a microscope when using unpolarised light without any polariser and analyser – something that the Jones method is unable to address. We first detail the experimental and numerical setup used, and then present and discuss our results.4.1 Experimental setup
We focused on one particular type of liquid crystal droplet, namely twisted bipolar droplets obtained at the thermodynamic coexistence between the nematic and isotropic phase. Twisted bipolar droplets are characterised by their planar anchoring (the molecules prefer to align parallel to the surface of the droplet), the existence of two diametrically opposed topological defects of rank +1 (in agreement with the Poincaré–Hopf theorem applied to a sphere), and a double twist internal structure for the director field of the droplet. This last characteristic can be experimentally induced either by using a cholesteric liquid crystal (in which case the director field has a spontaneous twist of fixed handedness) or an achiral nematic liquid crystal in which twist elastic deformations cost a negligible amount of free energy in comparison to splay and/or bend elastic deformations34 (in which case the director field prefers to be twisted in order to decrease the energy of the surface defects). In the latter case, the twist can be left-handed or right-handed with a 50/50 probability since it is due to energetically-induced spontaneous symmetry breaking in an achiral system.In our experiment, we exploited this spontaneous symmetry breaking by using a lyotropic chromonic suspension of Sunset Yellow FCF (SSY) in water with a mass fraction 29 wt%. In confined geometries filled with this mixture – such as the droplets studied here – a twist can be observed because of the giant elastic anisotropy of SSY suspensions, as reported by several authors.35–38 The protocol to prepare the sample and create twisted bipolar droplets was already described in a previous article.38 Briefly, an aqueous suspension of SSY was contained between two parallel glass plates separated by nylon wires of calibrated diameter 110 μm. The glass plates of the sample were spin-coated beforehand with polyvinyl alcohol (PVA) and annealed at 120 °C in order to favor wetting of the sample plate by the isotropic phase of the SSY suspension. Once filled, the sample was sealed with UV glue and sandwiched by two transparent ovens separately regulated within 0.01 °C. A detailed description of these ovens is available in ref. 39. Note that two thin layers of glycerol were added between the sample and the ovens in order to improve the thermal contact.
The sample was observed through the objective of a Leica microscope under bright-field illumination conditions (halogen lamp producing unpolarised white light, Köhler illumination setup allowing us to uniformly light the sample, no polariser and analyser). Note that the condenser diaphragm of the microscope was closed as much as possible in order to get normal illumination on the sample (which is assumed in our numerical method). The temperatures of the ovens were adjusted to be inside the coexistence range between the nematic and isotropic phase of the SSY sample. Thanks to the surface treatment of the sample plate, the nematic domains dewetted the walls and formed droplets in the bulk of the sample. The radius of the observed droplets was then adjusted to be typically R ≈ 25 μm by changing the temperature of the ovens while staying inside the coexistence range. By setting slightly different temperatures for the top and bottom ovens, we noticed that the droplets forming in the sample only have two possible orientations: parallel or orthogonal to the induced vertical temperature gradient. We chose to focus only on droplets with the polar axis orthogonal to the view direction by centering the sample stage appropriately.
Optical micrographs of the droplets were captured thanks to a CCD camera (C4742, Hamamatsu). Note that the incident unpolarised light was filtered using a red bandpass filter (λ ≈ 633 nm) in order to optimize the contrast of the micrographs. Since our goal is to study light deviation effects in the droplets, we systematically saved for each micrograph the vertical shift of the sample stage with respect to a reference position where the droplet is well-focused.
4.2 Numerical setup
The first step to numerically reconstruct the optical micrographs of the twisted bipolar droplets was to compute the director field associated with the observed SSY droplets. This was done using a trust-region finite-element minimisation (TR-FEM) of the total free energy of a spherical droplet with R = 25 μm. The details of this algorithm are given in another paper.12 Briefly, we assume that the anchoring strength at the nematic/isotropic interface is finite, which implies that the polar defects of the twisted bipolar droplets are only virtual (i.e. the Frank elastic energy stays finite near these defects). This allows us to neglect variations of the scalar order parameter and write the total free energy F[n] of the droplet as:| F[n] = Ff[n] + Fs[n] |
Here, la = K1/Wa is the anchoring length and Wa is the anchoring strength. Our TR-FEM algorithm allows us to iteratively minimize a discretised version of F[n] with finite elements using an efficient null space factorisation of the gradient and Hessian of the free energy and a robust calculation of the solution update which always decreases the energy and converges quadratically near a minimum of F[n]. We applied this algorithm to the case of SSY droplets by using the values of the material constants given in Table 2. The resulting director field, obtained on a mesh with approximately 2 × 106 vertices, is presented in Fig. 8.
| K 2/K1 | K 3/K1 | K 4/K1 | l a | λ |
|---|---|---|---|---|
| 0.161 | 1.43 | 0.58 | 3 μm | 633 nm |
| n glass | n glycerol | n water | n iso | n ⊥ | n ‖ |
|---|---|---|---|---|---|
| 1.52 | 1.47 | 1.33 | 1.43 | 1.47 | 1.41 |
Once the director field was computed, we used it in our ray-tracing code to propagate light through the system described in the previous section, including all the isotropic layers associated with the transparent ovens and the sample plates. Since we are only interested in the final micrographs and not in the bulk data of the Maxwell fields, we skipped step (A2.3) of our algorithm (see Section 2.4) and simply propagated forward the rays through the system using the values of the material constants in Table 2.
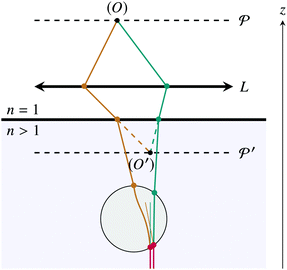
Under a real microscope, optical micrographs are obtained by propagating light through the objective to the final screen (here, the CCD image sensor). In our numerical method, we assume that the objective can be represented by an ideal lens, in which case the final screen 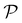 is conjugated through the lens to a virtual plane
is conjugated through the lens to a virtual plane 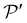 , which we call the back-focal plane. These planes are schematised in Fig. 9. Since we assumed that the lens is ideal, the final intensity field on the plane
, which we call the back-focal plane. These planes are schematised in Fig. 9. Since we assumed that the lens is ideal, the final intensity field on the plane 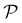 is perfectly equivalent (with a scaling transformation) to the intensity field on the virtual plane
is perfectly equivalent (with a scaling transformation) to the intensity field on the virtual plane 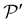 , which can be obtained by propagating backward the output rays as if the whole space was filled with air (dashed trajectories in Fig. 9). For this reason, we calculated the optical micrographs by combining all contributions of the ray families on the back-focal plane after propagating the rays forward through the system and backward to the virtual plane
, which can be obtained by propagating backward the output rays as if the whole space was filled with air (dashed trajectories in Fig. 9). For this reason, we calculated the optical micrographs by combining all contributions of the ray families on the back-focal plane after propagating the rays forward through the system and backward to the virtual plane 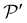 . Since an input polarisation must be specified in our method, the final BFOM is obtained by averaging incoherently the simulated POMs over all possible input polarisations.
. Since an input polarisation must be specified in our method, the final BFOM is obtained by averaging incoherently the simulated POMs over all possible input polarisations.
4.3 Results and discussion
A few observed and simulated BFOMs are presented in Fig. 10a and b for different vertical positions of the back-focal plane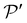 . The same contrast setting (Sz/S0 between 0.5 and 1.5) was applied to all micrographs for ease of comparison. As can been seen, the simulated micrographs correctly predict the existence of the almond-shaped high intensity region at the center of the droplet, which opens up and expands when the back-focal plane is moved upward. Let us remark that our first attempt to simulate the BFOMs of Fig. 10 was unsuccessful because we initially neglected the presence of all the additional isotropic layers associated with the sample plates and the transparent ovens of the experimental setup: in this simplified situation, the simulated micrographs were much more uniform (inexistent almond-shaped high intensity region) and therefore very different from the observations. The fact that the micrographs have a much sharper contrast when including the isotropic layers in the simulation can be interpreted as an amplification of the deflection effects on the back-focal plane
. The same contrast setting (Sz/S0 between 0.5 and 1.5) was applied to all micrographs for ease of comparison. As can been seen, the simulated micrographs correctly predict the existence of the almond-shaped high intensity region at the center of the droplet, which opens up and expands when the back-focal plane is moved upward. Let us remark that our first attempt to simulate the BFOMs of Fig. 10 was unsuccessful because we initially neglected the presence of all the additional isotropic layers associated with the sample plates and the transparent ovens of the experimental setup: in this simplified situation, the simulated micrographs were much more uniform (inexistent almond-shaped high intensity region) and therefore very different from the observations. The fact that the micrographs have a much sharper contrast when including the isotropic layers in the simulation can be interpreted as an amplification of the deflection effects on the back-focal plane  due to light refraction at the boundaries of the isotropic layers (see Fig. 9).
due to light refraction at the boundaries of the isotropic layers (see Fig. 9).
Although the agreement between the simulated and observed BFOMs is good, some discrepancies are clearly visible, especially outside the droplet and near its boundary. First, it is easy to see that the simulated interference rings outside the droplet are thicker and of higher contrast than in the experimental images. This discrepancy is probably due to the fact that we neglected all reflected rays on the boundary of the droplet. Second, optical artefacts are visible near the polar defects (left and right side of the droplet) when Δz < 0 in Fig. 10. These artefacts are associated with the presence of caustics, where the reconstructed Maxwell fields are highly inaccurate as shown in the previous section. Last, the crescent-shaped high intensity regions visible in the experimental micrographs when Δz > 0 are much thinner in the simulated micrographs. This discrepancy is not due to the presence of caustics (which can be directly checked in our result files by counting the number of rays arriving at one point of the micrograph); the most likely source of error is that the effective birefringence Δneff introduced in Section 2.3 is vanishingly small near the boundary of the droplet, where the director is almost parallel to the propagation axis. This implies that one of the main assumptions of our code (Mauguin number much bigger than 1) is broken near the droplet boundary, which explains the difference between the simulated and observed BFOMs near the crescent-shaped high intensity regions described above.
Nevertheless, we checked that the Mauguin number is reasonably high enough (≥10) at the center of the droplet and that the WKB expansion parameter |η| ≈ 1/(2k0R) is small enough (∼0.002), which explains why our ray-tracing method is robust enough to qualitatively predict the correct alternation of dark and bright bands in all micrographs. It should be noted that additional insight into the structure of the micrographs can be obtained by looking at the deflection maps of the extraordinary and ordinary rays, defined as the difference Δr(α) between the actual end point of a ray r(α) (α = e or o) and the virtual end point which would be obtained if there were no deflection of this ray. These deflection maps are plotted in the two bottom rows of Fig. 10. The ordinary deflection map always has rotational symmetry (which is expected since the ordinary index is constant inside the spherical droplet) and points outward for Δz < 0 and inward for Δz > 0, which explains the presence of interference rings outside the droplet when Δz < 0 and the dark bands near the boundary of the droplet when Δz > 0. The extraordinary deflection map has C2 symmetry (as expected because of the bipolar and twisted nature of the director field) and points inward for Δz < 0 and outward for Δz > 0, which explains why the almond-shaped high intensity region opens up and expands when Δz increases. Finally, we should clarify exactly what we meant by a “well-focused droplet” when defining the reference position of the back focal plane  (Δz = 0 in Fig. 10): here, “well-focused” simply means that the average deflection amplitude of the ordinary rays is minimal (as can be visually checked in Fig. 10d).
(Δz = 0 in Fig. 10): here, “well-focused” simply means that the average deflection amplitude of the ordinary rays is minimal (as can be visually checked in Fig. 10d).
5 Conclusion
To summarize, we presented an improved ray-tracing method allowing one to fully reconstruct the phase, polarisation and amplitude of the optical field inside a uniaxial birefringent medium. We demonstrated that this method is extremely fast in comparison to a full resolution of Maxwell's equations, and showed that the calculated solutions are accurate far from caustics, which only formed when the sample thickness is greater than a critical value. Finally, we showed how our method can be used to simulate bright-field optical micrographs of birefringent samples as seen under a microscope, with good agreement with experimental micrographs. Our method is thus able to address one of the main limitation of the Jones method, namely the inability to take into account ray deflection and simulate light propagation under bright-field illumination conditions. Contrary to the numerical methods mentioned in Section 1 (finite difference time domain, beam propagation method, eikonal differential equation…), our method is also able to support complex setups with thick isotropic layers. The main reason for this is that we do not have to solve a set of partial differential equations, we only have to propagate rays and reconstruct the electric fields along these rays.Note that the simplicity and effectiveness of our method are largely due to the fact that we neglected any exchange of energy between the extraordinary and ordinary modes. This assumption is only valid if the Mauguin number is much bigger than 1. As discussed in Sections 3 and 4, this was mainly the case for the systems studied here. In the future, it would be interesting to further improve our numerical method by relaxing this assumption and deriving general transport equations for the amplitude of the extraordinary and ordinary modes outside the adiabatic regime. Such a generalised method could then be applied to highly chiral birefringent systems, in which the twist of the polarisation is non-negligible everywhere in the sample.
On a parallel note, although our method was mainly applied to the calculation of optical micrographs, one could imagine a number of other applications. For example, our method could be used to analyze the diffraction patterns of the LC-based diffraction gratings mentioned in the introduction, by setting the final target plane of our method to the output plane of the LC layer, and then applying the usual far-field formula. The optical properties of flat LC diffractive lenses40 could also be analyzed either by using the ray trajectories computed by our method or by using the reconstructed fields on the output surface of the LC layer.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors warmly thank P. Oswald for giving access to the experimental setup used in this paper. Funding is acknowledged from the ARSS (Javna Agencija za Raziskovalno Dejavnost RS) through grants P1-0099 and L1-8135, and from the European Union's Horizon 2020 programme through the Marie Skłodowska-Curie grant agreement No. 834256.References
- P. Oswald and P. Pieranski, Nematic and cholesteric liquid crystals: concepts and physical properties illustrated by experiments, CRC Press, 2006 Search PubMed.
- P. Oswald and P. Pieranski, Smectic and columnar liquid crystals: concepts and physical properties illustrated by experiments, CRC Press, 2006 Search PubMed.
- I.-C. Khoo, Liquid crystals: physical properties and nonlinear optical phenomena, Wiley-Interscience, Hoboken, N.J., 2nd edn, 2007 Search PubMed.
- M. Humar, M. Ravnik, S. Pajk and I. Muševič, Nat. Photonics, 2009, 3, 595–600 CrossRef CAS.
- P. J. Ackerman, Z. Qi, Y. Lin, C. W. Twombly, M. J. Laviada, Y. Lansac and I. I. Smalyukh, Sci. Rep., 2012, 2, 414 CrossRef PubMed.
- I. Nys, K. Chen, J. Beeckman and K. Neyts, Adv. Opt. Mater., 2018, 6, 1701163 CrossRef.
- M. Jiang, H. Yu, X. Feng, Y. Guo, I. Chaganava, T. Turiv, O. D. Lavrentovich and Q.-H. Wei, Adv. Opt. Mater., 2018, 1800961 CrossRef.
- Y. Tabe and H. Yokoyama, Langmuir, 1995, 11, 699–704 CrossRef CAS.
- I. Smalyukh, Mol. Cryst. Liq. Cryst., 2007, 477, 23–41 CrossRef CAS.
- T. Lee, R. P. Trivedi and I. I. Smalyukh, Opt. Lett., 2010, 35, 3447–3449 CrossRef CAS PubMed.
- M. Ravnik and S. Žumer, Liq. Cryst., 2009, 36, 1201–1214 CrossRef CAS.
- G. Poy, F. Bunel and P. Oswald, Phys. Rev. E, 2017, 96, 012705 CrossRef PubMed.
- G. Posnjak, S. Čopar and I. Muševič, Sci. Rep., 2016, 6, 26361 CrossRef CAS PubMed.
- U. Mur, S. Čopar, G. Posnjak, I. Muševič, M. Ravnik and S. Žumer, Liq. Cryst., 2017, 44, 679–687 CrossRef CAS.
- F. Grandjean, Bull. Soc. Fr. Mineral., 1919, 42, 42 Search PubMed.
- A. F. Oskooi, D. Roundy, M. Ibanescu, P. Bermel, J. Joannopoulos and S. G. Johnson, Comput. Phys. Commun., 2010, 181, 687–702 CrossRef CAS.
- A. Joets and R. Ribotta, Opt. Commun., 1994, 107, 200–204 CrossRef.
- J. A. Kosmopoulos and H. M. Zenginoglou, Appl. Opt., 1987, 26, 1714 CrossRef CAS PubMed.
- H. M. Zenginoglou and J. A. Kosmopoulos, Appl. Opt., 1989, 28, 3516 CrossRef CAS PubMed.
- M. Sluijter, D. K. G. de Boer and J. J. M. Braat, J. Opt. Soc. Am. A, 2008, 25, 1260 CrossRef PubMed.
- M. Sluijter, D. K. de Boer and H. P. Urbach, J. Opt. Soc. Am. A, 2009, 26, 317 CrossRef PubMed.
- G. D. Ziogos and E. E. Kriezis, Opt. Quantum Electron., 2008, 40, 733–748 CrossRef CAS.
- G. Panasyuk, J. Kelly, E. C. Gartland and D. W. Allender, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041702 CrossRef CAS PubMed.
- O. Runborg, Commun. Comput. Phys., 2007, 2, 827–880 Search PubMed.
- R. B. Dingle and R. Dingle, Asymptotic expansions: their derivation and interpretation, Academic Press, London, 1973, vol. 48 Search PubMed.
- H. L. Ong, J. Appl. Phys., 1988, 64, 614–628 CrossRef CAS.
- F. Lekien and J. Marsden, Int. J. Numer. Meth. Eng., 2005, 63, 455–471 CrossRef.
- A. Taflove and S. C. Hagness, Computational electrodynamics: the finite-difference time-domain method, Artech house, 2005 Search PubMed.
- S. Zhou, Y. A. Nastishin, M. M. Omelchenko, L. Tortora, V. G. Nazarenko, O. P. Boiko, T. Ostapenko, T. Hu, C. C. Almasan, S. N. Sprunt, J. T. Gleeson and O. D. Lavrentovich, Phys. Rev. Lett., 2012, 109, 037801 CrossRef PubMed.
- J. Nehring and A. Saupe, J. Chem. Phys., 1971, 54, 337–343 CrossRef CAS.
- S. Faetti and V. Palleschi, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 3241 CrossRef CAS.
- M. Rubin, Sol. Energy Mater., 1985, 12, 275–288 CrossRef CAS.
- J. Rheims, J. Köser and T. Wriedt, Meas. Sci. Technol., 1997, 8, 601–605 CrossRef CAS.
- R. D. Williams, J. Phys. A: Math. Gen., 1986, 19, 3211 CrossRef.
- L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163–5168 CrossRef CAS PubMed.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742–1747 CrossRef CAS PubMed.
- K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6, 8067 CrossRef CAS PubMed.
- J. Ignés-Mullol, G. Poy and P. Oswald, Phys. Rev. Lett., 2016, 117, 057801 CrossRef PubMed.
- P. Oswald and A. Dequidt, Phys. Rev. Lett., 2008, 100, 217802 CrossRef PubMed.
- P. Valley, D. L. Mathine, M. R. Dodge, J. Schwiegerling, G. Peyman and N. Peyghambarian, Opt. Lett., 2010, 35, 336–338 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The code of the numerical method presented in this article will be publicly disseminated mid-2019 as part of a general platform for light propagation in LCs. See DOI: 10.1039/c8sm02448k |
| ‡ In the Jones method, only the polarisation state of light changes along the rays. This implies that the Jones method will always predict a transmission of 1 in bright-field microscopy. |
| § Note that for the beam propagation method, the memory cost can still be acceptable since the propagation can be done layer by layer in the propagation direction z (only two-dimensional arrays are therefore kept in the computer memory); but for propagation distance >1 mm, this method still takes a lot of time since a great number of steps in the z-direction are needed. |
| ¶ This length can be rigorously defined as L = ‖ε‖∞/‖∇⊥ε‖∞, with ∇⊥ the gradient in the plane orthogonal to the propagation axis and ‖T‖∞ the maximum value of any component of a tensor field T. |
| || Usually, ray-tracing is done by solving the Euler–Lagrange equation of a minimization problem15 (i.e. by using the Lagrangian formalism). Here, we prefer to use Hamiltonian dynamics because the involved expressions are much simpler and easier to solve numerically. |
| ** Note that our method can support more complicated light sources such as a Gaussian beam or a tilted plane wave. For these general light sources, the initialization is however a bit more complicated since one needs to specify inhomogeneous distributions on the source plane for the eikonal functions, rescaled wavevectors and initial amplitudes. |
| This journal is © The Royal Society of Chemistry 2019 |