Open Access Article
Open Access ArticleVolume-controlled cavity expansion for probing of local elastic properties in soft materials
Shabnam
Raayai-Ardakani
 a,
Zhantao
Chen
b,
Darla Rachelle
Earl
a and
Tal
Cohen
a,
Zhantao
Chen
b,
Darla Rachelle
Earl
a and
Tal
Cohen
 *ab
*ab
aDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA, USA. E-mail: talco@mit.edu
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA, USA
First published on 3rd December 2018
Abstract
Cavity expansion can be used to measure the local nonlinear elastic properties in soft materials, regardless of the specific damage or instability mechanism that it may ultimately induce. To that end, we introduce a volume-controlled cavity expansion procedure and an accompanying method that builds on the Cavitation Rheology technique [J. A. Zimberlin et al., Soft Matter, 2007, 3, 763–767], but without relying on the maximum recorded pressure. This is achieved by determining an effective radius of the cavity that is based on the volume measurements, and is further supported by numerical simulations. Applying this method to PDMS samples, we show that it consistently collapses the experimental curves to the theoretical prediction of cavity expansion prior to the occurrence of fracture or cavitation, thus resulting in high precision measurement with less than 5% of scatter and good agreement with results obtained via conventional techniques. Moreover, since it does not require visual tracking of the cavity, this technique can be applied to measure the nonlinear elastic response in opaque samples.
1 Introduction
The ability to accurately measure the elastic properties of soft and biological materials can significantly advance our understanding of their mechanical behavior and can be applied in diagnostic applications to distinguish between healthy and diseased tissue. Elastic properties of biological materials are defined by the hierarchical organization in the tissue, hence they can be directly influenced by pathological changes or disease.1,2 Previous research has shown that changes in stiffness can indicate various diseases such as cancer,3,4 atherosclerosis,5–8 fibrosis,9 and glaucoma.10,11 Thus, imaging based methods such as elastography have been previously introduced and used to measure the elastic modulus of soft tissues in vivo.12,13 While such methods are able to qualitatively differ between stiff and soft regions in a tissue, which can be used comparatively, they are not able to produce reliable quantitative measures.14,15Indentation has also been employed for measuring the elastic properties of soft materials.2,3,15 In this method the sample is placed under an indenter and the displacement under an applied force is measured. Then, using the relationship between the displacement of the body under indenters of different shapes and the total applied force (found theoretically or through finite element modeling), the elastic modulus of the material is extracted.2,3,15–17 However, such methods usually require the material to be removed from its natural environment.
Tensile testing also requires the specimen to be cut or prepared in specific shapes. While this is easily applicable to metals and hard plastics, it becomes a tedious task in the case of soft and biological materials and results in limited reproducibility. Moreover, when it comes to biological organs and tissue, such tests would require pieces to be cut, not only damaging the tissue but also removing and testing the piece in an environment different from its habitat, thus affecting its elastic response.18 This heavily limits the capability of the current mechanical testing to be effectively used as a diagnostics tool for bio-medical researchers, medical professionals, or even to obtain quantitative measures to correlate with elastography tests.
To remedy this limitation, inspired by the cavitation phenomenon and the accompanying theory, Crosby and co-workers18–24 have developed the method of Cavitation Rheology (CR) to measure the elastic modulus and the surface energy of soft nonlinear materials and have demonstrated its applicability for various gels, biological materials, and even for single cells.24 In this method, by pressure-controlled inflation, a cavity is expanded at the tip of a needle. Through this inflation process, the pressure inside the cavity reaches a maximum that theoretically corresponds to the predicted cavitation instability limit, which can be used to determine the elastic modulus.18–23 This method has been successfully applied for measuring the elastic properties of biological tissue in vivo and, in particular, for the case of vitreous inside an eye. While reporting on the differences in the elastic modulus of the cortex and the nucleus, it was shown that removing the vitreous from the eye results in a reduction of the elastic modulus.18,22
Despite its success in the case of the vitreous and other soft and biological materials, in several instances the CR technique results in fracture of the sample prior to reaching the cavitation instability limit. Hashemnejad and Kundu25 have previously attempted to theoretically explain their experimental results in polymers that exhibit such failure, however they report questionably large surface energies. In a separate study, Pavlovskly et al.26 have performed CR experiments on poly(ethylene oxide) (PEO) mixed in water (at various weight ratios) and show that for the CR results to be comparable to results extracted from conventional rheometry techniques, a correction factor in the range 0.7–1.9 is required. Therefore, with materials that fracture before reaching the cavitation instability, it is difficult to obtain quantitative measures. Moreover, it cannot be determined a priori which expansion mechanism (i.e. elastic or crack propagation) the material is going to follow. Nonetheless, considering the simplicity of the CR method that can be applied in vivo and the availability of theoretical models of the material response in cavity expansion, it is still of interest to be able to use the CR technique as a method of measuring the local material properties, especially the elastic modulus. Thus, in this work, we explore a volume-controlled CR technique to precisely measure the local elastic properties of soft materials, from gathered pressure–volume results prior to the cavitation or fracture of the sample.
The paper is organized as follows: in Section 2 we present a summary of observations made using the conventional CR technique, followed by a theoretical formulation in Section 3. Next, in Section 4 we explain the experimental setup for our custom-designed volume-controlled CR method and the calibration technique used to measure the pressure–volume results from the raw data collected. In Section 5, we propose a method for analyzing the results which allows us to find the elastic properties of the samples by introducing an effective length scale of the cavity and fitting the appropriate constitutive model to the experimental results. Then in Section 6 we present the results of the experiments performed on PDMS samples with various degrees of base to cross-linker ratios and the elastic properties extracted using the proposed analysis. Lastly, in Section 7 we summarize the key points of this work.
2 Observations
With a custom designed CR setup (which will be discussed in detail in Section 4), we have performed quasi-static volume controlled experiments on PDMS samples of varying base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios, where the magnitude of the gauge pressure, and volume of the injected fluid are recorded as a function of time. For example the results of the case of a PDMS sample with 44
cross-linker ratios, where the magnitude of the gauge pressure, and volume of the injected fluid are recorded as a function of time. For example the results of the case of a PDMS sample with 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base
1 base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
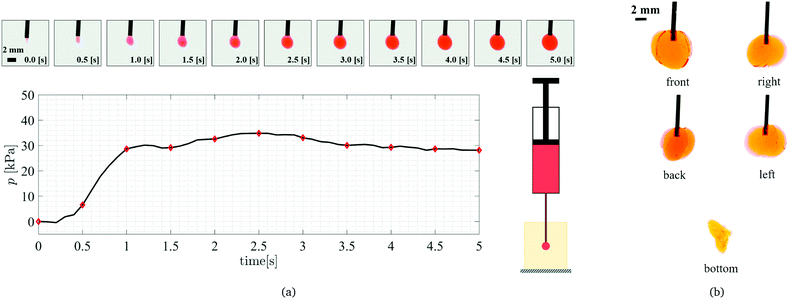
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratio are shown in Fig. 1a in the form of pressure as a function of time (volume change is linear with time). In addition, snapshots of the cavity at different time instances (every half a second) are shown above the figure (working fluid is dyed red to be distinguished from the transparent sample). Notice in the first snapshot (t = 0 s) an initial incision is already apparent; its shape and size are dependent on the experimental execution, and on the needle properties. In the beginning, as the cavity is filled (without any form of elastic expansion), no pressure change is recorded inside the cavity, however, after ∼0.2 s the initial cavity is fully filled and the additional injected volume will result in an increase of pressure inside the cavity. While, it is theoretically expected that the pressure monotonically increases up to a peak value, we notice that the pressure follows a non-monotonic and non-smooth path, with multiple local maxima visible in the results. This makes it difficult to choose an apparent maximum to compare with the maximum in the theory, as done in the conventional CR technique.
cross-linker ratio are shown in Fig. 1a in the form of pressure as a function of time (volume change is linear with time). In addition, snapshots of the cavity at different time instances (every half a second) are shown above the figure (working fluid is dyed red to be distinguished from the transparent sample). Notice in the first snapshot (t = 0 s) an initial incision is already apparent; its shape and size are dependent on the experimental execution, and on the needle properties. In the beginning, as the cavity is filled (without any form of elastic expansion), no pressure change is recorded inside the cavity, however, after ∼0.2 s the initial cavity is fully filled and the additional injected volume will result in an increase of pressure inside the cavity. While, it is theoretically expected that the pressure monotonically increases up to a peak value, we notice that the pressure follows a non-monotonic and non-smooth path, with multiple local maxima visible in the results. This makes it difficult to choose an apparent maximum to compare with the maximum in the theory, as done in the conventional CR technique.
To evaluate the applicability of the conventional CR technique we apply the method to PDMS samples of different base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
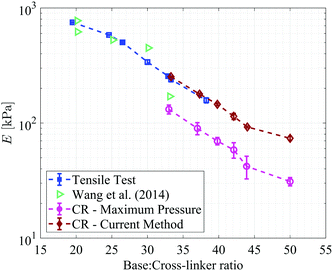
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios and compare them with results of tensile test measurements (with dog-bone shaped specimens mounted on an Instron universal testing machine) and with values reported in literature.27 As seen in Fig. 2, the CR technique (analyzed using the maximum recorded pressure) consistently measures an elastic modulus lower than the results measured via tensile testing. In addition, scatter in the measurements of the maximum pressure leads to rather large error bars on the figure.
cross-linker ratios and compare them with results of tensile test measurements (with dog-bone shaped specimens mounted on an Instron universal testing machine) and with values reported in literature.27 As seen in Fig. 2, the CR technique (analyzed using the maximum recorded pressure) consistently measures an elastic modulus lower than the results measured via tensile testing. In addition, scatter in the measurements of the maximum pressure leads to rather large error bars on the figure.
 | ||
| Fig. 2 Comparison between the elastic moduli of PDMS samples measured using the CR analysis proposed in this paper and the results of conventional CR method (denoted by circles), tensile measurements, and previous work reported by Wang and coworkers.27 Results of the current method are discussed in Section 6. | ||
Due to the non-smooth and non-monotonic behavior, it is also not clear whether the cavity growth is solely due to the elastic expansion (as predicted by the cavitation theory), or if it involves irreversible processes, such as crack propagation.28,29 Although the snapshots of the cavity expansion suggest that the cavity is expanding in a nearly spherical shape, snapshots of the final cavity shape taken from 5 different sides of the sample (as shown in Fig. 1b) clearly show that the expansion is due to a combination of fracture and elastic expansion.
Ultimately, we aim to design a technique to extract the constitutive response of the material without relying on the visual tracking of the cavity expansion process. Based on these observations, we find that to be able to consistently do so, we must eliminate issues related to the specific execution of the experiments and the initial incision. Additionally, it is desirable to use the pressure–volume curves without a priori assumption on the instability mechanism.
3 Theoretical formulation
Based on our observations, we seek to determine the material properties by employing a method that is not based on the cavitation instability limit. Therefore, we are interested in studying the mechanical response prior to its occurrence.Although cavitation literature often considers an unbounded body, for the practical application considered here we aim to determine the influence of the dimension of the body and the initial cavity size. The geometry of a finite body undergoing spherically symmetric expansion is illustrated in Fig. 3a. The radial coordinate in the initial and deformed configurations is defined by R and r, respectively. The corresponding inner and outer radii of the body in the undeformed and deformed configurations are A, B and a, b, respectively. The circumferential stretch is λθ = λϕ = r/R and we denote its value at the cavity wall by λ = a/A.
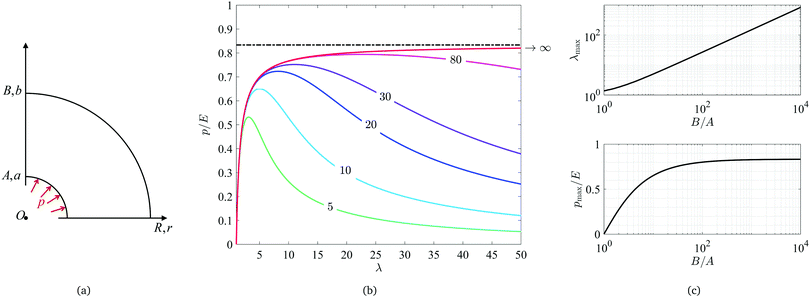 | ||
| Fig. 3 (a) Schematic illustration of the cavity expansion problem. (b) Curves of pressure as a function of stretch calculated using eqn (2) and (6) with different radii ratios B/A. In this plot pressure is normalized by the elastic modulus and the dashed line shows the asymptotic limit for the case of infinitely large geometries. (c) The maximum pressure pmax and the corresponding stretch λmax at onset of the instability for varying B/A values. | ||
Limiting our attention to incompressible materials, we can write the radial stretch λr = λθ−2. Additionally, for any spherical sub-region incompressibility implies r3 − a3 = R3 − A3, which for the entire body reads
| b3 − a3 = B3 − A3. | (1) |
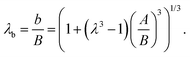 | (2) |
Now, considering a material whose response is modeled by an arbitrary free energy density function W = Ŵ(λr,λθ,λϕ), which is written here as a function of the principal stretch components, pressure applied at the cavity wall is readily derived in the integral form
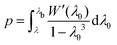 | (3) |
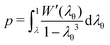 | (4) |
In the present work we will demonstrate our technique using the noe-Hookean model, since it is found to be well suited to capture the response of PDMS. Nonetheless, any alternative constitutive response can be considered. Several such solutions are available in the literature for both quasi-static and dynamic expansion. Some example are; Mooney–Rivlin (compressible and incompressible),30,31 power law,32 Blatz-Ko,33 elastoplastic,34–37 generalized Varga material,38 composite and anisotropic nonlinear materials,39–41 viscoelastic,42 and porous elastoplastic.43
Although our formulation applies for any hyperelastic constitutive relation, our analysis of the technique, presented in Sections 5 and 6, has been conducted for a family of materials whose response can be determined by a single elastic coefficient. If multiple material coefficients need to be determined from the cavity expansion procedure, a more complex fitting algorithm should be employed (compared to the one detailed in Section 5.2). Nonetheless, a similar approach can be used.
The special case of cavity expansion in an unbounded neo-Hookean body (B/A → ∞) has been considered by several researchers.44–48 Then the energy density has the form Ŵ = (E/6)(λr2 + λθ2 + λϕ2 − 3) with E being the elastic modulus at small strains, and by eqn (4) the internal pressure (p) can be written as
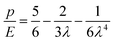 | (5) |
We plot eqn (5) using the red curve in Fig. 3b showing a monotonic increase of pressure as the cavity expands (i.e. λ increases), up to an asymptotic limit of p = 5/6E at which the cavity grows indefinitely. This phenomenon is known as the cavitation instability limit and was first reported by Gent and Lindley.44 They discussed it in terms of the cracking stress in cylindrical test samples of vulcanized rubber and identified that the measured cracking stresses were linearly dependent on the elastic modulus rather than the extensibility. Later, Lindsey49 discussed the cavitation phenomenon in terms of fracture and nucleation of a point of weakness in the material. The strong relationship between cavitation and fracture continues to be indicated in recent years. Lin and Hui50 studied the cavity inflation for various constitutive equations in terms of crack growth in soft materials and energy release rate during the cavity expansion. Kang et al.51 used finite element modeling to investigate the propagation of a ring crack in a spherical cavity and the effect of the crack size on the stable and unstable crack propagation. In addition, based on experimental observations of the nucleation of internal cavities and their transition to cracks, at high spatial and temporal resolutions, Poulain et al.29 conclude that the internal damage in soft material should be viewed as a fracture phenomenon.
A relation for the internal pressure for the case of a finite neo-Hookean body is readily derived from eqn (3) and written as†
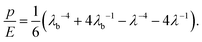 | (6) |
The pressure as function of λ (eqn 6), for bodies with various B/A ratios are plotted in Fig. 3b. It is shown that in contrast to the case with B/A → ∞, the pressure has a non-monotonic behavior and goes through a maximum as λ is increased. The location of the maximum is highly sensitive to the radii ratio. The sensitivities of the maximum pressure pmax and the corresponding stretch λmax are presented in Fig. 3c, showing that up to B/A ≈ 100 the maxima are clearly smaller than the asymptotic limit for the case of an infinite body. As B/A is increased, the stretch at which the maximum pressure takes place keeps increasing and for B/A > 100, λmax is expected to be larger than 27 (or a strain of 2600%). Notice that although sensitivity of the instability limit is considerable, in smaller ranges of the stretch (i.e. λ < 3), the curves of p–λ for bodies of B/A > 10 show nearly no sensitivity to the size as presented in Fig. 3b. Although we have demonstrated this point for the neo-Hookean material, based on Saint-Venant's principle it is possible to determine a range of stretches in which the pressure is insensitive to the outer dimension of the body for any hyperelastic material with sufficiently large radii ratio B/A. Within this range we can employ eqn (4).
The conventional CR method measures the elastic modulus of soft materials18–23 by determining the value of the maximum pressure from the experiment and comparing it with the asymptotic maximum predicted by the theory, which for the case of a neo-Hookean material is found as E = 6/5pmax.‡ This assumption is valid as long as B/A ≫ 1, as assumed in the conventional CR technique. In the present study, to eliminate the effect of the sample dimensions, we will present a method for employing the experimental data within a limited range of stretch prior to instability. For the neo-Hookean material this range is 1 < λ < 3.
4 Experimental method
Based on conclusions of the theoretical investigation, it is clear that the pressure alone is insufficient to determine the state of the cavity. Hence, we have developed an experimental setup that allows us to conduct volume-controlled cavity expansion experiments and to extract the cavity pressure and corresponding volume with high precision.4.1 Experimental setup
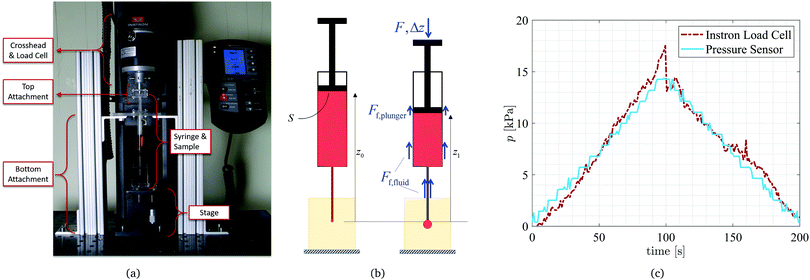
Our custom designed CR setup consists of a set of two attachments to an Instron universal testing machine as shown in Fig. 4a. The bottom attachment consists of two columns holding a horizontal platform. This part is stationary and attached to the optical breadboard at the base of the Instron machine. The flange of the syringe slides through the opening in the horizontal platform keeping the syringe fixed. This setup allows for both downward and upward movement of the piston (i.e. fluid injection and withdrawal). The top attachment is connected to the load cell and moves with the Instron crosshead. The plunger of the syringe is fixed to the top attachment and thus its movement is controlled and recorded with the movement of the crosshead. These two attachments turn the Instron machine into a customized syringe pump for the purpose of the CR experiments. In all the experiments 3 mL BD syringes were used (internal diameter of D = 8.66 mm). Any incompressible fluid can be used in these volume-controlled experiments. The reported tests were conducted using glycerol (dyed in red for visualization purposes).A manual vertical translation stage (Optics Focus) is fixed to the base of the machine (shown in Fig. 4a) and is used to move the sample up and down to insert the fixed needle into the sample. Hence, although the bottom of the sample is kept stationary, it is not confined on any of the other five faces, to obtain a closer resemblance to a traction-free boundary condition on the samples.
4.2 Pressure calibration
The Instron testing machine gives us the ability to precisely control the movement (i.e. vertical location of the plunger, z) and thus the volumetric fluid discharge from the syringe and needle system. The load cell of the Instron machine allows for accurate measurement of the force (F) applied to the plunger (shown in the free body diagram of Fig. 4b). The measured force is then used to find the pressure inside the cavity. Initially the load cell is balanced to zero and using hydrostatic formulation for the working fluid we can write the gauge pressure p0 as ρgz0, where ρ is the density of the working fluid, g is the gravitational acceleration, and z0 is the initial vertical location with respect to the tip of the syringe (as shown in Fig. 4b). Then, after the start of the experiment, as the crosshead is lowered to inflate the cavity (by injecting the working fluid) the load cell records the force F exerted on the plunger. In addition, there is a frictional force between the plunger tip and the internal surface of the barrel (Ff,plunger) and another frictional force between the fluid and the needle/syringe walls (Ff,fluid) as shown on the free-body diagram of Fig. 4b. Combining these two frictional components into Ff = Ff,plunger + Ff,fluid, during the experiment, the gauge pressure in the cavity is found as p1 = ρgz1 + (F − Ff)/S where S is the cross sectional area of the syringe piston (i.e. the cross sectional area of the inside of the barrel). Therefore, using the above relations, pressure acting on the cavity (corresponding to p in eqn (5)) is found as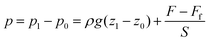 | (7) |
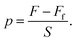 | (8) |
To measure the total frictional force in the system (between the plunger tip and the syringe barrel, as well as between fluid and the walls), we perform an identical test as the one performed in the CR measurements, but without the sample attached to the system. With the needle open to atmospheric pressure at all times (i.e. p = 0), the measured force is equal to the total frictional force in the system (F = Ff). This process is repeated prior to every experiment to find the Ff response to be used to calculate the pressure. It is important to note that in all cases a transient response is observed in the frictional force (Ff) followed by a steady value. This transient response is highly dependent on the specific syringe in use. To assure a correct measurement of the pressure, we consider data that has been collected during the steady response. This will be further explained in Section 5.
To validate our calibration method, a fluid filled syringe has been connected to an empty tube system connected to a pressure sensor (Omega) and the pressure was measured in a quasi-static injection-withdrawal test as shown in Fig. 4c (measured data were recorded using a National Instruments data acquisition system (USB-6002) accompanied by a custom Labview program). Simultaneously, the force measurement has been recorded through the Instron Blue Hill software and turned into pressure using the above calibration (eqn (8)). The results are presented in Fig. 4(c) showing very close agreement between the pressure measured using the pressure sensor and the corrected pressure calculated from the force measurements.
In addition to finding the pressure from the measured force, we can find the total injected volume of fluid from the recorded displacement of the crosshead. Since the plunger is connected to the crosshead through the top attachment, the total injected volume at every time instance is found as V = SΔz where Δz is the downward displacement as shown in Fig. 4(b). In this work, experiments on samples numbered 1, 2, 3 and 4 have been performed at four different rates of 0.03, 0.05, 0.07 and 0.09 mm s−1, respectively which correspond to 1.77, 2.95, 4.12 and 5.13 μL s−1. However, the results do not present any sensitivity to the rates used, thus confirming that the tests are conducted in the quasi-static limit. Similarly gauge 19 and 21 needles have been used (to avoid any effects of surface tension) in these experiments and did not present any differences thus confirming our expectation.
4.3 Sample preparation
To be able to vary the elastic properties of the samples, in this work we use soft PDMS (Polydimethylsiloxane) rubber samples (Sylgard 184, Dow Corning) with various base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linking agent ratios of 33
cross-linking agent ratios of 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 37
1, 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 40
1, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 42
1, 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 44
1, 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 50
1, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. To prepare the samples, the two parts were mixed and de-gassed using a vacuum pump. Then the samples were poured into molds of rectangular cuboid shape with a square cross sectional area of 30 × 30 mm2 and a height of 50 mm. Molds were filled with about ∼33–38 mm of the mixture resulting in average heights of about 35 mm after the end of de-gassing process. All the samples were cured in a 40 °C oven for 72 hours. Afterwards samples were retrieved from the oven and left to cool to room temperature. All the experiments were performed at room temperature.
1. To prepare the samples, the two parts were mixed and de-gassed using a vacuum pump. Then the samples were poured into molds of rectangular cuboid shape with a square cross sectional area of 30 × 30 mm2 and a height of 50 mm. Molds were filled with about ∼33–38 mm of the mixture resulting in average heights of about 35 mm after the end of de-gassing process. All the samples were cured in a 40 °C oven for 72 hours. Afterwards samples were retrieved from the oven and left to cool to room temperature. All the experiments were performed at room temperature.
5 Determining the elastic coefficient
The experimental results acquired using the current setup are reported in the form of pressure (adjusted using the calibration discussed in Section 4.2) as a function of the injected volume. However, as presented in Section 3, the theoretical curves are reported in the form of pressure as a function of the circumferential stretch ratio, λ (defined based on the radius of the cavity wall). Thus, to be able to analyze the data, extract the constitutive behavior, and the elastic modulus of the material at hand, we need to transform the experimental results from p–V to p–λ.Based on available literature55 PDMS is expected to rupture at strains in the range 20–100% (stretch of 1.2 < λ < 2) depending on the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratio, curing method, and curing temperature. Therefore, in cavitation experiments, PDMS is not able to experience stretches beyond λ ≈ 2 and fractures. After the point of fracture, the results of CR experiments do not follow the theoretical trend and the pressure is not able to reach the maximum predicted cavitation pressure.
cross-linker ratio, curing method, and curing temperature. Therefore, in cavitation experiments, PDMS is not able to experience stretches beyond λ ≈ 2 and fractures. After the point of fracture, the results of CR experiments do not follow the theoretical trend and the pressure is not able to reach the maximum predicted cavitation pressure.
For samples used in this work, the initial outer radius is estimated to be ∼15 mm and the radius of the cavity is estimated based on the outer diameter of the needle used (∼0.5 mm). Thus with a B/A ≈ 30 as an initial size estimate, the maximum pressure would be expected to take place at around λ ≈ 11 (i.e. strain of 1000%) which is beyond the rupture strain previously reported for PDMS samples. Hence, to extract the constitutive relations and elastic modulus of the materials from the collected results, instead of depending on the maximum pressure recorded, we aim to use the results prior to any indication of fracture which manifests itself in different ways such as sudden drops in pressure or changes in the trend. To do so, we require a method to transform the instantaneous volumetric data to a length scale that adequately represents the radius of the cavity wall at every instance.
To analyze the results, first let us consider the general p–λ relation for a material whose response is determined by a single elastic coefficient in eqn (4), and substitute λ = a/A to write
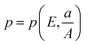 | (9) |
5.1 Effective cavity radius
Our CR experiments are performed using a volume-controlled protocol and thus we have access to exact volume of the cavity at every time instance. We thus use the volume of the injected fluid as a means of determining an effective length scale in the problem. For simplicity, assume that at every instance, we can think of the cavity to take the shape of an “effective” sphere, having an “effective” radius (i.e. length scale). Therefore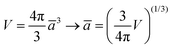 | (10) |
To further support the use of an effective radius, here we present the results of the finite element (FE) analysis (using ABAQUS) of the case of the cavity expansion inside a neo-Hookean body for two non-spherical cavities; one in the form of two cones connected at the base (revolution of a triangle) and another in the form of a cylinder (revolution of a rectangle). In both cases the outer boundary of the body is of spherical shape. Calculating the volume of the cavity at every time step of the simulation and using eqn (10) to calculate an effective stretch λ = ā/Ā, it can be seen that the results are nearly indistinguishable with the theoretical p–λ curve for the case of a spherical cavity as shown in Fig. 5.
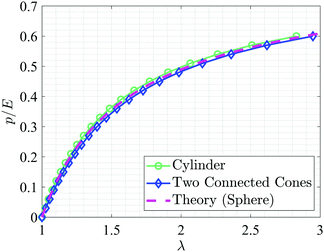 | ||
| Fig. 5 Plots of pressure versus effective stretch for cavities of two different initial shapes; two cones connected at the base, and cylinder. The stretch is calculated using the effective radius as defined by eqn (10). The theoretical results for the case of a spherical cavity is shown with a broken line. | ||
Clearly, comparing these lines one can see that even though the process of cavity expansion initially started from a non-spherical cavity, we can still base our fitting on an effective p–λ relation. These two examples demonstrate that not knowing the exact geometry of the cavity while only knowing its total volume is enough for finding a cavity length scale which can be effectively used to analyze the experimental results within the elastic range. This also confirms the report of Hutchens and Crosby56 that the shape of the cavity does not affect the overall results in CR.
5.2 Fitting method
Having determined the effective cavity radius, we are left to fit the data (prior to the point of fracture) with eqn (9) to extract the values of Ā and E. Different methods can be used to fit the experimental data to the theoretical prediction, and different constitutive relations can be considered to obtain the best fit. Here we limit our attention to materials whose response can be determined by a single elastic coefficient. In the demonstration of this method to determine the response of PDMS at varying base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios, we employ the neo-Hookean model, which is found to fit well to our experimental curves.
cross-linker ratios, we employ the neo-Hookean model, which is found to fit well to our experimental curves.
Our fitting method is based on the identification that the maximal (positive) slope in the experimental curve is associated with the point of maximum elastic resistance. Accordingly, we require that our fitted curve crosses through this point with the same slope. Additionally, we use this point to determine a useful range in the experimental data.§
The steps of the method used here are as follows:
(1) First we write the measured pressure as a function of the effective radius of the cavity found using eqn (10). For example, for a sample of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, the experimental results of F/S, Ff/S, and p are plotted as a function of the calculated effective radius and presented in Fig. 6(a). Notice the transient regime in the measurement of the friction force extends to ā ∼ 1.1 mm. Hence, for the fitting in this case we employ data obtained beyond this value.
1 PDMS, the experimental results of F/S, Ff/S, and p are plotted as a function of the calculated effective radius and presented in Fig. 6(a). Notice the transient regime in the measurement of the friction force extends to ā ∼ 1.1 mm. Hence, for the fitting in this case we employ data obtained beyond this value.
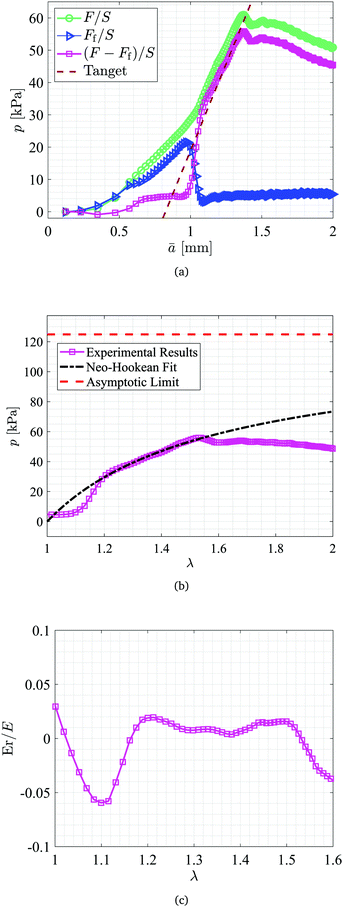 | ||
| Fig. 6 (a) Measured total force and frictional force normalized by the surface area of the plunger (F/S and Ff/S) and calculated pressure p in the cavity as a function of ā defined using eqn (10). The red dashed line presents the tangent line to the data at the point with the largest slope (away from the region impacted by the transient friction at the start-up). (b) The resulting p–λ curve using the current method and the corresponding neo-Hookean fit to the data. (c) The value of error Er calculated and normalized by the elastic modulus for the stretch range of 1 < λ < 1.6. | ||
(2) Next, we search for the largest slope (α) in the p–ā curve and determine the line tangent to the data at this point (αā + β where β is the ordinate intercept, as shown by the dashed line in Fig. 6(a)).
(3) Returning to the theoretical analysis of eqn (5) and Fig. 3(b), one can see that the slope of the p–λ curve is the largest at λ = 1 (slope = 4/3E) and decreases as λ is increased. To efficiently initiate a trial and error procedure, we use this tangent as a starting measure to find a first guess for Ā. We define a starting guess for the initial radius of the cavity (Āg) by finding the line's abscissa intercept. With this guessed value we define a guess for the stretch λg as
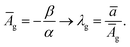 | (11) |
(4) Now, as it is clearly seen in Fig. 6(a), Āg requires a correction to get closer to the correct fitting. Therefore, to adjust the value of the effective initial radius, we introduce a correction factor M as
| λ = Mλg. | (12) |
To find the elastic modulus we then differentiate (4) using Leibniz's rule to write (see details in the Appendix)
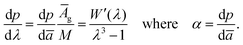 | (13) |
For the neo-Hookean material the above relation can be reorganized using the maximum slope α found earlier to find the value of E as
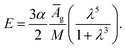 | (14) |
(5) Using the elastic modulus, E, from eqn (14) we then calculate the difference (e.g. error) between the measured value of pressure and the corresponding fit and define 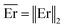 as an average error.
as an average error.
(6) Since M is not known a priori, we repeat steps (4) and (5) for a range of correction factors, (typically 0.5 < M < 1.5) and record the average error 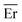 for all the cases. Then, among all the above cases, we search for the M, and E combination that gives minimum average error. This value of M (or equivalently Ā = Āg/M) and the corresponding E are the fitting parameters.
for all the cases. Then, among all the above cases, we search for the M, and E combination that gives minimum average error. This value of M (or equivalently Ā = Āg/M) and the corresponding E are the fitting parameters.
For the example tests presented here, a stretch range of [1.2–1.5] was employed resulting in A = 8.1725 × 10−4 m and M = 1.094. The resulting neo-Hookean fit is presented in Fig. 6(b) and the corresponding error, Er normalized by the elastic modulus (149.85 kPa) is shown in Fig. 6(c).
6 Results and discussion
The measured values of pressure versus volume for PDMS with various base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios (50
cross-linker ratios (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 144
1, 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 42
1, 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 40
1, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 37
1, 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 33
1, and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) have been analyzed using the above algorithm. The results are presented in Fig. 7 and Table 1. For example, experimental results for PDMS 50
1) have been analyzed using the above algorithm. The results are presented in Fig. 7 and Table 1. For example, experimental results for PDMS 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 samples are presented in Fig. 7(a) in the form of p–λ curves for four different tests. As shown in the figure, within a range of 1 < λ < 1.5 the results collapse onto a curve that corresponds to a neo-Hookean material with elastic modulus of 73.65 ± 2.95 kPa. Notice that the point of departure of the results from the neo-Hookean behavior varies among the different tests and is observed within a range of λ ∼ 1.2–1.4 (17 < p < 22 kPa). Moreover this point is clearly distinct from the point of maximum pressure recorded during the tests. The average maximum recorded pressure for these samples is 25.85 ± 2.12 kPa which is about 35% of the elastic modulus calculated through the fitting.
1 samples are presented in Fig. 7(a) in the form of p–λ curves for four different tests. As shown in the figure, within a range of 1 < λ < 1.5 the results collapse onto a curve that corresponds to a neo-Hookean material with elastic modulus of 73.65 ± 2.95 kPa. Notice that the point of departure of the results from the neo-Hookean behavior varies among the different tests and is observed within a range of λ ∼ 1.2–1.4 (17 < p < 22 kPa). Moreover this point is clearly distinct from the point of maximum pressure recorded during the tests. The average maximum recorded pressure for these samples is 25.85 ± 2.12 kPa which is about 35% of the elastic modulus calculated through the fitting.
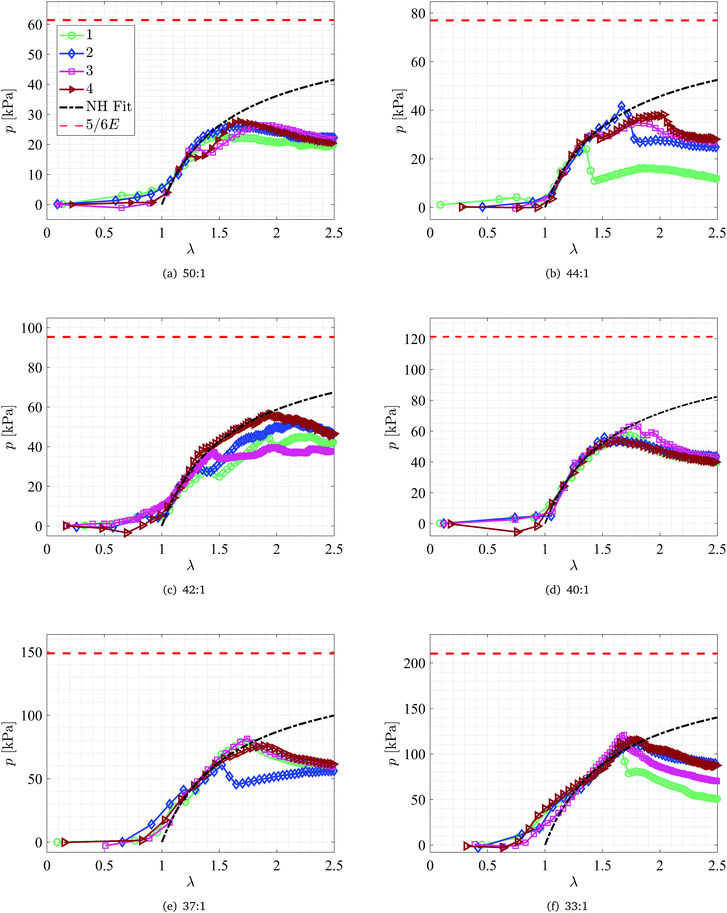 | ||
Fig. 7 Plots of p–λ curves for PDMS with four different base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios: (a) 50 cross-linker ratios: (a) 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (b) 44 1, (b) 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (c) 42 1, (c) 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (d) 40 1, (d) 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (e) 37 1, (e) 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and (f) 33 1, and (f) 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The corresponding neo-Hookean fitting parameters are presented in Table 1 and the neo-Hookean fit based on the average elastic modulus is plotted with a black dash-dot line. The asymptotic limit for an infinite neo-Hookean block (5/6E) is shown with red dashed line. Data in the range 0 < λ < 1 corresponds to the early time when the cavity is being filled and does not represent compression. 1. The corresponding neo-Hookean fitting parameters are presented in Table 1 and the neo-Hookean fit based on the average elastic modulus is plotted with a black dash-dot line. The asymptotic limit for an infinite neo-Hookean block (5/6E) is shown with red dashed line. Data in the range 0 < λ < 1 corresponds to the early time when the cavity is being filled and does not represent compression. | ||
| Sample | M | Ā g (m) | E (kPa) | p max (kPa) |
|---|---|---|---|---|
| 50-1 | 1.022 | 8.7779 × 10−4 | 69.49 | 22.90 |
| 50-2 | 1.043 | 8.5305 × 10−4 | 75.05 | 26.02 |
| 50-3 | 0.995 | 7.8534 × 10−4 | 76.26 | 26.58 |
| 50-4 | 1.002 | 8.0037 × 10−4 | 73.78 | 27.92 |
| 44-1 | 1.049 | 9.6097 × 10−4 | 90.38 | 24.40 |
| 44-2 | 0.987 | 7.7068 × 10−4 | 91.88 | 42.75 |
| 44-3 | 0.995 | 7.4101 × 10−4 | 93.92 | 34.82 |
| 44-4 | 1.022 | 8.4074 × 10−4 | 93.32 | 38.32 |
| 42-1 | 0.990 | 7.1154 × 10−4 | 104.02 | 45.63 |
| 42-2 | 0.995 | 7.5830 × 10−4 | 118.03 | 52.98 |
| 42-3 | 1.076 | 11.4262 × 10−4 | 115.54 | 39.78 |
| 42-4 | 1.018 | 7.6021 × 10−4 | 119.79 | 56.39 |
| 40-1 | 1.040 | 8.7512 × 10−4 | 140.98 | 57.54 |
| 40-2 | 1.094 | 8.1752 × 10−4 | 149.85 | 55.99 |
| 40-3 | 1.057 | 8.5193 × 10−4 | 144.77 | 64.32 |
| 40-4 | 1.055 | 8.7386 × 10−4 | 146.47 | 54.59 |
| 37-1 | 1.065 | 9.332 × 10−4 | 177.87 | 80.23 |
| 37-2 | 1.066 | 9.1536 × 10−4 | 175.88 | 61.86 |
| 37-3 | 1.011 | 9.3838 × 10−4 | 183.05 | 81.52 |
| 37-4 | 1.084 | 8.7437 × 10−4 | 177.44 | 76.11 |
| 33-1 | 1.123 | 8.5990 × 10−4 | 258.39 | 110.74 |
| 33-2 | 1.058 | 8.8030 × 10−4 | 250.47 | 109.83 |
| 33-3 | 1.096 | 11.0033 × 10−4 | 250.89 | 121.03 |
| 33-4 | 1.201 | 9.6268 × 10−4 | 249.20 | 97.33 |
A summary of the measured properties using the current and the conventional CR techniques are presented in Table 2. Note that the maximum pressure measured in all the cases is within a range of 35–45% of the elastic moduli found through the fitting analysis used here (recall that in conventional CR technique pmax = 5/6E). In addition, a larger standard deviation is recorded in the maximum pressures when compared to the standard deviation reported for the fitted elastic moduli.
| Ratio | E [kPa] (current method) | E [kPa] (conventional CR) |
|---|---|---|
| 50 | 73.65 ± 2.95 | 25.85 ± 2.13 |
| 44 | 92.37 ± 1.58 | 35.07 ± 7.82 |
| 42 | 114.34 ± 7.10 | 48.70 ± 7.45 |
| 40 | 145.52 ± 3.69 | 58.11 ± 4.31 |
| 37 | 178.56 ± 3.11 | 74.93 ± 9.02 |
| 33 | 252.34 ± 4.11 | 109.73 ± 9.70 |
In comparison to the theoretical predictions we find that the point of departure from the neo-Hookean trend happens within a range of λ ≈ 1.2–1.9 which is well below the cavitation instability threshold (λmax in Fig. 3(c)). We thus interpret the departure from the neo-Hookean trend as a manifestation of a mode-I crack propagation that results in a sudden growth of the cavity (defect) and relieving the pressure inside the cavity. This process can be clearly seen in nearly all the samples and for example dominates the response of the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 40
1 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 samples after the point of departure from the neo-Hookean behavior.
1 samples after the point of departure from the neo-Hookean behavior.
In some of the samples, the pressure relief is followed by local increases in the pressure, with additional pressure releases. This behavior can be explained as a combination of crack propagation and cavity expansion processes occurring simultaneously. Each sudden fracture and crack opening leads way to initiation of a new and larger cavity which results in a pressure relief. However, as we increase the volume, this larger cavity goes through an entirely new cavitation process (possibly starting from a not stress-free state) until another crack starts to propagate leading to another pressure relief.
It should be noted that even though the pressure relief in some of the samples shows a gradual trend (not sudden like the ones in 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 33
1 and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 samples), it should not be mistaken by the cavitation response of a finite size body. Using the effective initial radius of the cavity, calculated through the fitting, one can clearly see that the bodies have a mean B/Ā ≈ 14–18. The corresponding maximum pressure thus takes place in the range of 5.6 < λ < 7.6 (see Fig. 3(c)). However, the maximum pressure recorded in the samples is within the range 1.4 < λ < 1.8. Hence, the behavior reported here for PDMS is dominated by the gradual pressure relief due to crack propagation as more volume is injected into the cavity. In addition, using the radius of the needle as an estimate of the initial radius of the cavity is not an appropriate measure of length scale in this problem and fitting the data for the elastic modulus and the initial radius presents more accurate results. However, since the calculated B/Ā is larger than 10, we can still use eqn (9) for the curve fitting purposes within 1 < λ < 2.
1 samples), it should not be mistaken by the cavitation response of a finite size body. Using the effective initial radius of the cavity, calculated through the fitting, one can clearly see that the bodies have a mean B/Ā ≈ 14–18. The corresponding maximum pressure thus takes place in the range of 5.6 < λ < 7.6 (see Fig. 3(c)). However, the maximum pressure recorded in the samples is within the range 1.4 < λ < 1.8. Hence, the behavior reported here for PDMS is dominated by the gradual pressure relief due to crack propagation as more volume is injected into the cavity. In addition, using the radius of the needle as an estimate of the initial radius of the cavity is not an appropriate measure of length scale in this problem and fitting the data for the elastic modulus and the initial radius presents more accurate results. However, since the calculated B/Ā is larger than 10, we can still use eqn (9) for the curve fitting purposes within 1 < λ < 2.
Finally, we plot the results of the extracted elastic moduli calculated using the proposed method as a function of the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios as shown in Fig. 2. It can be seen that the current measurements capture the expected magnitude and trend in the elastic modulus of PDMS and the results agree with both our tensile measurements and the previously reported numbers. In addition, one should note that the current method is able to capture the neo-Hookean trend of the material behavior in addition to capturing the elastic modulus. Also, comparing the results of the fitting method proposed here and the use of the maximum pressure for analysis of the CR results shows that the conventional technique consistently predicts a lower bound and only captures up to 43% of the value of the elastic modulus with a larger standard deviation (Table 2). In addition, the proposed technique can be performed in opaque samples (i.e. does not depend on the visualization of the cavity) and allows us to determine an effective radius of the cavity at every instance.
cross-linker ratios as shown in Fig. 2. It can be seen that the current measurements capture the expected magnitude and trend in the elastic modulus of PDMS and the results agree with both our tensile measurements and the previously reported numbers. In addition, one should note that the current method is able to capture the neo-Hookean trend of the material behavior in addition to capturing the elastic modulus. Also, comparing the results of the fitting method proposed here and the use of the maximum pressure for analysis of the CR results shows that the conventional technique consistently predicts a lower bound and only captures up to 43% of the value of the elastic modulus with a larger standard deviation (Table 2). In addition, the proposed technique can be performed in opaque samples (i.e. does not depend on the visualization of the cavity) and allows us to determine an effective radius of the cavity at every instance.
7 Conclusions
In this work, we present a volume controlled cavitation rheology (CR) technique for measuring the elastic modulus of soft materials with rupture strains lower than the limit of cavitation instability. A custom-designed CR system provides high precision measurement of the injected volume and the pressure inside the cavity. Due to the non-spherical initial geometry of the cavity, the experimental data is analyzed by employing the notion of a volume based effective cavity radius, to determine an effective value of the circumferential stretch. The validity of this assumption is confirmed using numerical simulations. The resulting curves for pressure versus stretch are then fitted to the theoretical cavity expansion curve. The presented fitting method is limited to materials whose response can be determined by a single elastic coefficient. Future work should center on extending this technique to consider more complex materials that require additional material parameters.Applying this method to PDMS samples that are fabricated with different base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cross-linker ratios shows good agreement with measurements reported using conventional tensile/compression testing. Moreover, it allows us to capture both the neo-Hookean behavior of the PDMS samples and the elastic modulus, even though the samples fracture much earlier than the cavitation instability is observed.
cross-linker ratios shows good agreement with measurements reported using conventional tensile/compression testing. Moreover, it allows us to capture both the neo-Hookean behavior of the PDMS samples and the elastic modulus, even though the samples fracture much earlier than the cavitation instability is observed.
Comparing this method to the conventional CR technique that is based on the maximum pressure that appears at onset of the instability, one can see that due to the failure and crack propagation in PDMS, the conventional CR technique captures about 43% of the elastic modulus of the samples with a larger scatter in the results. Finally, this approach is insensitive to the respective size of the sample and the needle, it can be performed in opaque samples (i.e. without observing the cavity expansion), and does not make any preliminary assumption on the specific rupture mechanism, hence it can potentially be applied in future for measurement of nonlinear material properties in vivo.
Conflicts of interest
There are no conflicts to declare.Appendix
The spherically symmetric expansion illustrated on Fig. 3(a), results in an equi-biaxial deformation state. By limiting our attention to incompressible materials, the principal stretch components have the form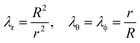 | (A1) |
In spherical coordinates, the equilibrium requirement reduces to a single non-trivial equation
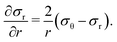 | (A2) |
Considering an isotropic hyperelastic material, we can write the elastic energy density in the general form W = Ŵ(λr,λθ,λϕ) and the principal stress difference is readily derived as
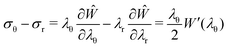 | (A3) |
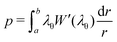 | (A4) |
| σr(a) = −p, σr(b) = 0. | (A5) |
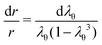 | (A6) |
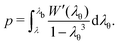 | (A7) |
Now, the slope of this pressure-stretch curve can be found by differentiation of this integral employing Leibniz's rule. In particular, for λb = 1 the slope is
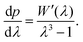 | (A8) |
Notes and references
- Y. C. Fung, Biomechanics: mechanical properties of living tissues, Springer Science & Business Media, 2013 Search PubMed.
- C. T. McKee, J. A. Last, P. Russell and C. J. Murphy, Tissue Eng., Part B, 2011, 17, 155–164 CrossRef PubMed.
- A. Samani and D. Plewes, Phys. Med. Biol., 2007, 52, 1247 CrossRef PubMed.
- M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo and D. Boettiger, et al. , Cancer Cell, 2005, 8, 241–254 CrossRef CAS PubMed.
- K. Hayashi, K. Ide and T. Matsumoto, J. Biomech. Eng., 1994, 116, 284–293 CrossRef CAS PubMed.
- T. Imura, K. Yamamoto, T. Satoh, T. Mikami and H. Yasuda, Atherosclerosis, 1988, 73, 149–155 CrossRef CAS PubMed.
- F. Wuyts, V. Vanhuyse, G. Langewouters, W. Decraemer, E. Raman and S. Buyle, Phys. Med. Biol., 1995, 40, 1577 CrossRef CAS PubMed.
- M. Claridge, G. Bate, P. Hoskins, D. Adam, A. Bradbury and A. Wilmink, Atherosclerosis, 2009, 205, 477–480 CrossRef CAS PubMed.
- W.-C. Yeh, P.-C. Li, Y.-M. Jeng, H.-C. Hsu, P.-L. Kuo, M.-L. Li, P.-M. Yang and P. H. Lee, Ultrasound Med. Biol., 2002, 28, 467–474 CrossRef PubMed.
- J. A. Last, T. Pan, Y. Ding, C. M. Reilly, K. Keller, T. S. Acott, M. P. Fautsch, C. J. Murphy and P. Russell, Invest. Ophthalmol. Visual Sci., 2011, 52, 2147–2152 CrossRef PubMed.
- P. Russell and M. Johnson, Invest. Ophthalmol. Visual Sci., 2012, 53, 117 CrossRef PubMed.
- J. Ophir, I. Cespedes, H. Ponnekanti, Y. Yazdi and X. Li, Ultrason. Imaging, 1991, 13, 111–134 CrossRef CAS PubMed.
- J.-L. Gennisson, T. Deffieux, M. Fink and M. Tanter, Diagn. Interv. Imaging, 2013, 94, 487–495 CrossRef PubMed.
- S. Franchi-Abella, C. Elie and J.-M. Correas, Diagn. Interv. Imaging, 2013, 94, 497–501 CrossRef CAS PubMed.
- A. Samani, J. Bishop, C. Luginbuhl and D. B. Plewes, Phys. Med. Biol., 2003, 48, 2183 CrossRef PubMed.
- Y. Hu, X. Chen, G. M. Whitesides, J. J. Vlassak and Z. Suo, J. Mater. Res., 2011, 26, 785–795 CrossRef CAS.
- S. Budday, R. Nay, R. de Rooij, P. Steinmann, T. Wyrobek, T. C. Ovaert and E. Kuhl, J. Mech. Behav. Biomed. Mater., 2015, 46, 318–330 CrossRef PubMed.
- J. A. Zimberlin, J. J. McManus and A. J. Crosby, Soft Matter, 2010, 6, 3632–3635 RSC.
- J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763–767 RSC.
- A. J. Crosby and J. J. McManus, Phys. Today, 2011, 64, 62–63 CrossRef.
- J. A. Zimberlin and A. J. Crosby, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1423–1427 CrossRef CAS.
- J. Cui, C. H. Lee, A. Delbos, J. J. McManus and A. J. Crosby, Soft Matter, 2011, 7, 7827–7831 RSC.
- A. Delbos, J. Cui, S. Fakhouri and A. J. Crosby, Soft Matter, 2012, 8, 8204–8208 RSC.
- A. Blumlein, N. Williams and J. J. McManus, Sci. Rep., 2017, 7, 7346 CrossRef PubMed.
- S. M. Hashemnejad and S. Kundu, Soft Matter, 2015, 11, 4315–4325 RSC.
- L. Pavlovsky, M. Ganesan, J. G. Younger and M. J. Solomon, Appl. Phys. Lett., 2014, 105, 114105 CrossRef PubMed.
- Z. Wang, A. A. Volinsky and N. D. Gallant, J. Appl. Polym. Sci., 2014, 131, 41050 CrossRef.
- V. Lefèvre, K. Ravi-Chandar and O. Lopez-Pamies, Int. J. Fract., 2015, 192, 1–23 CrossRef.
- X. Poulain, V. Lefèvre, O. Lopez-Pamies and K. Ravi-Chandar, Int. J. Fract., 2017, 205, 1–21 CrossRef CAS.
- A. Gent, Int. J. Non Linear Mech., 2005, 40, 165–175 CrossRef.
- J. Ganghoffer and J. Schultz, Int. J. Fract., 1995, 72, 1–20 CrossRef.
- C. O. Horgan and D. Polignone, Appl. Mech. Rev., 1995, 48, 471–485 CrossRef.
- C. O. Horgan and R. Abeyaratne, J. Elasticity, 1986, 16, 189–200 CrossRef.
- D. T. Chung, C. O. Horgan and R. Abeyaratne, Int. J. Solids Struct., 1987, 23, 983–988 CrossRef.
- H. Hang-Sheng and R. Abeyaratne, J. Mech. Phys. Solids, 1992, 40, 571–592 CrossRef.
- D. Durban and R. Masri, Int. J. Solids Struct., 2004, 41, 5697–5716 CrossRef.
- T. Cohen, R. Masri and D. Durban, Int. J. Solids Struct., 2009, 46, 3643–3650 CrossRef.
- C. O. Horgan, Int. J. Solids Struct., 1992, 29, 279–291 CrossRef.
- C. O. Horgan and T. Pence, J. Elasticity, 1989, 21, 61–82 CrossRef.
- D. A. Polignone and C. O. Horgan, J. Elasticity, 1993, 33, 27–65 CrossRef.
- D. A. Polignone and C. O. Horgan, Int. J. Solids Struct., 1993, 30, 3381–3416 CrossRef.
- T. Cohen and A. Molinari, Int. J. Solids Struct., 2015, 69, 544–552 CrossRef.
- T. Cohen and D. Durban, Acta Mech., 2013, 224, 1695–1707 CrossRef.
- A. Gent and P. Lindley, Proc. R. Soc. London, Ser. A, 1959, 249, 195–205 CrossRef.
- A. Gent and D. Tompkins, J. Appl. Phys., 1969, 40, 2520–2525 CrossRef CAS.
- C. O. Horgan and T. Pence, J. Appl. Mech., 1989, 56, 302–308 CrossRef.
- M. S. Chou-Wang and C. O. Horgan, Int. J. Eng. Sci., 1989, 27, 967–973 CrossRef.
- M. S. Chou-Wang and C. O. Horgan, Int. J. Solids Struct., 1989, 25, 1239–1254 CrossRef.
- G. H. Lindsey, J. Appl. Phys., 1967, 38, 4843–4852 CrossRef CAS.
- Y. Y. Lin and C. Hui, Int. J. Fract., 2004, 126, 205–221 CrossRef CAS.
- J. Kang, C. Wang and S. Cai, Soft Matter, 2017, 13, 6372–6376 RSC.
- Z. Chen, MSc thesis, Massachusetts Institute of Technology, 2018.
- N.-S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288 CrossRef CAS.
- A. Volk and C. J. Kähler, Exp. Fluids, 2018, 59, 75 CrossRef.
- R. Seghir and S. Arscott, Sens. Actuators, A, 2015, 230, 33–39 CrossRef CAS.
- S. B. Hutchens and A. J. Crosby, Soft Matter, 2014, 10, 3679–3684 RSC.
Footnotes |
| † For the full derivation of this formula see also ref. 52. |
| ‡ This relation was applied to determine the elastic modulus shown in Fig. 2, by circle markers. It is obtained from (5) with λ → ∞. |
| § Note that the chosen range of data applied for the fitting can be further tuned throughout the process to obtain a best fit over a maximal range, nonetheless it excludes the range in which transient changes in friction may affect the measurements. |
| This journal is © The Royal Society of Chemistry 2019 |