Anisotropic mechanics and dynamics of a living mammalian cytoplasm

Abstract

During physiological processes, cells can undergo morphological changes that can result in a significant redistribution of the cytoskeleton causing anisotropic behavior. Evidence of anisotropy in cells under mechanical stimuli exists; however, the role of cytoskeletal restructuring resulting from changes in cell shape in mechanical anisotropy and its effects remain unclear. In the present study, we examine the role of cell morphology in inducing anisotropy in both intracellular mechanics and dynamics. We change the aspect ratio of cells by confining the cell width and measuring the mechanical properties of the cytoplasm using optical tweezers in both the longitudinal and transverse directions to quantify the degree of mechanical anisotropy. These active microrheology measurements are then combined with intracellular movement to calculate the intracellular force spectrum using force spectrum microscopy (FSM), from which the degree of anisotropy in dynamics and force can be quantified. We find that unrestricted cells with aspect ratio (AR) ∼1 are isotropic; however, when cells break symmetry, they exhibit significant anisotropy in cytoplasmic mechanics and dynamics.

---

Introduction

Cytoplasm is a complex active material wherein numerous biochemical processes occur, which are critical for the functioning of a cell. Many of the biological processes, such as cell migration,^1–3 mechanotransduction,⁴ and cancer metastasis,^5–11 involve mechanical processes and are known to be critically regulated by cell mechanics. Consequently, numerous techniques have been developed to probe the mechanical properties of cells.^12–19 Most of the studies report mechanical measurements in terms of a stiffness or a shear modulus assuming that cells are isotropic.^12–20 However, the cytoplasm of a cell is a highly crowded, dynamic and heterogeneous microenvironment, which, under various physiological conditions, can undergo morphological changes resulting in polarity or anisotropy. In fact, Yeaman et al.²¹ proposed that the establishment of structural asymmetry in the plasma membrane was the first critical event for the orientation of cell polarity. Anisotropy in cells is critical and has been suggested to facilitate a diverse set of cellular processes such as directional cell migration,²² differentiation,²³ localized membrane growth,^24,25 activation of the immune system,²⁶ transport of molecules across cell layers,²⁷etc. There is also evidence that cell–cell and cell–extracellular matrix (ECM) interactions can also induce cell polarity, significantly affecting the internal organization of the cell and thereby playing a key role in developmental processes.²⁸ Therefore, a deeper insight into the directionally dependent changes of mechanical properties of the cytoplasm due to these structural changes will lend us greater understanding of the biological processes regulated by cell polarity. Some previous efforts have indeed demonstrated that redistribution of the cytoskeleton comprising actin filaments, microtubules and intermediate filaments governed by the morphological changes of the cell caused by physiological processes or external stimuli can regulate cellular stresses^29–32 and induce mechanical anisotropy in the cell.^28,33,34 Endothelial cells when subjected to continuous laminar flow shear stress suffer directional anisotropy resulting in temporal and spatial changes in cytoplasmic creep compliance in different directions;³⁴ smooth muscle cells under mechanical strain also modify their mechanics through cytoskeletal reorganization resulting in mechanical anisotropy.^35,36 Studies have also shown that the mechanical anisotropy of the plasma membrane can arise as a result of binding via specific molecular ligands.³⁷ However, most of these studies explored polarity in the context of generated traction forces and mechanics of the cortex. Therefore, a systematic study on the direction dependent mechanics of the inside of the cytoplasm is lacking in the present literature.

Cytoskeletal reorganization not only regulates the mechanics of the cytoplasm but can also critically determine intracellular dynamics as motor proteins work in conjunction with the cytoskeletal fibers.^38–42 As the cells operate out-of-equilibrium,^18,43–46 intracellular motion caused by the collective activity of molecular motors within the cells is highly correlated with not only mechanics but also intracellular forces. These forces are known to drive important functions at the level of the whole cell such as division,⁴⁷ migration,⁴⁸ and contraction⁴⁹ and therefore, understanding the effect of these forces in the context of cell polarity is critical for the complete understanding of the physical basis of biological phenomena in the cytoplasm.

In the present study, we investigate the effect of spatial restructuring of the cytoskeleton induced by morphological changes of the cells on intracellular mechanics and dynamics. We use a micro-contact printing technique to confine the width of the cells while allowing them to spread unrestricted in the other direction, resulting in cells with different aspect ratios. We use optical tweezers and microscopic particle tracking to investigate the mechanics and dynamics inside the cytoplasmic microenvironment in directions perpendicular and parallel to the principal cell axis. We find that both the mechanics of the intracellular environment and the motion of endocytosed tracer particles can be highly anisotropic depending on the cell morphology. Furthermore, we directly measure the spectrum of intracellular forces using force spectrum microscopy (FSM);^18,43 we find that the anisotropic cytoplasmic dynamics is governed by the cytoskeletal alignment of the fibers and actin based forces.

Materials and methods

Cell culture and pharmacological interventions

Mouse embryonic fibroblasts (mEFs)⁵⁰ are cultured in Dulbecco's minimal essential medium (Corning, NY, USA) supplemented with 10% fetal calf serum (Gibco, Life Technologies, Gaithersburg, MD, USA) and 1% penicillin–streptomycin (Gibco, Life Technologies, Gaithersburg, MD, USA) at 37 °C and 5% CO₂ in humid conditions. Cells are passaged onto 35 mm micropatterned dishes and allowed to grow overnight. Later, 500 nm fluorescent beads (Molecular Probes, Eugene, OR, USA) are mixed with culture media (at a concentration of 5 × 10⁵ microspheres per mL) for 24 hours to introduce them into the cytoplasm. Before imaging, beads that are not endocytosed are washed off with two washes using phosphate buffered saline (PBS). To depolymerize actin, cells are treated with cytochalasin D (Sigma Aldrich, MO, USA) at a working concentration of 500 nM for 30 min in an incubator.

Immunofluorescence, microscopy and image processing

Cells are fixed with 4% paraformaldehyde (Sigma Aldrich, MO, USA) and 0.1% Triton X-100 (Sigma Aldrich, MO, USA) in PBS for 15 min and then washed three times using PBS (Corning, NY, USA). Cells are then stained with rat anti-α-tubulin primary antibody (EMD Millipore, MA, USA), followed by Alexa Fluor 488 conjugated goat anti-rat (Invitrogen, CA, USA), using standard procedures. F-actin was stained using AlexaFluor 532 phalloidin (Molecular Probes, Eugene, OR, USA) for 30 min at room temperature. Nucleus is labelled using DRAQ5 (Invitrogen, CA, USA). Cells are imaged using excitation from a 488, 552 and 638 nm laser line and a 63×/1.2NA water immersion lens on a Leica TCS SP8 (Leica, Germany). Images were deconvolved using the Huygens deconvolution software (Huygens, Hilversum, Netherlands) using a theoretical point spread function. For cell and nuclear volume measurements, optical cross sections are recorded at 0.15 μm z-axis intervals to show intracellular, nuclear and cortical fluorescence. The volume is calculated by counting voxel number, after thresholding the stack. The precision of the cell volume measurement using 3D confocal microscopy has previously been confirmed by comparing it with measurements using AFM and super resolution structured illumination microscopy (SIM).^51,52 To quantify the local fiber orientation, Orientationj, an imagej plugin, is used, which uses an algorithm based on structure tensors as described previously.⁵³

Micro-contact printing

Micro-contact printing is used to confine cells and culture them in different aspect ratios using the protocol described previously.⁵⁴ We culture the cells on micropatterned strips with different widths of 10 μm, 20 μm and 40 μm to confine the cells in one direction while allowing them to spread unrestricted in the other direction; this results in cells with different aspect ratios. To calculate the aspect ratio, we choose the principal axes through the center of the cells and measure the cell lengths. The longer side is always chosen as the longitudinal direction and the shorter side as the transverse direction. Polydimethylsiloxane (PDMS) (Sylgard 184; Dow Corning, MI, USA) precursor and curing agent are mixed homogeneously in a 10 : 1 ratio and poured over a silicon wafer with micropatterned wells. To remove air bubbles from the PDMS mixture, the silicon wafer along with the PDMS mixture is degassed in a desiccator for 30 min and then cured in an oven at 65 °C for 3 h. Solidified PDMS is peeled off from the silicon wafer and cut into stamps, which are then oxidized using plasma. Later, 0.3 μg mL⁻¹ collagen-I is poured over each stamp; extra solution is wiped off with tissue and the stamp is allowed to dry for 15 min. After complete drying, the stamp is inverted onto the surface of a 35 mm dish (MatTek) with no. 1.5 glass coverslip (plasma treated) at the bottom for 2 min and then gently removed. Before seeding cells, the unpatterned surface of the coverslip is treated with 1% pluronic F-127 for 5 min and then washed twice with PBS and cell culture medium.

Active microrheology using optical tweezers

The beam from a single-mode continuous wave (CW) ytterbium fiber laser (10 W, 1064 nm; IPG Photonics, MA, USA) is steered through a series of Keplerian beam expanders to overfill the back aperture of a 100 × 1.45 numerical aperture microscope objective (CFI Plan Apo Lambda DM 100× Oil; Nikon Corp., Japan) to optically trap and manipulate 500 nm beads in the cytoplasm of living cells. Dual-axis acousto-optic deflectors (IntraAction Corp., IL, USA) are used to manipulate the beam in the plane of the microscope glass slide to steer the beam and manipulate the trapped bead. For detection, the bead is centered on a high-resolution position detection quadrant detector (Thorlabs Inc., NJ, USA) and illuminated using bright-field illumination from a 100 W lamp. The linear region of the detector is calibrated by trapping a bead identical to those used in the cells in water and moving it across the detector using the acousto-optic deflectors in known step sizes. The trap stiffness is calibrated to 0.05 pN nm⁻¹ using the mean-squared Brownian motion of a trapped bead in water at various laser power settings using the principle of energy equipartition, as previously described.⁵⁵ A trapped bead is oscillated at the natural frequency, f, across a frequency range f = 1–70 Hz using the acousto-optic deflectors, and the laser position and bead displacement are recorded simultaneously. The effective intracellular stiffness K(f) is determined from the resultant displacement of the bead, x(f), subjected to an applied sinusoidal trap oscillation with force F_s at frequency, ω, using |K(f)| = F_s(f)/x(f).

Tracking intracellular movements

Endocytosed fluorescent beads are imaged using a 63×/1.2NA water immersion lens on a Leica TCS SP8. The motion of the fluorescent particles is recorded every 100 ms for 30 s and the images are processed using a custom written particle tracking algorithm^56,57 in MATLAB (The MathWorks, Natick, MA). Particle centers are found in each image with an accuracy of 10 nm. To avoid the cell-boundary effects and any possible interaction between the mechanically distinct cell cortex and nucleus, particles greater than 1 micron deep within the cell and away from both the thin lamellar region and the nucleus are imaged.

Statistics

All values are reported as the mean ± SE unless otherwise noted. Statistics is performed using the unpaired Student's t-test (*p < 0.05, **p < 0.01, ***p < 0.001). Linear regression is performed by using Origin Pro (OriginLab Corporation, MA, USA). Circular statistics is performed using ORIANA 4 software (Kovach Computing Services, Angelsey, Wales). The Watson U² and Rayleigh tests are used to assess the degree of uniformity of the cytoskeletal fibers. To check if the distribution of the fiber orientation is normally distributed, the Shapiro–Wilk test is performed using Origin Pro (OriginLab Corporation, MA, USA). We find that the data is not normally distributed and thus, we use the two-sample Kolmogorov–Smirnov test, a general non-parametric test, to compare the cytoskeletal distribution of the fibers.

Results

Geometric control of cell aspect ratio

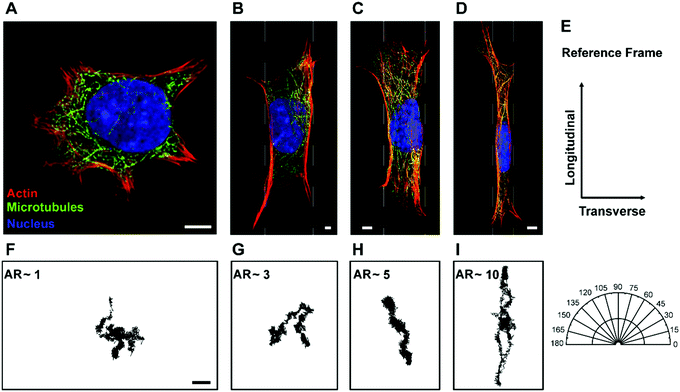
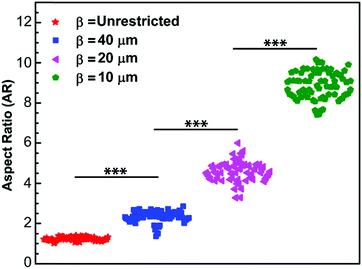
To naturally achieve cells with different aspect ratios, mEFs are cultured on unpatterned, β = unrestricted, and micropatterned strips of different widths, β = 10 μm, 20 μm and 40 μm (see Materials and methods) to confine the cells in one direction while allowing them to spread unrestricted in the other direction (Fig. 1A–D). To calculate the aspect ratio, we choose the principal axes through the center of the cells and measure the cell lengths. The longer side is always chosen as the longitudinal direction and the shorter side as the transverse direction (Fig. 1E). The distribution of aspect ratio of the cells grown on the unpatterned glass substrate, β = unrestricted, and cells cultured on the micropatterned strips of widths β = 10 μm, 20 μm and 40 μm are found to be AR = 1.24 ± 0.08, 8.88 ± 0.67, 4.62 ± 0.49 and 2.34 ± 0.28, respectively (n = 70) (mean ± SD) (Fig. 2). Control cells grown on the unpatterned strips are typically isotropic; however, as the width of the pattern decreases, cell morphology elongates.

Fig. 1 Geometric control of cell aspect ratio. (A–D) Fluorescent images of mEFs cultured on collagen strips of different widths, β = unrestricted, 40 μm, 20 μm and 10 μm, respectively, resulting in cells of different aspect ratios, AR ∼ 1, 3, 5 and 10, respectively, using micro-contact printing stained for actin (red), microtubules (green) and nucleus (blue) (scale bar: 5 μm). (E) Reference frame used in the present study. (E–G) Representative trajectories of a 500 nm endocytosed polystyrene bead in cells with different aspect ratios (scale bar: 0.2 μm). Movement of beads inside cells becomes highly anisotropic with increasing cell aspect ratio.

Fig. 2 Distribution of cell aspect ratio cultured on collagen strips of different widths, β = unrestricted, 40 μm, 20 μm and 10 μm, respectively, using micro-contact printing technique. As the width of the pattern decreases, an increase in the aspect ratio is observed.

Cell aspect ratio modifies cytoskeletal organization

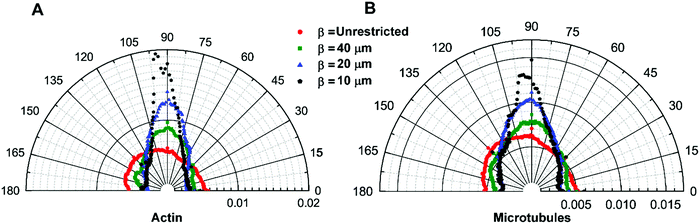
To understand how morphological changes affect the cytoskeletal organization of the cytoplasm, we stain actin filaments and microtubules to quantify their local orientation distribution (see Materials and methods). For the isotropic cells, β = unrestricted, both actin filaments and microtubules are isotropically distributed with uniform fractions of fibers oriented in every direction (Fig. 3A and B). This is confirmed by the Watson U² test and Rayleigh test for uniformity. As the aspect ratio of the cells increases, i.e., when they break symmetry, the distribution of the cytoskeletal fibers, namely, actin filaments and microtubules, becomes aligned preferentially in the longitudinal direction (Fig. 3A and B). We observe that the orientation of fibers is not normally distributed (Shapiro–Wilk test); therefore, we use a two-sample Kolmogorov–Smirnov test, a general non-parametric test, to compare the cytoskeletal distribution of the fibers and observe that the orientation of actin filaments and microtubules for different pattern widths is significantly different (Table S1, ESI†). For cells with the highest aspect ratio achieved in our study with width β = 10 μm, we observe significant cytoskeletal remodeling; the majority of actin and microtubules are aligned in the longitudinal direction as compared to the transverse direction. This confirms that cell shape can modify the cytoskeletal organization and can induce the network anisotropy of the cytoskeleton (Fig. 3A and B).

Fig. 3 Quantification of cytoskeletal anisotropy. (A and B) Histograms of actin and microtubule orientation as a function of aspect ratio, β. Data at each point represent the fraction of actin or microtubules aligned at a particular angle. Cells with low aspect ratio have an isotropic distribution of filaments; however, alignment of fibers in higher aspect ratio cells is biased in a particular direction (n = 25 cells per width (β)).

Cell aspect ratio induces anisotropy in cytoplasmic mechanics

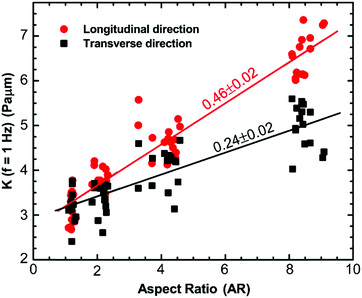
To investigate how the cytoskeletal reorganization modified due to changes in cell morphology alters the mechanical properties of the cells, we perform active microrheology measurements using optical tweezers to measure the micromechanical properties of the cytoplasm in the longitudinal and transverse directions. 500 nm diameter polystyrene beads are endocytosed into the cytoplasm of the cells. These beads go through the endocytic pathway and therefore are covered with lipid bi-layers. Consequently, occasionally, they are directionally transported along microtubules; however, most of the time, they exhibit random movement, as shown previously.^16,58 A bead is optically trapped and a sinusoidally oscillating force F_s(f) at the natural frequency, f, across a frequency range of 1–70 Hz, is applied using a piezo stage. This force results in the displacement, x(f), of the bead and thus, the effective spring constant of the intracellular environment can be calculated by K(f) = F_s(f)/x(f).^16,59 All the measurements are made using particles away from both the thin lamellar region and nucleus to prevent any contribution to the cytoplasmic stiffness from these mechanically distinct regions of the cells. For measurements in both directions within cells of different aspect ratios, an increase in the intracellular spring constant with frequency is observed, which follows the power-law form, |K(f)| ∝ f^α, with α ranging from 0.1 to 0.15 (Fig. S1A, B and Table S1, ESI†). This weak power-law behavior is consistent with that observed previously for cells and biopolymer networks.^16,43,59,60 Although a similar behavior in terms of frequency dependence is observed for all cases, the intracellular stiffness in both directions increases with an increase in the aspect ratio of the cells (Fig. S1A and B, ESI†). It is observed that unrestricted cells behave as an isotropic material where the intracellular stiffness, K(f), is of similar magnitude in both directions. However, when cells break symmetry, they start to exhibit anisotropic behavior. This behavior is consistent for all frequencies (Fig. S1B inset, ESI†). Specifically, at 1 Hz, we perform linear regression to show the dependence of intracellular stiffness on aspect ratio in both directions. It is observed that with an increase in aspect ratio, the intracellular stiffness increases for both directions; however, the increase in the longitudinal direction is faster than the transverse direction (Fig. 4). We also perform an unpaired Student's t-test to compare intracellular stiffness in both directions and find that they are significantly different (p < 0.0001). It increases with a slope of 0.46 ± 0.02 Pa μm with aspect ratio for the longitudinal direction; whereas, it increases with a slope of 0.24 ± 0.02 Pa μm in the transverse direction. As mentioned earlier, we find that for cells with aspect ratio AR ∼ 1, the cytoplasm behaves as an isotropic material showing that the ratio of the stiffness in different directions is ∼1; however, as the aspect ratio of the cell increases, the ratio of intracellular stiffness in the longitudinal and transverse directions increases at different rates, suggesting that the cells become anisotropic (Fig. 4). This behavior is consistent over the entire frequency range of the present study and can be explained by the fact that for cells with aspect ratio AR ∼ 1, the cytoskeletal filaments are uniformly distributed in all spatial directions, as shown in Fig. 3A and B, therefore, the cytoplasm behaves as an isotropic material; however, an increase in the cell aspect ratio introduces a bias in the distribution of cytoskeletal filaments, causing mechanical anisotropy.

Fig. 4 The variation of cytoplasmic stiffness, K, with aspect ratio measured using active microrheology with optical tweezers at 1 Hz in longitudinal and transverse directions. Solid lines are linear fits to the data. With increasing aspect ratio, the intracellular stiffness in the longitudinal direction increases at a rate faster compared to that of the transverse direction. Cells become mechanically anisotropic as the aspect ratio of the cells increases. Each data point is a single microrheology measurement in a cell (n = 60 cells).

Cell volume correlates with cell aspect ratio

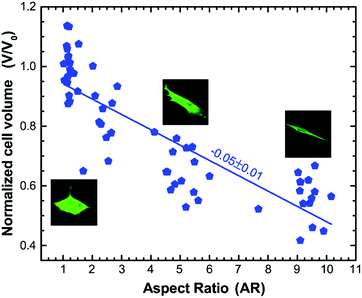
It has recently been shown that changes in cell volume correlate with changes in the mechanical properties of both the cytoplasm and the cell cortex.^51,52 To check if the change in mechanical properties observed due to varying cell aspect ratio also correlates with the change in cell volume, we use CellTracker™ and DRAQ5™ to label the cytoplasm and nucleus, respectively, and use three dimensional (3D) confocal microscopy to measure the volume of cells with different aspect ratios (see Materials and methods). The cell volume is normalized with the average volume of the cell grown on an unpatterned substrate (β = unrestricted), V₀ = 4376.75 μm³. We then perform linear regression to demonstrate the dependence of the normalized cell volume on aspect ratio. We find that the normalized volume of the cell decreases with a slope of −0.05 ± 0.01 with the increase in the cell aspect ratio (Fig. 5). This trend of decreasing cell volume with increase in the stiffness of the cytoplasm is consistent with that observed previously,^51,52 suggesting that the increase in overall stiffness of the cell with increasing aspect ratio is correlated to the reduction in cell volume.

Fig. 5 Normalized cell volume as a function of cell aspect ratio. The cell volume is normalized with the average volume of the cell grown on the unpatterned substrate (β = unrestricted). Cell volume decreases with an increase in the cell aspect ratio. Solid line is a linear fit to the data (n = 60 cells).

Cell aspect ratio regulates anisotropy in intracellular motion

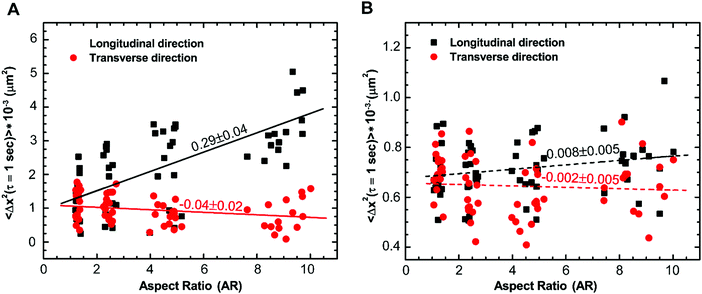
To confirm that cytoskeletal reorganization indeed changes the intracellular motion inside the cytoplasm, we quantify the movement of 500 nm endocytosed particles for cells with different aspect ratios. Mean square displacements (MSDs) of tracer particles in longitudinal and transverse directions are measured using confocal microscopy. We find the centers of fluorescent particles in each image, track their trajectories (Fig. 1F–I) and measure the one-dimensional time- and ensemble-averaged MSD, 〈Δx²(τ)〉, where, Δx(τ) = x(t + τ) − x(t), in both directions. Particles imaged are greater than 1 micron deep within the cell and away from both the thin lamellar region and the nucleus to avoid any effects from the cell cortex and the mechanically distinct regions. The MSD in the longitudinal direction monotonically increases with increasing aspect ratio or decreasing width of the micropatterned strip (Fig. S2A, ESI†). However, a reverse trend showing a decrease in MSD with an increase in aspect ratio in the transverse direction is observed (Fig. S2B, ESI†). This anisotropic behavior of intracellular motion is more evident at long time scales as active forces become highly dominant in this regime (Fig. S2B inset, ESI†).^18,43 For a specific lag time, τ = 1 s, we again perform linear regression to show the dependence of MSD on aspect ratio. The MSD in the longitudinal direction increases with a slope of 0.29 ± 0.04 μm² and decreases marginally with a slope of −0.04 ± 0.02 μm² with an increase in aspect ratio (Fig. 6A). Moreover, using the unpaired Student's t-test, we confirm that the MSDs are significantly different in both directions (p < 0.0001). For unrestricted cells, the intracellular motion appears to be isotropic as 〈Δx²〉_Longitudinal/〈Δx²〉_Transverse is ∼1; however, as the aspect ratio of cells increases, this ratio deviates from 1, suggesting that the intracellular motion becomes anisotropic. These results show that the cytoskeletal reorganization induced by cell morphology not only causes mechanical anisotropy but also results in anisotropy of the intracellular movement.

Fig. 6 The MSD, 〈Δx²(τ)〉, of 500 nm tracer particles in longitudinal and transverse directions at τ = 1 s. (A) MSD is observed to increase in longitudinal direction and marginally decrease in transverse direction with an increase in aspect ratio. (B) For cytochalasin D treated cells, MSDs in longitudinal and transverse directions at τ = 1 s remain similar in both directions upon an increase in aspect ratio magnitude suggesting anisotropy in intracellular movement can possibly be attributed to alignment of actin and related forces in the longitudinal direction. Solid lines are linear fits to the data that have a slope significantly different from zero. Dotted lines are linear fits to the data that have a slope not significantly different from zero. Each data point is a single measurement in a cell (n = 60 cells).

The majority of intracellular fluctuations are typically attributed to a combination of thermal agitation and random active forces such as that generated by myosin II motors that bind with actin filaments to cause acto-myosin contractility.^16,49,61 Therefore, to investigate if the alignment of actin structures is the major cause of the dynamic anisotropy, we disrupt the actin cytoskeleton by treating cells with cytochalasin D. We find that the MSD curves for different aspect ratios collapse in both the longitudinal and transverse directions regardless of the cell aspect ratio; the anisotropic behavior disappears (Fig. S3A and B, ESI†) and this behavior is consistent for all values of lag time (Fig. S3B inset, ESI†). We plot the distribution of MSDs with aspect ratio at lag time τ = 1 s and perform linear regression to show the dependence with increasing aspect ratio. It is observed that it is indistinguishable with a slope that is not significantly different from zero in both the longitudinal and transverse directions (Fig. 6B). This result suggests that actin cytoskeleton and its associated activities are crucial for the anisotropic intracellular motion.

Cell aspect ratio regulates anisotropy in intracellular forces

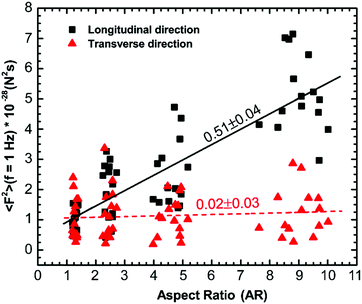
Our results suggest that cytoskeletal reorganization due to changes in cell morphology leads to anisotropy in the intracellular forces. To confirm this, we use force spectrum microscopy (FSM)⁴³ to measure the spectrum of forces for cells with different aspect ratios in both the longitudinal and transverse directions. FSM can be used to directly measure the spectrum of aggregate fluctuating forces that drive the intracellular motion by combining the MSD of tracer particles and independent micromechanical measurements of the intracellular environment using 〈F²(f)〉 = |K(f)|²〈x²(f)〉. The force in the longitudinal direction increases monotonically with an increase in the aspect ratio of cells; however, the force spectrum in the transverse direction remains indistinguishable with an increase in the aspect ratio (Fig. S4A and B, ESI†). We quantify the anisotropy in intracellular forces in terms of the ratio of forces in the longitudinal and transverse directions, 〈F²〉_Longitudinal/〈F²〉_Transverse, over the entire frequency range of the present study (Fig. S4 inset, ESI†). For forces below frequencies of ∼2 Hz, the trend of increasing anisotropy with aspect ratio observed is consistent as the forces are active in origin; however, at higher frequencies, the thermal noise is dominant and the thermal fluctuating forces are similar in magnitude and indistinguishable.^18,43 It is worth mentioning that the spectrum of active force fluctuations varies with a slope of ∼−2 with frequency, which is consistent with previous studies^18,43 and does not change significantly with a change in aspect ratio. We find that the intracellular forces in different directions are significantly different (p < 0.0001) and then use linear regression to demonstrate the dependence of intracellular forces in different directions at a frequency of 1 Hz. The longitudinal intracellular force fluctuation increases with a slope of 0.51 ± 0.04 N² s and the transverse force fluctuation remains indistinguishable with an increase in aspect ratio (Fig. 7). The slope of force in the transverse direction with increasing aspect ratio calculated from linear regression was 0.02 ± 0.03 N² s, which was not significantly different from zero. Our force measurements also reveal an overall increase in the intracellular force when the cell aspect ratio increases. Therefore, the intracellular force fluctuations appear to be isotropic for cells with aspect ratio AR ∼ 1; however, the intracellular force fluctuations become anisotropic as the cell aspect ratio increases. This shows that the cytoskeletal reorganization induced by cell morphology results in anisotropic forces.

Fig. 7 Variation of cytoplasmic force, 〈F²(f)〉, calculated from intracellular movement and active microrheology measurement using force spectrum microscopy in longitudinal and transverse directions with aspect ratio at f = 1 Hz. Force is observed to increase in the longitudinal direction and remain unchanged in the transverse direction with an increase in aspect ratio. Solid lines are linear fits to the data that have a slope significantly different from zero. Dotted lines are linear fits to the data that have a slope not significantly different from zero. Each data point is a single measurement in a cell (n = 60 cells).

Discussion

The cytoplasm of a living cell experiences significant redistribution of the cytoskeletal components such as actin filaments and microtubules while undergoing morphological changes; in particular, when the cell shape deviates from isotropicity. This induces anisotropic behavior in both the mechanics and dynamics of the cytoplasm. We use micro-contact printing to confine cells in one direction and let them grow unrestricted in another direction to achieve cells with different aspect ratios (Fig. 1 and 2) and we measure the local orientation of actin filaments and microtubules. Unrestricted cells with aspect ratio AR ∼1 have randomly distributed actin filaments and microtubules, suggesting an isotropic distribution; however, as the aspect ratio increases, cytoskeletal filaments preferentially align in the longitudinal direction (Fig. 3). This causes structural anisotropy of the cytoplasm, resulting in directionally dependent intracellular mechanics and dynamics. Our active microrheology measurements using optical tweezers show that cells with aspect ratio AR ∼ 1 have a similar value of intracellular stiffness in both the longitudinal and transverse directions, indicating isotropic behavior. As the cell aspect ratio increases, the intracellular mechanics deviates from isotropicity, showing an increase in stiffness in both the longitudinal and transverse directions with different rates; intracellular stiffness increases faster in the longitudinal direction in comparison to the transverse direction with an increase in cell aspect ratio (Fig. 4). This can be explained by the fact that mechanical stress in the plane parallel to the cytoskeletal fibers primarily results in the stretching of the fibers, whereas in the plane perpendicular to the fibers, the deformation is dominated by bending. The bending modulus of major cytoskeletal fibers, such as F-actin and microtubules, has been shown to be significantly lower compared to its stretching elastic modulus and thus, this results in a greater stiffness in the longitudinal direction for elongated cells.^62–65

Moreover, to investigate the potential cause of the increase in stiffness in both directions upon increasing cell aspect ratio, we measure the volume of cells with different aspect ratios. We find that an increase in the cell aspect ratio results in a significant reduction of cell volume (Fig. 5). The observed increase in stiffness with reduction in cell volume is consistent with previous findings where cell volume reduction due to cellular water efflux increased the cytoplasmic stiffness by increasing the concentration of the intracellular components.^51,52

It is evident that changes in cell morphology induce cytoskeletal remodeling (Fig. 1 and 3) and as molecular motors work in conjunction with the cytoskeletal fibers, this could possibly change the intracellular movement. By quantifying the motion of 500 nm tracer particles in terms of MSD, we show that the intracellular movement also becomes anisotropic when cells break symmetry. The cells with aspect ratio AR ∼ 1 behave as an isotropic material as the MSD in both longitudinal and transverse directions is of similar magnitude. However, as the cell aspect ratio increases, we observe a marked increase of MSD in the longitudinal direction and decrease in the transverse direction, demonstrating that the intracellular motion becomes anisotropic (Fig. 6A). It has been shown that actin cytoskeleton is a major player in random intracellular fluctuations; we thus use cytochalasin D to disrupt actin cytoskeleton to investigate its role in regulating anisotropic dynamics in the cytoplasm. We observe that MSDs in both the longitudinal and transverse directions collapse and the anisotropy in intracellular dynamics disappears (Fig. 6B). This suggests that alignment of actin filaments is the major player in regulating anisotropy in intracellular dynamics in elongated cells. However, this idea of actin structure regulating the anisotropic movement is non-trivial as the active forces and the cytoskeletal structures are correlated. This arises due to the fact that molecular motors, which are the major source of forces inside the cells, work in conjunction with the structure of the cytoskeleton.^61,66 Moreover, the direction of forces due to polymerization and depolymerization of cytoskeletal filaments also correlates with the structure of the cytoskeleton.^67–69 Therefore, it is likely that the alignment of the actin cytoskeleton and the biased forces due to this alignment together result in the anisotropic dynamics when cells break symmetry. Nonetheless, this behavior of the anisotropic MSD with an increase in aspect ratio can be explained with our aggregate intracellular force measurements quantified using FSM. The intracellular force in the longitudinal direction increases with increasing aspect ratio. In fact, this increase in the force that drives the intracellular movement is more significant compared to the increase in resistance quantified in terms of stiffness, thereby, increasing the MSD in the longitudinal direction with increasing aspect ratio. The force in the transverse direction, however, remains unchanged as the aspect ratio increases; therefore, an increase in stiffness in this direction reduces the MSD correspondingly. FSM also reveals that for the unrestricted cells, the intracellular forces in the longitudinal and transverse directions are of comparable magnitude; this result further confirms that these cells have isotropic dynamics (Fig. 7). However, as the aspect ratio of the cells increases, they deviate from isotropicity and depict anisotropic or directionally dependent forces (Fig. 7), showing that anisotropy in intracellular force fluctuations can be caused as a result of changes in cell morphology. It is also interesting to note that the point of transition from the plateau (short time scale) to the apparent diffusive (long time scale) behavior of MSD occurs later in the transverse direction. This is possibly due to less power being injected by the active components in the transverse direction and is consistent with our force spectrum measurements (Fig. S2, ESI†). It is worth mentioning that it has recently been demonstrated that cells operate far from equilibrium;^43–45 therefore, the intracellular movement is determined by both the cytoplasmic mechanical properties and intracellular non-equilibrium forces. Hence, just observing the intracellular fluctuations does not provide us with information about the mechanical properties of the cell,^18,43–45 with an exception for high frequencies.¹⁸ For example, our approach of using active microrheology in combination with particle tracking reveals that the increase in MSD with aspect ratio is due to increased intracellular forces rather than a decrease in the stiffness in the longitudinal direction.

In conclusion, our results systematically show that cell morphology is a critical regulator of the anisotropic behavior of mechanics, dynamics, and forces within the cytoplasm. We demonstrate that the anisotropy in mechanics arises as a consequence of the alignment of cytoskeletal components and the anisotropy in dynamics is mainly due to the generation of anisotropic forces and biased cytoskeletal structures. It has been observed in previous studies with different cells such as endothelial cells, epithelial cells, fibroblasts, etc. that elongated cells have aligned cytoskeletal filaments.^70–72 The observed anisotropic mechanics, dynamics and forces in the present study are indeed a result of cytoskeletal remodeling into a more aligned structure when cells break symmetry. Therefore, we anticipate that these observations should hold generally for different cell types. Our results suggest that it is important to consider the directional dependence of intracellular mechanics, dynamics and forces under the conditions when the cell shape deviates from isotropicity. This fundamental understanding of how cell polarity influences the mechanics and dynamics of living mammalian cells will lend deeper insight into the physical understanding of biological processes such as migration, differentiation, cancer extravasation and intravasation, etc., where cell polarity is induced.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by National Cancer Institute Grant 1U01CA202123, and the Department of Mechanical Engineering at Massachusetts Institute of Technology.

References

1. J. R. Lange and B. Fabry, Cell and tissue mechanics in cell migration, Exp. Cell Res., 2013, 319(16), 2418–2423.
2. P. Recho, T. Putelat and L. Truskinovsky, Mechanics of motility initiation and motility arrest in crawling cells, J. Mech. Phys. Solids, 2015, 84, 469–505.
3. M. Mak, et al., Single-cell migration in complex microenvironments: mechanics and signaling dynamics, J. Biomech. Eng., 2016, 138(2), 021004.
4. N. Wang, J. P. Butler and D. E. Ingber, Mechanotransduction across the cell surface and through the cytoskeleton, Science, 1993, 260(5111), 1124–1127.
5. S. Suresh, Biomechanics and biophysics of cancer cells, Acta Biomater., 2007, 3(4), 413–438.
6. S. Heyden and M. Ortiz, Oncotripsy: targeting cancer cells selectively via resonant harmonic excitation, J. Mech. Phys. Solids, 2016, 92, 164–175.
7. J. E. Kim, et al., Characterization of the mechanical properties of cancer cells in 3D matrices in response to collagen concentration and cytoskeletal inhibitors, Integr. Biol., 2018, 10(4), 232–241.
8. M. Mak, et al., Integrated Analysis of Intracellular Dynamics of MenaINV Cancer Cells in a 3D Matrix, Biophys. J., 2017, 112(9), 1874–1884.
9. F. Spill, et al., Impact of the physical microenvironment on tumor progression and metastasis, Curr. Opin. Biotechnol., 2016, 40, 41–48.
10. M. H. Zaman, The role of engineering approaches in analysing cancer invasion and metastasis, Nat. Rev. Cancer, 2013, 13(8), 596.
11. S. E. Leggett, A. S. Khoo and I. Y. Wong, Multicellular tumor invasion and plasticity in biomimetic materials, Biomater. Sci., 2017, 5(8), 1460–1479.
12. G. Bao and S. Suresh, Cell and molecular mechanics of biological materials, Nat. Mater., 2003, 2(11), 715–725.
13. J. M. Maloney, et al., Mesenchymal Stem Cell Mechanics from the Attached to the Suspended State, Biophys. J., 2010, 99(8), 2479–2487.
14. R. M. Hochmuth, Micropipette aspiration of living cells, J. Biomech., 2000, 33(1), 15–22.
15. A. R. Bausch, W. Möller and E. Sackmann, Measurement of local viscoelasticity and forces in living cells by magnetic tweezers, Biophys. J., 1999, 76(1 Pt 1), 573–579.
16. M. Guo, et al., The Role of Vimentin Intermediate Filaments in Cortical and Cytoplasmic Mechanics, Biophys. J., 2013, 105(7), 1562–1568.
17. M. Dao, C. T. Lim and S. Suresh, Mechanics of the human red blood cell deformed by optical tweezers, J. Mech. Phys. Solids, 2003, 51(11), 2259–2280.
18. S. K. Gupta and M. Guo, Equilibrium and out-of-equilibrium mechanics of living mammalian cytoplasm, J. Mech. Phys. Solids, 2017, 107, 284–293.
19. J. Hu, et al., Size-and speed-dependent mechanical behavior in living mammalian cytoplasm, Proc. Natl. Acad. Sci. U. S. A., 2017, 201702488.
20. A. J. Ehrlicher, et al., Alpha-actinin binding kinetics modulate cellular dynamics and force generation, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(21), 6619–6624.
21. C. Yeaman, K. K. Grindstaff and W. J. Nelson, New perspectives on mechanisms involved in generating epithelial cell polarity, Physiol. Rev., 1999, 79(1), 73–98.
22. C. Hidalgo-Carcedo, et al., Collective cell migration requires suppression of actomyosin at cell-cell contacts mediated by DDR1 and the cell polarity regulators Par3 and Par6, Nat. Cell Biol., 2011, 13(1), 49.
23. J. Huelsken, et al., β-Catenin controls hair follicle morphogenesis and stem cell differentiation in the skin, Cell, 2001, 105(4), 533–545.
24. M. Ziman, et al., Subcellular localization of Cdc42p, a Saccharomyces cerevisiae GTP-binding protein involved in the control of cell polarity, Mol. Biol. Cell, 1993, 4(12), 1307–1316.
25. A. Wodarz, Tumor suppressors: linking cell polarity and growth control, Curr. Biol., 2000, 10(17), R624–R626.
26. R. M. Hershberg and L. F. Mayer, Antigen processing and presentation by intestinal epithelial cells–polarity and complexity, Immunol. Today, 2000, 21(3), 123–128.
27. D. G. Drubin, Development of cell polarity in budding yeast, Cell, 1991, 65(7), 1093–1096.
28. M. Théry, et al., Anisotropy of cell adhesive microenvironment governs cell internal organization and orientation of polarity, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(52), 19771–19776.
29. P. W. Oakes, et al., Geometry regulates traction stresses in adherent cells, Biophys. J., 2014, 107(4), 825–833.
30. A. Zemel, et al., Optimal matrix rigidity for stress-fibre polarization in stem cells, Nat. Phys., 2010, 6(6), 468–473.
31. N. Wang, et al., Micropatterning tractional forces in living cells, Cytoskeleton, 2002, 52(2), 97–106.
32. I. M. Tolić-Nørrelykke and N. Wang, Traction in smooth muscle cells varies with cell spreading, J. Biomech., 2005, 38(7), 1405–1412.
33. S. Hu, et al., Mechanical anisotropy of adherent cells probed by a three-dimensional magnetic twisting device, Am. J. Physiol.: Cell Physiol., 2004, 287(5), C1184–C1191.
34. J. C. Del Alamo, et al., Anisotropic rheology and directional mechanotransduction in vascular endothelial cells, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(40), 15411–15416.
35. P. G. Smith, et al., Mechanical strain increases cell stiffness through cytoskeletal filament reorganization, Am. J. Physiol.: Lung Cell. Mol. Physiol., 2003, 285(2), L456–L463.
36. J. Su, et al., Geometric Confinement Influences Cellular Mechanical Properties II-Intracellular Variances in Polarized Cells, Mol. Cell. Biomech., 2007, 4(2), 105.
37. M. Irmscher, et al., Probing the cell membrane by magnetic particle actuation and Euler angle tracking, Biophys. J., 2012, 102(3), 698–708.
38. N. Hirokawa, Kinesin and dynein superfamily proteins and the mechanism of organelle transport, Science, 1998, 279(5350), 519–526.
39. R. D. Vale, The molecular motor toolbox for intracellular transport, Cell, 2003, 112(4), 467–480.
40. J. Howard, Molecular motors: structural adaptations to cellular functions, Nature, 1997, 389(6651), 561–567.
41. K. E. Kasza and J. A. Zallen, Dynamics and regulation of contractile actin–myosin networks in morphogenesis, Curr. Opin. Cell Biol., 2011, 23(1), 30–38.
42. A. W. Lau, et al., Microrheology, stress fluctuations, and active behavior of living cells, Phys. Rev. Lett., 2003, 91(19), 198101.
43. M. Guo, et al., Probing the Stochastic, Motor-Driven Properties of the Cytoplasm Using Force Spectrum Microscopy, Cell, 2014, 158(4), 822–832.
44. É. Fodor, et al., Activity-driven fluctuations in living cells, EPL, 2015, 110(4), 48005.
45. N. Fakhri, et al., High-resolution mapping of intracellular fluctuations using carbon nanotubes, Science, 2014, 344(6187), 1031–1035.
46. C. Wilhelm, Out-of-equilibrium microrheology inside living cells, Phys. Rev. Lett., 2008, 101(2), 028101.
47. D. J. Sharp, G. C. Rogers and J. M. Scholey, Microtubule motors in mitosis, Nature, 2000, 407(6800), 41–47.
48. M. L. Gardel, et al., Mechanical integration of actin and adhesion dynamics in cell migration, Annu. Rev. Cell Dev. Biol., 2010, 26, 315–333.
49. M. Murrell, et al., Forcing cells into shape: the mechanics of actomyosin contractility, Nat. Rev. Mol. Cell Biol., 2015, 16(8), 486–498.
50. S. Mahammad, et al., Giant axonal neuropathy–associated gigaxonin mutations impair intermediate filament protein degradation, J. Clin. Invest., 2013, 123(5), 1964–1975.
51. M. Guo, et al., Cell volume change through water efflux impacts cell stiffness and stem cell fate, Proc. Natl. Acad. Sci. U. S. A., 2017, 201705179.
52. E. H. Zhou, et al., Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(26), 10632–10637.
53. R. Rezakhaniha, et al., Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy, Biomech. Model. Mechanobiol., 2012, 11(3), 461–473.
54. M. Théry and M. Piel, Adhesive micropatterns for cells: a microcontact printing protocol, Cold Spring Harbor Protocols, 2009, 2009(7) DOI:10.1101/pdb.prot5255.
55. C. Veigel, et al., The stiffness of rabbit skeletal actomyosin cross-bridges determined with an optical tweezers transducer, Biophys. J., 1998, 75(3), 1424–1438.
56. V. Pelletier, et al., Microrheology of microtubule solutions and actin-microtubule composite networks, Phys. Rev. Lett., 2009, 102(18), 188303.
57. J. C. Crocker and D. G. Grier, Methods of digital video microscopy for colloidal studies, J. Colloid Interface Sci., 1996, 179(1), 298–310.
58. A. G. Hendricks, E. L. Holzbaur and Y. E. Goldman, Force measurements on cargoes in living cells reveal collective dynamics of microtubule motors, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(45), 18447–18452.
59. D. Mizuno, et al., Nonequilibrium mechanics of active cytoskeletal networks, Science, 2007, 315(5810), 370–373.
60. B. Fabry, et al., Scaling the microrheology of living cells, Phys. Rev. Lett., 2001, 87(14), 148102.
61. M. Schliwa and G. Woehlke, Molecular motors, Nature, 2003, 422(6933), 759–765.
62. H. Higuchi, T. Yanagida and Y. E. Goldman, Compliance of thin filaments in skinned fibers of rabbit skeletal muscle, Biophys. J., 1995, 69(3), 1000–1010.
63. F. Gittes, et al., Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape, J. Cell Biol., 1993, 120, 923.
64. D. J. Needleman, et al., Radial compression of microtubules and the mechanism of action of taxol and associated proteins, Biophys. J., 2005, 89(5), 3410–3423.
65. J. Howard, Mechanics of motor proteins and the cytoskeleton, Sinauer Associates, Publishers. xvi, Sunderland, Mass., 2001, p. 367.
66. J. A. Spudich, How molecular motors work, Nature, 1994, 372(6506), 515–518.
67. A. Mogilner and G. Oster, Polymer motors: pushing out the front and pulling up the back, Curr. Biol., 2003, 13(18), R721–R733.
68. A. Desai and T. J. Mitchison, Microtubule polymerization dynamics, Annu. Rev. Cell Dev. Biol., 1997, 13(1), 83–117.
69. A. Mogilner and G. Oster, Force generation by actin polymerization II: the elastic ratchet and tethered filaments, Biophys. J., 2003, 84(3), 1591–1605.
70. M. Versaevel, T. Grevesse and S. Gabriele, Spatial coordination between cell and nuclear shape within micropatterned endothelial cells, Nat. Commun., 2012, 3, 671.
71. K. Lee, et al., Contribution of actin filaments and microtubules to cell elongation and alignment depends on the grating depth of microgratings, J. Nanobiotechnol., 2016, 14(1), 35.
72. T. Ishizaki, et al., Coordination of microtubules and the actin cytoskeleton by the Rho effector mDia1, Nat. Cell Biol., 2001, 3(1), 8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm01708e

---