Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling the dynamics of colloidal particles by critical Casimir forces
Alessandro Magazzù *a,
Agnese Callegari
*a,
Agnese Callegari b,
Juan Pablo Staforellic,
Andrea Gambassi
b,
Juan Pablo Staforellic,
Andrea Gambassi d,
Siegfried Dietrichef and
Giovanni Volpe
d,
Siegfried Dietrichef and
Giovanni Volpe ab
ab
aDepartment of Physics, University of Gothenburg, SE-41296 Gothenburg, Sweden. E-mail: alessandro.magazzu@physics.gu.se
bSoft Matter Lab, Department of Physics and UNAM – National Nanotechnology Research Center, Bilkent University, Ankara 06800, Turkey
cDepartment of Physics, University of Concepción, 160-C, Concepción, Chile
dSISSA – International School for Advanced Studies and INFN, 34136 Trieste, Italy
eMax Planck Institute for Intelligent Systems, 70569 Stuttgart, Germany
fIVth Institute for Theoretical Physics, University of Stuttgart, 70569 Stuttgart, Germany
First published on 23rd January 2019
Abstract
Critical Casimir forces can play an important role for applications in nano-science and nano-technology, owing to their piconewton strength, nanometric action range, fine tunability as a function of temperature, and exquisite dependence on the surface properties of the involved objects. Here, we investigate the effects of critical Casimir forces on the free dynamics of a pair of colloidal particles dispersed in the bulk of a near-critical binary liquid solvent, using blinking optical tweezers. In particular, we measure the time evolution of the distance between the two colloids to determine their relative diffusion and drift velocity. Furthermore, we show how critical Casimir forces change the dynamic properties of this two-colloid system by studying the temperature dependence of the distribution of the so-called first-passage time, i.e., of the time necessary for the particles to reach for the first time a certain separation, starting from an initially assigned one. These data are in good agreement with theoretical results obtained from Monte Carlo simulations and Langevin dynamics.
1 Introduction
Critical Casimir forces (CCFs) arise in a binary liquid mixture close to its critical point.1–5 Upon approaching the critical point, fluctuations of the composition of the mixture emerge. If these critical fluctuations are confined between neighboring objects (e.g., two colloids, or a colloid and a planar surface), they lead to effective forces between these objects. These so-called CCFs were first predicted theoretically in 1978 by M. E. Fisher and P. G. de Gennes1 in analogy to quantum-electrodynamical (QED) Casimir forces.6 Only recently have they been measured directly7–9 and proved to be relevant for soft matter.10–12 These CCFs have been enjoying significant interest both from basic research and because they are promising candidates for applications in nano-science and nano-technology, in order to manipulate objects (e.g., by controllable periodic deformations of chains), to assemble devices (e.g., via the self-assembly of colloidal molecules13,14), and to drive machines (e.g., by powering rotators15) at the nano- and micro-meter scale. In fact, their piconewton strength and nanometric ranges of action match the requirements of nano-technology. Furthermore, these forces show an exquisite dependence on the temperature of the environment and on the chemical surface properties of the objects involved.4,5,8,16,17 For example, if composition fluctuations are confined between particles with the same surface property (e.g., hydrophilic), attractive CCFs take hold, while they are repulsive between particles with opposite surface properties (e.g., hydrophilic vs. hydrophobic particles). With the exception of ref. 18, until now, the experimental studies have focused on the time-independent properties of CCFs and thus keeping their dynamics hidden. Here, we use blinking optical tweezers to reveal how CCFs affect the free dynamics of a pair of colloidal particles immersed in a binary solution.2 Experimental setup and methods
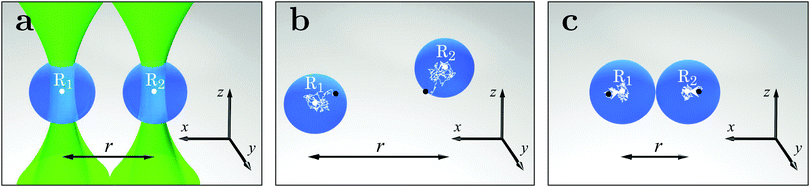
In our experiment, we use silica microspheres with diameter d = 2.06 ± 0.05 μm (Microparticles GmbH), dispersed in a critical mixture of water and 2,6-lutidine at the critical lutidine mass fraction ccL = 0.286, corresponding to a lower critical point at the temperature Tc ≃ 34 °C.19,20 In the bulk of the critical mixture, we generate two holographic optical traps21,22 at positions R0,1 and R0,2 in order to fix the positions R1 and R2 of the centers of two spherical colloids at their initial values, approximately equal to R0,1 and R0,2, respectively, with a specified center-to-center distance r0 = 2.40 μm (Fig. 1a). We have chosen this value for r0 such that the resulting surface-to-surface distance between the two colloids is of the order of 300 nm. Accordingly, the latter is significantly larger than the range of the electrostatic repulsion (which holds up to a surface-to-surface distance of about 100 nm, because the Debye screening length is![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≃ 13 nm9,20) and comparable with the largest range of the CCFs achieved in the present experiment (which here are always negligible beyond ≈300 nm). Given the sensitivity of CCFs to temperature, the sample temperature is stabilized to within ±2 mK9via a feedback controller, through the microscope objective. Although the objective is the closest metallic element to the trapping region, the actual temperature of the liquid mixture may differ slightly from the one measured at the objective. The values of the temperature reported in this paper are those of the mixture, which we infer a posteriori from the data analysis according to the method discussed in detail in ref. 9. The scheme of the experimental setup is presented in Fig. 2.
D ≃ 13 nm9,20) and comparable with the largest range of the CCFs achieved in the present experiment (which here are always negligible beyond ≈300 nm). Given the sensitivity of CCFs to temperature, the sample temperature is stabilized to within ±2 mK9via a feedback controller, through the microscope objective. Although the objective is the closest metallic element to the trapping region, the actual temperature of the liquid mixture may differ slightly from the one measured at the objective. The values of the temperature reported in this paper are those of the mixture, which we infer a posteriori from the data analysis according to the method discussed in detail in ref. 9. The scheme of the experimental setup is presented in Fig. 2.
We periodically chop the laser beam at the blinking frequency fb = 1.3 Hz so that the optical traps are periodically switched on and off (blinking optical tweezers23–25). We have chosen this value of fb because it is sufficiently low in order to be able to observe the effects of CCFs on the particle dynamics in the xy-plane and high enough to permit us to neglect the effects of gravity on the vertical position z of the particle. We record the ensuing motion of the colloids at 300 fps during the time windows in which the beam is blocked and hence the optical potential is not present. When the traps are turned on again, the two colloids are brought back to their initial positions by the restoring forces of the optical potentials. If the temperature T of the mixture is sufficiently far from Tc (i.e., ΔT = Tc − T ≳ 500 mK), the two particles freely diffuse in the solution as long as the optical traps are off (Fig. 1b). When ΔT → 0, critical order parameter fluctuations take hold associated with an increasing correlation length ξ. As ξ becomes comparable to the inter-particle distance r, the two hydrophilic particles experience attractive CCFs, which affect their dynamics and reduce their inter-particle distance (Fig. 1c). The entire blinking process is repeated about 400 times for each fixed value of ΔT → 0 in order to acquire sufficient statistics for the dynamics of the colloids.
We have analyzed the acquired videos using digital video microscopy22,26 in order to determine the trajectories r1(t) and r2(t) of the centers of the two particles projected onto the xy-plane, where rl(t) = (xl(t),yl(t)) with l = 1,2 labelling the particles. We correct the relative position of the particles r(t) = r2(t) − r1(t) and their relative distance r(t) = |r(t)| to account for artefacts which appear in digital video microscopy due to the proximity between the two particles.9,27
3 Data analysis and results
3.1 Particle trajectories and time evolution of the inter-particle distance probability density
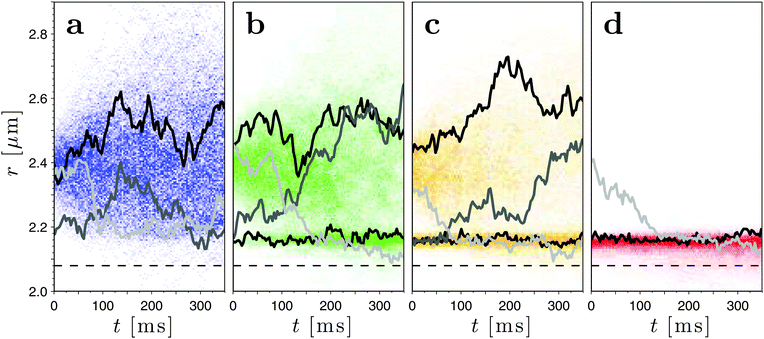
In Fig. 3 several inter-particle projected distances r(t) are reported for decreasing values of ΔT. For each value of ΔT, we plot the evolution of the inter-particle distance probability density as a function of time obtained from 400 particle trajectories by binning (colored background). We highlight a few selected trajectories to illustrate typical behaviors of the particles (solid lines). For ΔT = 456 ± 2 mK (Fig. 3a), the particles are diffusing freely and the CCFs do not affect their behavior. Heuristically, this is suggested by the fact that the probability density of the inter-particle distance is rather broad compared to what is observed closer to criticality. More quantitatively, the absence of CCFs is proved by the analysis presented further below. When ΔT is reduced to ΔT = 200 ± 2 mK (Fig. 3b) and 163 ± 2 mK (Fig. 3c), the CCFs arise and affect the dynamics of the colloids. Occasionally they cause adhesion as can be inferred from the emergence of a peak in the inter-particle distance probability density at r ≈ 2.16 μm. If ΔT is reduced further to ΔT = 108 ± 2 mK (Fig. 3d), strong attractive CCFs hinder the free diffusion of the particles, which often adhere to each other so that the values of r lie within a small region in which there is a balance between the repulsive electrostatic forces and the attractive CCFs.3.2 Equilibrium distributions and parameter fitting
At a specific temperature ΔT, the initial values r1,2(0) of the recorded trajectories are sampled from the equilibrium distribution of the two trapped particles exposed to the optical potentials Vot,1(R1) + Vot,2(R2), to the electrostatic repulsion Ves(ρ), and possibly to CCFs VC(ρ), i.e., to the total potential| V(R1,R2) = Vot,1(R1) + Vot,2(R2) + Ves(ρ) + VC(ρ), | (1) |
 | (2) |
For the electrostatic repulsion potential Ves, we consider the simple expression9,20
Ves(ρ) = kBTc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−(ρ−ρes)/ e−(ρ−ρes)/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D, D,
| (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D is the Debye screening length.9,20
D is the Debye screening length.9,20
For the potential VC of the CCFs, we adopt the theoretical prediction
 | (4) |
 , where we remind that rl is the projection of Rl onto the xy-plane. These distributions are reported in Fig. 4 for the same values of ΔT as considered in Fig. 3. The histograms represent the experimentally measured data, and the solid lines are the corresponding theoretical results obtained from the Monte Carlo integration of Peq(R1,R2), introduced above.
, where we remind that rl is the projection of Rl onto the xy-plane. These distributions are reported in Fig. 4 for the same values of ΔT as considered in Fig. 3. The histograms represent the experimentally measured data, and the solid lines are the corresponding theoretical results obtained from the Monte Carlo integration of Peq(R1,R2), introduced above.
 | ||
| Fig. 4 Equilibrium distribution Peq(r) of the inter-particle distance r(0) (i.e., when the optical tweezers are switched off) for two optically trapped colloids at temperatures (a) ΔT = 456 ± 2 mK, (b) 200 ± 2 mK, (c) 163 ± 2 mK, and (d) 108 ± 2 mK. Each histogram is obtained from 400 different experimental values. The solid black lines are the theoretical distribution of r(0), obtained via Monte Carlo integration (106 samples) of two optically trapped particles subjected to the theoretical total potential V(R1,R2) (eqn (1)). | ||
For ΔT = 456 ± 2 mK (Fig. 4a), Peq(r) can be very well approximated by a Gaussian distribution centered at the value r ≃ 2.40 μm, corresponding to the distance r0 between the minima of the two optical potentials. This result is expected for two optically trapped particles which do not interact with each other.22 Reducing ΔT (Fig. 4b–d), a peak arises at r ≃ 2.16 μm on the left flank of the Gaussian distribution, becoming more dominant at the expense of the Gaussian distribution. This is due to the gradual emergence of attractive CCFs between the particles, which causes them to adhere to each other also in the presence of the optical potentials. The peak position indicates the region where the repulsive electrostatic forces and the attractive CCFs are balanced.
By using Monte Carlo integration, we also calculated the distribution Peq(r) on the basis of the theoretical potential V(R1,R2). In particular, we have used Vot,l(Rl) (eqn (2)) and Θ(ρ/ξ) (eqn (4)) as input functions and ρes, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D, and ξ as fitting parameters. It is worth noting that the fitting parameters ρes and
D, and ξ as fitting parameters. It is worth noting that the fitting parameters ρes and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D are assumed to take the same values for all experimental acquisitions at the various temperatures, while the correlation length ξ is specific to each temperature and the corresponding values are determined from the best fit to the experimental data. Adjusting these fitting parameters of the theoretical potential, it is possible to match the experimental distribution Peq(r) at t = 0. By doing so, we have obtained the correlation length ξ of the order parameter fluctuations for each value of the temperature set at the objective,9 the constant parameters
D are assumed to take the same values for all experimental acquisitions at the various temperatures, while the correlation length ξ is specific to each temperature and the corresponding values are determined from the best fit to the experimental data. Adjusting these fitting parameters of the theoretical potential, it is possible to match the experimental distribution Peq(r) at t = 0. By doing so, we have obtained the correlation length ξ of the order parameter fluctuations for each value of the temperature set at the objective,9 the constant parameters ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≃ 13 nm and ρes ≃ 95 nm, which are in line with the values found in previous investigations.9,20 As anticipated in Section 2, the actual temperature T of the sample is expected to be a linear combination of the temperature TObj set at the microscope objective, which is varied during the experiment, and the fixed temperature TST = 304.65 K of the sample stage, i.e.,
D ≃ 13 nm and ρes ≃ 95 nm, which are in line with the values found in previous investigations.9,20 As anticipated in Section 2, the actual temperature T of the sample is expected to be a linear combination of the temperature TObj set at the microscope objective, which is varied during the experiment, and the fixed temperature TST = 304.65 K of the sample stage, i.e.,
| T = (1 − α)TST + αTObj | (5) |
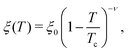 | (6) |
| ξ (nm) | T (K) | ΔT (mK) |
|---|---|---|
| 10 | 306.55 | 0.456 |
| 18 | 306.74 | 0.273 |
| 22 | 306.81 | 0.200 |
| 24 | 306.85 | 0.163 |
| 30 | 306.88 | 0.127 |
| 32 | 306.90 | 0.108 |
Once these parameters are fixed to their best-fit values, the resulting total potential Ves + VC, reported in Fig. 5 for the values of the parameters relevant for the current experiment, is used to simulate the ensuing evolution by Brownian dynamics, taking into account the distribution of the initial conditions. The core of a Brownian dynamics simulation is given by the Langevin equation, which is a stochastic differential equation describing the time evolution of a particle performing Brownian motion. It is integrated in time in order to create trajectories of the particle.32
We emphasise that, while the optical tweezers are switched off, i.e., with Vot,l = 0, the particles undergo Brownian motion and diffuse under the influence of the CCFs (due to VC) and of the electrostatic interaction (due to Ves).
3.3 Diffusion and drift velocity
The relative position and the distance between the two particles can be used to determine the values of their diffusion constant D(r) and of their drift velocity v(r) as functions of r.33 Given the experimental trajectories of the particles as a sequence of values ri, numbered by i and acquired at times i × ts, where ts is the time between sampling, one has
 | (7) |
 | (8) |
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = [〈(Δr)2〉 − 〈Δr〉2]/(2Δt), which is closer to the common definition of the diffusion constant and which highlights the sole effect of the Brownian noise, as it subtracts a possible mean drift 〈Δr〉 of the particles due to the action of external forces in the presence of overdamped dynamics. These two estimators are actually related by
= [〈(Δr)2〉 − 〈Δr〉2]/(2Δt), which is closer to the common definition of the diffusion constant and which highlights the sole effect of the Brownian noise, as it subtracts a possible mean drift 〈Δr〉 of the particles due to the action of external forces in the presence of overdamped dynamics. These two estimators are actually related by ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) = D − Δtv2/2 +
= D − Δtv2/2 + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ((Δt)2), where v = 〈Δr〉/Δt is the average relative velocity of the particles, and therefore they render the same value for sufficiently small Δt or whenever v vanishes due to the absence of external forces. In the present experiment, we considered the estimator D instead of
((Δt)2), where v = 〈Δr〉/Δt is the average relative velocity of the particles, and therefore they render the same value for sufficiently small Δt or whenever v vanishes due to the absence of external forces. In the present experiment, we considered the estimator D instead of ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) for three reasons: (a) Since 〈Δr〉, i.e., vΔt is affected by statistical errors, subtracting it from 〈(Δr)2〉 increases the resulting statistical error of
for three reasons: (a) Since 〈Δr〉, i.e., vΔt is affected by statistical errors, subtracting it from 〈(Δr)2〉 increases the resulting statistical error of ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) compared to that of D; (b) at distances r larger than ca. 2.2 μm, we expect all deterministic forces involved to vanish in the absence of the tweezers and therefore v = 0, such that D =
compared to that of D; (b) at distances r larger than ca. 2.2 μm, we expect all deterministic forces involved to vanish in the absence of the tweezers and therefore v = 0, such that D = ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ; (c) at smaller distances, but for sufficiently small values of Δt, i.e., for Δt ≪ D/v2, the two estimators
; (c) at smaller distances, but for sufficiently small values of Δt, i.e., for Δt ≪ D/v2, the two estimators ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) and D are anyhow approximately equal. Both estimators D(r) and
and D are anyhow approximately equal. Both estimators D(r) and ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) (r) render the actual diffusion coefficient as Δt → 0 but they are generically affected by (different) finite-time corrections which depend on r, are linear in Δt for small Δt, and are related as discussed above.†
(r) render the actual diffusion coefficient as Δt → 0 but they are generically affected by (different) finite-time corrections which depend on r, are linear in Δt for small Δt, and are related as discussed above.†
Due to the hydrodynamic interaction between the two colloids, the actual diffusion constant of these particles differs from the free one they would have in the bulk.34 As a result, the diffusion along the direction connecting the centers of the particles occurs with a diffusion constant which differs from that in the direction perpendicular to it (see eqn (5.5) in ref. 34). In order to compare our experimental results with these theoretical predictions, we decompose the ith displacement Δr(n)i = ri+n − ri into its parallel and perpendicular components:
Δr(n)i‖ = Δr(n)i·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) i i
| (9) |
Δr(n)i⊥ = Δr(n)i·(ẑ × ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) i), i),
| (10) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) i = ri/ri and ẑ is the unit vector along the z-direction, which is perpendicular to the xy-plane of observation where the position vectors ri lie. With these definitions, we can obtain the parallel and perpendicular diffusion coefficients defined with respect to the direction connecting the centers of the two particles:
i = ri/ri and ẑ is the unit vector along the z-direction, which is perpendicular to the xy-plane of observation where the position vectors ri lie. With these definitions, we can obtain the parallel and perpendicular diffusion coefficients defined with respect to the direction connecting the centers of the two particles:
 | (11) |
 | (12) |
 | (13) |
 | (14) |
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , stated after eqn (7), here applies to D‖, while D⊥ is not affected by the choice of the estimator because no forces are expected to act along the direction perpendicular to the segment joining the centers of the colloids. In Fig. 6 we report the experimental data (symbols) for D⊥ (upper set) and D‖ (lower set) as functions of the ratio r/d, together with the theoretical prediction obtained in ref. 34 (solid line) for no-slip boundary conditions. These quantities are normalized by the bulk inter-particle diffusion constant given by (see, e.g., eqn (5.6) in ref. 34)
, stated after eqn (7), here applies to D‖, while D⊥ is not affected by the choice of the estimator because no forces are expected to act along the direction perpendicular to the segment joining the centers of the colloids. In Fig. 6 we report the experimental data (symbols) for D⊥ (upper set) and D‖ (lower set) as functions of the ratio r/d, together with the theoretical prediction obtained in ref. 34 (solid line) for no-slip boundary conditions. These quantities are normalized by the bulk inter-particle diffusion constant given by (see, e.g., eqn (5.6) in ref. 34)
 | (15) |
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ‖ + v‖2Δt/2 in addition to those which characterize
‖ + v‖2Δt/2 in addition to those which characterize ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ‖. The experimental data for D⊥,‖ reported in Fig. 6 do not show any significant dependence on ΔT and ξ, apart from the finite-time effects mentioned above. A genuine temperature dependence of D⊥,‖ could be expected for Brownian particles diffusing near Tc in an external potential, provided by strongly temperature-dependent critical fluctuations which alter the dynamics (see, e.g., ref. 38 and 39 for a single trapped colloid). Accordingly, the absence of this dependence suggests that the effective interaction VC is valid, for all practical purposes, as if the colloidal particles were at rest in their instantaneous position. In our specific case, in fact, the typical timescale of colloid diffusion is 50 times larger than the relaxation time of critical fluctuations. Similarly, the distortion of the equilibrium order parameter profile around the colloids due to their deterministic motion is negligible, because the Péclet number which quantifies the magnitude of this effect (see ref. 40 for details) turns out to be at most 4 × 10−3, which is extremely small‡. This also implies that for the present experimental conditions the effects of retardation, observed numerically in ref. 41 during the aggregation of two identical colloids due to CCFs, are negligible.
‖. The experimental data for D⊥,‖ reported in Fig. 6 do not show any significant dependence on ΔT and ξ, apart from the finite-time effects mentioned above. A genuine temperature dependence of D⊥,‖ could be expected for Brownian particles diffusing near Tc in an external potential, provided by strongly temperature-dependent critical fluctuations which alter the dynamics (see, e.g., ref. 38 and 39 for a single trapped colloid). Accordingly, the absence of this dependence suggests that the effective interaction VC is valid, for all practical purposes, as if the colloidal particles were at rest in their instantaneous position. In our specific case, in fact, the typical timescale of colloid diffusion is 50 times larger than the relaxation time of critical fluctuations. Similarly, the distortion of the equilibrium order parameter profile around the colloids due to their deterministic motion is negligible, because the Péclet number which quantifies the magnitude of this effect (see ref. 40 for details) turns out to be at most 4 × 10−3, which is extremely small‡. This also implies that for the present experimental conditions the effects of retardation, observed numerically in ref. 41 during the aggregation of two identical colloids due to CCFs, are negligible.
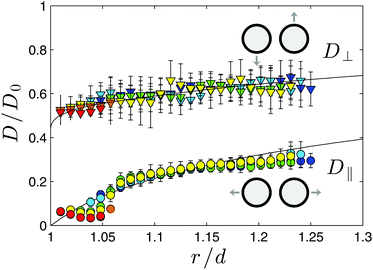 | ||
| Fig. 6 Experimental values of the normalized parallel D‖/D0 (circles) and perpendicular D⊥/D0 (triangles) diffusion constants as functions of the ratio between the inter-particle center-to-center distance r and the particle diameter d. The parallel and perpendicular directions refer to the line connecting the centers of the two colloids, and D0 is the bulk diffusion constant determined by eqn (15) and from available experimental data. The various colors refer to data taken at ΔT = 456 ± 2 mK (blue), 273 ± 2 mK (light blue), 200 ± 2 mK (green), 163 ± 2 mK (yellow), 127 ± 2 mK (orange), and 108 ± 2 mK (red). The solid lines represent the theoretical predictions accounting for the effect of the hydrodynamic interaction between the colloids.34 Error bars represent the standard deviation of the experimental values. There is good agreement between the theoretical predictions and the experimental results, which neither exhibit an appreciable dependence on temperature. The nature of the deviations observed in D‖ at short and long distances is discussed in the main text. | ||
In the first two columns of Fig. 7, we report the values of the experimental and simulated drift velocities v‖ and v⊥ as functions of r/d and for decreasing values of ΔT from top to bottom. The theoretical values of the drift velocities are calculated by employing eqn (13) and (14) for the simulated trajectories. These trajectories are obtained from Brownian dynamics simulations of two particles interacting via the total potential V = VC + Ves. We simulate a Langevin equation along the lines of ref. 32, with the diffusion coefficients D⊥,‖ following from eqn (5.5) and Fig. 3 in ref. 34 (see also Fig. 6 here) and based on the value of D0 as given by eqn (15). The parameters ξ, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D, and ρes are fixed to their best-fit values obtained by fitting the initial distribution Peq(r) as described above [see eqn (4) and (3)].
D, and ρes are fixed to their best-fit values obtained by fitting the initial distribution Peq(r) as described above [see eqn (4) and (3)].
At large values of ΔT (Fig. 7a and d), the parallel drift velocity v‖ is positive at small values of r/d because, on average, the particles are pushed away from each other by the dominating repulsive electrostatic potential Ves. Increasing the value of r/d, v‖ rapidly vanishes because, correspondingly, the electrostatic repulsion decays exponentially on a scale set by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D ≃ 13 nm, corresponding to
D ≃ 13 nm, corresponding to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) D/d ≃ 6 × 10−3 on the scale of the plot. Upon decreasing ΔT, as in Fig. 7g and j, v‖ becomes negative within a certain range of values of r/d. At these distances, the particles move on average towards each other due to the attractive critical Casimir interaction VC, which competes and eventually overcomes the electrostatic interaction Ves. However, at smaller values of r/d, Ves dominates and v‖ is no longer negative. If ΔT is reduced further, v‖ becomes quickly more negative (Fig. 7m and p), because the attractive critical Casimir interaction is so strong that it moves the particles towards each other until their velocity vanishes at contact. At larger distances, instead, v‖ vanishes and the particles undergo Brownian diffusion. We note that this range of distances can actually be explored only via numerical simulations with sufficiently high statistics. In the experiment, instead, the particles turn out to stick almost always together, and they explore the very limited range of distances indicated on the solid horizontal axes.
D/d ≃ 6 × 10−3 on the scale of the plot. Upon decreasing ΔT, as in Fig. 7g and j, v‖ becomes negative within a certain range of values of r/d. At these distances, the particles move on average towards each other due to the attractive critical Casimir interaction VC, which competes and eventually overcomes the electrostatic interaction Ves. However, at smaller values of r/d, Ves dominates and v‖ is no longer negative. If ΔT is reduced further, v‖ becomes quickly more negative (Fig. 7m and p), because the attractive critical Casimir interaction is so strong that it moves the particles towards each other until their velocity vanishes at contact. At larger distances, instead, v‖ vanishes and the particles undergo Brownian diffusion. We note that this range of distances can actually be explored only via numerical simulations with sufficiently high statistics. In the experiment, instead, the particles turn out to stick almost always together, and they explore the very limited range of distances indicated on the solid horizontal axes.
The experimental and numerical determination of the orthogonal component v⊥ of the drift velocity (eqn (14)) is reported in the second column of Fig. 7. Here, v⊥ vanishes in all the cases investigated because all the forces at play in the present experiment act along the direction which connects the centers of the particles. Accordingly, v⊥ shows no temperature dependence.
The third column of Fig. 7 reports the total force field (resulting from the sum of the electrostatic force and of the attractive CCF) in the xy-plane used in the numerical simulation. The length of the arrows corresponding to each point in that plane is proportional, for the purpose of visualization, to the logarithm of the magnitude of the total force. Blue arrows indicate repulsive forces, whereas red arrows indicate attractive ones.
It is noteworthy that the agreement observed in Fig. 6 and 7 between the experimental and simulated data confirms the reliability of the model we have used.
3.4 First passage times
In order to highlight the effect of CCFs on the dynamics of the two colloidal particles, we consider the first-passage time t1, i.e., the time it takes that the particles reach for the first time a reference separation rref, starting from a certain initial distance rin. Heuristically, this quantity provides a measure of how much the interaction effectively speeds up or slows down the relative diffusion process of the two particles, t1 being the minimal time required by the colloids to realize a certain configuration.The first-passage time is a random variable which changes for each realization of the diffusion process. Accordingly, it can be characterized by its cumulative probability distribution P1(t) that t1 is smaller than a given time t, which depends on the choice of rin and rref. (In order to smooth out statistical fluctuations of the experimental data, it is convenient here to focus on the cumulative distribution of t1 instead of its probability distribution p(t1), which can in principle be obtained as p(t1) = (dP1(t)/dt)|t=t1.) In order to determine P1, for each value of ΔT and each repetition of the blinking process, in which the particles are initially separated by a distance rin, we measure the time t1 it takes them to reach the separation rref for the first time, while the optical traps are turned off. Based on these data, P1(t) at a certain time t is determined by the ratio between the number of occurrences for which t1 < t and the total number of collected data. The experimental results are presented in Fig. 8a and b for rin = 2.16 μm < rref and rin = 2.40 μm > rref, respectively, with rref = 2.22 μm in all cases.
First, we consider the case of the first passage time from rin = 2.16 μm to rref = 2.22 μm, as shown in Fig. 8a. Far from criticality (ΔT = 456 ± 2 mK), the repulsive electrostatic interaction (see Fig. 5 for the corresponding potentials) dominates for r < rref and therefore, as the particles are pushed away from each other, P1(t) rapidly reaches its maximal value 1. However, upon approaching criticality, the increasingly strong, attractive critical Casimir interaction, acting for r < rref, effectively slows down the separation of the particles, so that P1(t) approaches its maximum value 1 only at long times.
Setting the initial condition outside the range of action of the CCFs, i.e., for rin = 2.40 μm, P1(t) has a significantly less pronounced dependence on ΔT, at least within the range of parameters explored here (Fig. 8b). This is due to the fact that the temperature dependent CCFs are actually negligible for r > rref. In particular, the total potential does not change as a function of temperature, because this range of distances is anyhow much larger than that of the correlation length of the critical fluctuations explored in the present experiment. In fact, a behavior similar to that reported in Fig. 8a can be observed for r > rref only for values of the correlation length ξ significantly larger than those achieved here.
The results of corresponding Langevin-dynamics simulations are presented in Fig. 8c and d. These simulations are in very good agreement with the experimental data presented in Fig. 8a and b, respectively. This agreement further validates our simulation model, which is based on an interaction potential V(ρ) = VC(ρ) + Ves(ρ), as a function of the surface-to-surface distance ρ between the particles, with a diffusion term described according to eqn (11) and (12).9
The results reported in Fig. 8 can be made more quantitative by calculating the mean first-passage time 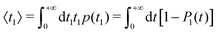 , which is reported in Fig. 9 as a function of the correlation length ξ corresponding to the values of ΔT used in Fig. 8. For rin = 2.16 μm and rref = 2.22 μm (Fig. 8a and c), 〈t1〉 increases upon increasing the correlation length ξ (Fig. 9a), because the attractive interaction due to VC slows down the diffusion of the particles. Instead, for rin = 2.40 μm and rref = 2.22 μm (Fig. 8b and d), no significant dependence of 〈t1〉 on ξ is observed (Fig. 9b), because the CCFs are negligible for r ≳ rref within the range of values of ξ explored here.
, which is reported in Fig. 9 as a function of the correlation length ξ corresponding to the values of ΔT used in Fig. 8. For rin = 2.16 μm and rref = 2.22 μm (Fig. 8a and c), 〈t1〉 increases upon increasing the correlation length ξ (Fig. 9a), because the attractive interaction due to VC slows down the diffusion of the particles. Instead, for rin = 2.40 μm and rref = 2.22 μm (Fig. 8b and d), no significant dependence of 〈t1〉 on ξ is observed (Fig. 9b), because the CCFs are negligible for r ≳ rref within the range of values of ξ explored here.
 | ||
| Fig. 9 Mean first-passage time 〈t1〉, as a function of the correlation length ξ, to reach for the first time the reference distance rref = 2.22 μm from the initial distance (a) rin = 2.16 μm and (b) 2.40 μm. Symbols with error bars represent the experimental data while black solid lines with greyly shaded area correspond to simulation data and their uncertainties. The color code for the temperatures is the same as the one used in Fig. 6 and 7. Here, 〈t1〉 is reported as a function of the associate correlation lengths ξ instead of ΔT; specifically, ξ = 10 nm (blue), 18 nm (light blue), 22 nm (green), 24 nm (yellow), 30 nm (orange), and 32 nm (red). | ||
4 Conclusions
We have shown that by using blinking optical tweezers it is possible to investigate the dynamics of a pair of colloidal particles, dispersed in a critical, binary liquid solution of water and 2,6-lutidine, in the absence of optical potentials and, thus, occurring under the influence of their effective inter-particle interaction only. Digital video microscopy facilitated to track the positions of the particles and to determine the effects of the CCFs on the time evolution of their center-to-center distance r upon approaching the critical temperature of the solvent. In order to infer the correlation length ξ of the critical fluctuations and the strength of the corresponding CCF, we have compared the experimental data for the equilibrium distribution of the inter-particle distance in the presence of optical traps with the results of a Monte Carlo integration of the expected Boltzmann distribution. The resulting fitted parameters have been used to perform a simulation of the dynamics of the two interacting colloids immersed in the same solvent. The very good agreement between the experimental data and the corresponding numerical simulations based on Langevin dynamics has validated the theoretical description of the forces involved and of the dynamics, which does not require accounting for the possible effects of retardation.41 This holds at least within the range of parameters explored here. The agreement between theory and experiment has also provided information about the correlation length ξ of the critical fluctuations and about the CCF field, for various temperatures approaching the critical point. Moreover, the knowledge of the first passage time relative to a start and a final configuration, in which the particles are essentially fully separated, is crucial for understanding the dynamics and to eventually control the self-assembly process of many colloidal particles. In particular, the model used here can be exploited to create a base protocol for the application and for the fine tuning of CCFs towards their use for nanotechnology. This offers new possibilities for the design and realization of self-assembled nano-structures and for driving nano-devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the ERC Starting Grant ComplexSwimmers (grant no. 677511) and by Vetenskapsrådet (grant no. 2016-03523). A. C. acknowledges partial financial support from TUBITAK (grant no. 116F111). J. P. S. acknowledges partial financial support from FONDECYT (grant no. 117103).Notes and references
- M. E. Fisher and P. G. de Gennes, C. R. Acad. Sci., Paris, 1978, 287, 207 CAS
.
- M. Krech, Casimir Effect in Critical Systems, World Scientific, Singapore, 1994 Search PubMed
.
- G. Brankov, N. S. Tonchev and D. M. Danchev, Theory of Critical Phenomena in Finite-Size Systems, World Scientific, Singapore, 2000 Search PubMed
.
- A. Gambassi, J. Phys.: Conf. Ser., 2009, 161, 012037 CrossRef
.
- A. Gambassi and S. Dietrich, Soft Matter, 2011, 7, 1247 RSC
.
- H. B. G. Casimir, Proc. K. Ned. Akad. Wet., 1948, 51, 793 Search PubMed
.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172 CrossRef CAS PubMed
.
- F. Soyka, O. Zvyagolskaya, C. Hertlein, L. Helden and C. Bechinger, Phys. Rev. Lett., 2008, 101, 208301 CrossRef PubMed
.
- S. Paladugu, A. Callegari, Y. Tuna, L. Barth, S. Dietrich, A. Gambassi and G. Volpe, Nat. Commun., 2016, 7, 11403 CrossRef CAS PubMed
.
- D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. Wegdam and P. Schall, Phys. Rev. Lett., 2009, 103, 156101 CrossRef PubMed
.
- A. Gambassi and S. Dietrich, Phys. Rev. Lett., 2010, 105, 059601 CrossRef PubMed
.
- R. Piazza, S. Buzzaccaro, A. Parola and J. Colombo, J. Phys.: Condens. Matter, 2011, 23, 194114 CrossRef PubMed
.
- E. Marino, T. E. Kodger, J. B. ten Hove, A. H. Velders and P. Schall, Sol. Energy Mater. Sol. Cells, 2016, 158, 154 CrossRef CAS
.
- T. A. Nguyen, A. Newton, D. J. Kraft, P. G. Bolhuis and P. Schall, Materials, 2017, 10, 1265 CrossRef PubMed
.
- F. Schmidt, A. Magazzù, A. Callegari, L. Biancofiore, F. Cichos and G. Volpe, Phys. Rev. Lett., 2018, 120, 068004 CrossRef PubMed
.
- U. Nellen, L. Helden and C. Bechinger, Europhys. Lett., 2009, 88, 26001 CrossRef
.
- M. Tröndle, O. Zvyagolskaya, A. Gambassi, D. Vogt, L. Harnau, C. Bechinger and S. Dietrich, Mol. Phys., 2011, 109, 1169 CrossRef
.
- I. A. Martnez, C. Devailly, A. Petrosyan and S. Ciliberto, Entropy, 2017, 19, 77 CrossRef
.
- C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516 CrossRef CAS
.
- A. Gambassi, A. Maciołek, C. Hertlein, U. Nellen, L. Helden, C. Bechinger and S. Dietrich, Phys. Rev. E, 2009, 80, 061143 CrossRef CAS PubMed
.
- D. G. Grier, Nature, 2003, 424, 810 CrossRef CAS PubMed
.
- P. H. Jones, G. Volpe and O. Maragò, Optical Tweezers: Principles and Applications, Cambridge University Press, 2015 Search PubMed
.
- D. G. Grier, Curr. Opin. Colloid Interface Sci., 1997, 2, 264 CrossRef CAS
.
- G. Pesce, G. Rusciano and A. Sasso, Opt. Express, 2010, 18, 2116 CrossRef CAS PubMed
.
- G. Pesce, G. Volpe, G. Volpe and A. Sasso, Phys. Rev. E, 2014, 90, 042309 CrossRef PubMed
.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS
.
- J. Baumgartl and C. Bechinger, Europhys. Lett., 2005, 71, 487 CrossRef CAS
.
- O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, EPL, 2007, 80, 60009 CrossRef
.
- O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, Phys. Rev. E, 2009, 79, 041142 CrossRef CAS PubMed
.
- M. Hasenbusch, Phys. Rev. B, 2012, 85, 174421 CrossRef
.
- E. Gülari, A. F. Collings, R. L. Schmidt and C. J. Pings, J. Chem. Phys., 1972, 56, 6169 CrossRef
.
- G. Volpe and G. Volpe, Am. J. Phys., 2013, 81, 224 CrossRef CAS
.
- T. Brettschneider, G. Volpe, L. Helden, J. Wehr and C. Bechinger, Phys. Rev. E, 2011, 83, 041113 CrossRef PubMed
.
- G. K. Batchelor, J. Fluid Mech., 1976, 74, 1 CrossRef
.
- J. C. Clunie and J. K. Baird, Phys. Chem. Liq., 1999, 37, 357 CrossRef CAS
.
- A. Stein, S. J. Davidson, J. C. Allegra and G. F. Allen, J. Chem. Phys., 1972, 56, 6164 CrossRef CAS
.
- J. C. Nieuwoudt and J. V. Sengers, J. Chem. Phys., 1989, 90, 457 CrossRef CAS
.
- Y. Fujitani, J. Phys. Soc. Jpn., 2017, 86, 114602 CrossRef
.
- Y. Fujitani, J. Phys. Soc. Jpn., 2016, 85, 044401 CrossRef
.
- A. Onuki, Phase transition dynamics, Cambridge University Press, 2002 Search PubMed
.
- A. Furukawa, A. Gambassi, S. Dietrich and H. Tanaka, Phys. Rev. Lett., 2013, 111, 055701 CrossRef PubMed
.
Footnotes |
† In order to illustrate the emergence of these corrections via using a simple example, we assume that the dynamics of the distance r under the sole effect of the interparticle potential Ves + VC is described by the overdamped Langevin equation 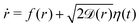 , where f(r) is proportional to the deterministic forces acting on the particles (due to that potential), η(t) is a Gaussian noise with 〈η(t)〉 = 0, and 〈η(t)η(t′)〉 = δ(t − t′), while , where f(r) is proportional to the deterministic forces acting on the particles (due to that potential), η(t) is a Gaussian noise with 〈η(t)〉 = 0, and 〈η(t)η(t′)〉 = δ(t − t′), while ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r) > 0 is the position-dependent diffusion constant. This stochastic differential equation is interpreted according to the Îto convention, while here we neglect the fact that r is actually the projection of the interparticle distance onto the xy-plane. A relatively simple but lengthy calculation shows that by defining D(r) as in eqn (7), i.e., from the conditional expectation of the increments Δr of the variable r within a time interval of finite duration Δt, one finds D(r) = (r) > 0 is the position-dependent diffusion constant. This stochastic differential equation is interpreted according to the Îto convention, while here we neglect the fact that r is actually the projection of the interparticle distance onto the xy-plane. A relatively simple but lengthy calculation shows that by defining D(r) as in eqn (7), i.e., from the conditional expectation of the increments Δr of the variable r within a time interval of finite duration Δt, one finds D(r) = ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r) + (Δt/2)c1(r) + (r) + (Δt/2)c1(r) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ((Δt)2), where c1(r) = f2(r) + 2 ((Δt)2), where c1(r) = f2(r) + 2![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r)f′(r) + (r)f′(r) + ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ′(r)f(r) + ′(r)f(r) + ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r) (r)![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ′′(r) is the leading finite-time bias of the estimator D of the actual diffusion ′′(r) is the leading finite-time bias of the estimator D of the actual diffusion ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) . We emphasize that c1(r) vanishes at large separations because, correspondingly, f(r) generically decays to zero while . We emphasize that c1(r) vanishes at large separations because, correspondingly, f(r) generically decays to zero while ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r) approaches its bulk, r-independent value. In addition, the sign of c1(r) may change as a function of r. In particular, one has c1(r) < 0 when r approaches a point r0 of stable mechanical equilibrium [i.e., with f(r0) = 0 and f′(r0) < 0] with (r) approaches its bulk, r-independent value. In addition, the sign of c1(r) may change as a function of r. In particular, one has c1(r) < 0 when r approaches a point r0 of stable mechanical equilibrium [i.e., with f(r0) = 0 and f′(r0) < 0] with ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ′′(r0) < 0, as in the case of the theoretical diffusion coefficients reported in Fig. 6. ′′(r0) < 0, as in the case of the theoretical diffusion coefficients reported in Fig. 6. |
| ‡ The typical timescale of a colloidal diffusion process can be estimated by the time tcoll the colloid takes to diffuse across a reference distance L (e.g., its radius d/2): tcoll = L2/D0, where D0 = kBT/(6πηd/2) is the diffusion constant of a colloid with diameter d in a fluid with dynamic viscosity η. Similarly, according to mode coupling theory,40 the mutual diffusion constant Dξ of the order parameter fluctuations is given by Dξ = kBT/(6πηξ), where ξ is the correlation length of the critical fluctuations, which in the present experiment ranges between 10 and 30 nm (see Table 1). Accordingly, the typical timescale tξ of the diffusion of critical fluctuations is tξ = L2/Dξ and the ratio of these two typical timescales is tcoll/tξ = Dξ/D0 ≃ 50, as reported in the main text. Similarly, the deterministic motion of the colloid may cause a distortion of the order parameter profile around the colloids, which was investigated in ref. 40. The magnitude of this effect turns out to be quantified by the Péclet number40 Pe = ξ|ν0|/Dξ, where ν0 is the typical velocity of the motion, which, in the present experiment (see Fig. 7), takes a maximal value of approximately 0.5 μm s−1. Accordingly, the maximum value of Pe turns out to be approximately 4 × 10−3, which is an extremely small value. |
| This journal is © The Royal Society of Chemistry 2019 |