Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A modeling framework to assess specific energy, costs and environmental impacts of Li-ion and Na-ion batteries†
Simon F.
Schneider
 ab,
Christian
Bauer
ab,
Christian
Bauer
 b,
Petr
Novák
b,
Petr
Novák
 a and
Erik J.
Berg
a and
Erik J.
Berg
 *ac
*ac
aElectrochemistry Laboratory, Paul Scherrer Institute, 5232 Villigen PSI, Switzerland. E-mail: erik.berg@kemi.uu.se
bLaboratory for Energy Systems Analysis, Paul Scherrer Institute, 5232 Villigen PSI, Switzerland
cDepartment of Chemistry, Uppsala University, 75121 Uppsala, Sweden
First published on 20th August 2019
Abstract
Li-ion batteries (LIBs) are among the most advanced technologies for energy storage. Due to the potential criticality of lithium raw materials, Na-ion batteries (NIBs) are frequently suggested as a low-cost, environmentally benign alternative to eventually complement or even replace LIBs. Herein, we present a holistic modeling framework to assess the potential of NIB cells from a performance, cost, and environmental impact perspective. To this end, we employ a physics-based battery cell model to project practical specific energies of LIB and NIB cells subjected to varying discharge rates. The derived performance metrics are subsequently used to parameterize a bottom-up battery cell cost model and to assess life cycle greenhouse gas (GHG) emission. Benchmarking model results obtained for NIBs (NaNi1/3Co1/3Mn1/3O2vs. hard carbon) against state-of-the-art LIBs (LiNi1/3Co1/3Mn1/3O2vs. graphite), we find that NIBs made from currently available active materials cannot compete with LIBs in terms of performance, costs, and environmental impact. Identifying battery performance as a key parameter driving manufacturing costs and GHG emissions, we argue that in order to make NIBs competitive to LIBs, one of the main priorities of NIB research should be the development of anode and cathode materials offering specific charges, voltages, and cycle life times comparable to or higher than for LIB active materials.
1. Introduction
Renewable energy sources (RES) play a critical role to decarbonize the energy system. A major challenge of many RES, such as solar and wind energy, is their intermittent availability, which requires complementary technologies to ensure reliable energy supply. Energy storage is therefore increasingly deployed to aid the system-integration of RES. LIBs are particularly suitable for energy storage due to their fast response time, low self-discharge, high round-trip efficiency, and scalability.1,2 Apart from stationary energy storage, LIBs are of crucial importance for mobile and portable applications, such as electric vehicles, laptops, and mobile phones.3 Their unmatched specific energy and reliable operation makes them one of the most advanced battery technologies, which is reflected in the worldwide LIB market size of 24 bn € in 2017.4 Due to rising concerns regarding the future costs and availability of lithium raw materials, Na-ion batteries (NIBs) are frequently discussed as a promising low-cost and environmentally more benign alternative to eventually complement LIBs.5–8 Based on the larger size of Na+ charge carriers compared to their Li+ counterparts and less negative standard potential (E0(Na+/Na) = −2.71 V (ref. 9) vs. E0(Li+/Li) = −3.04 V (ref. 9)) of the governing electrochemical reaction, it is often argued that NIBs are not likely to be competitive with LIBs in terms of specific energy. Whereas such considerations inherent to the thermodynamic properties of a battery chemistry are relevant when assessing theoretical specific energies,10 it is often overlooked that the larger size of Na+ charge carriers favors enhanced electrolyte mass transport11 and faster reaction kinetics11–14 at the electrode/electrolyte interface. Aiming for a better understanding of the trade-offs existing between thermodynamic and kinetic parameters in LIB and NIB cells, we present a modeling framework to assess practical specific energies of LIB and NIB cells subjected to varying discharge rates. Based on this framework, we quantify costs and manufacturing-related environmental impacts of LIB and NIB cells from a life-cycle perspective.State-of-the-art modeling approaches for battery cell assessment include the Argonne National Laboratory Battery Performance and Cost (BatPaC) model,15 the TIAX model,16 the simplified Energy-Cost model by Berg et al.,17 and other18–20 valuable studies evaluating performance and costs. Many of these contributions enjoy widespread appreciation in both academia and industry as they help uncover trade-offs existing between competing battery chemistries and can provide guidelines to improve battery cell design. More recently, comparative studies have been performed to assess costs21 and environmental impacts6 of LIBs and NIBs. A common shortcoming of the above-discussed modeling approaches is that they typically rely on generic battery performance assumptions, e.g. in terms of constraints imposed on battery cell design to meet discharge power requirements instead of performance metrics derived from detailed physics-based models. Therefore, these models are not suited to study the impact of fundamental thermodynamic and kinetic parameters on the performance of different battery technologies. In order to fill this research gap, we integrated a pseudo-two-dimensional (P2D) physics-based electrochemical battery cell model22 into a modeling framework to consistently assess specific energies, costs, and manufacturing-related GHG emissions of LIB and NIB cells. To evaluate the impact of faster kinetics in NIBs, the performance projections are performed for LIB and NIB cells subjected to varying discharge rates. Overall, the presented modeling framework helps to pinpoint key parameters governing the technical, economic, and environmental viability of LIB and NIB cells.
2. Methods
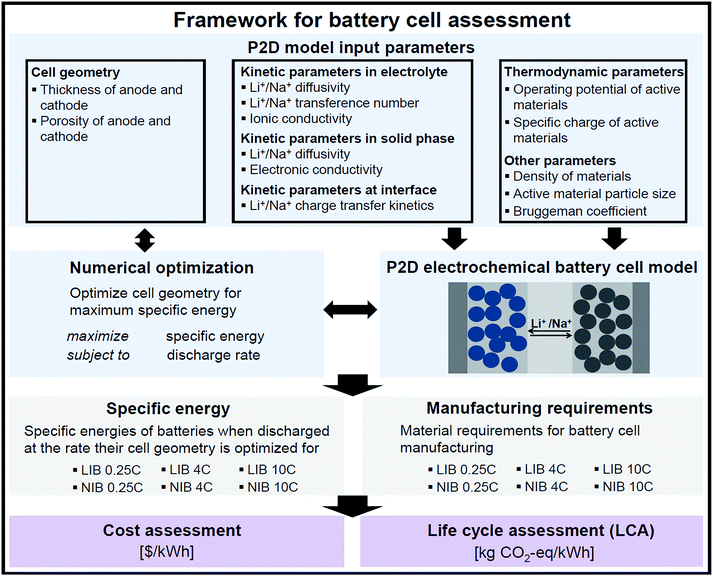
2.1 Methods overview
Fig. 1 summarizes the modeling framework developed in this study to assess performance, costs, and environmental impacts of LIB and NIB cells. In a first step, a pseudo-two-dimensional (P2D) physics-based battery cell model is employed to project practical specific energies of LIB and NIB cells subjected to varying discharge rates. In a second step, the P2D model output, i.e. battery cell performance and material requirements for battery cell manufacturing, enables the parameterization of a bottom-up cost model and life cycle inventories. In a third step, battery cell manufacturing costs are computed and life cycle assessment (LCA) is performed to quantify manufacturing-related GHG emissions. We used the established modeling framework to assess NIB cells with the active material configuration NaNi1/3Co1/3Mn1/3O2 (cathode) vs. hard carbon (anode) and benchmarked the cells against model results obtained for their state-of-the-art LIB analogue, i.e. LiNi1/3Co1/3Mn1/3O2vs. graphite. Please note that, although not strictly applicable to secondary batteries, we refer to anode for the negative electrode and cathode for the positive one throughout this paper as this is common in battery-related publications.Whereas the further advancement of LIBs has received significant attention from academia and industry since their commercialization by Sony ca. 30 years ago, NIBs are currently a less mature technology in their prototyping stage.3 We therefore expect that ongoing research activities will eventually lead to the development of NIB active materials offering higher voltage and specific charges than NIB active materials available today. We therefore additionally aim for a second assessment, which is not affected by differing development stages of the two technologies, but represents a hypothetical scenario where differences in battery performance originate solely from fundamental thermodynamic and kinetic disparities inherent to LIBs and NIBs. For this scenario, we consider NIB active materials that display the same specific charges and gravimetric densities as LiNi1/3Co1/3Mn1/3O2 and graphite, respectively. Although the cell voltage is thermodynamically solely linked to the Gibbs free energy change of the cell reaction,23 we furthermore assume that the lower voltage in NIB compared to LIB cells amounts only to the difference in the electrochemical standard potentials, i.e. 0.33 V.
The remainder of the methods chapter is structured as follows: Chapter 2.2 provides an overview of the P2D battery cell model and a critical discussion of key input parameters. In Chapter 2.3, we summarize life cycle inventories collected for this study and present the empirical bottom-up battery cell cost model established by distilling key insights from Patry et al.19 and Berckmans et al.24
2.2 P2D model
Based on porous electrode theory of de Levi25 and further developed by Newman, Doyle, and coworkers,26,27 the P2D battery cell model is one of the most widely used physics-based electrochemical battery cell models. The P2D model consists of a system of nonlinear partial differential equations (PDEs) for the conservation of mass and charge in the anode, separator, and cathode section of the battery cell. The model has repeatedly proven suitable to accurately simulate the discharge behavior of batteries and for cell design optimization.22,28,29In this study, we adapted the numerical implementation of the P2D model developed by Torchio et al.22 for MATLAB to project practical specific energies of LIB and NIB cells subjected to discharge rates of respectively 0.25C, 4C, and 10C. Current densities associated with these discharge rates were computed as the ratio of the theoretical specific charges of active materials and the duration of full galvanostatic discharge, i.e. 4 h, 15 min, and 6 min, respectively. Table 1 shows key input parameters for the P2D model. As discussed above, we consider two distinct active material configurations for the NIB, denoted as “present” (NaNi1/3Co1/3Mn1/3O2 and hard carbon active materials; referring to the present state of development) and “hypothetical” (yet unknown active materials) scenarios, respectively. The hypothetical scenario is intended to reflect the battery cell performance that we would expect NIBs to display in the hypothetical situation that they had enjoyed the same cumulative research and development efforts as LIBs today. Whereas a comparison of such hypothetical NIBs with current LIBs is not supposed to represent a comparison of future cells (since LIBs will also undergo further development), it allows evaluating achievable development goals of NIBs in terms of performance.
| Scenario label | LIB | NIB present base | NIB present optimistic | NIB present pessimistic | NIB hypothetical base | NIB hypothetical optimistic | NIB hypothetical pessimistic |
|---|---|---|---|---|---|---|---|
| Electrolyte conductivity (κel) | f(cLi+) | 1.2 × κel,LIB | 1.5 × κel,LIB | 1.0 × κel,LIB | 1.2 × κel,LIB | 1.5 × κel,LIB | 1.0 × κel,LIB |
| Electrolyte diffusivity (Del) | 3 × 10−10 m2 s−1 | 1.28 × Del,LIB | 2.00 × Del,LIB | 1.00 × Del,LIB | 1.28 × Del,LIB | 2.00 × Del,LIB | 1.00 × Del,LIB |
| Transference number (t+) | 0.4 | 0.5 | 0.5 | 0.4 | 0.5 | 0.5 | 0.4 |
| Charge transfer rate (kct) | 2 × 10−11 m2.5 mol−0.5 s−1 | 102 × kct,LIB | 103 × kct,LIB | 1 × kct,LIB | 102 × kct,LIB | 103 × kct,LIB | 1 × kct,LIB |
| Specific charge anode | 372 Ah kg−1 | 329 Ah kg−1 | 329 Ah kg−1 | 329 Ah kg−1 | 372 Ah kg−1 | 372 Ah kg−1 | 372 Ah kg−1 |
| Specific charge cathode | 155 Ah kg−1 | 119 Ah kg−1 | 119 Ah kg−1 | 119 Ah kg−1 | 155 Ah kg−1 | 155 Ah kg−1 | 155 Ah kg−1 |
| Open circuit voltage | See S1 | See S1 | See S1 | See S1 | LIB – 0.33 V | LIB – 0.33 V | LIB – 0.33 V |
| Gravimetric density anode | 2200 kg m−3 | 1700 kg m−3 | 1700 kg m−3 | 1700 kg m−3 | 2200 kg m−3 | 2200 kg m−3 | 2200 kg m−3 |
| Gravimetric density cathode | 4750 kg m−3 | 4750 kg m−3 | 4750 kg m−3 | 4750 kg m−3 | 4750 kg m−3 | 4750 kg m−3 | 4750 kg m−3 |
In order to account for uncertainties in the kinetic parameters that exist for NIBs because of limited experimental data available, three different sub-scenarios are considered for each active material configuration, referred to as “pessimistic”, “base”, and “optimistic”. Conceptually, the total number of six NIB parameter sets gives rise to six different types of NIB cells considered. Kinetic parameters in the electrode materials (i.e. solid phase diffusion coefficients and electronic conductivities) are not listed in Table 1 as they are assumed to be identical for NIB and LIB cells. A comprehensive discussion of P2D model parameters is provided in S1.† Compared to kinetic and thermodynamic input parameters, which are an intrinsic property of active materials, electrolyte solution, and other constituents of the battery cell, cell design parameters, i.e. electrode thickness and electrode porosity can be chosen by battery manufactures such as to best match the technical requirements of the battery. In this regard, one may conceptually distinguish between “high energy” cells with thick electrodes and low electrode porosity and “high power” cells with thin electrodes and high electrode porosity. Whereas “high energy” cells have higher theoretical specific energy, they show inferior performance in high-power applications compared to “high power” cells, which retain a larger fraction of their theoretical specific energy when subjected to fast discharge. In the context of this study, the optimal battery cell design is not only dependent on the anticipated discharge rate but also on battery chemistry and the optimal set of design parameters is thus not ex ante known. For that purpose, we coupled the P2D model to an optimization algorithm to numerically optimize the cell design parameters for maximum practical specific energy at the different discharge rates. Formally, this gives rise to a nonlinear optimization problem with bound constraints:
| Maximize Es(ta,εa,εc) | (1) |
| Subject to lb ≤ [ta,εa,εc]T ≤ ub | (2) |
In eqn (1), the objective function is the practical specific energy as evaluated with the P2D model for a particular set of cell design parameters {ta,εa,εc}. ta, εa, and εc denote the thickness of the anode, porosity of anode, and porosity of cathode, respectively. Note that the objective function is not dependent on the thickness of the cathode tc as it can be computed from {ta,εa,εc}. This is because balanced capacities are assumed for the anode and cathode, thus the four cell design parameters {ta,tc,εa,εc} are not independent (see ESI† 1.2.4 for more details). Eqn (2) introduces lower (lb) and upper (ub) bound constraints to restrict the cell design parameter values to physically meaningful ranges. It should be noted that the objective function in (1) is nonsmooth and typically nonconvex, thus the optimization solver should be selected with care. Previous studies have relied either on derivative-based local solvers18,30 or derivative-free global approaches18,31 to tackle the challenge of optimizing battery cell geometry. In this work, we employed the fmincon interior-point solver from the MATLAB optimization toolbox. The solver was run from 500 randomly selected start points 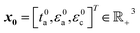 to ensure (near-)global optimality of the solution. The effectiveness of this strategy was verified using particle swarm optimization from the MATLAB optimization toolbox. Whereas similar results were obtained employing the two solvers, particle-swarm optimization tends to be more effective in terms of the number of required objective function evaluations and thus run-time. The MATLAB scripts needed to reproduce the results are available upon request. A list of computed practical specific energies and optimized cell design parameters is shown in S2.†
to ensure (near-)global optimality of the solution. The effectiveness of this strategy was verified using particle swarm optimization from the MATLAB optimization toolbox. Whereas similar results were obtained employing the two solvers, particle-swarm optimization tends to be more effective in terms of the number of required objective function evaluations and thus run-time. The MATLAB scripts needed to reproduce the results are available upon request. A list of computed practical specific energies and optimized cell design parameters is shown in S2.†
2.3 Manufacturing costs and LCA
Practical specific energies and optimized LIB and NIB cell designs derived using the P2D model form the basis to compute material requirements needed to assess costs and manufacturing-related life cycle GHG emissions. Table 2 lists battery cell components and associated material purchase costs and relevant data sets for LCA. In this study, the functional unit for both the cost assessment and LCA is the manufacturing of 1 kWh of battery cell capacity without considering battery use phase and end of lifetime aspects. GHG emissions were computed according to IPCC 2013 (100 year time frame) using the Python-based Brightway LCA framework37 and ecoinvent version 3.3 (system model “Allocation, cut-off by classification”)38 served as the background database providing GHG emissions of all modeled battery materials and energy carriers with the associated supply chains. Python code in the form of a Jupyter notebook is provided in S4.† The calculations were performed for battery cells in standard industrial pouch format where multiple electrode “sandwiches” consisting of anode current collector, anode, separator, cathode, and cathode current collector are stacked on top of each other. Because of the stacked arrangement of electrode sandwiches, the current collector thickness specified in Table 2 corresponds to half of the actual thickness of the copper and aluminum sheets. Due to unavailability of industrial data, we assume that the thickness of the NIB anode aluminum current collector is equal to the thickness of the LIB anode copper one. We note, however, that this assumption is possibly favouring NIBs as it is currently not clear whether the mechanical stability of aluminum allows for the processing of aluminum sheets with a thickness of only 8 μm. Following Patry et al.,19 a scrap rate of 9% is assumed for all components of the battery cell “sandwich”.| Component | Materials and processing steps | Material purchase costs | Relevant data sets for LCA |
|---|---|---|---|
| Current collectors LIB | - Aluminum current collector, thickness 10 μm (cathode side) | - Aluminum: 15 $ per kg (ref. 42) | - Market for aluminum scrap, new |
| - Sheet rolling aluminum | - Copper: 25 $ per kg (ref. 42) | - Market for copper | |
| - Copper current collector, thickness 4 μm (anode side) | - Sheet rolling | ||
| - Sheet rolling copper | |||
| Current collectors NIB | - Aluminum current collector, thickness 10 μm (cathode side) | - Aluminum: 15 $ per kg (ref. 42) | - Market for aluminum scrap, new |
| - Aluminum current collector, thickness 4 μm (anode side) | - Sheet rolling | ||
| - Sheet rolling aluminum | |||
| Anode paste LIB | - 93 wt%: graphite (active material) | - Graphite: 15 $ per kg (ref. 21) | - Market for anode, graphite, for Li-ion battery |
| - 3 wt%: binder (70 wt% CMC + 30 wt% SBR) | - Binder: 10 $ per kg (ref. 17) | - Market for CMC, powder | |
| - 4 wt%: carbon additive | - Carbon additive: 20 $ per kg (ref. 42) | - Market for SBR | |
| - Market for carbon black | |||
| Anode paste NIB | - 93 wt%: hard carbon (active material) | - Hard carbon: 15 $ per kg (ref. 21) | - Hard carbon from sugar precursor, inventory from Peters et al.6 |
| - 3 wt%: binder (70 wt% CMC + 30 wt% SBR) | - Binder: 10 $ per kg (ref. 17) | - Market for CMC, powder | |
| 4 wt%: carbon additive | - Carbon additive: 20 $ per kg (ref. 42) | - Market for SBR | |
| - Market for carbon black | |||
| Cathode paste LIB | - 93 wt%: LiNi1/3Co1/3Mn1/3O2 (active material) | - LiNi1/3Co1/3Mn1/3O2: 20 $ per kg (ref. 21) | - LiNi1/3Co1/3Mn1/3O2 |
| - 3 wt%: PVF (binder), proxy for PVDF43,44 | - Binder: 10 $ per kg (ref. 17) | - Market for PVF, proxy for PVDF43,44 | |
| - 4 wt%: carbon additive | - Carbon additive: 20 $ per kg (ref. 42) | - Market for carbon black | |
| - NMP solvent | - NMP solvent included in process costs | - Market for NMP | |
| Cathode paste NIB | - 93 wt%: NaNi1/3Co1/3Mn1/3O2 (active material) | - NaNi1/3Co1/3Mn1/3O2: 12.8 $ per kg (computed) | - NaNi1/3Co1/3Mn1/3O2 inventory adapted from ref. 41 |
| - 3 wt%: PVF (binder), proxy for PVDF43,44 | - Binder: 10 $ per kg (ref. 17) | - Market for PVF, proxy for PVDF43,44 | |
| - 4 wt%: carbon additive | - Carbon additive: 20 $ per kg (ref. 42) | - Market for carbon black | |
| - NMP solvent | - NMP solvent included in process costs | - Market for NMP | |
| Electrolyte LIB | - 12.7 wt%: LiPF6 salt | - Electrolyte (salt + solvent): 18 $ per kg (ref. 42) | - Market for LiPF6 |
| - 87.3 wt%: electrolyte solvent (30 wt% EC + 70 wt% DMC) | - Market for ethylene carbonate (proxy for electrolyte solvent mixture) | ||
| Electrolyte NIB | - 14.0 wt%: NaPF6 salt | - Electrolyte (salt + solvent): 17.6 $ per kg (computed) | - NaPF6 inventory from Peters et al.6 |
| - 86.0 wt%: electrolyte solvent (30 wt% EC + 70 wt% DMC) | - Market for ethylene carbonate (proxy for electrolyte solvent mixture) | ||
| Separator LIB/NIB | - Separator, thickness 25 μm, porosity 39% (50 wt% PP + 50 wt% PE) | - Separator: 120 $ per kg (ref. 42) | - Market for PP |
| - Extrusion, plastic film | - Market for PE | ||
| - Market for extrusion, plastic film | |||
| Cell container | - Mass breakdown LIB/NIB cell: | - Cell container costs included in process costs | - Tab aluminum |
| • 97 wt% electrode “sandwich” | - Tab copper | ||
| • 3 wt% cell container | - Multilayer pouch | ||
| Water for cell manufacturing | - LIB 4C cell: 32.55 kg per kWh of capacity | - Included in process costs | - Market for water, decarbonized, at user |
| - Other cells: proportional to process costs | |||
| Energy for cell manufacturing | - LIB 4C cell: 40 kWh per kWh of capacity (50% electricity, 50% heat)39 | - Included in process costs | - Market for electricity, medium voltage, country: South Korea41 |
| - Other cells: proportional to process costs | - Heat production, natural gas, furnace | ||
For the assessment of battery cell costs we adapted the empirical bottom-up cost model developed by Patry et al.,19 modeling total manufacturing costs as the sum of material purchase costs, process costs, and overhead costs. To account for increasing worldwide manufacturing capacities since the publication of their study, we apply learning curves for the computation of battery process and overhead costs. Assuming an average annual growth of the Li-ion battery manufacturing capacity of 26% (ref. 4) between 2014 and 2019, we discount process costs by a factor Dprocess = 0.396 and overhead costs by a factor Doverhead = 0.629 (see (ref. 24) and SI3† for more details). While material purchase costs can be computed directly from the P2D model output, process costs were estimated based on the underlying idea that they are dependent on the occupation time of production lines per kWh of battery cell capacity manufactured.19 We assume that production line occupation times are inversely proportional to the areal specific energy of the electrode sandwiches the battery cells are composed of. More precisely, we model process costs ($ per kWh) as the sum of a constant cost term cconst and a term that scales inversely with the areal specific energy of the electrode sandwich Asandwich. Asandwich,ref denotes the areal specific energy of a reference sandwich and cvar is a proportionality factor.
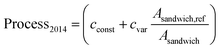 | (3) |
| Process2019 = Dprocess × Process2014 | (4) |
The process cost modelling approach employed in this study differs somewhat from the original one19 mainly in that we model process costs as a function of areal specific energy instead of electrode thickness. We believe that our generalized approach is suitable for LIB and NIB cells with disparate electrode porosities (anode porosities 17–30% and cathode porosities 18–47%, see S2†). We define Asandwich,ref as the areal specific energy of LIB 4C sandwiches (Asandwich,ref = 83 W h m−2) and set the process costs of LIB 4C cells equal to process costs specified by Patry et al.19 for an automotive NMC battery cell with 50 μm anode thickness, i.e. Process2014 = 69 $ per kWh). A comparison with process costs specified for automotive NMC battery cells with 100 μm anode thickness (Process2014 = 44 $ per kWh)19 allows to parameterize eqn (3) (cconst = 20 $ per kWh and cvar = 49 $ per kWh, respectively). Energy requirements for LCA calculations are based on (ref. 39) (see Table 2 for more details). We furthermore assume that water and energy requirements for battery cell manufacturing are proportional to process costs. This modeling approach is based on the rationale that water and energy requirements are dependent on the occupation time of production lines in a similar functional manner as are process costs. Although our approach allows only for an approximate estimation of the true water and energy requirements, we believe that it is well suited for the purpose of the comparative assessment performed in this study.
Overhead costs ($ per kWh) are computed from the material purchase and process costs according to the below empirical formula:19
| Overhead2014 = 0.66 × Process2014 + 0.056 × (Purchase + 1.66 × Process2014) | (5) |
| Overhead2019 = Doverhead × Overhead2014 | (6) |
A complete documentation of the battery cell cost model and life cycle inventories in excel sheet format is provided in S3.†
3. Results and discussion
3.1 Present NIBs
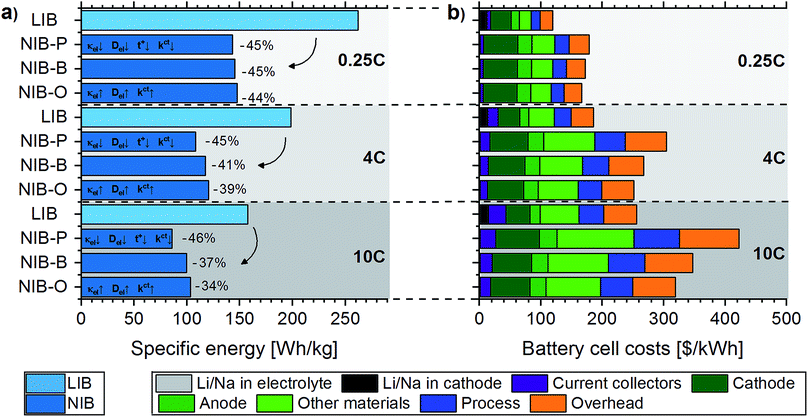
Fig. 2a compares practical specific energies projected for LIB (LiNi1/3Co1/3Mn1/3O2vs. graphite) and NIB (NaNi1/3Co1/3Mn1/3O2vs. hard carbon) cells subjected to discharge rates of 10C, 4C, and 0.25C, respectively. Serving as a first validation of the modeling framework developed in this study, we find good agreement between practical specific energies projected for LIB 4C cells and NMC-based LIB cells currently used in electric vehicles (this study: 198.6 W h kg−1 (without cell packaging) and 192.6 W h kg−1 (including cell packaging); automotive cells: typically ca. 150–200 W h kg−1 (ref. 45)). Compared to their LIB counterparts, we project lower practical specific energies for NIB cells at all discharge rates. However, a closer look at Fig. 2a reveals that the gap in specific energy between NIB and LIB cells is dependent on the discharge rate; for the “base” scenario, the gap in specific energy decreases from 45% (0.25C) to 41% (4C) and 37% (10C). These findings show that the enhanced kinetic processes in NIB cells have a significant impact on the high-power performance. However, for the particular NIB considered, this effect is not sufficient to compensate for the lower specific charges and voltage of the active materials.Please note that the practical specific energies computed for LIB and NIB cells are of course sensitive to the parameterization of the P2D model and the choice of input parameters.46 In order to account for this uncertainty, we consider for instance with respect to the kinetic input parameters not only a base scenario, but also a pessimistic and optimistic one for NIB cells. We believe that this approach yields reliable ranges for the practical specific energy of NIB cells, thus accounting for the main sources of uncertainty present in the analysis. Furthermore, we perform an additional battery performance assessment, where practical specific energies of current LIB cells are compared to optimized theoretical specific energies of NIB cells. For fixed battery active materials and cell design, such an assessment provides a theoretical upper bound for the specific energy that may be expected from NIB cells. Assuming the same cell designs as for the NIB-B cells shown in Fig. 2a, theoretical specific energies amount to 152 W h kg−1 (0.25C cell design), 131 W h kg−1 (4C cell design), and 120 W h kg−1 (10C cell design), respectively. It is evident that the theoretical specific energies of NIB cells are significantly lower than practical specific energies of their LIB counterparts (262 W h kg−1, 199 W h kg−1, and 158 W h kg−1, respectively).
Fig. 2b shows LIB (LiNi1/3Co1/3Mn1/3O2vs. graphite) and NIB (NaNi1/3Co1/3Mn1/3O2vs. hard carbon) cell manufacturing costs computed as the sum of material purchase costs, process costs, and overhead costs. A comparison of both the cost structure and total cell costs with industrial data evidences that our modeling framework provides accurate cost estimates: while we project 186 $ per kWh for LIB 4C cells, (ref. 47) specifies 180 $ per kWh for automotive LIB cells (NMC cathode); material purchase costs account for respectively 65% (this study) and 60–70% (ref. 47) of total cell costs. Within material purchase costs we further distinguish between costs related to lithium (Li2CO3) and sodium (Na2CO3) raw materials, current collectors (i.e. aluminum and copper sheets), cathode active material costs (without Li/Na), anode active material costs, and contributions from other cell components. While sodium raw material costs are almost negligible (1.0–1.4 $ per kWh NIB cell capacity), lithium raw material costs are ca. 10 times higher (12–15 $ per kWh LIB cell capacity). However, it needs to be emphasized that despite ongoing discussions about rising lithium costs in the last years,21 lithium raw material costs amount to only 5.8–10.2% of total LIB cell manufacturing costs. Note that this calculation is based on the annual average price of battery-grade Li2CO3 in the year 2017, which was 13.9 $ per kg.40 Even in the case of an increase of the Li2CO3 price to 25 $ per kg, which may be considered the “worst-case” scenario,48 lithium raw material costs would only amount to 22–27 $ per kWh LIB cell capacity. In addition to replacing lithium by sodium-based materials, additional cost savings can be achieved in NIBs by using aluminum instead of copper as the anode current collector. These cost savings are most pronounced for high-power cells (LIB 10C vs. NIB 10C), where the combined expenditures for aluminum and copper can be reduced by 8.9 $ per kWh. Total material purchase costs are consistently higher for NIB than LIB cells, which can be attributed to lower practical specific energies of NIB cells and thus higher material requirements per kWh of capacity. Similarly, higher process costs are projected for NIB cells due to longer production line occupation times as a result of larger electrode areas per kWh of capacity.
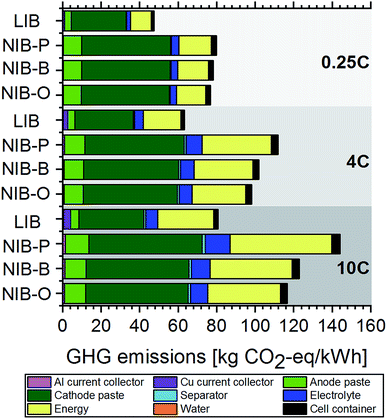
In line with the above discussion of battery cell manufacturing costs, we project higher GHG emissions for NIB cells (see Fig. 3), which we again attribute to lower practical specific energies and thus higher material and material processing requirements. Due to comparatively high GHG emissions associated with cathode active materials (LiNi1/3Co1/3Mn1/3O2 and NaNi1/3Co1/3Mn1/3O2) and large quantities required, the cathode paste accounts for 41–60% of total GHG emissions. Energy requirements for battery cell manufacturing contribute 20–37% to total GHG emissions, while the sum of all other contributions is, on average, only 21%. Comparing our results to an existing study evaluating NIBs from a life cycle perspective,6 we arrive at somewhat different conclusions. While Peters et al.6 found GHG emissions of NIBs to be in the same range or even slightly lower compared to LIBs, we project 45–78% higher GHG emissions for NIBs. Although the authors of this study homogenized battery cell manufacturing energy requirements and electricity mixes to improve the comparability of the results with existing LCA studies on LIBs, they state that the comparability is still limited. We ascribe the poor comparability in part to the lack of consistency in the battery performance assumptions, i.e. specific energies of LIBs and NIBs collected from different literature sources. As our study relies on more consistent performance data due to the use of a physics-based battery cell model for the parameterization of life cycle inventories, the results presented here should be more reliable.
3.2 Hypothetical NIBs
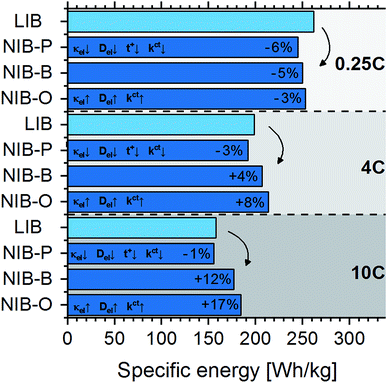
We now shift the discussion from battery cells manufactured with active materials available today to an assessment of LIB and NIB cells that is not affected by differing development stages, but intended to be governed solely by the underlying electrochemical disparities of the two technologies. For this scenario, Fig. 4 compares projected practical specific energies of LIB cells (LiNi1/3Co1/3Mn1/3O2vs. graphite) and hypothetical NIB cells. Importantly, while assuming same specific charges and gravimetric densities for LIB and NIB active materials, we expect NIB cells to display an open circuit voltage 0.33 V lower than LIB cells, corresponding to the difference in the standard electrochemical potentials of Li+/Li and Na+/Na. At low discharge rates of 0.25C, we project lower practical specific energies for NIB cells as explained by their lower voltage. Interestingly, the higher the discharge rate, the better NIB cells perform relative to their LIB counterparts. For the “base” scenario, the practical specific energy of NIB cells is 4% higher at 4C discharge and 12% higher at 10C discharge. At fast discharge rates, even in the absence of faster kinetic processes (“pessimistic” scenario), we project almost the same practical specific energy for NIB cells. This is because of the increasing impact of the low-mass aluminum anode collector in NIB cells with decreasing electrode thickness, i.e. the lower mass of the aluminum current collector compared to the copper one can compensate for the lower NIB cell voltage.The strong inverse correlation found between practical specific energy and both costs and GHG emissions suggests that NIBs can only reasonably compete with LIBs if similar specific energies can be achieved for NIB cells. In comparison, other drivers, such as the choice of Li-ion and Na-ion based materials and anode current collector (copper vs. aluminum) will only play a secondary role as long as the supply chains of lithium raw materials and copper are not endangered. As we found that NIBs could potentially reach similar or even slightly higher specific energies than LIBs in high-power applications, we envision that NIBs can become a viable alternative to LIBs even in the absence of interrupted lithium supply. In this study we refrain, however, from performing a quantitative assessment of costs and GHG emissions as the chemical composition of active materials for hypothetical NIBs and future material supply chains, location of production, and commodity prices are hard to predict, thus the results of such an assessment would not be meaningful in the light of these uncertainties.
4. Conclusions
Intrigued by the promises of the NIB research community, the goal of this study was to perform a realistic assessment of current and prospective (hypothetical) NIB cells, taking into consideration three key metrics indispensable for successful NIB market implementation: (1) battery performance, i.e. practical specific energies at different discharge rates; (2) costs; (3) environmental impacts evaluated based on manufacturing-related GHG emissions from a life cycle perspective. To ensure consistency in the assessment of the different metrics, we employed a physics-based electrochemical battery cell model to parameterize a bottom-up cost model and life cycle inventories. Comparing model results obtained for active material configurations considered representative for LIBs and NIBs (i.e. LiNi1/3Co1/3Mn1/3O2vs. graphite and NaNi1/3Co1/3Mn1/3O2vs. hard carbon) our findings suggest that NIBs need further improvement in order to become competitive with LIBs in terms of the three metrics assessed. We identified a strong inverse correlation between battery practical specific energy and both manufacturing costs and environmental impact, implying that the specific energy provides a key lever to reduce battery costs and GHG emissions. Since we found other drivers, such as cost savings due to replacement of lithium-based raw materials by sodium-based ones, to play a minor role, we argue that NIBs are most likely to become a viable alternative to LIBs only if they can achieve similar performance. In a second part of this paper, we evaluate if from a fundamental technical perspective NIBs have the potential to become competitive with LIBs. Aiming for an assessment that is not affected by the currently differing development stages of the two chemistries, we considered a hypothetical scenario in which the voltage of NIB cells is only 0.33 V lower compared to LIB cells and assumed that NIB and LIB active materials offer the same specific charges. We find that under these conditions NIBs are likely to reach practical specific energies close to (high-energy cells) or even somewhat higher (high-power cells) than their lithium competitors. Overall, this study underlines the importance of NIB active materials offering high voltage and specific charges for battery performance, costs, and environmental impact. Although not addressed in this study, it should be emphasized that future NIBs additionally have to comply with safety and lifetime requirements of mobile, automotive, and stationary applications. For instance, if longer cycle life can be attained with the NIB chemistry compared to LIB, the cost and environmental benefits could be significant and turn the conditions in favour of the deployment of NIBs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank Christopher Mutel, Xiaojin Zhang, and Brian Cox for their support in Python code writing to perform LCA calculations. This work was partially funded by the Commission for Technology and Innovation in Switzerland (CTI) within the Swiss Competence Centre for Energy Research in Heat and Electricity Storage (SCCER-HaE), contract number 1155000153.References
- H. C. Hesse, M. Schimpe, D. Kucevic and A. Jossen, Energies, 2017, 10, 1–42 Search PubMed.
- M. Aneke and M. Wang, Appl. Energy, 2016, 179, 350–377 CrossRef.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed.
- I. Tsiropoulos, D. Tarvydas and N. Lebedeva, Li-ion batteries for mobility and stationary storage applications, JRC Science for policy report, 2018 Search PubMed.
- J. Tang, A. D. Dysart and V. G. Pol, Curr. Opin. Chem. Eng., 2015, 9, 34–41 CrossRef.
- J. Peters, D. Buchholz, S. Passerini and M. Weil, Energy Environ. Sci., 2016, 9, 1744–1751 RSC.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- C. Delmas, Adv. Energy Mater., 2018, 8, 1–9 Search PubMed.
- P. Vanysek, Electrochemical Series, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, 99th edn, Internet Version, 2018 Search PubMed.
- J. Betz, G. Bieker, P. Meister, T. Placke, M. Winter and R. Schmuch, Adv. Energy Mater., 2019, 9, 1803170 CrossRef.
- A. Ponrouch, D. Monti, A. Boschin, B. Steen, P. Johansson and M. R. Palacín, J. Mater. Chem. A, 2015, 3, 22–42 RSC.
- T. R. Jow, S. A. Delp, J. L. Allen, J. Jones and M. C. Smart, J. Electrochem. Soc., 2018, 165, A361–A367 CrossRef CAS.
- V. A. Nikitina, S. S. Fedotov, S. Yu. Vassiliev, A. Sh. Samarin, N. R. Khasanova and E. V. Antipov, J. Electrochem. Soc., 2017, 164, A6373–A6380 CrossRef CAS.
- K. L. Browning, R. L. Sacci and G. M. Veith, J. Electrochem. Soc., 2017, 164, A580–A586 CrossRef CAS.
- P. A. Nelson, K. G. Gallagher and I. Bloom, BatPaC (Battery Performance and Cost) Software, Argonne National Lab, http://www.cse.anl.gov/BatPaC/ Search PubMed.
- J. Rempel, B. Barnett and Y. Hyung, PHEV battery cost assessment, https://www.energy.gov/sites/prod/files/2014/03/f13/es001_barnett_2013_o.pdf Search PubMed.
- E. J. Berg, C. Villevieille, D. Streich, S. Trabesinger and P. Novák, J. Electrochem. Soc., 2015, 162, A2468–A2475 CrossRef CAS.
- N. Xue, W. Du, T. A. Greszler, W. Shyy and J. R. R. A. Martins, Appl. Energy, 2014, 115, 591–602 CrossRef.
- G. Patry, A. Romagny, S. Martinet and D. Froelich, Energy Sci. Eng., 2015, 3, 71–82 CrossRef.
- R. Petri, T. Giebel, B. Zhang, J. H. Schünemann and C. Herrmann, International Journal of Precision Engineering and Manufacturing-Green Technology, 2015, 2, 263–268 CrossRef.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef.
- M. Torchio, L. Magni, R. B. Gopaluni, R. D. Braatz and D. M. Raimondo, J. Electrochem. Soc., 2016, 163, A1192–A1205 CrossRef CAS.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 RSC.
- G. Berckmans, M. Messagie, J. Smekens, N. Omar, L. Vanhaverbeke and J. Van Mierlo, Energies, 2017, 10, 1314 CrossRef.
- R. De Levie, Electrochim. Acta, 1963, 8, 751–780 CrossRef.
- J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41 CrossRef CAS.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526 CrossRef CAS.
- G. Lenze, F. Röder, H. Bockholt, W. Haselrieder, A. Kwade and U. Krewer, J. Electrochem. Soc., 2017, 164, A1223–A1233 CrossRef CAS.
- V. Ramadesigan, P. W. C. Northrop, S. De, S. Santhanagopalan, R. D. Braatz and V. R. Subramanian, J. Electrochem. Soc., 2012, 159, R31–R45 CrossRef CAS.
- N. Xue, W. Du, A. Gupta, W. Shyy, A. M. Sastry and J. R. R. A. Martins, J. Electrochem. Soc., 2013, 160, A1071–A1078 CrossRef CAS.
- Y. Dai and V. Srinivasan, J. Electrochem. Soc., 2016, 163, A406–A416 CrossRef CAS.
- K. Wang, Y. Jin, S. Sun, Y. Huang, J. Peng, J. Luo, Q. Zhang, Y. Qiu, C. Fang and J. Han, ACS Omega, 2017, 2, 1687–1695 CrossRef CAS.
- D. W. McCall and D. C. Douglass, J. Phys. Chem., 1965, 69, 2001–2011 CrossRef CAS.
- E. R. Logan, E. M. Tonita, K. L. Gering, J. Li, X. Ma, L. Y. Beaulieu and J. R. Dahn, J. Electrochem. Soc., 2018, 165, A21–A30 CrossRef CAS.
- M. Sathiya, K. Hemalatha, K. Ramesha, J. M. Tarascon and A. S. Prakash, Chem. Mater., 2012, 24, 1846–1853 CrossRef CAS.
- A. Ehrl, J. Landesfeind, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A826–A836 CrossRef CAS.
- C. Mutel, Journal of Open Source Software, 2017, 2, 236 CrossRef.
- G. Wernet, C. Bauer, B. Steubing, J. Reinhard, E. Moreno-Ruiz and B. Weidema, Int. J. Life Cycle Assess., 2016, 21, 1218–1230 CrossRef.
- B. Cox, C. Bauer, A. M. Beltran, D. P. van Vuuren and C. L. Mutel, Appl. Energy, 2019 Search PubMed , submitted.
- U.S. Geological Survey, Mineral commodity summaries 2018, U.S. Geological Survey, 2018 Search PubMed.
- T. S. Schmidt, M. Beuse, X. Zhang, B. Steffen, S. F. Schneider, A. Pena-Bello, C. Bauer and D. Parra, Environ. Sci. Technol., 2019, 53, 3379–3390 CrossRef CAS PubMed.
- E. J. Berg and S. Trabesinger, J. Electrochem. Soc., 2018, 165, A5001–A5005 CrossRef CAS.
- L. A. W. Ellingsen, G. Majeau-Bettez, B. Singh, A. K. Srivastava, L. O. Valoen and A. H. Stromman, J. Ind. Ecol., 2014, 18, 113–124 CrossRef CAS.
- J. F. Peters and M. Weil, J. Cleaner Prod., 2018, 171, 704–713 CrossRef.
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278 CrossRef CAS.
- B. Rajabloo, A. Jokar, M. Désilets and M. Lacroix, J. Electrochem. Soc., 2017, 164, A99–A105 CrossRef CAS.
- C. Pillot, Avicenne Energy, http://www.charles-hatchett.com/public/images/documents/2018/dr_christophe_pillot_current_status_and_future_trends_of_the_global_li-ion_battery_market.pdf Search PubMed.
- R. E. Ciez and J. F. Whitacre, J. Power Sources, 2016, 320, 310–313 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9se00427k |
| This journal is © The Royal Society of Chemistry 2019 |