Resistance-based analysis of limiting interfaces in multilayer water splitting photocathodes by impedance spectroscopy

Abstract

Photoabsorber materials such as Cu₂O, which are normally prone to degradation reactions in aqueous environment, have regained attention for photoelectrochemical water splitting (PEC) due to the use of protective overlayers. Furthermore, by implementing an additional interlayer between the photoabsorber and protective layer, the photovoltage and the overall device efficiency can be enhanced due to the increased built-in voltage at the p–n junction. The detailed analysis of these multilayer PEC photoelectrodes under operando conditions is challenging due to the multiplicity of interfaces and charge carrier processes. To facilitate routine investigation of such multilayer systems, we have established a resistance-based method using electrochemical impedance spectroscopy (EIS) to identify the underlying potential-dependent processes of water splitting photocathodes under operation, which quickly reveals the problematic interfaces in these structures. Cu₂O/Ga₂O₃/TiO₂/RuO_x and p–Si/TiO₂/RuO_x photocathodes were investigated, with varying thicknesses of both interlayer and protection layer. The main limitations in the Cu₂O devices were found to be the Ga₂O₃/TiO₂ interface and the surface properties of the cuprous oxide absorber (most likely Cu²⁺ at the surface). We demonstrate that a commonly applied etching procedure of the Cu₂O to remove surface impurities reduced the associated resistance, but was not sufficient to achieve an ideal interface to the electron accepting layer. The analysis scheme enabled us to shed light on most of the involved charge carrier processes taking place in these complex systems, and we expect that this method will be applicable to other multilayer systems, facilitating a more routine and powerful operando characterization method for water splitting photoelectrodes. Furthermore the knowledge gained in this investigation will pave the way for the development of a complete equivalent circuit model of these protected buried heterojunction photocathodes.

---

Introduction

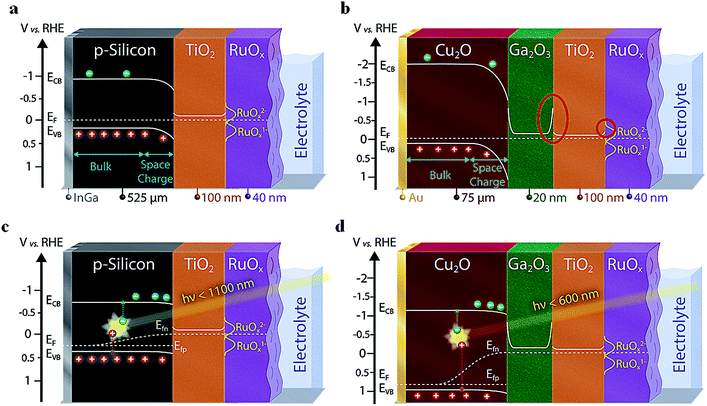
Several promising photocathode absorber materials for PEC applications—normally prone to (photo)corrosion in aqueous electrolyte solution—can be stabilized by using protective overlayers such as TiO₂, generating “buried junctions” where the photovoltage is generated at a solid-state junction underneath the semiconductor-electrolyte junction. Amongst these promising semiconductors are Cu₂O,^1,2 CuO,³ Si,^4–7 III–V semiconductors,^8,9 Cu₂BaSnS₄,¹⁰ Cu₂ZnSnS₄,¹¹ and BiVO₄.^12,13 Additionally, semiconducting buffer layers such as Ga₂O₃ (ref. 2 and 14) or CdS³ can be inserted between the photoabsorber and protection layers to increase the built-in voltage, the charge separation and the overall device efficiency. A scheme of these multi-layer structures is presented in Fig. 1.

Fig. 1 Band energy diagrams at equilibrium in the dark for (a) p-type silicon-based and (b) Cu₂O-based devices (the red circles show potential barriers for the photogenerated electrons); (c) a Si- and (d) a Cu₂O-based photocathode under illumination.

Due to the high complexity of these photoelectrodes along with the involved charge carrier processes, in-depth routine analysis is challenging. So far, there are few reports on the systematic study on interface and charge transport limitations through the multilayered structure under operational conditions. A scheme of the most common photophysical and electrochemical processes taking place in PEC devices are depicted in Fig. S1.† Electrochemical impedance spectroscopy (EIS) is a powerful non-destructive characterization method widely applied in different fields such as solar cells^15–18 and PEC systems.^19–21 Devices can be investigated under operando conditions both in the dark and under illumination. In the dark, measurements are normally performed to facilitate a Mott–Schottky analysis, which gives access to the band alignment of the semiconductors as well as the doping density and type of the majority carriers (electrons or holes).^22–24 In contrast, under illumination, the light induced processes, which are normally dominated by the minority charge carriers, can be evaluated and their implications for the device efficiency understood.

In PEC research, EIS under illumination has been applied to a variety of photoelectrodes, though interpretation of the data is not trivial, since an equivalent circuit (EC) model is required that sufficiently mimics the underlying photophysical and electrochemical processes in the system under study.^19,21 Even for such a relatively simple and well investigated system as Fe₂O₃, several EC models have been developed, as surface treatments, nanostructuring and/or fabrication process conditions alter the properties of the material.^20,25–28 Furthermore, the EI spectra can be complicated to analyze if two or more processes take place in the same time domain, as they can usually not be separated during the fitting procedure. On the other hand, the overall resistance of the two processes can be determined, which enables one to draw conclusions on their nature, especially if their potential dependence is investigated. Normally the capacitive elements distinguish the EC models, as the detected resistances are normally all in series (see Fig. S2†). Here, we apply a resistance-based analysis using EIS as a facile and generally applicable method to quickly identify the problematic layers and/or interfaces in these complex device architectures.

We investigated two systems, a more traditional photoabsorber material with relatively simple architecture (p-Si/TiO₂/RuO_x) as a well-behaved standard, and one based on the emerging material cuprous oxide (Cu₂O/Ga₂O₃/TiO₂/RuO_x), which features a buffer layer and therefore contains additional interfaces. The heterojunction with Ga₂O₃ is of particular interest due to the high photovoltage that can be obtained (1.2 V).²⁹

The n-type layer in the investigated photocathodes that is in contact with the electrolyte solution serves as both a protective layer and as an electron accepting layer. Commonly, TiO₂ is used due to its good (photo)electrochemical stability over a wide range of pH. On the other hand, the built-in voltage between Si or Cu₂O with TiO₂ is relatively low. By implementing ZnO or AZO,³⁰ ZnS,³¹ or Ga₂O₃ (ref. 14) as an interlayer, the built-in voltage and therefore also the photovoltage can be greatly increased for the Cu₂O-based devices.²⁹ The increased photovoltage is reflected in an earlier onset potential in J–V curves. The shift in onset potential of the photocurrent by the Ga₂O₃ interlayer is between 500 to 600 mV as compared to the devices with a direct Cu₂O/TiO₂ contact, reflecting the increased built-in voltage in the semiconductor heterojunction.

Results and discussion

Photocathodes in the dark

We first performed a Mott–Schottky analysis of the two photocathode types and of the ALD Ga₂O₃ to understand the energetic alignment of the different materials. The results on the built-in voltage (combined with the optical bandgap and the calculated distance of the E_F to the valence and conduction band) are presented in Fig. 1. A more detailed description of the Mott–Schottky plots and the processing of the resulting data can be found in the ESI (Fig. S3, S4 and Table S2†). The position of the reduced redox states of the RuO_x hydrogen evolving catalyst (namely Ru(III)O_x¹⁻ and Ru(II)O_x²⁻) have been implemented based on literature values and our own measurements (see Fig. S5† and main text below).^32–34

By evaluating the band diagrams in Fig. 1, potential barriers for photogenerated charge carriers are revealed. Such unfavorable band bending can lead to a limited charge transfer for electrons at the junction if the space charge forming the barrier is not thin enough (preventing tunneling). Indeed, we can conclude on the basis of Fig. 1a (for silicon) and Fig. 1b (for Cu₂O) that there is one limiting junction for the charge transfer of electrons from the TiO₂ to the catalyst, and in case of the Cu₂O-based devices a second one between the Ga₂O₃ and the TiO₂ (see red circles in Fig. 1b). Especially this latter one between the two n-type ALD layers could cause resistive limitations for the electron flow. We emphasize at this point that Mott–Schottky plot analysis must be taken as a first approximation of the actual band alignments in the PEC photocathodes. For example, the conduction band edges of the Ga₂O₃ with the photoabsorber and the TiO₂ will most probably not be symmetrical, but will still show the two potential barriers between Cu₂O/Ga₂O₃ and Ga₂O₃/TiO₂ as indicated in Fig. 1b.

Photocathodes under illumination

Typical J–V curves of the two systems are presented in Fig. 2. The photocurrent onset is shifted ∼0.6 V for the Cu₂O-based device, showing the higher built-in voltage as compared to the silicon devices. On the other hand, the J–V curve of the Cu₂O-based devices is more resistive, showing a lower fill factor (FF). When plotting the photocurrent logarithmically, three distinct regions are observed, which are also found in the resistances extracted from the EIS spectra (Fig. 3). In region I, at most positive potentials, a small (photo)anodic current is observed (nA to μA cm⁻²). This phenomenon can also be observed for other photocathodes^35–38 and originates from the leakage current of the majority carriers. In region II, the electron quasi Fermi level is negative enough (on the RHE scale) so that the catalyst is reduced from RuO_x to RuO_x⁻¹ by injecting electrons into the Gaussian shaped density of states (DOS) of the catalyst, showing photocathodic current (μA cm⁻²).³² Still most of the photogenerated charge carriers are subject to recombination as the electrochemical potential of the H₂ evolution has not yet been reached. In region III, the hydrogen evolution current can be observed as the electron quasi Fermi level has reached the second reduction step of the catalyst and the hydrogen evolution potential. The protons present in the electrolyte solution then act as electron acceptor, now enabling the charge transfer and the photocurrent generation.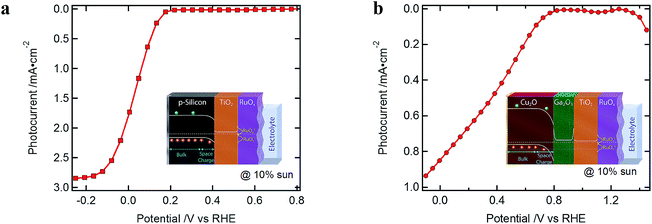

Fig. 2 Typical J–V curves (a) of a silicon-(100 nm ALD TiO₂ and RuO_x) and (b) of a Cu₂O-(20 nm ALD Ga₂O₃, 100 nm ALD TiO₂ and RuO_x) based standard device, under white light illumination of 10% sun.

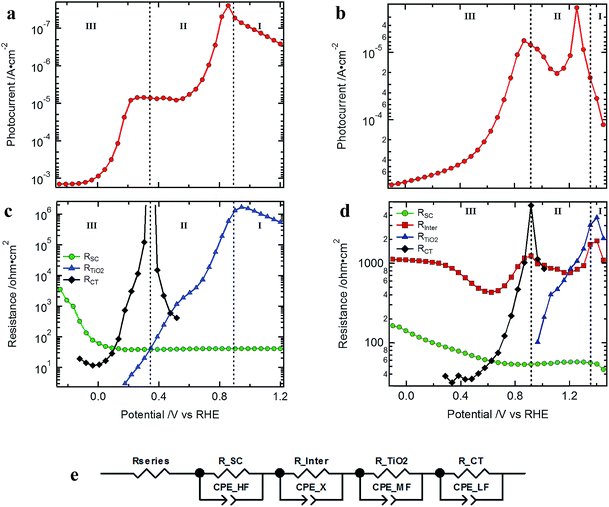Fig. 3 Logarithm of the photocurrent of the devices presented in Fig. 2: (a) Si- and (b) Cu₂O-based standard devices (light intensity of 10%); resistances from the EIS fitting procedure of the (c) Si- and (d) Cu₂O-based standard devices; (e) EC model used to fit the EIS data (for the silicon devices the RC element of R_inter is omitted as it was not present).

Comparing the different resistances determined for the Si and Cu₂O devices by EIS analysis (see Nyquist and Bode plots in Fig. S6 and S7† as well as Table S1† for associated frequencies), we can also observe three distinct potential regions, which coincide with those of the photocurrent plots (Fig. 3c and d). Furthermore, clear similarities in the potential dependent behavior of the resistances can be noted between the different photocathode types. The low frequency resistance R_CT (charge transfer resistance) has a strong potential dependence for both photocathode types. Also, R_TiO2 and R_SC (related to the TiO₂ layer and the recombination resistance inside the semiconductor junction, respectively) show clear changes with applied potential. R_inter (discussed in detail below), in contrast, is only present in the Cu₂O-based devices and is rather constant with potential, though showing a valley at ∼0.6 V vs. RHE and another one at ∼1.2 V vs. RHE.

The similarities between the resistances of the different photocathodes are even more evident when accounting for the different photovoltages in each system: after shifting the data to give the same quasi-Fermi level of electrons (set by the onset of the hydrogen evolution current as determined by R_CT at the beginning of region III), the J–V curves and extracted resistances of the Si and Cu₂O devices overlap with one another, enabling a direct comparison (Fig. S8†). The detection of the onset potential via R_CT is more sensitive as compared to the extrapolation of the photocurrent to the voltage axis or by setting an arbitrary (low) photocurrent as a measure.

The low frequency resistance, R_CT, mirrors the shape of the J–V curves in potential region III (Fig. 3c and d) and represents the hydrogen-generating charge transfer over the hydrogen evolving catalyst (HEC) into the electrolyte solution (R_CT–H₂ in Fig. 4). Prior to the onset of hydrogen evolution in potential region II, R_TiO2 shows a deviation from exponential behavior representing the increased current flow for the HEC reduction (Fig. S9†). In part of this potential region, R_CT is convoluted with R_TiO2. For the Si-based devices, the separation of R_CT and R_TiO2 could be achieved by extrapolating an exponential decrease of R_TiO2 and subtracting it in the potential region of the first HEC reduction (R_CT–RuO_x in Fig. 4). In the case of the Cu₂O devices, the separation did not yield reliable results due to the interference with the additional resistance R_inter.

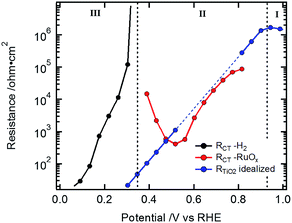Fig. 4 Data from Si sample in Fig. 2a: exponential extrapolation of R_TiO2 (blue dotted line) and the residual resistance (R_CT–RuO_x) relating to the current for the HEC reduction.

R _CT–RuO_x itself mirrors the current flow for the first reduction step of RuO_x to form RuO_x⁻¹ (from Ru(IV) to Ru(III)), which is a prerequisite for hydrogen evolution.^{32–34,39,40} Notably, the shape of R_CT–RuO_x reflects the DOS of the catalyst. RuO_x as the HEC can be seen as a protonic electrochemical capacitor due to H⁺ exchange with the electrolyte solution: RuO_x(OH)_y + δH⁺ + δe⁻ ↔ RuO_x−δ(OH)_y+δ (see also ESI and Fig. S5† for further discussion on the redox states of the HEC).^39,40 The charge inside the HEC can be visualized by its storage and release process during transient photocurrent decay measurements (TPC).^32,41 In the TPC experiments, a steady state white light bias was applied (10% sun). The wavelengths of the light pulse to generate the photocurrent transients was either 447 nm (Fig. 5a) or 530 nm (Fig. 5b), which led to an excitation of charge carriers near the surface of the photoabsorber. The possible excitation at 627 nm (red) is near the absorption onset of the Cu₂O and would therefore probe the bulk of the semiconductor with the deeper penetration depth of this wavelength (see Niu et al.).² As the focus in the TPC experiments was the detection of the charge inside the HEC, we have used a perturbation pulse with 5 to 10% of a sun as light intensity (i.e. 50 to 100% of the actual white light bias). Therefore, our TPC measurements are not “small” perturbation experiments near equilibrium but rather photocurrent transients similar to the investigations by Laskowski et al. with a strong perturbation.⁴¹ The TPC measurements were performed similar to the EIS measurements at different bias potentials to further observe the potential dependent changes of the accumulated charge.

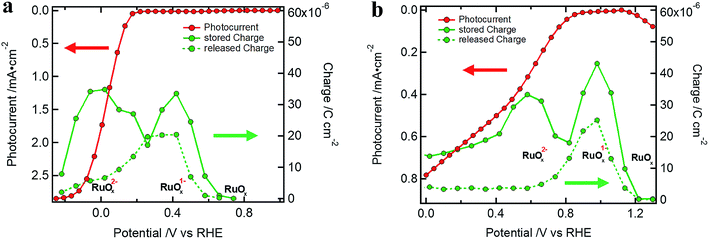Fig. 5 Stored and released charge in the TPC (measurements with 10% sun white light bias) showing the charging of the RuO_x catalyst for (a) a Si device (excitation at 447 nm (5% sun), same sample as in Fig. 2a) and (b) a Cu₂O standard device (excitation at 530 nm (10% sun)), Cu₂O standard device) device.

During the light pulse, normally a double-exponential decay of the photocurrent was observed. The fast component of the decay is associated with the recombination of photogenerated charge carriers while the slow one is related to the formation of RuO_x¹⁻ or RuO_x²⁻ species.³² After the light pulse is turned off, the photocurrent steeply drops and changes sign before returning to the steady state white light bias current. The photocurrent with inverted sign represents the release of stored charge inside the HEC (the decay back to steady state white light bias current was normally mono-exponential). Examples of the TPC transients can be found in Fig. S10† together with a table of the exponential fittings (Tables S3 and S4†).

The charge in a current transient was determined from the integral of the exponential decay of the current density over pulse duration (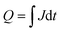; with Q as the charge per cm², J as the current density and t as time). The amount of charge determined in the TPC experiments for the storage (from the slow component of the photocurrent decay during the light pulse) and release (after the light pulse has been turned off) process are very similar and show the capacitive loading of the HEC at its different redox states (Fig. 5, see also Table S5†). As the release of stored charge is competing with the hydrogen evolution reaction, normally the amount of released charge detected is lower as compared to the initially stored charge, especially near the RuO_x²⁻ redox potential.

R _TiO2 is a strongly potential dependent resistance at intermediate frequencies present in potential regions I and II (Fig. 3). At very positive potentials R_TiO2 dominates the photoanodic current flow. In region II R_TiO2 decreases exponentially but shows a deviation in the form of a valley as discussed above. After the formation of RuO_x⁻¹, R_TiO2 further decreases exponentially. As both the Si and Cu₂O-based systems possess the TiO₂ protection layer and the associated interfaces (TiO₂/catalyst or the TiO₂/electrolyte solution), one possibility is that R_TiO2 is related to a resistive transport inside the TiO₂, or a second possibility is that it is related to a potential barrier at the aforementioned interfaces (for both of these cases, R_TiO2 manifests as a series resistance). To differentiate these options, we varied the protection layer thickness between 50, 100 and 150 nm. A transport related resistance should show a significant increase for the thicker protection layers while a resistance related to a potential barrier at the TiO₂/RuO_x interface would not be influenced by the different thicknesses of the TiO₂ layer. The results for Cu₂O and silicon (Fig. S11†) did not show any significant change in the resistance with increasing thickness of the ALD TiO₂ layer. A charge transport resistance within the TiO₂ can therefore be excluded. Considering the observation in Fig. 1a and b of the unfavorable band bending at the TiO₂ contact to the catalyst we can conclude that R_TiO2 represents the resistive limitation at this interface. The implications, however, for the overall device efficiency of this series resistance are limited to the photocurrent rise, as it is low or vanished when the surface potential approaches the thermodynamic HER potential. An additional observation is that the thickness of the TiO₂ layer did not have any significant influence on the V_OC nor on the photocurrent.

The resistance at the highest frequencies, R_SC, is mainly constant in the potential regions I and II and increases in region III. It is related to the recombination current of the photogenerated charge carriers and the steeper its increase in potential region III the better the FF of the J–V curves. The increase of R_SC with increasing reverse bias after passing the H₂ evolution potential represents the reduced recombination of photogenerated electron hole pairs (i.e. higher recombination resistance) as now the band bending in the space charge of the photoabsorber increases and acceptor states are available inside the electrolyte solution to enable the flow of photocurrent. It should be noted that in PEC photoelectrodes, the system is effectively in open-circuit until the surface potential is in a region where charge transfer can occur. Thus, if the quasi Fermi level of the electrons has not reached the second reduction step of the catalyst and the energetic position of the hydrogen evolution potential, the photogenerated charge must recombine (i.e. low recombination resistance, potential region I and II).⁴² The observation that R_SC increases more slowly in the case of the Cu₂O as compared to the Si samples (see Fig. 3 and S8†) originates from an additional series resistance that is present in the metal oxide-based devices, namely R_inter.

So far, the three different resistances described have been observed in both photocathode types. In the case of the fourth resistance, R_inter, observed only in the cuprous oxide devices, it stands to reason that it is related to the Ga₂O₃ layer or the Cu₂O surface (or interface). Though R_inter shows as mentioned one valley around the second reduction of the catalyst, the valley at the first reduction step is not always clearly visible and is therefore disregarded in the analysis.

Generally, one would expect a reduction of R_inter similar to R_TiO2 with increasing negative potential if it is purely related to a potential barrier at the Ga₂O₃/TiO₂ interface. Compared to R_TiO2 this reduction of the barrier would appear only after the electron quasi Fermi level reaches the redox potential of the H₂ evolution potential, as only then the barrier at the Ga₂O₃/TiO₂ interface would begin to reduce. This behavior is what we can observe in the descent into the valley starting from 0.8 V vs. RHE in Fig. 3d and 6 (for devices with Ga₂O₃ layer).

Fig. 6 (a) J–V curves of Cu₂O devices without and with 20 and 70 nm ALD Ga₂O₃ (and with 100 nm ALD TiO₂ and RuO_x); (b) J–V curves adjusted to the hydrogen evolution onset as determined by R_CT; (c) R_inter as determined from the EIS measurements and (d) R_inter adjusted by R_CT.

However, R_inter starts to increase again after passing 0.6 V vs. RHE, indicating that it is a superposition of different contributions. To better understand R_inter, Cu₂O-based devices without the ALD Ga₂O₃ layer were fabricated and evaluated. In Fig. 6, the J–V curves and R_inter of devices without and with 20 and 70 nm ALD Ga₂O₃ layer are plotted before (a and c) and after (b and d) adjusting to the H₂ evolution onset potential by R_CT. As expected, the built-in voltage (see Fig. S3b†) and the photovoltage for devices without Ga₂O₃ layer are lower but interestingly R_inter is still present, albeit with a different potential dependence. It has a constant and low value in potential region I and II at positive potentials before the onset of the photocurrent (∼90 ohm cm² as compared to ∼1000 ohm cm² for the case with 20 nm Ga₂O₃ interlayer, Fig. 6), and then increases at more negative potentials.

This observation shows that the Cu₂O surface properties are of crucial importance for high device efficiencies, as surface traps or an unwanted overlayer are limiting the charge transfer to the n-type semiconductor (discussed in more detail below). The magnitude of the R_inter (for devices with Ga₂O₃ layer) in potential region II correlates with the increased V_OC observed in the devices. And in potential region III R_inter represents the series resistance that dominates the fill factor of the J–V curves (Fig. S12†), pinpointing the main limitation for the FF of the Cu₂O photocathodes.

These observations on R_inter (series resistance in Region III, V_OC correlation in region II, and existence even without the Ga₂O₃ interlayer (though in latter case with a different potential dependence)) imply that it is composed of at least two components (see Fig. S13†). One component, as visible for the case with 0 nm of Ga₂O₃, must be related to the Cu₂O surface properties (R_surface). The second contribution must be related to the ALD Ga₂O₃ interlayer (R_Ga) at the Ga₂O₃/TiO₂ interface. The height of R_Ga in potential region II is accompanied with a higher built-in voltage and V_OC (see also Mott–Schottky plots in Fig. S3b†). With 20 nm Ga₂O₃ still no bulk of the buffer layer can be formed as the layer is to thin and the full heterojunction potential is therefore lower as compared to 70 nm of buffer layer (in which the bulk can be already formed, see Fig. S14a–c†). Higher built-in voltage in turn increases the barrier height at the Ga₂O₃/TiO₂ interface and the associated resistance.

To better understand the potential dependence of R_Ga we have to consider the interplay of the redox potential in solution, the applied potential and the position of the conduction bands of Ga₂O₃ and TiO₂. Before the H₂ onset potential, the barrier between Ga₂O₃ and TiO₂ remains unchanged (Fig. S14d†). At the onset of the H₂ evolution the potential barrier at the interface between the Ga₂O₃ and the TiO₂ will start to decrease as the Fermi level inside the TiO₂ layer is now pinned by the redox potential of the hydrogen evolution potential inside the electrolyte solution. On the other hand, the conduction band of Ga₂O₃ will continue to move to higher energies with scanning to more negative potentials (Fig. S14e and f†), reducing the barrier between the two n-type metal oxides. This will manifest as an exponential decrease of the R_Ga if it is related to a potential barrier (as for the case of R_TiO2).

Indeed, R_Ga is, like R_TiO2, reducing exponentially with increasing reverse bias, limiting its influence on the J–V curve mainly to the region of the hydrogen evolution current onset (see Fig. 6d). The relation between the built-in voltage and the change of R_Ga further supports our interpretation that it represents the potential barrier predicted by the Mott–Schottky plots (in Fig. 1d).

It is known that Cu₂O in ambient conditions undergoes surface oxidation to Cu²⁺ species such as Cu(OH)₂ or CuO, which can limit the performance of the devices.⁴³ According to Lee et al.²⁹ a reduction of the Cu²⁺ species by the gallium ALD precursor is possible as the authors have shown by XPS measurements which should improve the surface quality. Still we have implemented an additional etching of the Cu₂O surface as a first cleaning process.⁴³ Therefore, the as-prepared Cu₂O sample was immersed in nitric acid (1 : 1 of H₂O and 65% HNO₃) for 10 seconds, followed by rinsing with DI water and sonication in isopropanol for 30 seconds. Finally, the foil was dried under nitrogen flow and immediately transferred into the ALD chamber for the ALD buffer layer deposition.

In Fig. 7, the results for devices with and without etching are presented. Devices were measured without the Ga₂O₃ layer to avoid superposition with the R_Ga component of R_inter. The performance of the pre-etched devices showed an increased FF due to the reduced R_surface at the Cu₂O/TiO₂ contact (which could also be observed for the case with ALD Ga₂O₃ buffer layer, Fig. S15†). Nevertheless, R_surface is still present after the etching, implying that the surface treatment is not sufficient to achieve a defect free interface. This resistance is probably induced by an energetically low-lying energy state at the surface through which the electrons must flow in order to cross over to the buffer layer. In contrast to R_Ga, the Cu₂O surface resistance, R_surface, would not reduce with further reverse bias. It increases as the conduction band of Ga₂O₃ shifts up at more negative applied potential, increasing the barrier for the electrons that have to be transferred through the limiting Cu₂O surface layer (see Fig. S14d–f†).

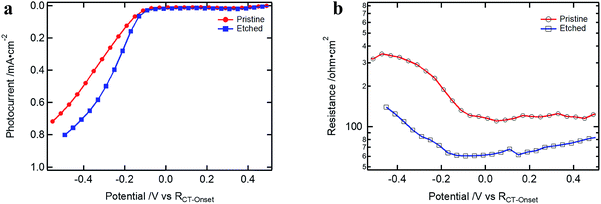Fig. 7 (a) J–V curves of Cu₂O-based devices with and without etching treatment (devices are without ALD Ga₂O₃ but 100 nm ALD TiO₂ and RuO_x); (b) R_surface of the samples presented in (a).

Combining the knowledge about the potential dependence of R_inter with and without the Ga₂O₃ layer, we can conclude that R_inter is the source of the main limitations observed in the J–V curves. We can achieve high photovoltages, but the fill factor is limited by the resistive components of R_inter. Our results can explain now e.g. why Lee et al. observed for their Cu₂O/Ga₂O₃-based solar cell devices high photovoltages of 1.2 V but a hampered FF of only 45%.²⁹

The resistances observed in the EIS spectra under illumination have been assigned to the relevant charge carrier processes, and we can understand their influence on the J–V curves, a precondition to make sophisticated routine analysis and to facilitate the development of a generally applicable EC. Further investigations are being conducted to tackle the limitations observed in the Cu₂O devices. On the one hand, we expect that the decrease of the space charge layer width through increased doping of the Ga₂O₃ layer would reduce the potential barrier and therefore the associated resistance for the electrons at the Ga₂O₃/TiO₂ interface, and may enable both high V_OC and FF. Furthermore, the higher doping would enable to achieve a higher built-in voltage at lower buffer layer thickness. On the other hand, with the presented analysis approach, we can evaluate the effect of different surface treatments on R_surface and optimize the surface cleaning process, which should finally lead to a better FF and overall device efficiency.

Conclusion

We have investigated silicon- and Cu₂O-based multilayer photocathode devices by EIS in the dark and under illumination to pinpoint the limitations for the J–V curves and device efficiencies. Based on the dark measurements we have identified potential barriers at the TiO₂/RuO_x and Ga₂O₃/TiO₂ interfaces. Under illumination conditions we have analyzed the EIS data in terms of the potential dependence of the determined resistances. We have shown that shifting the data to align the hydrogen onset potential in the different samples (determined by the onset of the hydrogen evolution via the charge transfer resistance) enables the comparison of similar device types with different photovoltage and even different photocathode absorber materials. The resistances were assigned to the related photophysical or electrochemical processes, namely, the recombination of photogenerated charge carriers in the bulk or space charge region of the semiconductor, the charge transfer into the electrolyte solution, and the limited charge transfer due to a potential barrier between the TiO₂ and the electrolyte solution. In the case of the Cu₂O-based devices, an additional resistance appears, convoluting several different processes such as charge transfer from the absorber to the n-type semiconductor and a potential barrier at the Ga₂O₃/TiO₂ interface. Based on our analysis we can conclude that this emerging photocathode material is hampered by its surface quality (i.e. interface defects), limiting the charge transfer between the Cu₂O and the buffer layer and therefore the fill factor for these devices. The series resistance associated with the Cu₂O surface could be reduced by a commonly applied etching treatment of the Cu₂O surface, but our analysis shows directly that such a pre-treatment is not sufficient to achieve an ideal or nearly ideal surface that enables reproducibly high efficiency devices. We further identified a potential barrier for the photogenerated electrons at the Ga₂O₃/TiO₂ interface which limits the rise of the photocurrent at the onset of the hydrogen evolution. By this analysis scheme we have opened the way for a fast and better understanding of the interplay of the different materials and interfaces and how to evaluate optimization treatments in complete multilayer device structures. Finally, the knowledge gained on the determined resistances and their associated photophysical and electrochemical processes will advance the development of a generally applicable EC of these multilayer photocathode systems.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The University of Zurich Research Priority Program (URPP) LightChEC, and the Swiss National Science foundation (AP Energy Grant # PYAPP2 160586) are gratefully acknowledged for financial support.

References

1. L. Pan, J. H. Kim, M. T. Mayer, M.-K. Son, A. Ummadisingu, J. S. Lee, A. Hagfeldt, J. Luo and M. Grätzel, Nat. Catal., 2018, 1, 412.
2. W. Niu, T. Moehl, W. Cui, R. Wick-Joliat, L. Zhu and S. D. Tilley, Adv. Energy Mater., 2018, 8, 1702323.
3. W. Septina, R. R. Prabhakar, R. Wick, T. Moehl and S. D. Tilley, Chem. Mater., 2017, 29, 1735.
4. D. Bae, T. Pedersen, B. Seger, M. Malizia, A. Kuznetsov, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, Energy Environ. Sci., 2015, 8, 650.
5. B. Seger, T. Pedersen, A. B. Laursen, P. C. K. Vesborg, O. Hansen and I. Chorkendorff, J. Am. Chem. Soc., 2013, 135, 1057.
6. A. G. Scheuermann, J. P. Lawrence, K. W. Kemp, T. Ito, A. Walsh, C. E. D. Chidsey, P. K. Hurley and P. C. McIntyre, Nat. Mater., 2016, 15, 99.
7. S. W. Boettcher, J. M. Spurgeon, M. C. Putnam, E. L. Warren, D. B. Turner-Evans, M. D. Kelzenberg, J. R. Maiolo, H. A. Atwater and N. S. Lewis, Science, 2010, 327, 185.
8. J. Gu, Y. Yan, J. L. Young, K. X. Steirer, N. R. Neale and J. A. Turner, Nat. Mater., 2016, 15, 456.
9. W.-H. Cheng, M. H. Richter, M. M. May, J. Ohlmann, D. Lackner, F. Dimroth, T. Hannappel, H. A. Atwater and H.-J. Lewerenz, ACS Energy Lett., 2018, 3, 1795.
10. J. Ge, P. J. Roland, P. Koirala, W. Meng, J. L. Young, R. Petersen, T. G. Deutsch, G. Teeter, R. J. Ellingson, R. W. Collins and Y. Yan, Chem. Mater., 2017, 29, 916.
11. K. Wang, D. Huang, Y. Le, H. Gu, S. Ikeda and F. Jiang, J. Colloid Interface Sci., 2019, 536, 9.
12. D. Lee, A. Kvit and K.-S. Choi, Chem. Mater., 2018, 30, 4704.
13. M. T. McDowell, M. F. Lichterman, J. M. Spurgeon, S. Hu, I. D. Sharp, B. S. Brunschwig and N. S. Lewis, J. Phys. Chem. C, 2014, 118, 19618.
14. C. Li, T. Hisatomi, O. Watanabe, M. Nakabayashi, N. Shibata, K. Domen and J.-J. Delaunay, Energy Environ. Sci., 2015, 8, 1493.
15. I. Mora-Seró, Y. Luo, G. Garcia-Belmonte, J. Bisquert, D. Muñoz, C. Voz, J. Puigdollers and R. Alcubilla, Sol. Energy Mater. Sol. Cells, 2008, 92, 505.
16. I. Mora-Seró, G. Garcia-Belmonte, P. P. Boix, M. A. Vázquez and J. Bisquert, Energy Environ. Sci., 2009, 2, 678.
17. J.-H. Yum, E. Baranoff, F. Kessler, T. Moehl, S. Ahmad, T. Bessho, A. Marchioro, E. Ghadiri, J.-E. Moser, C. Yi, M. K. Nazeeruddin and M. Grätzel, Nat. Commun., 2012, 3, 631.
18. R. Scheer and H. W. Schock, Chalcogenide photovoltaics. Physics, technologies, and thin film devices, Wiley-VCH, Weinheim, Germany, 2011.
19. L. Bertoluzzi and J. Bisquert, J. Phys. Chem. Lett., 2012, 3, 2517.
20. B. Klahr, S. Gimenez, F. Fabregat-Santiago, J. Bisquert and T. W. Hamann, J. Am. Chem. Soc., 2012, 134, 16693.
21. Photoelectrochemical solar fuel production. From basic principles to advanced devices, ed. S. Giménez and J. Bisquert, Springer International Publishing, Cham, 2016.
22. W. P. Gomes and D. Vanmaekelbergh, Electrochim. Acta, 1996, 41, 967.
23. R. de Gryse, W. P. Gomes, F. Cardon and J. Vennik, J. Electrochem. Soc., 1975, 122, 711.
24. O. Almora, C. Aranda, E. Mas-Marzá and G. Garcia-Belmonte, Appl. Phys. Lett., 2016, 109, 173903.
25. T. Lopes, L. Andrade, H. A. Ribeiro and A. Mendes, Int. J. Hydrogen Energy, 2010, 35, 11601.
26. C. Y. Cummings, F. Marken, L. M. Peter, K. G. U. Wijayantha and A. A. Tahir, J. Am. Chem. Soc., 2012, 134, 1228.
27. V. Aroutiounian, Int. J. Hydrogen Energy, 2002, 27, 33.
28. F. Le Formal, S. R. Pendlebury, M. Cornuz, S. D. Tilley, M. Grätzel and J. R. Durrant, J. Am. Chem. Soc., 2014, 136, 2564.
29. Y. S. Lee, D. Chua, R. E. Brandt, S. C. Siah, J. V. Li, J. P. Mailoa, S. W. Lee, R. G. Gordon and T. Buonassisi, Adv. Mater., 2014, 26, 4704.
30. A. Paracchino, V. Laporte, K. Sivula, M. Grätzel and E. Thimsen, Nat. Mater., 2011, 10, 456.
31. P. Dai, W. Li, J. Xie, Y. He, J. Thorne, G. McMahon, J. Zhan and D. Wang, Angew. Chem., Int. Ed., 2014, 53, 13493.
32. E. Pastor, F. Le Formal, M. T. Mayer, S. D. Tilley, L. Francàs, C. A. Mesa, M. Grätzel and J. R. Durrant, Nat. Commun., 2017, 8, 14280.
33. K. Doblhofer, M. Metikoš, Z. Ogumi and H. Gerischer, J. Phys. Chem., 1978, 82, 1046.
34. E. Watanabe, H. Ushiyama, K. Yamashita, Y. Morikawa, D. Asakura, M. Okubo and A. Yamada, J. Phys. Chem. C, 2017, 121, 18975.
35. M. J. Choi, J.-Y. Jung, M.-J. Park, J.-W. Song, J.-H. Lee and J. H. Bang, J. Mater. Chem. A, 2014, 2, 2928.
36. J. Feng, M. Gong, M. J. Kenney, J. Z. Wu, B. Zhang, Y. Li and H. Dai, Nano Res., 2015, 8, 1577.
37. M. G. Mali, H. Yoon, B. N. Joshi, H. Park, S. S. Al-Deyab, D. C. Lim, S. Ahn, C. Nervi and S. S. Yoon, ACS Appl. Mater. Interfaces, 2015, 7, 21619.
38. L. Zhang, Y. Li, C. Li, Q. Chen, Z. Zhen, X. Jiang, M. Zhong, F. Zhang and H. Zhu, ACS Nano, 2017, 11, 12753.
39. S. Ardizzone, G. Fregonara and S. Trasatti, Electrochim. Acta, 1990, 35, 263.
40. J. Juodkazytė, R. Vilkauskaitė, B. Šebeka and K. Juodkazis, Trans. IMF, 2007, 85, 194.
41. F. A. L. Laskowski, J. Qiu, M. R. Nellist, S. Z. Oener, A. M. Gordon and S. W. Boettcher, Sustainable Energy Fuels, 2018, 2, 1995.
42. W. Cui, W. Niu, R. Wick-Joliat, T. Moehl and S. D. Tilley, Chem. Sci., 2018, 9, 6062.
43. C. Xiang, G. M. Kimball, R. L. Grimm, B. S. Brunschwig, H. A. Atwater and N. S. Lewis, Energy Environ. Sci., 2011, 4, 1311.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9se00248k

---