Open Access Article
Open Access ArticleThe energetic implications of introducing lithium-ion batteries into distributed photovoltaic systems
Simon
Davidsson Kurland
 *abc and
Sally M.
Benson
bc
*abc and
Sally M.
Benson
bc
aDepartment of Space, Earth and Environment, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden. E-mail: simon.davidsson@chalmers.se; Tel: +46 31 772 6311
bGlobal Climate and Energy Project (GCEP), Stanford University, Stanford, CA 94305, USA
cDepartment of Energy Resources Engineering, Stanford University, Stanford, CA 94305, USA
First published on 18th March 2019
Abstract
Batteries for stationary applications can prove to be crucial for enabling high penetration of solar energy, but production and use of batteries comes with an energetic cost. This study quantifies how adding a lithium-ion (Li-ion) battery affects the energetic performance of a typical residential photovoltaic (PV) system under a wide range of climatic conditions. If all generated power is either self-consumed or made available via an existing distribution grid, the PV system will have an energy return on investment (EROI) of between 14 (Alaska) and 27 (Arizona). While adding a 12 kW h Li-ion battery increases self-consumption considerably, this has a negative effect of decreasing the EROI by more than 20%. In a situation where all excess power generation is curtailed, the EROI can be as low as 7 (Alaska and Washington), although it can also be as high as 15 (Florida). Introducing a battery increases the EROI but it is still considerably lower than in cases where excess power generation is added to the grid. Doubling the battery size increases the average self-consumption marginally, but further decreases the EROI of the system because the extra energy invested to build the additional battery is used inefficiently. The results show that installing PV systems in locations with good solar resources and a grid that can accept excess production is desirable for maximizing the net energy return from distributed PV systems. Batteries have a benefit when excess electricity generation cannot be fed into the grid. Oversizing batteries has the effect of significantly reducing the EROI of the PV system.
Introduction
Solar energy from photovoltaics (PVs) is one of the leading candidates for large scale deployment of low-carbon energy.1 A wide range of scenarios suggest rapid growth of both utility-scale and distributed PV installations in coming decades.2 As PV generation contributes significant shares of an electricity mix, an increasing fraction of the generated power could be curtailed, unless it can be stored and used at a later time.3 Most storage capacity in power systems installed to date has been in the form of pumped storage hydropower (PSH), but electrochemical storage technologies are emerging quickly and are becoming increasingly dominated by lithium-ion (Li-ion) batteries.4 Costs are declining rapidly as installations of Li-ion batteries for both utility scale and residential stationary applications grow, a development that is expected to continue.5The availability of lower-cost batteries for residential use makes it possible for home owners with PV installations to decrease their reliance on the central grid.6,7 Increased self-consumption of PV generation has the potential to increase profits, decrease stress on the distribution grid, and enable the integration of more PV capacity in power systems.8,9 However, it has been suggested that the use of batteries for power system applications can have negative implications, such as increased greenhouse gas (GHG) emissions and energy use.10,11 The manufacturing of batteries also requires substantial amounts of energy and associated GHG emissions exist.12,13 For a complete analysis of the consequences of large scale deployment of batteries the entire life-cycle of the system should be considered: the use phase, manufacturing, and recycling or disposal.
With rapid growth of energy technologies, a fraction of their output of energy is, in theory, required to drive the continued growth of the technology.14 Therefore, net energy analysis (NEA) has been suggested as a suitable tool for guiding research, policy, and investment towards sustainable energy systems.15 A wide range of studies have investigated net energy return ratios (NER) of modern PV installations, and the energy return on investment (EROI) appears to be positive and increasing with time.16–18 Attempts have been made to create a theoretical framework for how storage affects the EROI of energy systems.3 However, there are uncertainties regarding exactly how storage technologies should be incorporated into NEA metrics, especially when applied to real-world systems.19 Attempts have been made to include EROI impacts of optimizing relations between storage, renewable energy capacity, and curtailment.20 As batteries become more widely available for consumers, it is also interesting to analyze the impact of a decision to install a battery or promote the use of batteries.
The aim of this study is to assess the energetic implications of introducing Li-ion batteries into PV systems, taking into account both the use phase and the manufacturing of the battery. Focus is given to differences in useful energy outputs and use of a battery under varying climatic conditions and capabilities to make excess generation available through the distribution grid, unlike most previous studies focusing on the energy inputs required. New and transparent EROI estimates of realistic residential PV-battery systems are created to use the NEA methodology to assess realistic cases that could be used as a basis for actual decision and policy making.
Methods
Net energy analysis
NEA has developed side by side with life cycle assessment (LCA) methodology and these methodological frameworks share many similarities.21 Results from an NEA can be presented in the form of energy return on investment (EROI):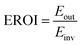 | (1) |
All generated electricity is generally considered useful and to have a positive impact on the EROI. However, the power generated from a PV installation varies with the time of the day and year, not necessarily in a way correlating with demand; hence curtailment of power generation can start occurring as solar penetration increases.23 It has been suggested that curtailment of power can be included in the EROI concept by expressing the fraction of curtailed power as ϕ, creating an alternative metric:
| EROIcurt = (1 − ϕ)EROI | (2) |
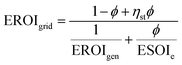 | (3) |
 | (4) |
Early theoretical estimates suggested that the ESOIe of Li-ion batteries was higher than that for other electrochemical storage technologies, but much lower than PSH and compressed air energy storage (CAES).25 After converting the energy inputs to electrical energy equivalents, it was concluded that the ESOIe of Li-ion battery technologies is 32 and the EROI of modern PV systems is 8.3 Instead of relying on these generic theoretical metrics, we calculate case specific EROI and ESOIe by estimating ϕ(t) at every time step of the service life of typical residential PV systems under different climatic conditions.
A typical residential PV system
About 94% of the total PV modules produced globally in 2016 were based on silicon wafer technology, and 70% were multi-crystalline silicon (mc-Si) modules.26 A model of a roof-top mounted mc-Si PV system representing a typical modern residential PV installation in the United States is created in the System Advisor Model (SAM) from the National Renewable Energy Laboratory (NREL).27 The main properties of the PV system are described in Table 1.| a The average efficiency of commercial wafer-based silicon modules in 2016.26 b The median size of residential PV systems in the US in 2016 was just over 6 kWp.47 c Default assumption in the SAM, corresponding to the median degradation value estimated by Jordan and Kurtz (2013).48 | |
|---|---|
| PV cell type | mc-Si |
| Installation type | Roof-top |
| Module efficiency | 17.0%a |
| Area (m2) | 35.6 |
| Installed capacity (kWp) | 6.0b |
| Expected PV service life (years) | 25 |
| Annual degradation | 0.5%c |
A wide range of different lithium-ion battery chemistries are available on the residential electrochemical storage market. Lithium iron phosphate (LFP) batteries with LiFePO4 as the cathode material have relatively low specific energy but are considered to have large potential for power system applications as they are safe, durable, and use abundant materials compared to most other lithium-ion battery chemistries.28 An LFP battery is included in the SAM. The main properties of the battery system are summarized in Table 2.
| a Standard assumptions for specific energy and degradation for a LFP battery in the SAM.27 b Median calendar life of a LFP battery in the Batt-DB database.31 | |
|---|---|
| Battery type | Lithium iron phosphate (LFP) |
| Nominal bank capacity (kW hn) | 12.0 (24.0) |
| Maximum depth of discharge | 80% |
| Specific energy (kW h kg−1) | 93.1a |
| Degradation | Modeled in SAMa |
| Calendar lifetime (years) | 15b |
| Battery connection | AC connected |
There is no common practice for sizing battery systems for PV systems as cost and characteristics of commercial batteries vary significantly.29 The size of the battery here is not optimized to fit any of the specific circumstances to maximize economic profit, but is the same in the different cases. Assuming a C-rate of 0.5, the battery used with a nominal capacity of 12 kW hn is large enough to temporarily accept the entire maximum power output from the PV system and is within the range of sizes available on the U.S. market. To investigate the importance of the battery size, an alternative case with a battery of double the size (24 kW hn) is also introduced.
Degradation of batteries is a complicated process, in which calendar and cycle aging are affected by both external conditions and usage.30 LFP batteries are considered to have a longer life expectancy than most other Li-ion battery technologies and have an expected calendar life of around 15 years.31 We assume that the battery is replaced after 15 years, meaning that a total of two 12 kW hn batteries are installed over the life time of the PV system.
Calculating useful energy outputs
The total energy outputs from the system, as well as the direct use, excess generation, and battery use are modelled using the SAM.27,32,33 To account for the differences in solar resource and residential load profiles in different climates, the system is modelled in five different locations in distinct climate zones (Table 3).34 Hourly weather data of a typical meteorological year (TMY) are used in the SAM to model PV power generation.35 Hourly load profiles of typical residential buildings (base load model) in the same TMY3 locations are used to estimate the direct use of the generated power.36 These annual load profiles are depicted in Fig. 1 and are assumed to remain the same over the 25 year expected service life of the PV system. The power generation from the PV system that is used to fulfil the residential load either directly, or via storage, is commonly referred to as self-consumption.8| AK | WA | NY | FL | AZ | |
|---|---|---|---|---|---|
| TMY3 location | Anchorage Intl AP | Seattle-Tacoma Intl AP | New York-LaGuardia AP | Miami Intl AP | Phoenix-Sky Harbor Intl AP |
| Climate zone | Very cold | Marine | Mixed-humid | Hot-humid | Hot-dry |
| Annual load (kW h) | 9270 | 7800 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
| Peak load (kW) | 2.45 | 2.02 | 3.55 | 3.7 | 4.39 |
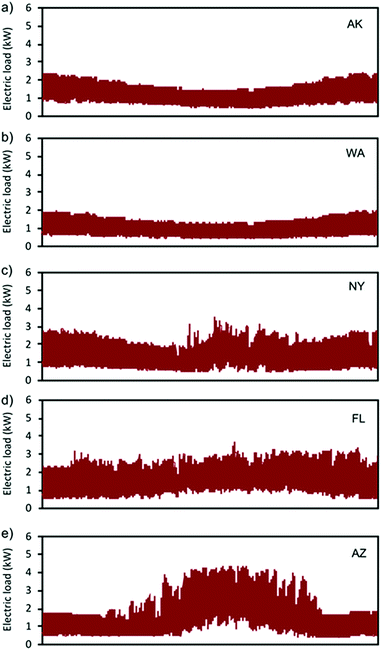 | ||
| Fig. 1 Hourly residential load over the year in the five different locations: (a) Alaska, (b) Washington, (c) New York, (d) Florida, and (e) Arizona. | ||
The power generated from the PV system is always used directly to fulfil the residential load if possible. In the base case, all excess generation can be made useful through the grid and the total useful energy can be expressed as:
| Eout1 = EPV–load + EPV–grid | (5) |
The manual battery dispatch model in the SAM is used to add a battery to the system.33 PV generation is first used to directly meet the residential load, secondly charges the battery, and thirdly exports power to the grid. There is no possibility to charge the battery with grid power. The useful energy outputs from the system with a battery can be expressed as:
| Eout1s = EPV–load + Ebatt–load + EPV–grid | (6) |
| Eout1s = EPV–load + ηbattEPV–batt + EPV–grid | (7) |
As an alternative scenario, it is assumed that no excess power generation can be made useful through the distribution grid. The useful energy outputs can then be expressed as:
| Eout2 = EPV–load. | (8) |
Adding a battery to this scenario gives:
| Eout2s = EPV–load + Ebatt–load | (9) |
| Eout2s = EPV–load + ηbattEPV–batt | (10) |
Summing up, this leads to four distinct estimates of useful energy outputs over the lifetime of the PV system in the different locations. The alternative grid case is likely not representative of the situation at the locations studied here but works as a comparison for potential future situations with congested distribution grids or attempts to go completely off-grid using PV-battery systems.
This can also be used to calculate other metrics describing the level of self-sufficiency (φ) and self-consumption of the system.8 The absolute self-sufficiency can be expressed as:
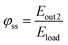 | (11) |
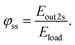 | (12) |
Since one of our cases includes the possibility of making excess generation available through the grid, we also introduce a metric expressing self-sufficiency equivalence representing the relationship between the total power generation and the total demand:
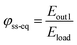 | (13) |
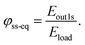 | (14) |
Self-consumption can be defined as:
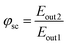 | (15) |
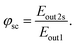 | (16) |
Energy inputs
The estimated primary energy used to manufacture the PV system is based on a study by de Wilde-Scholten utilizing transparent data of a rooftop mounted mc-Si system.38 Two different estimates are presented using different assumptions on electricity mix leading to a quite significant difference in primary energy inputs. We use the estimate based on Chinese electricity mix for two reasons. Firstly, China (and Taiwan) makes up around 70% of global PV module production, making it the most representative choice. Secondly, the primary energy inputs are converted to el-eq based on the efficiency of the Chinese electricity used in the study by de Wilde-Scholten. Data based on module area are used when possible, implicitly taking into account the improved panel efficiency of our system of study compared to the data source (Table 4).| Primary energy inputsa (MJPE-eq m−2) | Primary energy inputsb (MJPE-eq kWp−1) | El-eq inputc (kW hel kWp−1) | |
|---|---|---|---|
| a Based on primary energy demand for mc-Si panels manufactured in China with rooftop installation from de Wild-Scholte.38 b Figures in MJ m−2 are converted into MJ kWp−1 to account for the higher efficiency of the system studied. The inverter estimate for MJ kWp−1 is used directly.38 c Converted into electrical energy equivalents using a primary energy factor of 0.32, which is the conversion factor used by Wild-Scholte according to the ESI of Bhandari et al.42 | |||
| Feedstock | 1050 | 6185 | 550 |
| Ingot/crystal + wafer | 637 | 3752 | 334 |
| Cell | 233 | 1372 | 122 |
| Laminate | 450 | 2651 | 236 |
| Frame | 154 | 907 | 80.6 |
| Mounting | 125 | 736 | 65.4 |
| Cables + connectors | 12.5 | 74 | 6.5 |
| Inverter | — | 2290 | 204 |
| Total | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
1597 |
The primary energy inputs for the battery are based on the GREET model from the Argonne National Laboratory (Table 5).39–41 The estimated primary energy inputs are converted to el-eq based on the same estimate of efficiency of Chinese electricity mix as the solar panel.42
| Primary energy demand (MJPE-eq kg−1) | Primary energy demand (MJPE-eq kW−1 hn−1) | El-eq inputsc (kW hel kW−1 hn−1) | |
|---|---|---|---|
| a Calcluated for LFP batteries with the cathode prepared with a hydrothermal technique and specific energy of the studied system.39,41 b Process energy consumption specified by Dai et al. as 0.161 mmBtu where 82.4% is natural gas 17.6% electricity. This is converted into primary energy using the default energy intensity of electricity (2.179 mmBtu mmBtu−1) and natural gas (1.108 mmBtu mmBtu−1) in GREET 2017.40,41 c Converted into electrical energy equivalents using the same conversion factor for Chinese electricity mix as for the PV system (0.32).42 | |||
| Battery materials | 79.6a | 855 | 76.0 |
| Battery assembly | — | 220b | 19.5 |
| Total | — | 1075 | 95.5 |
The energy input estimates used are similar, but not exactly the same as previous numbers based on meta-analysis of studies.3,14,17,25,43 There are studies reaching significantly higher estimates for energy inputs for PV systems, using significantly broader system boundaries.44,45
Results
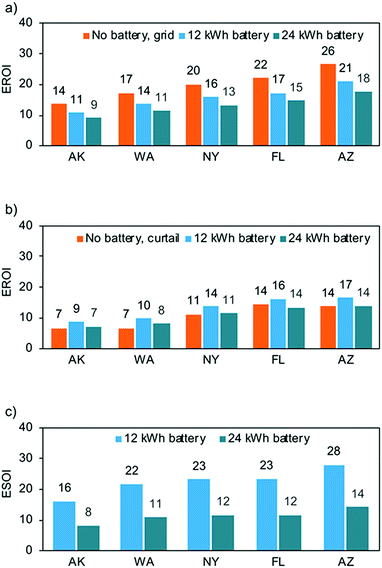
The hourly energy output from the PV system varies with the time of the day and year (Fig. 2), leading to highly different capacity factors and total lifetime electricity generation in the different locations (Table 6). The PV system generates an equivalent of between 56 and 85% of the total power demand of the residential loads (Table 6). If all the generated power is either used directly to fulfil the residential load or made available via the distribution grid (eqn (5)), the EROI (eqn (1)) of the PV system is between 14 and 27 depending on the location (Fig. 4a). Adding a 12 kW hn battery in this case decreases the useful energy outputs (eqn (6)) and the EROI drops by about 21%, as this both increases the energy inputs to the system and decreases the useful energy output due to battery conversion losses. Doubling the battery size to 24 kW hn induces around 34% decrease of the EROI compared to having no battery.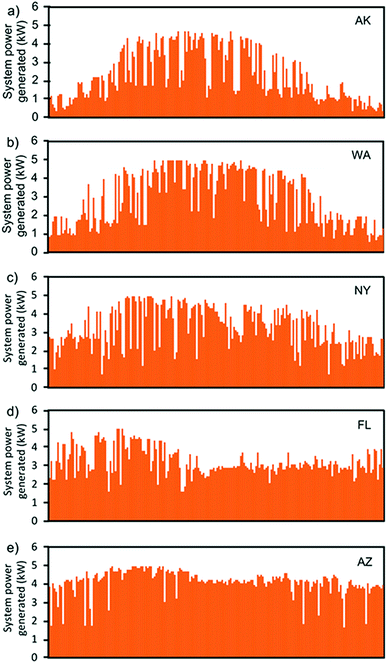 | ||
| Fig. 2 Hourly power generation over a year from the studied PV installation in the five different locations: (a) Alaska, (b) Washington, (c) New York, (d) Florida, and (e) Arizona. | ||
| AK | WA | NY | FL | AZ | |
|---|---|---|---|---|---|
| a 12 kW h battery (24 kW h battery). | |||||
| Total lifetime power generation (MW h) | 131 | 166 | 194 | 212 | 256 |
| Capacity factor | 0.10 | 0.13 | 0.15 | 0.17 | 0.20 |
| Total power to battery (MW h)a | 40.5 (49.5) | 54.2 (67.3) | 58.0 (80.6) | 58.7 (72.1) | 70.3 (106) |
| No self-consumption battery | 50.7% | 39.8% | 56.5% | 65.7% | 52.0% |
| Self-consumption batterya | 79.3% (85.7) | 69.8% (77.0) | 84.0% (94.7) | 91.1% (97.0) | 77.3% (90.2) |
| Battery losses (MW h)a | 3.23 (3.90) | 4.34 (5.31) | 4.69 (6.43) | 4.76 (5.78) | 5.68 (8.43) |
| No absolute self-sufficiency battery | 28.6% | 33.9% | 34.9% | 38.0% | 41.2% |
| Absolute self-sufficiency batterya | 44.7% (48.3) | 59.5% (65.7) | 56.5% (58.5) | 52.6% (56.0) | 61.2% (71.4) |
| Self-sufficiency equivalent | 56.4% | 85.3% | 61.7% | 57.8% | 79.2% |
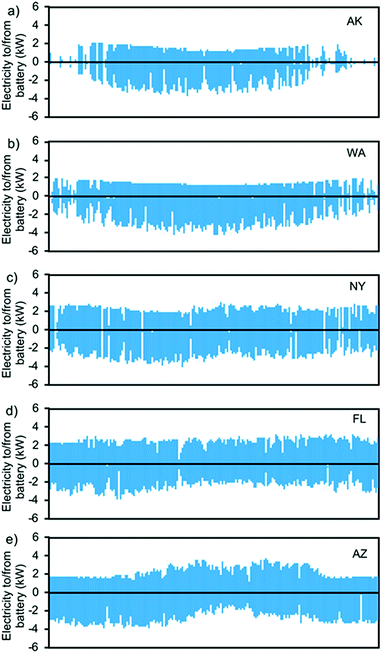 | ||
| Fig. 3 Hourly power to and from the 12 kW hn battery in the five different locations: (a) Alaska, (b) Washington, (c) New York, (d) Florida, and (e) Arizona. | ||
For the PV only scenarios, the degree of self-consumption (eqn (15)) is between 40% and 66%, which is only enough to provide between 29 and 41% of the total power demand (eqn (11)), demonstrating the mismatch between the PV supply and residential demand (Table 6). If the power that is not self-consumed is curtailed, the EROI of the PV system drops by more than half in Washington compared to the situation where excess generation can be made useful via the grid (Fig. 4a). The highest rate of self-consumption is in Florida, where the power demand is well correlated to the generation and reaches up to 66% self-consumption, and the EROI is still around 14 even when excess power is curtailed. However, in Alaska and Washington the EROI is as low as 7.
When it is not possible to provide excess power generation to the grid, adding a 12 kW hn battery to the PV system increases self-consumption to between 72 and 93%, but absolute self-sufficiency is still only from 44 to 61%, demonstrating that the grid still plays an important role in providing reliable power. Adding the battery increases the EROI in all of the locations, but the impact varies and is as low as 12% in Florida. Doubling the battery size to 24 kW hn is sufficient to reach close to 100% self-consumption in locations such as Florida, but it remains around 80% where the demand is poorly correlated to power generation. The increased energy input and conversion losses from the larger battery decreases the EROI to a level similar to when having no battery and excess PV generation is curtailed.
The hourly charge and discharge of the 12 kW hn battery in the first year is depicted in Fig. 3, indicating some of the variation in the use of the battery between different locations. The total energy stored over the lifetime differs by about 70% between the highest and the lowest case (Table 6) and the ESOI of the system varies between 16 and 28 (Fig. 4c). The fractional charge/discharge loss of the battery is around 8% in all cases and the total loss over the lifetime adds up to between 3.2 MW h and 5.7 MW h. This can be compared to the assumed total energy inputs in the two batteries used over the lifetime of the PV system of around 2.3 MW hel-eq (4.6 MW hel-eq in the larger battery case). A large part of the decreased EROI of the larger battery can be explained by looking at how the batteries are used since doubling the battery size to 24 kW hn increases the use of the battery and associated losses between 22 and 55%, while doubling the total energy input. This is also reflected in the drop in the ESOI with increasing battery size.
Discussion
Previous estimates for PV systems have suggested that the EROI of wafer based PVs is around 8, but with significant spread between studies.3 A mean value of 9.2 has been proposed specifically for polysilicon PVs but it may be significantly higher if outdated data are excluded or with technological advances in PV manufacturing.16 For these calculations it is commonly assumed that all generated power contributes positively to the net energy return in NEA and LCA studies of PV systems; therefore, most of the spread in these estimates is associated with uncertainties in the energy inputs to manufacturing and installation.Here, we take a different approach that focuses on the energy outputs, which depend on location, demand profiles, and how excess generation is managed. Output from a PV system installed in a good solar location such as Arizona is almost double to one in a worse location, such as Alaska. These circumstances are comparable to many other locations around the world and can be both better and worse in other climates not covered in this study. However, the EROI calculated here is significantly higher than the 8–9 cited above (EROI from 14 to 27), even in a low-solar location such as Alaska, as long as the grid can be used to make all generated power useful.
Adding a battery to a grid-connected PV system where excess power can be put onto the grid always decreases the EROI of the system. Therefore, the rationale for adding batteries to grid-connected residential systems needs to be motivated by other reasons.
The electric load profiles also vary with different locations and correlate differently to the generated power. This leads to different degrees of self-consumption of residential PV systems (and the corresponding potentially curtailed power ϕ). In situations where excess generation cannot be made available via the grid, analysing the local load can provide useful information on the total energetic value of a PV installation. As distributed and utility-scale PV generation grows, unless new loads are added that are coincident with solar generation, it is increasingly likely that grids will in fact not be able to accept more power.
Early theoretical estimates of the difference in electrical energy stored over the lifetime compared to the energy inputs required (ESOIe) of a generic Li-ion battery was 32.3 Our estimates are all lower than this, despite the considerably lower estimate for required energy inputs used. This is largely due to the lower utilization of a battery with a large storage capacity not being used during large parts of the year compared to theoretical cases. An increased battery size only makes this situation worse, with large decreases in the ESOI being the result of doubling the battery size.
The size of neither the PV array nor the battery is optimized to fit the different loads in the geographical locations studied. This is done on purpose, to enable a just comparison of the EROI of the system in different locations. Transparency has been pointed out as important when presenting EROI results, together with the level of analysis and caution when comparing results to other studies.46 One of the aims here is to provide transparent data and methods that can be modified to fit actual situations and future developments. The assumptions used here are considered representative of a typical PV system installed in the United States in 2016 and can be used as analogies for other locations with similar climate in other parts of the world. If the methodology described is to be used to analyse actual systems, the data for both the PV system and battery can be updated to suit the specific situation. If done properly, net energy analysis can provide useful information on the impacts of installing PV systems in different parts of the world, and especially, the implications of large-scale deployment of stationary batteries.
Conclusions
Understanding the energetic benefits of residential PV plus storage systems is needed to establish performance goals, R&D priorities, and set a sound policy. As these residential energy systems grow to provide a significant fraction of our power, the consequences of our decisions will have a large impact on the cost, efficiency, and reliability of the grid. Here we use a number of metrics, namely EROI, ESOI, self-consumption, and self-sufficiency, to quantify the benefits of typically sized residential PV plus storage systems for 5 selected locations covering a broad range of climatic zones. Location-specific hourly generation profiles are combined with hourly residential load over the course of the year. Recent literature on the energy intensity of manufacturing and installing PV systems and Li-ion batteries is used to assess energy inputs. Major conclusions from this study include:(1) The energy return on investment (EROI) for a 6 kW hp multi-crystalline silicon PV system without storage ranges from 14 to 27 in the five investigated climatic conditions, when excess hourly generation is made available for other customers of grid power. These high values for EROI demonstrate the energy benefits of PVs across a wide range of geographical regions in the U.S., and by analogy, elsewhere.
(2) Compared to simply providing excess generation to the grid, adding a 12 kW hn Li-ion battery to this system decreases the EROI by 21%. Doubling the battery size decreases the EROI by 34% compared to the case without a battery. The addition of batteries to residential PV systems decreases the EROI due to a combination of energy-intensive battery manufacturing and losses associated with the round-trip efficiency of charge/discharge cycles. From the perspective of energy return on investment, it is difficult to justify adding batteries to residential PV systems as long as excess generation can be made available for other users of the grid.
(3) If excess generation is curtailed instead of being sent to the grid or stored, the EROI of the PV system drops to between 7 and 14. Adding a 12 kW hn battery to avoid curtailment increases the EROI by about 12 to 42%, but the EROI still remains below the systems providing power to the grid, and doubling the battery size can decrease the total system EROI to levels similar to those of the systems curtailing all excess generation. This shows that a battery can increase the EROI of a PV system in cases where excess generation is otherwise curtailed. However, it can never reach the same levels as a system with the potential to export power to the grid and oversizing the battery can easily eat up all this gain in the total EROI.
(4) The energy stored on energy invested (ESOIe) for the 12 kW hn battery varies between 16 and 28 depending on how much the battery is used. This is considerably less than the earlier estimates of 32 which assume optimal use of the battery over its lifetime. Doubling the battery size decreases the ESOI by around 50%.
(5) In all the installations with batteries considered here, 40 to 55% of the residential electricity demand is still met by the grid due to the mismatch between PV generation and loads. Doubling the size of the battery reduced this to 30 to 50%. Increasing battery sizes to enable a higher degree of absolute self-sufficiency results in the battery remaining idle during large parts of the year, decreasing the ESOI and EROI of the total system.
A major transformation of the electricity system is now underway, driven by the need to decarbonize, the availability of low cost renewable generation, and the digital revolution. Wise choices about what we invest in, where we place new generation and storage assets, and policies regarding behind-the-meter energy assets are crucial for sustaining rapid progress and incentivizing cost-effective investments. The results provided here demonstrate how net energy analysis can be used to maximize the contributions of low-carbon power from distributed generation. Our results highlight the value of placing PV generation systems in geographical locations with high insolation, policies that encourage sales of excess generation back to the grid, and judicious use of battery storage to avoid curtailment. They also demonstrate the need for R&D to reduce energy inputs for manufacturing batteries and PVs, improve battery round-trip energy efficiency for charge–discharge cycles, and increase the cycle and calendar life of batteries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was made possible by financial support from the Global Climate and Energy Project (GCEP). We express our sincere gratitude to Adam Brandt for numerous interesting discussions and helpful suggestions during the work on the study.Notes and references
- J. Jean, P. R. Brown, R. L. Jaffe, T. Buonassisi and V. Bulović, Energy Environ. Sci., 2015, 8, 1200–1219 RSC.
- C. Breyer, D. Bogdanov, A. Gulagi, A. Aghahosseini, L. S. N. S. Barbosa, O. Koskinen, M. Barasa, U. Caldera, S. Afanasyeva, M. Child, J. Farfan and P. Vainikka, Prog. Photovolt.: Res. Appl., 2017, 25, 727–745 CrossRef.
- C. J. Barnhart, M. Dale, A. R. Brandt and S. M. Benson, Energy Environ. Sci., 2013, 6, 2804–2810 RSC.
- IEA, Tracking Clean Energy Progress 2017, International Energy Agency, OECD, 2017 Search PubMed.
- O. Schmidt, A. Hawkes, A. Gambhir and I. Staffell, Nat. Energy, 2017, 2, 17110 CrossRef.
- P. Hanser, R. Lueken, W. Gorman and J. Mashal, Utilities Policy, 2017, 46, 22–32 CrossRef.
- E. Hittinger and J. Siddiqui, Utilities Policy, 2017, 45, 27–35 CrossRef.
- R. Luthander, J. Widén, D. Nilsson and J. Palm, Appl. Energy, 2015, 142, 80–94 CrossRef.
- R. Luthander, J. Widén, J. Munkhammar and D. Lingfors, Energy, 2016, 112, 221–231 CrossRef.
- R. L. Fares and M. E. Webber, Nat. Energy, 2017, 2, 17001 CrossRef CAS.
- E. S. Hittinger and I. M. L. Azevedo, Environ. Sci. Technol., 2015, 49, 3203–3210 CrossRef CAS PubMed.
- J. F. Peters, M. Baumann, B. Zimmermann, J. Braun and M. Weil, Renewable Sustainable Energy Rev., 2017, 67, 491–506 CrossRef CAS.
- L. A.-W. Ellingsen, C. R. Hung and A. H. Strømman, Transp. Res. D, 2017, 55, 82–90 CrossRef.
- M. Carbajales-Dale, C. J. Barnhart and S. M. Benson, Energy Environ. Sci., 2014, 7, 1538–1544 RSC.
- M. Carbajales-Dale, C. J. Barnhart, A. R. Brandt and S. M. Benson, Nat. Clim. Change, 2014, 4, 524–527 CrossRef.
- R. H. E. M. Koppelaar, Renewable Sustainable Energy Rev., 2017, 72, 1241–1255 CrossRef.
- M. Dale and S. M. Benson, Environ. Sci. Technol., 2013, 47, 3482–3489 CrossRef CAS PubMed.
- M. Görig and C. Breyer, Environ. Prog. Sustainable Energy, 2016, 35, 914–923 CrossRef.
- G. Palmer, BioPhysical Economics and Resource Quality, 2017, 2, 6 CrossRef.
- G. Limpens and H. Jeanmart, Energy, 2018, 152, 960–973 CrossRef.
- D. J. Murphy, M. Carbajales-Dale and D. Moeller, Energies, 2016, 9, 917 CrossRef.
- M. Raugei, Methodological Guidelines on Net Energy Analysis of Photovoltaic Electricity, IEA-PVPS Task 12, 2016 Search PubMed.
- P. Denholm, M. O'Conell, G. Brinkman and J. Jorgenson, Overgeneration from Solar Energy in California: A Field Guide to the Duck Chart, National Renewable Energy Laboratory, 2015 Search PubMed.
- M. A. Pellow, C. J. M. Emmott, C. J. Barnhart and S. M. Benson, Energy Environ. Sci., 2015, 8, 1938–1952 RSC.
- C. J. Barnhart and S. M. Benson, Energy Environ. Sci., 2013, 6, 1083–1092 RSC.
- Fraunhofer ISE, Photovoltaics Report, Fraunhofer Institute for Solar Energy Systems ISE, 2018 Search PubMed.
- National Renewable Energy Laboratory (NREL), SAM 2017.9.5, 2017 Search PubMed.
- G. Zubi, R. Dufo-López, M. Carvalho and G. Pasaoglu, Renewable Sustainable Energy Rev., 2018, 89, 292–308 CrossRef.
- J. Cervantes and F. Choobineh, Appl. Energy, 2018, 216, 105–115 CrossRef.
- A. Barré, B. Deguilhem, S. Grolleau, M. Gérard, F. Suard and D. Riu, J. Power Sources, 2013, 241, 680–689 CrossRef.
- M. Baumann, J. F. Peters, M. Weil and A. Grunwald, Energy Technol., 2017, 5, 1071–1083 CrossRef CAS.
- N. Blair, A. P. Dobos, J. Freeman, T. Neises, M. Wagner, T. Ferguson, P. Gilman and S. Janzou, System Advisor Model, Sam 2014.1. 14: General Description, National Renewable Energy Laboratory (NREL), Golden, CO, 2014 Search PubMed.
- N. DiOrio, A. Dobos, S. Janzou, A. Nelson and B. Lundstrom,Technoeconomic Modeling of Battery Energy Storage in SAM, National Renewable Energy Lab (NREL), Golden, CO (United States), 2015 Search PubMed.
- M. C. Baechler, T. L. Gilbride, P. C. Cole, M. G. Hefty and K. Ruiz, Building America Best Practices Series: Volume 7.3: Guide to Determining Climate Regions by County, Pacific Northwest National Laboratory (PNNL), Richland, WA (US), 2015 Search PubMed.
- NREL, National Solar Radiation Database (NSRDB): 1991-2005 Update: TMY3, http://rredc.nrel.gov/solar/old_data/nsrdb/1991-2005/tmy3/, accessed August 16, 2017 Search PubMed.
- U.S. DOE, Commercial and Residential Hourly Load Profiles for all TMY3 Locations in the United States, https://openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states, accessed May 23, 2018 Search PubMed.
- L. I. Dulău, M. Abrudean and D. Bică, Procedia Technol., 2014, 12, 681–686 CrossRef.
- M. J. (Mariska) de Wild-Scholten, Sol. Energy Mater. Sol. Cells, 2013, 119, 296–305 CrossRef.
- J. B. Dunn, L. Gaines, J. C. Kelly, C. James and K. G. Gallagher, Energy Environ. Sci., 2015, 8, 158–168 RSC.
- Q. Dai, J. Dunn, J. C. Kelly and A. Elgowainy, Update of Life Cycle Analysis of Lithium-Ion Batteries in the GREET Model, Argonne National Laboratory, 2017 Search PubMed.
- Argonne National Laboratory, GREET2 Model, 2017 Search PubMed.
- K. P. Bhandari, J. M. Collier, R. J. Ellingson and D. S. Apul, Renewable Sustainable Energy Rev., 2015, 47, 133–141 CrossRef.
- Z. Zhou and M. Carbajales-Dale, Energy Environ. Sci., 2018, 11, 603–608 RSC.
- M. Raugei, S. Sgouridis, D. Murphy, V. Fthenakis, R. Frischknecht, C. Breyer, U. Bardi, C. Barnhart, A. Buckley, M. Carbajales-Dale, D. Csala, M. de Wild-Scholten, G. Heath, A. Jæger-Waldau, C. Jones, A. Keller, E. Leccisi, P. Mancarella, N. Pearsall, A. Siegel, W. Sinke and P. Stolz, Energy Policy, 2017, 102, 377–384 CrossRef.
- F. Ferroni and R. J. Hopkirk, Energy Policy, 2016, 94, 336–344 CrossRef.
- M. Carbajales-Dale, M. Raugei, V. Fthenakis and C. Barnhart, Proc. IEEE, 2015, 103, 995–999 Search PubMed.
- G. Barbose, N. R. Darghouth, D. Millstein, K. LaCommare, N. DiSanti and R. Widiss, Tracking the Sun 10: The Installed Price of Residential and Non-residential Photovoltaic Systems in the United States, Lawrence Berkeley National Laboratory, 2017 Search PubMed.
- D. C. Jordan and S. R. Kurtz, Prog. Photovolt.: Res. Appl., 2013, 21, 12–29 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |