View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/C9SC04185K (Edge Article) Chem. Sci., 2019, 10, 10318-10330

Enolization rates control mono- versus di-fluorination of 1,3-dicarbonyl derivatives†

Neshat Rozatian a, Andrew Beeby a, Ian W. Ashworth b, Graham Sandford a and David R. W. Hodgson *a
aChemistry Department, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: d.r.w.hodgson@durham.ac.uk
bAstraZeneca, Pharmaceutical Technology & Development, Macclesfield, SK10 2NA, UK

Received 21st August 2019 , Accepted 16th September 2019

First published on 16th September 2019

Abstract

Fluorine-containing 1,3-dicarbonyl derivatives are essential building blocks for drug discovery and manufacture. To understand the factors that determine selectivity between mono- and di-fluorination of 1,3-dicarbonyl systems, we have performed kinetic studies of keto–enol tautomerism and fluorination processes. Photoketonization of 1,3-diaryl-1,3-dicarbonyl derivatives and their 2-fluoro analogues is coupled with relaxation kinetics to determine enolization rates. Reaction additives such as water accelerate enolization processes, especially of 2-fluoro-1,3-dicarbonyl systems. Kinetic studies of enol fluorination with Selectfluor™ and NFSI reveal the quantitative effects of 2-fluorination upon enol nucleophilicity towards reagents of markedly different electrophilicity. Our findings have important implications for the synthesis of α,α-difluoroketonic compounds, providing valuable quantitative information to aid in the design of fluorination and difluorination reactions.

1. Introduction

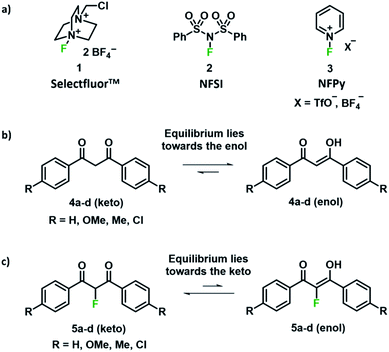
Fluorinated compounds have fundamental roles within the pharmaceutical, agrochemical and materials industries.1–4 The presence of a fluorine atom imparts profound effects upon the physical, chemical and biological properties of drugs and plant protection agents such as Prozac™, Lipitor®, ciprofloxacin and diclosulam.5 Such compounds are often synthesised from fluorine-containing building blocks;6 a key example is the antifungal agent voriconazole,7 which is synthesised from a 5-fluoropyrimidine intermediate that is prepared from a 2-fluoro-1,3-ketoester derivative. In this context, finding selective and efficient routes towards the fluorination of 1,3-dicarbonyl derivatives has been the subject of significant interest. Early work involved fluorinating reagents such as ClO3F,8 CF3OF,9 XeF2 (ref. 10,11) and CsSO4F;12 however, the low selectivities, difficulties regarding preparation, high reactivities and toxicities of these reagents halted their adoption in discovery and manufacturing processes. Elemental fluorine (F2) has been successfully used for the fluorination of 1,3-dicarbonyl systems, using both batch and flow techniques on laboratory and manufacturing scales, but this reagent requires specialist handling techniques that are not readily available in most laboratories.13–18

With the introduction of shelf-stable, crystalline electrophilic fluorinating reagents of the N–F class, such as Selectfluor™, NFSI and N-fluoropyridinium salts (Fig. 1a), that do not present any handling problems, numerous reports followed regarding the electrophilic fluorination of 1,3-dicarbonyl derivatives. Procedures include catalyst-free reactions,19 microwave-assisted methods,20 transition metal (Ti and Ru) catalysed methods,21–23 solvent-free reactions assisted by milling,24,25 fluorinations in ionic liquids,26 and reactions conducted in water.27,28 In many cases, difficulties in controlling mono- versus difluorination were reported, leading to challenging separations of the product mixtures. Therefore, finding synthetic routes that allow selective fluorination by such widely used reagents would be of great use.


image file: c9sc04185k-f1.tif
Fig. 1 (a) Commonly used N–F reagents: Selectfluor™, N-fluorobenzenesulfonimide (NFSI) and N-fluoropyridinium salts (NFPy). (b) Tautomerism in compounds 4a–d. (c) Tautomerism in the fluorine-containing compounds 5a–d.

Bioactive compounds bearing CF2 groups are found in both drugs and agrochemicals (e.g. gemcitabine, pantoprazole, sedaxane).29 In particular, carbonyl and dicarbonyl compounds containing α,α-difluoromethylene moieties are highly desirable bioactive compounds. When adjacent to a carbonyl group, the difluoromethylene moiety greatly increases the electrophilicity of the carbonyl group, leading to very facile nucleophilic additions. These include the additions of nucleophilic residues of enzyme active sites to α,α-difluoroketonic compounds,30,31 which have led to the application of α,α-difluoroketones as enzyme inhibitors.32–34 For example, difluorostatone compounds have been identified as potent inhibitors of HIV-1 protease35 and of a serine protease in the malaria parasite.36

Despite the importance of organofluorine compounds in the life sciences, very few kinetics studies on fluorination reactions are present in the literature and there have been no quantitative studies on the introduction of two fluorine atoms to form a difluoromethylene unit. Furthermore, although water and formic acid have been used as solvents or co-solvents in electrophilic fluorination reactions,13,28 their effects upon keto–enol tautomerism of 1,3-dicarbonyl derivatives and subsequent fluorinations are not fully understood. We have previously reported a quantitative reactivity scale for electrophilic N–F fluorinating reagents, where absolute and relative rate constants were determined for the monofluorination of a series of para-substituted 1,3-diaryl-1,3-dicarbonyl derivatives by 10 different N–F reagents, in acetonitrile.37 An independent study reported at the same time by Mayr et al.38 provided a scale of electrophilicity of the N–F reagents which was in very good agreement. A recent report by Nelson and co-workers39 gave further evidence supporting the SN2 mechanism for fluorinations by Selectfluor™.

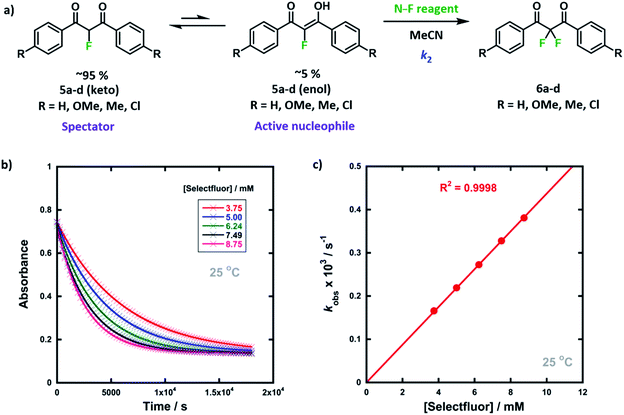
We were intrigued by the keto–enol tautomerism phenomena displayed by our aromatic 1,3-dicarbonyls and their monofluorinated analogues (Fig. 1b and c) and how we could take advantage of their photochemical interconversion properties to study tautomerism and fluorination processes. The mechanism of fluorination proceeds via reaction of the enol tautomer with an electrophilic fluorinating reagent,14,19 so a full understanding of the factors that affect keto–enol tautomerism would be beneficial in improving selective mono- and difluorinations of 1,3-dicarbonyls. The photochemistry and photo-physics of 1,3-diaryl-1,3-dicarbonyl derivatives have been extensively studied.40,41 In the 1970s, the groups of Markov42,43 and Mazur44–46 reported photoisomerization of 1,3-dicarbonyl compounds, whereby the keto–enol equilibrium was perturbed towards the keto tautomer upon irradiation. This process reverses to attain the tautomeric equilibrium by a non-photochemical reaction in darkness. The effects of solvents and additives (ethanol, triethylamine) on the rate of photoketonization were studied by Mazur et al.;44 however, relaxation kinetics that provided insights into enolization rates were not performed. We therefore identified the photoketonization approach as a means of studying the kinetics of enolization within our nucleophile systems.

Our efforts towards the quantification of the factors which affect mono- versus difluorination are two-fold; in the first instance, we focus on the effects of different reaction conditions on the keto–enol tautomerism of the 1,3-diaryl-1,3-dicarbonyl derivatives 4a–d and 5a–d. Secondly, we explore and discuss the kinetics of fluorination of enols 4a–d and fluoroenols 5a–d and the effects of solvent composition upon these processes.

2. Results and discussion

2.1 Kinetics of keto–enol tautomerism in compounds 4a–d

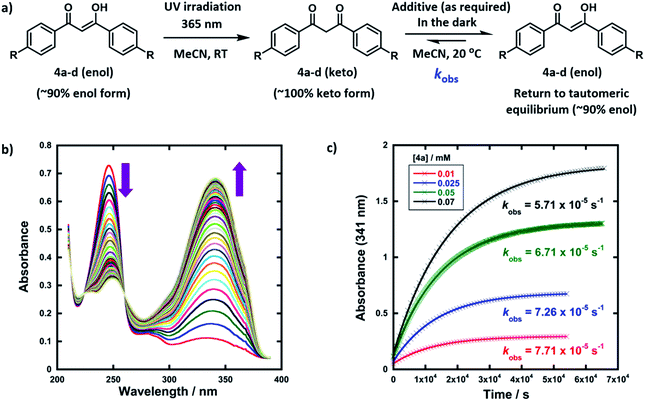
The enol forms of 1,3-diaryl-1,3-dicarbonyl derivatives 4a–d show markedly different absorption spectra to their keto tautomers and are thus convenient systems for the study of tautomerization kinetics by UV-vis spectrophotometry. Compounds 4a–d were synthesised using previously reported methods,47 and they exist predominantly in their enol forms (∼90% in MeCN). The enol tautomers were converted to their keto forms by irradiation of solutions of 4a–d in quartz cuvettes using a 0.5 W UV LED lamp at 365 nm (Fig. 2a). Spectrophotometric monitoring of the photoketonization of each system showed that these processes took several hours (see ESI Section 3.3† for corresponding spectra). The re-equilibration (relaxation) kinetics of 4a-keto in the dark were monitored using time-arrayed multi-wavelength analysis (Fig. 2b). As relaxation occurred, the enol absorbance band at λmax = 341 nm increased while the keto absorbance band at λmax = 250 nm decreased. The tautomeric equilibrium was regained after ∼14 hours, and clean isosbestic points were observed during both the photoketonization and the relaxation processes showing that there was no detectable build-up of additional intermediates during the tautomerization processes on the timescales that we monitored. The re-equilibration of 4a-keto was studied at four different concentrations and observed first-order rate constants (kobs) were obtained from plots of absorbance at λmax = 341 nm over time (Fig. 2c). When the concentration of 4a was doubled, there was a small decrease in kobs, which could reflect interaction between substrate molecules at higher concentrations.48
image file: c9sc04185k-f2.tif
Fig. 2 (a) Reaction scheme for photoketonization (step 1) and relaxation (step 2) of compounds 4a–d in MeCN. (b) Time-arrayed multi-wavelength analysis for relaxation of 4a (0.025 mM) in the dark, each spectrum acquired at 15 min intervals at 20 °C. (c) Relaxation of 4a-keto at different concentrations (0.01 mM, 0.025 mM, 0.05 mM and 0.07 mM); kobs values obtained at each concentration of 4a are shown.

In order to gain insight into the potential effects of species that are present in widely-employed electrophilic fluorination protocols upon enolization, we explored the effects of water, formic acid, DABCO and ClCH2-DABCO+BF4− upon re-equilibration kinetics. In addition, because keto–enol equilibration is a reversible process with significant proportions of both keto- and enol-tautomers being present at equilibrium, we also considered the effects of additives upon equilibrium position (Ke). The observed rate constants kobs for re-equilibration of 4a-keto and the equilibrium constants Ke in the presence of the additives are summarized in Table 1. Forward and reverse rate constants kfor(H) and krev(H), respectively, were estimated from kobs values using measured Ke and eqn (1) and (2):

 
kobs = kfor(H) + krev(H)(1)
 
Ke = kfor(H)/krev(H)(2)

Table 1 Summary of ketone relaxation of non-fluorinated 1,3-dicarbonyl systems. The kobs values for relaxation of photo-ketonized forms of 4a–d (0.025 mM) were determined in MeCN at 20 °C in the presence of additives. Percentages represent volumes of additive in MeCN. Equilibrium constants Ke were determined by NMR spectroscopy or by linear interpolation, extrapolation or averaging of the measured data. Forward and reverse rate constants, kfor(H) and krev(H), for enolization and ketonization processes, of the non-fluorinated 1,3-dicarbonyl systems, respectively were calculated using eqn (1) and (2)
Aryl substituent Additive Quantity of additive k obs/s−1 Approx. t1/2 K e(H) k for(H)/s−1 k rev(H)/s−1 k for(H) {with additive}/kfor(H) {MeCN}
a Measured by 1H NMR spectroscopy in MeCN-d3. b Measured by 1H NMR spectroscopy in MeCN-d3 in the presence of additive (for details see ESI Section 3.2†). c Value based on average of measured values or interpolation of measured values. d K e(H) value was assumed to be the same as Ke(H) in MeCN-d3 alone.
4a (R = H) None — 7.26 × 10−5 2.7 h 10.5a 6.63 × 10−5 6.31 × 10−6 1.0
Water 15% 8.44 × 10−5 2.3 h 7.8c 7.48 × 10−5 9.59 × 10−6 1.1
20% 1.79 × 10−4 1.1 h 6.9b 1.56 × 10−4 2.27 × 10−5 2.4
25% 1.84 × 10−4 1 h 6.6c 1.60 × 10−4 2.42 × 10−5 2.4
35% 3.39 × 10−4 34 min 6.3c 2.93 × 10−4 4.64 × 10−5 4.4
50% 7.29 × 10−4 15 min 5.7b 6.20 × 10−4 1.09 × 10−4 9.4
Formic acid 0.5% 1.92 × 10−3 6 min 10.3c 1.75 × 10−3 1.70 × 10−4 26
1% 4.16 × 10−3 3 min 10.0b 3.78 × 10−3 3.78 × 10−4 57
2% 4.89 × 10−3 2 min 10.5b 4.46 × 10−3 4.25 × 10−4 67
3% 6.29 × 10−3 2 min 9.5b 5.69 × 10−3 5.99 × 10−4 86
DABCO 2.5 μM 2.92 × 10−3 4 min 6.7c 2.54 × 10−3 3.80 × 10−4 39
12.5 μM 1.34 × 10−2 1 min 6.7c 1.17 × 10−2 1.74 × 10−3 176
25 μM (1 eq.) 2.49 × 10−2 30 s 6.7b 2.17 × 10−2 3.24 × 10−3 327
37.5 μM 4.08 × 10−2 17 s 6.7c 3.55 × 10−2 5.30 × 10−3 536
50 μM 5.22 × 10−2 13 s 6.7b 4.54 × 10−2 6.78 × 10−3 685
ClCH2-DABCO+BF4− 12.5 μM 1.04 × 10−4 2 h 9.1c 9.37 × 10−5 1.03 × 10−5 1.4
25 μM (1 eq.) 1.20 × 10−4 1.6 h 9.1b 1.08 × 10−4 1.19 × 10−5 1.6
50 μM 1.32 × 10−4 1.5 h 9.1c 1.19 × 10−4 1.31 × 10−5 1.8
625 μM 1.00 × 10−4 2 h 9.1c 9.01 × 10−5 9.90 × 10−6 1.4
1.25 mM 5.12 × 10−5 4 h 9.1c 4.61 × 10−5 5.07 × 10−6 0.7
2.5 mM 2.04 × 10−5 9 h 9.1c 1.84 × 10−5 2.02 × 10−6 0.3
20% water and ClCH2-DABCO+BF4− 20%/12.5 μM 2.05 × 10−4 1 h 6.9c 1.79 × 10−4 2.59 × 10−5 2.7
n Bu4N+BF4− 240 mM 1.44 × 10−4 1.3 h 9.1b 1.30 × 10−4 1.43 × 10−5 2.0
4b (R = OMe) None — 1.29 × 10−5 15 h 4.0a 1.03 × 10−5 2.58 × 10−6 1.0
Water 50% 1.47 × 10−4 1.3 h 3.7b 1.16 × 10−4 3.13 × 10−5 11
Formic acid 2% 8.27 × 10−3 1.4 min 5.3b 6.96 × 10−3 1.31 × 10−3 674
DABCO 2.5 μM 8.24 × 10−4 14 min 5.1b 6.89 × 10−4 1.35 × 10−4 67
ClCH2-DABCO+BF4− 50 μM 7.11 × 10−6 27 h 5.0b 5.93 × 10−6 1.19 × 10−6 0.6
4c (R = Me) None — 5.67 × 10−5 3.5 h 8.0a 5.04 × 10−5 6.30 × 10−6 1.0
Water 50% 3.15 × 10−4 37 min 8.0d 2.80 × 10−4 3.50 × 10−5 5.6
DABCO 2.5 μM 8.03 × 10−4 14 min 8.0d 7.14 × 10−4 8.92 × 10−5 14
4d (R = Cl) None — 1.07 × 10−4 2 h 12.5a 9.91 × 10−5 7.93 × 10−6 1.0
Water 50% 2.13 × 10−3 5 min 12.5d 1.97 × 10−3 1.58 × 10−4 20
DABCO 2.5 μM 7.69 × 10−3 1.5 min 12.5d 7.12 × 10−3 5.70 × 10−4 72
ClCH2-DABCO+BF4− 25 μM 7.35 × 10−5 2.6 h 12.5d 6.81 × 10−5 5.44 × 10−6 0.7

Given that the enol forms of 4a–d are dominant at equilibrium, kobs and kfor(H) values are in the same order. With water as the additive (15–50% of the reaction mixture by volume), increased rates of re-enolization were observed (Fig. 3a), with a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 MeCN/water solvent system giving a 10-fold increase in kfor(H) compared to MeCN. The position of the keto–enol equilibrium changed marginally upon moving from MeCN to 1[thin space (1/6-em)]:[thin space (1/6-em)]1 MeCN/water, with Ke values of 10.5 and 5.7 respectively. This is consistent with previous studies on 1,3-dicarbonyl systems which show limited variations of Ke values upon changes from single- to mixed-polar solvent systems.49 Photophysical studies on di-substituted 1,3-diphenyl-1,3-propanedione compounds have shown that MeCN supports very slow exchange between tautomeric states, whereas protic solvents, including MeCN-water mixtures, enhance rates significantly.50,51 Water is often used as a solvent or co-solvent in fluorination reactions to aid solubility of Selectfluor™.28 Our studies show that the solubility limit of Selectfluor™ in water is ∼500 mM, compared to ∼50 mM in MeCN. Here, we have shown that the addition of water also increases the rate of enolization, facilitating the conversion of the small amounts of residual diketone to the nucleophilic enol tautomer, which reacts with the fluorinating reagent.


image file: c9sc04185k-f3.tif
Fig. 3 Trends observed in the rates of relaxation (kobs) of 4a (0.025 mM) upon addition of different quantities of additives, in MeCN at 20 °C: (a) water, (b) formic acid, (c) DABCO, (d) 0.5–2 equivalents of ClCH2-DABCO+BF4−.

The addition of small amounts of formic acid had limited effects on the position of the keto–enol equilibria with all Ke values being ∼10, however, greatly enhanced rates of keto-to-enol relaxation were observed (Fig. 3b). Thus, the rate constant for enolization kfor(H) increased 86-fold upon addition of 3% formic acid in comparison to MeCN alone.

The addition of DABCO also increased the relaxation rates significantly. For example, with one equivalent (25 μM), a 330-fold acceleration of the enolization process kfor(H) was observed. Even with 0.1 equivalents (2.5 μM) of DABCO, the tautomeric equilibrium was regained rapidly. When kfor(H) values for relaxation were plotted against DABCO concentration (Fig. 3c), a simple linear (i.e. first order) correlation was observed, giving the second-order rate constant, k2 = 9.13 × 102 M−1 s−1. In terms of basicity, DABCO (pKaH(MeCN) = 18.29)52 is insufficiently basic to quantitatively deprotonate 4a-keto (for 4a-keto estimated pKa(MeCN) = pKa(DMSO) + 12.9 (ref. 53) = 13.4 (ref. 54) + 12.9 = 26.3). Thus our data suggest that DABCO may operate as a general base catalyst.

Upon delivery of electrophilic fluorine, N–F reagents give amines as by-products, which could promote keto–enol tautomerism, and hence the rate of fluorination, if they remain unprotonated. Fluorination reactions using Selectfluor™ result in the formation of ClCH2-DABCO+BF4− and when 0.5 to 2 equivalents of ClCH2-DABCO+BF4− were added to 4a-keto, very small (1.4 to 2-fold) increases in kobs and kfor(H) were observed (Fig. 3d). However, the addition of greater quantities of ClCH2-DABCO+BF4− (25–100 equivalents) resulted in reduced kfor(H) values (see ESI Section 3.4.5†). For example, with 100 equivalents of ClCH2-DABCO+, kfor(H) was reduced three-fold. While the ClCH2-DABCO+ cation is unlikely to remain unprotonated and thus will be unable to function as a base, this series of experiments suggested the possibility of salt effects upon the relaxation processes. Consequently, relaxation experiments were performed in the presence of 2–100 equivalents of LiBF4 and similar reductions in kfor(H) were observed (for related spectra see ESI Section 3.4.7†). Li salts are known to form chelates with 1,3-diketones,54 thus we explored the effects of adding nBu4NBF4, a non-chelating salt. In order to mimic the salt concentrations in synthetic-scale processes, we studied the effect of adding 240 mM nBu4NBF4 to solutions of 4a-keto. Under these conditions, kfor(H) increased 2-fold in comparison to experiments in the absence of salts. In summary, the effects of ‘spent’ Selectfluor™ (i.e. ClCH2-DABCO+BF4−) and other ionic species upon enolization kinetics of 4a–d are measurable, but marginal and potentially complex in nature.

We also explored the effects of the amine derivative of NFSI, dibenzenesulfonimide ((PhSO2)2NH, pKa(MeCN) ∼11.3)55 upon the rate of relaxation of 4a-keto. Interestingly, the presence of 5 equivalents of (PhSO2)2NH resulted in a 40-fold decrease in the relaxation rate constant rate, however, 10 equivalents of (PhSO2)2NH gave only a 16-fold decrease (see ESI Section 3.4.8–3.4.9†). The addition of the conjugate base form, (PhSO2)2N−Na+, also showed a similar effect, with one equivalent causing a significant reduction in relaxation rate and larger concentrations showing less-pronounced reductions. In this case, the reduction in kfor(H) is likely due to chelation of the Na+ ion to diketone 4a, an interaction previously described by Bordwell.54

The relaxation kinetics of keto forms of 4b–d were explored using the same photoketonization procedure, in the presence and absence of additives, and corresponding kobs, Ke, kfor(H) and krev(H) values are reported in Table 1. There were little variations in measured Ke values for 4b across the range of conditions that we employed. For 4c and 4d, we assumed that the Ke(H) values in the presence of additives would be the same as Ke(H) in MeCN-d3 alone under conditions where measured values were not obtained. The effects of the para-substituents within 4a–d on kfor(H) in MeCN were studied by Hammett correlation analysis. The use of σp+ values in the construction of the Hammett plot gave better correlations than with σp values (see ESI Section 3.5†). A ρ+ value of +1.06 was obtained, where this positive value indicates small increases in electron density on the aryl rings of the substrates during the limiting C–H removal step of enolization. Compound 4d (R = Cl) relaxed most rapidly, whereas compound 4b (R = OMe) was the slowest, which suggests that rate limiting proton transfer from carbon proceeds towards an anionic intermediate rather than through pre-protonation of the ketone.

2.2 Kinetics of keto–enol tautomerism in compounds 5a–d

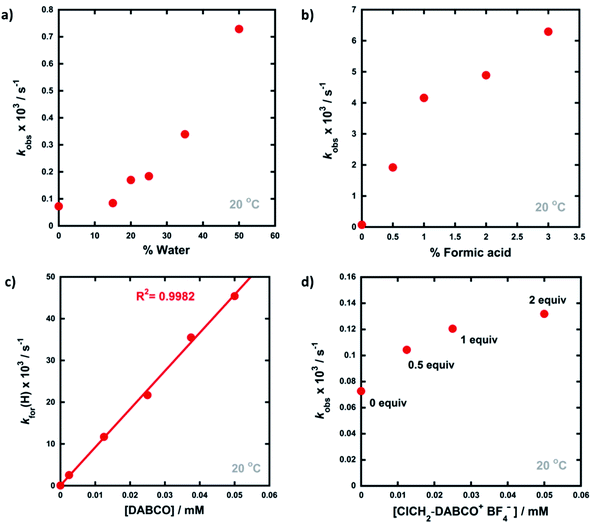
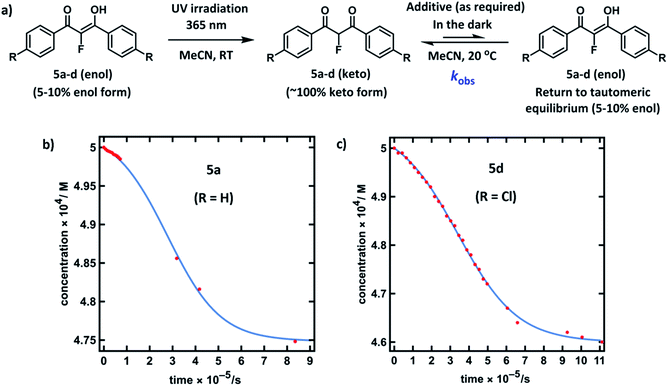
Compounds 5a–d were synthesised using our previously reported methods,37 in good yields. Following purification by recrystallization, we obtained the fluorinated 1,3-diaryl-1,3-dicarbonyls as mixtures of both keto and enol tautomers, where the keto form comprised ∼95% of 5a and 5b, and ∼90% of 5c and 5d (as determined by 19F NMR spectroscopy in MeCN-d3, see ESI Section 3.2†). We determined Ke values for 5a across a range of additives and, in a similar vein to the non-fluorinated systems, we found Ke to be broadly constant. The fluoroenol- and fluoroketo-tautomers of 5a–d have distinct absorbance bands at ∼350 nm and ∼250 nm, respectively. Therefore, in much the same way as for compounds 4a–d, we were able to monitor the tautomerism processes of the fluorinated derivatives via changes in absorbance of the fluoroenol tautomers. Photoketonization experiments were conducted on 0.50 mM solutions of 5a–d in MeCN in the absence of additives (Fig. 4a). Following irradiation, spectrophotometric kinetic assays for relaxation were conducted, and they showed very slow restoration of the thermodynamic ratio between the two tautomeric forms. Plots of diketone concentration versus time for 5a–d were constructed. In the case of 5a and 5d (Fig. 4b and c), sigmoidal behaviours were clearly discernible, which suggested autocatalysis of the processes, and fitting of the data to a model for reversible autocatalysis gave strong support for this hypothesis (for kinetic fittings performed using Wolfram Mathematica see ESI Sections 3.9.1 and 3.12.1†). In the case of 5b and 5c, reaction progress was extremely slow, and kobs values were estimated using an initial rates approach (see ESI Sections 3.10.1 and 3.11.1†).
image file: c9sc04185k-f4.tif
Fig. 4 (a) Reaction scheme for photoketonization (step 1) by irradiation with a 0.5 W UV LED lamp at 365 nm for 4–5 hours, followed by relaxation (step 2) of 5a–d in MeCN. (b) Plot of [5a-keto] versus time obtained from a time-arrayed single-wavelength kinetic analysis for relaxation of 5a-keto showing the return to the tautomeric equilibrium (0.50 mM, 20 °C, spectra acquired over 11 days). (c) Plot of [5d-keto] versus time obtained from a time-arrayed single-wavelength kinetic analysis for relaxation of 5d-keto showing the return to the tautomeric equilibrium (0.50 mM, 20 °C, spectra acquired over 13 days).

We then explored the effects of additives on the rates of relaxation of diketone tautomers of 5a–d, and the corresponding kfor(F) and krev(F) values were obtained via Ke values (Table 2). In general, the effects of additives upon kfor(F) were much greater than for the non-fluorinated series 4a–d. With 20% water in MeCN, 5a-ketokfor(F) was 160-fold larger than in the absence of water, whereas for system 4a-keto, only a 2.4-fold enhancement in kfor(H) was observed. When the quantity of water in MeCN was increased to 50%, kfor(F) for 5a-keto was further increased to 930-fold greater than in the absence of water. For compounds 5b and 5d, kfor(F) increased 3000-fold in 50% water, while 5c showed a 10[thin space (1/6-em)]000-fold increase. Addition of formic acid (3% in MeCN) led to an increase in kfor(F) of 220-fold, whereas DABCO proved to be an effective agent for de-fluorination of the substrate 5a (see ESI Section 3.2.1† for related spectra, and previous reports56,57 of bromomalonitriles acting as brominating agents). ‘Spent’ Selectfluor™ (ClCH2-DABCO+BF4−, 0.025 mM) offered a 4-fold increase in kfor(F), whereas the increase in kfor(H) for 4a with this additive was ∼2-fold, and only marginally discernible above salt-related medium effects (see ESI Section 3.9† for spectra).

Table 2 Summary of diketone relaxation of 2-fluorinated-1,3-dicarbonyl systems. The kobs values for relaxation of photoketonized forms of 5a–d (0.50 mM) were determined in MeCN at 20 °C in the presence of additives. Percentages represent volumes of additive in MeCN. Equilibrium constants Ke were determined by NMR spectroscopy or by linear interpolation, extrapolation or averaging of the measured data. Forward and reverse rate constants, kfor(F) and krev(F), for enolization and ketonization processes, of the 2-fluorinated-1,3-dicarbonyl systems, respectively were calculated using eqn (1) and (2)
Aryl substituent Additive Quantity of additive k obs/s−1 Approx. t1/2 K e(F) k for(F)/s−1 k rev(F)/s−1 k for(F){with additive}/kfor(F){MeCN}
a System displayed non-first order autocatalytic behaviour. b Measured by 19F NMR spectroscopy in MeCN-d3 or MeCN-d3/D2O. c Second order rate constant for autocatalytic process in units of M−1 s−1. d Value based on average of measured values or interpolation of measured values. e A 19F NMR spectroscopy measurement in 20% H2O/MeCN-d3 gave Ke(F) = 0.042. f Defluorination was observed. g Measured in the presence of 300 mM nBu4N+BF4−. h Extremely slow process, where rate constant was determined by initial rates method. i K e(F) for 50% H2O was assumed to be the same as Ke(F) in MeCN-d3.
5a (R = H) None — —a — 0.053b 3.66 × 10−8 (1.58 × 10−2)c 6.91 × 10−7 (0.298)c 1.0
Water 10% 4.98 × 10−5 4 h 0.053d 2.49 × 10−6 4.73 × 10−5 68
20% 1.19 × 10−4 1.6 h 0.053d,e 5.95 × 10−6 1.13 × 10−4 163
30% 2.23 × 10−4 0.9 h 0.053d 1.12 × 10−5 2.12 × 10−4 305
40% 3.77 × 10−4 0.5 h 0.053d 1.89 × 10−5 3.58 × 10−4 515
50% 6.78 × 10−4 0.3 h 0.053b 3.39 × 10−5 6.44 × 10−4 926
Formic acid 3% 1.64 × 10−4 1.2 h 0.053b 8.20 × 10−6 1.56 × 10−4 224
DABCO 2.5 μM 1.42 × 10−3 8 min —f —f —f —f
ClCH2-DABCO+BF4− 12.5 μM 1.01 × 10−6 8 d 0.053d 5.05 × 10−8 9.60 × 10−7 1.4
25 μM (1 eq.) 2.93 × 10−6 2.7 d 0.053d 1.47 × 10−7 2.78 × 10−6 4.0
20% water and ClCH2-DABCO+BF4− 20%/12.5 μM 1.91 × 10−4 1 h 0.053d 9.55 × 10−6 1.81 × 10−4 261
n Bu4N+BF4− 240 mM 8.38 × 10−5 2.3 h 0.043g 3.42 × 10−6 8.04 × 10−5 94
5b (R = OMe) None — 1.46 × 10−7h 60 d 0.020b 2.92 × 10−9 (n.d.)c 1.43 × 10−7 (n.d.)c 1.0
Water 20% 3.22 × 10−5 6 h 0.033d 1.04 × 10−6 3.12 × 10−5 355
30% 5.39 × 10−5 3.6 h 0.040d 2.06 × 10−6 5.18 × 10−5 706
40% 9.23 × 10−5 2.1 h 0.046d 4.07 × 10−6 8.82 × 10−5 1396
50% 1.71 × 10−4 1.1 h 0.053b 8.55 × 10−6 1.62 × 10−4 2928
Formic acid 2% 1.73 × 10−5 11 h 0.031b 5.19 × 10−7 1.68 × 10−5 178
DABCO 2.5 μM 1.32 × 10−5 15 h 0.020b 2.64 × 10−7 1.29 × 10−5 90
5c (R = Me) None — 8.64 × 10−8h 90 d 0.149b 1.12 × 10−8 7.52 × 10−8 1.0
Water 50% 9.15 × 10−4 0.2 h 0.149i 1.19 × 10−4 7.96 × 10−4 10[thin space (1/6-em)]594
5d (R = Cl) None — —a — 0.087b 5.37 × 10−8 (1.11 × 10−2)c 6.18 × 10−7 (0.128)c 1.0
Water 50% 1.97 × 10−3 6 min 0.087i 1.58 × 10−4 1.81 × 10−3 2936

Overall, these data suggest that the tautomerization reactions of the fluoro-systems 5a–d are accelerated much more significantly in the presence of polar additives than those of the non-fluorinated systems.

2.3 Kinetics of enol and fluoroenol fluorination

We previously reported the kinetics of fluorination of enols 4a–d in MeCN.37 We confirmed that fluorination of 5a occurs only via the fluoroenol form with the aid of NMR experiments, and that the fluoroketo tautomer acts as a spectator during the addition of the second fluorine atom to 5a-enol, owing to its slow enolization in MeCN. Here we explore the effects of additives upon the rates of fluorination of enols 4a–d and make comparisons with their effects upon the rates of fluorination of fluoroenols 5a–d. Together, these data allow us to explore the role of 2-fluorination upon enol nucleophilicity and potentially tune conditions, through the addition of e.g. water, towards favouring the formation of 2,2-difluoro-1,3-dicarbonyls 6a–d (Fig. 5a). Furthermore, on account of the greatly increased rates of enolization in the presence of additives, we also take account of in situ enolization of 5a.
image file: c9sc04185k-f5.tif
Fig. 5 (a) Reaction scheme for fluorination reactions of 1,3-dicarbonyls 5a–d with Selectfluor™ or NFSI in MeCN at controlled temperatures. (b) Exponential decays of absorbance of 5a-enol at 350 nm with different concentrations of Selectfluor™, in MeCN at 25 °C. (c) Correlation of kobs values for fluorination of 5a-enol with [Selectfluor™], in MeCN at 25 °C.

By monitoring the decays in absorbance of the fluoroenol tautomers of 5a–d at λ ∼350 nm, the kinetics of fluorination reactions were conveniently monitored by UV-vis spectrophotometry. To achieve pseudo-first order conditions, all kinetics experiments were carried out using excess electrophile. Clean exponential decays of absorbance of the nucleophile were observed in all runs in MeCN alone (representative examples are shown in Fig. 5). The first-order rate constants kobs were obtained from the fitting of plots of absorbance versus time (Fig. 5b). When kobs values were plotted against electrophilic fluorine concentration, linear (i.e. first order) correlations were observed (Fig. 5c), which projected cleanly through the origin in each case. The direct dependence upon electrophilic fluorine concentration demonstrates rate-limiting fluorination of the fluoroenol that is present in the mixture, and thus the slopes of these graphs gave the second-order rate constant k2 [M−1 s−1] according to the rate eqn (3). The rate constants for the reactions of 5a–d with each fluorinating reagent are summarized in Table 3.

 
image file: c9sc04185k-t1.tif(3)

Table 3 Second-order rate constants (k2) for the reactions of Selectfluor™ 1 and NFSI 2 with nucleophiles 5a–d, in MeCN at 25 °C, and relative rates compared to the reactions of Selectfluor™ and NFSI with 4a–d
Nucleophile Electrophile k 2 (25 °C)/M−1 s−1 k rel
a Using k2 values for reactions measured at 20 °C.
5a-enol (R = H) Selectfluor™ 1 4.37 × 10−2 1.0 (1.1)a
NFSI 2 4.59 × 10−4 46
5b-enol (R = OMe) Selectfluor™ 1 6.77 × 10−1 1.1 (1.1)a
NFSI 2 6.11 × 10−4 4.4
5c-enol (R = Me) Selectfluor™ 1 1.32 × 10−1 1.1
5d-enol (R = Cl) Selectfluor™ 1 3.07 × 10−2 1.7
NFSI 2 2.47 × 10−4 43

A Hammett plot was constructed for the reactions of fluoroenols 5a–d with Selectfluor™ 1 (see ESI Section 3.13.5†). The use of σp+ values led to a better correlation than with σp constants, and ρ+ = −1.5 was obtained, with R2 of > 0.99. This value is similar to the ρ+ values we obtained for fluorination of enols 4a–d by several N–F reagents, including Selectfluor™ 1 and NFSI 2.37 Activation parameters (ΔG‡, ΔH‡ and ΔS‡) were calculated from kinetic data obtained at different temperatures for the reactions of Selectfluor™ with 5a-enol and 5b-enol (see ESI Section 3.13.5†). As with our previous publication, the moderately negative values of ΔS‡, alongside the values for ρ+, support an SN2-type mechanism for the fluorination reactions.

The rates of fluorination of 5a–d by Selectfluor™ 1 and NFSI 2 were compared with the rate constants that we previously obtained for the fluorinations of 4a–d,37 using krel values, defined in eqn (4).

 
image file: c9sc04185k-t2.tif(4)

The k2 values obtained for fluorination of fluoroenols 5a–d by Selectfluor™ are slightly higher than those for fluorination of enols 4a–d, with krel values of 1.0–1.7 being observed. With NFSI, the rate enhancement is more pronounced, and the addition of the second fluorine atom to form the CF2 group is 46-fold faster for 5a-enol, 4-fold greater for 5b-enol and 43-fold faster for 5d-enol.

One might expect that the presence of a highly electronegative fluorine atom would lead to a lowering of the nucleophilicity of the fluoroenol and much lower rates of fluorination. On the other hand, the strong pi-donor ability of the fluorine atom could lead to ground-state destabilization of fluorine atoms at sp2 centres and thus enhanced nucleophilicity of the fluoroenol. Our results suggest that a balance between these opposing effects is observed for fluorinations in MeCN with the more reactive Selectfluor™ system, however, with the less reactive NFSI reagent the fluoroenols 5a–d are more reactive. The origins of this disparity could lie in the less early transition state structure that is to be expected from the less reactive NFSI system, coupled with the different charge state of the electrophile–nucleophile pair, and thus differing requirements for solvation.

Our findings of enhanced nucleophilicity for fluoroenols 5a–d over enols 4a–d align with studies conducted by Dolbier et al.58–60 on the kinetic impact of vinylic fluorine substituents upon cyclization reactions. They reported that the presence of a fluorine atom at an sp2 centre was disfavoured relative to the sp3 hybridised analogue, therefore, cyclization reactions occurred readily to form butadiene compounds. Chambers et al.13,14 reported that during electrophilic fluorination by elemental fluorine, the second fluorination step is much slower than the first. However, our results show that addition of the second fluorine atom proceeds at a rate that is similar to or even greater than the first fluorination step. The previously reported slow rate of difluorination is due to rate-limiting enolization of the mono-fluoro-diketone compound rather than the fluorination process itself. As we have shown in Section 2.2, the rate of enolization can be enhanced by the addition of catalytic amounts of water, salt, acid or base, which in turn contributes to an increase in the overall rate of the difluorination mechanism. Furthermore, in related carbanion systems, the reactivity was found to be enhanced by the presence of an α-fluorine atom compared to the non-fluorinated carbanion.61,62 Indeed, the effect of the α-fluorine was even greater in these studies, probably because of the increased repulsion between the oxyanionic charge and fluorine lone pairs in comparison to our systems.

We also studied the fluorinations of 4a-enol and 5a-enol by Selectfluor™ with 20% water in MeCN using an initial rates approach to overcome the complications associated with the presence of substantial keto–enol tautomerization and the formation of the hydrate of 6a under these conditions (for spectra see ESI Sections 3.15 and 3.18†). The presence of water (20% in MeCN) during the fluorination of 5a-enol gave a ∼50-fold larger second-order rate constant, k2, compared to without water, however, the k2 value for fluorination of 4a-enol was little changed (Table 4). We also explored the effects of adding formic acid (3–20%) on the rates of fluorination of 5a-enol and found that there was little effect on the k2 values (see ESI Section 3.16†). The presence of nBu4NBF4 (240 mM) during the fluorination of 5a-enol by Selectfluor™ afforded a ∼2600-fold increase in rate, where this large increase is likely due to the combined effects of the salt itself and inadvertent addition of water owing to the hygroscopic nature of tetraalkylammonium systems.63 Taken together, the effects of additives upon k2 further support the idea of differential solvation and medium effects along the reaction co-ordinates of the fluorination and tautomerization processes of the enol and fluoroenol systems, however, their underlying origins are not clear at this stage.

Table 4 Second-order rate constants (k2) for the reactions of Selectfluor™ with nucleophiles 4a-enol and 5a-enol in 20% water in MeCN at 20 °C
Nucleophile k 2 (20 °C)/M−1 s−1
a In MeCN only, k2 = 2.68 × 10−2 M−1 s−1 at 20 °C for fluorination of 4a-enol.37 b At 20 °C in MeCN only, k2 = 2.95 × 10−2 M−1 s−1 for fluorination of 5a-enol.
4a-enol (R = H) 2.49 × 10−2a
5a-enol (R = H) 1.43b

2.4 Application of kinetic data to synthesis

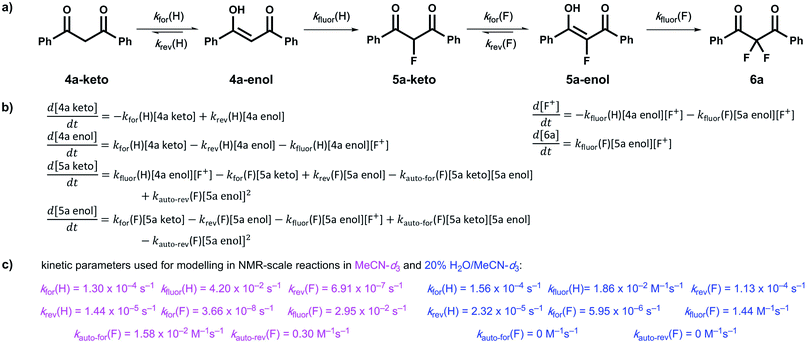
Our kinetic studies show that additives, such as water, facilitate enolization of 1,3-dicarbonyl species 4 and 5, with especially dramatic effects upon 2-fluoro-1,3-dicarbonyls 5. The presence of additives also has clear effects on the fluorination processes of 4a and 5a with Selectfluor™. In order to demonstrate the quantitative applicability of our data to synthetic scenarios, both in the presence and absence of water, we performed NMR experiments (Fig. 6a–d) to monitor the kinetics of fluorination of 4a with Selectfluor™ and compared measured data with a numerically-solved differential model (Fig. 7a–c) of the overall processes based upon the microscopic rate constants we have determined.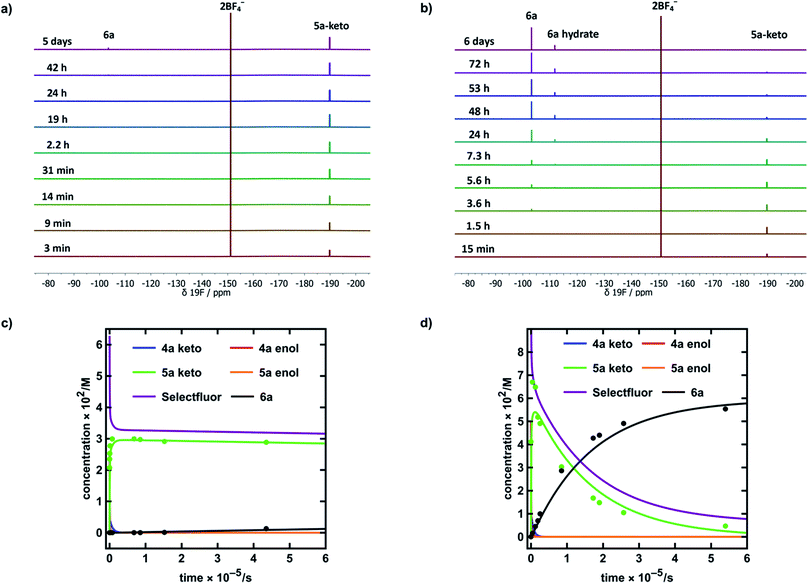
image file: c9sc04185k-f6.tif
Fig. 6 (a) 19F NMR time profile for the reaction between 1,3-dicarbonyl 4a (30 mM) and Selectfluor™ (62.5 mM) in MeCN-d3. (b) 19F NMR time profile for the reaction between 1,3-dicarbonyl 4a (59.5 mM) and Selectfluor™ (125 mM) in 20% water in MeCN-d3. (c) Integrated 19F NMR-time data for the reaction between 4a (30 mM) and Selectfluor™ (62.5 mM) in MeCN-d3. (d) Integrated 19F NMR-time data for the reaction between 4a (59.5 mM) and Selectfluor™ (125 mM) in 20% water in MeCN-d3. Some over-estimation of the concentration of 5a-keto was evident in the NMR experiment and the origin of this is discussed further in the ESI Section 4.†

image file: c9sc04185k-f7.tif
Fig. 7 (a) Overall kinetic model for the difluorination of compound 4a with Selectfluor™. (b) Differential representations for the rates of formation of each species within the kinetic model, where [F+] represents the concentration of Selectfluor™. (c) Rate constants used for kinetic fitting of fluorination processes in MeCN-d3 (pink) and in 20% water in MeCN-d3 (blue). Values for kfor(H) and krev(H) were based on those observed in the presence of 240 mM nBu4NBF4, where these values were chosen to mimic the effect of salt. When a similar approach was adopted for kfor(F) and krev(F), poor fitting was observed. We attribute this to the extreme sensitivity of the tautomerization processes of the fluoro-system 5a, described by these parameters, to the presence of small amounts of water that arise from the highly hygroscopic nature of the tetrabutylammonium salt.

In MeCN-d3 alone, we reacted 4a (30 mM) with Selectfluor™ 1 (2.1 equivalents) and the evolution of species was monitored by 19F NMR spectroscopy over 6 days. Without water, 5a-keto (δ = −190 ppm) was formed rapidly from the large reservoir of 4a-enol (∼90% of total 4a), with a second kinetic phase of 5a-keto formation associated with enolization of residual 4a-keto (Fig. 6a and green dots in Fig. 6c). On the basis of our UV-vis kinetic data, the formation of 5a-enol was expected to be extremely slow, with the formation of 6a (δ = −103 ppm) being similarly slow as a result. This was borne out by the very slow appearance of 2,2-difluoro-1,3-dicarbonyl 6a, with its formation only being evident at a level of ∼4% after 5 days.

The reaction conducted with 20% H2O in MeCN-d3 allowed for the use of higher concentrations of Selectfluor™ owing to its enhanced solubility in this medium, thus concentrations of 4a = 60 mM and Selectfluor™ = 125 mM were used. The reaction profile showed rapid build-up of 5a-keto (δ = −190 ppm) as a result of the large starting concentration of 4a-enol. Owing to the presence of water, enolization of 5a-keto was expected to occur more readily, and this was evidenced by the more rapid reduction in the signal for 5a-keto (Fig. 6b and green dots in Fig. 6d) and the formation of 7.5% 6a (δ = −103 ppm) after ∼3.5 h (Fig. 6d black dots), with complete conversion to 6a being achieved over 6 days (fluorination was expected to be rapid, and this was supported by very low levels of 5a-enol being detected in the steady state). An additional peak was present at δ = −111.9 ppm (Fig. 6b) which is likely to correspond to a hydrate of 6a. The formation of a hydrate is expected, as difluoroketones are known to form stable tetrahedral adducts.32 We also observed this peak in our 19F NMR-monitored synthetic reaction to obtain an authentic sample of 6a, however, upon work-up we did not isolate any 6a-hydrate.

In order to further validate our kinetic model (Fig. 7a and b), the microscopic rate constants (Fig. 7c) that we have measured by UV-vis spectrophotometry were inserted into the model and numerical methods were used to solve the differential equations (Fig. 7b). The resulting predicted concentration–time profiles of all species were plotted (lines in Fig. 6c and d) to allow comparison with experimental data (dots in Fig. 6c and d).

Pleasingly, for the experiment performed in the absence of added water, the rapid evolution of 5a-keto was modelled well by using ketonization and enolization rate constants (Table 1) for 4a in MeCN. The addition of kinetic terms related to the auto-catalytic keto–enol tautomerism of 5a were critical to the quantitative agreement between model and experiment for the formation of 6a, with the formation of 6a being predicted to reach only 1.7% after ∼5 days in the absence of this contribution, but 2.9% (versus ∼4% by experiment) when these terms were taken into account.

In the presence of 20% water, the build-up and break-down of 5a-keto was modelled well alongside the profile for the formation of 6a. We did not detect the presence of autocatalysis of the keto–enol equilibration of 5a by our UV-vis kinetic studies, and thus did not include them in the model. However, at the higher concentrations employed in this NMR study, any such terms could become more sizeable and could contribute to improving the model.

3. Conclusions

We have utilized a photo-switching method for the determination of the effects of additives on keto–enol tautomerism in the 1,3-diaryl-1,3-dicarbonyls 4a–d and the corresponding fluorinated derivatives 5a–d. We have shown through kinetics studies that the addition of water is a simple method for increasing the rate of enolization and thus increasing the rate of formation of 2,2-difluoro-1,3-dicarbonyl 6a. We found that small quantities of formic acid and DABCO greatly increased the enolization rate of 4a and formic acid also increased the enolization rate of 5a. The presence of DABCO resulted in the de-fluorination of 5a, as evidenced by NMR studies, whereas 5b was not de-fluorinated by DABCO. The non-fluorinated product of Selectfluor™, ClCH2-DABCO+BF4−, which is rarely considered in synthetic application, had small but detectable effects on keto–enol equilibration kinetics, however, the nature of the effects is not clear.

We also obtained kinetic data on the fluorination of mono-fluoroenols 5a–d with Selectfluor™ 1 and NFSI 2 under a variety of conditions. We have shown that the addition of a second fluorine atom occurs at a rate greater than or similar to that of the addition of the first fluorine atom. The rate-limiting step in the overall difluorination mechanism is therefore the enolization of the mono-fluoroketo tautomer, represented by kfor(F) in Fig. 7a.

Our kinetics studies correlate very well with previous synthetic studies: Banks et al.19 first reported the selective monofluorination of 4a using Selectfluor™ in MeCN, which gave 100% crude and 84% pure yields. We also observed complete conversion of 4a to 5a by both spectrophotometric and NMR methods, due to the high enol content of 4a. Yi and co-workers64,65 reacted a series of aromatic 1,3-dicarbonyl compounds with 2.1 equivalents of Selectfluor™ in 10[thin space (1/6-em)]:[thin space (1/6-em)]1 MeCN/H2O at 25 °C for 1–2 days, to obtain a range of 2,2-difluoro-1,3-diketones in approx. 90% yield. This matches our conclusion that water must be present to facilitate the enolization of 5a-keto and thus allow difluorination to occur within reasonable timescales. Pattison et al.66 attempted the difluorination of an aromatic β-ketoester with Selectfluor™ (2.5 equivalents) under reflux conditions in MeCN, which gave an 8[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio of mono- and difluorinated products. This was attributed to the lower enol content of β-ketoesters compared to 4a.66 Since water was not used in the reaction, the enolization of the β-ketoester was presumably slow, which explains the low conversion to the difluorinated product. Stavber et al.28 reported monofluorinations of cyclic 1,3-diketones and β-ketoesters in water using Selectfluor™ (1.1 equivalents), obtaining yields of 74–91%. The difluorinations of acyclic 1,3-diketones and β-ketoesters via Selectfluor™ (2.2 equivalents) in water gave yields of 78–89%. All reactions were conducted at 70 °C for 4–10 h. Fluorination of the acyclic 1,3-dicarbonyls could not be selectively stopped at the monofluorination stage, but by using 2.2 equivalents of Selectfluor™ the 2,2-difluoro-1,3-dicarbonyls were obtained without additional activation of the starting material. Syntheses of α,α-difluoro-β-ketoamides have been achieved using H2O:PEG-400 solvent mixtures in the presence of K2CO3,67 as well as very recently reported H2O:MeCN systems68 in green chemistry research programs, for which our experiments provide supporting mechanistic evidence of the crucial roles of water and base.

Our studies give direct evidence that water plays an essential role in accelerating the enolization of mono-fluorodiketone derivatives to allow the formation of difluorodiketones. Our findings have important implications for synthetic fluorination procedures: the addition of small quantities of water to partially enolic 1,3-dicarbonyl derivatives increases rates of keto to enol tautomerism, supporting the formation of the key enol intermediates required for both the first and second fluorination steps. Furthermore, water also enhances the rate of fluorination of fluoroenols, again supporting the expedited formation of pharmaceutically relevant α,α-difluoroketonic compounds.

4. Methods

The ESI contains details of methods, kinetics experiments and product analyses.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We are grateful to AstraZeneca and Durham University Science Faculty for providing doctoral funding to N. R. D. R. W. H thanks D. Jardine and M. Miller for their recommendation of numerical fitting software.

References

  1. D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308–319 RSC.
  2. S. Purser, P. R. Moore, S. Swallow and V. Gouverneur, Chem. Soc. Rev., 2008, 37, 320–330 RSC.
  3. K. Muller, C. Faeh and F. Diederich, Science, 2007, 317, 1881–1886 CrossRef PubMed.
  4. T. Liang, C. N. Neumann and T. Ritter, Angew. Chem., Int. Ed., 2013, 52, 8214–8264 CrossRef CAS PubMed.
  5. E. A. Ilardi, E. Vitaku and J. T. Njardarson, J. Med. Chem., 2014, 57, 2832–2842 CrossRef CAS PubMed.
  6. A. Harsanyi and G. Sandford, Org. Process Res. Dev., 2014, 18, 981–992 CrossRef CAS.
  7. M. Butters, J. Ebbs, S. P. Green, J. MacRae, M. C. Morland, C. W. Murtiashaw and A. J. Pettman, Org. Process Res. Dev., 2001, 5, 28–36 CrossRef CAS.
  8. B. L. Shapiro and M. M. Chrysam, J. Org. Chem., 1973, 38, 880–893 CrossRef CAS.
  9. W. J. Middleton and E. M. Bingham, J. Am. Chem. Soc., 1980, 102, 4845–4846 CrossRef CAS.
  10. B. Zajc and M. Zupan, J. Chem. Soc., Chem. Commun., 1980, 759 RSC.
  11. B. Zajc and M. Zupan, J. Org. Chem., 1982, 47, 573–575 CrossRef CAS.
  12. E. H. Appelman, L. J. Basile and R. C. Thompson, J. Am. Chem. Soc., 1979, 101, 3384–3385 CrossRef CAS.
  13. R. D. Chambers, M. P. Greenhall and J. Hutchinson, J. Chem. Soc., Chem. Commun., 1995, 21–22 RSC.
  14. R. D. Chambers, M. P. Greenhall and J. Hutchinson, Tetrahedron, 1996, 52, 1–8 CrossRef CAS.
  15. R. D. Chambers and J. Hutchinson, J. Fluorine Chem., 1998, 92, 45–52 CrossRef CAS.
  16. R. D. Chambers, D. Holling, R. C. H. Spink and G. Sandford, Lab Chip, 2001, 1, 132 RSC.
  17. R. D. Chambers, M. A. Fox and G. Sandford, Lab Chip, 2005, 5, 1132 RSC.
  18. C. B. McPake and G. Sandford, Org. Process Res. Dev., 2012, 16, 844–851 CrossRef CAS.
  19. R. E. Banks, N. J. Lawrence and A. L. Popplewell, J. Chem. Soc., Chem. Commun., 1994, 343–344 RSC.
  20. J.-C. Xiao and J. M. Shreeve, J. Fluorine Chem., 2005, 126, 473–476 CrossRef.
  21. L. Hintermann and A. Togni, Angew. Chem., Int. Ed., 2000, 39, 4359–4362 CrossRef CAS PubMed.
  22. S. Piana, I. Devillers, A. Togni and U. Rothlisberger, Angew. Chem., Int. Ed., 2002, 41, 979–982 CrossRef CAS PubMed.
  23. M. Althaus, C. Becker, A. Togni and A. Mezzetti, Organometallics, 2007, 26, 5902–5911 CrossRef CAS.
  24. G. Stavber, M. Zupan and S. Stavber, Tetrahedron Lett., 2007, 48, 2671–2673 CrossRef CAS.
  25. J. L. Howard, Y. Sagatov and D. L. Browne, Tetrahedron, 2018, 74, 3118–3123 CrossRef CAS.
  26. A. S. Reddy and K. K. Laali, Tetrahedron Lett., 2015, 56, 5495–5499 CrossRef CAS.
  27. G. Stavber, M. Zupan, M. Jereb and S. Stavber, Org. Lett., 2004, 6, 4973–4976 CrossRef CAS PubMed.
  28. G. Stavber and S. Stavber, Adv. Synth. Catal., 2010, 352, 2838–2846 CrossRef CAS.
  29. D. E. Yerien, S. Barata-Vallejo and A. Postigo, Chem.–Eur. J., 2017, 23, 14676–14701 CrossRef CAS PubMed.
  30. W. R. Dolbier, Guide to Fluorine NMR for Organic Chemists, John Wiley and Sons Inc., 2nd edn, 2016 Search PubMed.
  31. W. Peng and J. M. Shreeve, J. Org. Chem., 2005, 70, 5760–5763 CrossRef CAS PubMed.
  32. G. Pattison, Eur. J. Org. Chem., 2018, 2018, 3520–3540 CrossRef CAS.
  33. M. H. Gelb, J. P. Svaren and R. H. Abeles, Biochemistry, 1985, 24, 1813–1817 CrossRef CAS PubMed.
  34. J. T. Welch and S. Eswarakrishnan, Fluorine in Bioorganic Chemistry, John Wiley and Sons, New York, 1991 Search PubMed.
  35. D. Schirlin, S. Baltzer, V. Van Dorsselaer, F. Weber, C. Weill, J. M. Altenburger, B. Neises, G. Flynn, J. M. Rémy and C. Tarnus, Bioorg. Med. Chem. Lett., 1993, 3, 253–258 CrossRef CAS.
  36. S. Giovani, M. Penzo, S. Brogi, M. Brindisi, S. Gemma, E. Novellino, L. Savini, M. J. Blackman, G. Campiani and S. Butini, Bioorg. Med. Chem. Lett., 2014, 24, 3582–3586 CrossRef CAS PubMed.
  37. N. Rozatian, I. W. Ashworth, G. Sandford and D. R. W. Hodgson, Chem. Sci., 2018, 9, 8692–8702 RSC.
  38. D. S. Timofeeva, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2018, 140, 11474–11486 CrossRef CAS PubMed.
  39. S. Wood, S. Etridge, A. Kennedy, J. Percy and D. J. Nelson, Chem.–Eur. J., 2019, 25, 5574–5585 CrossRef CAS PubMed.
  40. R. A. Morton, A. Hassan and T. C. Calloway, J. Chem. Soc., 1934, 883–901 RSC.
  41. P. Markov, Chem. Soc. Rev., 1984, 13, 69–96 RSC.
  42. P. Markov and E. Radeva, J. Photochem., 1975, 4, 179–183 CrossRef CAS.
  43. P. Markov and I. Petkov, Tetrahedron, 1977, 33, 1013–1015 CrossRef CAS.
  44. D. Veierov, T. Bercovici, Y. Mazur and E. Fischer, J. Org. Chem., 1978, 43, 2006–2010 CrossRef CAS.
  45. D. Veierov, T. Bercovici, E. Fisher, Y. Mazur and A. Yogev, J. Am. Chem. Soc., 1973, 95, 8173–8175 CrossRef CAS.
  46. D. Veierov, T. Bercovici, E. Fischer, Y. Mazur and A. Yogev, J. Am. Chem. Soc., 1977, 99, 2723–2729 CrossRef CAS.
  47. K. Sato, G. Sandford, K. Shimizu, S. Akiyama, M. J. Lancashire, D. S. Yufit, A. Tarui, M. Omote, I. Kumadaki, S. Harusawa and A. Ando, Tetrahedron, 2016, 72, 1690–1698 CrossRef CAS.
  48. R. M. Claramunt, C. López, M. D. Santa María, D. Sanz and J. Elguero, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 49, 169–206 CrossRef CAS.
  49. M. T. Rogers and J. L. Burdett, Can. J. Chem., 1965, 43, 1516–1526 CrossRef CAS.
  50. I. Andrae, A. Bringhen, F. Böhm, H. Gonzenbach, T. Hill, L. Mulroy and T. G. Truscott, J. Photochem. Photobiol., B, 1997, 37, 147–150 CrossRef CAS.
  51. A. Cantrell and D. J. McGarvey, J. Photochem. Photobiol., B, 2001, 64, 117–122 CrossRef CAS.
  52. J. F. Coetzee and G. R. Padmanabhan, J. Am. Chem. Soc., 1965, 87, 5005–5010 CrossRef CAS.
  53. B. G. Cox, Acids and Bases: Solvent Effects on Acid-Base Strength, Oxford University Press, 2013 Search PubMed.
  54. W. N. Olmstead and F. G. Bordwell, J. Org. Chem., 1980, 45, 3299–3305 CrossRef CAS.
  55. A. Kütt, I. Leito, I. Kaljurand, L. Sooväli, V. M. Vlasov, L. M. Yagupolskii and I. A. Koppel, J. Org. Chem., 2006, 71, 2829–2838 CrossRef PubMed.
  56. A. Kundu, S. Pathak, K. Debnath and A. Pramanik, Tetrahedron Lett., 2014, 55, 3960–3968 CrossRef CAS.
  57. S. Pathak, A. Kundu and A. Pramanik, RSC Adv., 2014, 4, 10180–10187 RSC.
  58. W. R. Dolbier, G. D. Purvis III, M. J. Seabury, G. E. Wicks and C. R. Burkholder, Tetrahedron, 1990, 46, 7991–8004 CrossRef CAS.
  59. W. R. Dolbier, X. X. Rong and Y.-H. He, Tetrahedron Lett., 1993, 34, 5185–5188 CrossRef CAS.
  60. W. R. Dolbier and X. X. Rong, Tetrahedron Lett., 1996, 37, 5321–5324 CrossRef CAS.
  61. L. A. Kaplan and H. B. Pickard, J. Chem. Soc. D, 1969, 1500–1501 RSC.
  62. Z. Zhang, Á. Puente, F. Wang, M. Rahm, Y. Mei, H. Mayr and G. K. S. Prakash, Angew. Chem., Int. Ed., 2016, 55, 12845–12849 CrossRef CAS PubMed.
  63. R. McMullan and G. A. Jeffrey, J. Chem. Phys., 1959, 31, 1231–1234 CrossRef CAS.
  64. J. Qian, W. Yi, X. Huang, J. P. Jasinski and W. Zhang, Adv. Synth. Catal., 2016, 358, 2811–2816 CrossRef CAS.
  65. Y. Lin, W. Yi, W. Shen and G. Lu, Org. Lett., 2016, 18, 592–595 CrossRef CAS PubMed.
  66. D. J. Leng, C. M. Black and G. Pattison, Org. Biomol. Chem., 2016, 14, 1531–1535 RSC.
  67. Z. Zhang, J. Bi, Q. Liu and G. Zhang, J. Fluorine Chem., 2013, 151, 45–49 CrossRef CAS.
  68. L. Tang, Z. Yang, J. Jiao, Y. Cui, G.-D. Zou, Q. Zhou, Y.-Q. Zhou, W.-H. Rao and X. Ma, J. Org. Chem., 2019, 84, 10449–10458 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04185k
This journal is © The Royal Society of Chemistry 2019