Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selectivity of tungsten mediated dinitrogen splitting vs. proton reduction†
Bastian
Schluschaß
a,
Josh
Abbenseth
a,
Serhiy
Demeshko
a,
Markus
Finger
a,
Alicja
Franke
b,
Christian
Herwig
c,
Christian
Würtele
a,
Ivana
Ivanovic-Burmazovic
b,
Christian
Limberg
 c,
Joshua
Telser
c,
Joshua
Telser
 d and
Sven
Schneider
d and
Sven
Schneider
 *a
*a
aGeorg-August-Universität, Institut für Anorganische Chemie, Tammannstrasse 4, 37077 Göttingen, Germany. E-mail: sven.schneider@chemie.uni-goettingen.de
bLehrstuhl für Bioanorganische Chemie, Department Chemie und Pharmazie, Friedrich-Alexander-Universität Erlangen, Egerlandstrasse 3, 91058 Erlangen, Germany
cInstitut für Chemie, Humboldt Universität zu Berlin, Brook-Taylor-Strasse 2, 12489 Berlin, Germany
dDepartment of Biological, Physical and Health Sciences, Roosevelt University, 430 S. Michigan Avenue, Chicago, Illinois 60605, USA
First published on 24th September 2019
Abstract
Mo complexes are currently the most active catalysts for nitrogen fixation under ambient conditions. In comparison, tungsten platforms are scarcely examined. For active catalysts, the control of N2vs. proton reduction selectivities remains a difficult task. We here present N2 splitting using a tungsten pincer platform, which has been proposed as the key reaction for catalytic nitrogen fixation. Starting from [WCl3(PNP)] (PNP = N(CH2CH2PtBu2)2), the activation of N2 enabled the isolation of the dinitrogen bridged redox series [(N2){WCl(PNP)}2]0/+/2+. Protonation of the neutral complex results either in the formation of a nitride [W(N)Cl(HPNP)]+ or H2 evolution and oxidation of the W2N2 core, respectively, depending on the acid and reaction conditions. Examination of the nitrogen splitting vs. proton reduction selectivity emphasizes the role of hydrogen bonding of the conjugate base with the protonated intermediates and provides guidelines for nitrogen fixation.
Introduction
Homogeneous N2 fixation under ambient conditions has made remarkable progress over the past 15 years.1 Nishibayashi and co-workers recently obtained over 4000 equiv. of NH3 with the proton coupled electron transfer (PCET) reagent H2O/SmI2 as H+/e− sources and a molecular Mo pincer catalyst.2 Accordingly, nitrogen reduction (NR) via electrochemically or light-driven PCET with related systems has attracted a lot of attention.3,4 Lindley et al. estimated a suitable overpotential window of 1–1.5 V for selective NR (in MeCN) prior to competing hydrogen reduction (HR) at a glassy carbon cathode.5 However, besides the thermochemical framework, mechanistic models that account for NR vs. HR selectivities of molecular catalysts are generally poorly developed.Several M(NxHy) intermediates relevant to N2 fixation (Scheme 1) exhibit low N–H bond dissociation free energies (BDFEs) below that of free H2 (BDFE(H2, gas) = 97.2 kcal mol−1) as possible branching points into HR.6,7 Computational evaluation of NR vs. HR selectivities for a series of Fe catalysts pointed at bimolecular H2 loss from species with low N–H BDFEs.8,9 Attempts to stabilize such Fe(NxHy) species by hydrogen bonding with pendant bases so far resulted in shutdown of catalysis.10 But, in fact, such secondary interactions might also be relevant for Nishibayashi's catalyst as indicated by selectivities obtained with 2,6-lutidinium acids ([LutH]+[X]−) as the proton source. These strongly depend on the X− counter anion: NH3/H2 (X−) = 7.0 (Cl−), 0.9 (OTf−), and 0.14 (BAr4−).11
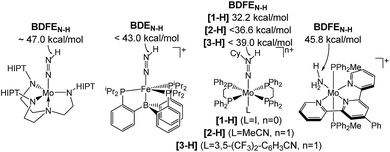 | ||
| Scheme 1 Transition metal species relevant to N2 fixation with a low BDFEN–H.7 | ||
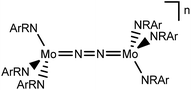
In this contribution, we address the role of hydrogen bonding for the selectivity of proton induced N2 splitting into molecular nitrides vs. proton reduction. N2 splitting has evolved as an entry into N2 functionalization for a wide variety of metals12 and was proposed as the key step in N2 fixation with Mo pincer catalysts.2,13 Cleavage of Cummins' seminal complex 1 (Fig. 1) was attributed to the {π12π22π32π42π51π61} configuration of the Mo2N2-core, which enables population of a destabilizing σ-antibonding molecular orbital (MO) in the transition state.14,15 In contrast, the {π8} oxidation product 22+ exhibits strong N2 activation (Table 1) but lacks two electrons to form stable MoVI(N3−) nitrides.16
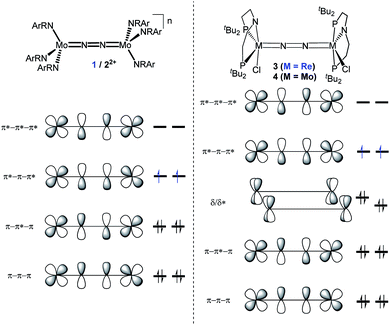 | ||
| Fig. 1 Qualitative molecular orbital schemes for 1, 22+, 3 and 4, illustrating the isolobal relationship of 1 {π10}/3 {π10δ4} and 22+ {π8}/4 {π8δ4}, respectively. | ||
| Compound | 1 | — | 22+ | 3 (M = Re) | 4 (M = Mo) | 6 (M = W) | 7+ (M = W) | 82+ (M = W) |
| n | 0 | +1 | +2 | 0 | 0 | 0 | +1 | +2 |
| Configuration | {π10} | {π9} | {π8} | {π10δ4} | {π8δ4} | {π8δ4} | {π8δ3} | {π8δ2} |
| d(NN) [Å] | 1.212(2)/1.217(2) | 1.239(4) | 1.265(5) | 1.202(10) | 1.258(9) | 1.33(4)/1.27(8) | 1.277(5) | 1.266(12) |
| ν(NN) [cm−1] | 1630 | 1503 | 1349 | 1771* | 1343 | 1392 | 1414 | 1400 |
| S | 1 | 1/2 | 0 | 1 | 0 | 0 | 1/2 | 1 |
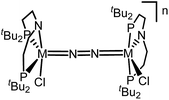
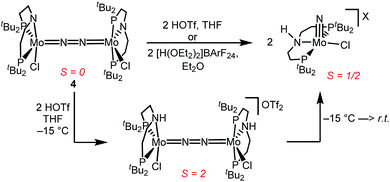
Similar electronic structure considerations can be applied to metal pincer platforms developed by our group. For example, the square-pyramidally coordinated dinuclear Re complex [(N2){ReCl(PNP)}2] (3, PNP = N(CH2CH2PtBu2)2) also splits into nitrides at r.t. and exhibits a {π10δ4} configuration that is isolobal with 1 (Fig. 1).17,18 In contrast, the {π8δ4} complex [(N2){MoCl(PNP)}2] (4) features stronger N2-activation comparable to 22+ (Table 1), but is thermally stable.19 Unexpectedly, splitting of 4 at r.t. was obtained upon protonation of the pincer backbone (Scheme 2), which was rationalized by a protonation induced low-spin {π8δ4} to high-spin {π10δ2} transition that facilitates electron transfer to N2.
Given the impressive N2 fixation rates with Mo pincer catalysts which possibly proceed via N2 splitting;2,13 W nitride formation from N2 is surprisingly rare.20 We here report tungsten mediated N2 splitting that competes with proton reduction upon protonation of a {W2N2} pincer complex. Our results provide evidence for the significance of hydrogen bonding for the reaction selectivity.
Results and discussion
Synthesis of the [(N2){WCl(PNP)}2]n+ (n = 0–2) redox series
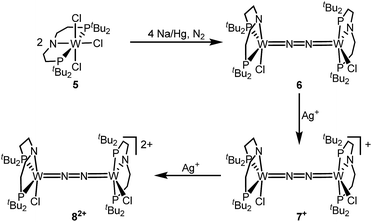
The reaction of WCl4 with HPNP in the presence of NEt3 gives the pincer complex [WCl3(PNP)] (5) in yields of up to 60%. In the absence of a signal in the 31P{1H} NMR spectrum, the paramagnetically shifted 1H NMR signals and the solution magnetic moment derived by Evans' method (μeff = 2.8 ± 0.1 μB) are in line with a d2 high-spin (S = 1) configuration. The molecular structure obtained by X-ray diffraction closely resembles previously reported compounds [MCl3(PNP)] (M = Re and Mo).18a,19Reduction of 5 with Na/Hg (2 equiv.) under N2 (1 atm) in THF gives the green, N2-bridged dinuclear complex [(N2){WCl(PNP)}2] (6) in up to 66% isolated yield (Scheme 3). In the solid state (Fig. 2) 6 is isostructural with the molybdenum analogue 4, regarding the N2 binding mode, the approximate C2 symmetry due to mutually twisted {WCl(PNP)}-fragments (Cl1-W1-W1#-Cl1#: 89.59°/92.27°), and the distorted square-pyramidal metal coordination (τ = 0.35).21 The short W–N2 bond (1.78(2)/1.82(4) Å) indicates multiple bonding character. In turn, the N–N bond (1.33(4)/1.27(8) Å) is at the higher end for N2-bridged ditungsten complexes.22 The two 31P{1H} NMR signals (δP = 92.9, 87.8 ppm) with large trans-coupling (2JPP = 147 Hz), the singlet 15N NMR resonance (δN = 31.1 ppm), and the 1H NMR signature of 6 support a C2 symmetric structure also in solution on the NMR timescale.
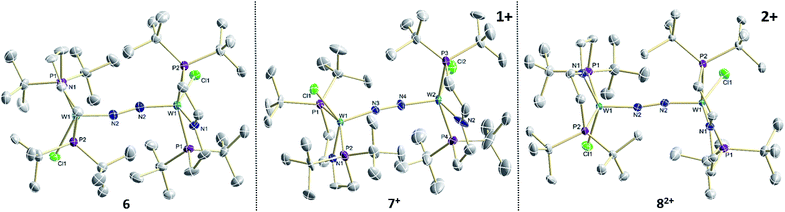 | ||
| Fig. 2 Molecular structures of 6, 7+ and 82+ in the crystal obtained by single crystal X-ray diffraction. Hydrogen atoms and anions are omitted for clarity. | ||
The N2 stretching vibration of 6 was assigned to the Raman signal at 1392 cm−1 (λexc = 457 nm, THF solution; 15N2 isotopologue: 1347 cm−1) supporting strong N2-activation with a formal N–N bond order below the double bonding character (trans-diazene: νNN = 1529 cm−1).23 The closed-shell ground state and degree of N2 activation are in line with the covalent bonding picture described in Fig. 1. The {π8δ4} configuration of the W2N2 core can be rationalized to arise from two low-spin WII ions. The twisted conformation enables strong back bonding of each metal ion with one π*-MO of the N2 bridge, respectively, resulting in net transfer of approximately two electrons as judged from the Raman data. This picture is corroborated by DFT computations, which confirm the {π8δ4} configuration of the W2N2 core, analogous to the Mo analogue 4 and Cummins' 22+. The blue-shifted N2 stretching vibration of 6vs.4 (ΔνNN = 49 cm−1; Table 1) indicates slightly reduced back-bonding by the 5d metal.
The redox chemistry of 6 was examined to probe the electronic structure model. Cyclic voltammetry (CV) in THF shows no reduction feature down to −2.9 V (vs. FeCp2+/FeCp2). In contrast, two reversible oxidation waves (Eo1 = −1.39 V; Eo2 = −0.91 V) are observed. Both redox events are cathodically shifted by 250 mV with respect to the Mo analogue 4, supporting metal centered oxidation. The oxidation products [(N2){WCl(PNP)}2]+ (7+) and [(N2){WCl(PNP)}2]2+ (82+) could be isolated in yields beyond 80% upon chemical oxidation of 6 with one and two equivalents of silver salts, respectively (Scheme 3). Stabilization of 82+ requires a weakly coordinating anion, which was introduced with Ag[Al(OC(CF3)3)4] as the oxidant.
In the solid state, 7+ and 82+ resemble the twisted conformation found for 6 (Fig. 2). Distinctly different bond lengths around the two tungsten ions of the mixed-valent complex 7+ indicate valence localization, which is further supported in solution by the large comproportionation constant (Kc ≈ 108)24 and the X-band EPR spectrum at r.t. The isotropic signal (gav = 1.93) of the low-spin (S = 1/2) complex exhibits hyperfine interaction (HFI) with only one tungsten (A(183W) = 220 MHz) and two phosphorous nuclei (A(31P) = 56 MHz), respectively. HFIs with the N2-bridge are not found and the 14N2- and 15N2-isotopologues give identical spectra, further supporting metal centered oxidation. In fact, the degree of N2 activation is almost invariant within the redox series 6/7+/82+ as judged from the invariance of the N–N stretching vibrations and the N–N bond lengths of the W2N2 cores (Table 1). Notably, the 1H NMR spectrum of 7+ features four signals assignable to tBu groups, in agreement with the averaged C2 symmetry and therefore valence delocalization on the slow NMR timescale.
The double oxidation product 82+ exhibits paramagnetically shifted, yet relatively sharp 1H NMR signals. Magnetic characterization by SQUID magnetometry reveals a χMT product of about 0.6 cm3 mol−1 K−1 at r.t., which gradually drops to 0 at about 20 K. The data can be fitted to a model with two weakly antiferromagnetically coupled (J = −59 cm−1) low-spin (S = 1/2) ions. The g-value (gav = 1.90) indicates an orbital contribution in the typical range for WV complexes with multiply bound hard ligands, such as oxo or nitrido complexes.25
Characterization of the redox series 6/7+/82+ supports the electronic structure picture with {π8δ4}/{π8δ3}/{π8δ2} configurations for the WIILS/WIILS (6), WIILS/WIIILS (7+) and WIIILS/WIIILS (82+) complexes, respectively (Fig. 1 and Table 1). The spin orbitals of 7+ and 82+ are orthogonal to the W2N2 core resulting in weak mutual coupling via the N2 bridge (J(82+) = −59 cm−1). In consequence, all three complexes of the redox series exhibit strong back bonding to the N2 bridge with only weakly affected degrees of N2 activation. These interpretations are corroborated by DFT (ESI†). Doublet {π8δ12δ21} (7+) and open-shell singlet {π8δ11δ21} (82+) ground states, respectively, were computed with a low lying triplet state for 82+ due to weak antiferromagnetic coupling of the metal centered spins (JDFT = −184 cm−1).
Protonation induced N2 splitting vs. proton reduction
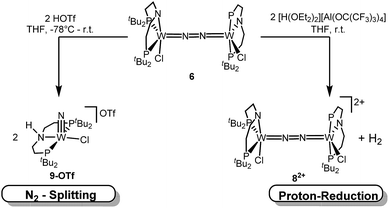
N2 splitting of 6 into the nitride [W(N)Cl(HPNP)]OTf (9OTf, Scheme 4) as the only detectable tungsten species (NMR/EPR spectroscopy, HR-ESI-MS) was achieved upon adding 2 equiv. of triflic acid at −78 °C and gradual warming to r.t. Complex 9OTf could be isolated in over 60% yield and was fully characterized. The tungsten(V) nitride is NMR silent and features an isotropic signal (gav = 1.93) in the X-band EPR spectrum (THF, r.t.) with HFIs with the tungsten and phosphorous nuclei (A(183W) = 220 MHz; A(31P) = 56 MHz). The W![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibration is found in the IR spectrum at 1058 cm−1 (15N-9OTf: Δν = 29 cm−1). In the solid state (Fig. 3), 9+ is isostructural with the molybdenum analogue,19 featuring square-pyramidally coordinated tungsten with the nitride ligand in the apical site. Hydrogen bonding of the amine proton with the triflate anion is indicated by the short NH…O distance (2.03(3) Å). The W
N stretching vibration is found in the IR spectrum at 1058 cm−1 (15N-9OTf: Δν = 29 cm−1). In the solid state (Fig. 3), 9+ is isostructural with the molybdenum analogue,19 featuring square-pyramidally coordinated tungsten with the nitride ligand in the apical site. Hydrogen bonding of the amine proton with the triflate anion is indicated by the short NH…O distance (2.03(3) Å). The W![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond length (1.679(2) Å) is in the typical range found for the related tungsten nitrides.1,17a,26
N bond length (1.679(2) Å) is in the typical range found for the related tungsten nitrides.1,17a,26
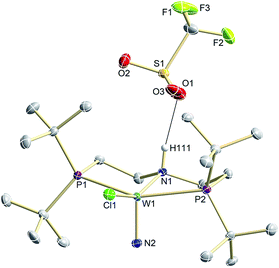 | ||
| Fig. 3 Molecular structure of 9OTf in the crystal obtained by single crystal X-ray diffraction. Hydrogen atoms are omitted for clarity except H111. | ||
In contrast to the Mo analogue 4 (Scheme 2), the selectivity of protonation induced N2 splitting strongly varies with the reaction conditions. The addition of HOTf (2 equiv.) to 6 at r.t. results in low nitride yields and substantial amounts of the oxidation products 7+ and 82+. Furthermore, 2 equiv. of strong acids with weakly coordinating anions, such as [H(OEt2)2] [Al(OC(CF3)3)4] and [H(OEt2)2]BArF24 (BArF24− = B(C6H3-3,5-(CF3)2)4−), exclusively gave dicationic 82+ both at low (−70 °C) and ambient temperatures (Scheme 4). Concomitant H2 evolution was confirmed by gas chromatography. Reaction of 6 at r.t. with 1 equiv. of these and other acids (HOTf, (2,6-lutidinium)OTf, [HNEt3][BArF24], [H(OEt2)2][BArF24], and [H(OEt2)2] [Al(OC(CF3)3)4]) selectively gives the oxidation product 7+ in all cases.
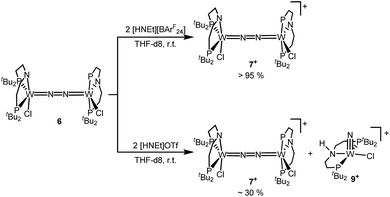
Next, the influence of the acid counteranion on the selectivity was probed. Upon protonation with [HNEt3][BArF24] (2 equiv.), 7+ was found exclusively (Scheme 5). The second oxidation is hampered by the higher pKa of this acid vs. HOTf, which prevents protonation of the monocationic product. Importantly, this selectivity changes with [HNEt3]OTf (2 equiv.): in this case, 7+ is obtained in spectroscopic yields of up to only 30%. In situ HR-ESI-MS examination indicates that nitride 9+ is formed as the only other product. This observation is reminiscent of acid dependent selectivities reported by Nishibayashi for catalytic nitrogen fixation (see above).11 For this reason, [HNEt3]Cl (2 equiv.) was also used. Unfortunately, sluggish mixtures of products were obtained, including substantial amounts of trichloride 5. In the next sections, experimental and computational mechanistic examinations with only [HNEt3]X (X− = BArF24−, OTf−) are therefore reported.
Mechanistic examinations
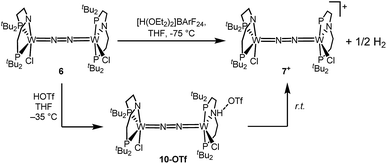
Stoichiometric protonation at low temperatures was carried out to obtain spectroscopic information about intermediates. With 1 equiv. of HOTf at low T (−35 °C), the NMR data are in agreement with pincer protonation to diamagnetic dinuclear C1-symmetric [(HPNP)ClW(μ-N2)WCl(PNP)]OTf (10OTf), analogous to the respective Mo system (Scheme 6).19Notably, immediate formation of the oxidation product 7+ was observed with [H(OEt2)2][BArF24], even at temperatures down to −75 °C. The enhanced stability of 10OTf suggests an interaction of the immediate protonation product with the triflate anion. Contact-ion pair formation is confirmed by 19F and 1H DOSY NMR spectroscopy at −35 °C. The diffusion coefficient of the triflate anion in 10OTf (D = 2.29 × 10−6 cm2 s−1) is in the same range as that of the cation (D = 2.18–2.14 × 10−6 cm2 s−1) and significantly reduced compared to free triflic acid (D = 5.11 × 10−6 cm2 s−1). We tentatively attribute the solution ion-pairing to hydrogen bonding of the triflate with the pincer N–H proton, as found in the solid state for 9OTf (Fig. 3).
Protonation of 6 with 2 equiv. of HOTf at low temperatures in THF is associated with a color change from green to yellow. The absence of a signal in the 31P{1H} NMR spectrum and the broadened and strongly shifted 1H NMR signals indicate the formation of a paramagnetic product. The magnetic moment for the presumable product, [(N2){WCl(HPNP)}2]OTf2 (11OTf2), was estimated with Evans' method at −60 °C (μeff = 4.7 μB), i.e. close to the spin-only value for a quintet ground state (4.9 μB). Increasing the temperature leads to fading of the color and disappearance of all 1H NMR signals, as expected for selective N2-splitting into the pale, NMR silent nitride product 9OTf.
Mechanistic information about proton reduction was obtained from kinetic studies. For this purpose, [HNEt3][BArF24] was used as the acid, which selectively gives 7+ at r.t. within a convenient timescale even under pseudo first-order conditions. Addition of the acid to 6 in THF leads to an immediate drop of absorbance without significant change of the absorption maxima, suggesting only small changes in the electronic structure. The acid concentration dependence of the absorbance allowed for estimating the equilibrium constant and forward rate of the initial protonation of 6 (K1 = 1592 ± 578 M−1, k1 = 163 ± 47 M−1 s−1; Scheme 7 and Fig. S25 and S26 in the ESI†). This step is followed by a much slower, mono-exponential decay, which was monitored over 5 h (Fig. 4, left). Under pseudo first order conditions in acid (c(HNEt3+)0/c(6)0 = 10–25), the rate constant (kobs(2)) linearly depends on the acid concentration (Fig. 4, right), which is in agreement with a slow, irreversible second protonation after the initial, fast pre-equilibrium K1. However, the non-zero intercept indicates the presence of at least one competitive pathway at a low acid concentration. The rate constant kobs(2) for the formation of 7+ was therefore expressed as eqn (1) which results from the minimum kinetic model outlined in Scheme 7:
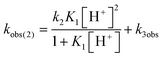 | (1) |
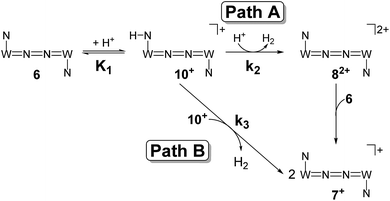 | ||
| Scheme 7 Proposed mechanistic pathways for proton reduction at high (Path A) and low (Path B) acid concentrations. | ||
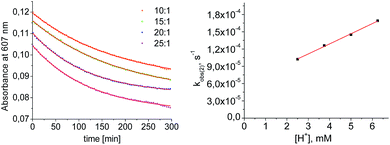 | ||
| Fig. 4 Left: plot of the absorbance at 607 nm vs. time for different concentrations of [HNEt3+]. Results from fitting to the rate law are indicated by red lines. Right: plot of kobs(2)vs. [HNEt3+]. | ||
The first term accounts for the initial protonation of 6 to give 10+, followed by irreversible H2 release from acid and 10+. Rapid, subsequent comproportionation of the resulting 82+ with 6 to 2 × 7+ is in line with the electrochemical results (Kc ≈ 108, see above). The second term in eqn (1) is ascribed to bimolecular decay of 10+ as an alternative path at low acid concentrations. The rate constant k2 = 0.018 ± 0.001 M−1 s−1 was derived from fitting the experimental data to eqn (1) (with preserved K1) under pseudo first order conditions in acid (10–25 equiv.). The rate constant k3 = 0.4 M−1 s−1 for the bimolecular path at low acid concentrations was obtained from the initial rate of the reaction of 6 and an equimolar amount of [HNEt3][BArF24].‡
Kinetic analysis suggests two pathways for H2 formation which both go through the spectroscopically characterized common intermediate 10+ (as 10OTf). Path B (Scheme 7) explains the decay of 10+ even in the absence of the acid and reflects a bimolecular H2 formation route as proposed by Matson and Peters for an iron diazenide N2-fixation intermediate.8 However, path A is predominant with excess acid. Besides these routes for hydrogen evolution, splitting of the N2 bridge is observed in the presence of triflate as the counteranion and is even selective at lower temperatures. These effects are rationalized computationally in the next section.
Computational examinations
Protonation with [NEt3H][BArF24] was first examined computationally with trimethylammonium as the model acid (Scheme 8). Two different sites, a metal ion and a pincer nitrogen atom, respectively, were considered for the first protonation step. A hydride product [(PNP)W(H)Cl(μ-N2)WCl(PNP)]+ (12+) adopts an electronic singlet (S = 0) ground state and was found to be the global protonation minimum at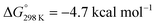 below 6 and [NMe3H]+. Hence, the model computation is in excellent agreement with the experimental equilibrium constant K1. The computed structure of 12+ features a bridging hydride between the metal ion and a pincer phosphorous atom. A similar structure was previously found experimentally by Schrock and co-workers for the protonation of a PCP molybdenum(IV) nitride by [NEt3H][BArF24].27 All efforts to experimentally verify hydride intermediates like 12+ were unfortunately unsuccessful. However, pincer protonation to 10+ is only slightly less exergonic
below 6 and [NMe3H]+. Hence, the model computation is in excellent agreement with the experimental equilibrium constant K1. The computed structure of 12+ features a bridging hydride between the metal ion and a pincer phosphorous atom. A similar structure was previously found experimentally by Schrock and co-workers for the protonation of a PCP molybdenum(IV) nitride by [NEt3H][BArF24].27 All efforts to experimentally verify hydride intermediates like 12+ were unfortunately unsuccessful. However, pincer protonation to 10+ is only slightly less exergonic 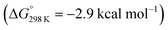 . Importantly, this state is further stabilized upon use of [NEt3H]OTf as the acid due to hydrogen bonding of the pincer amine moiety with the triflate anion by
. Importantly, this state is further stabilized upon use of [NEt3H]OTf as the acid due to hydrogen bonding of the pincer amine moiety with the triflate anion by 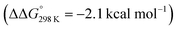 . In contrast, the hydride ligand is not involved in hydrogen bonding, rendering 10OTf
. In contrast, the hydride ligand is not involved in hydrogen bonding, rendering 10OTf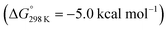 the global minimum of the first protonation in the presence of triflate. Overall, the metal and pincer protonation products 12+ and 10+ (and 10OTf in the presence of triflate) should be in rapid equilibrium under these conditions, which is slightly shifted towards pincer protonation by hydrogen bonding with the counteranion. Notably, hydrogen bonding with the conjugate base NMe3 was not observed, presumably for steric reasons.
the global minimum of the first protonation in the presence of triflate. Overall, the metal and pincer protonation products 12+ and 10+ (and 10OTf in the presence of triflate) should be in rapid equilibrium under these conditions, which is slightly shifted towards pincer protonation by hydrogen bonding with the counteranion. Notably, hydrogen bonding with the conjugate base NMe3 was not observed, presumably for steric reasons.
Starting from the amine/hydride equilibrium, the second protonation with [NMe3H]+ can ultimately lead to hydrogen evolution or N2 splitting, respectively. The formation of H2 and dicationic 82+, which represents Path A (Scheme 7), was computed to be exergonic by 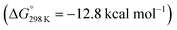 with respect to 6. The most reasonable pathway (Scheme 8, right branch) proceeds via hydride protonation of 12+ leading to the dihydrogen intermediate [(PNP)W(H2)Cl(μ-N2)WCl(PNP)]2+ (132+), which is unstable and readily releases H2 without barriers. While the transition state that leads from 12+ to 132+ could not be reliably located due to the flat potential energy profile of protonation, the free energy of 132+ (
with respect to 6. The most reasonable pathway (Scheme 8, right branch) proceeds via hydride protonation of 12+ leading to the dihydrogen intermediate [(PNP)W(H2)Cl(μ-N2)WCl(PNP)]2+ (132+), which is unstable and readily releases H2 without barriers. While the transition state that leads from 12+ to 132+ could not be reliably located due to the flat potential energy profile of protonation, the free energy of 132+ (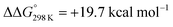 with respect to 12+) was used as an estimate for the kinetic barrier of hydride protonolysis.§ Notably, this value is in excellent agreement with the experimentally derived barrier for Path A (k2 = 0.018 M−1 s−1; ΔG‡eff = 19 kcal mol−1).
with respect to 12+) was used as an estimate for the kinetic barrier of hydride protonolysis.§ Notably, this value is in excellent agreement with the experimentally derived barrier for Path A (k2 = 0.018 M−1 s−1; ΔG‡eff = 19 kcal mol−1).
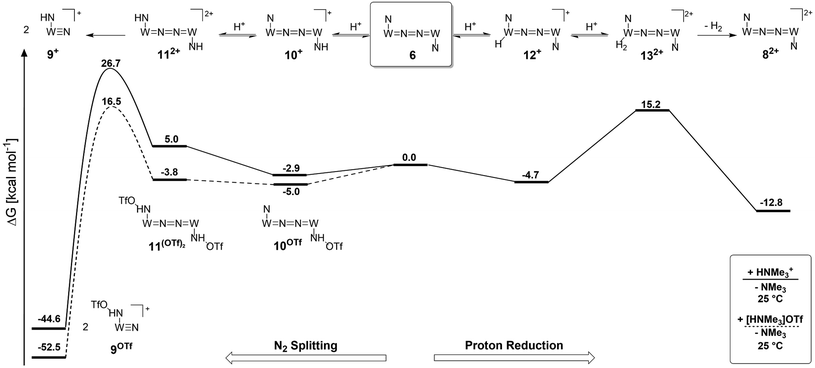
Alternatively, splitting of the dinitrogen bridge (Scheme 8, left branch) was computed to proceed via protonation of the second pincer nitrogen. In the absence of triflate, [(N2){WCl(HPNP)}2]2+ (112+) was located at 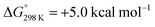 vs.6 (
vs.6 (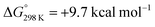 vs. the global first protonation minimum 12+) adopting an electronic quintet (S = 2) ground state in accordance with the experimental findings for 11OTf2. From there, N2 cleavage into the nitrides 9+ was computed to be strongly exergonic
vs. the global first protonation minimum 12+) adopting an electronic quintet (S = 2) ground state in accordance with the experimental findings for 11OTf2. From there, N2 cleavage into the nitrides 9+ was computed to be strongly exergonic 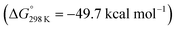 with a kinetic barrier (ΔG‡298 K = 21.7 kcal mol−1) that is comparable to the experimentally derived barriers for [(N2){MoCl(HPNP)}2]2+ (ΔG‡298 K = 19.5 kcal mol−1) and [(N2){ReCl(PNP)}2] (ΔG‡298 K = 19.8 kcal mol−1), respectively. For the tungsten system, this gives rise to an overall effective barrier for protonation induced N2 splitting from the most stable monoprotonation intermediate, hydride 12+, of ΔG‡eff = 31.4 kcal mol−1. This value is considerably higher than the estimate for the hydrogen evolution pathway (ΔΔG‡eff = +11.5 kcal mol−1), which is in line with selective proton reduction with [NEt3H][BArF24] as the acid.
with a kinetic barrier (ΔG‡298 K = 21.7 kcal mol−1) that is comparable to the experimentally derived barriers for [(N2){MoCl(HPNP)}2]2+ (ΔG‡298 K = 19.5 kcal mol−1) and [(N2){ReCl(PNP)}2] (ΔG‡298 K = 19.8 kcal mol−1), respectively. For the tungsten system, this gives rise to an overall effective barrier for protonation induced N2 splitting from the most stable monoprotonation intermediate, hydride 12+, of ΔG‡eff = 31.4 kcal mol−1. This value is considerably higher than the estimate for the hydrogen evolution pathway (ΔΔG‡eff = +11.5 kcal mol−1), which is in line with selective proton reduction with [NEt3H][BArF24] as the acid.
Importantly, the relative energetics of these two reaction channels are perturbed in the presence of triflate as the counteranion. As was found for the first pincer protonation (see above), triflate hydrogen bonding stabilizes the pincer diprotonation product 11OTf2 by −8.8 kcal mol−1. Consequently, the estimated effective barrier for hydrogen evolution (ΔG‡298 K = 20.2 kcal mol−1vs. the global first protonation minimum in the presence of triflate 10OTf) is slightly raised. On the other hand, the N2 splitting pathway (ΔG‡298 K = 21.5 kcal mol−1vs.10OTf) is almost isoenergetic, in full agreement with the experimental findings. The triflate induced effect on selectivity is therefore attributed to Curtin–Hammett controlled reactivity wherein N–H hydrogen bonding to the counteranion modifies the energetics of the protonation pre-equilibria.
A similar picture evolves for the reaction with triflic acid (see the ESI, Scheme S1†). However, the potential energy of protonation is augmented by the higher driving force with the stronger acid (pKTHFa(Et3NH+) − pKTHFa(HOTf) = 4.7).28 This affects the selectivity as the effective barrier for the N2 splitting branch versus hydrogen evolution is close in energy. Furthermore, all rate determining states are below the starting point 6. In consequence, under these conditions (HOTf as the acid at r.t.), Curtin–Hammett conditions do not apply resulting in the experimentally observed low selectivity.
Reduction of the temperature to −80 °C further perturbs the relative energetics of the two reaction pathways with HOTf. The computed amine 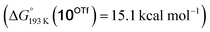 vs. hydride
vs. hydride 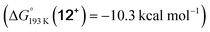 equilibrium is even more shifted towards the amine due to the lower entropic penalty for hydrogen bonding at low T. The negligible population of the hydride tautomer is in agreement with the exclusive experimental observation of 10OTf and 11OTf2 upon single and double protonation with HOTf at −80 °C. From 11OTf2, the dihydrogen complex 132+
equilibrium is even more shifted towards the amine due to the lower entropic penalty for hydrogen bonding at low T. The negligible population of the hydride tautomer is in agreement with the exclusive experimental observation of 10OTf and 11OTf2 upon single and double protonation with HOTf at −80 °C. From 11OTf2, the dihydrogen complex 132+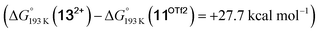 is much higher in free energy than the barrier for N2 splitting (ΔG‡193 K = 19.9 kcal mol−1), in line with selective N2 splitting upon double protonation with HOTf at −80 °C and slow warming.
is much higher in free energy than the barrier for N2 splitting (ΔG‡193 K = 19.9 kcal mol−1), in line with selective N2 splitting upon double protonation with HOTf at −80 °C and slow warming.
Concluding remarks
In summary, an anion effect on the selectivity of proton induced dinitrogen splitting (NR) vs. hydrogen evolution (HR) at the N2 bridged ditungsten complex 6 was demonstrated and rationalized. Our spectroscopic, kinetic and computational studies suggest some guidelines to improve NR over HR yields:(a) Nitrogen vs. metal protonation offers separate reaction channels with a proposed hydride isomer leading to hydrogen evolution analogous to the highly active Mo-oxo polypyridyl HR catalysts.29 The tautomerisation equilibrium can be offset by hydrogen bonding with protic N–H hydrogen atoms favoring the use of an acid [BH]+X− where the anion X− is prone to form H-bonds for high NR selectivity.
(b) Protonation under Curtin–Hammett control with weak acids can become irreversible with strong acids. Hence, the pKa of the acid can have a decisive kinetic effect on the selectivity.
(c) Lower temperatures favour hydrogen bonding interactions due to the reduced entropic penalty as a strategy for increased NR yields.
Besides the immediate application to the current system, these findings might be considered as a model reaction for nitrogen fixation schemes. The studies of Peters and of Nishibayashi have emphasized the importance of proton coupled electron transfer for N2 fixation under ambient conditions. Our kinetic model might therefore offer some general strategies regarding the choice of acid to improve NR selectivities with respect to unproductive proton reduction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the European Research Council (ERC Grant Agreement 646747). The authors thank Dr C. Volkmann for X-ray diffraction analysis of compounds 5 and 6, Dr S. Dechert for recording Raman spectra of 6 and 7+ and Dr C. Stückl for EPR measurements of 7+ and 9+.Notes and references
- (a) R. Schrock, Angew. Chem., Int. Ed., 2008, 47, 5512–5522 CrossRef CAS; (b) J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501, 84–87 CrossRef CAS PubMed; (c) K. C. MacLeod and P. Holland, Nat. Chem., 2013, 5, 559–565 CrossRef CAS PubMed; (d) H. Tanaka, Y. Nishibayashi and K. Yoshizawa, Acc. Chem. Res., 2016, 49, 987–995 CrossRef CAS PubMed.
- Y. Ashida, K. Arashiba, K. Nakajima and Y. Nishibayashi, Nature, 2019, 568, 536–540 CrossRef CAS PubMed.
- (a) N. Thompson, M. Green and J. Peters, J. Am. Chem. Soc., 2017, 139, 15312–15315 CrossRef CAS PubMed; (b) M. J. Chalkley, T. J. Del Castillo, B. D. Matson and J. Peters, J. Am. Chem. Soc., 2018, 140, 6122–6129 CrossRef CAS PubMed.
- (a) D. Wang, F. Loose, P. J. Chirik and R. R. Knowles, J. Am. Chem. Soc., 2019, 141, 4795–4799 CrossRef CAS; (b) F. Loose, D. Wang, L. Tian, G. D. Scholes, R. R. Knowles and P. J. Chirik, Chem. Commun., 2019, 55, 5595–5598 RSC.
- B. M. Lindley, A. M. Appel, K. Krogh-Jespersen, J. M. Mayer and A. J. M. Miller, ACS Energy Lett., 2016, 1, 698–704 CrossRef CAS.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS PubMed.
- (a) D. J. Yandulov and R. R. Schrock, Inorg. Chem., 2005, 44, 1103–1117 CrossRef CAS PubMed; (b) J. Rittle and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 3161–3170 CrossRef CAS PubMed; (c) M. J. Bezdek and P. Chirik, Dalton Trans., 2016, 45, 15922 RSC; (d) M. J. Bezdek, S. Guo and P. J. Chirik, Science, 2016, 354, 730–733 CrossRef CAS PubMed.
- B. D. Matson and J. C. Peters, ACS Catal., 2018, 8, 1448–1455 CrossRef CAS PubMed.
- T. J. Del Castillo, N. B. Thompson and J. C. Peters, J. Am. Chem. Soc., 2016, 138, 5341–5350 CrossRef CAS.
- S. E. Creutz and J. C. Peters, Chem. Sci., 2017, 8, 2321–2328 RSC.
- K. Arashiba, Y. Miyake and Y. Nishibayashi, Nat. Chem., 2011, 3, 120–125 CrossRef CAS.
- I. Klopsch, E. Y. Yuzik-Klimova and S. Schneider, Top. Organomet. Chem., 2017, 60, 71 CrossRef.
- K. Arashiba, A. Eizawa, H. Tanaka, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Bull. Chem. Soc. Jpn., 2017, 90, 1111 CrossRef CAS.
- C. E. Laplaza and C. C. Cummins, Science, 1995, 268, 861 CrossRef CAS PubMed.
- C. E. Laplaza, M. J. A. Johnson, J. C. Peters, A. L. Odom, E. Kim, C. C. Cummins, G. N. George and I. J. Pickering, J. Am. Chem. Soc., 1996, 118, 8623–8638 CrossRef CAS.
- J. J. Curley, T. R. Cook, S. Y. Reece, P. Müller and C. C. Cummins, J. Am. Chem. Soc., 2008, 130, 9394–9405 CrossRef CAS PubMed.
- (a) I. Klopsch, M. Finger, C. Würtele, B. Milde, D. B. Werz and S. Schneider, J. Am. Chem. Soc., 2014, 136, 6881 CrossRef CAS PubMed; (b) B. M. Lindley, R. S. van Alten, M. Finger, F. Schendzielorz, C. Würtele, A. J. M. Miller, I. Siewert and S. Schneider, J. Am. Chem. Soc., 2018, 140, 7922 CrossRef CAS.
- (a) I. Klopsch, M. Kinauer, M. Finger, C. Würtele and S. Schneider, Angew. Chem., Int. Ed., 2016, 55, 4786 CrossRef CAS; (b) I. Klopsch, F. Schendzielorz, C. Volkmann, C. Würtele and S. Schneider, Z. Anorg. Allg. Chem., 2018, 644, 916 CrossRef CAS; (c) F. Schendzielorz, M. Finger, J. Abbenseth, C. Würtele, V. Krewald and S. Schneider, Angew. Chem., Int. Ed., 2019, 58, 830 CrossRef CAS PubMed.
- G. Silantyev, M. Förster, B. Schluschaß, J. Abbenseth, C. Würtele, C. Volkmann, M. C. Holthausen and S. Schneider, Angew. Chem., Int. Ed., 2017, 56, 5872 CrossRef CAS.
- (a) A. J. Keane, W. S. Farrell, B. L. Yonke, P. Y. Zavalij and L. R. Sita, Angew. Chem., Int. Ed., 2015, 54, 10220–10224 CrossRef CAS; (b) L. M. Duman, W. S. Farrell, P. Y. Zavalij and L. R. Sita, J. Am. Chem. Soc., 2016, 138, 14856–14859 CrossRef CAS PubMed.
- A. W. Addison, N. T. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349 RSC.
- (a) M. R. Churchill, Y. J. Li, K. H. Theopold and R. R. Schrock, Inorg. Chem., 1984, 23, 4472–4476 CrossRef CAS; (b) R. C. Murray and R. R. Schrock, J. Am. Chem. Soc., 1985, 107, 4557–4558 CrossRef CAS; (c) M. R. Churchill and Y. J. Li, J. Organomet. Chem., 1986, 301, 49–59 CrossRef CAS; (d) M. Scheer, J. Müller, M. Schiffer, G. Baum and R. Winter, Chem. - Eur. J., 2000, 6, 1252–1257 CrossRef CAS PubMed; (e) P. P. Fontaine, B. L. Yonke, P. Y. Zavalij and L. R. Sita, J. Am. Chem. Soc., 2010, 132, 12273–12285 CrossRef CAS PubMed.
- (a) J. R. Durig, M. G. Griffin and R. W. MacNamee, J. Raman Spectrosc., 1975, 3, 133 CrossRef CAS; (b) N. C. Craig and I. W. Levin, J. Chem. Phys., 1979, 71, 400 CrossRef CAS.
- For critical discussion of Kc as a descriptor of valence tautomerism see: W. Kaim and B. Sarkar, Coord. Chem. Rev., 2007, 251, 584–594 CrossRef CAS.
- Representative examples: (a) W. Levason, C. A. McAuliffe and F. P. McCullough Jr., Inorg. Chem., 1977, 16, 2911–2916 CrossRef CAS; (b) K. Frick, S. Verma, J. Sundermeyer and M. Hanack, Eur. J. Inorg. Chem., 2000, 1025–1030 CrossRef CAS; (c) S. Sproules, A. A. Eagle, M. K. Taylor, R. W. Gable, J. M. White and C. G. Young, Inorg. Chem., 2011, 50, 4503–4515 CrossRef CAS PubMed.
- (a) K. Dehnicke and J. Strähle, Angew. Chem., Int. Ed., 1981, 20, 413–426 CrossRef; (b) M. H. Chisholm, D. M. Hoffman and J. C. Huffman, Inorg. Chem., 1983, 22, 2903–2906 CrossRef CAS; (c) C. R. Clough, J. B. Greco, J. S. Figueroa, P. L. Diaconescu, W. M. Davis and C. C. Cummins, J. Am. Chem. Soc., 2004, 126, 7742–7743 CrossRef CAS PubMed; (d) K. R. McClain, C. O'Donohue, A. Koley, R. O. Bonsu, K. A. Abboud, J. C. Revelli, T. J. Anderson and L. McElwee-White, J. Am. Chem. Soc., 2014, 136, 1650–1662 CrossRef CAS PubMed; (e) A. Lackner and A. Fürstner, Angew. Chem., Int. Ed., 2015, 54, 12814–12818 CrossRef CAS PubMed.
- T. J. Hebden, R. R. Schrock, M. K. Takase and P. Müller, Chem. Commun., 2012, 48, 1851–1853 RSC.
- A. Kütt, S. Selberg, I. Kaljurand, S. Tshepelevitsh, A. Heering, A. Darnell, K. Kaupmees, M. Piirsalu and I. Leito, Tetrahedron Lett., 2018, 59, 3738–3748 CrossRef.
- D. Z. Zee, T. Chantarojsiri, J. R. Long and C. J. Chang, Acc. Chem. Res., 2015, 48, 2017–2036 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1943888–1943892. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc03779a |
‡ An alternative pathway via reduction of 10+ with 6 is less likely based on the derived rate constant 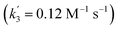 , which is considerably smaller than k3. , which is considerably smaller than k3. |
| § A transition state for the direct protonation of 12+ with HNMe3+ at the hydride ligand was located at 25.4 kcal mol−1 above 6 and two equivalents of [HNMe3]+. However, this activation free energy is considerably higher than the experimentally determined value (ΔG‡eff = 19 kcal mol−1). It is not clear if this deviation can be attributed to the computational truncation of the acid or to a lower competing pathway. We therefore prefer to use the experimental value for the discussion of the selectivity. See also the ESI for further discussion.† |
| This journal is © The Royal Society of Chemistry 2019 |