Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A model for dinitrogen binding in the E4 state of nitrogenase†
Albert Th.
Thorhallsson
ab,
Bardi
Benediktsson
 a and
Ragnar
Bjornsson
a and
Ragnar
Bjornsson
 *ab
*ab
aScience Institute, University of Iceland, Dunhagi 3, 107 Reykjavik, Iceland
bDepartment of Inorganic Spectroscopy, Max-Planck-Institut für Chemische Energiekonversion, Stiftstrasse 34-36, 45470 Mülheim an der Ruhr, Germany. E-mail: ragnar.bjornsson@cec.mpg.de
First published on 15th October 2019
Abstract
Molybdenum nitrogenase is one of the most intriguing metalloenzymes in nature, featuring an exotic iron–molybdenum–sulfur cofactor, FeMoco, whose mode of action remains elusive. In particular, the molecular and electronic structure of the N2-binding E4 state is not known. In this study we present theoretical QM/MM calculations of new structural models of the E4 state of molybdenum-dependent nitrogenase and compare to previously suggested models for this enigmatic redox state. We propose two models as possible candidates for the E4 state. Both models feature two hydrides on the FeMo cofactor, bridging atoms Fe2 and Fe6 with a terminal sulfhydryl group on either Fe2 or Fe6 (derived from the S2B bridge) and the change in coordination results in local lower-spin electronic structure at Fe2 and Fe6. These structures appear consistent with the bridging hydride proposal put forward from ENDOR studies and are calculated to be lower in energy than other proposed models for E4 at the TPSSh-QM/MM level of theory. We critically analyze the DFT method dependency in calculations of FeMoco that has resulted in strikingly different proposals for this state. Importantly, dinitrogen binds exothermically to either Fe2 or Fe6 in our models, contrary to others, an effect rationalized via the unique ligand field (from the hydrides) at the Fe with an empty coordination site. A low-spin Fe site is proposed as being important to N2 binding. Furthermore, the geometries of these states suggest a feasible reductive elimination step that could follow, as experiments indicate. Via this step, two electrons are released, reducing the cofactor to yield a distorted 4-coordinate Fe2 or Fe6 that partially activates N2. We speculate that stabilization of an N2-bound Fe(I) at Fe6 (not found for Fe2 model) via reductive elimination is a crucial part of N2 activation in nitrogenases, possibly aided by the apical heterometal ion (Mo or V). By using protons from the sulfhydryl group (to regenerate the sulfide bridge between Fe2 and Fe6) and the nearby homocitrate hydroxy group, we calculate a plausible route to yield a diazene intermediate. This is found to be more favorable with the Fe6-bound model than the Fe2-bound model; however, this protonation is uphill in energy, suggesting protonation of N2 might occur later in the catalytic cycle or via another mechanism.
Introduction
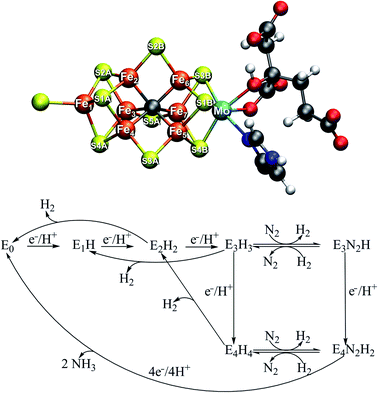
The mechanism of biological nitrogen reduction, catalyzed by the bacterial nitrogenase enzymes, has remained an unsolved problem in bioinorganic chemistry despite decades of research involving many experimental and theoretical research groups. The nitrogenases are metalloenzymes that catalyze the reduction of dinitrogen to two molecules of ammonia for each molecule of dinitrogen, impressively at ambient conditions.1,2 The molybdenum-dependent form is the most active and the best characterized, yet there is no consensus on the dinitrogen binding site on the cofactor nor is there a basic mechanism in place. The complete enzyme consists of a transient complex of the MoFe protein and the Fe protein. The function of the Fe protein is electron transfer to the MoFe protein via an [Fe4S4] cluster in an ATP-dependent process while dinitrogen reduction takes place in the MoFe protein. The active site of the MoFe protein, includes a complex [MoFe7S9C] cofactor (FeMoco, shown in Fig. 1) where dinitrogen binds. The kinetic studies by Lowe and Thorneley3 resulted in a model for dinitrogen catalysis linking different redox states of the cofactor (denoted En, with n indicating the number of added electrons and protons) together. The obligatory formation of one molecule of H2 per molecule of N2 is an intriguing aspect of the model, suggesting the unusual stoichiometry and the apparent waste of 2 electrons and 4 molecules of MgATP to produce this extra molecule of H2.4| N2 + 8e− + 8H+ + 16MgATP → 2NH3 + H2 + 16MgADP |
Curiously, in the Lowe–Thorneley model (a simplified scheme is shown in Fig. 1), dinitrogen does not bind to the iron–molybdenum cofactor until either the E3 or E4 state (after 3 or 4 added electrons and protons to the resting state E0), concomitant with formation of one molecule of H2. This obligatory H2 evolution step (as N2 binds) is thus directly part of the mechanism (rather than being one of the known side-reactions).4 Most kinetic and spectroscopic studies have been directed towards the E4 state as it is EPR active, its population can be increased by specific mutations and it has been argued to be the primary state for N2 binding.3,4
The FeMoco cluster is a highly unusual metallocofactor with a molecular structure that took many years to characterize; it consists of 7 iron ions, 1 molybdenum ion, 9 sulfides and an interstitial carbide5,6 (see Fig. 1). Its electronic structure is deeply complicated owing to the open-shell nature of the metal ions and their complex spin coupling in a highly covalent cluster (including an unusual carbide ligand).7 The iron oxidation states of the resting state FeMoco are formally Fe(II) and Fe(III) (typical in iron–sulfur clusters) while the Mo ion was determined via Mo K-edge and L-edge XAS spectroscopy to be in a Mo(III) oxidation state and theoretical calculations have shown it to be in an unusual spin-coupled low-spin state, likely due to metal–metal bonding interactions with the Fe ions.8,9 Recent X-ray magnetic circular dichroism experiments demonstrated the presence of the unusual spin-coupled state of Mo(III) in a related [MoFe3S4] model cubane.10 The charge of the cofactor in the resting state has been determined to be [MoFe7S9C]1− according to Mössbauer analysis, spatially resolved anomalous dispersion refinement and comparison of calculated and crystallographic metal–metal distances.11–13 Recent studies of the electronic structure from broken-symmetry (BS) DFT studies reveals a complicated electronic structure featuring both antiferromagnetic coupling, mixed-valence delocalization and partial metal–metal bonding.8,11,13
Other redox states of FeMoco are less well-characterized but we note recent spectroscopic studies of the E1 state14,15 and the E2 state.16,17 The binding site of dinitrogen is far from obvious from inspection of the cluster in its resting state (E0) and since little is known about the structure of the E4 redox state (which has been argued to be the primary state for N2 binding during turnover3,4), this is one of the most pressing questions in nitrogenase research. Even less is known about the E3 state and its proposed N2 binding as the state is EPR silent. A correct structural model for E4 would arguably reveal (or at least strongly suggest) how dinitrogen can favourably bind to FeMoco and how this typically inert molecule is activated for protonation. An accumulated S = 1/2 E4 state was originally probed by EPR spectroscopy in a mutant (α-70Val→Ile) of MoFe protein and ENDOR spectroscopy revealed that the structure contains 2 chemically near-equivalent bridging hydrides, likely storing the 4 reducing equivalents.18 Later, the EPR signal and ENDOR hyperfine signals associated with this state were found in the wild-type protein as well.19 The reductive elimination of H2 from these two hydrides was furthermore proposed to explain the obligatory H2 evolution in the mechanism4,20 and how dinitrogen is activated for protonation and there is now ample experimental evidence for this proposal.19,21 There is, however, no consensus on the structure of the E4 state, neither the precise coordination of the hydrides, nor is the N2 binding site agreed upon. Mutation studies have previously implicated the Fe2–Fe3–Fe6–Fe7 face as a likely binding site for dinitrogen as no dinitrogen reduction is observed when the residue α-70Val is mutated into the bulkier α-70Ile.22 Recent joint experimental–computational studies have proposed E4 models featuring bridging hydrides23–25 (the favoured model features bridging hydrides between Fe3–Fe7 and Fe2–Fe6) while other computational studies have suggested mixed bridging/terminal hydride models26,27 or even, surprisingly, structures featuring a protonated carbide with/without bridging hydrides.28–31 Additionally, recent crystal structures of a CO-bound form32 of MoFe protein (CO being an inhibitor) and an XH-ligand-bound (X = N or O) form33 of VFe protein have emerged, that show CO/XH replacing the Fe2–Fe6 bridging sulfide in a bridging binding mode (we recently showed via QM/MM calculations that the XH ligand in the FeVco structure is more consistent with an OH).34 These crystal structures demonstrate the lability of the sulfide bridges, which hints at a possible binding site of dinitrogen or perhaps a binding site of hydrides as discussed by Einsle et al.33,35 Overall, there is no consensus on the nature of the E4 state.
The present study proposes new structural models for the E4 state of FeMoco as well as a model for dinitrogen binding based on theoretical calculations. A state-of-the-art QM/MM protocol using the broken-symmetry DFT approach is used that has been previously validated on the resting E0 state.13 We compare the new structural models to previous proposals by calculating all models at the same QM/MM level of theory. The DFT method dependence of the relative energies is discussed and is put into context with the ability of different computational protocols to describe the electronic structure of the resting state correctly. Two energetically favourable models appear to be consistent with the bridging hydride proposal from experimental ENDOR studies and while favourable dinitrogen binding to both is possible, the E4 model featuring an open coordination site at Fe6 binds N2 slightly stronger. Concomitant H2 evolution with N2 binding via the reductive elimination proposal can be explained using our model due to close proximity of the hydrides (favoured over a hydride-proton reaction) and this leads to the stabilization of an N2-bound Fe(I) intermediate at Fe6 (or alternatively to an N2-bound Fe(II) intermediate at Fe2). A possible protonation step to yield a FeMoco-bound diazene intermediate is discussed.
Computational details
The QM/MM models for E4 were based on our model for the E0 resting state model that has been previously described.13 It is a spherical QM/MM model (42 Å radius and ∼37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) centered on the carbide of FeMoco that includes roughly half of the tetrameric MoFe protein; see ESI† for details about the QM/MM model preparation. In the QM/MM geometry optimizations of E4 models the active region consists of 1003 atoms and a QM region of 136 atoms while calculations of E0 used a smaller QM region of 54 atoms. All QM/MM calculations were performed in Chemshell36,37 using the built-in MM code DL_POLY38 with the CHARMM36 forcefield39 and ORCA version 4.0 (ref. 40) as QM code. The 136 atom QM region (see Fig. S4 in ESI†) contains the FeMoco cofactor, singly protonated homocitrate and the sidechains of residues α-70Val, α-96Arg, α-191Gln, α-195His, α-275Cys, α-278Ser, α-359Arg, α-380Glu, α-381Phe and α-442His. The QM region thus contains the main residues critical to describing the coordination, electrostatic environment, asymmetry, and hydrogen-bonding environment around FeMoco. This includes residues directly coordinating FeMoco (α-442His, α-275Cys), neighboring charged residues (α-96Arg, α-359Arg, α-380Glu), those capable of participating in hydrogen bonding (α-195His, α-191Gln, α-278Ser), as well as spatially close residues (α-70Val, α-381Phe). α-195His is calculated to be in the Nδ protonation state, assuming the residue has donated a proton from Nε to the cofactor and has been reprotonated at Nδ. All QM/MM calculations used electrostatic embedding, and hydrogen link atoms were used to terminate the QM–MM border together with the charge-shift procedure as implemented in Chemshell. The E4 QM calculations primarily used the TPSSh hybrid density functional,41,42 a ZORA scalar relativistic Hamiltonian,43,44 the relativistically recontracted def2-TZVP basis set45,46 on all metal, sulfur, carbide, homocitrate and hydride/SH/CH atoms (def2-SVP on other atoms) and a D3BJ dispersion correction.47,48 The RIJCOSX approximation49,50 with a decontracted Coulomb auxiliary basis set by Weigend51 was used. All DFT calculations used tight integration grids (Grid5 Finalgrid6 settings in ORCA). Single-point energy calculations of E4 models were performed at the TPSS,41 B3LYP52–55 and M06-2X56 levels using the same basis set. M06-2X calculations used a very large grid (Grid7 in ORCA) due to the grid-dependence associated with this functional.57 QM/MM geometry optimizations of the E0 state with other functionals always used the D3BJ dispersion correction except in the case of M06-2X where a D3(0) correction was used. Functionals used for E0 geometry optimizations were BP86,52,58 TPSS,41 B3LYP, PBE0,59,60 BHLYP,61 M06-2X and ωB97M-D3BJ.62,63 Broken-symmetry solutions of the E4 models were found by flipping spins on Fe atoms converging to the MS = 1/2 solution. Four different broken-symmetry solutions were explored (with Fe ions 235, 346, 247 or 147 spin down; atom numbering as in crystal structure) as discussed later. Vibrational frequencies of N2-bound models were calculated from a numerical QM/MM partial Hessian. While all QM/MM calculations minimized the QM/MM energy function, we primarily discuss the polarized QM energy rather than the total QM/MM energy as the former is less sensitive to the unrelated MM energy changes of the MM region.
000 atoms) centered on the carbide of FeMoco that includes roughly half of the tetrameric MoFe protein; see ESI† for details about the QM/MM model preparation. In the QM/MM geometry optimizations of E4 models the active region consists of 1003 atoms and a QM region of 136 atoms while calculations of E0 used a smaller QM region of 54 atoms. All QM/MM calculations were performed in Chemshell36,37 using the built-in MM code DL_POLY38 with the CHARMM36 forcefield39 and ORCA version 4.0 (ref. 40) as QM code. The 136 atom QM region (see Fig. S4 in ESI†) contains the FeMoco cofactor, singly protonated homocitrate and the sidechains of residues α-70Val, α-96Arg, α-191Gln, α-195His, α-275Cys, α-278Ser, α-359Arg, α-380Glu, α-381Phe and α-442His. The QM region thus contains the main residues critical to describing the coordination, electrostatic environment, asymmetry, and hydrogen-bonding environment around FeMoco. This includes residues directly coordinating FeMoco (α-442His, α-275Cys), neighboring charged residues (α-96Arg, α-359Arg, α-380Glu), those capable of participating in hydrogen bonding (α-195His, α-191Gln, α-278Ser), as well as spatially close residues (α-70Val, α-381Phe). α-195His is calculated to be in the Nδ protonation state, assuming the residue has donated a proton from Nε to the cofactor and has been reprotonated at Nδ. All QM/MM calculations used electrostatic embedding, and hydrogen link atoms were used to terminate the QM–MM border together with the charge-shift procedure as implemented in Chemshell. The E4 QM calculations primarily used the TPSSh hybrid density functional,41,42 a ZORA scalar relativistic Hamiltonian,43,44 the relativistically recontracted def2-TZVP basis set45,46 on all metal, sulfur, carbide, homocitrate and hydride/SH/CH atoms (def2-SVP on other atoms) and a D3BJ dispersion correction.47,48 The RIJCOSX approximation49,50 with a decontracted Coulomb auxiliary basis set by Weigend51 was used. All DFT calculations used tight integration grids (Grid5 Finalgrid6 settings in ORCA). Single-point energy calculations of E4 models were performed at the TPSS,41 B3LYP52–55 and M06-2X56 levels using the same basis set. M06-2X calculations used a very large grid (Grid7 in ORCA) due to the grid-dependence associated with this functional.57 QM/MM geometry optimizations of the E0 state with other functionals always used the D3BJ dispersion correction except in the case of M06-2X where a D3(0) correction was used. Functionals used for E0 geometry optimizations were BP86,52,58 TPSS,41 B3LYP, PBE0,59,60 BHLYP,61 M06-2X and ωB97M-D3BJ.62,63 Broken-symmetry solutions of the E4 models were found by flipping spins on Fe atoms converging to the MS = 1/2 solution. Four different broken-symmetry solutions were explored (with Fe ions 235, 346, 247 or 147 spin down; atom numbering as in crystal structure) as discussed later. Vibrational frequencies of N2-bound models were calculated from a numerical QM/MM partial Hessian. While all QM/MM calculations minimized the QM/MM energy function, we primarily discuss the polarized QM energy rather than the total QM/MM energy as the former is less sensitive to the unrelated MM energy changes of the MM region.
Results and discussion
A. Computational modelling of the E4 state
Theoretical modelling of the E4 state (here defined as the state after addition of 4e− and 4H+ to the resting state E0 of FeMoco) has been pursued recently by many groups and their models will be discussed and compared. It is helpful to first discuss criteria that, in our view, a realistic model for the E4 state should ultimately fulfil. These criteria are: (i) consistency with available spectroscopic data, (ii) the model being a thermodynamically viable state, (iii) demonstration of favorable N2 binding and consistency with isotope substitution experiments and, (iv) computational consistency.Regarding criterion i, regrettably, spectroscopic data for the E4 state are scarce and are primarily available in the form of EPR and ENDOR data, and primarily on a mutant form of the protein (which appears though to have the same spectroscopic signature as the wild type19). The EPR data indicates a spin state of S = 1/2 and analysis of the 1H hyperfine tensors from 1H ENDOR spectroscopy led to the proposal that the state contains two near-identical metal-bound hydrides, that are bridging rather than terminal and bound to Fe ions rather than the Mo ion according to 95Mo ENDOR.64 Furthermore, 57Fe ENDOR indicates that the overall iron redox level of E4 is the same as in the E0 state,65 which suggests that the two hydrides are acting as carriers of the four added electrons. A recent high-resolution ENDOR study of the same state has additionally revealed signals from two other hydrogens, likely present as protons bound to sulfides.25 As quantum chemical calculations of FeMoco are currently mostly limited to broken-symmetry DFT approaches (where pure spin states are not calculated) and spin projection schemes are problematic for non-Heisenberg systems like FeMoco, this unfortunately makes a direct comparison of the calculations to magnetic spectroscopy data from EPR and ENDOR difficult. However, an indirect comparison is still possible, i.e. a comparison of computed structures to the bridging hydride structural motif suggested by the ENDOR analysis.
Regarding thermodynamic stability i.e. criterion ii, kinetic studies of MoFe protein under turnover, indicates the E4 state is only fleetingly stable. The state can be freeze-trapped in a turnover sample with a small population but will evolve H2 with fast rates to fall back to an E2 state (that in turn further evolves H2 and falls back to E0).66 The fleeting nature of this state and the fact that the mechanisms of reduction and protonation are not entirely clear, indicates that thermodynamics alone cannot be the only guiding principle for differentiating between models for E4; however, thermodynamic stability must still be relevant to its formation.
Criterion iii implies that the model should ideally demonstrate favourable N2 binding. Experimental studies indicate N2 binding to be unfavourable in the early redox states, suggesting that the unknown E4 state features a structural component that makes N2 binding favourable (e.g. an empty coordination site), unlike redox states E0–E2 (E3 has also been proposed to bind N2). Furthermore, a model for E4 should offer a plausible explanation or mechanism for the obligatory H2 evolution resulting from the reductive elimination of H2 from two hydrides (as shown by isotope substitution studies) as N2 binds to FeMoco.
Finally, we propose computational consistency as criterion iv, that the computational E4 model should satisfy. By this, we mean that the computational protocol used to propose the model should also be shown to be consistent with other important experimental data of the system such as data for the other redox states. The 1.0 Å crystal structure of the E0 state6 is in our view the most accessible experimental data for gauging the quality of the computational protocols. The quality of the crystal structure of MoFe protein has improved steadily in recent years and has a bond length uncertainty of ∼0.02 Å. We consider a satisfactory agreement of the computed resting state structure to the crystal structure to be vital to any computational protocol that is used to suggest new redox state models of FeMoco.
All models that we consider in this study were structurally optimized at the same QM/MM level of theory that we have previously used to describe the resting state E0 and we considered multiple broken-symmetry states for each model. As recently discussed by Raugei et al.,24 the protein environment and the quality of the computational model can make a surprisingly large difference regarding the relative stability of an E4 isomer. Raugei et al. demonstrated e.g. that a protonated-carbide model for E4 was only stable for small cluster models of the active site but became unstable when larger cluster models were considered. As our QM/MM model accounts for the explicit protein environment from the beginning (and avoids potentially artificial constraints on residues) and furthermore utilizes a large QM-region (including important charged and hydrogen-bonding residues near FeMoco), our calculations should suffer much less from such artifacts. Our QM/MM methodology has previously been validated by detailed comparison of the calculated molecular structure of the cofactor in the resting state to the available high-resolution crystal structure, giving better agreement for the basic metal framework than cluster models.13 As before, we primarily utilize the TPSSh level of theory (a 10% Hartree–Fock (HF) exchange TPSS hybrid), a ZORA scalar relativistic Hamiltonian, dispersion correction and a flexible polarized triple-zeta basis set (on the cofactor). The functional dependency of calculations is discussed in chapter C.
Due to the complex open-shell nature of the [MoFe7S9C] cluster, the spin coupling problem of FeMoco is far from trivial. The broken-symmetry DFT methodology used here, flips individual spins on atoms and converges to broken-symmetry SCF solutions with localized alpha and beta spins on different atoms. These BS states likely correspond well to some of the low energy electronic states of FeMoco, but the methodology cannot capture the full multiplet spectrum of such a complex spin-coupled metal-sulfur cluster. Additionally, as discussed in recent multiconfigurational wavefunction theory studies, simplified model Hamiltonians (Heisenberg and Double Exchange Hamiltonians) are likely too simple to give a realistic description for spin-coupled iron–sulfur systems,67 preventing the use of spin-projection schemes. For the resting state, the BS7 class of solutions (that appears to maximize antiferromagnetic interactions) has been consistently found to be most favourable in multiple studies5,8,68–71. The three BS7 solutions, here labelled according to which Fe ions are spin-down (crystal structure numbering): BS-235, BS-346 and BS-247 have been found to be within ∼1 kcal mol−1 of each other (QM/MM-TPSSh level of theory) and in previous work13 we found that the BS-235 solution was in better agreement with the crystal structure than the other spin isomers. As E4 is a different redox state, however, the spin coupling may well have changed completely due to binding of hydrides and in fact the experimental spin state changes from S = 3/2 (E0) to S = 1/2 (E4). Thus a similar BS state to the one in E0 cannot simply be assumed to apply to E4. Cao et al.27 have shown, however, in their work where many different E1–E4 models were considered (featuring many of the models studied herein) that the BS solutions that are consistently lowest in energy are the BS7 class of solutions, thus supporting the hypothesis that maximizing antiferromagnetic coupling remains important, even when hydrides are bound. In this work we have primarily considered the BS7 solutions (BS-235, BS-346 and BS-247) as the most relevant broken-symmetry solutions as well as the BS-147 solution. The BS7 solutions are similar in energy and feature a very similar electronic structure in the resting state E0 (as discussed in ref. 11 and 13); the differing positions of spin-down Fe atoms though has the effect of changing the iron oxidation state at each site, as the mixed-valence pairs or localized ferric/ferrous irons will then involve different atoms in the structure. This local oxidation state interpretation of the different broken-symmetry states has been previously discussed.11,13,15 A BS-147 solution features ferromagnetic alignment of atoms Fe2 and Fe6. As some of the models in this study feature structural changes at these Fe ions, it seems possible that such a solution could become more favourable than other BS solutions. To aid in the computational problem involving many models and many BS states at an expensive level of theory, we have restricted ourselves to performing geometry optimizations with the BS-235, BS-247, BS-346, BS-147 solutions to explore the energetics of all models in Fig. 2. We additionally explored all 35 BS solutions of two models (l and o) at the single-point level (see ESI, Fig. S5 and S6† respectively). All models assumed a final MS = 1/2 spin state, consistent with the experimental S = 1/2 spin state of E4.
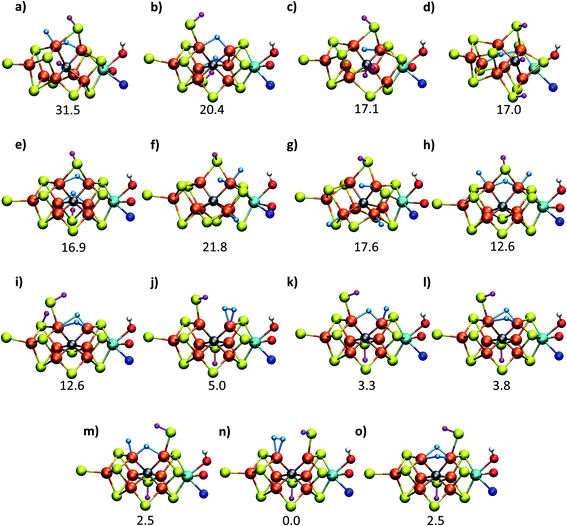 | ||
| Fig. 2 Structures and relative polarized electronic energies (EQM in kcal mol−1) of all FeMoco models for the E4 state considered in this study. All models were minimized using the same QM/MM level of theory using the TPSSh-D3 functional, ZORA–def2-TZVP basis set and a ZORA scalar relativistic Hamiltonian. See Tables 1 and S1 and S2† for information on all BS solutions tested. A large QM region of 136 atoms was used in the calculations but only the cofactor geometry is shown here. Hydrides are colored in light blue and carbide/sulfide-bound protons in magenta. | ||
B. QM/MM calculations of models of the E4 state
Fig. 2 shows the molecular structures of various proposed E4 models from previous work and new ones, featuring a variety of hydride binding modes and/or sulfide/carbide protonation scenarios. We are aided here by the work of Cao et al.,27 who performed a systematic study of a large number of protonation positions in the E0–E4 redox states. Thus, we have included the most stable E4 models found in their study (the study lacks, however, open sulfide-bridge models) according to the levels of theory employed in their study (TPSS and B3LYP), as well as models from other groups. All models, shown in Fig. 2, can be grouped according to whether they contain a protonated carbide (model a, c and d),27,29,30 whether they feature terminal/bridging hydrides with an intact sulfide bridge (models e, f, g and h)24,26,27 or whether they feature hydrides with an open sulfide bridge in the form of a terminal sulfhydryl group (models b, i, j, k, l, m, n, o).Models n, m and o were previously discussed as models close in energy to the favoured model e in work by Raugei et al. In this study we introduce models l and model o (though a model like o has been discussed by Raugei et al.24) as plausible candidates for E4 as well as models j and k, being similar to models m and n, and model b featuring two terminal sulfhydryl groups and two bridging hydrides. Model i also has a terminal sulfhydryl group like l but has a different sulfide protonation state.72 The models with a terminal sulfhydryl group at Fe2/Fe6 (rather than at Fe4/Fe5 or Fe3/Fe7) seem consistent with crystal structures of ligand-bound states32,33 lacking S2B (that bridges Fe2 and Fe6), suggesting some lability of this particular sulfide bridge. Fig. 2 and Table 1 contains data for the lowest energy BS solution but data for all broken-symmetry solutions can be found in Tables S1–S5† along with Mulliken spin populations for each state.
| TPSSh | Single-point QM energies (EQM) | |||||||
| Model (BS-state) | E QM | E QM/MM | Model | TPSS | Model | B3LYP | Model | M06-2X |
| a (147) | 31.46 | 23.67 | a (235) | 37.77 | a (147) | 36.83 | a (147) | 59.26 |
| b (247) | 20.40 | 17.66 | b (247) | 15.77 | b (147) | 26.84 | b (346) | 47.33 |
| c (247) | 17.14 | 14.73 | c (247) | 36.81 | c (147) | 2.46 | c (147) | 0.00 |
| d (147) | 16.96 | 17.58 | d (147) | 26.12 | d (346) | 15.70 | d (147) | 41.68 |
| e (147) | 16.88 | 11.23 | e (147) | 12.81 | e (235) | 34.70 | e (235) | 61.35 |
| f (346) | 21.80 | 22.55 | f (346) | 3.43 | f (235) | 43.19 | f (235) | 114.39 |
| g (346) | 17.60 | 13.02 | g (346) | 4.07 | g (235) | 38.21 | g (147) | 104.64 |
| h (247) | 12.56 | 11.37 | h (346) | 2.87 | h (247) | 33.04 | h (247) | 100.05 |
| i (247) | 12.55 | 10.91 | i (247) | 12.08 | i (247) | 19.60 | i (247) | 58.24 |
| j (147) | 4.99 | 3.35 | j (235) | 3.50 | j (147) | 12.34 | j (247) | 31.41 |
| k (147) | 3.29 | 1.95 | k (235) | 0.37 | k (147) | 13.18 | k (147) | 57.42 |
| l (147) | 3.75 | 2.44 | l (235) | 2.28 | l (147) | 14.52 | l (147) | 55.05 |
| m (346) | 2.47 | 2.04 | m (235) | 0.21 | m (346) | 0.00 | m (346) | 10.29 |
| n (346) | 0.00 | 0.00 | n (346) | 6.73 | n (346) | 1.40 | n (235) | 26.54 |
| o (147) | 2.48 | 2.25 | o (147) | 0.00 | o (346) | 12.96 | o (346) | 44.50 |
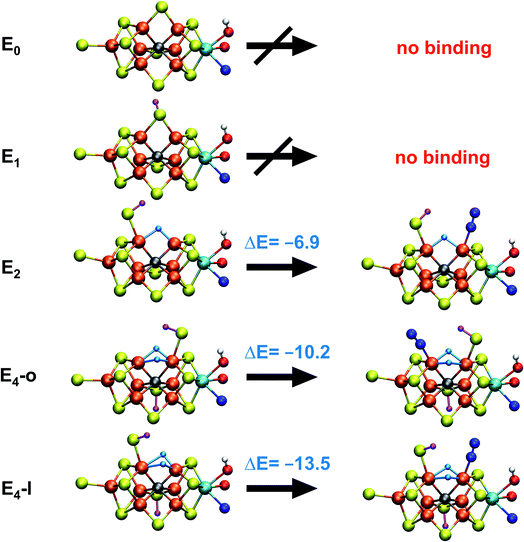
As shown in Fig. 2 and Table 1, the relative energies (polarized QM energies at QM/MM geometries) at the TPSSh level of theory indicate models featuring protonated carbides (a, c, d) are strongly disfavoured, appearing much too high in energy (17–32 kcal mol−1 higher in energy than the lowest energy model n) to be likely candidates for the E4 state. Additionally, models e, f, g, h, featuring an intact sulfide bridge also appear rather high in energy ranging from 13–22 kcal mol−1. Only open sulfide bridge models, j–o, featuring a terminal sulfhydryl group at Fe2 or Fe6 are found to be similarly low in energy, suggesting that it is generally thermodynamically favourable to alter the coordination of a protonated sulfide bridge to aid stabilizing hydrides (bridging, terminal or dihydrogen-like). Model b with two open sulfide bridges is an exception to this trend. This energetic analysis suggests that models j–o are the most viable models for the E4 state (at the TPSSh-QM/MM level). Open sulfide-bridge models like j–o were not considered in the study by Cao et al.27 but some open-sulfide bridge models were discussed by Raugei et al.24 and were found to be similar in energy as model e, which, however, is not in agreement with our results. We attribute this disagreement to different modelling aspects, i.e. cluster modelling vs. QM/MM modelling, as well as BS-solution dependence and functional dependence, which will be discussed in the next section.
C. Computational protocol dependence
As has recently been discussed in the literature, by Raugei et al.24 and especially by Cao et al.27,73 there is a considerable functional dependency present in calculations of FeMoco, affecting e.g. whether carbide protonation is favoured or not, or the structure of FeMoco. Thus, when hybrid density functionals with ≥20% HF exchange such as B3LYP (20% HF exchange) and M06-2X (54% HF exchange) have been used in the computational protocol, carbide protonation models have been found to be favoured over models with only hydrides. This is at odds with our relative energy comparison at the TPSSh level (10% HF exchange), shown in Fig. 2. We have been able to confirm some of this behaviour by performing single-point energy calculations using these functionals with the TPSSh-optimized geometries. As shown in Table 1, the energy comparison of models is dramatically altered when these hybrid functionals are considered. Meanwhile, results from the non-hybrid functional TPSS are more similar to the TPSSh results. As an example of this strong functional dependency, model c (a protonated carbide model found in the study by Cao et al.), is predicted to be only ∼2.5 kcal mol−1 higher in energy than the lowest energy model (m) at the B3LYP level of theory but ∼17 kcal mol−1 higher in energy than the lowest model (n) at the TPSSh level of theory. Structural optimization at the same level of theory would likely further stabilize model c. This effect of using a higher HF exchange hybrid is further magnified when using the M06-2X functional (having 54% HF exchange); this even leads to model c becoming the most stable model as seen in Table 1 (and the energy gap between models becoming 114 kcal mol−1). The M06-2X functional has been used to suggest carbide protonation as an important aspect of the mechanism.29The large energy changes seen for different functionals echo the results of Cao et al.73 We also note the pronounced sensitivity w.r.t. which BS-solution is calculated (see Tables S1–S2†), underlining the importance of studying multiple BS states in calculations of FeMoco. Such a large functional dependency of the relative energies (even when the same TPSSh geometries are used) naturally calls into question the reliability of the DFT calculations to distinguish energetically between E4 models of these complex systems. In fact, these results strongly suggest that the different functionals are describing the electronic structure of the FeMoco E4 state very differently. Such a different description of electronic structure with different functionals for FeMoco in the E4 state should be apparent in the E0 state as well (despite an absence of hydrides and protonated sulfides/carbide). In fact, when different functionals are used to describe the electronic structure of FeMoco in the E0 state, there are notable differences in the spin populations and isosurface plots of the spin density (see ESI, Fig. S13 and S14, Tables S9 and S11†). These differences can partly be attributed to the differing delocalization of electrons in FeMoco as well as the strength of Mo–Fe interactions (as discussed in previous studies the Mo electrons are partially delocalized towards the Fe ions, suggesting some Mo–Fe bonding7,8,11,13). A functional such as B3LYP for example shows a slightly more localized description of unpaired electrons in FeMoco and this effect is magnified when going to functionals with more HF exchange like BHLYP or M06-2X. In fact, when QM/MM geometry optimizations of the E0 state are performed with hybrid functionals with HF exchange ≥20% (such as B3LYP, BHLYP and M06-2X), large structural changes occur. This can be seen for Mo–Fe, Fe–Fe and Fe–C distances in Fig. 3 which shows the mean deviation of specific atom–atom distances w.r.t. crystal structure (more data available in the ESI, Fig. S10–S12†). Especially noteworthy is the up to 0.8 Å deviation seen for the Mo–Fe1 distance (see ESI, Fig. S10†) that suggests that the basic structure of the cofactor is very badly described at some of these same hybrid levels. As discussed further in the ESI,† the largest structural deviations involve Mo–Fe distances, and for BHLYP and M06-2X, this can be attributed to a completely different electronic structure on the molybdenum, giving rise to a high-spin Mo(IV) instead of the non-Hund Mo(III) configuration. The oxidation state of Mo as Mo(III) in FeMoco is now firmly established from Mo K-edge and L-edge XAS spectroscopy and theoretical calculations.8,9 Additionally, the unusual spin-coupled non-Hund Mo(III) configuration, first proposed by theoretical calculations8 has now experimental support via recent Mo L-edge and XMCD spectra.10 Thus, computational protocols giving rise to long Mo–Fe5/Fe6/Fe7 distances (>3 Å) by stabilizing a high-spin Mo(IV) ion are not only incompatible with the experimental molecular structure data (high resolution crystallography) but experimental electronic structure data (XAS and XMCD) as well. The QM/MM B3LYP results in Fig. 3 and the ESI† show considerable deviations with respect to the crystal structure (though not as large as the BHLYP and M06-2X results); however, this effect is further magnified if the QM/MM model is replaced by a simpler cluster model instead. The B3LYP cluster model data shown in the figures are from Siegbahn74 and give deviations as bad as the BHLYP and M06-2X QM/MM data. As shown in the ESI† there are also dramatic changes in the electronic structure of the B3LYP cluster model, especially regarding the oxidation state of Mo, again indicating a Mo(IV) oxidation state. It is also worth noting that overestimated Fe–C bond lengths (suggesting destabilized Fe–C chemical bonds) are seen from functionals/protocols that show more favourable carbide protonation according to Table 1 and these functionals/protocols have been used in studies that suggest carbide protonation occurring in reduced states of FeMoco. The non-hybrid functionals, BP86 and TPSS, give structures in better agreement with the experimental crystal structure (though showing underestimation of distances instead of overestimation). TPSS shows relative energies of E4 models more similar to TPSSh than the hybrid functionals, at least regarding the stability of carbide-protonation models. FeMoco is thus an interesting example of where there is quite a strong relationship between electronic structure (and hence reaction energies) and molecular structure.
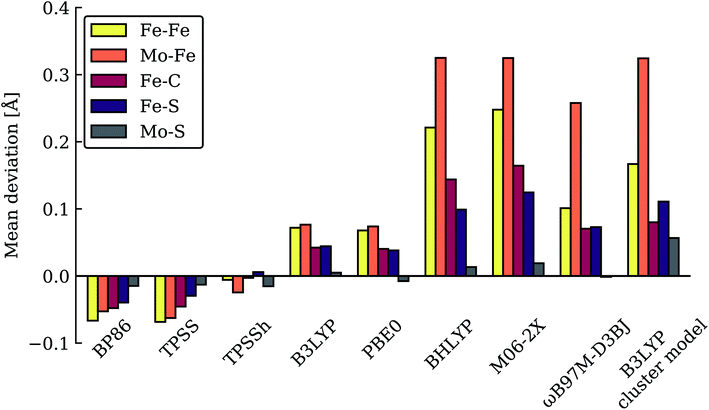 | ||
| Fig. 3 Mean deviations (Å) of Fe–Fe, Mo–Fe, Fe–C, Fe–S and Mo–S distances of resting state FeMoco (relative to crystal structure), calculated with various functionals using the same QM/MM protocol. Also shown is a B3LYP cluster model from Siegbahn.74 | ||
The good agreement seen between our TPSSh-QM/MM E0 structure and the high resolution crystal structure of E0 strongly suggests that we are describing the electronic structure of the system more correctly with TPSSh, clearly much better than the higher exchange hybrids and also better than non-hybrid functionals such as BP86 and TPSS. We note that our calculations include dispersion corrections, a large polarized triple-zeta basis set (on the cofactor) that should be close to the basis set limit, as well as scalar relativistic effects (via ZORA) and we account for the explicit protein environment from the beginning; the good agreement seen with our TPSSh calculations should thus primarily be due to a more correct description of the electronic structure rather than being due to accidental error cancellations of both model and method errors. Whether this ability to describe the resting state FeMoco well, carries over to describing the relative stability of hydrides and protonation of a metal-carbide is not as clear. We note though that the TPSSh functional has been shown to be a reliable functional for many problems in inorganic and bioinorganic chemistry giving both good structures75 and reaction energies.76 It appears most likely to us that the higher HF exchange in hybrids such as B3LYP, BHLYP and M06-2X is responsible for introducing severe artifacts in the basic electronic structure of FeMoco, that would carry over to the description of all redox states. Results from these functionals, such as a tendency to favour protonated carbides (not found with functionals that describe the E0 structure well), should therefore be regarded with high suspicion, in our view, as 20% or higher HF exchange appears to destabilize metal–ligand and metal–metal bonding in FeMoco (resulting even in a wrong Mo oxidation state) that is arguably crucial to its reactivity.
In our view, the relative energy comparison at the TPSSh level is at this point the most reliable as only this level of theory describes the electronic structure of the cofactor accurately in the resting state. This comparison indicates E4 models j–o as the most energetically favourable E4 models. We note that the stability of such open sulfide-bridge models is for the most part also found at the non-hybrid level of theory (TPSS) while the higher HF exchange hybrids predict a very different energy landscape. Geometry optimizations with these hybrid functionals (B3LYP, M06-2X) would no doubt further change the energy landscape of E4 models (likely further stabilizing protonated carbide models), however, this would not lead to any useful comparison, in view of the aforementioned electronic structure artifacts.
Thus, models j–o appear to be viable choices for the E4 state of FeMoco. We hesitate to distinguish further between these models based on their energetics. There is ample uncertainty regarding the reliability of relative energies with our DFT level of theory but it is also worth noting that the E4 state is thermodynamically not stable with respect to H2 formation (that leads back to the E2 state) according to experiments. The E4 state must then be a state that is kinetically trapped behind a barrier, and not necessarily at the lowest energy configuration (prior to H2 dissociation). The E4-n model is the lowest in energy according to our energetic comparison but this is a state where H2 has already formed, bound to Fe2 with a Kubas-type metal-dihydrogen geometry. Our calculations indicate an almost barrierless H2 dissociation from this state (a path leading to the E2 redox level) and this H2 formation (involving hydrides) would thus occur without N2 involvement which is inconsistent with isotope-substitution experiments. Those experiments showed that N2 is necessary for H2 formation via the hydrides (criterion iii from Section A.). Additionally, the E4-n model does not feature bridging hydrides, at odds with the structural interpretation of the ENDOR studies (criterion i from Section A.). The E4-n state, while energetically favourable, may thus be a state never formed under experimental conditions, it most likely represents an alternative path towards E4→E2 relaxation, but likely one that would not be seen experimentally.
If we focus on models that seem broadly consistent with the ENDOR proposal of two almost chemically equivalent bridging hydrides then models E4-l and E4-o (see Fig. 4) appear to be the most appealing models as these models feature two almost equivalent hydrides with considerable bridging character. These two models are also among the most thermodynamically stable models according to our TPSSh protocol and there is very likely a kinetic barrier towards H2 formation involving these hydrides that could be affected by N2 binding, making a reductive elimination step possible.
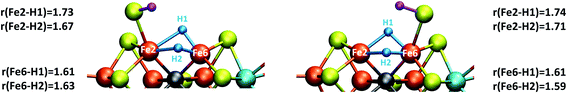 | ||
| Fig. 4 Close-up view of the hydride structures in E4-l (left) and E4-o (right) with Fe–H bond lengths (Å) indicated. | ||
On the other hand, model E4-e has been previously suggested by Hoffman and coworkers to be a structure that is consistent with the ENDOR data. In a very recent study,25 a case was made for this model being in the best agreement with even higher resolution ENDOR data while a structure similar to model E4-o was considered less likely. This comparison was based on calculated hyperfine tensor orientations with a simplified point-dipole approximation where the metal ions are assumed to all be high-spin and to behave as localized “spherical balls of spin”. The latter seems questionable, in our view, considering the strong delocalization of electrons seen in calculations of FeMoco and we also note that calculated spin populations of almost all E4 models (including E4-l, E4-o and E4-e, see Tables S2–S5†) show reduced spin populations on some Fe ions, calling into question the high-spin nature of all Fe ions in the E4 models. A direct calculation of the 1H hyperfine tensors of the hydrides of these models via multireference wavefunction theory may in fact be required to confidently tell apart models based on the hyperfine tensors. Such calculations are unfortunately still out of reach but may become possible in the near future. Our QM/MM calculations of E4-e do not suggest the state as a thermodynamically favourable model for the E4 state compared to open-sulfide bridge models (with no functional tested). Further studies will be required to determine whether such a model could be favourable under some conditions or even whether such a model represents a kinetically trapped state.
The energetically favourable E4-l and E4-o models (at TPSSh level of theory), featuring bridging hydrides (in agreement with ENDOR analysis), will be studied further in the next section. The energy surface and barriers that connects all of the states j–o will be reported on later; at present it is not clear whether all of these states are accessible to each other and this requires careful mapping of the minimum energy paths between them.
D. Molecular and electronic structure of E4-l and E4-o
The two models E4-l and E4-o both feature the same bridging hydride structure with the hydrides between Fe2 and Fe6 but the models differ in the position of the terminal sulfhydryl group (Fe2vs. Fe6) derived from sulfide S2B (Fig. 4). Sulfide S5A is also protonated in these models but remains bridging. The two hydrides in these models are mostly but not completely bridging between Fe2 and Fe6. For model E4-l, both hydrides are slightly more associated with Fe6 (Fe6–H distances of 1.61 and 1.63 Å) than Fe2 (Fe2–H distances of 1.73 and 1.67 Å) and for model E4-o, we see similarly stronger binding to Fe6 as well, with Fe6–H distances of 1.61 and 1.59 Å and Fe2–H distances of 1.71 and 1.74 Å. The coordination of these two new ligands to Fe2 and Fe6 change the geometry of these Fe ions from approximate tetrahedral to five- and six-coordinate geometries (distorted octahedral geometries), which naturally has a pronounced effect on the electronic structure of both Fe ions. In fact, the electronic structure of the two models reveal a change in the local spin state of both Fe ions in the lowest energy solution found for both, BS-147. With hydrides known to act as strong-field ligands and the change in four-coordinate local tetrahedral geometry to five or six-coordinate geometry this is perhaps not surprising. The change in local spin state is revealed in the change of spin population at Fe2 and Fe6 (from >3 to 2.4–2.5, see Table S6† for spin populations) and the localized orbitals reveal more clearly spin-pairing occurring at Fe2 and Fe6. The electronic structure appears consistent with intermediate spin S = 3/2 Fe(III) ions but this will require further study. In this context it is worth noting that such a double-hydride bridging geometry between two Fe ions has precedent in the form of synthetic dimeric Fe compounds from the groups of Peters77 and Holland78 though these synthetic compounds have a planar Fe–H–Fe–H geometry.A bridging hydride structure, with two hydrides between Fe2 and Fe6, has also been discussed by Einsle and coworkers as a possible E4 structure.33,79 However, that structure assumed an absent sulfide, in line with the hypothesis that the sulfide S2B leaves to open up a binding site, as crystal structures have shown that the sulfide can be displaced by CO or NH/OH.12,33 Importantly, in our E4 models, the S2B sulfide is protonated and remains present as a terminal sulfhydryl group on either Fe2 or Fe6. Dance has recently explored the thermodynamic feasibility of completely dissociating S2B in the form of SH− or H2S and found it not to be favourable80 and our own preliminary results suggest this as well. It is presently not clear under what conditions (or when in the cycle) complete sulfide removal from the cofactor (as shown by the crystal structures) occurs.
Based on the similarity of models E4-l and E4-o in terms of structure and energy, we cannot easily distinguish between them. Both appear reasonable candidates for the E4 state; only one of them may be formed under turnover conditions, however, and this may depend on the precise way that protons and electrons get introduced into the active site. Unfortunately, these mechanisms are not well established.
E. Dinitrogen binding to E4-l and E4-o
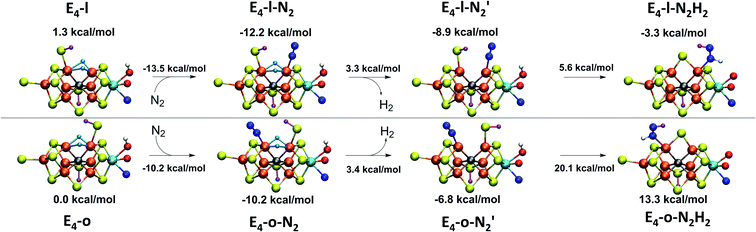
With the change in coordination by introduction of bridging hydrides, one of the Fe ions in each state is coordinatively unsaturated with respect to a six-coordinate octahedral geometry. This makes N2 binding to Fe6 (in E4-l) or Fe2 (in E4-o) a feasible scenario. In fact the synthetic Fe(II)–(μH)2–Fe(II) dimer by Peters and coworkers featured a bound N2 ligand on one of the Fe ions and 1-electron reduction to give a Fe(II)–Fe(I) dimer resulted in a large increase in the binding affinity of a second N2.77 There is thus precedent for a similar bridging-hydride dimer structure to be capable of favorable N2 binding.We explored N2 binding to the empty coordination site at Fe6/Fe2 for both E4-l and E4-o models to give N2-bound models E4-l-N2 and E4-o-N2 (shown in Fig. 5). N2 binding is found to be thermodynamically favourable (w.r.t. free N2) for both E4-l (bound to Fe6) and E4-o (bound to Fe2) states, with an electronic binding energy of ΔE = −13.5 kcal mol−1 for the E4-l-N2 state and a slightly weaker binding of ΔE = −10.2 kcal mol−1 is found for the E4-o-N2 state. We note that accounting for translational entropy (10.7 kcal mol−1 based on gas phase statistical mechanics) would reduce these electronic binding energies by that amount, leading to slightly endothermic 0.5 kcal mol−1 binding for E4-o and exothermic 2.8 kcal mol−1 for E4-l. Different broken-symmetry solutions (BS-235, BS-346, BS-247 and BS-147) were tested for the N2-bound states E4-l-N2 and E4-o-N2 that turned out to be crucial, as the energies of different states differed by up to 14 kcal mol−1 (see ESI, Table S6†), with some BS states not showing favorable N2 binding. For E4-l-N2 and E4-o-N2 models, the BS-235 and BS-346 solutions were lowest in energy, respectively. We note that these results are in sharp contrast with a recent study by Raugei et al.24 that found N2 binding (in a bridging geometry between Fe2 and Fe6) to be endothermic by 5 kcal mol−1 (ΔE).
N2 binds end-on to Fe6/Fe2 in these E4-l-N2 and E4-o-N2 structures resulting in an unusual distorted octahedral geometry at the participating Fe. This favorable binding of N2 to a FeMoco redox state is notable; N2 will unsurprisingly not bind to FeMoco at the E0 redox level in our calculations (no minimum found) but the same applies to a 1-electron reduced state. Our model for the E1 redox state (one of two favoured models from a recent joint EXAFS-QM/MM study15) involves an added electron to the [MoFe3S3C] sub-cubane and a protonated S2B sulfide bridge (multiple BS states with MS = 2 were calculated). Even when the E1-N2 optimization is started from a structure with a terminal sulfhydryl group bound to Fe2 and N2 in close proximity to Fe6, then N2 spontaneously dissociates. Thus neither 1-electron reduction of the cofactor or protonation of the sulfide bridge alone is sufficient for favorable N2 binding to occur at the cofactor. N2 will also not bind favorably to other Fe ions in the E4-l model; while a stable minimum is found when N2 is placed at Fe7, the binding is endothermic (∼5.5 kcal mol−1).
These results suggest that the hydride ligands at Fe2 and Fe6 in E4-l and E4-o are responsible for the favorable formation of the N2-binding states, E4-l-N2 and E4-o-N2, likely due to the unique ligand-field now found at these Fe ions. In support of this, we have also calculated a model for the E2 state of FeMoco, analogous to E4-l (with a sulfhydryl group at Fe2) but with only one bridging hydride between Fe2 and Fe6. This state (BS-235 and MS = 3/2) interestingly features favorable N2 binding (−6.9 kcal mol−1), about half of the binding energy to the E4-l state. The calculated N2 binding of this E2 model may, however, not be enough to overcome entropy and implies that the presence of two hydrides at the same Fe may be required for favorable dinitrogen binding.
Electronic structure aspects of dinitrogen binding of FeMoco will be explored in more detail in a future study. Our current interpretation of the electronic structure behind the favorable Fe6–N2 binding in the E4-l→E4-l-N2 step is that the low-spin configuration found at Fe6 in E4-l-N2 (spin population of −0.46) is a vital aspect of the N2 binding. The localized orbital analysis of Fe6 in E4-l-N2 reveals that this iron can be interpreted as a low-spin octahedral S = 1/2 Fe(III) ion with doubly occupied dxz and dyz orbitals. This low-spin configuration must arise via the strong-field hydride ligands as well as due to the N2 ligand. The double occupation of the dxz and dyz orbitals should allow increased backbonding to the N2 π* orbitals and the localized orbitals reveal some N2 character in these orbitals (see Fig. S8†). Taken together, the results in this section imply that a change from a high-spin to a low-spin Fe configuration may be vital to N2 being able to bind to FeMoco in the first place. The same argument holds for the E4-o-N2 model.
While the N2 ligand binds more strongly to Fe6 in our E4-l-N2 structure than to Fe2 in the E4-o-N2 structure, the difference is not large enough to confidently tell the two scenarios apart. The N2 ligand has a slightly elongated N–N bond length of 1.109 and 1.112 Å (for E4-l-N2 and E4-o-N2 respectively), a shift of 0.014/0.017 Å compared to free N2 at the same level of theory. The shift in N–N vibrational frequency (compared to free N2 at our level of theory) of 172 cm−1 (E4-l-N2) and 202 cm−1 (E4-o-N2) also indicates weak N2 activation for both states.
F. Reductive elimination
As is now well established from experiments, H2 is eliminated from the E4 state as N2 binds, via a reductive elimination mechanism involving the hydrides.4,19–21 Due to the proximity of the two hydrides in the E4 and E4-N2 models discussed in the previous chapters, one can imagine how such a reductive elimination step could proceed from our models. Isotope substitution experiments indicate that H2 evolution via reductive elimination can only proceed in the presence of N2. Experiments performed in the absence of N2, indicate that a regular hydride-proton reaction is responsible for the H2 formed from the E4 state (leading to the unproductive E4→E2 side-reaction). This implies that as N2 binds to the E4 state, either the H2 formation via reductive elimination is favoured thermodynamically over a hydride-proton reaction or it is kinetically favoured by lowering of the barrier for reductive elimination (relative to a hydride-proton reaction).A future study will explore in detail the reaction barriers for H2 formation via both reductive elimination and hydride-proton mechanisms from our E4 models. However, there is a simple argument in favour of reductive elimination over a more normal hydride-proton reaction that applies to both E4-l-N2 and E4-o-N2 models. The simplest hydride-proton reaction would involve combining one of the bridging hydrides with the proton from a sulfhydryl group (the closest accessible proton). The required deprotonation of the terminal sulfhydryl group (to act as proton donor) would be highly unfavoured as the terminal deprotonated sulfide is prevented from recombining with Fe6/Fe2 to reform the sulfide-bridge due to the presence of the other hydride in this position (in fact, calculations indicate such a step to be uphill by 15.1 kcal mol−1). The dinitrogen ligand would furthermore block a hydride-proton pathway involving the hydroxy proton from the Mo-bound homocitrate and possibly other proton donors. The molecular structures of the E4-l-N2 and E4-o-N2 models thus appear to offer an intuitive explanation for why the reductive elimination step can only occur in the presence of N2. Without the N2 ligand (i.e. in the absence of N2 gas), a hydride-protonation reaction (i.e. a E4→E2 step) should be more likely to occur, probably due to a lower barrier of a hydride-proton reaction compared to a hydride–hydride reaction. This could occur e.g. by hydride protonation via the hydroxy group on Mo-bound homocitrate or via the sulfhydryl group (and a possible transformation of the remaining bridging hydride to a terminal hydride and reformation of the sulfide bridge). With the N2 ligand present, however, reductive elimination could be the only favoured H2 evolution pathway.
This reductive elimination step involving two hydrides (formally storing four electrons) releases two electrons in the form of H2 and makes two electrons now available to the cofactor in states we call 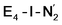 and
and 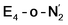 (see Fig. 6). Our calculations predict an electronic energy change (ΔE) of +3 kcal mol−1 uphill. While this step is predicted to be mildly endothermic according our calculations, this result is not in strong disagreement with experiment. In fact, kinetic studies show this step to be reversible,81 meaning the step is close to thermoneutral. Additionally, the translational entropy contribution to the free energy would favour the elimination of H2. We have opted for not adding gas phase translational entropy corrections (−8.4 kcal mol−1 for H2 elimination) to our energies as the entropic contribution could be more complicated for a complex condensed phase macromolecular system such as nitrogenase (as has been discussed by Reiher and coworkers82), however, the entropy contribution would likely be the same magnitude as the gas phase value. The fact that the
(see Fig. 6). Our calculations predict an electronic energy change (ΔE) of +3 kcal mol−1 uphill. While this step is predicted to be mildly endothermic according our calculations, this result is not in strong disagreement with experiment. In fact, kinetic studies show this step to be reversible,81 meaning the step is close to thermoneutral. Additionally, the translational entropy contribution to the free energy would favour the elimination of H2. We have opted for not adding gas phase translational entropy corrections (−8.4 kcal mol−1 for H2 elimination) to our energies as the entropic contribution could be more complicated for a complex condensed phase macromolecular system such as nitrogenase (as has been discussed by Reiher and coworkers82), however, the entropy contribution would likely be the same magnitude as the gas phase value. The fact that the 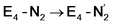 step is predicted to be close to thermoneutral (ΔE) according to our calculations is due to the nature of the reductive elimination. A regular H2 formation step should be quite exothermic (our calculations for hydride-proton reactions for an E4 → E2 predict exothermicity of ∼ −20 kcal mol−1). The lack of strong exothermicity for
step is predicted to be close to thermoneutral (ΔE) according to our calculations is due to the nature of the reductive elimination. A regular H2 formation step should be quite exothermic (our calculations for hydride-proton reactions for an E4 → E2 predict exothermicity of ∼ −20 kcal mol−1). The lack of strong exothermicity for 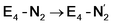 step stems from the fact that the metal cofactor is reduced (by 2 electrons) during the reaction, as previously the four electrons were stored in the form of the hydrides and two leave in the form of H2. This rather unfavorable two-electron reduction of the metal cofactor may thus be offset via the exothermicity of the H2 formation.
step stems from the fact that the metal cofactor is reduced (by 2 electrons) during the reaction, as previously the four electrons were stored in the form of the hydrides and two leave in the form of H2. This rather unfavorable two-electron reduction of the metal cofactor may thus be offset via the exothermicity of the H2 formation.
The molecular and electronic structure of the 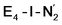 and the
and the 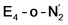 states is thus of interest as the metal ions of the cofactor are now more reduced than before and the structures lack the hydrides that previously helped bind N2. The local Fe geometries of the Fe2/Fe6 ions in
states is thus of interest as the metal ions of the cofactor are now more reduced than before and the structures lack the hydrides that previously helped bind N2. The local Fe geometries of the Fe2/Fe6 ions in 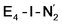 and
and 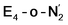 are unusual. A terminal sulfhydryl group is still present on Fe2 or Fe6. Attempts to reform the sulfide bridge (with sulfide still protonated) were not successful as the system returns to a geometry with the terminal sulfhydryl group. Clearly, the distorted geometries at Fe2/Fe6 are stable, though this is presently not well understood. Using the τ4 and
are unusual. A terminal sulfhydryl group is still present on Fe2 or Fe6. Attempts to reform the sulfide bridge (with sulfide still protonated) were not successful as the system returns to a geometry with the terminal sulfhydryl group. Clearly, the distorted geometries at Fe2/Fe6 are stable, though this is presently not well understood. Using the τ4 and 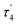 structural metrics83,84 for 4-coordinate compounds, we find that the Fe2 and Fe6 in both
structural metrics83,84 for 4-coordinate compounds, we find that the Fe2 and Fe6 in both 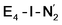 and
and 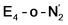 models are about halfway between a tetrahedral geometry and a seesaw geometry (see ESI, Tables S7 and S8,† for calculated τ4 and
models are about halfway between a tetrahedral geometry and a seesaw geometry (see ESI, Tables S7 and S8,† for calculated τ4 and 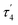 parameters for all Fe ions in multiple E4 models). We note that such geometries have previously been found in DFT calculations of FeMoco.85,86
parameters for all Fe ions in multiple E4 models). We note that such geometries have previously been found in DFT calculations of FeMoco.85,86
Analysis of the electronic structure suggests that the distorted N2-bound Fe2 ion in 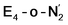 can be described as an S = 1 Fe(II) ion. However, remarkably, the distorted Fe6 ion in
can be described as an S = 1 Fe(II) ion. However, remarkably, the distorted Fe6 ion in 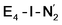 best fits the description of an S = 3/2 Fe(I) ion according to the localized orbitals (see ESI, Fig. S9†), revealing a stark difference between the two states and the nature of the different binding site. Both
best fits the description of an S = 3/2 Fe(I) ion according to the localized orbitals (see ESI, Fig. S9†), revealing a stark difference between the two states and the nature of the different binding site. Both 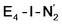 and
and 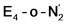 states feature doubly occupied dxz and dyz orbitals that likely account for the favorable dinitrogen binding via metal backbonding (similarly to the E4-l-N2 and E4-o-N2 models despite the absence of hydrides).
states feature doubly occupied dxz and dyz orbitals that likely account for the favorable dinitrogen binding via metal backbonding (similarly to the E4-l-N2 and E4-o-N2 models despite the absence of hydrides).
While distinguishing between the E4-l and E4-o pathways is not quite clear based on the calculated energies, it is tempting to attribute the presence of Fe(I) in 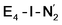 as a potentially important aspect of the mechanism when going forward. The interpretation of the reductive elimination is then that the electrons in the reductive elimination step are used to reduce the N2-binding Fe6 ion to an Fe(I) ion. Compared to the resting state E0, the mixed-valent delocalized Fe6(2.5)–Fe7(2.5) pair has then been reduced to a pair of localized Fe6(I) and Fe7(II) ions. Thus, the reductive elimination step could be imagined as a specific mechanism towards stabilizing an Fe(I)–N2 species without going to the strongly negative potentials such as those required for mononuclear complexes. Indeed, low-valent mononuclear iron complexes from Jonas Peters and coworkers have been found to act as catalysts for N2 reduction; this is accomplished via the use of strong reductants (KC8) to access low (Fe(I), Fe(0) and Fe(−I)) oxidation states that bind and activate N2.87–89 Reductive elimination could thus enable reduction of an Fe ion to Fe(I) while using the same low potential of the Fe protein.
as a potentially important aspect of the mechanism when going forward. The interpretation of the reductive elimination is then that the electrons in the reductive elimination step are used to reduce the N2-binding Fe6 ion to an Fe(I) ion. Compared to the resting state E0, the mixed-valent delocalized Fe6(2.5)–Fe7(2.5) pair has then been reduced to a pair of localized Fe6(I) and Fe7(II) ions. Thus, the reductive elimination step could be imagined as a specific mechanism towards stabilizing an Fe(I)–N2 species without going to the strongly negative potentials such as those required for mononuclear complexes. Indeed, low-valent mononuclear iron complexes from Jonas Peters and coworkers have been found to act as catalysts for N2 reduction; this is accomplished via the use of strong reductants (KC8) to access low (Fe(I), Fe(0) and Fe(−I)) oxidation states that bind and activate N2.87–89 Reductive elimination could thus enable reduction of an Fe ion to Fe(I) while using the same low potential of the Fe protein.
The N2 ligand in 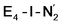 and
and 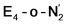 is only weakly activated as seen in a small increase in N–N bond length of 0.021 and 0.023 Å for
is only weakly activated as seen in a small increase in N–N bond length of 0.021 and 0.023 Å for 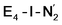 and
and 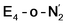 respectively, when compared to free N2 and by the decrease in N–N vibrational frequency of 242 and 255 cm−1 for
respectively, when compared to free N2 and by the decrease in N–N vibrational frequency of 242 and 255 cm−1 for 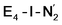 and
and 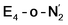 respectively, when compared to free N2. The N2 activation is greater though than in the E4-l-N2 and E4-o-N2 models (N–N bond length shifts of 0.014 and 0.017 Å and frequency shifts of 172 cm−1 and 202 cm−1). A high-spin Fe(I)–N2 complex was first synthesized by Harman and coworkers.90 Unlike the
respectively, when compared to free N2. The N2 activation is greater though than in the E4-l-N2 and E4-o-N2 models (N–N bond length shifts of 0.014 and 0.017 Å and frequency shifts of 172 cm−1 and 202 cm−1). A high-spin Fe(I)–N2 complex was first synthesized by Harman and coworkers.90 Unlike the 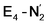 states proposed here, the synthetic Fe(I)–N2 complex has C3v symmetry and the dinitrogen activation is stronger with a N–N stretching frequency shift of 372 cm−1 compared to free N2.
states proposed here, the synthetic Fe(I)–N2 complex has C3v symmetry and the dinitrogen activation is stronger with a N–N stretching frequency shift of 372 cm−1 compared to free N2.
While activation of the N2 ligand in the in 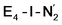 and
and 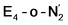 states is thus still considered weak, and protonation might be considered unlikely, we tested simple protonation reactions by transferring nearby protons to the nitrogen atoms of the ligand. Two possible protonation agents seem likely, one being the terminal sulfhydryl group on Fe2/Fe6 and the hydroxy group of homocitrate another. The hydroxy proton on homocitrate was found to be present in the resting state FeMoco according to a previous QM/MM study by us13 and by Cao et al.91 In this context it is of note that homocitrate is experimentally known to be important for dinitrogen reduction.92 Transferring a proton from the hydroxy group to either the distal or proximal nitrogen of either
states is thus still considered weak, and protonation might be considered unlikely, we tested simple protonation reactions by transferring nearby protons to the nitrogen atoms of the ligand. Two possible protonation agents seem likely, one being the terminal sulfhydryl group on Fe2/Fe6 and the hydroxy group of homocitrate another. The hydroxy proton on homocitrate was found to be present in the resting state FeMoco according to a previous QM/MM study by us13 and by Cao et al.91 In this context it is of note that homocitrate is experimentally known to be important for dinitrogen reduction.92 Transferring a proton from the hydroxy group to either the distal or proximal nitrogen of either 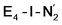 or
or 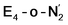 resulted in high energy intermediates of 34.3–36.3 kcal mol−1. If a double proton-transfer step is calculated, however, using both the sulfhydryl group and the hydroxy group, we get lower-energy diazene intermediates E4-l-N2H2 and E4-o-N2H2 instead. While the E4-l-N2H2 diazene intermediate is predicted to be higher in energy than the
resulted in high energy intermediates of 34.3–36.3 kcal mol−1. If a double proton-transfer step is calculated, however, using both the sulfhydryl group and the hydroxy group, we get lower-energy diazene intermediates E4-l-N2H2 and E4-o-N2H2 instead. While the E4-l-N2H2 diazene intermediate is predicted to be higher in energy than the 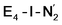 state by 5.6 kcal mol−1, it is interestingly much more favorable than the E4-o-N2H2 intermediate (uphill by 20.1 kcal mol−1), demonstrating very different reactivity of the Fe sites in the two models. Furthermore, the
state by 5.6 kcal mol−1, it is interestingly much more favorable than the E4-o-N2H2 intermediate (uphill by 20.1 kcal mol−1), demonstrating very different reactivity of the Fe sites in the two models. Furthermore, the 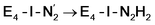 pathway, being in close proximity to the hydroxy group appears more plausible for direct proton transfer. These results indicate that protonation of the N2 ligand may not occur until later in the cycle (e.g. in the E5 redox state) or possible via another protonation mechanism not considered here.
pathway, being in close proximity to the hydroxy group appears more plausible for direct proton transfer. These results indicate that protonation of the N2 ligand may not occur until later in the cycle (e.g. in the E5 redox state) or possible via another protonation mechanism not considered here.
Experimentally, via a quench-cryoannealing relaxation protocol and varying H2/N2 concentrations, a reaction intermediate was shown to accumulate following reductive elimination, at the same redox level as E4.81 While this intermediate is denoted as E4(2N2H) by Hoffman and coworkers and discussed as “a state in which FeMo-co binds the components of diazene, which may be present as N2and two [e−/H+] or as diazene itself”81 EPR and ENDOR studies of this same intermediate93,94 showed 15N hyperfine coupling (using 15N2) but no hyperfine coupling from hydrogens was seen. A single 15N hyperfine signal was found, suggesting end-on binding which fits well with our 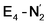 models. A recent EPR/ENDOR study of synthetic mononuclear Fe–N2 compounds by Peters and coworkers of states featuring either a single and double protonated N2 ligand: Fe–N2H and Fe–N2H2 (distal protonation) revealed a clear hyperfine signal from the hydrogens.95 These experiments may thus be an indication that the experimental dinitrogen-bound intermediate, “E4(2N2H)” is still unprotonated. Based on our computational modelling, it is possible that the experimental intermediate “E4(2N2H)” could correspond to the
models. A recent EPR/ENDOR study of synthetic mononuclear Fe–N2 compounds by Peters and coworkers of states featuring either a single and double protonated N2 ligand: Fe–N2H and Fe–N2H2 (distal protonation) revealed a clear hyperfine signal from the hydrogens.95 These experiments may thus be an indication that the experimental dinitrogen-bound intermediate, “E4(2N2H)” is still unprotonated. Based on our computational modelling, it is possible that the experimental intermediate “E4(2N2H)” could correspond to the 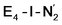 model (or possibly
model (or possibly 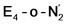 ) rather than a diazene-bound intermediate like E4-l-N2H2/E4-o-N2H2. An alternative explanation is that the hyperfine couplings from the hydrogens in a diazene intermediate may be too weak to be measured. Additional spectroscopy is required to clarify the nature of this intermediate.
) rather than a diazene-bound intermediate like E4-l-N2H2/E4-o-N2H2. An alternative explanation is that the hyperfine couplings from the hydrogens in a diazene intermediate may be too weak to be measured. Additional spectroscopy is required to clarify the nature of this intermediate.
Conclusions
We have presented QM/MM calculations of possible models for the E4 state of nitrogenase and how dinitrogen can bind to some of these models. In view of the thermodynamic stability of our model for the E4 state and the favourable dinitrogen binding we have presented, our work looks promising as a step towards a mechanistic understanding of biological dinitrogen reduction. Questions remain about the reliability of calculated reaction energies for this complicated cofactor and a stronger connection to experiment would be much desired, requiring more spectroscopy on nitrogenase intermediates.In this context, we should note that a recent ENDOR study25 combined with calculations has presented evidence in favour of another model (model e in article) as the structure of the E4 state. Our QM/MM calculations of that model suggest it to be higher in energy than all open-sulfide bridge models (with all calculated functionals) and this model has not been found to bind dinitrogen favorably.24 Additional spectroscopic data on the E4 state to sort out this disagreement would therefore be desirable.
Our proposed mechanism for binding of dinitrogen and reductive elimination suggests a role for many of the components of the complicated cofactor of nitrogenase. The size of the cofactor and the nature of the fused iron–sulfur double-cubane may play a primary role of favourably accepting electrons and storing them as hydrides at the same potential as provided by the Fe protein; the stability of the hydride geometries being facilitated by a labile sulfide bridge between cubanes. Furthermore, our calculations suggest the strong-field nature of the hydrides to aid the binding of dinitrogen by a local high-spin→low-spin electronic structure change at Fe6 or Fe2. The reductive elimination step then maintains the low-spin structure while doubly reducing the cofactor and partially activating the N2 ligand. The carbide may play a role in tuning the redox potential for the reduction steps but it may also play a role in either binding or activation of N2. The carbide being approximately trans to the N2 ligand in our 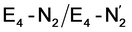 structures, suggests a link to the model chemistry of Peters and coworkers87,88 where carbide and boride-containing mononuclear trigonal bipyramidal Fe complexes were found to be active catalysts for dinitrogen reduction. Similar to the model compounds, the carbide in FeMoco may aid in pushing electron density into the π-accepting orbitals of the N2 ligand. The molybdenum ion likely also has an effect on the redox potential of the cofactor (the redox potential can in fact be tuned by heterometal substitution as known by synthetic [XFe3S4] chemistry where X = Mo, V, W96,97). We speculate that the role of the molybdenum may also be vital in stabilizing the N2-bound Fe(I) ion in
structures, suggests a link to the model chemistry of Peters and coworkers87,88 where carbide and boride-containing mononuclear trigonal bipyramidal Fe complexes were found to be active catalysts for dinitrogen reduction. Similar to the model compounds, the carbide in FeMoco may aid in pushing electron density into the π-accepting orbitals of the N2 ligand. The molybdenum ion likely also has an effect on the redox potential of the cofactor (the redox potential can in fact be tuned by heterometal substitution as known by synthetic [XFe3S4] chemistry where X = Mo, V, W96,97). We speculate that the role of the molybdenum may also be vital in stabilizing the N2-bound Fe(I) ion in 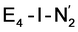 , formed after the reductive elimination step, making the electrons available for partial activation of the N2 ligand. The homocitrate ligand likely plays a role in protonation steps and the proton on the Mo-bound alcohol group of homocitrate is in an ideal position to protonate the N2 ligand when bound to Fe6 in the
, formed after the reductive elimination step, making the electrons available for partial activation of the N2 ligand. The homocitrate ligand likely plays a role in protonation steps and the proton on the Mo-bound alcohol group of homocitrate is in an ideal position to protonate the N2 ligand when bound to Fe6 in the 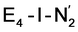 state; it may also help deliver protons in the early redox states (becoming protonated sulfides or hydrides).
state; it may also help deliver protons in the early redox states (becoming protonated sulfides or hydrides).
Finally, we emphasize that this work presents only a preliminary mechanism for dinitrogen binding to FeMoco that relies primarily on calculated energies with density functional theory approximations (where a large functional dependency is seen) and where only a small part of chemical space has been explored. More experimental data on the E4 and E4-N2 states are urgently needed to further constrain the mechanistic possibilities of FeMoco as well as to help benchmark the theoretical methodology employed. The precise way in which the N2 ligand is activated for protonation is also not clear from our results. At the very least this computational study has presented falsifiable ideas about the mechanism of biological nitrogen reduction that can be confirmed or ruled out by suitable experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
RB acknowledges support from the Icelandic Research Fund, Grants No. 141218051 and 162880051 and the University of Iceland Research Fund. The Max Planck society is acknowledged for funding. Serena DeBeer is thanked for support. Some of the computations were performed on resources provided by the Icelandic High Performance Computing Centre at the University of Iceland.References
- B. K. Burgess, Chem. Rev., 1990, 90, 1377–1406 CrossRef CAS
.
- L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Annu. Rev. Biochem., 2009, 78, 701–722 CrossRef CAS PubMed
.
-
R. N. F. Thorneley and D. J. Lowe, in Molybdenum Enzymes, ed. T.G. Spiro, Wiley, New York, 1985, pp. 221–284 Search PubMed
.
- B. M. Hoffman, D. Lukoyanov, Z. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114(8), 4041–4062 CrossRef CAS PubMed
.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977 CrossRef CAS PubMed
.
- T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Science, 2011, 334, 940 CrossRef CAS PubMed
.
- R. Bjornsson, F. Neese, R. R. Schrock, O. Einsle and S. DeBeer, J. Biol. Inorg Chem., 2015, 20, 447–460 CrossRef CAS PubMed
.
- R. Bjornsson, F. A. Lima, T. Spatzal, T. Weyhermller, P. Glatzel, E. Bill, O. Einsle, F. Neese and S. DeBeer, Chem. Sci., 2014, 5, 3096–3103 RSC
.
- R. Bjornsson, M. Delgado, F. A. Lima, D. Sippel, J. Schlesier, T. Weyhermüller, O. Einsle, F. Neese and S. DeBeer, Z. Anorg. Allg. Chem., 2015, 641, 65–71 CrossRef CAS PubMed
.
- J. Kowalska, J. T. Henthorn, C. Van Stappen, C. Trncik, O. Einsle, D. Keavney and S. DeBeer, Angew. Chem., Int. Ed., 2019, 58, 9373–9377 CrossRef CAS PubMed
.
- R. Bjornsson, F. Neese and S. DeBeer, Inorg. Chem., 2017, 56, 1470–1477 CrossRef CAS PubMed
.
- T. Spatzal, J. Schlesier, E.-M. Burger, D. Sippel, L. Zhang, S. L. A. Andrade, D. C. Rees and O. Einsle, Nat. Commun., 2016, 7, 10902–10907 CrossRef CAS PubMed
.
- B. Benediktsson and R. Bjornsson, Inorg. Chem., 2017, 56, 13417–13429 CrossRef CAS
.
- C. Van Stappen, R. Davydov, Z.-Y. Yang, R. Fan, Y. Guo, E. Bill, L. C. Seefeldt, B. M. Hoffman and S. DeBeer, Inorg. Chem., 2019, 58, 12365–12376 CrossRef CAS PubMed
.
- C. Van Stappen, A. Th. Thorhallsson, L. Decamps, R. Bjornsson and S. DeBeer, Chem. Sci., 2019 10.1039/C9SC02187F
.
- N. Khadka, R. D. Milton, S. Shaw, D. Lukoyanov, D. R. Dean, S. D. Minteer, S. Raugei and B. M. Hoffman, J. Am. Chem. Soc., 2017, 139, 13518–13524 CrossRef CAS PubMed
.
- D. Lukoyanov, N. Khadka, Z. Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Inorg. Chem., 2018, 57, 6847–6852 CrossRef CAS PubMed
.
- R. Y. Igarashi, M. Laryukhin, P. C. Dos Santos, H. I. Lee, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2005, 127, 6231–6241 CrossRef CAS PubMed
.
- D. Lukoyanov, N. Khadka, Z. Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2016, 138, 10674–10683 CrossRef CAS PubMed
.
- B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2013, 46, 587–595 CrossRef CAS PubMed
.
- Y. Y. Yang, N. Khadka, D. Lukoyanov, B. M. Hoffman, D. Dean and L. C. Seefeldt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16327–16332 CrossRef PubMed
.
- B. M. Barney, R. Y. Igarashi, P. C. Dos Santos, D. R. Dean and L. C. Seefeldt, J. Biol. Chem., 2004, 279, 53621–53624 CrossRef CAS PubMed
.
- D. Lukoyanov, N. Khadka, D. R. Dean, S. Raugei, L. C. Seefeldt and B. M. Hoffman, Inorg. Chem., 2017, 56, 2233–2240 CrossRef CAS PubMed
.
- S. Raugei, L. C. Seefeldt and B. M. Hoffman, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10521–E10530 CrossRef CAS PubMed
.
- V. Hoeke, L. Tociu, D. A. Case, L. C. Seefeldt, S. Raugei and B. Hoffman, J. Am. Chem. Soc., 2019, 141, 11984–11996 CrossRef CAS PubMed
.
- I. Dance, J. Am. Chem. Soc., 2007, 129, 1076–1088 CrossRef CAS PubMed
.
- L. Cao, O. Caldararu and U. Ryde, J. Chem. Theory Comput., 2018, 14, 6653–6678 CrossRef CAS
.
- M. L. McKee, J. Phys. Chem. A, 2016, 120, 754–764 CrossRef CAS
.
- L. Rao, X. Xu and C. Adamo, ACS Catal., 2016, 6, 1567–1577 CrossRef CAS
.
- P. E. M. Siegbahn, J. Am. Chem. Soc., 2016, 138, 10485–10495 CrossRef CAS PubMed
.
- P. E. M. Siegbahn, J. Comput. Chem., 2018, 39, 743–747 CrossRef CAS PubMed
.
- T. Spatzal, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Science, 2014, 345, 1620–1623 CrossRef CAS PubMed
.
- D. Sippel, M. Rohde, J. Netzer, C. Trncik, J. Gies, K. Grunau, I. Djurdjevic, L. Decamps, S. L. A. Andrade and O. Einsle, Science, 2018, 359, 1484–1489 CrossRef CAS PubMed
.
- B. Benediktsson, A. T. Thorhallsson and R. Bjornsson, Chem. Commun., 2018, 54, 7310–7313 RSC
.
- M. Rohde, D. Sippel, C. Trncik, S. L. A. Andrade and O. Einsle, Biochemistry, 2018, 57, 5497–5504 CrossRef CAS PubMed
.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28 CrossRef CAS
.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110 CAS
.
- W. Smith and T. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS
.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. Mackerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 73–78 Search PubMed
.
- J. Tao, J. Perdew, V. Staroverov and G. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed
.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS
.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS
.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392 CrossRef
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- D. A. Pantazis, X. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS
.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef
.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed
.
- A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2010, 6, 395–404 CrossRef CAS
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS
.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed
.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS
.
- D. Lukoyanov, Z. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2010, 132, 2526–2527 CrossRef CAS PubMed
.
- P. E. Doan, J. Telser, B. M. Barney, R. Y. Igarashi, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2011, 133, 17329–17340 CrossRef CAS PubMed
.
- D. F. Harris, Z. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Biochemistry, 2018, 57, 5706–5714 CrossRef CAS PubMed
.
- S. Sharma, K. Sivalingam, F. Neese and G. K. Chan, Nat. Chem., 2014, 6, 927–933 CrossRef CAS
.
- D. Lukoyanov, V. Pelmenschikov, N. Maeser, M. Laryukhin, T. C. Yang, L. Noodleman, D. Dean, D. A. Case, L. C. Seefeldt and B. Hoffman, Inorg. Chem., 2007, 46, 11437–11449 CrossRef CAS
.
- J. Kastner and P. E. Blöchl, J. Am. Chem. Soc., 2007, 129, 2998–3006 CrossRef PubMed
.
- T. V. Harris and R. K. Szilagyi, Inorg. Chem., 2011, 50, 4811–4824 CrossRef CAS PubMed
.
- I. Dance, Inorg. Chem., 2011, 50, 178–192 CrossRef CAS
.
-
J. Vertemara, PhD thesis, Università degli Studi di Milano-Bicocca, 2018 Search PubMed
.
- L. Cao and U. Ryde, Phys. Chem. Chem. Phys., 2019, 21, 2480–2488 RSC
.
- P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2019, 21, 15747–15759 RSC
.
- M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282–1290 CrossRef PubMed
.
- K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365 CrossRef CAS PubMed
.
- J. Rittle, C. C. L. McCrory and J. C. Peters, J. Am. Chem. Soc., 2014, 136, 13853–13862 CrossRef CAS PubMed
.
- S. M. Bellows, N. A. Arnet, P. M. Gurubasavaraj, W. W. Brennessel, E. Bill, T. R. Cundari and P. L. Holland, J. Am. Chem. Soc., 2016, 138, 12112–12123 CrossRef CAS PubMed
.
- M. Rohde, D. Sippel, C. Trncik, S. L. A. Andrade and O. Einsle, Biochemistry, 2018, 57, 5497–5504 CrossRef CAS PubMed
.
- I. Dance, Dalton Trans., 2019, 48, 1251–1262 RSC
.
- D. Lukoyanov, Z. Y. Yang, N. Khadka, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2015, 137, 3610–3615 CrossRef CAS
.
- M. Reiher and B. A. Hess, Chem. - Eur. J., 2002, 8, 5332–5339 CrossRef CAS
.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC
.
- A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Polyhedron, 2015, 90, 47–57 CrossRef CAS
.
- J. Kästner and P. E. Blöchl, J. Am. Chem. Soc., 2007, 129, 2998–3006 CrossRef PubMed
.
- P. P. Hallmen and J. Kästner, Z. Anorg. Allg. Chem., 2015, 641, 118–122 CrossRef CAS
.
- J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501, 84–87 CrossRef CAS PubMed
.
- S. E. Creutz and J. C. Peters, J. Am. Chem. Soc., 2014, 136, 1105–1115 CrossRef CAS PubMed
.
- T. J. Del Castillo, N. B. Thompson and J. C. Peters, J. Am. Chem. Soc., 2016, 138, 5341–5350 CrossRef CAS PubMed
.
- A. McSkimming and W. H. Harman, J. Am. Chem. Soc., 2015, 137(28), 8940–8943 CrossRef CAS PubMed
.
- L. Cao, O. Caldararu and U. Ryde, J. Phys. Chem. B, 2017, 121, 8242–8262 CrossRef CAS PubMed
.
- J. Imperial, T. R. Hoover, M. S. Madden, P. W. Ludden and V. K. Shah, Biochemistry, 1989, 28, 7796–7799 CrossRef CAS PubMed
.
- B. M. Barney, T. C. Yang, R. Y. Igarashi, P.
C. Dos Santos, M. Laryukhin, H. I. Lee, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, J. Am. Chem. Soc., 2005, 127, 14960–14961 CrossRef CAS PubMed
.
- B. M. Barney, D. Lukoyanov, R. Y. Igarashi, M. Laryukhin, T. C. Yang, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Biochemistry, 2009, 48, 9094–9102 CrossRef CAS PubMed
.
- M. A. Nesbit, P. H. Oyala and J. C. Peters, J. Am. Chem. Soc., 2019, 141, 8116–8127 CAS
.
- D. V. Fomitchev, C. C. McLauchlan and R. H. Holm, Inorg. Chem., 2002, 41, 958–966 CrossRef CAS PubMed
.
- D. Hong, Y. Zhang and R. H. Holm, Inorg. Chim. Acta, 2005, 358, 2303–2311 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Further information on all broken-symmetry solutions calculated for all models. Details of the QM/MM model preparation. Spin populations of all models. Localized orbital analysis of selected models. Geometry analysis of E0 state calculated with different functionals and electronic structure analysis. Cartesian coordinates for the QM regions of all optimized structures available as XYZ files. See DOI: 10.1039/c9sc03610e |
| This journal is © The Royal Society of Chemistry 2019 |