Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computationally aided design of a high-performance organic semiconductor: the development of a universal crystal engineering core†
Anthony J.
Petty
II
a,
Qianxiang
Ai
a,
Jeni C.
Sorli
b,
Hamna F.
Haneef
c,
Geoffrey E.
Purdum
b,
Alex
Boehm
a,
Devin B.
Granger
 a,
Kaichen
Gu
b,
Carla Patricia Lacerda
Rubinger
d,
Sean R.
Parkin
a,
Kenneth R.
Graham
a,
Kaichen
Gu
b,
Carla Patricia Lacerda
Rubinger
d,
Sean R.
Parkin
a,
Kenneth R.
Graham
 a,
Oana D.
Jurchescu
a,
Oana D.
Jurchescu
 c,
Yueh-Lin
Loo
c,
Yueh-Lin
Loo
 be,
Chad
Risko
be,
Chad
Risko
 af and
John E.
Anthony
af and
John E.
Anthony
 *af
*af
aDepartment of Chemistry, University of Kentucky, Lexington, Kentucky 40506-0055, USA. E-mail: anthony@uky.edu
bDepartment of Chemical and Biological Engineering, Princeton University, Princeton, New Jersey 08544, USA
cDepartment of Physics and Center for Functional Materials, Wake Forest University, USA
dPhysics and Chemistry Institute, Federal University of Itajubá, 37500-903, Itajubá, MG, Brazil
eAndlinger Center for Energy and the Environment, Princeton University, Princeton, New Jersey 08544, USA
fCenter for Applied Energy Research, University of Kentucky, Lexington, Kentucky 40511, USA
First published on 7th October 2019
Abstract
Herein, we describe the design and synthesis of a suite of molecules based on a benzodithiophene “universal crystal engineering core”. After computationally screening derivatives, a trialkylsilylethyne-based crystal engineering strategy was employed to tailor the crystal packing for use as the active material in an organic field-effect transistor. Electronic structure calculations were undertaken to reveal derivatives that exhibit exceptional potential for high-efficiency hole transport. The promising theoretical properties are reflected in the preliminary device results, with the computationally optimized material showing simple solution processing, enhanced stability, and a maximum hole mobility of 1.6 cm2 V−1 s−1.
Introduction
The solid-state arrangement of molecules in crystalline films is the determining parameter for the performance of organic semiconductors. While numerous crystal engineering paradigms exist for tuning molecules functionalized with a variety of supramolecular synthons1 for exploration of improved pharmaceuticals,2 tuning of solid-state reactivity,3 photochemistry,4,5 and crystal mechanical properties,6 the crystalline order of the simple nonpolar aromatic molecules used as semiconductors is typically more difficult to control. Apart from alignment induced by the van der Waals interactions of long hydrocarbon chains (the so-called “zipper” or “fastener” effect),7 few reliable approaches exist that can improve solubility and control solid-state order in simple aromatic structures. Nearly twenty years ago, we introduced silylethyne substitution as a simple method to increase stability, improve solubility, and induce π-stacking in aromatic molecules.8,9 This functionalization strategy has been applied to acenes,10–16 heteroacenes,17–25 indenofluorenes,26 benzo-thiadiazoles,27 zethrene,28 and others,29–32 typically via a simple alkynylation sequence,33 to yield new materials for transistor,34–38 photovoltaic,39–44 imaging,45 light-emitting,46,47 and other applications.48–50 While this approach is relatively general in scope, it cannot be applied to a number of promising chromophores due to difficulties in preparing the necessary precursors, or to the delicacy of certain chromophores that preclude ethynylation.In order to both apply silylethyne functionality to a more general class of materials and, at the same time, integrate computation-based guidance to assess a derivative's likelihood for high performance in an application, we envisioned developing a “universal crystal engineering core” that could be orthogonally derivatized to allow manipulation of the properties of the aromatic backbone while still exploiting the versatility of silylethyne-based crystal engineering strategies to modify the solid-state ordering. Through simple functionalization strategies our universal crystal engineering core could be used, along with feedback from computation, to develop high-performance materials. The design parameters we required for a universal crystal-engineering core are straightforward – simple and scalable preparation, amenable to addition of functionalized alkynes to tune crystal packing, and halogen “handles” to allow attachment of the chromophores of interest. Further, silylethyne-based crystal engineering typically works best with roughly linear molecules, which suggests that the core should terminate in five-membered rings; as such, a benzodithiophene (BDT) core appeared to be an ideal scaffold. We report here our first example of our modular crystal engineering approach to new organic materials; the development of stable, new molecules for organic field-effect transistors (OFETs).
Results and discussion
Design and synthesis of universal crystal engineering core
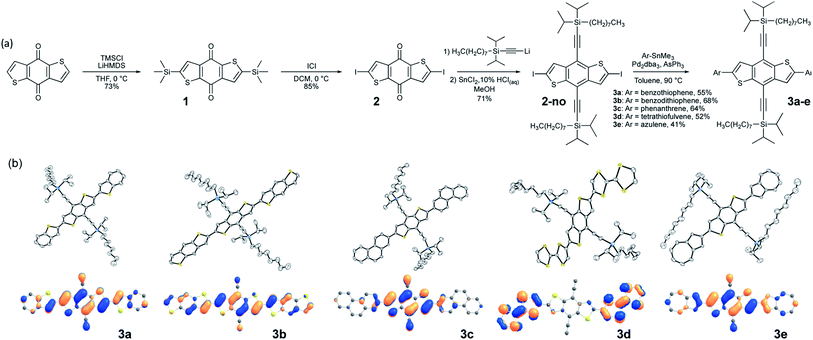
Our approach begins with the development of a multi-gram synthetic approach to diiodo-benzodithiophene quinone, 2, through a novel, scalable method that obviates the need for cryogenic temperatures (Fig. 1a).51 The crystal engineering silylethyne handle is added by routine ethynylation/deoxygenation sequence to provide the desired core.The size of the trialkylsilyl group can be modified depending on the combined size of core and pendant; our previous work produced a model for controlling solid-state order that relates the nature of π-stacking to the diameter of the solubilizing group relative to the length of the chromophore.10 Since even small chromophores appended to this core will yield molecules with substantial aspect ratio, commercially available trialkylsilyl groups are unlikely to yield appropriate π-stacking motifs. For our initial studies, we employed the n-octyldiisopropylsilyl derivative as the trialkylsilyl group, which has shown promise in large aromatic systems such as the bistetracenes.30
Screening of aromatic pendants
We employed modified (Farina) Stille coupling conditions52,53 to attach the pendant to the crystal engineering core, first appending benzothiophene and BDT to 2-no, giving products 3a and 3b. Yields were generally good after minimal optimization, producing stable, soluble materials that were purified by standard chromatographic techniques. Crystals suitable for X-ray analysis were easily grown from slow cooling of saturated solutions, and the diffraction measurements confirmed the planarity of the chromophores and π-stacked order of the materials, consistent with previous reports on bithiophene linkages.54 To determine whether linking 6-membered aromatic rings to core 2-no would also yield the planar systems required for efficient π-stacking, we appended phenanthrene to 2-no to give 3c. Crystallographic analysis showed a planar molecule, with strong π-stacking interactions and significant intermolecular overlap. Finally, applying this approach to some of the more delicate chromophores of interest to the organic electronics community, we coupled both tetrathiafulvalene (TTF)55 and azulene to 2-no. Here again, the products were stable, soluble, crystalline materials with planar backbones and strongly π-stacked arrangements in the solid state. All structures have been submitted to the Cambridge Crystallographic Data Centre – registry numbers can be found in the ESI.†The photophysical properties of the chromophore-core-chromophore systems are determined by the appended groups (Fig. S1†). When there is little donor–acceptor character between the core and pendant groups (benzothiophene, benzodithiophene, phenanthrene) minimal absorption shifts are observed. The azulene-pendant compound 3e, which has a highest-occupied molecular orbital (HOMO) that is predominately localized on the BDT core (Fig. 1b, bottom row), caused a substantial red shift in absorption (the LUMOs were similarly localized, see Fig. S11†). Similarly, the strongly red-shifted and relatively featureless absorption for the TTF derivative 3d suggests charge-transfer between the TTF unit and the core, with the HOMO localized to the pendants and the LUMO localized to the core.
To gain a measure of the difference in stability between the materials prepared from our benzodithiophene core compared to a prototypical organic semiconductor, tri-isopropylsilylethynyl pentacene (TIPS-pentacene), the decay observed in the solution absorption spectra of 3b and TIPS-pentacene were followed under intense external lighting as a function of time (Fig. S2†). While the TIPS-pentacene absorption declined rapidly, with a half-life of less than 15 minutes, 3b exhibited no appreciable decomposition after 7 hours under the same conditions. A high degree of solution stability is important for development of viable semiconductor inks.
With the exception of the TTF derivative 3d, all synthesized derivatives adopt extended π-stacked arrangements (Fig. S3†) in the 1-D slipped-stack motif, with reasonably close contacts between the stacks. In our prior studies on acenes, such packing arrangements typically arose in systems where the solubilizing trialkylsilyl groups were not sufficiently large to induce the 2-D “brickwork” packing motif that is more desirable for charge tranpsort.10 In contrast, 3d adopted an end-to-end arrangement that yielded a chevron pattern similar to that seen in the orthorhombic polymorph of rubrene (Fig. S3†).56
Computational selection of candidates for device evaluation
The frontier molecular orbitals (MO) of 3a–e were evaluated by density functional theory (DFT) calculations at the ωB97X-D/Def2SVP level of theory after geometry optimization (Fig. 1b, bottom row).57,58 The intermolecular overlaps of the HOMOs in the solid state are critical for hole transport, thus for this application materials where this orbital spans the length of the molecule are preferred. We observe that the HOMOs are delocalized along the long axes of the chromophores to different degrees depending on the pendant groups (Fig. 1b, bottom row). The HOMOs of 3a and 3b are delocalized along the entire chromophore, whereas the HOMOs are localized on the central BDT core in 3c and 3d, and is localized on the pendant azulene moieties in 3e. Thus, the BDT pendant 3b, showing HOMO delocalization along the entire conjugated backbone, was selected for further crystal engineering efforts.57,58Crystal engineering to improve crystal packing
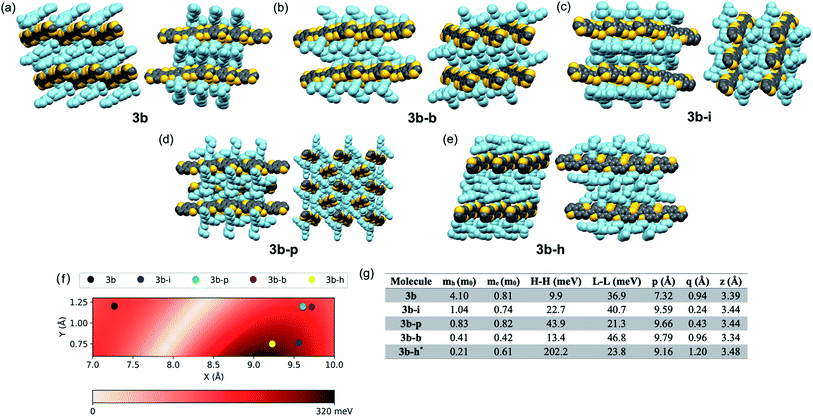
While 3b demonstrated good delocalization of the HOMO, its crystal packing was still not optimized for use in devices where charge transport is the key metric; the trialkylsilyl group required further tuning to optimize crystal packing for the desired application. Due to the large aspect ratio of the molecule, we focused on the synthesis of silyl derivatives containing relatively long alkyl groups, such as tri(iso-butyl)silyl (3b–i), tri(n-butyl)silyl (3b–b), tri(n-pentyl)silyl (3b–p), and tri(n-hexyl)silyl (3b–h). The syntheses simply required addition of the relevant alkynes to 2, followed by coupling of the BDT pendant to the new cores, allowing rapid screening of solid-state order as a function of the size of the trialkylsilyl group. Single crystals were grown and analyzed for all five derivatives. Molecules 3b–b and 3b–i yielded a crystal packing that was in-between the 1D slip-stack and the 2D-brickwork π-stacking motifs,10 with both showing a clear co-facial overlap of π-surfaces in one direction (Fig. 2b and c, left), but with slight geometric overlap in the second direction (Fig. 2b and c, right). The crystal packing of 3b–p showed insulated 1D π-stacks (Fig. 2d). However, 3b–h exhibited exceptional overlap of the π-surfaces in both directions, clearly demonstrating the archetypal 2D-brickwork packing (Fig. 2e). Unfortunately, full structural refinement of crystals of 3b–h was not possible due to extensive disorder of both the backbone and side chains, and as such the solved but unrefined structure is presented here strictly to demonstrate the overall packing motif.Looking more closely at these crystal structures, careful assessment of the occupancies of the sulfur atoms of adjacent BDT units in 3b derivatives revealed that many consist of a mixture of anti and syn conformers in adjacent BDT units. This disorder is unpredictable and varied between derivatives. 3b showed an ∼80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 anti
20 anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) syn relationship whereas 3b–b showed a 96
syn relationship whereas 3b–b showed a 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 anti
4 anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) syn relationship (Fig. 3a). 3b–i was peculiar as its crystal structure revealed the adjacent BDT units exhibited a majority syn relationship (Fig. 3b). The presence of this conformational disorder may present challenges, as the mixture conformations has been related to decreased device performance due to increased disorder59 but could also lead to stronger electronic couplings.60 Unfortunately, with the present system it is not possible to deconvolute the effect that the rotational disorder may have on the material properties, nor to quantify the precise amount of rotational disorder in thin films of the materials. We will report our approach to mitigate this disorder issue in future work.
syn relationship (Fig. 3a). 3b–i was peculiar as its crystal structure revealed the adjacent BDT units exhibited a majority syn relationship (Fig. 3b). The presence of this conformational disorder may present challenges, as the mixture conformations has been related to decreased device performance due to increased disorder59 but could also lead to stronger electronic couplings.60 Unfortunately, with the present system it is not possible to deconvolute the effect that the rotational disorder may have on the material properties, nor to quantify the precise amount of rotational disorder in thin films of the materials. We will report our approach to mitigate this disorder issue in future work.
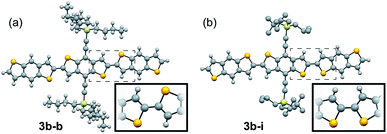 | ||
| Fig. 3 Ball and stick representation of the major conformers of 3b–b, anti, (a) and 3b–i, syn, (b) as determined from their respective crystal structures. Inset shows relevant atom positions. | ||
Computational assessment of electronic couplings
Intermolecular electronic couplings among the frontier MOs were calculated at the ωB97X-D/Def2SVP level of theory based on dimers extracted from the molecular crystals. The largest electronic couplings are shown in Fig. 2f, along with the carrier effective masses calculated based on parabolic approximation from the electronic band structure determined by periodic DFT calculations, as shown in Fig. S10 and S11 (see ESI for computational details†). While the transport properties largely depend on the crystal packing arrangements, it is worth noting that intermolecular slip could have a non-trivial effect on electronic couplings – i.e., electron–phonon couplings could play an important role in charge-carrier transport. To give a qualitative description of this effect, we calculated the HOMO–HOMO electronic coupling as a function of relative in-plane slip within a dimer model. After optimizing the geometry of the 3b core where the side chains are trimmed down to alkynyl groups, we built the dimer model with a set of slips defined by the long and short molecular axes and the intermolecular axis of the dimer. The HOMO–HOMO electronic coupling is plotted against varying long/short axis slips while the intermolecular distance is fixed at 3.4 Å, as shown in Fig. 2f. From this analysis, it is clear that there are regions with very small or large electronic couplings, as expected.60,61 In our crystals, the displacements of 3b–h put this derivative near the region featuring the largest electronic couplings. We note the effect of side chain trimming seems to be negligible as the difference in HOMO–HOMO electronic coupling between trimmed/untrimmed dimers of 3b–i is calculated as less than 3 meV. On the other hand, the electronic couplings of 3b derivatives extracted from Fig. 2f and g are generally larger than those from dimer models built from experimentally determined crystal structures, which implies the importance of nuances in atomic positions. In 3b–h, the HOMO–HOMO coupling reaches more than 200 meV, and the hole effective mass is only 0.21m0, making it a prime candidate for device evaluation. While a small electronic coupling in the dimer model is typically related to heavy carriers, in 3b–b the hole effective mass is rather small, suggesting some limitation in approximating the crystal electronic structure with isolated dimer models, and it too may be a strong candidate for device evaluation. Notably, the electronic couplings are sensitive to even sub-Å slips of these large backbones; for instance, the HOMO–HOMO couplings in 3b–b and 3b–h are quite different even though the slips are similar. This result points to the potential further limitation of evaluating these systems with such a static (e.g. single-point calculation) representation, and that non-local electron–phonon couplings could play an important role in these systems.62,63Device performance of computationally selected derivatives
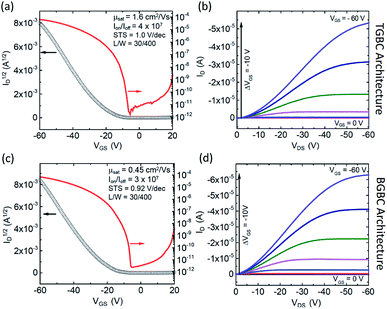
Using the information gleaned from the electronic structure calculations, compounds 3b–b and 3b–h were selected and evaluated for their performance in organic field-effect transistors. Details on device fabrication can be found in the ESI.† Devices of 3b–b and 3b–h were fabricated using an aligned drop-cast method,64 and exhibited average hole mobilities of 0.15 ± 0.04 cm2 V−1 s−1 and 0.7 ± 0.3 cm2 V−1 s−1, with maximum mobilities of 0.21 cm2 V−1 s−1 and 1.52 cm2 V−1 s−1, respectively (Fig. S6†). Devices fabricated from 3b–h also demonstrated low threshold voltages, (1 ± 5 V) and subthreshold swings of 1.5 ± 0.5 V dec−1.Since compound 3b–h showed the most encouraging performance in OFETs, along with the highest calculated electronic couplings, we further explored performance in devices with different architectures. Bottom-gate, bottom contact (BGBC) OFETs were fabricated by spin coating the organic semiconductor over a Si/SiO2 substrate with pentafluoro benzenethiol (PFBT)-treated gold source and drain electrodes. Standard procedures were adopted to characterize and analyze these transistors.65 Measurements performed under N2 on 45 devices yielded a maximum mobility of 0.45 cm2 V−1 s−1 and an average of 0.23 ± 0.07 cm2 V−1 s−1 in this configuration. The mobility histogram and the current–voltage characteristics of the best performing device are included in Fig. S7†, 4c and d, respectively. These devices typically exhibit large on/off current ratios (106–107) and sharp turn on (subthreshold swings around 1 V dec−1), however the threshold voltage is relatively large and negative (−20 to −30 V) suggesting that this material interacts strongly with traps at the interface with the SiO2 dielectric.66 Since co-planar contacts typically produce large contact resistance and SiO2 creates significant scattering at the semiconductor/dielectric interface,65,67,68 we incorporated the same compound in OFETs with a top-gate bottom contact (TGBC) architecture,69 employing parylene as the top-gate dielectric. These OFETs provided mobilities as high as 1.6 cm2 V−1 s−1 (Fig. 4a and b) with an average of 0.7 ± 0.3 cm2 V−1 s−1 obtained on 34 devices.
The curvature of the current–voltage curves at low VDS (Fig. 4b and d) present in both architectures is a typical signature of high contact resistance, suggesting that the mobility in these devices is limited by charge injection. Such injection barriers may be attributed to a number of different variables, including an energetic barrier to hole injection, local microstructural differences near the electrode that impede charge transport from the contact to the accumulation layer, dipoles formed at the semiconductor/electrode interface, or tunnelling resistance of the PFBT layer.70 To further assess this issue, we measured the ionization energies of both 3b–b and 3b–h using ultraviolet photoelectron spectroscopy, yielding values between 5.2 and 5.3 eV (Fig. S12 and S13†). Device performance could thus likely be further enhanced by improving the contacts.
GIXD evaluation of thin-film structure
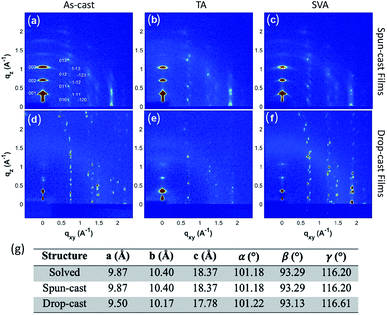
To fully characterize the structures accessed in thin-films of 3b–h, and explore the possibility of thin-film polymorphism in these materials, grazing incidence X-ray diffraction (GIXD) was employed on both the aligned drop-cast films64 and spin-cast films. The as-cast films were also subjected to post-deposition thermal annealing (TA) and solvent vapor annealing (SVA)71 to assess polymorphic stability, as these techniques have demonstrated the ability to induce polymorphic transformations in organic small molecules.72–743b–h is crystalline as-deposited by both spin-casting (Fig. 5a) and aligned drop-casting (Fig. 5d). This is notably different from other trialkylsilyl functionalized organic semiconductors, such as TIPS-pentacene, which are amorphous upon spin-coating. The spin-cast film accesses the known crystal structure with the (001) plane parallel to the substrate; however, the dropcast film adopts a slightly shifted structure from the solved bulk crystal structure (Fig. 5g), possibly explaining why the drop-cast devices show inferior transfer characteristics compared to spin-cast devices. Both spin- and drop-cast films are unaffected by post-deposition processing through either SVA or TA (Fig. 5b, c, e and f, respectively). The lack of polymorphic transformation as a result of post-deposition processing is supported by the presence of short interlayer contacts observed in the crystal structure, which have been shown to screen for kinetically stable polymorphs in organic molecular solids.75
Conclusions
We presented a robust and simple strategy for inducing π-stacking in aromatic chromophores by using a universal aromatic core molecule containing a trialkylsilylethynyl group to tune crystal packing, to which one can attach a wide variety of π-conjugated pendants. Each pendant screened here yielded soluble, easily crystallized derivatives that adopted planar, π-stacked arrays in the solid state. Selecting the BDT pendant to demonstrate optimization of crystal packing for OFET applications, simple manipulation of the trialkylsilyl group afforded a champion material, 3b–h, which exhibited hole mobility as high as 1.6 cm2 V−1 s−1. As π-stacking was observed in all derivatives, careful choice of pendant group may allow this strategy to be applied beyond OFET materials, as molecules with more localized orbitals, like those observed in 3d and 3e, could ostensibly be used for photonic applications76 by undertaking crystal engineering efforts to specifically optimize the crystal packing or aggregation for the desired application.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
The work was supported by the National Science Foundation Designing Materials to Revolutionize and Engineer our Future (NSF DMREF) program under Awards 1627428 (UKY), 1627453 (Princeton) and 1627925 (WFU). Supercomputing resources on the Lipscomb High Performance Computing Cluster were provided by the University of Kentucky Information Technology Department and Center for Computational Sciences (CCS). Crystallography was supported by NSF-MRI awards CHE-0319176 and CHE-1625732.Notes and references
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- K. Biradha and R. Santra, Chem. Soc. Rev., 2013, 42, 950–967 RSC.
- V. Ramamurthy and K. Venkatesan, Chem. Rev., 1987, 87, 433–481 CrossRef CAS.
- Q. Chu, A. J. E. Duncan, G. S. Papaefstathiou, T. D. Hamilton, M. B. J. Atkinson, S. V. S. Mariappan and L. R. MacGillivray, J. Am. Chem. Soc., 2018, 140, 4940–4944 CrossRef CAS PubMed.
- C. M. Reddy, G. R. Krishna and S. Ghosh, CrystEngComm, 2010, 12, 2296–2314 RSC.
- H. Inokuchi, G. Saito, P. Wu, K. Seki, T. B. Tang, T. Mori, K. Imaeda, T. Enoki, Y. Higuchi and K. Inaka, Chem. Lett., 1986, 15, 1263–1266 CrossRef.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483 CrossRef CAS PubMed.
- J. E. Anthony and A. G. Jones, in Organic Electronics II – an Industrial Perspective, ed. H. Klauk, Wiley-VCH, Berlin, 2012 Search PubMed.
- J. E. Anthony, D. L. Eaton and S. R. Parkin, Org. Lett., 2002, 4, 15–18 CrossRef CAS PubMed.
- D. Chun, Y. Cheng and F. Wudl, Angew. Chem., 2008, 120, 8508–8513 CrossRef.
- M. L. Tang, A. D. Reichardt, P. Wei and Z. Bao, J. Am. Chem. Soc., 2009, 131, 5264–5273 CrossRef CAS PubMed.
- X. Zhang, X. Jiang, J. Luo, C. Chi, H. Chen and J. Wu, Chem.–Eur. J., 2009, 16, 464–468 CrossRef PubMed.
- D. Lehnherr, H. Murray Adrian, R. McDonald and R. Tykwinski Rik, Angew. Chem., 2010, 122, 6326–6330 CrossRef.
- V. S. Barlier, C. W. Schlenker, S. W. Chin and M. E. Thompson, Chem. Commun., 2011, 47, 3754–3756 RSC.
- R. Bula, M. Fingerle, A. Ruff, B. Speiser, C. Maichle-Mössmer and F. Bettinger Holger, Angew. Chem., Int. Ed., 2013, 52, 11647–11650 CrossRef CAS PubMed.
- M. M. Payne, S. A. Odom, S. R. Parkin and J. E. Anthony, Org. Lett., 2004, 6, 3325–3328 CrossRef CAS PubMed.
- J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- M. L. Tang, A. D. Reichardt, T. Siegrist, S. C. B. Mannsfeld and Z. Bao, Chem. Mater., 2008, 20, 4669–4676 CrossRef CAS.
- D. Lindner Benjamin, U. Engelhart Jens, O. Tverskoy, L. Appleton Anthony, F. Rominger, A. Peters, H.-J. Himmel and H. F. Bunz Uwe, Angew. Chem., Int. Ed., 2011, 50, 8588–8591 CrossRef CAS PubMed.
- D. Lehnherr, R. Hallani, R. McDonald, J. E. Anthony and R. R. Tykwinski, Org. Lett., 2012, 14, 62–65 CrossRef CAS PubMed.
- H. F. Bunz Uwe, U. Engelhart Jens, D. Lindner Benjamin and M. Schaffroth, Angew. Chem., Int. Ed., 2013, 52, 3810–3821 CrossRef CAS PubMed.
- Q. Miao, Adv. Mater., 2014, 26, 5541–5549 CrossRef CAS PubMed.
- U. H. F. Bunz, Acc. Chem. Res., 2015, 48, 1676–1686 CrossRef CAS PubMed.
- Z. Wang, P. Gu, G. Liu, H. Yao, Y. Wu, Y. Li, G. Rakesh, J. Zhu, H. Fu and Q. Zhang, Chem. Commun., 2017, 53, 7772–7775 RSC.
- C. K. Frederickson, B. D. Rose and M. M. Haley, Acc. Chem. Res., 2017, 50, 977–987 CrossRef CAS PubMed.
- B. D. Lindner, F. Paulus, A. L. Appleton, M. Schaffroth, J. U. Engelhart, K. M. Schelkle, O. Tverskoy, F. Rominger, M. Hamburger and U. H. F. Bunz, J. Mater. Chem. C, 2014, 2, 9609–9612 RSC.
- P. Hu and J. Wu, Can. J. Chem., 2016, 95, 223–233 CrossRef.
- R. R. Parkhurst and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 15351–15356 CrossRef CAS PubMed.
- L. Zhang, A. Fonari, Y. Liu, A.-L. M. Hoyt, H. Lee, D. Granger, S. Parkin, T. P. Russell, J. E. Anthony, J.-L. Brédas, V. Coropceanu and A. L. Briseno, J. Am. Chem. Soc., 2014, 136, 9248–9251 CrossRef CAS PubMed.
- X. Cui, J. J. Hoff, J. D. Ji, T. Albers, J. Zhao, W. He, L. Zhu and S. Miao, Inorg. Chim. Acta, 2016, 442, 145–150 CrossRef CAS.
- J. Wei, D. Meng, L. Zhang and Z. Wang, Chem.–Asian J., 2017, 12, 1879–1882 CrossRef CAS PubMed.
- L. Marshall Jonathan, D. Lehnherr, D. Lindner Benjamin and R. Tykwinski Rik, ChemPlusChem, 2017, 82, 967–1001 CrossRef.
- S. K. Park, D. A. Mourey, S. Subramanian, J. E. Anthony and T. N. Jackson, Appl. Phys. Lett., 2008, 93, 043301 CrossRef.
- G. R. Llorente, M.-B. Dufourg-Madec, D. J. Crouch, R. G. Pritchard, S. Ogier and S. G. Yeates, Chem. Commun., 2009, 3059–3061 RSC.
- J. Smith, R. Hamilton, I. McCulloch, N. Stingelin-Stutzmann, M. Heeney, D. D. C. Bradley and T. D. Anthopoulos, J. Mater. Chem., 2010, 20, 2562–2574 RSC.
- G. Giri, E. Verploegen, S. C. B. Mannsfeld, S. Atahan-Evrenk, D. H. Kim, S. Y. Lee, H. A. Becerril, A. Aspuru-Guzik, M. F. Toney and Z. Bao, Nature, 2011, 480, 504 CrossRef CAS PubMed.
- M. R. Niazi, R. Li, E. Qiang Li, A. R. Kirmani, M. Abdelsamie, Q. Wang, W. Pan, M. M. Payne, J. E. Anthony, D.-M. Smilgies, S. T. Thoroddsen, E. P. Giannelis and A. Amassian, Nat. Commun., 2015, 6, 8598 CrossRef CAS PubMed.
- M. T. Lloyd, A. C. Mayer, S. Subramanian, D. A. Mourey, D. J. Herman, A. V. Bapat, J. E. Anthony and G. G. Malliaras, J. Am. Chem. Soc., 2007, 129, 9144–9149 CrossRef CAS PubMed.
- K. N. Winzenberg, P. Kemppinen, G. Fanchini, M. Bown, G. E. Collis, C. M. Forsyth, K. Hegedus, T. B. Singh and S. E. Watkins, Chem. Mater., 2009, 21, 5701–5703 CrossRef CAS.
- D. S. Chung, J. W. Park, W. M. Yun, H. Cha, Y.-H. Kim, S.-K. Kwon and C. E. Park, ChemSusChem, 2010, 3, 742–748 CrossRef CAS PubMed.
- Z. Li, Y.-F. Lim, J. B. Kim, S. R. Parkin, Y.-L. Loo, G. G. Malliaras and J. E. Anthony, Chem. Commun., 2011, 47, 7617–7619 RSC.
- Y. Shu, Y.-F. Lim, Z. Li, B. Purushothaman, R. Hallani, J. E. Kim, S. R. Parkin, G. G. Malliaras and J. E. Anthony, Chem. Sci., 2011, 2, 363–368 RSC.
- L. Zhang, B. Walker, F. Liu, N. S. Colella, S. C. B. Mannsfeld, J. J. Watkins, T.-Q. Nguyen and A. L. Briseno, J. Mater. Chem., 2012, 22, 4266–4268 RSC.
- N. M. Pinkerton, C. Frongia, V. Lobjois, B. K. Wilson, M. J. Bruzek, R. K. Prud'homme, J. Anthony, F. Bolze and S. Chassaing, RSC Adv., 2016, 6, 65770–65774 RSC.
- M. A. Wolak, J. Delcamp, C. A. Landis, P. A. Lane, J. Anthony and Z. Kafafi, Adv. Funct. Mater., 2006, 16, 1943–1949 CrossRef CAS.
- M. Ganschow, S. Koser, S. Hahn, F. Rominger, J. Freudenberg and H. F. Bunz Uwe, Chem.–Eur. J., 2017, 23, 4415–4421 CrossRef CAS PubMed.
- L. Feng, W. Tang, J. Zhao, R. Yang, W. Hu, Q. Li, R. Wang and X. Guo, Sci. Rep., 2016, 6, 20671 CrossRef CAS PubMed.
- P.-Y. Gu, Z. Wang and Q. Zhang, J. Mater. Chem. B, 2016, 4, 7060–7074 RSC.
- Y. Seo, H. Lee Jung, E. Anthony John, V. Nguyen Ky, H. Kim Yeon, W. Jang Ho, S. Ko, Y. Cho and H. Lee Wi, Adv. Mater. Interfaces, 2017, 5, 1701399 CrossRef.
- M. Mamada, D. Kumaki, J.-i. Nishida, S. Tokito and Y. Yamashita, ACS Appl. Mater. Interfaces, 2010, 2, 1303–1307 CrossRef CAS PubMed.
- C. Cordovilla, C. Bartolomé, J. M. Martínez-Ilarduya and P. Espinet, ACS Catal., 2015, 5, 3040–3053 CrossRef CAS.
- V. Farina and B. Krishnan, J. Am. Chem. Soc., 1991, 113, 9585–9595 CrossRef CAS.
- Z. Fei, P. Boufflet, S. Wood, J. Wade, J. Moriarty, E. Gann, E. L. Ratcliff, C. R. McNeill, H. Sirringhaus, J.-S. Kim and M. Heeney, J. Am. Chem. Soc., 2015, 137, 6866–6879 CrossRef CAS PubMed.
- M. Bendikov, F. Wudl and D. F. Perepichka, Chem. Rev., 2004, 104, 4891–4946 CrossRef CAS PubMed.
- O. D. Jurchescu, A. Meetsma and T. T. M. Palstra, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 330–334 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. K. Hailey, A. J. Petty II, J. Washbourne, K. J. Thorley, S. R. Parkin, J. E. Anthony and Y.-L. Loo, Adv. Mater., 2017, 29, 1700048 CrossRef PubMed.
- K. J. Thorley and C. Risko, J. Mater. Chem. C, 2016, 4, 4040–4048 RSC.
- J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804 CrossRef PubMed.
- X. Xie, A. Santana-Bonilla and A. Troisi, J. Chem. Theory Comput., 2018, 14, 3752–3762 CrossRef CAS PubMed.
- Z. Tu, Y. Yi, V. Coropceanu and J.-L. Brédas, J. Phys. Chem. C, 2018, 122, 44–49 CrossRef CAS.
- K. Nakayama, Y. Hirose, J. Soeda, M. Yoshizumi, T. Uemura, M. Uno, W. Li, M. J. Kang, M. Yamagishi, Y. Okada, E. Miyazaki, Y. Nakazawa, A. Nakao, K. Takimiya and J. Takeya, Adv. Mater., 2011, 23, 1626–1629 CrossRef CAS PubMed.
- Z. A. Lamport, H. F. Haneef, S. Anand, M. Waldrip and O. D. Jurchescu, J. Appl. Phys., 2018, 124, 071101 CrossRef.
- V. Podzorov, E. Menard, A. Borissov, V. Kiryukhin, J. A. Rogers and M. E. Gershenson, Phys. Rev. Lett., 2004, 93, 086602 CrossRef CAS PubMed.
- P. J. Diemer, Z. A. Lamport, Y. Mei, J. W. Ward, K. P. Goetz, W. Li, M. M. Payne, M. Guthold, J. E. Anthony and O. D. Jurchescu, Appl. Phys. Lett., 2015, 107, 103303 CrossRef.
- Y. Mei, P. J. Diemer, M. R. Niazi, R. K. Hallani, K. Jarolimek, C. S. Day, C. Risko, J. E. Anthony, A. Amassian and O. D. Jurchescu, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E6739 CrossRef CAS PubMed.
- Z. A. Lamport, K. J. Barth, H. Lee, E. Gann, S. Engmann, H. Chen, M. Guthold, I. McCulloch, J. E. Anthony, L. J. Richter, D. M. DeLongchamp and O. D. Jurchescu, Nat. Commun., 2018, 9, 5130 CrossRef PubMed.
- O. Fenwick, C. Van Dyck, K. Murugavel, D. Cornil, F. Reinders, S. Haar, M. Mayor, J. Cornil and P. Samorì, J. Mater. Chem. C, 2015, 3, 3007–3015 RSC.
- A. M. Hiszpanski, S. S. Lee, H. Wang, A. R. Woll, C. Nuckolls and Y.-L. Loo, ACS Nano, 2013, 7, 294–300 CrossRef CAS PubMed.
- G. E. Purdum, N. Yao, A. Woll, T. Gessner, R. T. Weitz and Y.-L. Loo, Adv. Funct. Mater., 2016, 26, 2357–2364 CrossRef CAS.
- A. M. Hiszpanski, A. R. Woll, B. Kim, C. Nuckolls and Y.-L. Loo, Chem. Mater., 2017, 29, 4311–4316 CrossRef CAS.
- A. M. Hiszpanski, C. J. Dsilva, I. G. Kevrekidis and Y.-L. Loo, Chem. Mater., 2018, 30, 3330–3337 CrossRef CAS PubMed.
- G. E. Purdum, N. G. Telesz, K. Jarolimek, S. M. Ryno, T. Gessner, N. C. Davy, A. J. Petty, Y. Zhen, Y. Shu, A. Facchetti, G. E. Collis, W. Hu, C. Wu, J. E. Anthony, R. T. Weitz, C. Risko and Y.-L. Loo, J. Am. Chem. Soc., 2018, 140, 7519–7525 CrossRef CAS PubMed.
- J. Zyss and I. Ledoux, Chem. Rev., 1994, 94, 77–105 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic details, characterization of synthesized materials, absorption spectra, and additional information on computational details and device fabrication. CCDC 1833615–1833619 and 1922871–1922873. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc02930c |
| This journal is © The Royal Society of Chemistry 2019 |