Open Access Article
Open Access ArticleMining predicted crystal structure landscapes with high throughput crystallisation: old molecules, new insights†
Peng
Cui
a,
David P.
McMahon
b,
Peter R.
Spackman
bc,
Ben M.
Alston
ac,
Marc A.
Little
 a,
Graeme M.
Day
a,
Graeme M.
Day
 *b and
Andrew I.
Cooper
*b and
Andrew I.
Cooper
 *ac
*ac
aDepartment of Chemistry and Materials Innovation Factory, University of Liverpool, Liverpool, L7 3NY, UK. E-mail: aicooper@liverpool.ac.uk
bComputational Systems Chemistry, School of Chemistry, University of Southampton, SO17 1BJ, UK. E-mail: g.m.day@soton.ac.uk
cLeverhulme Research Centre for Functional Materials Design, Department of Chemistry and Materials Innovation Factory, University of Liverpool, Liverpool, L7 3NY, UK
First published on 17th September 2019
Abstract
Organic molecules tend to close pack to form dense structures when they are crystallised from organic solvents. Porous molecular crystals defy this rule: they contain open space, which is typically stabilised by inclusion of solvent in the interconnected pores during crystallisation. The design and discovery of such structures is often challenging and time consuming, in part because it is difficult to predict solvent effects on crystal form stability. Here, we combine crystal structure prediction (CSP) with a robotic crystallisation screen to accelerate the discovery of stable hydrogen-bonded frameworks. We exemplify this strategy by finding new phases of two well-studied molecules in a computationally targeted way. Specifically, we find a new ‘hidden’ porous polymorph of trimesic acid, δ-TMA, that has a guest-free hexagonal pore structure, as well as three new solvent-stabilized diamondoid frameworks of adamantane-1,3,5,7-tetracarboxylic acid (ADTA). Beyond porous solids, this hybrid computational–experimental approach could be applied to a wide range of materials problems, such as organic electronics and drug formulation.
Introduction
Organic crystalline solids are useful in many applications, such as organic semiconductors,1,2 in pharmaceutical formulations,3 and for molecular separations using porous crystals.4,5 To achieve the optimum functionality for a given application, we must be able to produce crystal structures with specific packings of the molecular building blocks. This is because different polymorphs are known to have different bulk material properties.6 For example, porous molecular organic crystals are known to have polymorph-dependent gas adsorption properties, and this has been used to modulate gas selectivity.7,8 Control over the crystallisation of organic molecules is a long-standing problem, and the field of ‘crystal engineering’9–11 predates developments in bonded frameworks such as metal organic frameworks (MOFs)12–14 and covalent organic frameworks (COFs).15,16 Indeed, the huge success of MOFs and COFs can be explained by the structural predictability that ensues when the less directional and weaker non-covalent interactions in molecular crystals are replaced by stronger, more directional metal–organic bonding and covalent bonding in framework materials. There are reasons, however, to consider non-bonded crystalline molecular frameworks for certain applications: for example, it has proved challenging to produce large, high-quality single crystals for MOFs17 and COFs,18–20 whereas high-quality organic crystals are often more accessible. By contrast, in the specific case of porous molecular crystals, preservation of this crystallinity upon desolvation may be more challenging. Further, molecular crystals can change their structure in response to guest inclusion, and this has led to applications in porosity “switching”7,8 and in the separation of organic hydrocarbons.21–23It remains difficult, however, to predict how a candidate molecule will crystallise and, hence, to design new function: in this regard, molecular crystals are at a disadvantage with respect to MOFs and COFs. To tackle this, we have used crystal structure prediction (CSP)24–27 to guide the discovery of molecular crystals with porous host structures.28,29 In a recent study, calculated energy-structure-function maps29,30 were used to pre-screen the probable function of molecules in silico prior to experiment; in this case, for porosity, methane storage capacity, and guest molecule selectivity. This led to the discovery of hydrogen bonded organic frameworks (HOFs) based on rigid triptycene benzimidazalones with unprecedentedly low bulk densities (0.41 g cm−3) and apparent Brunauer–Emmett–Teller surface area (SABET) as high as 3230 m2 g−1.29 The experimental porous crystal structures were found to correspond to low density, stable regions, or ‘spikes’ on the energy-density representation of the predicted crystal energy landscape. We proposed that such features might be used to predict the formation of other porous HOFs in the future.
HOFs31–35 are a sub-class of porous solids whose structures are driven by hydrogen bonding, which is typically weaker than the directional coordination bonding in MOFs.36 Hence, assumptions about crystal packing based on intuitive ‘rules’ are more prone to fail.37–39 For example, even though the hydrogen bonding in the benzimidazalone molecules that we studied29 is particularly strong and directional, there are at least four competing porous polymorphs that are all defined by 1-dimensional hydrogen-bonded tapes. There is no single dominant porous form, and although all four porous polymorphs can be identified as low-energy structures on the CSP landscape, the specific polymorph that is produced by experiment is influenced by the choice of crystallisation solvent.
More generally, hydrogen bonding has been used to control the supramolecular assembly of a huge range of organic building blocks,40 most commonly using carboxylic acid groups. The study of hydrogen bonded nets can be traced back to 1969, when Duchamp et al.41 reported the ‘α-polymorph’ of trimesic acid (TMA; Fig. 1a), which comprises triply interlocked pleated hexagonal networks of TMA molecules. Seventeen years later, Herbstein reported the first non-catenated hexagonally arranged networks of TMA, which were stabilized in an offset arrangement by disordered alkane guests.42 Herbstein also showed that TMA can be crystallised from the vapor, by condensation onto a cold surface, to produce a γ-polymorph,43 which was recently shown to adsorb acetic acid reversibly after activation.44 Zaworotko reported a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 TMA
1 TMA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetic acid solvate, which features triply inclined interpenetration between truncated 1D and hexagonal 2D nets.45 The 2-D ordering of TMA on metal surfaces has also been investigated,46 and TMA is an archetypal ligand for MOF synthesis (e.g., HKUST-1).47 As such, TMA has been widely studied by the crystal engineering community for decades. The continued fascination with this molecule results from the complexity of its solid form landscape and the large number of competing structures that can be produced.
acetic acid solvate, which features triply inclined interpenetration between truncated 1D and hexagonal 2D nets.45 The 2-D ordering of TMA on metal surfaces has also been investigated,46 and TMA is an archetypal ligand for MOF synthesis (e.g., HKUST-1).47 As such, TMA has been widely studied by the crystal engineering community for decades. The continued fascination with this molecule results from the complexity of its solid form landscape and the large number of competing structures that can be produced.
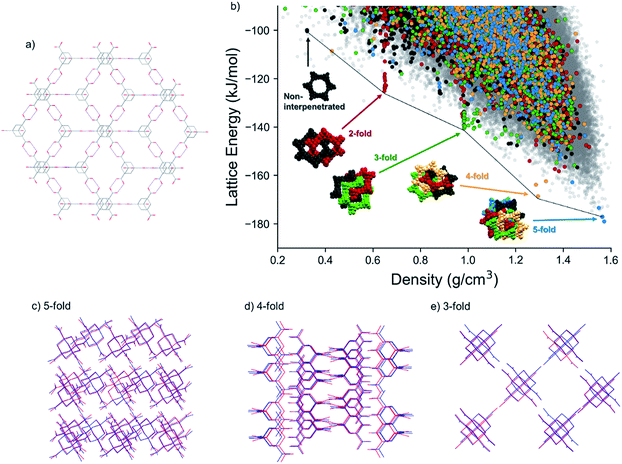
A second archetypal example is adamantane-1,3,5,7-tetracarboxylic acid (ADTA, Fig. 1b), which was reported in 1988 by Ermer to form a 5-fold interpenetrated diamondoid hydrogen-bonded net.48 Broadly speaking, the molecular assembly followed the intuitive design rules; that is, the tetrahedral node led to a 3-D diamondoid net. However the 5-fold interpenetration could (presumably) not have been predicted a priori, although an analysis of crystal density did show that a 5-fold form matched experiment (1.65 g cm−3), while a hypothetical non-interpenetrated diamondoid net was suggested to have a density of just 0.336 g cm−3.10,48 To modulate the interpenetration, Ermer later functionalized the adamantane core with dioxo or dimethylidene groups to sterically direct the formation of 3-fold and 2-fold interpenetrated networks, respectively.49
In this study, we use CSP calculations to uncover the underlying structural landscapes for carboxylic acid-bearing molecules, using the classic TMA and ADTA systems as examples. These molecules were studied as part of wider computational screening for latent porous structures within the predicted crystal structures of small molecules. CSP highlighted TMA as an attractive target for further crystallisation experiments. These molecules introduce a new challenge: unlike the triptycene benzimidazalones in our previous study,29 which can be considered as rigid molecules with a single conformation, the carboxylic acids in TMA and ADTA can adopt different possible conformations that must be accounted for in the CSP search.
While CSP can provide valuable insights into a molecule's structural preferences, we are not yet able to account for the effect of crystallisation solvent in a computationally affordable way.24–27,50 This is a particularly acute problem when searching for porous molecular crystals, where solvent stabilization increases the energetic range of possible structures on the lattice energy landscape, sometimes up to thousands of candidates. As such, experimental crystallisation screens are needed to identify the conditions needed to access interesting predicted structures in the laboratory. High throughput crystallisation screening has previously been used to explore the solid form diversity of active pharmaceutical ingredient.51,52 In this study, we develop a high-throughput robotic crystallisation screening protocol to search for polymorphs of interest that are predicted by CSP.
Results and discussion
Crystal structure prediction – TMA
The energy-density distribution of predicted TMA crystal structures is shown in Fig. 2a (further information about the CSP methodology is provided in the Experimental section). The expense of searching the crystal packing space with multiple independent, conformationally flexible molecules in the asymmetric unit limited us to predicting crystal structures with 1 and 2 molecules in the asymmetric unit (Z′ = 1 and 2). Hence, our landscape of predicted structures does not contain the known Z′ = 6 α-TMA,43,44 nor the Z′ = 3 γ-TMA structures.42 For comparison to the CSP structures, the energies of α- and γ-TMA were calculated from ordered approximations of their high-Z′ disordered structures (see Fig. 2a). Approximations in the treatment of disorder and of the conformational strain in these structures means that these models will be less stable than the true α and γ polymorphs. Still, their energies are within 7.7 (α) and 8.2 (γ) kJ mol−1 of the CSP global minimum, which is within the usual energetic range of polymorphism,53 and lie on the low energy edge of the energy-density distribution, where observed structures are often found. Furthermore, we find hexagonal networks of hydrogen bonding, as seen in α-TMA and γ-TMA, across the crystal structure landscape; predicted crystal structures containing this motif are shown as orange points (Z′ = 1) and red points (Z′ = 2) in Fig. 2a.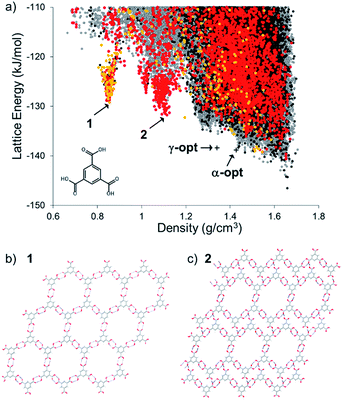 | ||
| Fig. 2 (a) CSP map for TMA (Z′ = 1 black, Z′ = 2 grey) with structures containing hexagonal hydrogen bonded sheets colored orange (Z′ = 1) and red (Z′ = 2). Energies and densities of the optimised versions of the known α and γ polymorphs are indicated by crosses (see text and ESI† for details); (b) hypothetical porous structure corresponding to the energy-density spike minimum structure, 1, at 0.855 g cm−3, and; (c) the spike minimum energy structure, 2, at 1.11 g cm−3. | ||
The CSP results show the usual overall trend towards higher lattice energies at lower crystal density. However, we observe two clear low-energy ‘spikes’ of unusually stable, low density structures in the density regions around ∼0.8 and 1.1 g cm−3, significantly below the densities of the known α (ρ = 1.44 g cm−3) and γ (ρ = 1.34 g cm−3) forms. The minimum of the lower density spike, whose structure, 1, is shown in Fig. 2b, has a density of 0.85 g cm−3 and an energy 17.3 kJ mol−1 above the global minimum predicted structure, while the minimum of the higher density spike, 2, shown in Fig. 2c, is 14.8 kJ mol−1 above the global minimum. These ‘spike’ features are reminiscent of the low-energy, low-density spikes corresponding to isolable porous structures on the crystal structure landscape of triptycenetrisbenzimidazolone.29 The shape of the energy-density distribution suggests that these sets of crystal structures occupy deep, low energy regions of the lattice energy surface separated from the region of densely-packed structures by a large energy barrier. Moreover, the predicted lattice energies for 1 and 2 are both within 20 kJ mol−1 of the predicted global minimum structure. Given that we previously isolated polymorphs of triptycene benzimidazalone molecules that were predicted to be 49.6 kJ mol−1 above the global minimum but stabilized by crystallisation solvent,29 this gave us confidence that 1 and 2 might be accessible by experiment.
The lowest energy crystal structure (1) in the 0.85 g cm−3 spike features hexagonal arranged networks of hydrogen bonded TMA molecules, as in α- and γ-TMA. Importantly, these hexagonal nets are planar and aligned in the crystal structure, in contrast to previously reported TMA solvate structures42 that feature offset arrangements of hexagonal TMA nets. Other low energy structures in this spike are very similar, but differ in conformation of TMA within the hexagonal sheets, distortion of the hexagonal pores or breaking of the hydrogen bonded hexagons to form hydrogen bond interactions between layers of TMA. Hexagonal pores in the 1.1 g cm−3 predicted structure, 2, are collapsed in one direction of the hydrogen bonded sheets (Fig. 2c), forming a structure that is intermediate between the open hexagonal sheets and the ‘flower’ TMA monolayers sometimes seen at liquid–substrate interfaces.54,55 As in predicted structure 1, the remaining hexagonal pores in 2 are aligned, forming open channels.
Neither of the low-energy structures in these pronounced spikes on the CSP landscapes corresponds to a previously reported crystal structure of TMA. Thus, these predicted crystal structures and their expected stability provided a strong impetus to re-examine the crystallisation behaviour of TMA, for which we developed a HT crystallisation screen.
Crystallisation screen – TMA
For the HT crystallisation screen with TMA, we screened 224 ‘good–bad’ solvent combinations and 56 ‘good–good’ solvent combinations (where, ‘good solvents’ dissolved TMA at concentration of ≥15 mg mL−1 at RT, and ‘bad solvents’ dissolved TMA at concentration of <15 mg mL−1 at RT). Hence, we screened a total of 280 crystallisation conditions using a Chemspeed robot platform. After evaporation of the ‘good solvents’ at room temperature, as well as all or part of the ‘bad solvents’, we collected the crystalline products and recorded PXRD data after drying the samples in air. Using a library of simulated PXRD patterns for previously reported TMA crystal structures obtained from the Cambridge Structure Database (CSD) and the literature (see ESI, Table S3†), we identified six potential ‘hits’ (see ESI, Fig. S5†), which produced structures that appeared to be unknown. We determined all six structures using single crystal X-ray diffraction (Table 1, see ESI, Tables S5 and S6† for full refinement details); as a result of the hexagonal layered packing of the TMA molecules in these six solvates, we observed a close similarity between the simulated PXRD pattern of the a priori predicted low-density polymorph, 1 (Fig. 2b), and the experimental PXRD patterns (see ESI, Fig. S5†). This shows that CSP, coupled with HT crystallisation screening, can identify new forms of ‘old’, well-studied molecules in a targeted way.| Structure codea | Good solventb | Bad solventc | Space group |
|---|---|---|---|
| a Structure codes correspond to crystallisation solvents numbers listed in ESI, Table S2. The structures with hexagonal layered packing of TMA molecules are: 2-33, 3-31, 3-36, 7-35, 8-32, and 8-35. Both 4-18 and 6-18 are non-hexagonal forms that show hydrogen bonding to the crystallisation solvent. b Solvents that dissolved TMA at concertation ≥15 mg mL−1 at RT. c Solvents that dissolved TMA at concentration <15 mg mL−1 at RT. | |||
| TMA_2-33 | THF | n-Butylbenzene | P3121 |
| TMA_3-31 | EtOH | Cyclohexanone | C2/c |
| TMA_3-36 | EtOH | Ph2O |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| TMA_4-18 | 2-Propanol | EtOAc | C2/c |
| TMA_6-18 | 1-Propanol | EtOAc |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| TMA_7-35 | 1,4-Dioxane | 1,3-Dimethoxybenzene | C2/m |
| TMA_8-32 | 1-Butanol | Mesitylene | P3221 |
| TMA_8-35 | 1-Butanol | 1,3-Dimethoxybenzene | C2/m |
The need for HT methods is clear: only 6/280 (∼2%) of the experimental conditions trialled gave a crystalline form with a PXRD pattern that was similar to that of the predicted structure, 1. The vast majority of crystallisation conditions led to either direct crystallisation to the known α-polymorph or produced an unstable, transient phase that transformed into the α-polymorph upon loading onto the PXRD plate. This explains why δ-TMA has remained hidden for 50 years.41
We also identified two other structures in this HT screen, crystallised from 2-propanol/EtOAc and 1-propanol/EtOAc (TMA_4-18 and TMA_6-18, Table 1), which feature hydrogen bonds between the TMA molecules and hydroxyl groups in the solvent molecules; these structures are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates (see ESI, Table S7†).
1 solvates (see ESI, Table S7†).
We next focused on determining the properties of the six new hexagonally-packed TMA phases in more detail.
For the hexagonally packed TMA structures, we observed differences in the crystallographic symmetry due to the stacking geometry of the hexagonal TMA networks. Among these structures, we found a close structural match, based on comparable simulated and experimental PXRD patterns, between the predicted low-density polymorph, 1 (Fig. 2b), and the two solvates; 1,4-dioxane/1,3-dimethoxybenzene (TMA_7-35) and 1-butanol/1,3-dimethoxybenzene (TMA_8-35) (see ESI, Fig. S5†). Hence, even though solvent affects the packing of TMA molecules in these structures, we could identify crystal structures that closely match the predicted low-density polymorph, 1 (Fig. 2b).
To investigate the stability of the hexagonally packed TMA structures (TMA_2-33, 3-31, 3-36, 7-35, 8-32, and 8-35) in the absence of the crystallisation solvent, we exchanged the solvent in the pores with the n-pentane and then activated the crystals by evacuating at room temperature for 2 hours. PXRD analysis showed that all six of the resulting n-pentane solvates transformed to the same phase after activation.
The experimental PXRD pattern of the resulting, activated material was compared to the simulated patterns of the full set of predicted crystal structures using constrained dynamic time-warping (see ESI† for details), which highlights a high similarity of the activated material to the predicted structures in the 0.8 g cm−3 spike on the CSP energy-density map (Fig. 3a). Visual comparison shows that all of the evacuated samples match the simulated PXRD pattern of the predicted polymorph, 1 (Fig. 3b; ESI, Fig. S6–S11†). These results show the potential for automated matching of materials from HT crystallisation screens against databases of predicted structures, which could rapidly identify likely structures of new materials.
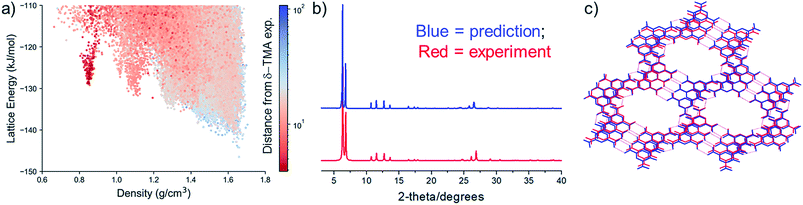 | ||
| Fig. 3 (a) Computed similarity in PXRD patterns of activated δ-TMA against all CSP structures of TMA, using constrained dynamic time-warping (see ESI† for details). Similarity is plotted on a logarithmic scale, where the most similar PXRD patterns correspond to dark red shaded points; (b) comparison between predicted and experimental δ-TMA PXRD patterns (the predicted structure is TMA structure 1 (Fig. 2b)); (c) overlay of the predicted (blue) and the experimental (red) δ-TMA structures. The experimental structure was derived from solvent exchange followed by activation of TMA_2-33. | ||
We next studied the transformation and activation in more detail using the THF/n-butylbenzene solvate (TMA_2-33). After complete exchange of the crystallisation solvent with n-pentane, which was determined using 1H NMR (see ESI, Fig. S12†), we used thermogravimetric analysis (TGA) to determine the n-pentane solvent evaporation rate from the crystal pores at room temperature (see ESI, Fig. S13†). Using single crystal XRD, we showed that the pentane-solvated TMA_2-33 structure undergoes a single-crystal to single-crystal transformation to a solvent free form, δ-TMA (Table 2, see ESI, Table S7 and Fig. S14, S15†). The crystal packing of TMA molecules in the single crystal structure of δ-TMA are in excellent agreement with the predicted low density packing in 1, not only in the hexagonal packing on TMA molecules, but also in the stacking of these sheets. The structural similarity was assessed using an overlay of atomic positions of the predicted and single crystal structures within a cluster of molecules taken from each structure, using the COMPACK algorithm; this yielded an RMSD of 0.345 Å for a 20-molecule comparison. Unit cells are compared in Table 2 and an overlay of predicted and single crystal structures is shown in Fig. 3c.
| Space group | a/Å | b/Å | c/Å | β/° | V/Å3 | |
|---|---|---|---|---|---|---|
| Pred. | C2/m | 26.27 | 16.92 | 3.72 | 93.87 | 1651.8 |
| Expt. | C2/m | 26.08 | 16.48 | 3.68 | 95.08 | 1573.3 |
From experimental PXRD patterns, we found that δ-TMA was thermally stable up to 110 °C (see ESI, Fig. S16†). In addition, δ-TMA is porous to nitrogen and has a SABET of 910 m2 g−1 at 77.3 K (see ESI, Fig. S17†). However, the PXRD pattern recorded after gas sorption analysis indicated that there was a small amount of the non-porous α-TMA polymorph in the sample (see ESI, Fig. S18†). Investigating this further, we found that δ-TMA transforms to α-TMA at 130 °C (see ESI, Fig. S16 and S19†), after 6 hours under dynamic vacuum at room temperature (see ESI, Fig. S20†), or after standing in humid air after activation (see ESI, Fig. S21†), indicating that δ-TMA is metastable, as often observed for porous molecular crystals with low densities. This might explain why δ-TMA (1) was not discovered before; conceivably, it might never have been discovered without the guidance provided by CSP. By contrast, we did not find any experimental evidence for predicted form 2; this might be because 1 is more effectively stabilized by solvent,29,50 and hence 2 is not competitive.
Crystal structure prediction – ADTA
Encouraged by our success with δ-TMA, we applied CSP to explore the space of possible crystal structures of ADTA. The known, dense crystal structure of ADTA features double hydrogen bonds at each carboxylic acid group (Fig. 4a) and close packing is achieved via 5-fold interpenetration of the resulting diamondoid networks.A group of predicted crystal structures at the global minimum of the CSP landscape (Fig. 4b) contain this 5-fold interpenetrated diamondoid hydrogen bonding. One of these predicted structures, 5.6 kJ mol−1 above the global minimum, reproduces the known crystal structure accurately (Fig. 4c), with a root mean squared deviation in atomic positions of 0.28 Å within a cluster of 20 molecules taken from the observed and predicted crystal structures (Table 3, Fig. 4c). The low-energy, high density region also contains crystal structures that are not based on the diamondoid hydrogen bonding framework.
| Space group | a/Å | c/Å | V/Å3 | |
|---|---|---|---|---|
| Predicted 5-fold form | I41/a | 7.28 | 22.94 | 1215.3 |
| Experimental 5-fold form (ADTA_3-3) | I41/a | 7.48 | 22.11 | 1235.6 |
| Predicted 4-fold form | I41/a | 16.11 | 23.32 | 6052.3 |
| Experimental 4-fold form (ADTA_2-2) | I41/a | 16.40 | 22.40 | 6024.5 |
| Predicted 3-fold form | I41/amd | 16.48 | 7.76 | 2108.5 |
| Experimental 3-fold form (ADTA_7-38) | I41/amd | 16.43 | 7.36 | 1986.0 |
| Experimental 2-fold form (ADTA_2-34) | I41/a | 16.24 | 22.38 | 5901.7 |
| Experimental 2-fold form (ADTA_2-27) |
Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
14.41 | 14.41 | 1484.4 |
| Experimental 2-fold form (ADTA_2-35) | P42/nnm | 11.43 | 11.43 | 1494.2 |
The same diamondoid hydrogen bonding as found in the known crystal structure, but with lower degrees of interpenetration, is found in many of the other predicted structures towards lower crystal densities and higher lattice energies. Fig. 4b highlights these structures, with different colors indicating the number of unique hydrogen-bond networks interpenetrated within each structure. While most of these structures occur within the bulk of the energy-density distribution of structures, the most stable predicted structures for each degree of interpenetration, from 5-fold (ρ = 1.57 g cm−3) down to 2-fold (ρ = 0.324 g cm−3) interpenetration, lie just below the low-energy ‘leading edge’ of the energy-density distribution. These structures corresponding to the lowest energy instances of each level of interpenetration are found at approximately equally-spaced intervals of density and they lose, on average, around 20 kJ mol−1 of lattice energy per lost degree of interpenetration of the hydrogen bonding networks (Fig. 4b). The energetic stability of these diamondoid hydrogen-bonded structures relative to other crystal packing arrangements is not as pronounced as the ‘spike’ of structures containing the new δ polymorph, 1, on the TMA landscape (Fig. 2a). However, this double hydrogen bonding motif clearly provides greater stability than any other hypothetical crystal packing of similar density in the cases of 3-fold, 4-fold and 5-fold interpenetration.
Within the nearly-linear energy-density relationship among the lowest energy structures with each degree of interpenetration, the predicted 4-fold interpenetrated structure is particularly stable, being located just 10.4 kJ mol−1 above the global minimum predicted 5-fold interpenetrated structure (and 4.8 kJ mol−1 above the known 5-fold crystal structure). This falls within the usual energetic range of polymorphism in organic crystals,56 and we expected therefore that this structure should be accessible under the right crystallisation condition. A large number of predicted structures with 3-fold interpenetrated diamondoid hydrogen bonded networks are found in the region around 1 g cm−3 (cluster of green points in Fig. 4b). The many possibilities for 3-fold interpenetration, compared to higher and lower degrees of interpenetration, can be rationalized by the number of available permutations for arriving at 3-fold interpenetrated structures by the removal of 2 networks from the 5-fold interpenetrated structure.
A non-interpenetrated diamondoid crystal structure is also found among the predicted structures, along the same roughly linear energy-density relationship as the lowest energy 2-fold, 3-fold, 4-fold and 5-fold interpenetrated forms. This non-interpenetrated structure, 78.6 kJ mol−1 above the global minimum 5-fold network, has a density of 0.324 g cm−3, in excellent agreement with the structure hypothesized by Ermer.48 However, the CSP results show that, at these low densities, there are many energetically preferable structures with similar densities and different hydrogen bonding. The presence of alternative, lower energy structures in this density region suggests that the non-interpenetrated structure is too unstable, so is unlikely to be observed. Moreover, even if it could be formed as a solvated structure, its position on the CSP landscape suggests that it might not occupy a sufficiently deep, isolated energy basin to be kinetically stable as an unsolvated structure.
Crystallisation screen – ADTA
By employing the same HT crystallisation workflow developed for TMA, we screened 192 ‘good–bad’ solvent combinations, and 36 ‘good–good’ solvent combinations for the crystallisation of ADTA (where, ‘good solvents’ dissolved ADTA at concentration of ≥3 mg mL−1 at RT, and ‘bad solvents’ dissolved TMA at concentration of <3 mg mL−1 at RT). Using the predicted 3-, 4-, and 5- fold structures as a reference (Table 3 and Fig. 4) along with experimental X-ray diffraction data (see ESI, Tables S8 and S9†), we found that 5 sets of conditions led to new ADTA crystal forms with 3-fold interpenetrated diamondoid hydrogen bonded networks, 81 conditions led to 4-fold interpenetration, and 77 conditions led to 5-fold interpenetration (Fig. 5; see ESI, Fig. S22†). We also identified 22 crystallisations that appeared to give a phase mixture of 4- and 5-fold interpenetrated structures (Fig. 5). The remaining conditions produced two amorphous samples, and 41 structures that could not be identified as one, or a mixture, of the 3-, 4-, or 5- fold structures by simply comparing PXRD patterns (see ESI, Fig. S23–S28†).We obtained a single crystal structure of the 4-fold interpenetrated form from the THF crystallisation (ADTA_2-2, see ESI, Table S8†). In ADTA·0.25 (THF), there are THF molecules located in extrinsic voids between ADTA molecules, rationalizing the formation of the 4-fold structure from this crystallisation solvent. The arrangement of ADTA molecules in this solvated structure was compared to CSP structures and found to agree very well with the lowest energy 4-fold interpenetrated structure from the CSP calculations: an overlay of 20-molecule clusters gave an RMSD in atomic positions of 0.379 Å, Fig. 4d (unit cell parameters are compared in Table 3). We found that the THF molecules were trapped in the extrinsic cavities, and TGA showed that the THF molecules remained in the crystal lattice until ∼210 °C (see ESI, Fig. S29–S32†). To remove THF solvent from the 4-fold structure, a sample of ADTA_2-2, was heated at 210 °C for 2.5 h, and NMR was used to check for THF in the desolvated sample (see ESI, Fig. S33†). After activation at 210 °C, this material was found to be non-porous to N2 at 77 K. Structural changes in the material were monitored in a subsequent variable temperature PXRD study (see ESI, Fig. S35†), which showed gradual transformation to the 5-fold interpenetrated structure. This transformation was complete at 350 °C.
The 3-fold structure was only clearly observed in the crystallisation screen when tetradecane was used as the ‘bad solvent’ (Fig. 5). We characterized the 3-fold structure using the ethanol/tetradecane (ADTA_3-38) and dioxane/tetradecane (ADTA_7-38) crystallisations. Disordered tetradecane solvent occupies 1-D pores in both of the 3-fold structures, rationalizing their formation with this ‘bad solvent’, but we observed slight differences in crystallographic symmetry for these structures; Fddd for ADTA_3-38 vs. I41/amd for ADTA_7-38 (see ESI, Table S8†). This finding can also be explained by the tetradecane solvent, which appeared to be more ordered in the FdddADTA_3-38 structure, distorting the interpenetrated packing of diamondoid networks. Again, based on comparison of ADTA atomic coordinates in the single crystal and predicted structures, we find good agreement between the ADTA arrangement in the observed structures and the predicted 3-fold interpenetrated structure (Fig. 4e, see also unit cell parameters in Table 3).
The PXRD patterns from the HT crystallisation screen that could not be assigned to 3-, 4-, or 5-fold structures were mostly crystallised using the structurally-related ‘bad solvents’ o-xylene, m-xylene, p-xylene, mesitylene, 1,2-dimethoxybenzene, and 1,3-dimethoxybenzene (ESI, Fig. S23–S28†). We used the THF crystallisations with the following ‘bad solvents’ to determine the X-ray crystal structures for three of these hits: o-xylene (ADTA_2-27), 1,2-dimethoxybenzene (ADTA_2-34), and 1,3-dimethoxybenzene (ADTA_2-35) (see ESI, Table S9†). In the crystal structure of ADTA_2-34 we found ordered 1,2-dimethoxybenzene between ADTA molecules, whereas the aromatic solvents in ADTA_2-27 and ADTA_2-35 were too disordered to model accurately. However, the three structures, ADTA_2-27, ADTA_2-34, and ADTA_2-35 have the same underlying 2-fold interpenetrated structure. The crystallised 2-fold interpenetrated structures that we isolated experimentally did not have exact matches on the crystal structure landscape. In the case of ADTA_2-34, there are two symmetrically inequivalent ADTA molecules in the structure, which was not considered in the CSP search. For the other observed structures with 2-fold interpenetration of hydrogen bond networks, the absence of exact experimental matches can be rationalized by the larger solvent content with respect to the 3-fold and 4-fold structures. Due to weak, non-directional interactions between interpenetrated hydrogen bonded networks, the solvent molecules have an important influence on the relative arrangement of the two hydrogen bonding networks of ADTA molecules that is not considered during CSP, which does not include solvent molecules. To test this, we manually removed the solvent molecules from the ADTA_2-35 structure, replaced the ADTA molecule with the lowest energy conformer used in CSP and lattice energy minimized the resulting structure. The packing in the optimized structure is found in some of the higher energy 2-fold interpenetrated CSP structures, differing mainly in the conformation of ADTA.
To characterize the experimental stability of the 2- and 3-fold structures, we subjected solvated crystals to direct activation under vacuum at 100 °C. We also activated the materials by first exchanging the crystallisation solvent with n-pentane and then evacuating at room temperature. However, we found that the 2-fold and 3-fold structures transformed in the solid state to the 5-fold structure after activation under both conditions (see ESI, Fig. S36–S40†); neither the 2-fold nor 3-fold interpenetrated packing of ADTA have been isolated as solvent-free crystals.
Overall, the experimental results correlate very well with the observations from the ADTA CSP energy landscape: structures with 5-, 4-, 3- and 2- fold interpenetration of diamondoid hydrogen bonding networks all fall along the low energy, leading edge of the energy-density distribution of structures and are all observed experimentally, whereas the non-interpenetrated structure is not in a stable region of the energy landscape and has not been observed. Furthermore, of those levels of interpenetration that are observed, only the 5-fold and 4-fold structures are stable without solvent inclusion. In the case of the 5-fold interpenetrated structure, this is due to close packing of ADTA molecules and this is the overall lowest energy packing mode of the molecule. For the 4-fold interpenetrated structure, the ability to maintain the structure after evacuation of solvent from the pores may relate to the particular stability of this structure on the energy landscape (Fig. 4b).
Conclusions
In summary, while both TMA and ADTA have been studied widely for decades, CSP calculations indicated that there were promising unknown porous crystal structures for both molecules. A number of these predicted phases were subsequently discovered in the laboratory using a HT method to rapidly screen hundreds of different crystallisation conditions. This integrated CSP/experimental screening strategy greatly accelerated the discovery of these new materials: indeed, they would likely have remained undiscovered without this approach. CSP can tell us whether to look and, if so, what to look for: this is a huge advantage over ‘blind screening’ approaches. For context, TMA and ADTA were selected from a broader array of candidate hydrogen-bonding molecules, most of which did not show interesting low-energy porous structures on their structure landscapes. As such, we would not have studied these molecules at all in the laboratory without the computationally-guided expectation that there were new structures to be found.Our hybrid computational/experimental approach allowed us to find new solvated structures for TMA, including the targeted hexagonal crystal packing, 1, and for ADTA, including structures with lower degrees of hydrogen bond network interpenetration that supplement the known 5-fold form. Furthermore, a desolvated porous polymorph of TMA, δ-TMA (SABET = 910 m2 g−1), was found by solvent exchanging one of these structures (TMA_2-33) with pentane. The crystal structure of δ-TMA matched well with the lowest-energy predicted structure from a pronounced ‘spike’ in the CSP landscape. This demonstrates that this combination of computation and HT crystallisation can accelerate discovery for materials with desirable physical properties, such as microporosity.
More generally, the combination of CSP with HT crystallisation screening has the potential to aid the discovery of materials for a wide range of other applications. Indeed, this approach is not limited to porous materials, but could be applied to a wide range of physical properties that are calculable from structure, such as charge transport57 and optoelectronic properties.
Experimental
Crystal structure prediction
Conformers for both TMA and ADTA were generated using the low-mode sampling method58,59 implemented in Schrödinger's Maestro package,60 with energies modelled using the OPLS2005 force field.61 All unique conformers were then re-optimized using density functional theory (DFT), at the B3LYP/6-311G(d,p) level of theory, leading to two conformers for TMA and six for ADTA. These conformers were used as starting points for CSP, which was performed with low discrepancy sampling of crystal packing variables, using the Global Lattice Energy Explorer62 software. Crystal structures were generated using all conformers of both TMA and ADTA in the 25 most common space groups with one molecule in the asymmetric unit, and with two molecules in the asymmetric unit for TMA (in 7 space groups). Crystal structures were lattice energy minimized using the crystal structure modelling software DMACRYS;56 intermolecular interactions within the predicted crystal structures were calculated using the FIT atom–atom force field,63 combined with atomic multipole electrostatics. Total energies were calculated as a sum of the force field intermolecular energy and the dispersion corrected DFT energy of the molecular conformer.Lattice energies of the known TMA polymorphs (α and γ) were calculated using the same force field, using molecular geometries obtained from constrained optimisation of the molecules taken from the experimental structures. The molecular energies, relative to the lowest energy gas phase conformer, were added to the force field calculated intermolecular energy. Due to disorder of carboxylic acid groups in both the α and γ polymorphs, calculations were based on one configuration, chosen to satisfy all expected hydrogen bonds (see ESI† for details).
Full details of the computational methods are provided in the ESI.†
High-throughput crystallisation screen
For the high-throughput (HT) crystallisation screen, we initially screened the solubility of TMA and ADTA in 44 commercially available aliphatic and aromatic solvents (see ESI, Table S1†), by attempting to dissolve TMA (15 mg) or ADTA (3 mg) in 1 mL of each solvent at room temperature. The solvents which dissolved ≥15 mg mL−1 of TMA, or ≥3 mg mL−1 of ADTA, at room temperature, and had boiling points <120 °C, were used as ‘good solvents’ for the crystallisation screens (see ESI, Table S2†). In total, we used 8 ‘good solvents’ for TMA (methanol, THF, ethanol, 2-propanol, tetrahydropyran, 1-propanol, 1,4-dioxane, and 1-butanol) and 6 ‘good solvents’ for ADTA (methanol, THF, ethanol, 2-propanol, 1-propanol, and 1-butanol) to prepare stock solutions of these molecules (15 mg mL−1 for TMA and 3 mg mL−1 for ADTA). The remaining organic solvents that dissolved <15 mg mL−1TMA, or <3 mg mL−1ADTA at room temperature were used as ‘bad solvents’ for the crystallisation screen. In total, we used 28 and 30 ‘bad solvents’ to direct the crystallisation of TMA and ADTA, respectively. Isooctane and tetradecane were not used for the TMA crystallisation screen because TMA solvates have been reported in the literature.42 The crystallisation screens were carried out on a Chemspeed Technologies SWING POWDERDOSE robot using the experimental design shown in the ESI† (Section 2.1.1 for full Experimental details). Using this robot, we could add the ‘bad solvents’ at different rates to create different crystallisation conditions. For the TMA crystallisations reported here, 1 mL of ‘good solvent’ and 1 mL of ‘bad solvent’ was added into each crystallisation vial. For the ADTA crystallisations, 2 mL of ‘good solvent’ and 2 mL of ‘bad solvent’ was added into each vial. After evaporation of the crystallisation solvent at room temperature over several days, the crystalline materials were transferred into HT 96-well PXRD plate with a mylar film base. PXRD patterns were recorded over the 2θ range 2–40, on a PANalytical Empyrean diffractometer (Cu Kα), operating in transmission geometry mode, and equipped with a HT screening XYZ sample stage and PIXcel detector. The PXRD patterns for the screened crystallisation conditions were compared with the simulated PXRD patterns for the predicted crystal structures and previously reported TMA and ADTA crystal structures from the literature (see ESI, Tables S3 and S4†) using PANalytical X'Pert HighScore software package (PW3212). X-ray crystal structures were determined using Rigaku MicroMax-007 HF rotating anode diffractometer (Mo Kα radiation, λ = 0.71073 Å, kappa 4-circle goniometer, Rigaku Saturn724 + detector); or at beamline I19, Diamond Light Source, Didcot, UK using silicon double crystal monochromated synchrotron radiation (λ = 0.6889 Å, Pilatus 2 M detector).Full details of the experimental methods are provided in the ESI.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
For funding, the authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC) (EP/N004884/1), the Leverhulme Trust via the Leverhulme Research Centre for Functional Materials Design and the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013) through grant agreement numbers 321156 (ERC-AG-PE5-ROBOT) and 307358 (ERC-stG-2012-ANGLE). P. C. thanks the China Scholarship Council for a PhD studentship. The authors thank Rob Clowes for assistance running isotherms. The authors acknowledge Diamond Light Source for access to beamlines I19 (MT15777) and I11 (EE17193). We acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton.Notes and references
- J. Ferraris, V. Walatka, J. H. Perlstei and D. O. Cowan, J. Am. Chem. Soc., 1973, 95, 948 CrossRef CAS.
- C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422 RSC.
- N. K. Duggirala, M. L. Perry, O. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640 RSC.
- J. R. Holst, A. Trewin and A. I. Cooper, Nat. Chem., 2010, 2, 915 CrossRef CAS PubMed.
- Y. He, S. Xiang and B. Chen, J. Am. Chem. Soc., 2011, 133, 14570 CrossRef CAS PubMed.
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, Oxford, 2007 Search PubMed.
- J. T. A. Jones, D. Holden, T. Mitra, T. Hasell, D. J. Adams, K. E. Jelfs, A. Trewin, D. J. Willock, G. M. Day, J. Bacsa, A. Steiner and A. I. Cooper, Angew. Chem., Int. Ed., 2011, 50, 749 CrossRef PubMed.
- M. Baroncini, S. d'Agostino, G. Bergamini, P. Ceroni, A. Comotti, P. Sozzani, I. Bassanetti, F. Grepioni, T. M. Hernandez, S. Silvi, M. Venturi and A. Credi, Nat. Chem., 2015, 7, 634 CrossRef CAS PubMed.
- C. B. Aakeroy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397 RSC.
- M. J. Zaworotko, Chem. Soc. Rev., 1994, 23, 283 RSC.
- G. R. Desiraju, Angew. Chem., Int. Ed., 1995, 34, 2311 CrossRef CAS.
- B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1990, 112, 1546 CrossRef CAS.
- M. Kondo, T. Yoshitomi, H. Matsuzaka, S. Kitagawa and K. Seki, Angew. Chem., Int. Ed., 1997, 36, 1725 CrossRef CAS.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276 CrossRef CAS.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166 CrossRef CAS PubMed.
- H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortes, A. P. Cote, R. E. Taylor, M. O'Keeffe and O. M. Yaghi, Science, 2007, 316, 268 CrossRef CAS PubMed.
- H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523 CrossRef CAS PubMed.
- D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830 CrossRef CAS PubMed.
- A. M. Evans, L. R. Parent, N. C. Flanders, R. P. Bisbey, E. Vitaku, M. S. Kirschner, R. D. Schaller, L. X. Chen, N. C. Gianneschi and W. R. Dichtel, Science, 2018, 361, 52 CrossRef CAS PubMed.
- T. Ma, E. A. Kapustin, S. X. Yin, L. Liang, Z. Zhou, J. Niu, L. H. Li, Y. Wang, J. Su, J. Li, X. Wang, W. D. Wang, W. Wang, J. Sun and O. M. Yaghi, Science, 2018, 361, 48 CrossRef CAS PubMed.
- K. Jie, M. Liu, Y. Zhou, M. A. Little, A. Pulido, S. Y. Chong, A. Stephenson, A. R. Hughes, F. Sakakibara, T. Ogoshi, F. Blanc, G. M. Day, F. Huang and A. I. Cooper, J. Am. Chem. Soc., 2018, 140, 6921 CrossRef CAS PubMed.
- K. Jie, M. Liu, Y. Zhou, M. A. Little, S. Bonakala, S. Y. Chong, A. Stephenson, L. Chen, F. Huang and A. I. Cooper, J. Am. Chem. Soc., 2017, 139, 2908 CrossRef CAS PubMed.
- W. Bury, A. M. Walczak, M. K. Leszczynski and J. A. R. Navarro, J. Am. Chem. Soc., 2018, 140, 15031 CrossRef CAS PubMed.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937 CrossRef CAS PubMed.
- S. L. Price, Acc. Chem. Res., 2009, 42, 117 CrossRef CAS PubMed.
- S. L. Price, Faraday Discuss., 2018, 211, 9 RSC.
- J. Nyman and S. M. Reutzel-Edens, Faraday Discuss., 2018, 211, 459 RSC.
- J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367 CrossRef CAS PubMed.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657 CrossRef CAS PubMed.
- G. M. Day and A. I. Cooper, Adv. Mater., 2018, 30, e1704944 CrossRef PubMed.
- M. Mastalerz and I. M. Oppel, Angew. Chem., Int. Ed., 2012, 51, 5252 CrossRef CAS PubMed.
- W. Yang, A. Greenaway, X. Lin, R. Matsuda, A. J. Blake, C. Wilson, W. Lewis, P. Hubberstey, S. Kitagawa, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2010, 132, 14457 CrossRef CAS PubMed.
- Y. He, S. Xiang and B. Chen, J. Am. Chem. Soc., 2011, 133, 14570 CrossRef CAS PubMed.
- R. Lin, Y. He, P. Li, H. Wang, W. Zhou and B. Chen, Chem. Soc. Rev., 2019, 48, 1362 RSC.
- M. K. Corpinot and D.-K. Bučar, Cryst. Growth Des., 2019, 19, 1426 CrossRef CAS.
- H. García and S. Navalón, Metal–Organic Frameworks: Applications in Separations and Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2018 Search PubMed.
- C. B. Aakeröy, N. R. Champness and C. Janiak, CrystEngComm, 2010, 1, 22–43 RSC.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342 CrossRef CAS PubMed.
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952 CrossRef CAS PubMed.
- L. R. MacGillivray and J. L. Atwood, Nature, 1997, 389, 469 CrossRef CAS.
- D. J. Duchamp and R. E. Marsh, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 5 CrossRef CAS.
- F. H. Herbstein, M. Kapon and G. M. Reisner, J. Inclusion Phenom., 1987, 5, 211 CrossRef CAS.
- F. T. Herbstein, M. Kapon and G. M. Reisner, Acta Crystallogr., Sect. A: Cryst. Phys., Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 348 CrossRef.
- M. Sanchez-Sala, O. Vallcorba, C. Domingo and J. A. Ayllon, Cryst. Growth Des., 2018, 18, 6621 CrossRef CAS.
- P. Vishweshwar, D. A. Beauchamp and M. J. Zaworotko, Cryst. Growth Des., 2006, 6, 2429 CrossRef CAS.
- A. Dmitriev, N. Lin, J. Weckesser, J. V. Barth and K. Kern, J. Phys. Chem. B, 2002, 106, 6907 CrossRef CAS.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148 CrossRef CAS PubMed.
- O. Ermer, J. Am. Chem. Soc., 1988, 110, 3747 CrossRef CAS.
- O. Ermer and L. Lindenberg, Helv. Chim. Acta, 1991, 74, 825 CrossRef CAS.
- D. P. McMahon, A. Stephenson, S. Y. Chong, M. A. Little, J. T. A. Jones, A. I. Cooper and G. M. Day, Faraday Discuss., 2018, 211, 383 RSC.
- S. L. Morissette, S. Soukasene, D. Levinson, M. J. Cima and Ö. Almarsson, Proc. Natl. Acad. Sci. U. S. A., 2003, 5, 2180 CrossRef PubMed.
- S. L. Morissette, Ö. Almarsson, M. L. Peterson, J. F. Remenar, M. J. Read, A. V. Lemmo, S. Ellis, M. J. Cima and C. R. Gardner, Adv. Drug Delivery Rev., 2004, 56, 275 CrossRef CAS PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154 RSC.
- S. Griessl, M. Lackinger, M. Edelwirth, M. Hietschold and W. M. Heckl, Single Mol., 2002, 3, 25 CrossRef CAS.
- M. Lackinger, S. Griessl, W. A. Heckl, M. Hietschold and G. W. Flynn, Polymorphism, 2005, 21, 4984 CAS.
- S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478 RSC.
- J. E. Campbell, J. Yang and G. M. Day, J. Mater. Chem. C, 2017, 5, 7574 RSC.
- I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011 CrossRef.
- I. Kolossváry and W. C. Guida, J. Comput. Chem., 1999, 20, 1671 CrossRef.
- MacroModel, V9.0, Schrodinger LLC, New York, NY, 2011 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657 CrossRef CAS PubMed.
- D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910 CrossRef CAS PubMed.
- D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational methodology, crystallographic data, robot configuration, NMR, TGA, DSC, and gas sorption data. CCDC 1915299–1915315. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc02832c |
| This journal is © The Royal Society of Chemistry 2019 |