Open Access Article
Open Access ArticleStereodynamical control of product branching in multi-channel barrierless hydrogen abstraction of CH3OH by F†
Dandan
Lu
 a,
Jun
Li
a,
Jun
Li
 *a and
Hua
Guo
*a and
Hua
Guo
 *b
*b
aSchool of Chemistry and Chemical Engineering, Chongqing University, Chongqing 401331, China. E-mail: jli15@cqu.edu.cn
bDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA. E-mail: hguo@unm.edu
First published on 9th July 2019
Abstract
Hydrogen abstraction from methanol (CH3OH) by F atoms presents an ideal proving ground to investigate dynamics of multi-channel reactions, because two types of hydrogen can be abstracted from the methanol molecule leading to the HF + CH3O and HF + CH2OH products. Using the quasi-classical trajectory approach on a globally accurate potential energy surface based on high-level ab initio calculations, this work reports a comprehensive dynamical investigation of this multi-channel reaction, yielding measurable attributes including integral and differential cross sections, as well as branching ratios. It is shown that while complex-forming and direct mechanisms coexist at low collision energies, these barrierless reaction channels are dominated at high energies by the direct mechanism, in which the reaction is only possible for trajectories entering into the respective dynamical cones of acceptance. Perhaps more importantly, the non-statistical product branching is found to be dictated by unique stereodynamics in the entrance channels.
I. Introduction
A main goal of reaction dynamics is to gain a microscopic understanding of chemical transformation by investigating quantum state resolved reactivity in the gas phase.1 Over the past few decades, our knowledge of how chemical reactions take place has reached an unprecedentedly high level, both theoretically and experimentally. Detailed measurements and sophisticated theoretical investigations have led to a thorough understanding of the dynamics for many prototypical reactions involving three or four atoms, such as the H/F/Cl/O/N/C + H2 and H/F/O/Cl + H2O reactions.2–7 Recent focus has been shifted to more complex ones, such as the H/F/Cl/O/OH + CH4 (the simplest hydrocarbon) reactions.8–11 These studies have played a pivotal role in advancing our understanding of fundamental mechanisms and dynamics in chemical reactions, and have shed valuable light on a wide array of important dynamical issues such as tunneling, resonance, mode specificity and bond selectivity, steric effects, and nonadiabatic effects.However, the aforementioned reactions with only a single type of reaction channel are not representative of most chemical reactions of larger molecules. For instance, many reactions involving organic molecules often have multiple reaction pathways, and one product may be highly desired. It is thus of great importance to understand product selectivity among competing reaction pathways.12–16 Theoretically, it is challenging to study the reaction dynamics of these systems because of the increased dimensionality, expensive electronic structure calculations, considerably more complex potential energy surfaces (PESs), and costly theoretical treatments of the nuclear motions, especially when quantum effects are present. Indeed, detailed dynamical studies of multi-channel reactions are still lacking except for a few well-known systems.12,15 The investment of substantial efforts to meet the challenges in multi-channel reactions is undoubtedly worthwhile because of the concomitant gains in understanding the rich reaction dynamics.
In this work, we examine the hydrogen abstraction from methanol by fluorine atoms, which has two competing hydrogen abstraction pathways, namely from the hydroxyl group of methanol to form methoxy radicals, CH3O,
| F(2P) + CH3OH → HF + CH3O, | (R1) |
| F(2P) + CH3OH → HF + CH2OH. | (R2) |
As shown in Fig. 1, both transition states (TSs) along the two abstraction pathways are submerged below the reactant asymptote,17–19 resulting in very fast reaction rates.17–19 Besides, both reaction channels are highly exothermic, with −28.40 and −37.74 kcal mol−1 for (R1) and (R2), respectively.18,19 The measured branching ratios, defined as the ratio of the thermal rate constants kR1/(kR1 + kR2), vary between 0.4 and 0.6,20–27 and are all greater than the 0.25 value expected from the statistical limit (one H out of four possible ones).
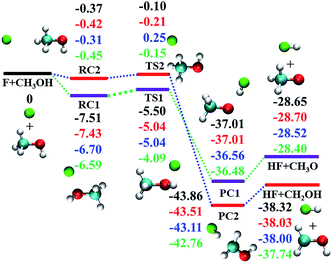 | ||
| Fig. 1 Reaction scheme for the electronic ground state of F + CH3OH → HF + CH3O/CH2OH. From top to bottom, the energies (in kcal mol−1) correspond to PIP-NN PES, CCSD(T)-F12a/AVDZ, CCSD(T)-F12a/AVTZ, and CCSD(T)/AVQZ as reported by Schaefer and co-workers,19 respectively. | ||
Methanol is widely used as a laboratory/industrial solvent and a promising alternative fuel.28 It is the simplest oxygenated polyatomic organic molecule with two functional groups, which makes it an ideal candidate for studying branching ratios and stereodynamics in reactions with atomic radicals.12 Its reaction with F has been used to generate CH3O or CH2OH radicals, which are important intermediates in combustion of hydrocarbon fuels, atmospheric chemistry, surface science, and interstellar chemistry.29–31 Therefore, a large number of investigations, in particular experimental ones, have been carried out on the kinetics, branching ratios of the two channels, and dynamics for reactions of F atoms with CH3OH and the various deuterated isotopologues, CD3OH, CH3OD, and CD3OD.17–27,29,32–42
Considerable attention has also been directed toward measuring product-state or energy distributions. Internal state distributions of the nascent HF product have been measured by infra-red chemiluminescence and laser induced fluorescence and found to be inverted in both product channels.33–35,37–39 Selective deuteration, employed to disentangle these results, showed that the HF product formed by hydrogen abstraction from the methyl group (R2) possesses greater internal energy than that formed by the abstraction from the hydroxyl group (R1), consistent with the exothermicities of the two channels as discussed above. On the other hand, only a small amount of energy is partitioned into the methoxy radical, with ca. 2% of the available energy in the C–O stretching mode, suggesting the spectator nature of the CH3O moiety, for the (R1) channel.37,38
The reaction channel (R1) has also been probed by the photodetachment of the F−(HOCH3) anion, whose geometry resembles TS1 for this neutral reaction.40,42,43 The photoelectron spectrum provides a direct probe of the vibrational structure and metastable resonances that are characteristic of the PES of the neutral reaction. In particular, the experiment revealed spectral features associated with manifold vibrational Feshbach resonances and bound states in the exit channel well.43
In sharp contrast to the numerous experimental investigations on the title reaction, relevant theoretical research is scarce, especially on the reaction dynamics. Based on the information of the stationary points computed with Mϕller–Plesset perturbation theory17,18 and at the G2 level of theory,18 the kinetics of the two reaction channels were investigated in an attempt to explain the observed anomalously large kR1/(kR1 + kR2) branching ratio. However, the agreement with experiments was quite poor. In 2015, Schaefer and co-workers reinvestigated this reaction at the level of coupled cluster theory with single, double, and perturbative triple excitations (CCSD(T)) associated with the augmented double, triple, and quadruple-zeta basis sets (AVDZ, AVTZ, and AVQZ),19 which revealed that the electronic structure theories used in the previous calculations were not sufficiently accurate.
More recently, we reported a global PES of the title reaction with all 15 internal degrees of freedom (DOFs) by fitting 121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points calculated at the explicitly correlated (F12a) version of CCSD(T) with the AVDZ basis set and core electrons frozen.43 This level of electronic structure theory was found to yield results comparable to the benchmark ab initio results obtained by Schaefer and co-workers.19 The chemically accurate fitting was performed with the permutation invariant polynomial-neural network (PIP-NN) method,44,45 which has been successfully applied to several reactive systems for high fidelity fitting of their PESs.46
000 points calculated at the explicitly correlated (F12a) version of CCSD(T) with the AVDZ basis set and core electrons frozen.43 This level of electronic structure theory was found to yield results comparable to the benchmark ab initio results obtained by Schaefer and co-workers.19 The chemically accurate fitting was performed with the permutation invariant polynomial-neural network (PIP-NN) method,44,45 which has been successfully applied to several reactive systems for high fidelity fitting of their PESs.46
Using this PES, the kinetics and the associated thermal branching ratio of the title reaction have been studied with the quasi-classical trajectory (QCT) method.47 The calculated canonical rate coefficients were in good agreement with experiments, both showing a slightly negative temperature dependence. In addition, the calculated thermal branching ratios of 0.40–0.43 at 200–1000 K are in good agreement with measurements.47 These results further confirmed the accuracy of the PES.
In this work, we report an extensive theoretical investigation on the reaction dynamics of this multi-channel system, focusing on the reaction mechanism, as well as stereodynamics and its impact on the microcanonical branching ratio. These calculations were carried out on the globally accurate PES, which has been used successfully to simulate the photoelectron spectrum43 and photoelectron–photoion coincidence spectrum of the F−(HOCH3) anion48 and to reproduce the experimental canonical rate coefficients and branching ratios well.47 Here, integral and differential cross sections are computed for both product channels using QCT, which shed light on the mechanism of this multi-channel reaction. It is found that the coexistence of capture and direct mechanisms at low collision energies gives way to an exclusively direct mechanism at high collision energies. Perhaps most interestingly, detailed analysis of the stereodynamics of the reaction revealed the origin of the non-statistical branching to the two product channels. These results shed valuable light on the dynamics of this multi-channel barrierless reaction prototype.
II. Results and discussion
The QCT method used to investigate the dynamics is well established and the details of the calculations can be found in the ESI.† Briefly, trajectories are calculated at collision energies of 1.0, 2.0, 3.0, 5.0, 10.0, 15.0, 20.0, 25.0, and 30.0 kcal mol−1 on the PIP-NN PES43 for the title reaction interfaced to the VENUS chemical dynamics program.49II-A. Reaction mechanisms
Excitation functions, namely the dependence of the integral cross sections (ICSs) on the collision energy (Ec), have been calculated for the ground ro-vibrational state of methanol and are shown in Fig. 2(a). It can be seen that the reactivity of both channels is quite large at low collision energies and all ICSs show no threshold in energy, consistent with the barrierless nature and a complex-forming mechanism for the two channels.5 The ICS of the (R1) (HF + CH3O) channel decreases monotonically with increasing collision energy. As shown in Fig. 1, (R1) features a barrierless entrance channel leading to a potential well (RC1) with a significant depth. At low collision energies, this feature of the PES is expected to capture the collision partners and guide them towards TS1. Indeed, the unique RC1 complex is similar to the reactant complex between F and H2O,50,51 and both are stabilized by a two-center-three-electron covalent bond formed between the unpaired electron of the F atom and a lone pair of the O atom.52 As the energy increases, faster collision partners are more difficult to capture and the reactivity decreases.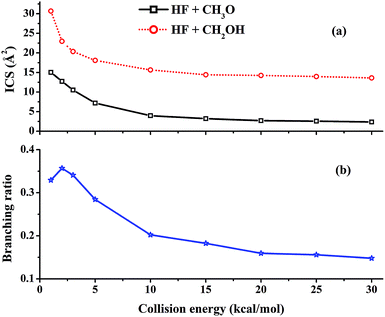 | ||
| Fig. 2 (a) ICSs of the two reactive channels and (b) the branching ratio of the HF + CH3O channel as a function of the collision energy. | ||
For the (R2) (HF + CH2OH) channel, the ICS is much larger than for (R1), due partly to the availability of three possible H atoms in the methyl group. It also decreases sharply with the collision energy and then becomes essentially flat at high collision energies, qualitatively similar to that for the (R1) reaction discussed above. This can be explained by the barrierless energetics along the (R2) channel and the weak complex RC2, which also enables capture at low collision energies.
Fig. 3 shows opacity functions of the two channels at different collision energies. At low collision energies, e.g., Ec = 1.0 kcal mol−1, both reaction channels are dominated by very large impact parameters, signifying significant capture. At higher collision energies, as discussed above, capture at large impact parameters becomes ineffective due to faster relative speed of the collision partners, and reactive trajectories can only be found at relatively small impact parameters. The dramatic change of the opacity functions suggests a change of the reaction mechanism from low energies to higher ones.
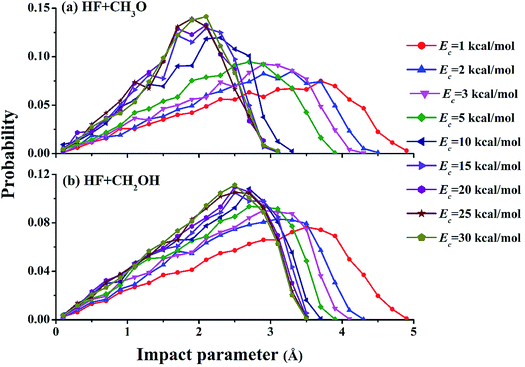 | ||
| Fig. 3 Opacity functions of both channels for the F + CH3OH reaction at different collision energies. | ||
The attractive PES topography at large reactant separation (R) underscores the universal capture at low collision energies. At high energies, however, the PES is dominated by repulsive walls with narrow cones of acceptance, which can only be accessed with small impact parameters and correct approaching angles.53 To illustrate this quantitatively, the cones of acceptance are determined as follows. At the reaction bottleneck, which is defined as the point where the forming bond distance F⋯H is 1.3 Å, the polar angle ∠FHO and the dihedral angle ∠FHOC (for the (R1) channel) or the polar angle ∠FHC and the dihedral angle ∠FHCO (for the (R2) channel) are calculated for reactive trajectories at collision energies of 1.0, 15.0, and 30.0 kcal mol−1. As shown in Fig. 4(a) and (b), the productive trajectories have a relatively narrow distribution in either ∠FHO or ∠FHC, although this distribution broadens somewhat at higher collision energies. On the other hand, the distributions of the dihedral angles, displayed in Fig. 4(c) and (d), show different characteristics for the two channels: for the (R1) channel, the distributions are quite narrow, peaking at around ±90°, which is quite close to the −82° of TS1, while for the (R2) channel, they are quite broad. The picture obtained from this analysis underscores the steric effect in this reaction: only trajectories that have the correct approach are productive in the reaction at high collision energies.
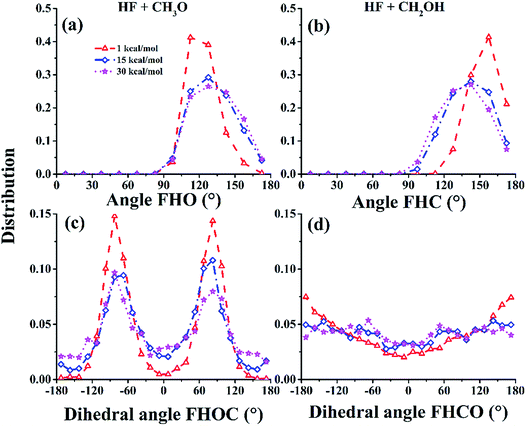 | ||
| Fig. 4 The distributions of the acceptable angles FHO (a)/FHC (b) and FHOC (c)/FHCO (d) for the CH3O/CH2OH channels at the bottleneck for Ec = 1.0, 15.0, and 30.0 kcal mol−1, respectively. | ||
Relative differential cross sections (DCSs) for the two channels with the methanol in its ground ro-vibrational state are plotted in Fig. 5. It is clear that at collision energies between 1.0 and 30.0 kcal mol−1, the DCSs in both channels are biased in the forward direction, although scattering occurs at all angles. This is quite different from the backward scattering dominated DCSs in F + H2O,50,54 which has a small barrier of about 2 kcal mol−1. As shown in Fig. 3, the isotropic capture contribution is only important at low collision energies. The dominant direct mechanism contains both backward and forward scattering, although the latter is favored.
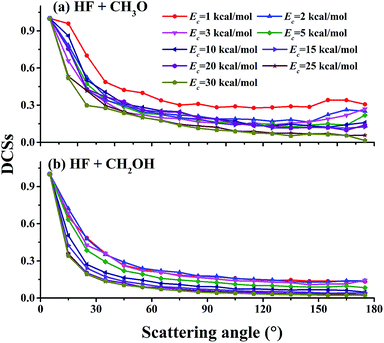 | ||
| Fig. 5 Relative product angular distributions (DCSs) at different collision energies: (a) for the (R1) (HF + CH3O) channel and (b) for the (R2) (HF + CH2OH) channel. | ||
To further understand the details of the DCSs, the correlation between the impact parameter and the scattering angle is shown in Fig. 6 for both reaction channels at Ec = 1.0, 15.0, and 30.0 kcal mol−1. From the figures, it is clear that there are two types of scattering, particularly in the (R1) channel. One features a large impact parameter scattering with near isotropic scattering angles, which points to a complex-forming mechanism with a lifetime longer than the rotational period.5 The other shows a strong correlation between the impact parameter and scattering angle. This latter mechanism is a direct one, in which small impact parameter collisions lead to backward scattering (rebound) while large impact parameter collisions result in forward scattering (stripping). It is clear that the former is significant at low collision energies but disappears at high collision energies. These observations are consistent with the opacity functions in Fig. 3, reinforcing the notion about the mechanistic transition from low collision energies to higher ones.
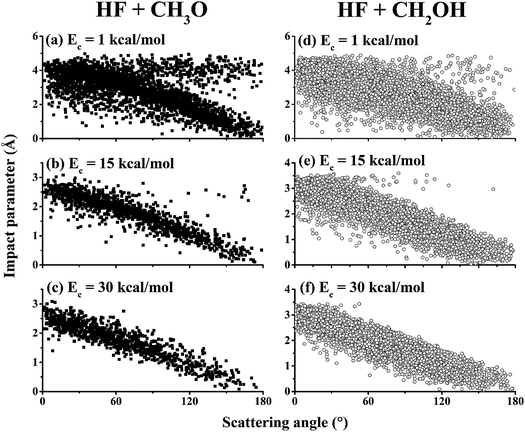 | ||
| Fig. 6 Correlation diagrams between the impact parameter and the scattering angle for the (R1) channel (HF + CH3O, left panels, (a–c)) and the (R2) channel (HF + CH2OH, right panels, (d–f)) at Ec = 1.0, 15.0, and 30.0 kcal mol−1. | ||
II-B. Branching ratio
In our previous work, the calculated thermal branching ratio of the HF + CH3O channel (R1) and its temperature dependence reproduced the experimental values well.47 In this work, the branching ratio of the HF + CH3O channel, which is defined as σR1/(σR1 + σR2), is calculated using the QCT method as a function of collision energy with the reactants in their ro-vibrational ground states. As shown in Fig. 2(b), the (R1) branching ratio decreases monotonically with increasing collision energy except for Ec = 1 kcal mol−1. This trend differs from our previous results for the thermal branching ratio.47,48 As discussed in the ESI,† this difference is due to the fact that rotational excitation of methanol significantly increases the reactivity of the (R1) reaction. A detailed analysis of mode specificity in this reaction will be discussed in a future publication.It is noted from Fig. 2(b) that the (R1) reactivity is larger than the 0.25 statistical value at low collision energies, but this trend is reversed for Ec > 5 kcal mol−1. In other words, this channel has a lower reactivity than the statistical limit at high collision energies. As discussed above, the reaction is dominated by capture at low collision energies. Due to the deeper RC1 well, the (R1) channel has a larger capture radius than the (R2) channel, as evidenced by the opacity functions shown in Fig. 3. As a result, it is not surprising that the (R1) channel has a large branching ratio at low collision energies compared to the statistical value.
As the collision energy increases, the capture mechanism gives way to a direct one. As discussed above, only those trajectories that enter the cones of acceptance are reactive. However, this is true for both the (R1) and (R2) channels and it follows that these two channels are thus expected to approach the statistical limit of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
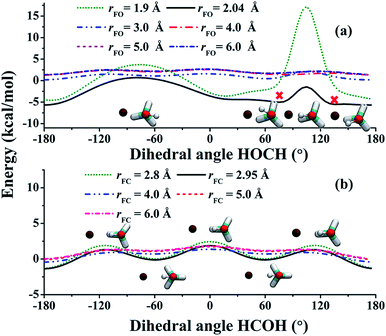
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. This is apparently not the case from Fig. 2(b)! To understand the lower branching ratio for the (R1) channel, we examine the stereodynamics associated with the floppy nature of the OH pseudo-rotation around the C–O axis of methanol. As shown in Fig. 7(a), the potential along the ∠H–O–C–H angle is quite flat when F is far away from methanol, due apparently to the near free rotation of the OH moiety. However, as F approaches methanol, the potential along this coordinate becomes highly anisotropic, featuring two equivalent entrance channels (∠H–O–C–H = 80° and 135°) corresponding to the TS1 geometry. As a result, only those OH moieties around these regions are likely to be reactive, as shown clearly in Fig. 8. For those OH configurations that happen to be away from these angles, the potential is quite repulsive, leading to non-productive collisions. The situation here is very different from the photodetachment of F−(HOCH3), where the OH group is locked to the F− anion in the precursor, and is thus not free to rotate.43
3 ratio. This is apparently not the case from Fig. 2(b)! To understand the lower branching ratio for the (R1) channel, we examine the stereodynamics associated with the floppy nature of the OH pseudo-rotation around the C–O axis of methanol. As shown in Fig. 7(a), the potential along the ∠H–O–C–H angle is quite flat when F is far away from methanol, due apparently to the near free rotation of the OH moiety. However, as F approaches methanol, the potential along this coordinate becomes highly anisotropic, featuring two equivalent entrance channels (∠H–O–C–H = 80° and 135°) corresponding to the TS1 geometry. As a result, only those OH moieties around these regions are likely to be reactive, as shown clearly in Fig. 8. For those OH configurations that happen to be away from these angles, the potential is quite repulsive, leading to non-productive collisions. The situation here is very different from the photodetachment of F−(HOCH3), where the OH group is locked to the F− anion in the precursor, and is thus not free to rotate.43
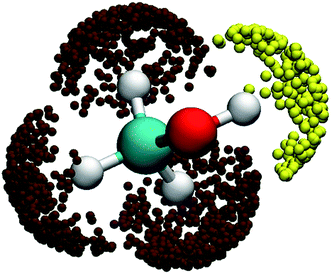 | ||
| Fig. 8 Three-dimensional angular distributions for reactive trajectories leading to the two reactive channels when the F–H distance is 1.3 Å. The yellow and brown symbols represent the (R1) and (R2) reactions. | ||
It should probably be noted that the stereodynamics described above is much more pronounced at high collision energies because of the fast relative collision velocity. At low collision energies, the slow-moving F allows the OH rotor to adiabatically adjust to the anisotropic potential. As a result, the steric effect is relatively minor.
The situation in the (R2) channel is completely different. The flat potential in the ∠H–C–O–H angle when F is far away becomes only slightly anisotropic, as shown in Fig. 7(b). This is because of the relative rigidity of the CH3 moiety, except for a three-fold internal rotation which is clearly seen in the figure. As a result, approaches of F in a wide range of the ∠H–C–O–H angle are productive, as shown by the distributions of reactive trajectories in Fig. 8.
The overall result is that the (R1) channel becomes less reactive at higher collision energies, leading to a branching ratio that is lower than the statistical limit. This strong stereodynamics in this channel can be considered as an example of the entropic effect, in which the nearly free OH internal rotation significantly reduces the reaction rate by a pre-exponential steric factor (ξ < 1).1 In other words, only a fraction of the OH orientation relative to the approaching F is reactive. This steric effect is absent in the (R2) channel.
We note in passing that stereodynamical control of product branching has been observed before.55–58 However, the previous examples are all restricted to branching between intrinsically equivalent product channels, made distinguishable by isotopic substitutions. For example, the branching between the HCl and DCl channels in the Cl + HD reaction was found to be influenced by a van der Waals well in the reactant channel.55 There, the two product channels (HCl vs. DCl) are chemically identical. However, the stereodynamical control in the system discussed here is for two chemically distinct product channels, which is much more relevant to real chemistry.
IV. Conclusions
The availability of accurate high-dimensional potential energy surfaces for complex reactive systems has ushered in an era in which complex reaction dynamics can be investigated in great detail. As demonstrated in this work, deep insights have been gained through theoretical scrutiny of the dynamics of a multi-channel reaction between F and CH3OH, which leads to two different product channels. Such a detailed investigation of reaction dynamics would be very difficult without the global potential energy surface.While both product channels are exothermic and barrierless, it is shown that dynamics play an indispensable role in the reaction. In particular, a complex-forming mechanism is favored at low collision energies, while a direct mechanism becomes increasingly dominant as the collision energy increases. This change of the reaction mechanism manifests in measurable attributes such as the differential cross sections. It is also our hope that the current work will stimulate future experimental investigations on this reaction.
More importantly, the branching ratio between the two product channels is energy dependent and non-statistical. Detailed analysis suggests that the non-statistical branching ratio at high collision energies can be attributed to stereodynamics, particularly in the (R1) channel. This is due to the floppy nature of the OH internal rotation, which significantly reduces the reactivity in this channel. Such a steric factor is not as pronounced for the (R2) channel, thanks to the relative rigidity of the CH3 moiety. Since both OH and CH3 moieties are quite common in organic molecules, the insights gained from this study can have significant implications concerning the product selectivity in organic reactions.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Contract No. 21573027 to J. L.). H. G. acknowledges support by the US Department of Energy (DE-SC0015997 to H. G.). Prof. Changjian Xie is acknowledged for helpful discussions on using VENUS.References
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, Cambridge, 2005 Search PubMed.
- F. Fernandez-Alonso and R. N. Zare, Annu. Rev. Phys. Chem., 2002, 53, 67–99 CrossRef CAS.
- N. Balucani, G. Capozza, F. Leonori, E. Segoloni and P. Casavecchia, Int. Rev. Phys. Chem., 2006, 25, 109–163 Search PubMed.
- X. Yang, Annu. Rev. Phys. Chem., 2007, 58, 433–459 CrossRef CAS.
- H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1–68 Search PubMed.
- J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667–4687 CrossRef CAS.
- D. H. Zhang and H. Guo, Annu. Rev. Phys. Chem., 2016, 67, 135–158 CrossRef CAS.
- W. Hu and G. C. Schatz, J. Chem. Phys., 2006, 125, 132301 CrossRef.
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839–2864 CrossRef.
- K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111 CrossRef CAS.
- B. Fu, X. Shan, D. H. Zhang and D. C. Clary, Chem. Soc. Rev., 2017, 46, 7625–7649 RSC.
- C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435–482 Search PubMed.
- B. Joalland, Y. Shi, A. D. Estillore, A. Kamasah, A. M. Mebel and A. G. Suits, J. Phys. Chem. A, 2014, 118, 9281–9295 CrossRef CAS.
- G. T. Dunning, D. R. Glowacki, T. J. Preston, S. J. Greaves, G. M. Greetham, I. P. Clark, M. Towrie, J. N. Harvey and A. J. Orr-Ewing, Science, 2015, 347, 530–533 CrossRef CAS.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969 CrossRef CAS.
- H. Pan, K. Liu, A. Caracciolo and P. Casavecchia, Chem. Soc. Rev., 2017, 46, 7517–7547 RSC.
- W. A. Glauser and M. L. Koszykowski, J. Phys. Chem., 1991, 95, 10705–10713 CrossRef CAS.
- J. T. Jodkowski, M. T. Rayez, J. C. Rayez, T. Berces and S. Dobe, J. Phys. Chem. A, 1998, 102, 9219–9229 CrossRef CAS.
- H. Feng, K. R. Randall and H. F. Schaefer III, J. Phys. Chem. A, 2015, 119, 1636–1641 CrossRef CAS.
- U. Meier, H. H. Grotheer and T. Just, Chem. Phys. Lett., 1984, 106, 97–101 CrossRef CAS.
- T. Khatoon and K. Hoyermann, Ber. Bunsenges. Phys. Chem., 1988, 92, 669–673 CrossRef CAS.
- P. Pagsberg, J. Munk, A. Sillesen and C. Anastasi, Chem. Phys. Lett., 1988, 146, 375–381 CrossRef CAS.
- J. A. McCaulley, N. Kelly, M. F. Golde and F. Kaufman, J. Phys. Chem., 1989, 93, 1014–1018 CrossRef CAS.
- D. J. Bogan, M. Kaufman, C. W. Hand, W. A. Sanders and B. E. Brauer, J. Phys. Chem., 1990, 94, 8128–8134 CrossRef CAS.
- J. L. Durant, J. Phys. Chem., 1991, 95, 10701–10704 CrossRef CAS.
- S. Dóbé, T. Bérces, F. Temps, H. G. Wagner and H. Ziemer, Symp. (Int.) Combust., 1994, 25, 775–781 CrossRef.
- E. Assaf, C. Schoemaecker, L. Vereecken and C. Fittschen, Phys. Chem. Chem. Phys., 2018, 20, 10660 RSC.
- T. S. Norton and F. L. Dryer, Int. J. Chem. Kinet., 1990, 22, 219–241 CrossRef CAS.
- K. Hoyermann, N. S. Loftfield, R. Sievert and H. G. Wagner, Symp. (Int.) Combust., 1981, 18, 831–842 CrossRef.
- C. K. Westbrook and F. L. Dryer, Symp. (Int.) Combust., 1981, 18, 749–767 CrossRef.
- R. D. Johnson and J. W. Hudgens, J. Phys. Chem., 1996, 100, 19874–19890 CrossRef CAS.
- M. E. Jacox, Chem. Phys., 1981, 59, 213–230 CrossRef CAS.
- D. J. Smith, D. W. Setser, K. C. Kim and D. J. Bogan, J. Phys. Chem., 1977, 81, 898–905 CrossRef CAS.
- R. G. Macdonald, J. J. Sloan and P. T. Wassell, Chem. Phys., 1979, 41, 201–208 CrossRef CAS.
- B. Dill and H. Heydtmann, Chem. Phys., 1980, 54, 9–20 CrossRef CAS.
- J. M. Dyke, A. R. Ellis, N. Jonathan, N. Keddar and A. Morris, Chem. Phys. Lett., 1984, 111, 207–210 CrossRef CAS.
- B. S. Agrawalla and D. W. Setser, J. Phys. Chem., 1984, 88, 657–660 CrossRef CAS.
- B. S. Agrawalla and D. W. Setser, J. Phys. Chem., 1986, 90, 2450–2462 CrossRef CAS.
- M. A. Wickramaaratchi, D. W. Setser, H. Hildebrandt, B. Korbitzer and H. Heydtmann, Chem. Phys., 1985, 94, 109–129 CrossRef CAS.
- S. E. Bradforth, D. W. Arnold, R. B. Metz, A. Weaver and D. M. Neumark, J. Phys. Chem., 1991, 95, 8066–8078 CrossRef CAS.
- P. Biggs, C. E. Canosa-Mas, J.-M. Fracheboud, D. E. Shallcross and R. P. Wayne, J. Chem. Soc., Faraday Trans., 1997, 93, 2481–2486 RSC.
- A. W. Ray, J. Agarwal, B. B. Shen, H. F. Schaefer and R. E. Continetti, Phys. Chem. Chem. Phys., 2016, 18, 30612–30621 RSC.
- M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950–955 CrossRef CAS.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- D.-d. Lu, C.-j. Xie, J. Li and H. Guo, Chin. J. Chem. Phys., 2019, 32, 84–88 CrossRef CAS.
- L. Guo, J. Li, J. Ma and H. Guo, J. Chem. Phys., 2019, 150, 044301 CrossRef.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- J. Li, R. Dawes and H. Guo, J. Chem. Phys., 2012, 137, 094304 CrossRef.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 074309 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, Chem. Sci., 2013, 4, 629–632 RSC.
- R. D. Levine, J. Phys. Chem., 1990, 94, 8872–8880 CrossRef CAS.
- J. Li and H. Guo, Chin. J. Chem. Phys., 2013, 26, 627–634 CrossRef CAS.
- D. Skouteris, D. E. Manolopoulos, W. Bian, H.-J. Werner, L.-H. Lai and K. Liu, Science, 1999, 286, 1713–1716 CrossRef CAS.
- S. Yan, Y. T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723–1726 CrossRef CAS.
- W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303–306 CrossRef CAS.
- F. Wang, J.-S. Lin and K. Liu, Science, 2011, 331, 900–903 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc02445j |
| This journal is © The Royal Society of Chemistry 2019 |