Open Access Article
Open Access ArticleIn the quest for a stable triplet state in small polyaromatic hydrocarbons: an in silico tool for rational design and prediction†
Madhumita
Rano
 ,
Sumanta K.
Ghosh
,
Sumanta K.
Ghosh
 and
Debashree
Ghosh
and
Debashree
Ghosh
 *
*
School of Chemical Sciences, Indian Association for the Cultivation of Science, Jadavpur, Kolkata 700 032, India. E-mail: pcdg@iacs.res.in; Tel: +91 033 2473 4971 ext. 1103
First published on 19th August 2019
Abstract
Combining the roles of spin frustration and geometry of odd and even numbered rings in polyaromatic hydrocarbons (PAHs), we design small molecules that show exceedingly small singlet-triplet gaps and stable triplet ground states. Furthermore, a computationally efficient protocol with a model spin Hamiltonian is shown to be capable of qualitative agreement with respect to high level multireference calculations and therefore, can be used for fast molecular discovery and screening.
1 Introduction
Oligoacenes,1–7 have formed the basis of intense research for a few decades due to their tunable optical gaps. Oligoacenes, up to undecacene,8–10 have been synthesized. Due to their fascinating properties, the theoretical aspects related to their π-bonding topology have been studied extensively,2,4,5,11–13 and their possible usage in singlet fission phenomena14–18 has been investigated.From a theoretical perspective, the electronic structure of oligoacenes has been the subject of intense debate. Stable triplet states in longer polyacenes have been predicted.2 Multi-reference calculations,11,19,20 however, did not observe triplet ground states, which have been corroborated by experiment.8 However, the exact nature of decay of the singlet triplet (ST) gap was extremely relevant to the synthesis of materials with functionalities important for organic electronics.21–27 Theoretical studies until recently showed that the optical gap decreases monotonically for long polyacenes.28,29 However, a recent study reports the non-monotonicity of the decay in the optical gap with the size of polyacenes.30 Therefore, our understanding of the electronic structure of polyacenes is incomplete to this day.
Azulene, consisting of fused five and seven membered rings, has been much less discussed.31 It is known that azulene has a significantly lower ST gap as compared to its acene isomer, naphthalene. Since the five and seven membered rings do not satisfy the (4n + 2) rule, the singlet state of azulene is significantly less stable, thereby reducing the ST gap. In fact, the dipole moment of the singlet state of azulene points towards charge (or electron) transfer from the seven to five membered ring, to attain a stable electronic state. Repeated fused azulene moieties show low ST gaps and a crossover of the triplet state as the ground state (as opposed to the singlet state).32 This observation is fundamentally different from that of the acenes and was also predicted from the UB3LYP level of theory.33 A previous study by Malrieu and co-workers investigated the development of spin bistability in donor–acceptor complexes and they have proposed a few succinct rules to achieve the goal.34 Much work has also been done in the understanding of the inherent aromaticity of such systems.35 Valence bond theory has been used to understand the root of bistability and radicaloid properties of hydrocarbons.36
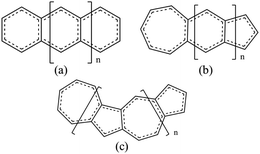
In our work, we will show that the UB3LYP method gives rise to certain artifacts and multireference calculations can change the quantitative findings quite significantly. We have designed a class of fused acene–azulenes (Fig. 1) that can reduce the ST gap much more effectively than only repeated azulene units. What is even more significant is that this class of fused acene–azulenes is as stable as polyazulenes, and yet shows a much lower ST gap. We also show that the determining factor behind this large ST gap reduction is multiple spin frustrated pairs or bonds. Thus, the number of spin frustrated bonds can form a simple design principle to effectively tune the ST gap. We have developed a simple protocol for parameterization of a model Hamiltonian that is capable of fast molecular screening and discovery.
2 Computational details
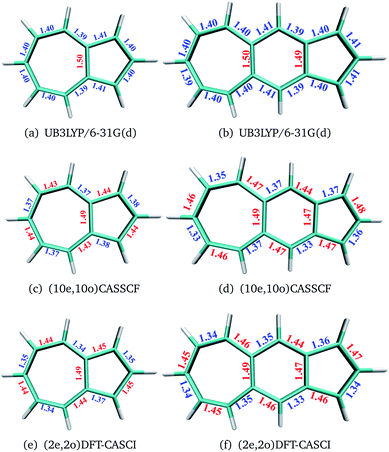
The geometries of polyacenes are taken from earlier work by Hachmann et al.11 and Bendikov et al.2 Geometries of the fused acene–azulenes and polyazulenes are optimized at the (2e,2o)CASCI/RB3LYP/6-31G(d), (10e,10o) CASSCF/6-31G(d) and UB3LYP/6-31G(d) levels of theory. All the optimized geometries for both singlet and triplet states are given in the ESI.† It was noticed that UB3LYP optimizations gave rise to qualitatively different geometries (different bond length alternation (BLA) patterns) as compared to full valence CASSCF optimizations for small PAHs (2 and 3 fused rings) (shown in Fig. 2(a)–(d)). On the other hand, the scheme of obtaining RB3LYP orbitals followed by a minimal CASCI (2e,2o) optimization (referred to as (2e,2o) CASCI/RB3LYP/6-31G(d)) gives the correct BLA pattern (shown in Fig. 2(e) and (f)).Therefore, this computationally affordable scheme of optimization has been used for larger PAHs. In the case of polyacenes, Yang and co-workers37 have also noticed that different levels of theory can give rise to different patterns of BLA and subsequent symmetries. With the minimal active space DFT-CASCI optimized geometries, DMRG (full valence 2pz active space),38–42 CASSCF (14e,14o)43 and CASPT2 (14e,14o)44 calculations have been performed using the cc-pVDZ basis set.45 CASSCF and CASPT2 calculations have been performed using the quantum chemistry software package Molpro 2018.2.46 We have used Block-1.5.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 for DMRG calculations and Q-Chem 5.1
47 for DMRG calculations and Q-Chem 5.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 for DFT optimizations.
48 for DFT optimizations.
2.1 Tuning the J parameter
For the calculations of the model Hamiltonian, we have considered each C atom as a spin-1/2 site which is antiferromagnetically coupled (favorable interaction between opposite spins) to its nearest neighboring sites with equal coupling parameter J. This essentially corresponds to bonding interactions between the nearest neighbor bonded C atoms. J parameters in the Heisenberg spin Hamiltonian of the polyacenes have been tuned to reproduce the adiabatic DMRG/cc-pVDZ ST gap of the molecular Hamiltonian. These tuned J values are used for isomeric polyazulenes and fused acene–azulenes.Non-empirical forms of the Heisenberg Hamiltonian have erstwhile49,50 been used to investigate the effect of ground state geometry on the excited state manifold of polyenes. In this work, we have included a simplified and empirical form of the Hamiltonian, in which the absolute energies of the singlet and triplet states have not been used. On the other hand the adiabatic ST gap (obtained from ab initio calculations) has been used to fit the J parameter for each acene. The same J parameter is used for all bonds for all isomers of acenes, i.e., polyazulene and the fused acene–azulene systems. Therefore, all the bonds in the model Hamiltonian are treated as equivalent and the only direct interactions that are considered are those across the bonds in the moiety.
3 Results and discussion
3.1 Adiabatic ST gap
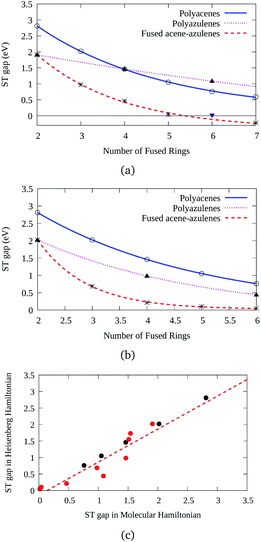
Three types of structures (shown in Fig. 1) are considered and compared – (a) polyacenes, (b) fused acene–azulenes and (c) polyazulenes. The adiabatic ST gaps, calculated at the DMRG/cc-pVDZ level of theory, for the fused rings of size 2–7 are shown in Fig. 3(a). The complete 2pz valence space is chosen as the active space. As expected, the azulene ST gap is significantly lower than that of its isomer, naphthalene. However, we notice that the rate of decay of the adiabatic ST gap for polyazulene is much lower than that of the polyacenes. Therefore, contrary to what has been observed at the model Hamiltonian32 and UDFT level of theory,33 accurate multireference calculations show that the polyazulenes do not form stable triplet states within 6 fused rings.Surprisingly a combined acene–azulene fused system (Fig. 1(b)) shows the lowest adiabatic ST gaps. Within 5 fused rings the ST gap of the fused acene–azulene system is close to the computational accuracy of the method (∼0.05 eV). The ST gaps with various levels of multireference theory (CASSCF and CASPT2) show the same qualitative trend (given in the ESI†). It is important to note that when the acenes and azulenes are fused in different orders,51i.e., structures with fused 7–5–6 or 7–5–6–6 rings, they show much higher (1.58 and 1.40 eV respectively) adiabatic ST gaps than 7–6–5 or 7–6–6–5 motifs (0.97 and 0.46 eV respectively) calculated at the DMRG/cc-pVDZ level of theory. Furthermore, a comparison of the stabilization energies per C atom of the isomeric systems of PAHs shows that the fused acene–azulenes systems (8–9 kcal mol−1) are comparable in stability with the polyazulenes (8–9 kcal mol−1). But both of these systems are somewhat less stable than the acene–azulene systems that have already been synthesized (10–11 kcal mol−1), such as 7–5–6 and 7–5–6–6 moieties.51 These stabilization energies were calculated with the help of isodesmic reactions of the form,
| PAH + n1CH4 → n2C2H4 + n3C2H6, | (1) |
The single reference UDFT calculations when compared to the multireference calculations show that for most of these systems the UDFT level of theory gives rise to quantitatively wrong results (preferential stabilization of triplet states). On the other hand, the multireference calculations are computationally expensive and cannot be routinely used for molecular design and screening. Therefore, we try to develop a model Hamiltonian based protocol to predict the ST gaps in a computationally affordable way. It is important to note that such model Hamiltonians have been suggested in the context of polyacenes in previous studies by a few groups.50,52,53 The ST gaps are calculated with a model Heisenberg Hamiltonian, given by,
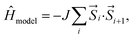 | (2) |
3.2 Spin frustration
The model Hamiltonian wavefunction gives us a simple paradigm to understand the physics behind ST gaps in these molecules. It is important to note that the spins in adjacent sites (bonded C atoms) are antiferromagnetically coupled, so as to model the bonding interactions between them. Thus, opposite spins on adjacent sites refer to bonding and therefore, stabilization, while same spins on adjacent sites destabilize the configurations. The even-membered rings can contain configurations with all anti-parallel adjacent spins (i.e. stable configurations), while this is not possible in the case of odd-membered rings. This leads to spin frustration,55 in the odd-membered rings. Examples of such configurations are shown in Fig. 4(a) for polyazulene and fused acene–azulene. There is effectively one frustrated pair for each azulene unit (2 fused rings). In case of fused acene–azulene, this situation may be exacerbated. It should be noted that in the fused acene–azulene system, configurations with at least 2 spin frustrations are possible. These observations can also be explained within generalizations of Ovchinnikov's rule.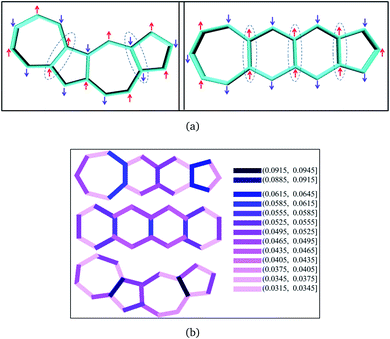 | ||
| Fig. 4 (a) Example configurations of spins on the polyazulene and fused acene–azulene systems. (b) Probabilities of same spins across bonds. | ||
The probability of finding same spins in adjacent sites can, therefore, form a measure of destabilization and is shown in Fig. 4(b). Since the acenes are made of even-membered rings only, there is a low probability of encountering the same spins on adjacent sites. However, in the case of both polyazulene and fused acene–azulene there are regions of high probabilities, especially across certain common bonds (bonds shared by two fused rings). To measure the instability in each system, the probabilities of the same spins across any bonds are computed. It is 0.22 for tetracene, 0.24 for 4-azulene and 0.24 for the 4-fused acene–azulene system. We notice that in the case of polyazulenes, each azulene (7–5 membered fused ring) forms a unit and the common bond between the 7 and 5 membered rings show a higher probability of the same spin configuration. In the case of fused acene–azulene, this trend is spread across all common bonds and sometimes even across the rings. These observations point towards the presence of spin frustration in polyazulenes and fused acene–azulenes, as opposed to acenes.
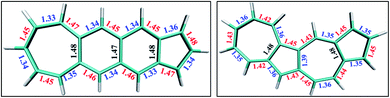
From the comparison of the probabilities it is expected that the polyazulenes and fused acene–azulenes would be of comparable stability in their singlet state and both these compounds would be less stable than acenes. This is indeed noticed from the ab initio calculations. Furthermore, one would expect that the regions of high same-spin probability would try to reduce the instability by introducing lattice degrees of freedom, i.e., change in molecular geometry. In line with our expectations, the geometries of the fused acene–azulene and polyazulene systems (shown in Fig. 5) show elongated bond lengths across the common bonds with high same-spin probability (Fig. 4(b)). This is akin to Peierls distortion in polyenes and polyacenes.
In the polyacenes we notice the expected BLA, where the fused bonds also participate in the BLA pattern.56 In the case of polyazulene (Fig. 5(a)), we notice that each azulene moiety forms a unit and the common bond in this unit is elongated. This common bond is almost a single bond in nature (1.48 Å), i.e., only minimally participates in conjugation. Thus, each azulene forms a pseudo ten membered conjugated ring pattern. However, the common bond between the two azulene moieties is shorter than a single bond (1.39 Å) and takes part in conjugation. The situation is quite different when we notice the bond lengths of the fused acene–azulene system (Fig. 5(b)). Here, all the common bonds are elongated to almost single bond lengths (1.47–1.48 Å) and all of these bonds are minimally present in conjugation. These observations are in accordance with that of the spin probabilities calculated in the model system.
3.3 Stability of the triplet state
The discussion till now considered only the relative stability of the singlet states and showed that both polyazulenes and fused acene–azulenes are expected to have low ST gaps. However, in the case of polyazulenes, the triplet state is destabilized with respect to that of fused acene–azulene (Fig. 6). This can be explained from the spin probabilities being in the same line of argument as those for singlets. The probabilities of finding the same spins in adjacent sites for the triplet states are 0.255 in polyazulene and 0.24 in fused acene–azulene, in isomeric C18H12. Thus, the ST gap of polyazulenes is not as low as expected due to its unstable singlet state. Polyazulenes do not show a ST crossover within 6 fused rings.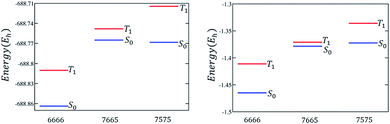 | ||
| Fig. 6 Molecular and model Hamiltonian energies for the singlet and triplet states are compared for 4-fused ring systems, i.e., tetracene, polyazulene and fused acene–azulene. | ||
As the size of the molecule grows, it is the triplet stabilization that takes over. For example, in isomers of C26H16, i.e., containing 6 rings, the singlet state of fused acene–azulene shows lower spin frustration than polyazulene. Since, fused acene–azulenes can form configurations with at least 2 spin frustrations as opposed to polyazulenes with 3 spin frustrations, this is to be expected. This is depicted in the same spin probabilities of the singlet states as 0.246 for polyazulene versus 0.240 for fused acene–azulene, in C26H16. Therefore, one would expect a lower ST gap for polyazulene from the consideration of the singlet state only. However, at these system sizes, it is the relative triplet state stabilities that result in the ST gaps of fused acene–azulenes being much lower than those of the polyazulenes. The same spin probabilities for the triplet states are 0.251 for polyazulene versus 0.240 for fused acene–azulene, in C26H16. Thus, we can notice that the probabilities of finding the same adjacent spins remain almost constant in the case of fused acene–azulene systems across system sizes, while in polyazulenes they increase as expected due to more number of spin frustrations.
Symmetry of the molecule also plays a minor role in the ST gaps. The difference in ST gaps of straight and kinked acenes has been reported before.57 The same is noticed here. The bent PAHs, i.e., polyazulenes, have higher ST gaps than the straight isomers, fused acene–azulene. It was further noticed that the fused acene–azulenes systems which were arranged in a bent topology also show relatively higher ST gaps. Therefore, if one were to design a low ST gap molecule, there are three considerations – (i) maximize spin frustrations in singlet states, (ii) minimize spin frustrations in triplet states and (iii) more symmetric molecules. With these considerations in mind, a large number of differently fused acene–azulene systems have been designed and screened. We notice that the lowest ST gap moiety consists of a fused ring motif of 7–6⋯6–5 membered rings.
3.4 Bond length alternation
Bond length alternation (BLA) patterns of the PAHs have been found to be quite different using different optimization schemes (details given in the ESI†). Furthermore, it is known in the context of polyenes that inclusion of only static correlation can give rise to more pronounced BLAs. In this study, we have used CASSCF and CASCI based approaches to ascertain the geometry and therefore, the BLA might be over-estimated. Therefore, it is important to understand the effect of lower BLAs on the ST gaps. Fig. 7(a) shows the effect of reduction in the BLAs on the vertical ST gaps of the hydrocarbons. The BLA is reduced to about half the amount obtained from DFT-CASCI optimization to understand the effect of reduction of BLA on the ST gaps. Furthermore, Fig. 7(b) shows the effect of change of BLA to different values on the tetracene (6–6–6–6), 7–5–7–5 and 7–6–6–5 systems, as a representative example. It can be seen from both the figures that as expected, the reduction in BLA stabilizes the triplet state and therefore, reduces the vertical ST gap. The comparison of the triplet and singlet state geometries further shows that low BLA is favored by triplet states and high BLA is favored by singlet states. Furthermore, it is interesting to note that the effect of BLA reduction on the ST gap of fused acene–azulenes is markedly more extensive than in the case of polyacenes and polyazulenes.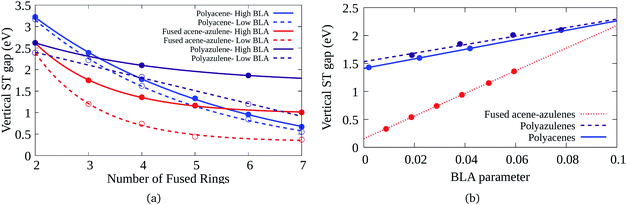 | ||
| Fig. 7 (a) Variation of the vertical ST gap with change in BLA in PAHs, (b) reduction of the vertical ST gap with the decrease of the BLA parameter for 7–5–7–5, 6–6–6–6, and 7–6–6–5 systems. | ||
4 Conclusions
In conclusion, we have developed a novel model Hamiltonian based approach for the design of PAHs with tunable ST gaps. This analogy between the molecular system and model spin lattice can be expressed as a generalization of Ovchinnikov's rule, which states the existence of ferromagnetic phases in infinite hydrocarbon systems of appropriate alternating or non-alternating patterns. While this rule discusses the existence of high spin states in infinite or large systems and can be easily correlated with odd membered ring systems such as poly-azulenes, we find it fascinating that fused acene–azulenes which can indeed be thought of as an acene system attached to two odd membered rings in its extremity can exacerbate the effect and give rise to high spin stable states with much smaller sizes.We have noticed that the ST gaps predicted by the model Heisenberg Hamiltonian approach are well correlated with the ab initio calculations. Therefore, this approach has been used to predict the smallest PAH with a negative ST gap. The stability of these species was tested with the help of isodesmic reactions and they were shown to be reasonably stable with respect to their acene analogues. We have further been able to propose a few succinct design principles which can be used to engineer low ST gap species. In this study, we have tested only the systems that are isomeric with polyacenes; however, we believe that this method can be used for other PAH systems as well.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Manoranjan Kumar and Ms. Debasmita Maiti, SNBNCBS, for helpful discussions, the IACS for computational resources and DST-SERB (EMR/2017/001054) for funding. M. R. and S. K. G. thank the CSIR and the UGC for fellowships.Notes and references
- E. Clar and R. Schoental, Polycyclic hydrocarbons, Springer, 1964, vol. 2 Search PubMed.
- M. Bendikov, H. M. Duong, K. Starkey, K. Houk, E. A. Carter and F. Wudl, J. Am. Chem. Soc., 2004, 126, 7416–7417 CrossRef CAS PubMed.
- Q. Ye and C. Chi, Chem. Mater., 2014, 26, 4046–4056 CrossRef CAS.
- R. Huang, H. Phan, T. S. Herng, P. Hu, W. Zeng, S.-q. Dong, S. Das, Y. Shen, J. Ding and D. Casanova, J. Am. Chem. Soc., 2016, 138, 10323–10330 CrossRef CAS PubMed.
- W. Zeng, T. Y. Gopalakrishna, H. Phan, T. Tanaka, T. S. Herng, J. Ding, A. Osuka and J. Wu, J. Am. Chem. Soc., 2018, 140, 14054–14058 CrossRef CAS PubMed.
- R. G. Harvey, Polycyclic aromatic hydrocarbons: chemistry and carcinogenicity, CUP Archive, 1991 Search PubMed.
- K. Müllen and G. Wegner, Electronic materials: the oligomer approach, John Wiley & Sons, 2008 Search PubMed.
- C. Tönshoff and H. F. Bettinger, Angew. Chem., 2010, 49, 4125–4128 CrossRef PubMed.
- B. Purushothaman, M. Bruzek, S. R. Parkin, A.-F. Miller and J. E. Anthony, Angew. Chem., 2011, 50, 7013–7017 CrossRef CAS PubMed.
- R. Zuzak, R. Dorel, M. Kolmer, M. Szymonski, S. Godlewski and A. M. Echavarren, Angew. Chem., 2018, 57, 10500–10505 CrossRef CAS PubMed.
- J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309 CrossRef PubMed.
- K. Fukuda, T. Nagami, J.-y. Fujiyoshi and M. Nakano, J. Phys. Chem. A, 2015, 119, 10620–10627 CrossRef CAS PubMed.
- T. Y. Gopalakrishna, W. Zeng, X. Lu and J. Wu, ChemComm, 2018, 54, 2186–2199 RSC.
- S. R. Yost, J. Lee, M. W. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao, K. Johnson, M. Y. Sfeir, M. G. Bawendi, T. M. Swager, R. H. Friend, M. A. Baldo and T. V. Voorhis, Nat. Chem., 2014, 6, 492 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- T. Zeng, R. Hoffmann and N. Ananth, J. Am. Chem. Soc., 2014, 136, 5755–5764 CrossRef CAS PubMed.
- P. M. Zimmerman, Z. Zhang and C. B. Musgrave, Nat. Chem., 2010, 2, 648 CrossRef CAS PubMed.
- B. Hajgató, D. Szieberth, P. Geerlings, F. De Proft and M. Deleuze, J. Chem. Phys., 2009, 131, 224321 CrossRef PubMed.
- C. U. Ibeji and D. Ghosh, Phys. Chem. Chem. Phys., 2015, 17, 9849–9856 RSC.
- M. Magoga and C. Joachim, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 4722 CrossRef CAS.
- D. J. Gundlach, J. E. Royer, S. Park, S. Subramanian, O. Jurchescu, B. H. Hamadanni, A. Moad, R. J. Kline, L. Teague, O. Kirillov, C. Richter, J. Kushmerick, L. Richter, S. Parkin, T. Jackson and J. Anthony, Nat. Mater., 2008, 7, 216 CrossRef CAS PubMed.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef PubMed.
- V. Mujica, M. Kemp, A. Roitberg and M. Ratner, J. Chem. Phys., 1996, 104, 7296–7305 CrossRef CAS.
- J. Chen, M. Reed, A. Rawlett and J. Tour, science, 1999, 286, 1550–1552 CrossRef CAS PubMed.
- F. Zahid, A. Ghosh, M. Paulsson, E. Polizzi and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245317 CrossRef.
- C. Zhou, M. Deshpande, M. Reed, L. Jones and J. Tour, Appl. Phys. Lett., 1997, 71, 611–613 CrossRef CAS.
- C. Raghu, Y. A. Pati and S. Ramasesha, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035116 CrossRef.
- H. Chakraborty and A. Shukla, J. Phys. Chem. A, 2013, 117, 14220–14229 CrossRef CAS PubMed.
- R. Korytár, D. Xenioti, P. Schmitteckert, M. Alouani and F. Evers, Nat. Commun., 2014, 5, 5000 CrossRef PubMed.
- T. Zeng, N. Ananth and R. Hoffmann, J. Am. Chem. Soc., 2014, 136, 12638–12647 CrossRef CAS PubMed.
- S. Thomas, S. Ramasesha, K. Hallberg and D. Garcia, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 180403 CrossRef.
- Z. Qu, S. Zhang, C. Liu and J.-P. Malrieu, Communication: A dramatic transition from nonferromagnet to ferromagnet in finite fused-azulene chain, 2011 Search PubMed.
- N. Guihery, D. Maynau and J.-P. Malrieu, New J. Chem., 1998, 22, 281–286 RSC.
- C. Angeli and J.-P. Malrieu, J. Phys. Chem. A, 2008, 112, 11481–11486 CrossRef CAS PubMed.
- J. R. Dias, Mol. Phys., 2013, 111, 735–751 CrossRef CAS.
- Y. Yang, E. R. Davidson and W. Yang, Proc. Natl. Acad. Sci. U.S.A., 2016, 113, E5098–E5107 CrossRef CAS PubMed.
- G. K.-L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462–4476 CrossRef CAS.
- G. K.-L. Chan, J. Chem. Phys., 2004, 120, 3172–3178 CrossRef CAS PubMed.
- G. K.-L. Chan, M. Kállay and J. Gauss, J. Chem. Phys., 2004, 121, 6110–6116 CrossRef CAS PubMed.
- D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117 CrossRef PubMed.
- G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed.
- B. O. Roos, P. R. Taylor and P. E. Si, et al. , Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2019.1, a package of ab initio programs, 2019 Search PubMed.
- S. Sharma and G. K.-L. Chan, J. Chem. Phys., 2012, 136, 124121 CrossRef PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. KuÅŻ, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. OâĂŃNeill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. StÃijck, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru- Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- M. Said, D. Maynau, J. P. Malrieu and M. A. Garcia-Bach, J. Am. Chem. Soc., 1984, 106, 571–579 CrossRef CAS.
- M. Said, D. Maynau and J. P. Malrieu, J. Am. Chem. Soc., 1984, 106, 580–587 CrossRef CAS.
- M. Murai, S. Iba, H. Ota and K. Takai, Org. Lett., 2017, 19, 5585–5588 CrossRef CAS PubMed.
- A. A. Ovchinnikov, Theor. Chem. Acc., 1978, 47, 297–304 Search PubMed.
- D. Klein and M. Garcia-Bach, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 877 CrossRef.
- G. Giri, D. Dey, M. Kumar, S. Ramasesha and Z. G. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 224408 CrossRef.
- D. Dai and M.-H. Whangbo, J. Chem. Phys., 2004, 121, 672–680 CrossRef CAS PubMed.
- L. Salem and H. C. Longuet-Higgins, Proc. R. Soc. London, Ser. A, 1960, 255, 435–443 CrossRef CAS.
- M. Huzak, B. Hajgató and M. Deleuze, Chem. Phys., 2012, 406, 55–64 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of cartesian coordinates of PAHs. Vertical ST gaps, ST gaps calculated at different levels of theory, triplet state energies and spin probability, effect of kinked geometry etc.. See DOI: 10.1039/c9sc02414j |
| This journal is © The Royal Society of Chemistry 2019 |