Open Access Article
Open Access ArticleInternal acidity scale and reactivity evaluation of chiral phosphoric acids with different 3,3′-substituents in Brønsted acid catalysis†
Kerstin
Rothermel
,
Maxime
Melikian
,
Johnny
Hioe
,
Julian
Greindl
,
Johannes
Gramüller
,
Matej
Žabka
 ,
Nils
Sorgenfrei
,
Thomas
Hausler
,
Fabio
Morana
and
Ruth M.
Gschwind
,
Nils
Sorgenfrei
,
Thomas
Hausler
,
Fabio
Morana
and
Ruth M.
Gschwind
 *
*
Institut für Organische Chemie, Universität Regensburg, Universitätsstraße 31, D-93053 Regensburg, Germany. E-mail: ruth.gschwind@chemie.uni-regensburg.de
First published on 6th September 2019
Abstract
The concept of hydrogen bonding for enhancing substrate binding and controlling selectivity and reactivity is central in catalysis. However, the properties of these key hydrogen bonds and their catalyst-dependent variations are extremely difficult to determine directly by experiments. Here, for the first time the hydrogen bond properties of a whole series of BINOL-derived chiral phosphoric acid (CPA) catalysts in their substrate complexes with various imines were investigated to derive the influence of different 3,3′-substituents on the acidity and reactivity. NMR 1H and 15N chemical shifts and 1JNH coupling constants of these hydrogen bonds were used to establish an internal acidity scale corroborated by calculations. Deviations from calculated external acidities reveal the importance of intermolecular interactions for this key feature of CPAs. For CPAs with similarly sized binding pockets, a correlation of reactivity and hydrogen bond strengths of the catalyst was found. A catalyst with a very small binding pocket showed significantly reduced reactivities. Therefore, NMR isomerization kinetics, population and chemical shift analyses of binary and ternary complexes as well as reaction kinetics were performed to address the steps of the transfer hydrogenation influencing the overall reaction rate. The results of CPAs with different 3,3′-substituents show a delicate balance between the isomerization and the ternary complex formation to be rate-determining. For CPAs with an identical acidic motif and similar sterics, reactivity and internal acidity correlated inversely. In cases where higher sterical demand within the binary complex hinders the binding of the second substrate, the correlation between acidity and reactivity breaks down.
Introduction
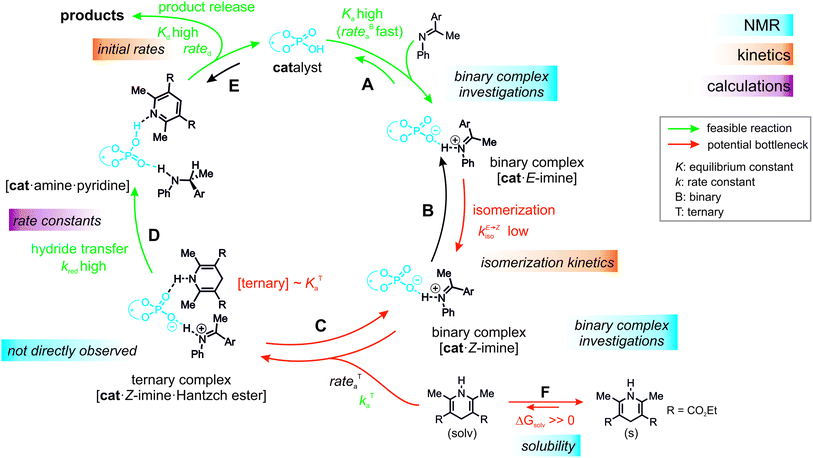
Over the past decade, a large number of reactions were developed, where enantioenriched products are formed using a chiral organic molecule with acidic functionality as catalyst.1–3 A prominent example of the so-called chiral Brønsted acid catalysis was a Strecker reaction catalyzed by peptide-based thiourea derivatives.1,4–6 One success factor of Brønsted acid catalysts in enantioselective transformations is the formation of a central hydrogen bond between catalyst and substrate, thus anchoring the structures, which favor one enantiotopic face over the other.1 Another milestone was the development of chiral phosphoric acid (CPAs) catalysts with BINOL (1,1′-bi-2-naphthol) backbones by Akiyama and Terada.7,8 These catalysts are applicable in several highly enantioselective reactions with imines such as transfer hydrogenations,9–11 reductive aminations,12,13 Mannich-type reactions14–16 and Strecker reactions.17 In particular, in the asymmetric reduction of imines with Hantzsch 1,4-dihydropyridine ester, these BINOL derived CPAs can achieve high yields as well as high enantioselectivities.12,18–20Rueping et al. proposed a catalytic cycle (Fig. 1a), where the imine is protonated by the phosphoric acid and forms a hydrogen bond assisted ion pair (step A).18 In the next step, the thermodynamically more stable E-imine is isomerized to the minor-populated Z-imine complex (step B). Calculations as well as our previous experimental study showed that the transition state of the Z-imine complex is energetically more favoured.21 Then, the Hantzsch ester approaches and a ternary complex is formed (step C). In the last step, the hydride transfer from the Hantzsch ester (step D) leads to the chiral amine (step E), while the pyridinium salt regenerates the Brønsted acid.18
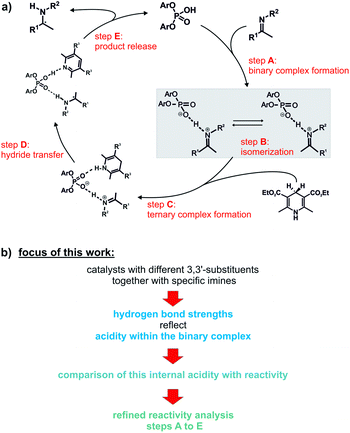 | ||
| Fig. 1 (a) Proposed catalytic cycle for the asymmetric transfer hydrogenation with CPAs;18 (b) the influence of different 3,3′-substituents of the catalyst on the hydrogen bond of the ion pair (highlighted in grey) was investigated. In addition, the effect of the varying internal acidities of the binary complexes on the overall reaction rate of the shown transfer hydrogenation was the focus of this work. | ||
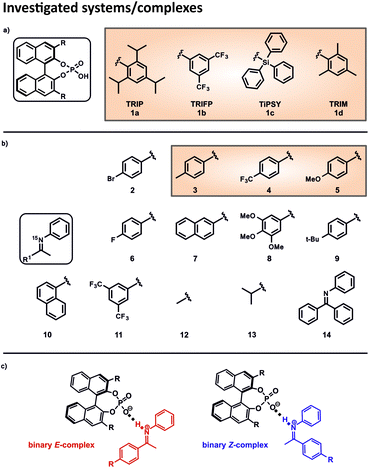
This asymmetric reduction of imines works with many different CPAs, which differ only in the 3,3′-substituents. Prominent examples are amongst others TRIP (3,3′-bis(2,4,6-triisopropylphenyl)-1,1′-binaphthyl-2,2′-diyl hydrogen phosphate), TRIFP (3,3′-bis(3,5-bis(trifluoromethyl)phenyl)-1,1′-binaphthyl-2,2′-diyl hydrogen phosphate) and TiPSY (3,3′-bis(triphenylsilyl)-1,1′-binaphthyl-2,2′-diyl hydrogen phosphate) (Fig. 2a).18,19,22 Thus, the 3,3′-substituents are the key to ee values and yields and sometimes even reverse stereoselectivity.23–26 The way that structures of the catalysts influence the outcome varies from reaction to reaction and, up to now, there have been few direct experimental measurements of relevant structural features.27 Thus, the screening of the catalysts to find the most effective BINOL-derived CPA is still the predominantly employed method in synthesis. On the contrary, in silico, the understanding of the occurring interactions and structures is by far more developed.28 One approach follows a multivariate regression model analysis, utilizing various parameters to develop a mathematical model that explains the relationship between structure and reactivity or selectivity. This model is capable of distinguishing certain crucial non-covalent interactions present between the catalyst and the substrate.29,30
In 2016, Goodman et al. introduced some parameters to describe the steric bulk of the 3,3′-substituents of the catalysts. Thus, they could show that the stereoselectivity of the asymmetric transfer hydrogenation of imines (Fig. 1a) is widely dependent on two parameters: the rotation barrier describing the proximal bulk and the AREA (θ) taking the distal bulk into account.31 Also, other groups investigated the influence of different 3,3′-substituents of CPAs in several reactions regarding the occurring transition states, the structural differences and/or the enantioselectivity by theoretical methods.32–40 Nevertheless, our recent NMR study about the influence of 3,3′ substituents on the structures and populations of binary CPA/imine complexes revealed a significant deviation of experimental populations compared to those calculated with the standard theoretical methods applied to these systems.41 In general, experimental insight into the structures involved in Brønsted acid catalysis is very rare.42,43 In earlier studies we revealed the hydrogen bond strengths and geometries of TRIP/imine complexes in detail.42 In addition, we could experimentally show that for TRIP, TRIFP, TiPSY and TRIM (3,3′-bis(2,4,6-trimethylphenyl)-1,1′-binaph-thyl-2,2′-diyl hydrogen phosphate) four different core structures of their binary CPA/imine complexes are omnipresent in solution (Type I/II E and Type I/II Z).41,43 The different 3,3′-substituents influence mainly the energetics/population of these binary complexes, however, much less their general sterically features and interaction patterns.41 Nevertheless, despite the crucial function of hydrogen bonds in Brønsted acid catalysis as structural anchor43 or regarding acidity/reactivity correlations44 detailed experimental insights about the effect of 3,3′ substituents on this hydrogen bond are elusive so far.
In general, the formation of hydrogen bonds in catalyst/substrate complexes is often highly relevant and plays a key role in the activation of the substrate. For example, in the field of asymmetric catalysis, the activation of electrophilic substrates such as carbonyls or imines seems to take place via a hydrogen bond.3,9,45,46 Also in photochemistry several examples are known, where the proposed mechanisms is based on a hydrogen-bonded species. For example, Knowles et al. could show that ketones, amides or alcohols can be converted by a proton-coupled electron transfer (PCET) and assumed hydrogen bond formation between the substrate and proton donor/acceptor prior to the electron transfer.47–49 Finally, there are various examples throughout organocatalysis, in which the substrate binding and activation via a hydrogen bonded species is proposed.50–54 However, the central hydrogen-bonded species are often in fast chemical exchange or have short lifetimes, therefore it is for most of the systems experimentally not possible to detect these hydrogen bonds.
In the literature, hydrogen bonds are described as the start of a proton transfer reaction.55,56 This means that the position of the proton inside the hydrogen bond varies depending on the acidity of the hydrogen bond donor respectively basicity of the acceptor. Limbach et al. developed on model systems a NMR spectroscopic access to the position of these hydrogen atoms inside the hydrogen bonds using an empirical correlation of the 1H and the 15N chemical shifts.57,58 This in combination with our recently developed access to the hydrogen bonds in CPA/imine complexes42 allows for the first time to tackle the effect of the 3,3′-substituent on the hydrogen bonds and thus on the acidity of the CPAs within the binary complex with NMR. This acidity may play a crucial role regarding reactivity. However, up to now there are only few experimentally determined pKa values of CPAs. In 2011, O'Donoghue et al. determined pKa values for TRIP and TRIFP in DMSO by using a spectrophotometric titration method.59,60 Here, variations of the 3,3′-substitents resulted in modulation of the pKa-values of the CPAs up to ∼1.5 pKa units (pKaTRIP (DMSO) = 4.22 and pKaTRIFP (DMSO) = 2.63).60 In acetonitrile, a similar variation range of experimental pKa values for five phosphoric acids between 12.5 and 14.0 is found (pKaTRIP (ACN) = 13.3).44 However, BINOL-derived N-triflyl-phosphoramides show significant smaller pKa values between 6.3 and 6.9.44 Thus, at least in acetonitrile, the acidity of the catalysts is significantly influenced by the acidic motif, while the 3,3′-substituents have minor effects.44 Most interestingly, in a Nazarov cyclization higher rates were found for more acidic Brønsted acids and a direct correlation between acidity and reactivity was postulated.44 Given the large deviations of CPA acidities between the previous studies and our access to hydrogen bonds in CPA imine complexes for TRIP this opens up the possibility to measure an internal acidity scale of the catalysts. Furthermore, this internal acidity analysis is of central interest for a reactivity analysis, because the acidity potentially influences any step in the catalytic cycle (see steps A to E in Fig. 1a).
Therefore, in this study, we used four CPAs with different 3,3′-substituents and several imines to develop for the first time an internal acidity scale for binary CPA/imine complexes. This scale is based on chemical shifts and 1JNH coupling constants of the binary complexes obtained by NMR at low temperatures. The resulting internal acidities of the catalysts were compared with their respective reactivity in the transfer hydrogenation. In addition, a multitude of experimental and theoretical data was used to identify the reaction steps contributing to the overall reaction rate.
Results and discussion
Investigated systems/complexes
In order to investigate the influence of different 3,3′-substituents on the acidity of CPAs and to correlate this internal acidity with the reactivity in transfer hydrogenations, we selected four different CPAs and twelve imines with different electronic and steric properties (Fig. 2). The binary complexes of the four CPAs 1a–1d with the imines 2 and 6–13 were used to cover the whole range of the Steiner–Limbach curve, while imines 3, 4 and 5 were chosen for a detailed hydrogen bond analysis within the binary complexes. Altogether, we screened 32 different binary complexes.15N labelling of the imines allowed the access to the 15N chemical shifts42 and CD2Cl2 was chosen as solvent, since CD2Cl2 provides the best chemical shift dispersion and smallest line widths of all solvents investigated. To reach the slow exchange regime of the hydrogen bonds all spectra were recorded at 180 K unless otherwise mentioned.Determination of the internal acidity of the CPAs
Since external pKa measurements/calculations are performed versus protons, whereas in the transfer hydrogenation a binding to an imine occurs, there is no reason why there necessarily should be a correlation between external acidity and reactivity. Therefore, an internal acidity scale for the CPAs was constructed within the binary CPA imine complexes to be later compared to the reactivity. The Steiner–Limbach correlation can be used to characterize hydrogen bonds in phosphoric acid catalyst/imine complexes as previously demonstrated for TRIP/imine complexes.42 By plotting the 1H chemical shift δ(OHN) of the acidic proton against the 15N chemical shift δ(OHN) of the basic nitrogen, a parabolic correlation curve can be fitted through the data points (see Fig. 3 and ESI† Chapter 3). All CPA/imine complexes investigated in this work feature a strong hydrogen bond with 1H chemical shifts ranging from 15 to 19 ppm (see highlighted points in Fig. 3a). Their referenced 15N chemical shifts (for details see ESI† Chapter 3.2) range from −90 to −150 ppm. Furthermore, for many of these binary complexes magnetisation transfers across the hydrogen bond via3hJPN and 2hJPH are detectable. All of these parameters are typical for a strong hydrogen bond with a substantial covalent character providing high geometrical preferences for a linear arrangement. The position of these binary complexes on the left side of the curve (highlighted in Fig. 3a) shows that these binary complexes have a partial ion pair character.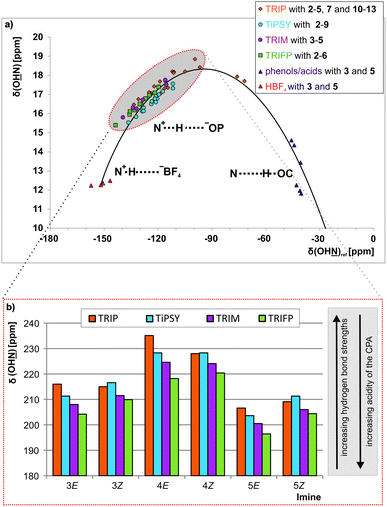 | ||
| Fig. 3 (a) In the Steiner–Limbach curve the δ(OHN) is plotted versus δ(OHN) of the hydrogen bonded complexes. All CPA/imine complexes are located on the left side of the curve (highlighted in grey) and form hydrogen-bond assisted ion pairs. The data for the complexes with TRIP, HBF4, phenols and carboxylic acids were taken from ref. 42 All 15N chemical shifts are referenced to {δ(OHN)ref = δ(OHN)exp − 340 ppm} (for details and exact values see ESI† Chapter 3); (b) the experimental δ(OHN) of the imines 3, 4 and 5 in the binary complexes with the CPAs 1a–1d are shown. | ||
Since in the first step of the asymmetric transfer hydrogenation the activation of the imine via a hydrogen bond formation is assumed (Fig. 1a), this hydrogen bond of the binary complex can be used to monitor the binding between catalyst and substrate. In general, three parameters can be used to determine the hydrogen bond strength: the chemical shifts of 1H and 15N as well as the 1JNH coupling constants. While the 1H chemical shift is known to be significantly influenced by anisotropic shielding effects e.g. from aromatic moieties and other neighbourhood effects, the 15N chemical shift of TRIP/imine complexes was shown to reflect directly the hydrogen bond situation.42 Therefore, the 15N chemical shift was used as a descriptor for the hydrogen bond strength and acidity of the catalyst, which also directly correlates with the 1JNH coupling constant (see discussion below).
Internal acidity: chemical shift analysis
The encircled area in the Steiner–Limbach curve in Fig. 3a and the corresponding graph in Fig. 3b, representing complexes with imines 3, 4 and 5, reveal different hydrogen bond strengths for the four catalysts and common trends for E- and Z-imines (for details see ESI† Chapter 3.6). In general, for all CPA/Z-imine complexes stronger hydrogen bonds are observed than for the complexes with E-imines, as indicated by the low field shift of the hydrogen atom as well as the nitrogen atom. Due to the reduced steric requirements of the imine in the Z-configuration the imine can approach closer to the catalyst. This is corroborated by the experimentally derived atomic distances of the hydrogen bonds of the TRIP complexes42 and further supported by the distances in the calculated structures of various binary complexes (for coordinates see ESI† Chapter 17). Furthermore, within the E- and Z-complexes different trends regarding the hydrogen bond strengths upon variation of the catalyst are observed: for the E-complexes TRIP forms the strongest hydrogen bonds (least negative 15N chemical shift), followed by TiPSY, TRIM and TRIFP. For Z-complexes TiPSY forms the strongest hydrogen bond directly followed by TRIP and then with a slight gap again followed by TRIM and TRIFP. These trends of the hydrogen bond strengths (TRIP > TiPSY > TRIM > TRIFP for E-complexes and TiPSY ≥ TRIP > TRIM > TRIFP for Z-complexes) were observed for imines 3–5 and could be confirmed by the 1JNH coupling constants (see below). The hydrogen bond strengths can be directly correlated with the internal acidity of the CPA,61 because with a given imine a variation of the acidity of the catalyst changes the position of the proton in the hydrogen bond. In case of the investigated hydrogen assisted ion pair complexes, which are located on the left side of the Steiner–Limbach curve, a higher acidity effects a weaker hydrogen bond. That means a higher acidity or lower pKa value of the CPA relates to a reduced 1H and 15N chemical shift (larger negative value for the referenced 15N) and an increased 1JNH coupling constant. In summary, the chemical shift analysis yielded two different internal acidity scales, i.e. scales for the binary E-complexes (pKaTRIP > pKaTiPSY > pKaTRIM > pKaTRIFP) and the Z-complexes (pKaTiPSY ≥ pKaTRIP > pKaTRIM > pKaTRIFP).Internal acidity: 1JNH coupling constants analysis
The analysis of the 1JNH coupling constants (Fig. 4) confirms the internal acidity of the catalyst for both E- and Z-complexes. Furthermore, the Hammett σpara values of the aryl substituents of the imines correlate with the coupling constants for E- and Z-complexes of imine 3–6 (see ESI† Chapter 5). Given the fact that the hydrogen bond of all investigated CPA/imine complexes tends towards ionic complexes, i.e. to a complete proton transfer, lower 1JNH coupling constants correspond to stronger hydrogen bonds. Within all investigated CPA/E-imine complexes TRIP shows the smallest 1JNH coupling constants, followed by TiPSY, TRIM and TRIFP. This is in accordance with the internal acidities (pKaTRIP > pKaTiPSY > pKaTRIM > pKaTRIFP) discussed before based on the 15N chemical shifts. For the Z-complexes, in almost all cases slightly smaller 1JNH coupling constants than for E-complexes were observed, corroborating the stronger hydrogen bonds derived from the chemical shift analysis (see above). For the CPA/Z-imine complexes 1JNH coupling constants for TiPSY are slightly smaller than for TRIP, suggesting stronger hydrogen bond and shorter distance from the catalyst, thus congesting the active catalyst pocket (Fig. 4).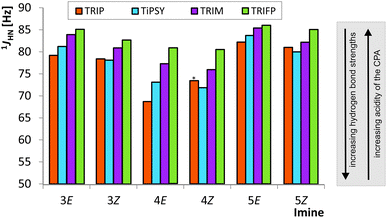 | ||
| Fig. 4 The experimental CPA/imine 1JHN coupling constants are shown for E- and Z-imines of 3, 4 and 5. The following trend is observed for the E-imines: 1JHN TRIP < 1JHN TIPSY < 1JHN TRIM < 1JHN TRIFP. For Z-complexes slightly different trend was found: 1JHN TIPSY < 1JHN TRIP < 1JHN TRIM < 1JHN TRIFP. Due to overlap the 1JHN of TRIP/4Z was determined from HN-HMBC spectra (marked by an asterisk; for all values see ESI† Chapter 3.3). | ||
In our theoretical calculations, the same qualitative trend for the scalar coupling constants (1JNH TRIP < 1JNH TiPSY < 1JNH TRIM < 1JNH TRIFP, for details see ESI† Chapter 4) could be reproduced for the E-complexes. For the Z-complexes, the switched order of TRIP and TiPSY is not reflected in the calculations.
Comparison of internal vs. calculated external acidity
Next, the developed internal acidities of the catalysts were compared to experimental and theoretical external acidities. The experimental, external acidities of TRIFP and TRIP as described by O'Donoghue (pKaTRIFP < pKaTRIP) in DMSO,60 correlate at least in their trend with our internal acidities. Absolute pKa values of many CPAs in DMSO (SMD) at 298 K using various thermodynamic cycles have been also computed at DFT level of theory.62 Thus, to compare the internal acidities in DCM at 180 K with the external acidity, we calculated the relative external acidity of TRIP, TRIM and TiPSY to TRIFP (Table 1). In general, the relative external acidities of the investigated CPAs in DCM confirm the previous calculated relative pKa values in DMSO within ∼0.5 pKa units. This indicates that the implicit solvent model may vary the absolute pKa values but not the order. Thus, regardless of the choice of dielectric medium, the relative external acidity scale deviates significantly from the internal acidity scale. Especially the almost identical internal acidities of TRIM and TiPSY are not reflected in the calculated external acidities. As a result, this internal acidity scale can be used as a direct experimental indicator for the importance of intermolecular interactions such as dispersion63,64 in Brønsted acid catalysis, which was already proposed for CPAs and other catalytic systems65,66 but so far only accessible via theoretical calculations/analyses or multicomponent experimental data such as reactivities.64,67,68| pKa,calc in DCM at 180 K (relative to TRIFP) | pKa,calc in DMSO at 298 K (relative to TRIFP)52 | |
|---|---|---|
| TRIP | +0.85 | +0.55 |
| TRIM | +1.57 | +2.26 |
| TiPSY | +6.00 | n.a. |
The presented first internal acidity scale of different CPAs in their binary CPA/imine complexes and to our knowledge the first systematic and broad experimental NMR-study about the trends in hydrogen bond strengths within catalyst/substrate complexes in enantioselective catalysis shows that the intermolecular interactions between catalyst and substrate and potentially also the modulated solvent interactions of the complex significantly affect even the relative acidities. Furthermore, the comparison of the internal with the external acidity may in the future represent a useful tool to evaluate the non-covalent interactions in these complexes and especially the interactions of the 3,3′-substituents, because at least for the imines 3–5 there are common internal acidity trends.
Comparison of reactivity and internal acidity
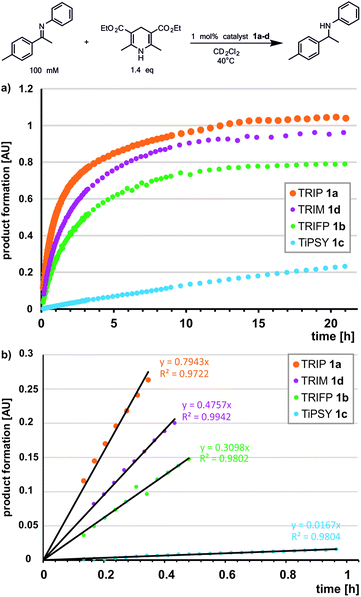
Previously, a correlation was postulated between the acidity of CPAs and their reactivity in a different system. In a Nazarov cyclisation, the highest reactivity was observed for the most acidic CPA catalyst.44 With the internal CPA acidities at hand, we tested whether this relationship is transferable to the transfer hydrogenation of imines. To compare the internal acidities with reaction rates, the reactivities were determined in CD2Cl2.In the transfer hydrogenation with imine 3 we identified TRIP as the most reactive catalyst. TRIM showed a slightly lower reactivity, followed by TRIFP, while for TiPSY a considerable drop in reactivity was observed (Fig. 5). For the transfer hydrogenation of imine 5 under identical conditions, the order of reactivity is conserved. However, we observed an overall significantly lower reaction rate, which correlated with the Hammett σpara values of the imine aryl substituents (for details see ESI† Chapter 7.3). Obviously, the order of reactivity for the investigated transfer hydrogenation (TRIP > TRIM > TRIFP ≫ TiPSY) does not match the internal acidity scale, which show that TRIP and TiPSY have similar acidities (weakest acids pKaTRIP ≥ pKaTiPSY > pKaTRIM > pKaTRIFP). Since the low reactivity of TiPSY (94.6% in the initial linear product build up compared to TRIFP) was already recognized in various reactions, e.g. a higher catalyst loading is often necessary, TiPSY might be an exception. Excluding TiPSY, the remaining catalysts TRIP, TRIM and TRIFP show an inverse correlation between reactivity and internal acidity of the catalyst, i.e. a direct correlation with H-bond strength.69 This is in contrast to the previously reported direct correlation with the catalyst acidity in a Nazarov cyclisation.44
Reactivity analysis
Next, it was investigated which of the individual steps of the reaction determines the reactivity to obtain a more detailed understanding and to rationalize TiPSY as an outlier.In general, there are five possible rate-determining steps for the investigated transfer hydrogenation catalytic cycle, all of them potentially affected by the internal acidity: binary complex formation (Fig. 6, step A), E- to Z-imine isomerization (step B), formation of the ternary complex (step C), hydride transfer (step D) and product release/product inhibition (step E).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and directly measuring its NMR spectra. The equilibrium between free imine and imine in the binary complex enables the experimental access to the association constant Kba of the binary complex. 1
1) and directly measuring its NMR spectra. The equilibrium between free imine and imine in the binary complex enables the experimental access to the association constant Kba of the binary complex. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-samples of the catalysts 1a–1d and imine 5 show for all catalysts approximately the same amount of free imine (TRIP: 26%, TRIFP: 16%, TRIM: 35% and TiPSY: 27% free imine; for Ka values see Table 2; for spectra see ESI† Chapter 8). The same outcome is observed even with sample preparation at 180 K (see ESI† Chapter 9). At this low temperature condition, no product formation takes place (see ESI† Chapter 10) proving that the binary complex formation (rateBa) is faster than the observed overall rate (rateobs). This indicates a sufficient association constant for this pre-equilibrium (especially at 1 mol% of catalyst, the imine is likely to saturate the catalyst) and suggests kinetics of the binary complex formation not contributing to the rate determining step.
1-samples of the catalysts 1a–1d and imine 5 show for all catalysts approximately the same amount of free imine (TRIP: 26%, TRIFP: 16%, TRIM: 35% and TiPSY: 27% free imine; for Ka values see Table 2; for spectra see ESI† Chapter 8). The same outcome is observed even with sample preparation at 180 K (see ESI† Chapter 9). At this low temperature condition, no product formation takes place (see ESI† Chapter 10) proving that the binary complex formation (rateBa) is faster than the observed overall rate (rateobs). This indicates a sufficient association constant for this pre-equilibrium (especially at 1 mol% of catalyst, the imine is likely to saturate the catalyst) and suggests kinetics of the binary complex formation not contributing to the rate determining step.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were reached. Next, the temperature was raised to 230 K, the light was switched off, and the decay curves of the thermal Z- to E-back-isomerization were recorded (for details see ESI† Chapter 11). Fitting of these curves allowed us to obtain the activation barriers for the Z- to E-isomerization of the binary complexes. From these data and the known Boltzmann distribution of the binary E- and Z-complexes in the thermodynamic equilibrium (1H spectra), the E- to Z-isomerization rates were calculated. This experimental access to the isomerization process is independent of the exact mechanism of isomerization (inversion, protonation-rotation and addition-rotation-elimination71–74), which may be differently operative dependent on the catalyst.
1 were reached. Next, the temperature was raised to 230 K, the light was switched off, and the decay curves of the thermal Z- to E-back-isomerization were recorded (for details see ESI† Chapter 11). Fitting of these curves allowed us to obtain the activation barriers for the Z- to E-isomerization of the binary complexes. From these data and the known Boltzmann distribution of the binary E- and Z-complexes in the thermodynamic equilibrium (1H spectra), the E- to Z-isomerization rates were calculated. This experimental access to the isomerization process is independent of the exact mechanism of isomerization (inversion, protonation-rotation and addition-rotation-elimination71–74), which may be differently operative dependent on the catalyst.
At 230 K, the experimentally determined isomerization process is fastest for TRIP/5 (kE→Z = 1.36 × 10−3 1 s−1) and similar for TiPSY/5 (kE→Z = 5.71 × 10−4 1 s−1) and TRIFP/5 (kE→Z = 4.45 × 10−4 1 s−1). While the similar offset in the isomerization rates, kiso(TRIP/5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kiso(TRIFP/5) = 3.05 and in the observed reaction rate, robs(TRIP/5)
kiso(TRIFP/5) = 3.05 and in the observed reaction rate, robs(TRIP/5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) robs(TRIFP/5) = 3.43 fit for TRIP and TRIFP, those for TRIP and TiPSY show a large deviation: kiso(TRIP/5)
robs(TRIFP/5) = 3.43 fit for TRIP and TRIFP, those for TRIP and TiPSY show a large deviation: kiso(TRIP/5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kiso(TiPSY/5) = 2.38 and robs(TRIP/5): robs(TiPSY/5) = 34.33 (see ESI† Chapter 7.3 for reaction kinetic of CPA/5). For TRIM such an analysis was not possible due to severe signal overlap. Thus, our results showed that the relative rate of transfer hydrogenation between TRIP and TRIFP is in the same qualitative trend with their relative isomerization rates. However, for the reaction with TiPSY, additional factors may contribute to the steps affecting the overall reaction rate.
kiso(TiPSY/5) = 2.38 and robs(TRIP/5): robs(TiPSY/5) = 34.33 (see ESI† Chapter 7.3 for reaction kinetic of CPA/5). For TRIM such an analysis was not possible due to severe signal overlap. Thus, our results showed that the relative rate of transfer hydrogenation between TRIP and TRIFP is in the same qualitative trend with their relative isomerization rates. However, for the reaction with TiPSY, additional factors may contribute to the steps affecting the overall reaction rate.
Additionally, the low solubility of Hantzsch ester (endergonic ΔGsolv in step F) in the organic solvents used in this study reduces the concentration of the ternary complex even further and thus amplifies the problem of a low to moderate association constant (KTa). Given these experimental results the ternary complex formation/concentration can contribute to the reaction rate or even become the rate determining step and thus influence the relative reactivities of the catalysts. In addition, for a non-isomerizable imine 14, a 1st order dependence of the dissolved Hantzsch ester concentration on the observed overall reaction rate was found (see ESI† Chapter 7.4). A similar shift of the rate determining step due to concentration modulations has been intentionally used in our previous mechanistic study of dienamines.78 Assuming the ternary complex formation contributes significantly to the steps determining the overall reaction rate and the solubility of Hantzsch ester is similar in all reactions, the origin of differences in reactivity with various catalysts lies in the alternation of association constant (KTa) and/or barrier for the ternary complex formation (kTa). Especially the bulkiness of the 3,3′-substituents and their effect on the size of the binding pocket is expected to affect the association constant (KTa) and barrier for formation (kTa).
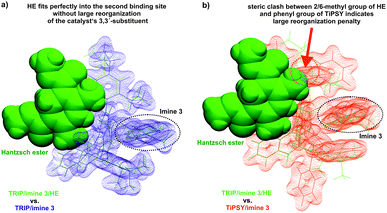
Indeed, the AREA (θ) value, a sterical descriptor introduced by Goodman et al., which describes the cone angle of the substrate binding pocket of the CPA is for TiPSY significantly smaller than for the other CPAs.31 These values (TiPSY: 29°, TRIFP: 62°, TRIM: 61°, TRIP: 51°)31 demonstrate that the 3,3′-substituents of TiPSY are sterically by far more demanding and may therefore hinder the formation of the ternary complex. Despite the largest sterical hindrance of TiPSY (smallest AREA (θ)), for the binary Z-complex the strongest hydrogen bond was found, i.e. the formation of the binary complex is not affected by the steric demands of the SiPh3-groups. Thus, the flexibility of the substituents allows the structural adaptation of the catalyst to the imine. This is also corroborated by the experiments, which showed comparable association constants Ka for all catalysts (Table 2). After the binary complex is formed, the degree of freedom of the 3,3′-substituents is reduced in order to maximize the interaction with the imine enthalpically. The structural comparison between TRIP/3 and TiPSY/3 revealed a sterical shield for the Hantzsch ester binding for TiPSY/3, which indicates a large reorganization penalty (Fig. 7). In contrast, for TRIP/3 almost no reorganization is required. Thus, the steric of the 3,3′-substituents can explain the large difference in the reactivity of TiPSY compared to the other structurally analogous CPAs.
Comprehensive reactivity analysis
All of the experimental data discussed above are summarized in Table 2. Based on the results presented there, a previously established correlation of an increased acidity of the catalyst giving higher reactivity in chiral phosphoric acid-catalysed reactions44 cannot be transferred to the asymmetric transfer hydrogenation of imines. However, a possible inverse relationship of the internal acidity for TRIP, TRIM and TRIFP with the reactivity could be observed, thus in our system, the less acidic catalysts give the fastest reactions (see Table 2). In contrast, TiPSY does not follow this trend. Despite having the strongest hydrogen bond, as well as a binary complex association constant Ka and an isomerization rate constant kiso, comparable to the other catalysts, the observed reactivity is by far the slowest. The only parameter deviating significantly from the other catalysts is the AREA (θ) value, which is extremely small. In addition, the blockage of the second binding site in TiPSY complexes may amplify the issue of the ternary complex formation within the steps determining the overall reaction rate (see discussion above and Fig. 7). The experimental and theoretical studies on aromatic imines provided, show that the formation of the binary complex as well as product inhibition can be neglected as rate determining steps. Furthermore, the rate constant of hydride transfer (kred) is by far higher than for the isomerization (kiso). Finally, isomerization and ternary complex formation have to be decisive for the observed overall reaction rate. Thus, the comparison of isomerization rates, reaction rates and ternary complex formation of CPAs with different 3,3′-substituents shows that in a delicate equilibrium isomerization rates and ternary complex formation determine the overall reaction rate. Thus, the presented results suggest that within a similar acidic motif and similar sterics of the CPAs the reactivity is inverse correlated to the internal acidity of the catalyst, i.e. directly correlated with the H-bond strength in the binary complex. For CPAs with small AREA (θ) values the steric bulk seem to overrule the internal acidity and the reactivity is significantly decreased.Conclusions
By means of NMR-spectroscopic studies, a hydrogen bond analysis of 32 CPA/imine complexes regarding 1H and 15N chemical shifts as well as 1JNH coupling constants was established. This allowed for the first time to implement an internal acidity scale of CPA/imine complexes as a direct experimental tool to probe a correlation between acidity of the catalyst and reactivity. All CPA/imine complexes form strong, charge-assisted hydrogen bonds. The analysis of the chemical shifts and the resulting hydrogen bond strengths of the four Brønsted acid catalysts TRIP, TiPSY, TRIM and TRIFP show two different acidity scales for E- and Z-imines complexes (E-imines: pKaTRIP > pKaTiPSY > pKaTRIM > pKaTRIFP; Z-imines. pKaTiPSY > pKaTRIP > pKaTRIM > pKaTRIFP). All investigated imines showed the same trend. The internal acidity analysis of the CPAs by chemical shifts was corroborated by experimentally determined 1JNH coupling constants and theoretical calculations of the complexes. Our calculated external acidity scale in DCM (pKaTRIFP < pKaTRIP < pKaTRIM < pKaTiPSY) deviates from the experimental internal acidity scale. This shows that intermolecular interactions in CPA/imine complexes are essential to describe the acidic properties of these complexes correctly and either experimental data or calculations of the binary complexes have to be accounted for.While the calculated external acidity scale does not exhibit any correlation with the reactivity of the transfer hydrogenation, the internal acidity at least of TRIP, TRIM and TRIFP shows an inverse correlation. Thus, the least acidic TRIP with the strongest hydrogen bond gives the highest reactivity. However, TiPSY does not follow this trend, demonstrating that for Brønsted acids with an identical acidic functional group, also other factors may contribute. Isomerization rates, reaction rates and ternary complex formation data of CPAs with different 3,3′-substituents show that a delicate balance between the isomerization and the ternary complex formation is potentially determining the overall reaction rate. The collected experimental data of TRIP, TRIM and TRIFP suggest that the lower the internal acidity of the catalyst, the higher the isomerization rates and the higher the reactivity in the transfer hydrogenation. This trend can be predicted by calculating internal acidities (i.e.1JNH coupling constants), which match the experimental results best. However, for a small binding pocket the correlation with the internal acidities fails, i.e. for TiPSY, still a very strong hydrogen bond is formed, but the reactivity breaks down most probably due to sterical congestion at the active site for the second binding partner.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial Support was provided by the European Research Council (ERC-CoG 614182 – IonPairsAtCatalysis) and intellectual support was provided by SPP 1807 dispersion.Notes and references
- M. Terada, Synthesis, 2010, 1929–1982 CrossRef CAS.
- D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047–9153 CrossRef CAS.
- M. Mahlau and B. List, Angew. Chem., Int. Ed., 2013, 52, 518–533 CrossRef CAS.
- M. S. Sigman and E. N. Jacobsen, J. Am. Chem. Soc., 1998, 120, 4901–4902 CrossRef CAS.
- M. S. Sigman, P. Vachal and E. N. Jacobsen, Angew. Chem., Int. Ed., 2000, 39, 1279–1281 CrossRef CAS.
- P. Vachal and E. N. Jacobsen, J. Am. Chem. Soc., 2002, 124, 10012–10014 CrossRef CAS.
- T. Akiyama, J. Itoh, K. Yokota and K. Fuchibe, Angew. Chem., Int. Ed., 2004, 43, 1566–1568 CrossRef CAS.
- D. Uraguchi and M. Terada, J. Am. Chem. Soc., 2004, 126, 5356–5357 CrossRef CAS.
- M. Rueping, T. Theissmann, M. Stoeckel and A. P. Antonchick, Org. Biomol. Chem., 2011, 9, 6844–6850 RSC.
- Q. Yin, S.-G. Wang and S.-L. You, Org. Lett., 2013, 15, 2688–2691 CrossRef CAS.
- T. Marcelli, P. Hammar and F. Himo, Chem.–Eur. J., 2008, 14, 8562–8571 CrossRef CAS.
- R. I. Storer, D. E. Carrera, Y. Ni and D. W. C. Macmillan, J. Am. Chem. Soc., 2006, 128, 84–86 CrossRef CAS.
- K. Saito and T. Akiyama, Chem. Commun., 2012, 48, 4573–4575 RSC.
- M. Yamanaka, J. Itoh, K. Fuchibe and T. Akiyama, J. Am. Chem. Soc., 2007, 129, 6756–6764 CrossRef CAS.
- X. Xu, Y. Qian, L. Yang and W. Hu, Chem. Commun., 2010, 47, 797–799 RSC.
- E. P. Ávila, R. M. S. Justo, V. P. Gonçalves, A. A. Pereira, R. Diniz and G. W. Amarante, J. Org. Chem., 2015, 80, 590–594 CrossRef PubMed.
- K. Shen, X. Liu, Y. Cai, L. Lin and X. Feng, Chem.–Eur. J., 2009, 15, 6008–6014 CrossRef CAS.
- M. Rueping, E. Sugiono, C. Azap, T. Theissmann and M. Bolte, Org. Lett., 2005, 7, 3781–3783 CrossRef CAS.
- S. Hoffmann, A. M. Seayad and B. List, Angew. Chem., Int. Ed., 2005, 44, 7424–7427 CrossRef CAS.
- M. Rueping, C. Azap, E. Sugiono and T. Theissmann, Synlett, 2005, 2367–2369 CrossRef CAS.
- P. Renzi, J. Hioe and R. M. Gschwind, J. Am. Chem. Soc., 2017, 139, 6752–6760 CrossRef CAS.
- S. G. Ouellet, A. M. Walji and D. W. C. Macmillan, Acc. Chem. Res., 2007, 40, 1327–1339 CrossRef CAS.
- S. Liao, I. Čorić, Q. Wang and B. List, J. Am. Chem. Soc., 2012, 134, 10765–10768 CrossRef CAS.
- X. Yu, Y. Wang, G. Wu, H. Song, Z. Zhou and C. Tang, Eur. J. Inorg. Chem., 2011, 3060–3066 CrossRef CAS.
- Q. Kang, Z.-A. Zhao and S.-L. You, Org. Lett., 2008, 10, 2031–2034 CrossRef CAS.
- Q. Gu, Z. Rong, C. Zheng and S. You, J. Am. Chem. Soc., 2010, 132, 4056–4057 CrossRef CAS PubMed.
- C. Min and D. Seidel, Chem. Soc. Rev., 2017, 46, 5889–5902 RSC.
- R. Maji, S. C. Mallojjala and S. E. Wheeler, Chem. Soc. Rev., 2018, 47, 1142–1158 RSC.
- A. J. Neel, A. Milo, M. S. Sigman and F. D. Toste, J. Am. Chem. Soc., 2016, 138, 3863–3875 CrossRef CAS.
- M. Orlandi, F. D. Toste and M. S. Sigman, Angew. Chem., Int. Ed., 2017, 56, 14080–14084 CrossRef CAS PubMed.
- J. P. Reid and J. M. Goodman, J. Am. Chem. Soc., 2016, 138, 7910–7917 CrossRef CAS PubMed.
- S. E. Wheeler, T. J. Seguin, Y. Guan and A. C. Doney, Acc. Chem. Res., 2016, 49, 1061–1069 CrossRef CAS.
- T. J. Seguin and S. E. Wheeler, Angew. Chem., Int. Ed., 2016, 55, 15889–15893 CrossRef CAS.
- T. J. Seguin and S. E. Wheeler, ACS Catal., 2016, 6, 7222–7228 CrossRef CAS.
- R. Maji, P. A. Champagne, K. N. Houk and S. E. Wheeler, ACS Catal., 2017, 7, 7332–7339 CrossRef CAS.
- M. Orlandi, M. J. Hilton, E. Yamamoto, F. D. Toste and M. S. Sigman, J. Am. Chem. Soc., 2017, 139, 12688–12695 CrossRef CAS PubMed.
- M. Orlandi, J. A. S. Coelho, M. J. Hilton, F. D. Toste and M. S. Sigman, J. Am. Chem. Soc., 2017, 139, 6803–6806 CrossRef CAS.
- R. B. Sunoj, Acc. Chem. Res., 2016, 49, 1019–1028 CrossRef CAS.
- J. P. Reid and J. M. Goodman, Chem.–Eur. J., 2017, 23, 14248–14260 CrossRef CAS.
- F. Duarte and R. S. Paton, J. Am. Chem. Soc., 2017, 139, 8886–8896 CrossRef CAS.
- M. Melikian, J. Gramüller, J. Hioe, J. Greindl and R. M. Gschwind, Chem. Sci., 2019, 10, 5226–5234 RSC.
- N. Sorgenfrei, J. Hioe, J. Greindl, K. Rothermel, F. Morana, N. Lokesh and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 16345–16354 CrossRef CAS.
- J. Greindl, J. Hioe, N. Sorgenfrei, F. Morana and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 15965–15971 CrossRef CAS.
- K. Kaupmees, N. Tolstoluzhsky, S. Raja, M. Rueping and I. Leito, Angew. Chem., Int. Ed., 2013, 52, 11569–11572 CrossRef CAS.
- M. S. Taylor and E. N. Jacobsen, Angew. Chem., Int. Ed., 2006, 45, 1520–1543 CrossRef CAS.
- R. J. Phipps, G. L. Hamilton and F. D. Toste, Nat. Chem., 2012, 4, 603–614 CrossRef CAS.
- Q. Zhu, D. E. Graff and R. R. Knowles, J. Am. Chem. Soc., 2018, 140, 741–747 CrossRef CAS.
- H. G. Yayla, H. Wang, K. T. Tarantino, H. S. Orbe and R. R. Knowles, J. Am. Chem. Soc., 2016, 138, 10794–10797 CrossRef CAS.
- G. Qiu and R. R. Knowles, J. Am. Chem. Soc., 2019, 141, 2721–2730 CrossRef CAS.
- K. Gratzer, V. Diemer and J. Clayden, Org. Biomol. Chem., 2017, 15, 3585–3589 RSC.
- A. Eisenhofer, J. Hioe, R. M. Gschwind and B. König, Eur. J. Inorg. Chem., 2017, 2194–2204 CrossRef CAS.
- H. Rahaman, Ú. Madarász, I. Pápai and P. M. Pihko, Angew. Chem., Int. Ed., 2011, 50, 6123–6127 CrossRef CAS.
- A. J. Neuvonen, T. Földes, Á. Madarász, I. Pápai and P. M. Pihko, ACS Catal., 2017, 7, 3284–3294 CrossRef CAS.
- T. Kano and K. Maruoka, Chem. Commun., 2008, 5465–5473 RSC.
- W. Tang, S. Johnston, J. A. Iggo, N. G. Berry, M. Phelan, L. Lian, J. Bacsa and J. Xiao, Angew. Chem., Int. Ed., 2013, 52, 1668–1672 CrossRef CAS.
- L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2008, 130, 8741–8747 CrossRef.
- H. Benedict, I. G. Shenderovich, O. L. Malkina, V. G. Malkin, G. S. Denisov, N. S. Golubev and H. H. Limbach, J. Am. Chem. Soc., 2000, 122, 1979–1988 CrossRef CAS.
- S. Sharif, G. S. Denisov, M. D. Toney and H. H. Limbach, J. Am. Chem. Soc., 2007, 129, 6313–6327 CrossRef CAS.
- A. Kuett, I. Leito, I. Kaljurand, L. Soovaeli, V. M. Vlasov, L. M. Yagupolskii and I. A. Koppel, J. Org. Chem., 2006, 71, 2829–2838 CrossRef CAS.
- P. Christ, A. G. Lindsay, S. S. Vormittag, J.-M. Neudörfl, A. Berkessel and A. C. O'Donoghue, Chem.–Eur. J., 2011, 17, 8524–8528 CrossRef CAS.
- S. Sharif, D. Schagen, M. D. Toney and H.-H. Limbach, J. Am. Chem. Soc., 2007, 129, 4440–4455 CrossRef CAS.
- C. Yang, X. S. Xue, J. L. Jin, X. Li and J. P. Cheng, J. Org. Chem., 2013, 78, 7076–7085 CrossRef CAS.
- S. Rösel, J. Becker, W. D. Allen and P. R. Schreiner, J. Am. Chem. Soc., 2018, 140, 14421–14432 CrossRef.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- R. Y. Liu, S. L. Buchwald, P. Liu, Y. Yang, G. Lu, D. S. Lambrecht and C. Fang, J. Am. Chem. Soc., 2017, 139, 16548–16555 CrossRef.
- X. Cai, A. Tohti, C. Ramirez, H. Harb, J. C. Fettinger, H. P. Hratchian and B. J. Stokes, Org. Lett., 2019, 21, 1574–1577 CrossRef CAS.
- D. Seebach, U. Groselj and W. B. Schweizer, Helv. Chim. Acta, 2010, 93, 1–16 CrossRef CAS.
- A. Armstrong, R. A. Boto, P. Dingwall, J. Contreras-García, M. J. Harvey, N. J. Mason and H. S. Rzepa, Chem. Sci., 2014, 5, 2057–2071 RSC.
- No absolute correlation between ee values and H-bond strength/internal acidity was identified. Relative correlations are under current investigation.
- C. Feldmeier, H. Bartling, E. Riedle and R. M. Gschwind, J. Magn. Reson., 2013, 232, 39–44 CrossRef CAS.
- C. H. Bushweller, J. W. O'Neil and H. S. Bilofsky, Tetrahedron, 1971, 27, 5761–5766 CrossRef CAS.
- C. H. Bushweller, J. W. O'Neil and H. S. Bilofsky, J. Am. Chem. Soc., 1970, 92, 6349–6350 CrossRef CAS.
- M. I. Rodríguez-Franco, I. Dorronsoro, A. Castro and A. Martínez, Tetrahedron, 2000, 56, 1739–1743 CrossRef.
- M. Dewar and B. Jennings, Tetrahedron Lett., 1970, 11, 339–342 CrossRef.
- L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2008, 130, 8741–8747 CrossRef.
- L. Simón and J. M. Goodman, J. Org. Chem., 2011, 76, 1775–1788 CrossRef.
- J. P. Reid, L. Simón and J. M. Goodman, Acc. Chem. Res., 2016, 49, 1029–1041 CrossRef CAS.
- A. Seegerer, J. Hioe, M. M. Hammer, F. Morana, P. J. W. Fuchs and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 9864–9873 CrossRef CAS.
- V. N. Wakchaure, P. S. J. Kaib, M. Leutzsch and B. List, Angew. Chem., Int. Ed., 2015, 54, 11852–11856 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc02342a |
| This journal is © The Royal Society of Chemistry 2019 |