Open Access Article
Open Access ArticleHammett neural networks: prediction of frontier orbital energies of tungsten–benzylidyne photoredox complexes†
Alexander M.
Chang
 ,
Jessica G.
Freeze
,
Jessica G.
Freeze
 and
Victor S.
Batista
*
and
Victor S.
Batista
*
Department of Chemistry, Energy Sciences Institute, Yale University, New Haven, CT 06520, USA. E-mail: victor.batista@yale.edu
First published on 12th June 2019
Abstract
The successful application of Hammett parameters as input features for regressive machine learning models is demonstrated and applied to predict energies of frontier orbitals of highly reducing tungsten–benzylidyne complexes of the form W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CArR)L4X. Using a reference molecular framework and the meta- and para-substituent Hammett parameters of the ligands, the models predict energies of frontier orbitals that correlate with redox potentials. The regressive models capture the multivariate character of electron-donating trends as influenced by multiple substituents even for non-aryl ligands, harnessing the breadth of Hammett parameters in a generalized model. We find a tungsten catalyst with tetramethylethylenediamine (tmeda) equatorial ligands and axial methoxyl substituents that should attract significant experimental interest since it is predicted to be highly reducing when photoactivated with visible light. The utilization of Hammett parameters in this study presents a generalizable and compact representation for exploring the effects of ligand substitutions.
CArR)L4X. Using a reference molecular framework and the meta- and para-substituent Hammett parameters of the ligands, the models predict energies of frontier orbitals that correlate with redox potentials. The regressive models capture the multivariate character of electron-donating trends as influenced by multiple substituents even for non-aryl ligands, harnessing the breadth of Hammett parameters in a generalized model. We find a tungsten catalyst with tetramethylethylenediamine (tmeda) equatorial ligands and axial methoxyl substituents that should attract significant experimental interest since it is predicted to be highly reducing when photoactivated with visible light. The utilization of Hammett parameters in this study presents a generalizable and compact representation for exploring the effects of ligand substitutions.
Introduction
The relationship between molecular structure and chemical reactivity is central for the design of catalytic systems. One of the most extensively investigated topics in structure–reactivity relationships has been the effect of substituents on the properties of aromatic compounds, as described by the Hammett equation:1–3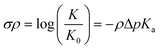 | (1) |
Eqn (1) provides a linear free energy relationship between the equilibrium or rate constants K0 and K, for chemical reactions of unsubstituted (K0) and substituted (K) benzoic acid derivatives, and the meta- and para-substituents.1–3 A demonstration of this relationship to ΔG can be seen in the ESI.†1 The substituent constant σ depends only on the nature and position of the substituent, determining the net electron-withdrawing or electron-donating character of that group, while ρ is the reaction constant that depends on the particular reaction of interest, type of molecule, and reaction conditions. Eqn (1) was initially tested by Hammett on 52 reactions,1–3 and since then many other reactions have been successfully investigated with parameters σ and ρ tabulated for hundreds of different meta- and para-substituents.2 However, ortho-substituents or poly-substituted compounds often deviate from the linear relationship due to the non-additive character of the contributions when steric or solvent effects are important. Here, we introduce a neural network and various linear models that are capable of predicting frontier orbital energies, based on the σ Hammett parameters from literature.1,2 The models bypass the usual limitations of the Hammett equation, including both aryl and non-aryl substitutions, allowing for the prediction of frontier orbital energies of tungsten–benzylidyne complexes (Fig. 1).
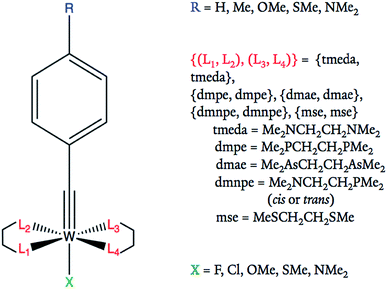 | ||
| Fig. 1 Tungsten–benzylidyne molecular framework and possible substituent ligand options at each site. All R groups are in the para position of the benzene ring. | ||
Tungsten–alkylidyne complexes represent a d2 family of the photoredox chromophores of the form W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)L4X (R′ = aryl group with organic substituent, L = neutral ligand, X = anionic ligand, where the W–X bond is trans to the alkylidyne ligand), with redox potentials that can be tuned over a broad range by ligand design.4–6 In fact, Hopkins and co-workers have shown that W(
CR′)L4X (R′ = aryl group with organic substituent, L = neutral ligand, X = anionic ligand, where the W–X bond is trans to the alkylidyne ligand), with redox potentials that can be tuned over a broad range by ligand design.4–6 In fact, Hopkins and co-workers have shown that W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)L4X complexes can have highly variable ligands allowing for tunable redox potentials and photophysical properties.4,5,7 For example, 32 different W(
CR′)L4X complexes can have highly variable ligands allowing for tunable redox potentials and photophysical properties.4,5,7 For example, 32 different W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)L4X compounds were synthesized and examined through variation of the R′, L, and X substituents.4 The redox active orbital of the synthesized W(
CR′)L4X compounds were synthesized and examined through variation of the R′, L, and X substituents.4 The redox active orbital of the synthesized W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)L4X complexes is the metal-centered dxy state (typically the HOMO), with an energy level that is strongly correlated to the redox potential of the complex (Fig. 2).4 Therefore, the ligands can be tuned to achieve highest reduction potential using the dxy orbital energy as a molecular descriptor. As applications to solar photoreduction also require the energy gap dxy–π* (usually the HOMO–LUMO gap) to be in the visible range, this energy gap can be used as a molecular descriptor as well. For the purposes of this study, we focused on tungsten–benzylidyne complexes of the form W(
CR′)L4X complexes is the metal-centered dxy state (typically the HOMO), with an energy level that is strongly correlated to the redox potential of the complex (Fig. 2).4 Therefore, the ligands can be tuned to achieve highest reduction potential using the dxy orbital energy as a molecular descriptor. As applications to solar photoreduction also require the energy gap dxy–π* (usually the HOMO–LUMO gap) to be in the visible range, this energy gap can be used as a molecular descriptor as well. For the purposes of this study, we focused on tungsten–benzylidyne complexes of the form W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CArR)L4X (Fig. 1), a subset of the tungsten–alkylidyne complex chemical space suggested by Hopkins and co-workers. Due to the large number of possible ligands,8,9 high-throughput screening could be a time-consuming and computationally expensive approach. Consequently, implementing systematic methods based on inverse design may prove a more cost-effective endeavor. Inverse design, as a general concept, involves searching over a descriptor space to find a desired descriptor value and then determining the structure that matches that descriptor. Because descriptor space contains the parameter or a related parameter that one is trying to optimize, inverse design is able to perform a directed search over possible structures in contrast to the often-random ligand combinations seen in methods like high-throughput screening.
CArR)L4X (Fig. 1), a subset of the tungsten–alkylidyne complex chemical space suggested by Hopkins and co-workers. Due to the large number of possible ligands,8,9 high-throughput screening could be a time-consuming and computationally expensive approach. Consequently, implementing systematic methods based on inverse design may prove a more cost-effective endeavor. Inverse design, as a general concept, involves searching over a descriptor space to find a desired descriptor value and then determining the structure that matches that descriptor. Because descriptor space contains the parameter or a related parameter that one is trying to optimize, inverse design is able to perform a directed search over possible structures in contrast to the often-random ligand combinations seen in methods like high-throughput screening.
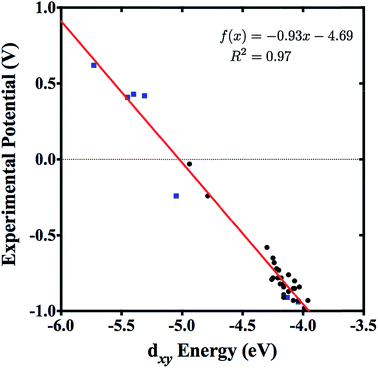 | ||
Fig. 2 Experimental potentials of 32 W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)L4X complexes plotted against their corresponding DFT (B3LYP) dxy energies, with basis set LANL2DZ used for W, Cl, Br, and I atoms, and basis set 6-311G* used for all other atoms. A structural benchmarking study by Rudshteyn et al. showed that this chosen level of theory was in agreement with experiment.6 Data was taken from ref. 6 including only reversible (black circles) and quasi-reversible (blue squares) experimental potentials. CR′)L4X complexes plotted against their corresponding DFT (B3LYP) dxy energies, with basis set LANL2DZ used for W, Cl, Br, and I atoms, and basis set 6-311G* used for all other atoms. A structural benchmarking study by Rudshteyn et al. showed that this chosen level of theory was in agreement with experiment.6 Data was taken from ref. 6 including only reversible (black circles) and quasi-reversible (blue squares) experimental potentials. | ||
Methods based on machine learning have received prominent attention in the chemistry community, and have been used to learn patterns of a training data set and accurately predict labels such as frontier orbital energies for novel molecules,10–16 bypassing the cost of exhaustive screening. However, incorporation of the Hammett substituent constants into these deep learning methods has not been explored. Here, we show that Hammett parameters can be used for training regressive machine learning models, varying the ligands of a given complex to render accurate quantitative descriptions. In order to determine the presence of non-linearity in the relationship between frontier orbital energies and Hammett parameter descriptors, we compare results between neural network and linear, ridge, LASSO, and stepwise regression methods, similar to the works of Sigman and co-workers.17 The reported findings thus contribute to the emerging field of machine learning in chemistry already explored in a wide range of important directions, including force field development,18,19 electronic structure calculations,20,21 drug discovery,22 new materials development,23,24 toxicity probing,25 prediction of chemical reactions26 and reaction yields,21 to mention a few.
The R, L, and X ligands are described according to their corresponding meta- and para-σ Hammett parameters, which are provided as input data for the regressive methods. The resulting models thus simultaneously account for the effects of multiple substituents, exploiting the capabilities of Hammett parameters as descriptors of electron-withdrawing/donating effects that correlate with redox potentials as well as HOMO/LUMO energies.27–34 In fact, due to their ability to capture electron-donating trends, the substituent constants should modulate the frontier orbital energies in the d2 W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CArR)L4X complexes, regardless of whether the corresponding ligands are aryl or not. However, the underlying correlation established by multiple Hammett constants and the frontier orbital energies has yet to be established.
CArR)L4X complexes, regardless of whether the corresponding ligands are aryl or not. However, the underlying correlation established by multiple Hammett constants and the frontier orbital energies has yet to be established.
In this paper, we explore the energy of the frontier orbital with predominant symmetry, dxy, and the dxy–π* energy gap for a series of 150 tungsten–benzylidyne complexes. All 150 energies were calculated after geometry optimization at density functional theory (DFT) level, as implemented in Gaussian 09,35 using the B3LYP functional36 and the Def2SVP basis set.37,38 The DFT energies, along with the Hammett parameters of the various substituent ligands, were then used to train and test linear and non-linear regressive models. The models were parameterized to predict the energies of the frontier orbitals from just the Hammett substituent constants of poly-substituted compounds, so that top reducing candidates can be determined and further evaluated at the DFT level while minimizing computational expense. Data set tests showed only training with 30 molecules, out of a total of 150 compounds in the set produced highly accurate frontier orbital energies, demonstrating the ability to produce accurate predictions from a modest number of calculations.
Methods
Computational modeling
The series of compounds W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CArR)L4X includes 5 substituent options for the R position, 6 for L and 5 for X (Fig. 1). Note that in this study R denotes the ligand on the aryl group as shown in Fig. 1 and is not R′ which includes the aryl group and the organic substituent, as in the previous paper.6 The ligands are commercially available or easily accessible, and are also synthetically viable options for the tungsten catalyst of interest. For the purpose of redox potential calculations, solvation energies were calculated using single point calculations under the SMD dielectric continuum model39 for the solvent THF (ε = 7.43),35 the most popular solvent used in studies of these tungsten–benzylidene complexes.4 The orbitals with symmetry dxy (typically the HOMO) and π* (typically the LUMO) were identified by visual inspection of DFT-optimized molecules, using Avogadro 1.2.0.32,40 Visual examples of these orbitals are displayed in the ESI.† The dxy energies and dxy–π* energy gaps were tabulated and analyzed as shown in Fig. 5.
CArR)L4X includes 5 substituent options for the R position, 6 for L and 5 for X (Fig. 1). Note that in this study R denotes the ligand on the aryl group as shown in Fig. 1 and is not R′ which includes the aryl group and the organic substituent, as in the previous paper.6 The ligands are commercially available or easily accessible, and are also synthetically viable options for the tungsten catalyst of interest. For the purpose of redox potential calculations, solvation energies were calculated using single point calculations under the SMD dielectric continuum model39 for the solvent THF (ε = 7.43),35 the most popular solvent used in studies of these tungsten–benzylidene complexes.4 The orbitals with symmetry dxy (typically the HOMO) and π* (typically the LUMO) were identified by visual inspection of DFT-optimized molecules, using Avogadro 1.2.0.32,40 Visual examples of these orbitals are displayed in the ESI.† The dxy energies and dxy–π* energy gaps were tabulated and analyzed as shown in Fig. 5.
Redox potentials (E1/2) were computed using the Born–Haber cycle at the DFT level of theory (B3LYP36/Def2SVP37,38), relative to the computed potential for the complex W(CPh)(dmpe)2Cl. The Def2SVP basis set is worse than the basis set used for this catalyst in the previous paper,6 but is cheaper for calculations and is shown to perform comparably to experimental values, like its predecessor, through the scaling procedure detailed below. The expression for E1/2 is given, as follows:
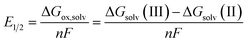 | (2) |
The previous study on this tungsten catalyst determined that dispersion corrections were only necessary for one of their potential catalysts.6 To show that these corrections are not necessary for our molecules, a selected ten of our 150 molecules were re-optimized using dispersion-corrected DFT (ωB97XD41/Def2SVP), with their resulting energies shown in the ESI.† It was found that the absolute energies of the dxy orbital and the dxy–π* gap are systematically altered, making their relative energies approximately the same as their non-dispersion-corrected energies. Therefore, we conclude that our machine learning models would capture the same trends regardless of the use of dispersion-corrected functionals, thereby rendering dispersion calculations of all of our candidates superfluous.
Data sets
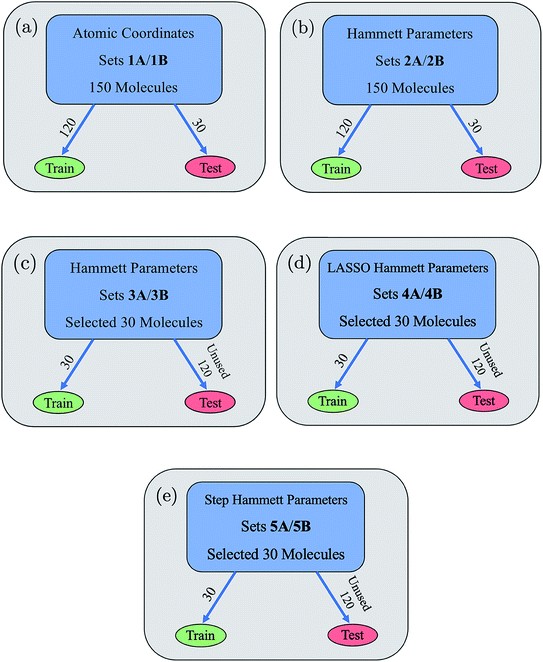
For most of the data sets used, each compound was defined by 11 parameters, consisting of an output label corresponding to the energy of the frontier orbital with dxy symmetry or energy gap dxy–π* and 10 input Hammett parameters associated with the substituent groups, including R, X, and 3 L ligands described by σm and σp. The fourth ligand L was determined by the other three choices of L since we imposed a symmetry constraint that should facilitate synthesis and assembly (Fig. 1). Note, ethyl groups were used in place of the alkyl chains of equatorial bidentate ligands, as shown in Table 1 (e.g., tmeda becomes two NEt2) since ethyl groups mimic the alkyl chains of the original ligands and the Hammett parameters of the bidentate ligands are not available. For the purposes of comparison, one data set used atomic coordinates instead of Hammett parameters as its input. In atomic coordinate input, the corresponding period and valence electron number of each connecting atom of a substituted ligand acted as input parameters. For example, substituting a methyl would give input parameters of 2 and 4 for that ligand. This led to a total of 10 input parameters for the 5 substitution positions. Regardless of parameterization, all molecules are labeled using the code RLX where R, L, and X are the corresponding codes for the ligands, as shown in Table 1 and Fig. 1. For example, complex 352 corresponds to OMe in the R position, cis-dmnpe for the L ligands, and Cl at the X site.| R | L1 | L2 | L3 | X | |
|---|---|---|---|---|---|
| 1 | H | NEt2 | NEt2 | NEt2 | F |
| 2 | Me | PEt2 | PEt2 | PEt2 | Cl |
| 3 | OMe | AsEt2 | AsEt2 | AsEt2 | OMe |
| 4 | SMe | SEt | SEt | SEt | SMe |
| 5 | NMe2 | NEt2 | PEt2 | PEt2 | NMe2 |
| 6 | NEt2 | PEt2 | NEt2 |
From these two parameterizations, ten data sets of 150 molecules each were formed and are shown in Fig. 3. Data sets 1A and 1B use a random 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 train
30 train![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test split, are described by the atomic coordinate input parameters, and use dxy energy (1A) or dxy–π* energy gap (1B) as the output parameters. Data sets 2A and 2B use a random 120
test split, are described by the atomic coordinate input parameters, and use dxy energy (1A) or dxy–π* energy gap (1B) as the output parameters. Data sets 2A and 2B use a random 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 train
30 train![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test split, are described by the ten Hammett parameters input, and use dxy energy (2A) or dxy–π* energy gap (2B) as the output parameters. Data sets 3A and 3B use a fixed 30
test split, are described by the ten Hammett parameters input, and use dxy energy (2A) or dxy–π* energy gap (2B) as the output parameters. Data sets 3A and 3B use a fixed 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 train
120 train![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test split, are described by the ten Hammett parameters input, and use dxy energy (3A) or dxy–π* energy gap (3B) as the output parameters. The 30 molecules used for training in the 3A/3B data sets were hand-chosen to cover the feature space as much as possible with equal representation amongst the various ligand options at each site. Sets 4A/4B and 5A/5B were formed via multivariate linear regression models performed on sets 3A/3B and will be further discussed in a later section. All data sets are provided in the ESI.†
test split, are described by the ten Hammett parameters input, and use dxy energy (3A) or dxy–π* energy gap (3B) as the output parameters. The 30 molecules used for training in the 3A/3B data sets were hand-chosen to cover the feature space as much as possible with equal representation amongst the various ligand options at each site. Sets 4A/4B and 5A/5B were formed via multivariate linear regression models performed on sets 3A/3B and will be further discussed in a later section. All data sets are provided in the ESI.†
Principal component analysis (PCA)
PCA was performed with RStudio 1.1.442,42 using the ‘factoextra’ library,43 for data sets 2A/2B to determine what correlations existed between the Hammett parameters and the labels used in the regressive methods. The resulting rotation matrix was used to determine which parameters covered the most variance in the output data, providing an effective way of predicting whether the regressive methods could derive a correlation pattern. The amount of correlation between input and labels provided insights into how much data was needed for each degree of freedom, leading to the construction of data sets 3A/3B.Neural network
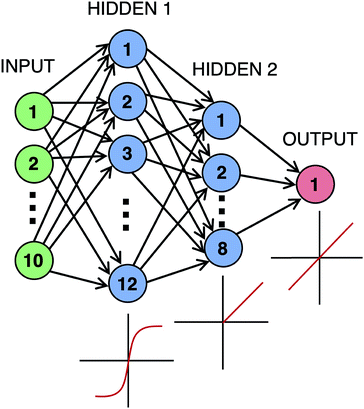
A neural network was coded in python using the Sequential model in the Keras library,44 with a Tensorflow backend. The network, shown in Fig. 4, included two hidden layers with 12 and 8 neurons along with the input and output layers of size 10 and 1, respectively. For compilation of the model, the mean-squared error (MSE) was used as the loss function while the ‘Adam’ algorithm45 with default parameters was used as the optimizer. A loss or cost function is a function used to tell how far the predicted results are from the actual results. This cost is then used with the Adam algorithm, which is a gradient based algorithm capable of dealing with noisy data, to determine how the weights are updated after every round of training. The hyperparameters, number of layers, nodes per layer, and activation functions employed were chosen because they produced optimal results. A trial and error procedure where hyperparameters, activation functions, and layer construction were adjusted one at a time until no improvement was observed was used to determine this optimality. A plausible explanation for why the hyperbolic tangent function works as a good first activation function could be because the domain of the Hammett substituent constants is centered around 0 and is mostly between −1 and 1.2 In addition, the PCA results below show both uncoupled and coupled ligand interactions contributing to the output parameters. With such complex interactions, the inclusions of a nonlinear function like hyperbolic tangent, a linear function, and ReLU, which is partially linear, offer the ability to describe these relationships. The optimization of network parameters during training of each data set required 220 epochs to reach convergence, with a batch size of 2. Convergence was defined as the number of epochs at which a minimum MSE occurred without overfitting. K-fold cross-validation was performed with a 90% training, 10% validation breakdown.The MSE of predicted energies relative to the DFT values was recorded for each round of 220 epochs for both training and testing data. The testing MSE values were averaged over 90 rounds for data sets 2A/2B and 30 for 1A/1B and 3A/3B. A standard deviation was calculated for each average MSE. The molecules chosen for the 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 training
30 training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) testing split for 1A/1B and 2A/2B are random for each round. For the data sets 3A/3B, the network evaluated the MSE based on the 120 unused molecules in the test set, which were the same for all rounds because the training set was pre-selected. The networks parametrized with 3A/3B were then used to predict the labels of all 150 molecules (including the 30 complexes used for training), which were then compared to their corresponding DFT values. Performing this test demonstrated the capabilities and limitations of the resulting networks as applied to predicting the full energy spectrum of frontier orbitals. Welch two sample t-tests were performed to see whether the models generalized well, comparing the average MSE of the predicted energies between the 30 molecules in 3A/3B and the remaining 120 not included in those sets. A significance level p = 0.05 was used to determine whether the means of the MSE of the two subsets deviated significantly from one another. If the average MSE of the 30 training molecules is statistically less significant than that of the other 120, then the model did not generalize well to the test candidates and may have been overfitted to the training data.
testing split for 1A/1B and 2A/2B are random for each round. For the data sets 3A/3B, the network evaluated the MSE based on the 120 unused molecules in the test set, which were the same for all rounds because the training set was pre-selected. The networks parametrized with 3A/3B were then used to predict the labels of all 150 molecules (including the 30 complexes used for training), which were then compared to their corresponding DFT values. Performing this test demonstrated the capabilities and limitations of the resulting networks as applied to predicting the full energy spectrum of frontier orbitals. Welch two sample t-tests were performed to see whether the models generalized well, comparing the average MSE of the predicted energies between the 30 molecules in 3A/3B and the remaining 120 not included in those sets. A significance level p = 0.05 was used to determine whether the means of the MSE of the two subsets deviated significantly from one another. If the average MSE of the 30 training molecules is statistically less significant than that of the other 120, then the model did not generalize well to the test candidates and may have been overfitted to the training data.
Alternative regressive models
Multivariate Linear, LASSO, Ridge, and Gaussian Process regressions were all implemented using the Scikit Learn package.46 The cost functions for each of the linear regressions can be seen below where xij are inputs, yi are the expected value, and wj are the weights. The Gaussian process regression used Algorithm 2.1 from Rasmussen and Williams with a radial basis function kernel (covariance).47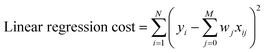 | (3) |
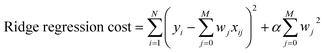 | (4) |
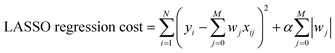 | (5) |
The parameter α in Ridge and LASSO was tested with the values 0, 0.001, 0.005, and 0.01. LASSO and Ridge methods were tested with and without cross validation. Cross-validation is a method used to prevent overfitting and improve a model's generalization by allocating a subset of data as validation data during each round of training that will be used as a test set to generate the cost. This cost is used to update the weights of the regressive method. Without cross-validation, this cost is determined by the training data. However, using the same training data every round may cause overfitting because the weights are being tuned precisely to the same data. Instead, if cross-validation is performed, the weights will be less biased towards the training data and will give a better estimate of the accuracy of the model on unseen data. Each method was tested using data sets 3A/3B as these data sets offered the most promise for utility and accuracy. The LASSO method has a built-in feature selection that was used on set 3A using α = 0.01 to select parameters for new data sets 4A/4B, which use dxy energy (4A) or dxy–π* energy gap (4B) as the output parameters. Similar to what was done with sets 3A/3B, these new data sets were trained on the neural network and tested on the energies of the 120 unused molecules. All of the previously mentioned regressive methods, including the neural network, were also tested with data sets 4A/4B in order to determine the effects of the LASSO feature selection.
Using stepwise regression, we found another set of alternative models that predicted the dxy energy and dxy–π* energy gap well. Forward selection, backward elimination, and bidirectional elimination stepwise regression were used with selection criterion of either Akaike information criterion (AIC)48 or Bayesian information criterion (BIC),49 giving a total of six regressions for each label. Formulas for AIC and BIC are displayed in eqn (6) and (7),
AIC = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L + 2p L + 2p | (6) |
BIC = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L + log(n)p L + log(n)p | (7) |
The MSE's for these multivariate regression models were calculated differently than those for the neural network comparison of data sets 1A/1B, 2A/2B, and 3A/3B (Table 3). For the MSE's seen in Table 4, the training sets 3A/3B, 4A/4B, and 5A/5B were used to predict the energies of the unused 120 molecules for those data sets following each round (220 epochs) of training. These test energies were averaged over 30 rounds of training, and then the MSE of those average energies was calculated. The reason why we calculated the MSE's differently for the neural networks in Table 3 was to show the standard deviation of the MSE's between our training rounds for the neural network. In contexts where there are restrictions on averaging over training rounds, it is important to know that the MSE for a given round of training does not deviate too significantly from its average. Moreover, Welch two sample t-tests identical to those used for the neural networks were performed on the training and testing MSE of all regression models on data sets 3A/3B to determine generalizability.
Results and discussion
DFT calculations
The DFT dxy energies and dxy–π* energy gaps of all 150 molecules in the sets (provided in the ESI†) were obtained after full geometry optimization. Consistent with changes in the coordination sphere of tungsten, we find that the dxy energies and dxy–π* energy gaps are most sensitive to changes in the L ligands. When nitrogen is in the L ligand (L = tmeda, cis-dmnpe, trans-dmnpe), the catalysts have much higher dxy energies than the other compounds. The axial ligands have a less significant effect on the dxy energy, consistent with the π* orbital being oriented along the z-axis of the molecule. The dxy–π* gaps remain in the UV-visible range (<4 eV) for all complexes, keeping the photoexcitation energies suitable for solar photocatalytic applications.Principal component analysis
PCA of data sets 2A/2B gave three major components, with percentages reported in Table 2 (rotation matrices provided in the ESI†). Each of the top three principal components corresponds to high correlation between one of the three varied substitutional sites and the output label. The rotation matrix of our analyses reveals that the equatorial ligands are responsible for the most significant variance in both data sets, consistent with earlier studies.4 The Hammett parameters in the L positions show anticorrelation with the dxy energy (therefore a positive correlation with the dxy–π* gap), which can be observed in the biplot shown in the ESI.† These results are consistent with the fact that substituents with more negative Hammett substituent constants are better electron-donors as usually observed in electron density trends. The second and third principal components, which mostly correspond to the X and R sites, do not correlate strongly with either label although they are responsible for about 15–18% of the variance. From the rotation matrices, the large isolation of each substitution site into the three highest variance principal components indicates, as expected, that the largest contributions to the energies are the uncoupled ligands which may be expected to give a linear relationship. Subsequent components which make up a total of 18.4% and 19.2% respectively of the variance in the dxy and dxy–π* gap are coupled ligand contributions that involve mixtures the of the R, L, and X substitution sites. These coupled mixtures may be non-linear in nature. Based on the R, L, and X components each being responsible for high amounts of variance, all features were kept for the 2A/2B data sets.| Label | PC1 | PC2 | PC3 |
|---|---|---|---|
| E(dxy) | 48.3% | 17.9% | 15.4% |
| E(π*)–E(dxy) | 47.2% | 17.9% | 15.7% |
Neural network
Table 3 shows the average MSE for each of the neural network data sets. These results show that the neural networks based on Hammett parameters perform better than those based on atomic coordinates and thereby better predict the dxy energies and dxy–π* energy gaps. With an MSE below 0.004, the 2A/2B model is in semiquantitative agreement with DFT. However, that level of accuracy results from a large data set including 80% of all possible molecules.| Data sets | E(dxy) MSE | E(π*)–E(dxy) MSE |
|---|---|---|
| 1A/1B | 0.0088(51) | 0.0106(28) |
| 2A/2B | 0.0036(14) | 0.0035(13) |
| 3A/3B | 0.0107(29) | 0.0068(15) |
Table 3 reports the average MSE for the sets 3A and 3B, highlighting the accuracy of the neural networks generated with a minimum amount of training. Note that 3A and 3B predicted both labels well, with an average MSE of 0.0107 for the dxy energy and 0.0068 for the dxy–π* gap, employing only a quarter of the amount of training data used by the full sets. Fig. 5a and b show the correlation plots for all 150 predicted values from the sets 3A/3B of energies dxy and dxy–π* gap, respectively, versus their corresponding DFT values. The slope and correlation coefficient near 1 highlight the level of correlation and prediction accuracy for both labels. We note that the 1A and 1B sets have the same level of performance as 3A and 3B but require 4 times more data (120 DFT calculations) for parameterization. Furthermore, there is evident clustering of data points in Fig. 5a; this clustering can be explained by the small amount of training data, as when 2A is trained and used to predict all 150 energies, the clustering disappears, which is shown in the ESI.†
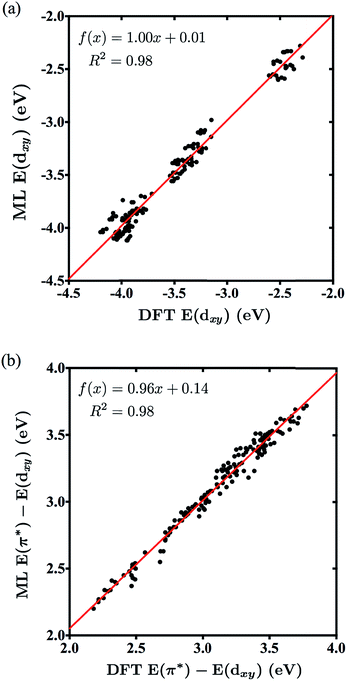 | ||
| Fig. 5 Correlation between the NN-predicted and DFT-obtained energies for the dxy orbitals (a) and dxy–π* gaps (b) of molecules in data sets 3A/3B. | ||
Molecule 515 is identified by the neural network (NN) for set 3A to be optimal as a reducing agent. According to DFT, however, 515 has the second-highest dxy energy with a reduction potential of −2.40 V vs. FeCp20/+, only 50 mV below that of 513 which is the most reducing catalyst. Nevertheless, 513 is predicted by the NN to be within the top 5% – i.e., within a standard deviation of the dxy energy of 515. Other complexes, such as 511, 313 and 315 with tmeda ligands also exhibit great reducing power. This is expected, as the stronger π-donating ability of tmeda compared to that of the other equatorial options raises the dxy orbital energy more and decreases stabilization due to π-backbonding. The predicted rankings are even more accurate for the dxy–π* gaps in set 3B. The two molecules with the largest dxy–π* gaps (521, 541) are identical for both the NN and DFT predictions, as well as the four molecules with the smallest gaps (114, 214, 414, 115). This is again consistent with the π-accepting trends in the equatorial plane, as the more π-accepting ligands have higher dxy–π* energy gaps because of the lowering of the dxy orbital energy due to stronger π-backbonding. Furthermore, the NN predicts that all dxy–π* gaps are within the UV-visible energy range, consistent with DFT. The parity plots formed from training sets 2A/2B containing predictions of all 150 energies, displayed in the ESI,† show a small set of outliers that all contain sulfur in the equatorial plane. Further exploration is needed to examine why the neural network fails to predict the energies of those molecules well.
Fig. 6 shows complex 513, which is the most promising photo-reducing complex since it has the highest dxy energy and a dxy–π* energy gap within the visible range.
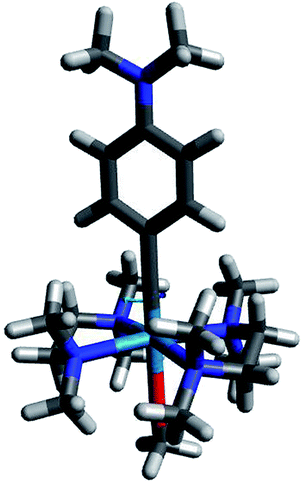 | ||
| Fig. 6 Compound 513, predicted to be highly reductive, with a redox potential of −2.45 V vs. FeCp20/+. Color code: gray = C; white = H; dark blue = N; red = O; light blue = W. | ||
These results suggest that the predicted potential for 513 of −2.45 V should be close to the actual experimental value since we have previously gauged the accuracy of our potentials to be in good agreement with the experimentally determined values.4 We have also performed a two-way t-test to compare the MSE's between the molecules used for training and the molecules used for testing for sets 3A and 3B. The p-values of the t-tests for 3A and 3B were both 0.52, well above the significance threshold of 0.05. Consequently, it is natural to conclude that our training from the 3A/3B has generalized well, as the mean contributions in MSE between the 30 training candidates and 120 test candidates are not significantly different. Furthermore, we have checked that our model did not overfit the data, as shown in the ESI† by the graph of the training and validation loss for dxy energies of all 150 molecules. These results underscore the computational power of the NN methodology, since the expense of training and testing is negligible compared to that of DFT calculations.
Alternative regressive models
The MSE results from the alternative regressive models and the neural network for data sets 3A/3B and 4A/4B are shown in Table 4. LASSO regression on set 3A generated 4A/4B, which have parameters R σm, R σp, L1σp, L2σm, L2σp, L3σp, and X σp as the input. As seen in Table 4, the best predictive models, as determined by lowest MSE, are linear and ridge regression for the dxy energy, and the neural network for the dxy–π* energy gap. While those are the best results purely by the absolute MSE's, it is important to note that the MSE's for every model in each column of Table 4 are very close with the exception of LASSO without cross validation. Without cross validation, LASSO is susceptible to completely removing important features as it did for the dxy–π* energy gap where the features selected were only R σp, L1σp, L2σp, L3σp. Note there is no longer a feature describing the X position ligand, which was shown by PCA to contain about 15% of the variance in both outputs. It is likely for this reason that the LASSO model had an MSE much higher than those of the other models using the 3B data set. Comparing the use of LASSO parameters between the 4A/3A data sets, it can be seen that the use of LASSO parameters improves the NN case. We note that the extra regularization does not improve the linear, ridge, or LASSO regressions. In fact, the use of the LASSO parameters worsens the cross validated LASSO and ridge cases. Using the LASSO parameters, which were derived from the dxy output, also increases the MSE for the dxy–π* cases. Combining the above results and the LASSO data set's failure to consistently produce better MSE's than other data sets, we conclude that further examination of the 4A/4B data sets is unnecessary. All LASSO and ridge regressions on the 3A/3B data sets, both with and without cross validation, are found to generalize well between training and testing data as seen in Table 5.| 5A | 4A | 3A | 5B | 4B | 3B | |
|---|---|---|---|---|---|---|
| a These models have identical models with the same MSE's. b The NN MSE's for 3A and 3B shown here are calculated differently than those for Table 3, as explained in the Methods. | ||||||
| Linear | 0.0026a | 0.0026 | 0.0026 | 0.0061a | 0.013 | 0.0059 |
| Ridge (α = 0.01) | — | 0.0026 | 0.0026 | — | 0.013 | 0.0060 |
| LASSO (α = 0.01) | — | 0.0092a | 0.0092a | — | 0.020a | 0.020a |
| NN (with CV) | 0.0056 | 0.0038 | 0.0081b | 0.0034 | 0.013 | 0.0034b |
| Ridge CV | — | 0.0033 | 0.0028 | — | 0.014 | 0.0088 |
| LASSO CV | — | 0.0032 | 0.0026 | — | 0.016 | 0.0079 |
| Stepwise | — | — | 0.0026a | — | — | 0.0061a |
| Gaussian process | — | 0.013 | 0.0079 | — | 0.060 | 0.0082 |
| dxyt-test | dxy–π* t-test | |
|---|---|---|
| Linear | 0.96 | 0.56 |
| Ridge (α = 0.01) | 0.96 | 0.50 |
| LASSO (α = 0.01) | 0.88 | 0.99 |
| NN (with CV) | 0.53 | 0.53 |
| Ridge CV | 0.96 | 0.56 |
| LASSO CV | 0.98 | 0.48 |
| Stepwise | 0.99 | 0.0009 |
| Gaussian process | 8.7 × 10−6 | 1.1 × 10−9 |
The six step regressions used for each label agreed on one particular model for the dxy energy and another one for the dxy–π* energy gap. For the dxy energy, the regression model suggested R σp, L1σm, L1σp, L2σm, L3σm, and X σp as the Hammett parameters; for the dxy–π* energy gap, the regression model suggested R σm, R σp, L1σp, L2σm, L2σp, X σm, and X σp. The linear regressions for the dxy energy and dxy–π* energy gap models gave MSE of 0.0026 and 0.0061 eV2, respectively, as shown in Table 4. We see in Table 5 that while the 5A data set's training generalizes well, the 5B data set's training does not. This could be easily explained by the step regression removing all parameters describing the L3 ligand for the dxy–π* energy gap model, which would introduce error in the prediction of the catalyst's frontier orbital energies when generalized to the unused 120 molecules.
In a comparison of ridge regression cases with and without cross validation, a predictable increase of MSE is seen when including cross validation. As ridge regression turned into linear regression when the hyperparameter α went towards zero (shown in the ESI†), it can be extrapolated that the same pattern of increased error would be seen between cross validated linear regression and normal linear regression. The increased error with cross validation is predictable because the model is made less dependent on individually picked training data, making it more generalizable which tends to make individual data points less well described. As a generalizable model is desired, this hit to accuracy is generally an acceptable tradeoff. However, since ridge regression only outperforms the NN in the dxy case and the NN does include cross validation, neither model can be considered distinctly better.
Comparing MSE's for our models using 3A, the neural network performed worse than the linear, ridge, and step regressions, while for 3B, the neural network had the lowest MSE. Similar results are found for sets 4A/4B and 5A/5B, as for both sets it is observed that the linear model outperforms the NN for the dxy energy but not for the dxy–π* energy gap. This suggests that there likely is more non-linear contribution from the Hammett parameters to the dxy–π* energy gap than to the dxy energy. Further exploration is needed to analyze the source behind these non-linear contributions.
It is seen that the linear, ridge, ridge cross-validated, and LASSO cross-validated regressions developed patterns of prediction similar to those of the neural network. For these regressions, once again the actual top reducing agent was found within the top 5% based off of dxy energies, and the actual second-best reducing agent was predicted to be the best. Furthermore, the largest DFT dxy–π* energy gap was correctly predicted by these models, and the second biggest was within the top 5%. As expected, the lack of generalization for the LASSO without cross-validation case is less accurate, finding the DFT second largest dxy–π* energy gap only in the top 10%. Gaussian process regression also had difficulty, only predicting the top reducing agents in the top 10%, and predicting the largest gap in the top 5% and the 2nd largest gap to be the biggest.
Conclusions
We have introduced the use of substituent Hammett parameters as features in regressive machine learning models and have applied the tested models to predict energies of frontier orbitals of highly reducing tungsten–benzylidyne complexes W(![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CArR)L4X with varied R, L, and X ligands. We have shown that these models can accurately predict frontier orbital energies, requiring only a modest computational training cost, thus bypassing the significant cost of high-throughput screening based on DFT. Using a constant molecular framework and the Hammett substituent constants of varied ligands, the methodologies were able to predict the reducing power of tungsten complexes by accurately identifying the candidates with the highest dxy energies. The linear, ridge, ridge cross-validated, LASSO cross-validated, and NN methods were thus able to capture the electron-withdrawing/donating trends of multiple substituents, aryl or not, showing that the resulting models efficiently harness the breadth of existing Hammett parameters in a new manner. The second-highest reducing catalyst, as predicted by the DFT dxy energy, was found to be the optimal candidate according to these models, while the highest was found within the top 5%. These models produced results that were even better for predictions of dxy–π* energy gaps, since the molecules with the largest and smallest gaps were predicted correctly. While the NN performed better for the dxy–π* energy gap than the alternative methods, the alternative methods proved to be better models for the dxy energy, suggesting that these alternative multivariate linear models should always be evaluated in addition to the NN for this methodology, with a keen focus on generalizability. The optimal catalyst has tetramethylethylenediamine (tmeda) equatorial ligands and axial OMe, with an oxidation potential of −2.45 V. It also satisfies the constraint of dxy–π* energy differences in the visible range, making it a promising candidate for a wide range of reactions, including reduction of CO2.
CArR)L4X with varied R, L, and X ligands. We have shown that these models can accurately predict frontier orbital energies, requiring only a modest computational training cost, thus bypassing the significant cost of high-throughput screening based on DFT. Using a constant molecular framework and the Hammett substituent constants of varied ligands, the methodologies were able to predict the reducing power of tungsten complexes by accurately identifying the candidates with the highest dxy energies. The linear, ridge, ridge cross-validated, LASSO cross-validated, and NN methods were thus able to capture the electron-withdrawing/donating trends of multiple substituents, aryl or not, showing that the resulting models efficiently harness the breadth of existing Hammett parameters in a new manner. The second-highest reducing catalyst, as predicted by the DFT dxy energy, was found to be the optimal candidate according to these models, while the highest was found within the top 5%. These models produced results that were even better for predictions of dxy–π* energy gaps, since the molecules with the largest and smallest gaps were predicted correctly. While the NN performed better for the dxy–π* energy gap than the alternative methods, the alternative methods proved to be better models for the dxy energy, suggesting that these alternative multivariate linear models should always be evaluated in addition to the NN for this methodology, with a keen focus on generalizability. The optimal catalyst has tetramethylethylenediamine (tmeda) equatorial ligands and axial OMe, with an oxidation potential of −2.45 V. It also satisfies the constraint of dxy–π* energy differences in the visible range, making it a promising candidate for a wide range of reactions, including reduction of CO2.
The introduced Hammett NN and alternative regressive machine learning models have been demonstrated as applied to the prediction of energies of frontier orbitals and could be generalized for a wide range of other molecular properties simply by training the models with calculations of the desired properties with DFT. Because the Hammett parameters are tabulated for hundreds of substituents, the Hammett NN could address a broad class of molecules simultaneously varying multiple sites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Air Force Office of Scientific Research Grant No. FA9550-17-0198 (V. S. B.). We acknowledge a generous allocation of computer time from NERSC and the high-performance computing facilities at Yale.References
- L. P. Hammett, The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives, J. Am. Chem. Soc., 1937, 59(1), 96–103 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, A survey of Hammett substituent constants and resonance and field parameters, Chem. Rev., 1991, 91(2), 165–195 CrossRef CAS.
- H. H. Jaffé, A Reëxamination of the Hammett Equation, Chem. Rev., 1953, 53(2), 191–261 CrossRef.
- D. E. Haines, D. C. O'Hanlon, J. Manna, M. K. Jones, S. E. Shaner, J. Sun and M. D. Hopkins, Oxidation-Potential Tuning of Tungsten–Alkylidyne Complexes over a 2 V Range, Inorg. Chem., 2013, 52(16), 9650–9658 CrossRef CAS PubMed.
- B. M. Lovaasen, J. V. Lockard, B. W. Cohen, S. Yang, X. Zhang, C. K. Simpson, L. X. Chen and M. D. Hopkins, Ground-State and Excited-State Structures of Tungsten–Benzylidyne Complexes, Inorg. Chem., 2012, 51(10), 5660–5670 CrossRef CAS PubMed.
- B. Rudshteyn, H. B. Vibbert, R. May, E. Wasserman, I. Warnke, M. D. Hopkins and V. S. Batista, Thermodynamic and Structural Factors that Influence the Redox Potentials of Tungsten–Alkylidyne Complexes, ACS Catal., 2017, 7(9), 6134–6143 CrossRef CAS.
- R. E. Da Re and M. D. Hopkins, Electronic spectroscopy and photophysics of metal–alkylidyne complexes, Coord. Chem. Rev., 2005, 249(13), 1396–1409 CrossRef CAS.
- W. L. Jorgensen, The many roles of computation in drug discovery, Science, 2004, 303(5665), 1813–1818 CrossRef CAS PubMed.
- D. Xiao, L. A. Martini, R. C. Snoeberger, R. H. Crabtree and V. S. Batista, Inverse Design and Synthesis of acac-Coumarin Anchors for Robust TiO2 Sensitization, J. Am. Chem. Soc., 2011, 133(23), 9014–9022 CrossRef CAS PubMed.
- R. M. Balabin and E. I. Lomakina, Neural network approach to quantum-chemistry data: Accurate prediction of density functional theory energies, J. Chem. Phys., 2009, 131(7), 074104 CrossRef PubMed.
- V. P. Solov'ev, Y. A. Ustynyuk, N. I. Zhokhova and K. V. Karpov, Predictive Models for HOMO and LUMO Energies of N-Donor Heterocycles as Ligands for Lanthanides Separation, Mol. Inf., 2018, 37, 1800025 CrossRef PubMed.
- X. Wang, L. Wong, L. Hu, C. Chan, Z. Su and G. Chen, Improving the Accuracy of Density-Functional Theory Calculation:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The Statistical Correction Approach, J. Phys. Chem. A, 2004, 108(40), 8514–8525 CrossRef CAS.
The Statistical Correction Approach, J. Phys. Chem. A, 2004, 108(40), 8514–8525 CrossRef CAS. - M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning, Phys. Rev. Lett., 2012, 108(5), 058301 CrossRef PubMed.
- F. Pereira, K. Xiao, D. A. R. S. Latino, C. Wu, Q. Zhang and J. Aires-de-Sousa, Machine Learning Methods to Predict Density Functional Theory B3LYP Energies of HOMO and LUMO Orbitals, J. Chem. Inf. Model., 2017, 57(1), 11–21 CrossRef CAS PubMed.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Machine learning of molecular electronic properties in chemical compound space, New J. Phys., 2013, 15(9), 095003 CrossRef.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. Von Lilienfeld, A. Tkatchenko and K.-R. Müller, Assessment and validation of machine learning methods for predicting molecular atomization energies, J. Chem. Theory Comput., 2013, 9(8), 3404–3419 CrossRef CAS PubMed.
- C. B. Santiago, J.-Y. Guo and M. S. Sigman, Predictive and mechanistic multivariate linear regression models for reaction development, Chem. Sci., 2018, 9(9), 2398–2412 RSC.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci., 2017, 8(4), 3192–3203 RSC.
- Y. Li, H. Li, F. C. Pickard, B. Narayanan, F. G. Sen, M. K. Y. Chan, S. Sankaranarayanan, B. R. Brooks and B. Roux, Machine Learning Force Field Parameters from Ab Initio Data, J. Chem. Theory Comput., 2017, 13(9), 4492–4503 CrossRef CAS PubMed.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K. R. Muller, Bypassing the Kohn-Sham equations with machine learning, Nat. Commun., 2017, 8(1), 872 CrossRef PubMed.
- M. Welborn, L. Cheng and T. F. Miller, Transferability in Machine Learning for Electronic Structure via the Molecular Orbital Basis, J. Chem. Theory Comput., 2018, 14(9), 4772–4779 CrossRef CAS PubMed.
- H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, The rise of deep learning in drug discovery, Drug Discovery Today, 2018, 23(6), 1241–1250 CrossRef PubMed.
- Y. Liu, T. Zhao, W. Ju and S. Shi, Materials discovery and design using machine learning, J. Materiomics, 2017, 3(3), 159–177 CrossRef.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9(5), 1064–1071 CrossRef CAS PubMed.
- T. Lei, F. Chen, H. Liu, H. Sun, Y. Kang, D. Li, Y. Li and T. Hou, ADMET Evaluation in Drug Discovery. Part 17: Development of Quantitative and Qualitative Prediction Models for Chemical-Induced Respiratory Toxicity, Mol. Pharm., 2017, 14(7), 2407–2421 CrossRef CAS PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, Neural Networks for the Prediction of Organic Chemistry Reactions, ACS Cent. Sci., 2016, 2(10), 725–732 CrossRef CAS PubMed.
- J. Frey, B. F. E. Curchod, R. Scopelliti, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and E. Baranoff, Structure–property relationships based on Hammett constants in cyclometalated iridium(iii) complexes: their application to the design of a fluorine-free FIrPic-like emitter, Dalton Trans., 2014, 43(15), 5667–5679 RSC.
- C. Alexiou and A. B. P. Lever, Tuning metalloporphyrin and metallophthalocyanine redox potentials using ligand electrochemical (EL) and Hammett (σp) parametrization, Coord. Chem. Rev., 2001, 216–217, 45–54 CrossRef CAS.
- J. K. Hino, L. Della Ciana, W. J. Dressick and B. P. Sullivan, Substituent constant correlations as predictors of spectroscopic, electrochemical, and photophysical properties in ring-substituted 2,2′-bipyridine complexes of rhenium(i), Inorg. Chem., 1992, 31(6), 1072–1080 CrossRef CAS.
- B. H. Solis and S. Hammes-Schiffer, Substituent Effects on Cobalt Diglyoxime Catalysts for Hydrogen Evolution, J. Am. Chem. Soc., 2011, 133(47), 19036–19039 CrossRef CAS PubMed.
- K. Tanekazu and M. Hiroshi, The Effect of Substituents on the Half-Wave Potential of the Polarographic Reduction of Pyridine N-Oxide Derivatives, Bull. Chem. Soc. Jpn., 1966, 39(10), 2057–2062 CrossRef.
- M. N. Ackermann, K. B. Moore, A. S. Colligan, J. A. Thomas-Wohlever and K. J. Warren, Tetracarbonylmolybdenum complexes of 2-(phenylhydrazino)pyridine ligands.: Correlations of spectroscopic data with pyridyl substituent effects, J. Organomet. Chem., 2003, 667(1), 81–89 CrossRef CAS.
- J. E. Heffner, C. T. Wigal and O. A. Moe, Solvent dependence of the one-electron reduction of substituted benzo- and naphthoquinones, Electroanalysis, 1997, 9(8), 629–632 CrossRef CAS.
- M. L. Dell'Arciprete, C. J. Cobos, J. P. Furlong, D. O. Mártire and M. C. Gonzalez, Reactions of Sulphate Radicals with Substituted Pyridines: A Structure–Reactivity Correlation Analysis, ChemPhysChem, 2007, 8(17), 2498–2505 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09, Rev. D, Gaussian, Inc., Wallingford CT, 2009.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1992, 98, 5648–5652 CrossRef.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4(1), 17 CAS.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620 RSC.
- RStudio, Integrated Development Environment for R, version 1.1.442, RStudio, Inc., Boston, MA, 2016 Search PubMed.
- A. Kassambara and F. Mundt, factoextra: Extract and Visualize the Results of Multivariate Data Analyses, 2017. https://CRAN.R-project.org/package=factoextra, accessed June 28, 2018 Search PubMed.
- F. Chollet, Keras, 2015, https://keras.io, accessed June 20, 2018 Search PubMed.
- D. P. Kingma and J. Ba, Adam: A method for stochastic optimization, 2014, arXiv:1412.6980. arXiv.org e-Print archive, https://arxiv.org/abs/1412.6980, accessed June 20, 2018.
- F. V. G. Pedregosa, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- H. Akaike, A New Look at the Statistical Model Identification, IEEE Trans. Autom. Control, 1974, 19, 716–723 CrossRef.
- G. Schwarz, Estimating the Dimension of a Model, Ann. Stat., 1978, 6(2), 461–464 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc02339a |
| This journal is © The Royal Society of Chemistry 2019 |